Abstract
Collagen fiber alignment derived from second harmonic generation (SHG) microscopy images can be important for disease diagnostics. Image processing algorithms are needed to robustly quantify the alignment in images with high sensitivity and reliability. Fourier transform (FT) magnitude, 2D power spectrum, and image autocorrelation have previously been used to extract fiber information from images by assuming a certain mathematical model (e.g. Gaussian distribution of the fiber-related parameters) and fitting. The fitting process is slow and fails to converge when the data is not Gaussian. Herein we present an efficient constant-time deterministic algorithm which characterizes the symmetricity of the FT magnitude image in terms of a single parameter, named the fiber alignment anisotropy R ranging from 0 (randomized fibers) to 1 (perfect alignment). This represents an important improvement of the technology and may bring us one step closer to utilizing the technology for various applications in real time. In addition, we present a digital image phantom-based framework for characterizing and validating the algorithm, as well as assessing the robustness of the algorithm against different perturbations.
OCIS codes: (180.6900) Three-dimensional microscopy, (100.2960) Imaging analysis, (180.4315) Nonlinear microscopy
1. Introduction
SHG microscopy is a powerful technology which allows for direct, non-invasive, and label-free three-dimensional visualization of collagen fiber architecture and extracellular matrix (ECM) of biological tissues. Many studies have shown that SHG microscopy can be used for disease diagnosis, and links have been established between ECM remodeling and disease formation and progression. Specifically, the risk of breast cancer initiation is associated with high collagen density [1], and it has been shown that cancer cells interact with ECM to promote metastasis [2, 3]. Pathological changes in collagen fiber network, e.g., in fiber alignment and waviness, have also been observed in ovarian cancers [4, 5]. In addition to cancer, SHG imaging is also useful for detecting fibrosis [6], bone diseases [7, 8], and potentially the risk of pre-term birth [9]. To capitalize on the ability of SHG microscopy of visualizing ECM, it is highly desirable to have the image-based information interpreted and converted into more objective classifications.
Image processing is playing an increasingly important role in SHG microscopy applications. Diseases are complex and often so heterogeneous that visual observation of structural changes in one location or from a single image (or even several images) is not enough. Thus, automatic quantification in multiple regions is needed. Moreover, it is desirable to develop deterministic unbiased algorithms, i.e., ones that can be applied to any image regardless of the image acquisition system. Lastly but not the least, processing speed is also critical so that the algorithm can be used for real-time analysis and display.
Commonly used SHG image processing methods can be categorized into two classes. The first class, which has been primarily applied so far, is based on extracting physical features such as collagen fiber diameter and orientation [10]. The second class consists of entirely computational machine-learning-based approaches which calculate a large matrix of different image-based features and then resort to automatic clustering to determine the relevant features that best separate the data into the classification groups (e.g. normal vs diseased) [11]. While extremely powerful, the disadvantage of the machine-learning approach is its disconnection with the physical parameters, which makes it hard to analyze and interpret the results in many cases. Selective use of a large number of metrics can often correctly classify a training set but the classification criteria might work poorly on another independent, unseen data set (i.e. overfitting) [12]; how to avoid overfitting and promote generalization of the learning algorithm remains a challenge.
Collagen fiber alignment is an important physical parameter and has been established as a marker in breast cancer [13], bone disease [8] and ovarian cancer [11]. Multiple research groups have presented the use of Fourier Transform (FT) to characterize the morphological properties of collagen fibers [14–16]. This has been performed in several ways, such as by thresholding and fitting the 2D image autocorrelation to a Gaussian function [16] or an ellipse [17], or alternatively by fitting the image power spectrum (squared magnitude of the FT output) to a line [14], or by fitting the angular distribution to a Gaussian function [8]. The fiber properties are then derived from the functional properties. While the previous approaches provide an excellent starting point to investigate fiber alignment, they do have some limitations. Image thresholding in general is tricky and can depend on the particular imaging system and imaging parameters. As a result, thresholding can dramatically influence the outcome of any analysis and therefore can be biased. Fitting data to a curve without a clear theoretical basis can also be problematic. While in many cases the data can resemble the function (for example a Gaussian), when that assumption fails, the results can be incorrect. In addition, fitting in general is a slow process, especially when there are multiple unknowns and perhaps even more time-consuming if the data is not actually complying with the target form. To overcome these limitations, we have developed a deterministic, unbiased approach, which does not require fitting or thresholding. In this paper we present this new method along with a robust validation, firstly on digital image phantoms and then on practical SHG images of biological tissues. The method is fast and robust, which is critical for real-time fiber alignment processing in in vivo imaging applications such as SHG endomicroscopy of biological tissues [9, 18].
2. Fiber alignment anisotropy quantification
The FT analysis of collagen fiber images provides a powerful tool for quantification of fiber alignment. Given an image , its 2D FT is calculated as follows where u and v are the 2D spatial frequency coordinates:
| (1) |
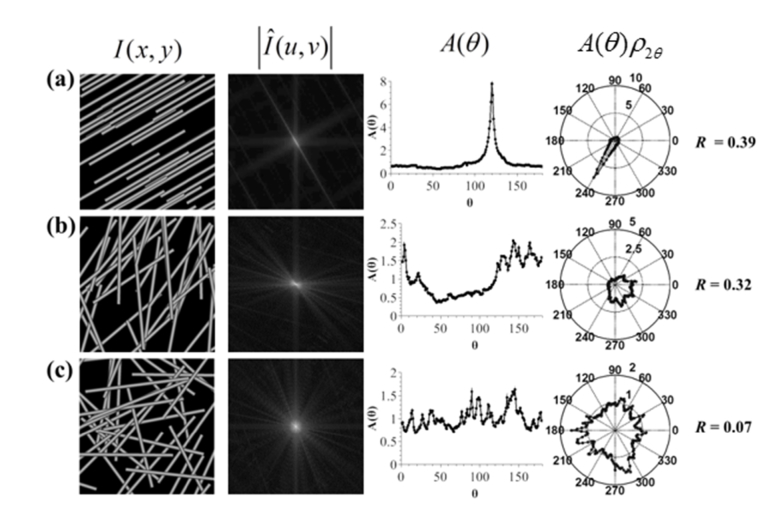
Figure 1 illustrates how the fiber alignment is translated to the Fourier domain, where , the magnitude of the FT of digital phantom images (the first column in Fig. 1; see Section 3 for detailed explanation of how the phantom images are generated) with varying degrees of alignment, are shown in the second column. Through comparison, we can tell the differences in , where a higher degree of fiber alignment is reflected in an increased level of angular non-uniformity around the origin.
Fig. 1.
Digital phantoms of fibers ranging from high (a) to intermediate (b) and random alignment (c). The first column shows the spatial images whereas the second column shows the corresponding FT magnitude image |(u,v)|. The third and fourth columns show the angular content distributions of |(u,v)| in a linear and polar manner, respectively. The computed R’s are shown for each case on the right.
As mentioned above, the alignment is encoded in the angular non-uniformity of around the origin. In order to quantify the non-uniformity without involving a fitting procedure, we can directly assess the content of at each angle θ (defined over 0° to 180°) using polar coordinates () and integrating over the radial coordinate along a line through the origin (at angle θ) from to . This can be written as:
| (2) |
Here the function represents angular projections or line integrals/averages of through the origin. This simplifies the problem from 2D to 1D. Now, it is desirable to quantify the alignment in terms of a single metric. There are multiple potential ways to calculate such a metric based on . We propose a simple method which involves distributing on a circle from 0° to 360°, where each real-valued data point of is mapped to a complex number (or vector) with the unit vector defined as pointing radially along the direction of . Then we summed up all the vectors into a single sum vector . For cases where there is a high degree of alignment, will be highly polarized and the sum vector will have a large magnitude . On the other hand if the alignment is random, will be almost uniform, and therefore the vectors ’s will cancel each other out, and final magnitude will be small. For convenience, we normalize R such that it has a range from 0 to 1 where 1 represents a perfect alignment and 0 represents completely isotropic or random distribution of collagen fibers. It is calculated as follows and we refer to it as the angular anisotropy parameter:
| (3) |
where is uniformly distributed from 0 to π with N values. Here Na is the total number of angles uniformly distributed between [0, π], and the discrete summation in the numerator is essentially a numerical evaluation of the following continuous integral, . In practice, we found that for a 512×512 phantom or real SHG image, setting Na > 200 is sufficient to capture the detailed undulation of , and throughout this report, we choose Na = 512 to guarantee numerical accuracy. The FT and angular analyses are shown for cases of increasing alignment in Figs. 1(a)-1(c), along with the ground-truth and computed values for (how to obtain the ground truth is explained shortly). By comparison, the numbers correlate well with the observed alignment.
The above method can be easily implemented with MATLAB, and it took about 28 ms to process an image of 512 × 512 pixels on a 3.3-GHz-CPU desktop computer with 3 GB of RAM. Thus, it could readily be used for real-time processing and display.
Also worth noting is the close relation between power spectrum and image autocorrelation, i.e., the power spectrum, calculated as , is the FT of the image-based autocorrelation. Therefore, these transforms are highly related and can be expected to give similar information, although in a slightly different fashion. For example, in the Fourier domain, small fibers will result in high frequency content, whereas in the autocorrelation (spatial domain) it would result in image content concentrated close to the origin.
As already mentioned, many of the previous alignment analysis methods utilized thresholding and/or fitting to a mathematical function to obtain information from the Fourier domain (or autocorrelation image). While this may work in many circumstances, it can also fail in many other situations. For example, looking at the FT magnitude and the angular distribution in the 2nd and 3rd columns of Fig. 1, a Gaussian fit to the angular distribution would not be even close to being perfect (except the uniform alignment case as shown in the 3rd column of Fig. 1(a)).
3. Digital phantom validation and calibration
The algorithm was characterized under multiple conditions using digital phantoms, i.e., images of fibers with various but controlled properties.
3.1 Digital phantom generation
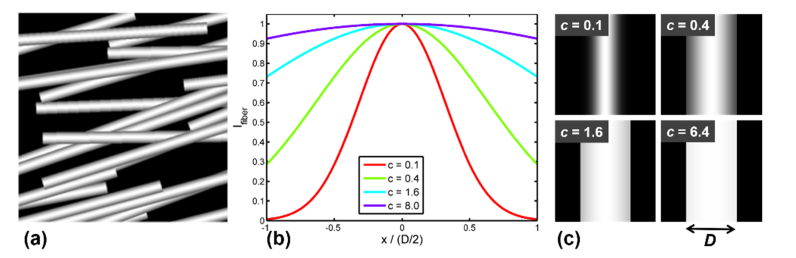
The mathematical model of the brightness of a single straight fiber along the y-direction is given by:
| (4) |
where D and L are the fiber diameter and length (Fig. 2), respectively, and c is a parameter that defines the contrast which is particularly important when fibers are overlapping.
Fig. 2.
Phantom generation for validation study. (a) Example of multi-fiber architecture on a black background. (b) Cross-sectional intensity profiles of fibers illustrating the influence of the contrast parameter c. (c) Illustration of the fibers in (b) in 2D images with a black background.
The phantom image consisting of multiple fibers (Fig. 2) is generated by superposition of myriad fibers with different orientations as follows:
| (5) |
where defines the center position of the nth fiber and θn its orientation angle. Nf is the total number of fibers within the phantom image. The function Rot(θn) represents an operator that rotates an image matrix by an angle of θ in the range [0°, 180°]. Note that for overlapping fibers, the value of the topmost fiber takes precedence. For phantoms used here, the central position of each fiber was randomized uniformly within the image area. To generate a specific angular distribution, we specified a mean angle and a range . Then each angle is determined as where is a random variable following uniform distribution in the range [-0.5, 0.5].
Knowing the actual value of each , we can calculate the actual angular anisotropy value of a given image phantom as follows:
| (6) |
where again we have , and Nf is the total number of fibers within the phantom image. The actual value is entirely dependent upon the angular distribution and represents the actual fiber alignment anisotropy information that we are trying to derive based on image analysis. The actual value can then serve as the ground truth for validation.
We notice that the ground-truth angular anisotropy defined as Eq. (6) in our manuscript is complementary to a previously established metric named directional variance or circular variance [19], defined as for a given set of unit vectors . Specifically, for the set of unit vector ’s, we have . Furthermore, the computed angular anisotropy defined by Eq. (3) can be regarded as a generalized version of above definitions by replacing the constant weight with a non-uniform normalized weight (or probability) , and thus it shares similar spirit as being complementary to the corresponding circular variance.
3.2 Digital phantom validation
To validate the performance of our algorithm, we conducted intensive simulation studies on numerous digital phantoms with different fiber morphological parameters. Specifically, for each phantom image, we randomized the following morphological parameters:
-
1)
Fiber density (or number of fibers per image): uniformly sampled from 63 to 162 fibers per phantom image.
-
2)
Contrast parameter : randomly selected from 0.1, 0.4, 1.6 and 6.4. Note that once selected, the contrast parameter is applied to all fibers within a given phantom image, i.e. we assume that all fibers in a phantom field of view share identical cross-sectional brightness profile.
-
3)
Mean fiber orientation angle : uniformly sampled from 0 to 180 degrees.
-
4)
Variance range spanned by all fibers: uniformly sampled from 0 to 180 degrees. Therefore the orientation angle of each individual fiber will be uniformly sampled within the range . Again, it is that mainly decides the fiber alignment anisotropy .
-
5)
Central location of each fiber: randomly chosen throughout the field of view.
-
6)
Mean fiber length : randomly chosen from the following values: 30, 50, and 70 µm. The variance range of fiber length was fixed to be 20 µm in our simulation. That is to say, the length of all fibers within a single digital phantom is uniformly sampled from one of the following intervals: 20−40 µm, 40−60 µm, and 60−80 µm, and the interval to use is randomly selected. These fiber length distributions were chosen based on previous report on typical collagen fiber lengths [16], as well as visual estimation of real-world SHG images from various collagen-rich tissues [20–22].
-
7)
Mean fiber diameter : randomly chosen from the following values: 1, 2, 3, and 4 µm (similar to the collagen fiber diameter range in biological tissues [20, 21]). The variance range of fiber diameter was fixed to be 1 µm in our simulation. That is to say, the diameter of all fibers within a digital phantom is uniformly sampled from one of the following intervals: 0.5−1.5 µm, 1.5−2.5 µm, 2.5−3.5 µm, and 3.5−4.5 µm, and the interval to use is randomly selected.
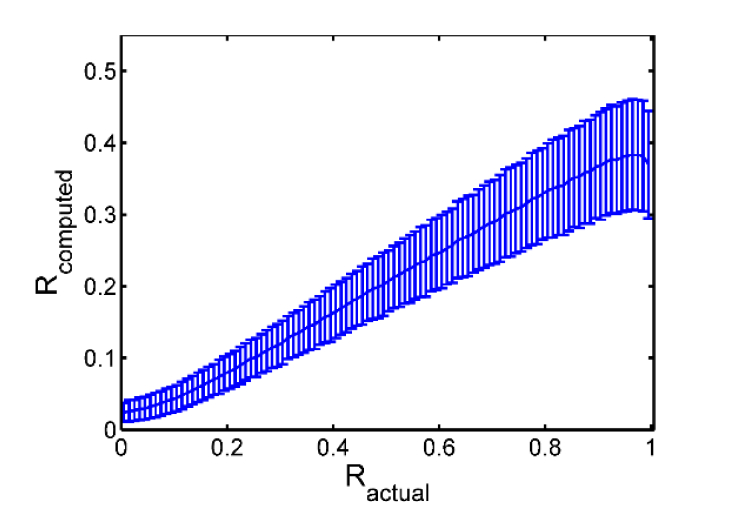
To fully cover all possible parameter combinations listed above, we generated more than 8 × 105 phantom images. For each image we calculated the actual angular anisotropy based on the known angular distribution and compared it with that obtained from the proposed approach (Eq. (3)). With all the anisotropy data, we can validate the effectiveness of our algorithm and investigate its robustness against different parameters, as detailed shortly. First, by discretizing the actual angular anisotropy into 0.01-wide intervals and grouping phantom images according to their values, we can estimate the mean and standard deviation of the corresponding computed R’s for each value (i.e. the corresponding group of phantom images), as shown in Fig. 3. As can be seen, there is a high level of correlation between the two values and the relationship is monotonic and quite linear, except when the actual exceeds 0.98 (i.e. approaching perfect alignment). Such discrepancy stems mainly from the fact that even when the phantom fibers are perfectly aligned, the spatial spectrum of the whole image does not reside purely along a single direction, but leaks substantially into a wide range of directions in the 2D Fourier domain, as exemplified in the 2nd column of Fig. 1(a). And therefore, the corresponding directional integral deviates considerably from an ideal delta function, resulting in a computed anisotropy far below 1.0 (see Fig. 1(a) and Fig. 3).
Fig. 3.
Distribution of the actual and computed angular anisotropy value R. Plotted in the figure are the mean value and standard deviation of versus corresponding extracted from multiple digital phantoms. The standard deviation is represented by the error bars.
Despite the slight decrease of average when the actual alignment anisotropy approaches 1.0, the overall increasing trend of with increasing alignment of phantom fibers could still be utilized to characterize the alignment of practical SHG images, especially considering perfectly aligned collagen fibers barely occur in biological tissues. To further investigate the sensitivity of our algorithm to fiber alignment, we conducted ANOVA analysis (MATLAB, MathWorks) of the groups of values (each group corresponds to a 0.01-wide interval in , as shown in Fig. 3), which yields a p-value = 0, implying that there is absolutely significant difference among all the groups (i.e. at least one group is significantly different from at least another group). Furthermore, multiple comparison of means reveals that, for the majority of , as long as the difference between and exceeds 0.03, there exists a significant difference between the distributions of and . This reflects the excellent sensitivity of the algorithm, i.e. a small difference of ~0.03 in actual is enough to yield a statistically different distribution of ’s.
4. Robustness and dependence on other parameters
The influence of parameters other than the angular fiber distribution on the image-derived values is important to assess the robustness of the proposed method. If robust, fiber diameter, fiber length, fiber density, contrast factor, and noise, which are independent of fiber orientation, should have minimal effects on .
4.1 Fiber diameter and contrast
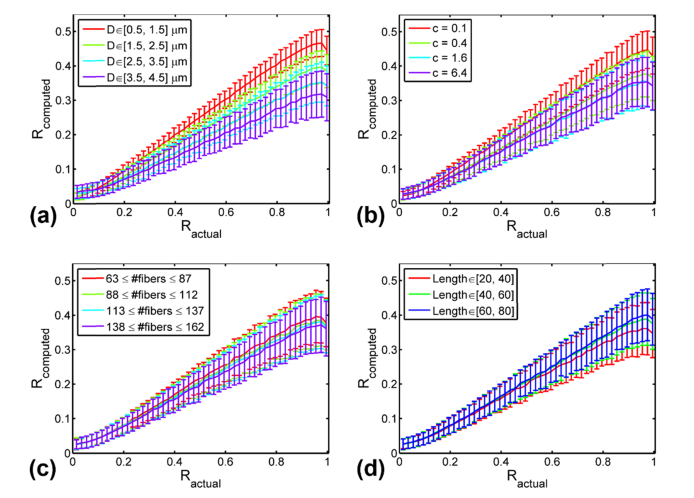
Figure 4(a) compares the image-derived anisotropy and actual R values for image phantoms with different average fiber diameters, ranging from 1 to 4 microns (similar to the diameter range of collagen fibers in biological tissues [20, 21]). While there is some influence from fiber diameter on , where the more aligned smaller fibers have a relatively higher , the correlation between the image-derived and actual values is still very good (with correlation coefficients of ~0.977 for D = 1 µm, ~0.963 for D = 2 μm, ~0.936 for D = 3 μm, and ~0.896 for D = 4 μm cases, respectively). The general trend we found is that thicker phantom fibers yield relatively lower values with higher standard deviations on average
Fig. 4.
Robustness evaluation of the algorithm against various morphological parameters. The average and standard deviation (represented by the error bars) of values are plotted versus for different fiber morphological parameter values (ranges), including: (a) fiber diameter, (b) fiber contrast, (c) fiber density, and (d) fiber lengths.
In Fig. 4(b), the fiber contrast parameter c was varied from 0.1, 0.4, 1.6 to 6.4. Again, there is slight influence of the contrast parameter c on , but the four pairs of and ’s correlate very well (with correlation coefficients of ~0.961 for c = 0.1, ~0.925 for c = 0.4, ~0.899 for c = 1.6, and ~0.901 for c = 6.4, respectively). We noticed that a larger contrast parameter c tends to yield a relatively lower value. Since fibers with a larger contrast parameter appear thicker, as shown in Fig. 2(c), this observation matches well our previous observation that thicker fibers tend to yield lower values, as presented in Fig. 4(a). Overall, we find that the proposed method is robust against reasonable variations in fiber diameter and contrast, producing a good correlation between the actual and image-derived R values under various circumstances.
4.2 Fiber density and length
Similar as in Section 4.1, we further investigated the robustness of our algorithm against fiber density and length, as shown in Figs. 4(c)-4(d). Specifically, to check the effect of fiber density on the algorithm, we divided the phantom images used for Fig. 3 into 4 subgroups, corresponding to the following fiber density ranges: [63, 87], [88, 112], [113, 137], and [138, 162]. To check the effect of fiber length on the algorithm, we divided the same set of images into 3 subgroups, and each subgroup has fiber length uniformly sampled from one of the following intervals: 20−40 µm, 40−60 µm, and 60−80 µm. The similarity between each individual curves in Figs. 4(c)-4(d) corroborates that there is no obvious dependence of the algorithm performance on fiber length or fiber density.
4.3 White noise in the spatial frequency domain
When computing the projection function , a white noise-style background residing in the Fourier domain (i.e. spatial frequency domain) can contribute to line integral along every angle in Eq. (2) unselectively, thus leading to a considerate quasi-uniform offset to . Such quasi-uniform offset will in turn pile up in scalar summation in the denominator of Eq. (3), but basically cancel out in the vector summation in the nominator, thereby attenuating the informative fluctuation carried by and resulting in reduced . It is noteworthy that white noise in the spatial frequency domain corresponds to delta function-style features in the image, which is commonly encountered in practical SHG images (e.g. polluted by salt-and-pepper noise).
To investigate the robustness of the proposed method to such Fourier-domain white noise, we consider a simplified case with the Fourier-domain angular projection function modeled as a predominant peak at angle (corresponding to perfectly aligned fibers in the image domain) superposed with a white noise-induced offset , as given by:
| (7) |
where is the delta function and θ ranges from 0° to 180°. The anisotropy value can then be deduced using Eq. (3) as:
| (8) |
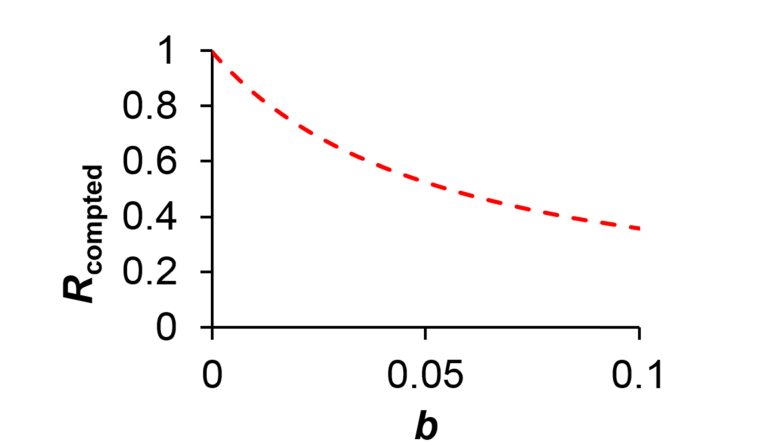
Figure 5 shows how the value depends on the white noise-induced offset b. As expected, decreases progressively with stronger white noise-induced offset . Therefore, when comparing values between images, one should keep in mind that the presence of spatially small features of random orientations could lead to a downward-biased estimation of the anisotropy . In contrast, a uniform or low-spatial frequency image background, upon Fourier transform, will contribute to only locally nearby the origin (i.e. u = v = 0), and thus would not exert much influence in practice to the final estimation of R. In light of this, one way to mitigate such affect from Fourier-domain white noise is low-pass filtering the image first (to remove any salt-and-pepper noise) before undertaking the anisotropy analysis.
Fig. 5.
Pronounced effect of white noise on the absolute R value for a perfectly aligned distribution. It is noted that white noise has no effect on the absolute R value for cases of completely random fiber orientation.
5. Tissue imaging validation
Shown in Fig. 6 are representative results of applying the proposed method to SHG images experimentally acquired from ex vivo mouse tail tendon and mouse cervical tissues at different gestation time points [9,21] using a recently developed nonlinear endomicroscopy technology as detailed elsewhere [9, 23–25] Collagen fibers in the mouse tail tendon are generally highly aligned, as shown in Fig. 6(a), and the computed R values ranges ~0.2-0.35; one can also see that increased waviness of collagen fibers generally leads to lowered R value (the 2nd and 3rd columns of Fig. 6(a)). Cervical collagen fibers of normal pregnant mice in the earlier gestation stage (day 6 as shown in Fig. 6(b)) exhibits a higher degree of alignment than those in the latter gestation stage (day 18 as shown in Fig. 6(c)), reflecting the dramatic remodeling process in cervical collagen architecture during pregnancy [21]. Overall, these experimental results demonstrate that the proposed algorithm performs well as expected, i.e., the trend in the R values are in accordance with the level of alignment seen visually.
Fig. 6.
Application of the proposed algorithm to SHG images acquired from various types of biological tissues. (a) Highly aligned collagen fibers from mouse tail tendon. (b) Moderately-aligned cervical collagen fibers of normal pregnant mice at gestation day 6. (c) More randomized cervical collagen fibers of normal pregnant mice at gestation day 18. All images shown here were acquired using the nonlinear endomicroscope we recently developed [23]. The excitation conditions were ~10 mW for mouse tail tendon (a), and of ~40 mW for cervical tissue sections (b-c) at 890 nm. Ten raw frames were averaged for (a) while twenty for (b-c), corresponding to an effective frame acquisition time of ~3.8 s (a) and ~7.6 s (b-c), respectively. The computed R’s are shown at the upper-left corner for each image. Scale bars: 20 µm.
6. Conclusion
We developed an algorithm for quantification of collagen fiber alignment in SHG microscopy images. The method was shown to be robust by validation on digital phantoms. It provides an improvement over previous related approaches in terms of speed and its unbiasedness. The method provides a single parameter output about the alignment, and could be very easy to use for clinical applications of the SHG imaging technology.
Disclosures
The authors declare that there are no conflicts of interest related to this article.
Funding
This project was supported in part by the National Institutes of Health under a grant R01CA153023 and the National Science Foundation under a grant CBET-1430040.
References and links
- 1.Provenzano P. P., Inman D. R., Eliceiri K. W., Knittel J. G., Yan L., Rueden C. T., White J. G., Keely P. J., “Collagen density promotes mammary tumor initiation and progression,” BMC Med. 6(1), 11 (2008). 10.1186/1741-7015-6-11 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Provenzano P. P., Eliceiri K. W., Campbell J. M., Inman D. R., White J. G., Keely P. J., “Collagen reorganization at the tumor-stromal interface facilitates local invasion,” BMC Med. 4(1), 38 (2006). 10.1186/1741-7015-4-38 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Conklin M. W., Eickhoff J. C., Riching K. M., Pehlke C. A., Eliceiri K. W., Provenzano P. P., Friedl A., Keely P. J., “Aligned Collagen Is a Prognostic Signature for Survival in Human Breast Carcinoma,” Am. J. Pathol. 178(3), 1221–1232 (2011). 10.1016/j.ajpath.2010.11.076 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Nadiarnykh O., LaComb R. B., Brewer M. A., Campagnola P. J., “Alterations of the extracellular matrix in ovarian cancer studied by Second Harmonic Generation imaging microscopy,” BMC Cancer 10(1), 94 (2010). 10.1186/1471-2407-10-94 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Williams R. M., Flesken-Nikitin A., Ellenson L. H., Connolly D. C., Hamilton T. C., Nikitin A. Y., Zipfel W. R., “Strategies for High-Resolution Imaging of Epithelial Ovarian Cancer by Laparoscopic Nonlinear Microscopy,” Transl. Oncol. 3(3), 181–194 (2010). 10.1593/tlo.09310 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Strupler M., Pena A. M., Hernest M., Tharaux P. L., Martin J. L., Beaurepaire E., Schanne-Klein M. C., “Second harmonic imaging and scoring of collagen in fibrotic tissues,” Opt. Express 15(7), 4054–4065 (2007). 10.1364/OE.15.004054 [DOI] [PubMed] [Google Scholar]
- 7.Nadiarnykh O., Plotnikov S., Mohler W. A., Kalajzic I., Redford-Badwal D., Campagnola P. J., “Second harmonic generation imaging microscopy studies of osteogenesis imperfecta,” J. Biomed. Opt. 12(5), 051805 (2007). 10.1117/1.2799538 [DOI] [PubMed] [Google Scholar]
- 8.Ambekar R., Chittenden M., Jasiuk I., Toussaint K. C., Jr., “Quantitative second-harmonic generation microscopy for imaging porcine cortical bone: Comparison to SEM and its potential to investigate age-related changes,” Bone 50(3), 643–650 (2012). 10.1016/j.bone.2011.11.013 [DOI] [PubMed] [Google Scholar]
- 9.Zhang Y., Akins M. L., Murari K., Xi J., Li M. J., Luby-Phelps K., Mahendroo M., Li X., “A compact fiber-optic SHG scanning endomicroscope and its application to visualize cervical remodeling during pregnancy,” Proc. Natl. Acad. Sci. U.S.A. 109(32), 12878–12883 (2012). 10.1073/pnas.1121495109 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Kakkad S. M., Solaiyappan M., Argani P., Sukumar S., Jacobs L. K., Leibfritz D., Bhujwalla Z. M., Glunde K., “Collagen I fiber density increases in lymph node positive breast cancers: pilot study,” J. Biomed. Opt. 17(11), 116017 (2012). 10.1117/1.JBO.17.11.116017 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Wen B. L., Brewer M. A., Nadiarnykh O., Hocker J., Singh V., Mackie T. R., Campagnola P. J., “Texture analysis applied to second harmonic generation image data for ovarian cancer classification,” J. Biomed. Opt. 19(9), 096007 (2014). 10.1117/1.JBO.19.9.096007 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Lehmann T. M., Güld M. O., Deselaers T., Keysers D., Schubert H., Spitzer K., Ney H., Wein B. B., “Automatic categorization of medical images for content-based retrieval and data mining,” Comput. Med. Imaging Graph. 29(2-3), 143–155 (2005). 10.1016/j.compmedimag.2004.09.010 [DOI] [PubMed] [Google Scholar]
- 13.Bredfeldt J. S., Liu Y., Conklin M. W., Keely P. J., Mackie T. R., Eliceiri K. W., “Automated quantification of aligned collagen for human breast carcinoma prognosis,” J. Pathol. Inform. 5(1), 28 (2014). 10.4103/2153-3539.139707 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Rao R. A., Mehta M. R., Toussaint K. C., Jr., “Fourier transform-second-harmonic generation imaging of biological tissues,” Opt. Express 17(17), 14534–14542 (2009). 10.1364/OE.17.014534 [DOI] [PubMed] [Google Scholar]
- 15.Lau T. Y., Ambekar R., Toussaint K. C., “Quantification of collagen fiber organization using three-dimensional Fourier transform-second-harmonic generation imaging,” Opt. Express 20(19), 21821–21832 (2012). 10.1364/OE.20.021821 [DOI] [PubMed] [Google Scholar]
- 16.Raub C. B., Unruh J., Suresh V., Krasieva T., Lindmo T., Gratton E., Tromberg B. J., George S. C., “Image correlation spectroscopy of multiphoton images correlates with collagen mechanical properties,” Biophys. J. 94(6), 2361–2373 (2008). 10.1529/biophysj.107.120006 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Ghazaryan A., Tsai H. F., Hayrapetyan G., Chen W.-L., Chen Y.-F., Jeong M. Y., Kim C.-S., Chen S.-J., Dong C.-Y., “Analysis of collagen fiber domain organization by Fourier second harmonic generation microscopy,” J. Biomed. Opt. 18(3), 031105 (2012). 10.1117/1.JBO.18.3.031105 [DOI] [PubMed] [Google Scholar]
- 18.Myaing M. T., MacDonald D. J., Li X., “Fiber-optic scanning two-photon fluorescence endoscope,” Opt. Lett. 31(8), 1076–1078 (2006). 10.1364/OL.31.001076 [DOI] [PubMed] [Google Scholar]
- 19. Mardia K. V., Jupp P. E., “Summary Statistics,” in Directional Statistics (John Wiley & Sons, Inc., 2008), pp. 13–24. [Google Scholar]
- 20.Campagnola P. J., Loew L. M., “Second-harmonic imaging microscopy for visualizing biomolecular arrays in cells, tissues and organisms,” Nat. Biotechnol. 21(11), 1356–1360 (2003). 10.1038/nbt894 [DOI] [PubMed] [Google Scholar]
- 21.Akins M. L., Luby-Phelps K., Mahendroo M., “Second harmonic generation imaging as a potential tool for staging pregnancy and predicting preterm birth,” J. Biomed. Opt. 15(2), 026020 (2010). 10.1117/1.3381184 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Chen X., Nadiarynkh O., Plotnikov S., Campagnola P. J., “Second harmonic generation microscopy for quantitative analysis of collagen fibrillar structure,” Nat. Protoc. 7(4), 654–669 (2012). 10.1038/nprot.2012.009 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Wu Y. C., Xi J. F., Cobb M. J., Li X. D., “Scanning fiber-optic nonlinear endomicroscopy with miniature aspherical compound lens and multimode fiber collector,” Opt. Lett. 34, 953–955 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Murari K., Zhang Y., Li S., Chen Y., Li M.-J., Li X. D., “Compensation-free, all-fiber-optic, two-photon endomicroscopy at 1.55 μm,” Opt. Lett. 36, 1299–1301 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Liang W., Hall G., Messerschmidt B., Li M.-J., Li X. D., “Nonlinear optical endomicroscopy for label-free functional histology in vivo,” Light: Sci. Appl. 6, e17082 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]