Chromophore decomposition in multispectral time-resolved diffuse optical tomography

Abstract

Multicomponent phantom measurements are carried out to evaluate the ability of multispectral time domain diffuse optical tomography in reflectance geometry to quantify the position and the composition of small heterogeneities at depths of 1-1.5 cm in turbid media. Time-resolved data were analyzed with the Mellin-Laplace transform. Results show good localization and correct composition gradation of objects but still a lack of absolute material composition accuracy when no a priori geometry information is known.

1. Introduction

Some molecules in biological tissues, called chromophores, absorb light allowing them to be detected, identified and quantified. For instance oxy and deoxy-hemoglobin (HbO₂ and Hb) have distinct spectral signatures in the Near InfraRed range (NIR) where the depth penetration of light is relatively large, allowing the probing of tissues non-invasively with a non-ionizing radiation at cm depth. As they are important constituents involved in physiological mechanisms, quantitative images of their spatial distribution and concentration would provide a very useful tool to diagnose or monitor pathologies of patients, or to better understand physiological mechanisms. It can permit to do functional measurements and detect vascular activity [1]. It may be used for instance to monitor brain activities during a variety of tasks [2], neoadjuvant hormone therapy [3] or autologous tissues (“flap”) in reconstruction surgery [4], just to quote few examples. From normal to abnormal tissue, vascularization can change therefore it may be used to diagnose pathologies like breast cancer, peripheral arterial diseases [5] or brain injuries like ischemia or hemorrhage. Other chromophores detectable in the NIR range bring physiological and pathological information such as collagen which can be a risk factor for breast cancer [6,7].

However, extracting the information of the chromophore composition of the tissue from an outgoing light that has travelled through it is a challenging task. This may be achieved with Diffuse Optical Tomography (DOT). To get this information, DOT explores the tissue by injecting light and then collecting it using a set of source-detector pairs. A tomographic map of the optical properties of the tissue can be obtained through a reconstruction algorithm.

This technique can be coupled to multispectral approach, i.e. using multiple wavelengths, to decompose results on a material basis and to obtain the absolute chromophore decomposition concentration of the main tissue components. In the literature, most of the studies using multispectral DOT yield reconstruction results usually by normalizing the image scale or relative values. Moreover, most of the authors have carried out measurements with only one kind of absorbing object while changing other parameters like the depth and/or the spatial resolution [8]. The DOT performances in quantification are in general not systematically addressed: indeed only few works show DOT reconstructions with absolute values of chromophores’ concentration. A clinical 3D reconstruction of Hb and HbO₂ from the breast of a human volunteer using Frequency Domain (FD) DOT system in a cylindrical geometry shows limited quantitation capability, but a relative increase of hemoglobin in the tumor region compared with the background [9]. In continuous wave domain (CW), chromophore decomposition (Hb, HbO₂, water and lipid) were obtained in simulation and in vivo with the expected localization and correct quantification by using wavelength optimization [10]. Another work has presented the potential of Time-Resolved (TR) DOT on the monitoring of neoadjuvant hormone therapy for breast cancer to give valuable physiological information [3]. In fact, during three case measurements around the treatment, the total hemoglobin concentration estimated using TR-DOT in transmittance geometry changed as expected.

For anatomical constraints and to design a hand-held probe, the reflectance geometry is preferable. TR approach is advisable for such a geometry since measurements contain specific information about the depth of light-matter interactions. Indeed, TR measurements are obtained using short-pulsed sources and time-resolved detectors, exploiting the time-of-flight of detected photons, which have traveled in different tissue layers. As time adds a further dimension to encode depth, by employing time-windowing or moments analysis, it is possible to separate contribution of photons according to their arrival times and thus separate the information depending on the depth. The use of raw TR data in DOT is strongly time-consuming and so it was demonstrated that the Mellin-Laplace transform is an effective analysis tool for time-domain signals enabling data compression, time-windowing and increasing the sensitivity for late times [11].

Furthermore, thanks to the development of new detectors and detection technologies, we gained in compactness, signal-to-noise ratio and maximized the photon harvest [12]. In particular, demonstrations of Silicon PhotoMultiplier (SiPM) in diffuse optics and TR DOT were presented in previous papers [13,14]. These and other cost-effective solutions (e.g. compact TRS systems [15]) can now open the way to next-generation, compact TR DOT systems.

In parallel with technological progress, the scientific community also experienced the need to standardize the performance assessment of newly developed system. In the literature, the formulation of a performance assessment and quantification protocol is more straightforward for homogenous samples (MEDPHOT [16]) and functional imaging (BIP [17] and NEUROPT [18]). In our previous paper [19], we have addressed the issue of DOT quantification of the absorption coefficient with a single wavelength for heterogeneous media and we have evaluated the quantified results in terms of linearity and accuracy: the two parameters have different clinical interests for example for the monitoring of neoadjuvant therapy or the determination of absolute chromophore concentrations.

This paper is not presenting a new system and/or its characterization, but it follows the aim to quantify chromophore concentrations to enable chromophore decomposition in depth using multispectral time-resolved diffuse optical tomography in reflectance geometry. To achieve this goal, we have conducted an extended experimental multi-wavelengths campaign on synthetic media (calibrated phantoms). Such media were built to mimic different Hb/HbO₂ concentrations. They consisted of one or two liquid inclusions with various material quantities immersed at various depths inside a homogeneous liquid. We have also explored the optimal choice of the set of wavelengths to use. The data processing is restricted to absorption variations in the space, while in principle it is feasible to refine it by considering scattering.

The paper is organized as follows: Section 2 describes the experimental setup, the homemade multichromophore phantom manufacturing and the reconstruction process. Section 3 displays the results with the single inclusions showing first the absorption quantification and then the material composition. Same for Section 4 but with two inclusions at 25 mm distance from each other. Section 5 summarizes the conclusions and opens a discussion on the current limits.

2. Material and methods

2.1 Experimental setup

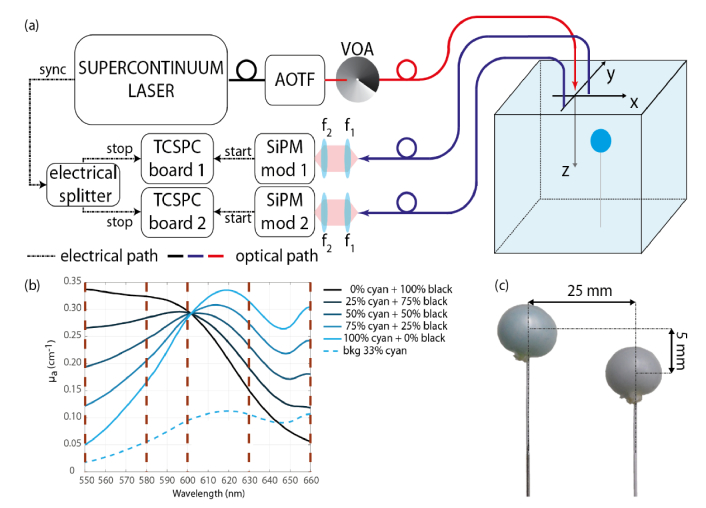
Figure 1(a) reports the setup used which is the same setup as in [13] except that we changed the laser source by a supercontinuum laser (SuperK EXTREME, NKT photonics, 10 ps pulse width) and added a fast wavelength selection system: an acousto-optical tunable filter (AOTF, NKT Photonics). The switching of the wavelength is fully automatized and controlled by a home-made measurement software.

Fig. 1.

(a) Schematics of the setup used (VOA: Variable Optical Attenuator, f₁ = f₂ = 30 mm). (b) Spectra of the various multichromophore compositions filled in the inclusion before adding scattering agent, with highlighted the five selected wavelengths (550-580-600-630-660 nm) for the scanning (purple dashed lines). (c) Picture of two balloon inclusions (Case 2, see Table 1).

As in the setup of [13], the backscattered light coming from the phantom was collected by two optical fibers at a distance of 30 mm from the excitation fiber (“source” in Fig. 1). Each collection fiber was connected to a SiPM module [20] coupled to a time-correlated single-photon counting (TCSPC) board. The whole scan over the phantom containing a single inclusion was done with 35 source positions (6 + 1 steps in x-direction and 5 steps in y-direction) and at 5 selected wavelengths (550, 580, 600, 630, 660 nm). During the scan the two SiPMs recorded the time-of-flight distribution simultaneously. As the reconstruction process is based on the perturbation approach, we used the measurements taken far from the inclusion (at x = −4 cm from the center of the inclusion, where the medium can be considered as homogenous) as reference acquisitions. For the multi-inclusion measurements, we enlarged the scanning area in the x-direction by adding three lines of scan in order to take the reference far from both perturbations.

2.2 Multichromophore phantoms

Currently, the most advanced multilaboratory validation of phantom materials for Diffuse Optics relies on water dilution of Intralipid and ink [21]. Nevertheless, optical phantoms containing heterogeneities are difficult to obtain and each lab has its own protocol [22,23]. For purely absorbing inclusions assessed at a single wavelength we preferred the Equivalent Black Volume (EBV) approach, which can mimic a wide Equivalence Class of realistic perturbations with different combination of volume, shape and absorption changes [24,25]. However, to cope with multichromophore problems we had to implement a different approach. In the present work, the inclusion consisted of a thin (< 0.1 mm) approximately spherical rubber balloon as a small container filled with a liquid mixture with calibrated optical properties, as described in the following subsection. To evaluate the effect of the container walls and/or the mismatch of the refraction index, we performed a measurement with inclusion filled with the same solution as the background medium.

The phantoms consisted in a homogeneous liquid background and one or two inclusion(s) immersed at depths 10 mm and 15 mm. The whole phantom was contained in a glass tank (volume 8.5 l). The background liquid is composed of a water-based solution made of Intralipid and cyan ink for jet printers (μ_s’ = 13.5 cm⁻¹ and μ_a = 0.095 cm⁻¹ at 600 nm) as exhibited in Fig. 1(b). To prepare the multichromophore liquid phantoms for the inclusions, we used the same cyan ink and a black one. We decided to work with these synthetic chromophores, since, in the visible range, their absorption spectrum somehow mimic the spectral behavior of a Hb/HbO₂ mixture in the NIR (see Fig. 1(b)). So far, we have not found any other colorants capable of mimicking the Hb/HbO₂ in the infrared range without introducing problems of stability or fluorescence. The obvious choice of using Hb/HbO₂ from blood would require a good control of oxygenation, which is far from straightforward [26]. To have the optimal separation between the two colorants, we decided to work in the optical window from 550 to 660 nm and defined the proportions to get a common absorption coefficient of approximately 0.3 cm⁻¹ at 600 nm. In order to assess the quantitation performances and to draw gradual quantified plots of absorbing heterogeneities, we realized five bi-chromophore inclusions with gradual compositions and one inclusion with the same solution as the background phantom. The absorption spectra of the gradual range of the liquid inclusions are represented in Fig. 1(b). The composition of the colored mixtures ranges from 100% of black ink solution (μ_a = 0.297 cm⁻¹ at 600 nm) up to 100% of cyan ink solution (μ_a = 0.284 cm⁻¹ at 600 nm) with a decrease or increase step of 25% of each ink. The background phantom corresponds to around 33% of cyan ink and 0% of black ink.

The absorption values of the pure constituents were derived using the procedure described in Ref [27]. Briefly, this method is based on the analysis of time-resolved measurements on water solutions of Intralipid adding ink at increasing concentrations. The slope of the retrieved μ_a as a function of ink concentration leads to the intrinsic absorption coefficient of ink, free from any scattering contributions (including the non-negligible effects of ink particles) and residual background absorption. The proportion between phantom’s components were obtained to have the desired optical properties at 600 nm (μ_a = 0.3 cm⁻¹ and μ_s’ = 13.5 cm⁻¹ for 100% cyan and 100% black while μ_a = 0.1 cm⁻¹ and μ_s’ = 13.5 cm⁻¹ for the background). Before adding the Intralipid, the ink and water solution was measured at the spectrophotometer so as to recover the absorption spectrum of the pure inks (100% cyan and 100% black, as well as those of the background).

To derive the spectra of the mixtures of inks (e.g. 25% cyan and 75% black), we made use of the Beer’s law of mixture which states that the final spectrum is a weighted average of the main components one, as reported in Eq. (1)

$${\mu }_a(\lambda )={\displaystyle \sum _{i=1}^{N_c}{\mu }_{a,i}(\lambda )}{p}_i$$ (1)

where λ is the wavelength, N_c is the number of chromophores in the medium (2 in this case), μ_a,i is the spectrum of the pure ink while p_i is the percentage of the i-th ink in the solution (e.g. 0.25 for the cyan and 0.75 for thr black).

Single inclusion

For the inclusions, we used a homemade rubber balloon to contain the liquid absorbers. To make it, we cut the finger of a laboratory disposable glove (made of natural latex and powder free, Ansell Ltd, color clear) used as container. The piece of glove was placed on an aluminum plate, previously drilled to obtain a small hole that fits the diameter of the output orifice of a syringe (without the needle). The syringe was then used to fill the piece of glove with 1 ml liquid phantom, since it was free to expand on the other side of the hole, thinning its thickness and becoming an almost spherical balloon. To close it, we made a knot with a white thin thread and fixed it to a white-painted metallic wire (0.5-mm music wire) in order reduce as much as possible the interference of the wire during the motion of the inclusion at different positions (see Fig. 1(c)), as already adopted in [25]. The diameter of these inclusions was about 11.5 mm on average with a standard deviation of 0.6 mm.

Each of the six gradual compositions inclusions were immersed within the homogeneous liquid background at 2 depths (10-15 mm). The depth is defined as the distance from the surface of the phantom to the center of the inclusion.

Multi-inclusions

The multi-inclusions phantoms were composed of two inclusions at a distance of 25 mm from their centroids (14 mm from their borders) (see Fig. 1(c)) immersed in the same liquid phantom as the experiments with the single inclusion. Various combinations (composition, volume, depth) of inclusion couple were realized and are summarized in Table 1. For example, two balloons of different compositions (left inclusion: 100% cyan ink solution; right inclusion: 50% cyan and 50% black inks solution) and same size (1 ml) were both embedded at 10 mm depth; it is Case 1.

Table 1. Summary of the characteristics of the different bi-inclusions phantoms tested. The corresponding spectra of each chromophore composition are displayed in Fig. 1(b).

	Inclusions	Ink composition	Volume	Depth
Case 1	Left	100% cyan	1 ml	10 mm
	Right	50% cyan + 50% black	1 ml	10 mm
Case 2	Left	100% cyan	1 ml	15 mm
	Right	50% cyan + 50% black	1 ml	10 mm
Case 3	Left	100% cyan	1 ml	10 mm
	Right	50% cyan + 50% black	1 ml	15 mm
Case 4	Left	50% cyan + 50% black	1 ml	10 mm
	Right	50% cyan + 50% black	1 ml	10 mm
Case 5	Left	50% cyan + 50% black	2 ml	10 mm
	Right	50% cyan + 50% black	1 ml	10 mm

2.3 Reconstruction process

We used the reconstruction technique detailed in [19] applied to each selected wavelength independently and we also supposed the reduced scattering coefficient, μ_s’, as known, homogenous and equal to 13.5 cm⁻¹ at 600 nm in the whole phantom.

The algorithm is based on the time-domain diffusion equation which is solved by Mellin-Laplace transform [28]. To linearize the inverse problem, we used a “Born approximation” perturbation approach which also permits to eliminate the instrument response function (IRF) in our reconstruction algorithm. Indeed, by performing the cross convolution Y_sd^(k)(t) between reference measurements -M^A(t)- actual measurements -M^B(t)- and their Green’s functions (known G^A)(t) and estimated G^B(k)(t) at iteration k), we get this linear system restricted for the study to absorption reconstruction:

$$\{\begin{array}{l}{M}_{sd}^A\left(t\right)=IR{F}_{sd}\left(t\right)\ast G_{sd}^A\left(t\right)\\ M_{sd}^B\left(t\right)=IR{F}_{sd}\left(t\right)\ast G_{sd}^B\left(t\right)\end{array}\Rightarrow \{\begin{array}{c}{Y}_{sd}^{(k)}\left(t\right)=M_{sd}^B\left(t\right)\ast G_{sd}^A\left(t\right)-M_{sd}^A\left(t\right)\ast G_{sd}^{B(k)}\left(t\right)\\ Y_{sd}^{(k)}\left(t\right)\approx -M_{sd}^A\left(t\right)\ast {\displaystyle \underset{\Omega }{\int }d\overrightarrow{r}.G_s^B\left(\overrightarrow{r},t\right)\ast G_d^{B(k)}\left(\overrightarrow{r},t\right).\delta {\mu }_a^{\left(k\right)}\left(\overrightarrow{r}\right)}\end{array}$$

where $\delta {\mu }_a^{\left(k\right)}\left(\overrightarrow{r}\right)$ is the difference between the actual absorption and the current absorption reconstructed at iteration k at position $\overrightarrow{r}$, and s and d are indexes on the source the detector and t is the time. We applied the Mellin-Laplace transform which is an effective analysis tool for time-domain signals enabling data compression and, time-windowing thus, increasing the sensitivity for late times. Additionally, the use of Mellin-Laplace transform and simplifies the system by transforming the time-convolution into a matrix multiplication, as demonstrated in Ref [28].

Then we solved the discretized problem by the weighted least squares using the conjugate gradient method. At each iteration, we updated the 3D map of the absorption coefficient of the unknown medium up to 10 iterations.

Constrained method

In the present work, we also evaluated the spatially constrained method defined in [19]. In this method the reconstruction is performed after having fixed the position and shape of the inclusions according to the actual physical configuration. In these conditions the reconstruction serves only to recover the absorption coefficient of the inclusion(s). We have demonstrated in [19] that this improves significantly the accuracy of the retrieved absorption coefficient. The assumption of a known geometry is justified when dealing with multimodal imaging techniques like for example the combination of diffuse optical imaging with ultrasound imaging [29–31].

Chromophore decomposition

With the multispectral approach after getting the reconstructed μ_a maps at each wavelength, we use the Beer’s law of mixtures (the same as that of Eq. (1), reported for each voxel in Eq. (2)) to determine the concentrations of each chromophore. The total absorption coefficient μ_a,m at voxel m of the mesh is the sum of the specific absorption coefficient μ_a,i or the molar extinction coefficient ε_i of the chromophores weighted by the proportions p_i or concentrations C_i of the chromophores i.

$${\mu }_{a,m}(\lambda )={\displaystyle \sum _{i=1}^{N_c}{\epsilon }_i(\lambda )C_i}={\displaystyle \sum _{i=1}^{N_c}{\mu }_{a,i}(\lambda )}{p}_i.$$ (2)

In our phantom experiments using inks, the chromophore decomposition is expressed in percent (%) because we have measured beforehand the specific absorption coefficients μ_a,i of each ink solution i (see Fig. 1b black curve for black ink and cyan curve for cyan ink) and thus we obtained the reconstructed chromophore decomposition results of black and cyan inks in proportions p_i which are converted in %.

This two-steps approach enables to test different combinations of wavelengths and to find the optimal combination to get the best chromophore decomposition for this study.

3. Results with single inclusion

With the reconstruction in two steps, we are able to detail the μ_a quantification before the chromophore decomposition results. The results with a single inclusion are shown in this section.

3.1 Multispectral results

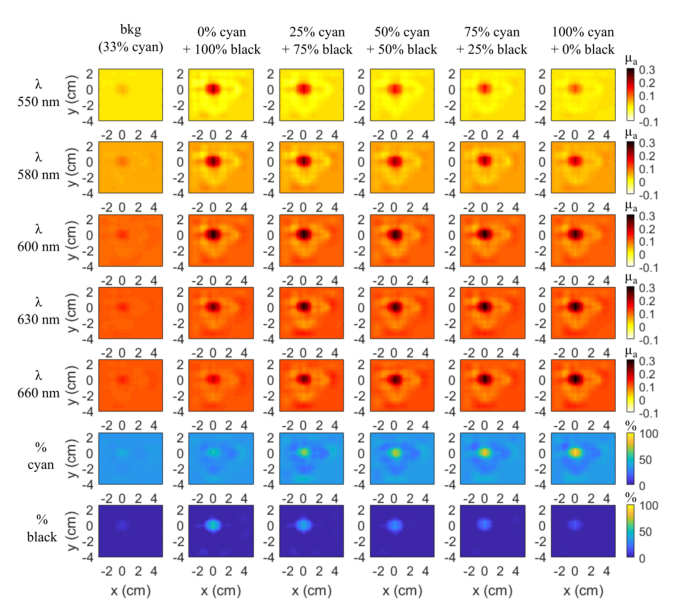
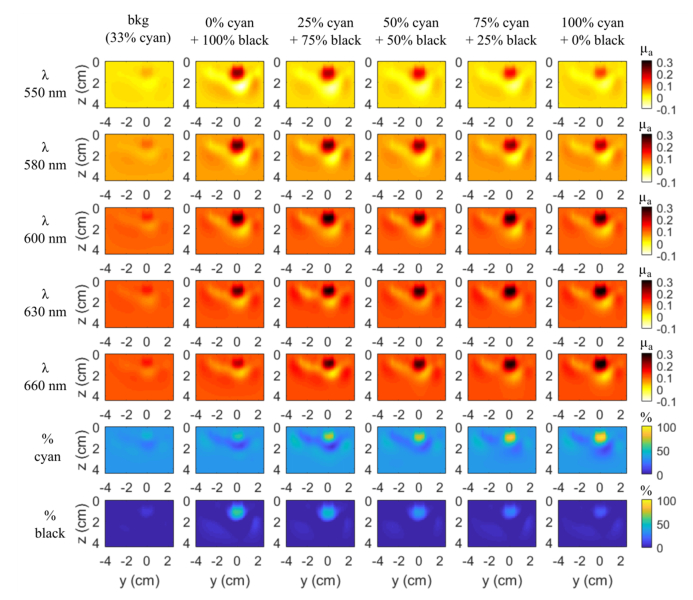
Figures 2 and 3 display the 3D reconstructed maps of the inclusions at 10 mm depth on two slices y-x and z-y respectively (z being the coordinate along the depth with the origin at the surface of the scattering medium). The scan probe is located on the z = 0 mm plane. The first five rows correspond to the absorption maps for each wavelength and the last two rows, which will be discussed in the next subsection, are the % of both inks maps deduced from the law of mixtures (Eq. (1)) taking into account their respective absorption spectra.

Fig. 2.

Slices y-x (z = 10 mm) of 3D reconstruction μ_a maps of each balloon inclusion at each wavelength at 10 mm depth and the chromophore decomposition in percent of cyan and black inks solutions by taking into account the 5 wavelengths (550-580-600-630-660 nm) (rows 6-7). Same colorbar for each line.

Fig. 3.

Slices z-y (x = 0 mm) of 3D reconstruction μ_a maps of each balloon inclusion for each wavelength at 10 mm depth and chromophore decomposition in percent of cyan and black inks by taking into account the 5 wavelengths. Same colorbar as Fig. 2 for each line.

We first checked for possible artefacts arising from the inclusion envelope and holder. To do so, we first acquired data with the rubber balloon filled with the same solution as the surrounding phantom. The reconstructions obtained from these measurements are shown in the first column of Figs. 2 and 3. A faint spot can be seen at the position of the heterogeneity but the value of the reconstructed absorption coefficient is weak. The contrast of this balloon inclusion is almost the same for all the wavelengths (about 9%). So, the combined effect of glove, thread and metallic wire seems to be wavelength independent and it will only add a small offset in the measurements.

For the whole set of experiments, the position of the reconstructed inclusion is accurate in x and y, where we expect x = 0 and y = 0 for its center (Fig. 2) and an important gradation can be observed for the extreme wavelengths (550 and 660 nm) from columns 2 to 6, in accordance with the ink absorption spectra (Fig. 1(b)), where the difference between the absorption spectra of each ink combination is the largest. At 600 nm, as expected, we get approximately μ_a = 0.3 cm⁻¹ for all the inclusions except for the inclusion filled with the background medium (column 1 of Fig. 2).

In the z-y plane (Fig. 3), all the inclusions show up in the reconstruction at the expected depth of 10 mm. A reconstruction artefact below the inclusion appears in every image with about the same shape. Of course, as for the y-x slices, the same gradation of the reconstructed composition is obtained.

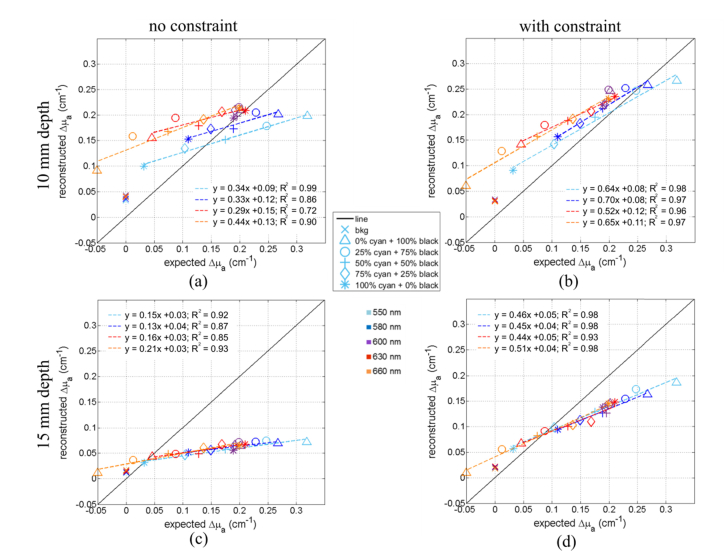
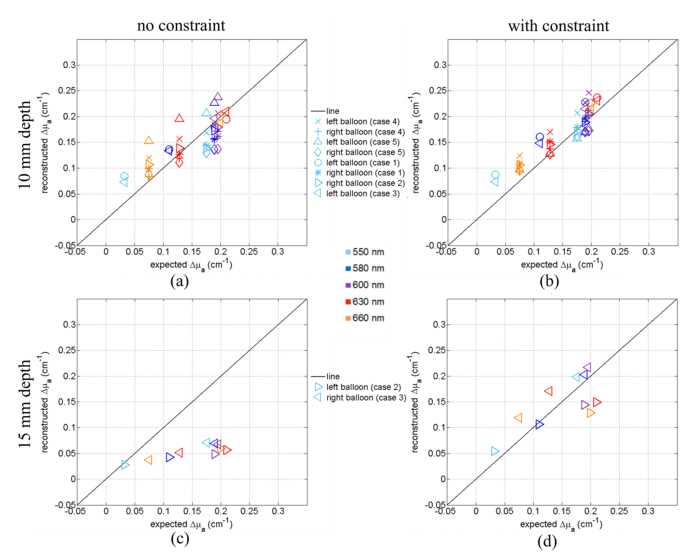
An evaluation of the accuracy of the quantification of the retrieved absorption coefficients can be estimated from Fig. 4. It shows for each wavelength and each inclusion the maximal value of Δμ_a, (the difference between the μ_a of the inclusion and that of the background liquid) retrieved from the reconstruction using the standard method (Figs. 4(a) and 4(c), left column) and the values retrieved using the spatial constraint method (Figs. 4(b) and 4(d), right column). The first and second rows of Fig. 4 correspond to depths 10 and 15 mm, respectively. As highlighted by the starting point of the x and y scale range, for one point (i.e. inclusion with 100% black ink solution at 660 nm), we expect to get a negative value because the absorption coefficient of the inclusion is below the absorption of the background medium (see Fig. 1(b)).

Fig. 4.

Comparison of the reconstructed and expected values of Δμ_a^max for all the balloon inclusion (markers) and various wavelengths (colors). The linear fits of each wavelength are plotted (dotted lines and equation of the fit). (a) and (b) Plots of Δμ_a^max of inclusions at 10 mm depth obtained with the standard reconstruction process and the spatially constrained method respectively. (c) and (d) Plots of Δμ_a^max of inclusions at 15 mm depth obtained with the standard reconstruction process and the spatially constrained method respectively.

At 10 mm depth, the standard method (no constraints, Fig. 4(a)) yields fairly acceptable values for 550, 580 and 600 nm. The data can be reasonably well fitted by a linear regression y = ax + b (in particular R² is very close to 1 for 550 nm) but the slope is about 3 times smaller than the expected value. Anyway, the consistency of the data is ascertained by the facts that for 600 nm the values retrieved for all the samples are very close, and this holds for all the wavelengths. The values retrieved for the sample filled with the same solution as the background (oblique crosses) are the same although they are not zero as they should be, as discussed in Figs. 2 and 3.

With the spatially constrained method (i.e. imposing in the reconstruction a spatial constraint for the position and size of the inclusion, Fig. 4(b)), the values come closer to the expected values (black line). The linear fit of the data yields slightly better R² coefficients (R² always larger than 0.93) with a slope ‘a’ which is still underestimated but comes closer to 1 as expected (about 0.7 instead of 0.35 with the standard reconstruction method).

Figures 4(c) and 4(d) show the Δμ_a^max reconstructed of all the inclusions but at 15 mm depth. The plot is less scattered, and the data can again be well represented by a linear fit although the slope is even more underestimated than at 10 mm depth. Such a depth effect on the slope has been observed already in our previous work [19]. By forcing the reconstruction on the expected shape and position of the inclusion, we slightly improve the linearity (R² slightly closer to 1) and the slopes of the linear fits are increased, still remain smaller than the values obtained at 10 mm depth. So, the depth has an effect of the quantification and can be partially corrected by the spatially constrained method.

3.2 Wavelength optimization

In the previous figures (rows 6 and 7 of Figs. 2 and 3), we have drawn the 3D concentration maps of the two chromophores by taking into account all the 5 wavelengths. As expected, the percentage of cyan ink increases gradually, while the one of black ink decreases gradually, but we get an important underestimation with around 55% of black ink instead of 100%.

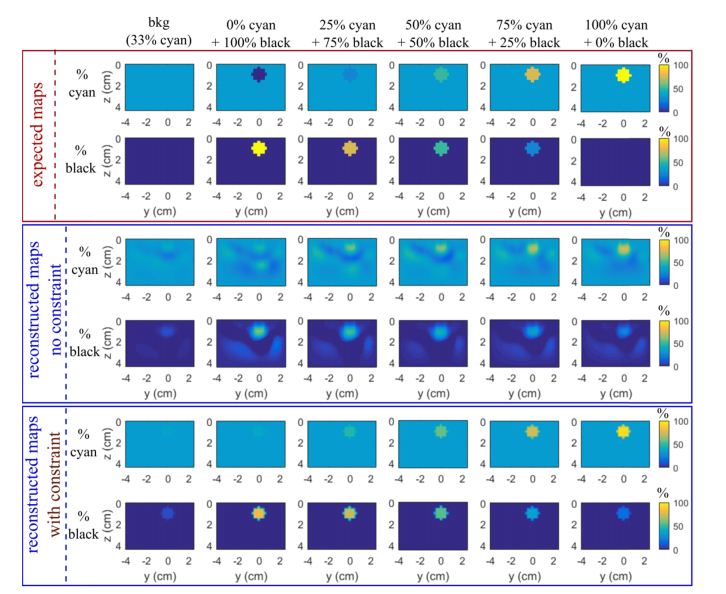
The data shown in the previous subsection and Fig. 4 suggest that the more accurate values are obtained extracting only the 3 wavelengths 550-580-600 nm. We obtained large reconstructed µ_a errors for 630 and 660 nm than for the other wavelengths for the cases with high percentage of black ink where expected Δμ_a^max are small. For unclear reasons, despite reconstructions obtained for these cases are globally satisfying, (see 0% Cyan + 100% black at wavelength 660 on Fig. 3), the inclusion being much fainter than for low wavelengths, there still remain high concentration spots which make the reported Δμ_a^max being overestimated. That is why, these two wavelengths were excluded for subsequent analyses. Figure 5 presents the chromophore decomposition results using wavelengths 550-580-600 nm compared with the expected values. The gradation in the concentration of both chromophores is much more marked than by combining all the 5 wavelengths. By forcing spatially the reconstruction (rows 5 and 6 of Fig. 5), the separation is evident and the quantification is encouraging. For both colorants, they are close to the expected values for 50%, 75% and 100% cyan. At 0% cyan, we retrieve a value corresponding to the liquid background (33% cyan) and not below as expected. Actually the reconstruction algorithm requires to be initiated by specifying for each wavelength some spatial distribution of μ_a (x,y,z). Here it is given using the liquid background corresponding to 33% cyan ink solution. With both reconstruction methods (standard and constrained) it seems that it is not possible to retrieve concentrations of cyan inks smaller than this initialization i.e. the current algorithm cannot reconstruct negative perturbation. For the black ink fraction, both reconstruction algorithms yield an erroneous value for the inclusion 100%cyan + 0%black. However, while the standard code yields 40% maximal error on black ink estimation the spatially constrained code yields only 20%. Thus compared to the results obtained with the standard code, the prior spatial information of the inclusion improves significantly the accuracy of the quantification.

Fig. 5.

Slices z-y (x = 0 mm) of 3D chromophore decomposition in percent of cyan and black inks of each inclusion at 10 mm depth with the optimal wavelength combination (550, 580 and 600 nm). Rows 1-2 the expected values, rows 3-4 reconstructed maps with the standard reconstruction process and rows 5-6 with the spatially constrained method.

4. Results with multi-inclusions

4.1 Absorption results

We now consider the results corresponding to phantoms containing two inclusions with various composition and depths (see Table 1). For all these cases Fig. 6 shows for each wavelength and both inclusions (“left” and “right”) the maximal value of Δμ_a (difference between μ_a of the inclusion and that of the background liquid) retrieved from the reconstruction using the standard method (“no constraint”, Figs. 6(a) and 6(c)) and the values retrieved using the spatial constraint method (Figs. 6(b) and 6(d)).

Fig. 6.

Comparison of the reconstructed and expected values of Δμ_a^max for the left and right balloon of each case defined in Table 1 (markers) and various wavelengths (colors). (a-b) Plots of Δμ_a^max of inclusions at 10 mm depth obtained with the standard reconstruction process and the spatially constrained method respectively. (c-d) Plots of Δμ_a^max of inclusions at 15 mm depth obtained with the standard reconstruction process and the spatially constrained method respectively.

At 10 mm depth most of the data points follow the black line meaning that the measurements are fairly accurate for this wavelength range. The spatial constraint reduces significantly the scattering of the data points. In particular, it reduces the overestimation of the absorption by the biggest inclusion (Case 5, triangle markers).

By contrast, it is evident from Fig. 6(c) that the absorption of the inclusion at z = 15 mm retrieved using the standard method is strongly underestimated, which is consistent with the observations shown on Fig. 4(c): The second inclusion at 25 mm distance is spatially well separated and does not affect the behavior observed for single inclusions. However, the spatially constrained method cures this problem (Fig. 6(d)) yielding quite satisfactory quantification results for inclusions at 15 mm depth.

4.2 Chromophore decomposition

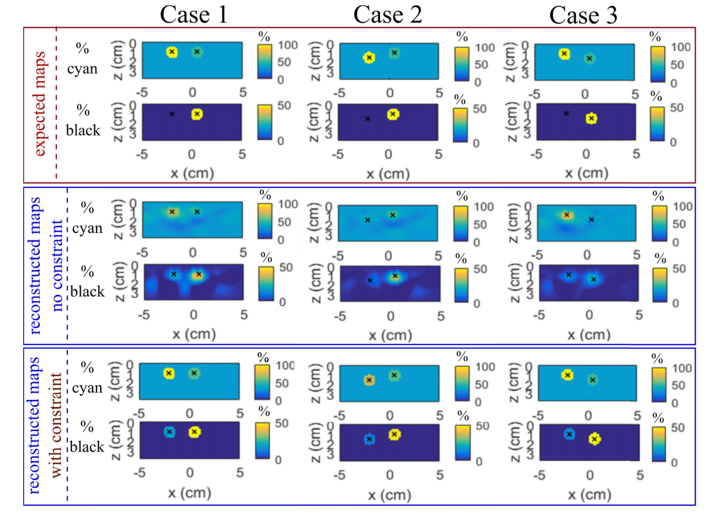
Figure 7 shows the z-y slices of the 3D chromophore decomposition with the 550-580-600-nm wavelength combination of the multi-inclusions phantoms of Case 1, 2 and 3 (i.e. a pair of balloons of the same size and different composition - 100% cyan and 50% cyan 50% black - placed one after the other from 10 to 15 mm depth; see Table 1). For the reconstructed maps, we can separate the two inclusions at a distance of 25 mm easily. Their positions are correctly reconstructed. So, we can well identify and localize the two inclusions.

Fig. 7.

Slices z-y of 3D chromophore decomposition in percent of cyan and black inks of the multi-inclusions phantoms Case 1, 2 and 3 defined in Table 1 with the optimal wavelength combination (550, 580 and 600 nm). Rows 1-2 the expected values, rows 3-4 reconstructed maps with the standard reconstruction and rows 5-6 with the spatially constrained method. The black crosses correspond to the expected center of the inclusions.

With no constraint the concentrations in the deeper balloon are underestimated for both cyan and black ink solutions (excepted for 0% black ink where it is overestimated since a non-zero concentration is retrieved). This is consistent with the fact that the slope of the retrieved absorbance vs the expected decreases with the depth as shown on Fig. 6(c) (and also on Fig. 4(c) compared to Fig. 4(a)). The spatial constraint significantly improves the accuracy of the retrieved composition, the most inaccuracy that remains being the fact that a non-zero concentration of black ink is retrieved when it should be 0%.

5. Discussion and conclusions

We acquired a unique set of measurements with a time-domain multispectral system on a large range of bi-materials and bi-inclusions phantoms so as to evaluate the performance of a complete diffuse optical tomography system (apparatus + reconstruction algorithm).

Working with synthetic media (phantoms) to get optical properties close to proportions of Hb/HbO₂ concentrations as in biological tissues is challenging. We have overcome it by building multichromophore calibrated phantoms with liquid ink solutions (where the fabrication process is validated by the community) and a homemade rubber balloon as inclusion to contain the liquid absorbent where the wall effect was checked and is fairly limited.

Results on the μ_a 3D reconstructions and the quantified plots show very good localization of inclusions at 10 or 15 mm depth, good separation of two objects at 25 mm distance, good linear behaviors, but still suffer from lack of quantitation accuracy. Moreover, with the multispectral approach, we performed chromophore decomposition and the results show good separation and gradation of the two chromophores also when there were two objects in the studied medium. When the inclusion is at 10 mm depth and in the range of absorption variation (compared to the background) between around 0.1 to 0.25 cm⁻¹, the maximal absolute absorption is correctly reconstructed with an error of less than 29%. Beyond these conditions with no a priori geometry information, absolute material composition accuracy is hard to obtain and even more when the object is immersed at 15 mm depth or deeper. Better results are obtained in the cases with a spatially constraint method. Thus compared to the results obtained with the standard code, the prior spatial information of the inclusion improves significantly the accuracy of the quantification and compensates the quantification degradation due to depth. These observations are in agreement with results reported in recent works [29–31], where the use of other techniques (such as ultrasound imaging) to detect the position and shape of the inclusions (i.e. the a priori information) have been demonstrated useful to improve tomographic reconstructions.

The two-steps reconstruction approach has allowed us to discuss the optimum wavelengths for different absorption chromophores and wavelength combinations, and we have provided optimum wavelength distributions for typical experimental scenarios which improve the chromophore decomposition.

We prove in this paper the progress of the TR DOT to be in the future a diagnostic medical device to quantify the concentration of chromophores such as oxy hemoglobin and deoxy-hemoglobin which is useful for biomedical applications from brain activity to oncology. In addition, the development of new TR DOT components [11] (e.g. laser, detector and time-tagging electronics) paves the way to more cost-effective and versatile multimodality systems complementing the morphological information provided form e.g. US or X-ray with the functional and chemical specificity of TR DOT. Such achievements will permit to feed the DOT acquisition with the a-priori information on shape and location yielding a satisfactory chromophore decomposition.

Nevertheless, we have identified some issues concerning the dependence of the initialization parameters on the reconstruction of medium which raise some concerns whenever the reference data cannot represent properly the background composition, and more complex, probably non-linear reconstruction approaches should be considered.

As a next step, special attention must be paid on data processing because we get the same quantification difficulties in simulations [19]. It is now performed by using the Born approximation and a cross convolution to eliminate the instrumental response, but such a procedure involving measurements convolution with Green’s functions might lead to information loss. A better procedure is now regarded so as to achieve better quantification.

Disclosures

The authors declare that there are no conflicts of interest related to this article.

Funding

European Union's Horizon 2020 programme under grant agreement no 654148 (Laserlab-Europe), and no 731877 (SOLUS).