Analysis of IgG kinetic stability by differential scanning calorimetry, probe fluorescence and light scattering

Abstract

Monoclonal antibodies of the immunoglobulin G (IgG) type have become mainstream therapeutics for the treatment of many life‐threatening diseases. For their successful application in the clinic and a favorable cost‐benefit ratio, the design and formulation of these therapeutic molecules must guarantee long‐term stability for an extended period of time. Accelerated stability studies, e.g., by employing thermal denaturation, have the great potential for enabling high‐throughput screening campaigns to find optimal molecular variants and formulations in a short time. Surprisingly, no validated quantitative analysis of these accelerated studies has been performed yet, which clearly limits their application for predicting IgG stability. Therefore, we have established a quantitative approach for the assessment of the kinetic stability over a broad range of temperatures. To this end, differential scanning calorimetry (DSC) experiments were performed with a model IgG, testing chaotropic formulations and an extended temperature range, and they were subsequently analyzed by our recently developed three‐step sequential model of IgG denaturation, consisting of one reversible and two irreversible steps. A critical comparison of the predictions from this model with data obtained by an orthogonal fluorescence probe method, based on 8‐anilinonaphthalene‐1‐sulfonate binding to partially unfolded states, resulted in very good agreement. In summary, our study highlights the validity of this easy‐to‐perform analysis for reliably assessing the kinetic stability of IgGs, which can support accelerated formulation development of monoclonal antibodies by ranking different formulations as well as by improving colloidal stability models.

Abbreviations

ANS

8‐anilinonaphthalene‐1‐sulfonate

CD

circular dichroism

C_H

constant domain of the heavy chain

DSC

differential scanning calorimetry

Fab

fragment antigen binding

Fc

fragment crystallizable

IgG

immunoglobulin G

PBS

phosphate‐buffered saline.

Introduction

Monoclonal antibodies based on the immunoglobulins G (IgG) format class are rapidly becoming a standard therapy for many human diseases.1 In an antibody discovery pipeline, after identifying lead candidates that specifically recognize one defined epitope with high affinity and specificity and good manufacturability properties, the next critical step is the development of suitable formulations, in which these IgG candidates display constant efficacy over an extended period of time. For therapeutic applications, it is not only required that the antibody maintains its native conformation but also that it does not form any aggregates. This is often challenging because of the low conformational stability of some of these molecules, leading to a significant population of partially unfolded species. At high concentrations, these partially unfolded molecules with exposed hydrophobic parts tend to form aggregates.2, 3, 4, 5

Importantly, unfolded and aggregated molecules may decrease the efficacy of these therapeutics, and aggregates can also induce a strong immunogenic response6 which might counteract their therapeutic effects or even preclude their clinical use altogether. To suppress these adverse reactions, specific formulations must be developed to stabilize the active conformation over months or years. Thus, it is no surprise that prior to any administration to patients, the stability properties of therapeutic IgGs and the testing of formulations is an essential part of the so‐called common technical documents submitted for market authorization and is critically reviewed by regulatory authorities.

Hence, the long‐term stability of therapeutic candidates in the pharmaceutical development of new biological drugs is the focus of intensive studies regarding both their conformational 7, 8, 9, 10, 11, 12, 13, 14 and colloidal 15, 16, 17, 18 stabilities. Thus, understanding factors determining IgG stability or predicting it at suitable storage temperatures is a critical goal in biopharmaceutical studies. As long‐time measurements at storage conditions are very time‐consuming, so‐called accelerated stability testing methods have been used to assess the shelf‐life of therapeutic proteins.19, 20, 21, 22, 23 These methods are based on a prediction of the shelf‐life of IgGs using an extrapolation of stability data from elevated temperatures to real‐life storage conditions. However, such extrapolations are only meaningful if there is a linear dependence of stability over a wide range of temperatures, i.e., from storage to denaturation temperatures. The validity of such an extrapolation needs to be confirmed over extended temperature ranges and by independent methods – however, this has not been done to date in a systematic approach.

Essentially all accelerated studies have so far focused on the colloidal stability of IgGs due to their apparent propensity to form aggregates after prolonged storage at high protein concentrations, even at low temperatures.18, 21, 22, 24 Methods that are able to predict the relative or absolute rates of aggregation are, therefore, of great practical interest in biopharmaceutical research and development.22 However, aggregation processes, particularly those induced by temperature, are very complex and show non‐Arrhenius behavior. In fact, the non‐Arrhenius temperature dependence of aggregation is quite typical, even over relatively small temperature windows. For this reason, low‐temperature extrapolations are challenging to interpret, if they are based simply on accelerated stability studies at high/denaturation temperatures.22, 25, 26

It is important to keep in mind that colloidal and conformational stabilities of proteins are closely related properties. In fact, the formation of non‐native aggregates depends on the presence of partially unfolded protein molecules, whose occurrence itself strongly depends on the conformational stability and dynamics of the native state of the protein under given conditions.2, 3 In other words, a prediction of the unfolding‐limited colloidal stability of the protein strongly depends on the proper determination of its conformational stability. Indeed, important factors that contribute to the temperature‐dependent nonlinearity in protein aggregation originate from both the nonlinearity of the temperature dependence of protein stability27 and a change in the rate‐limiting step of aggregation as a function of temperature.26

Recently, we have developed a kinetic model addressing the complex thermal denaturation of IgGs that consists of three consecutive steps: one reversible transition (corresponding to C_H2 domain unfolding) followed by two irreversible transitions, corresponding to the unfolding of the Fab and C_H3 domains, respectively.13 This model enabled us to determine parameters quantitatively describing each step of the IgG thermal denaturation, such as the equilibrium constant of the first transitions and the rate constants of the irreversible steps at any given temperature. In the present study, we address the question whether this model can also be used for accelerated stability studies and if the obtained rates can be validated by an independent approach. Moreover, we show that our model correctly calculates the molar fractions of individual intermediate states at different temperatures and thus provides important information for existing or future models addressing colloidal stability of IgGs.28

To this end, we performed detailed analyses of our model using differential scanning calorimetry (DSC), 8‐anilinonaphthalene‐1‐sulfonic acid (ANS) fluorescence and absorbance spectroscopy. We could show that the employed model correctly describes the thermal denaturation of IgG both over a broad concentration range (from 0.25 to 15 mg/ml) and also in the presence of non‐denaturing chaotropic formulations. The accuracy of the mathematical description is further supported by our finding that the rate constants of the first irreversible step obtained from DSC scans correlate very well with those determined by an orthogonal method, namely by measuring the kinetics of ANS binding to IgG at various temperatures. Finally, our analysis shows that thermal denaturation kinetics of IgGs are not affected by their aggregation, but on the other hand, IgG aggregation depends on its concentration. This suggests that the aggregation process is very complex, and depends on absolute concentrations of aggregation‐prone conformational state(s) of IgG, their particular aggregation rates and the temperature dependence of these rates.

Material and Methods

Purification of IgG

The well‐characterized IgG6B3 binds myoglobin and had been selected from the Human Combinatorial Antibody Library (HuCAL).29 Protein was produced from a stable HEK293 clone as described previously13, 30 as well as from transiently transfected FreeStyle 293‐F cells (Thermo Fisher Scientific) according to the protocol for HEK cell lines summarized by Hacker et al.31 Subsequently, IgGs were affinity‐purified from cleared supernatants on Protein A columns (GE Healthcare Life Sciences). Eluted fractions were pooled and dialyzed against PBS, pH 7.4, (Thermo Fisher Scientific) before proteins were used for subsequent analyses.

Absorbance measurements

The aggregation of IgG in the presence of increasing urea concentrations was determined by light scattering at 500 nm using a Specord S 300 UV VIS and Specord S 600 diode array spectrophotometer (Analytik Jena AG, Jena, Germany) equipped with a Peltier‐thermostated cell holder with a PTC 100 control unit. The temperature was increased from 20°C to 90°C with a heating rate of 1 K/min. The protein concentrations were 5 μM (i.e., 0.75 mg/ml) in cuvettes with 1 cm path length.

Circular dichroism (CD) measurements

A Jasco J‐810 spectropolarimeter (Tokyo, Japan) equipped with a Peltier type thermostated single cell holder (PTC‐423S) was used for circular dichroism measurements. Ellipticity in the far‐UV region was measured in a 1 mm pathlength quartz cuvette. All circular dichroism measurements were performed in PBS buffer pH 7.4 with an IgG6B3 concentration of 5 μM in the presence and absence of urea. The temperature was kept constant at 25°C.

ANS measurements

Thermal transitions of IgG in the presence of different concentrations of urea (0, 1, 2, and 3 M) were monitored by the fluorescence of 8‐anilinonaphthalene‐1‐sulfonate (ANS). Samples were mixed and incubated overnight at room temperature. The temperature was changed from 20°C to 90°C with a heating rate of 1 K/min. Thermograms were corrected by subtraction of the pre‐transition linear baseline of ANS fluorescence.

Kinetic measurements of ANS fluorescence, i.e., ANS binding to IgG, at various urea concentrations at different temperatures were followed after a two‐hour incubation of the IgG and ANS mixture at room temperature. The kinetic traces were corrected by subtraction of the value of ANS fluorescence at the start of the measurement. The ANS fluorescence was followed at 510 and 525 nm with an excitation wavelength of 395 nm. In all measurements, concentrations of IgG of 5 μM (i.e., 0.75 mg/ml) and ANS of 500 μM in PBS buffer, pH 7.4, were used. The fluorescence measurements were performed with a Varian Cary Eclipse fluorescence spectrophotometer (Varian Australia Pty Ltd) equipped with a Peltier multi‐cell holder.

The observed kinetic traces of ANS fluorescence were analyzed by two models:

(i) a one‐step irreversible reaction described by the following equation:

$$F_{\text{obs}}=F_{\max }\left(1-\exp (-k_{1}t)\right)$$ (1)

where F _obs and F _max correspond to the observed (measured) value and the maximum value (fitted parameter) of ANS fluorescence, respectively. The fitted parameter k ₁ corresponds to the rate constant of the irreversible step.

(ii) two consecutive irreversible first‐order steps, described by the following equation:32

$$F_{\text{obs}}=F_{\max }\left\{1+\frac{1}{k_1-k_2}\left[k_2\exp (-k_{1}t)-k_1\exp (-k_{2}t)\right]\right\}$$ (2)

where F _obs and F _max are defined as for Eq. (1), and the parameters k ₁ and k ₂ correspond to the rate constants of the consecutive steps. It needs to be stressed that the order of the steps cannot be distinguished solely on the basis of the measured rate constants.32 In this case, the final rate constant k of two consecutive irreversible steps was calculated from the following equation:

$$\frac{1}{k}=\frac{1}{k_1}+\frac{1}{k_2},\hspace{0.17em}\mathrm{i}.\mathrm{e}.\hspace{0.17em}k=\frac{k_1{k}_2}{k_1+k_2}$$ (3)

Differential scanning calorimetry

Differential scanning calorimetry (DSC) measurements were performed using a VP‐Capillary DSC system (Microcal Inc., acquired by Malvern Instruments Ltd.). Antibody concentrations were adjusted to 0.75 mg/ml prior to the measurement unless stated otherwise. The corresponding buffer, PBS at pH 7.4, was used as a reference. The samples were heated from 20°C to 90°C at the stated rates after an initial eight min of equilibration at 20°C. The filtering period, i.e., the time period during in which the signal is collected, was changed as a function of the scan rate, i.e., 50, 25, 10, and 8 s for the scan rates of 0.25, 0.5, 1.0, and 1.5 K/min, respectively. Thermograms were corrected by subtraction of the so‐called chemical baseline, i.e., the sigmoidal curve connecting the signal of excess heat capacity of the native and denatured states, and normalized to the molar concentration of the protein.

The experimental data of the excess heat capacity of IgG obtained from DSC were fitted by our recently derived equation13 which reflects the model of thermal denaturation of IgG consisting of three consecutive transitions (one reversible step followed by two irreversible transitions):

$$N\underset{}{\overset{K}{\rightleftarrows }}U\stackrel{k_2}{\to }D\stackrel{k_3}{\to }F$$ (4)

where N is the native state, U and D are intermediate states of thermal denaturation and F is the final (denatured) state of the IgG; K is the equilibrium constant of the first transition, k ₂ and k ₃ are the rate constants of the corresponding irreversible reactions. The excess heat capacity, being the parameter measured in the DSC experiments, is expressed by the general equation satisfying the model:

$$C_p^{\mathrm{e}\mathrm{x}\mathrm{c}\mathrm{e}\mathrm{s}\mathrm{s}}\left(T\right)=-{\Delta H}_1\left(\frac{d{n}_N}{dT}\right)+{\Delta H}_2\left(\frac{k_2{n}_U}{v}\right)+{\Delta H}_3\left(\frac{{\mathrm{k}}_3{n}_D}{v}\right)$$ (5)

where ΔH ₁, ΔH ₂, and ΔH ₃ are the molar enthalpy changes for the first, second and third steps, respectively. n _N, n _U and n _D are the molar fractions of corresponding states of the protein and ν is the scan rate in K/min. A detailed description of the derivation of Eq. (5) is provided in our previous work.13

DSC data were analyzed by numerical analysis in Microsoft Excel® by nonlinear regression using the Solver Add‐in. Regression statistics for the regression coefficient (the standard deviations of the regression coefficients and R ²), obtained by using the Solver Add‐in, were calculated by utilizing the Solvstat Add‐in.

Results

For the analysis of the kinetic stability of IgG with our previously derived mathematical model13 we chose the well‐characterized antibody IgG6B3, a human IgG1, that contains a heavy chain of subclass V_H6 and a light chain of the V_λ3 family.29, 30

Thermal denaturation of IgG in different formulations

For analysis of the thermal denaturation behavior of a given protein, one should examine the following three parameters of its thermal transition: (i) reversibility, (ii) scan rate dependence, and (iii) concentration dependence. Previously, we showed that the thermal denaturation of IgG6B3 is scan rate dependent and becomes irreversible upon heating to temperatures above ∼70°C in PBS buffer.13, 30 This is also valid for the thermal transition of IgG6B3 under all studied conditions in this work (Supporting Information Fig. S1A).

In our previous study, we showed the independence of the thermal transition for protein concentrations from 0.25 to 2.5 mg/ml.13 Here, we expanded this range to a concentration of 15 mg/ml, being more relevant for pharmaceutical formulations (Fig. 1). The combined results from our previous and the present work thus clearly show that even a 60‐fold increase in IgG6B3 concentration and an absolute concentration of 15 mg/ml had no apparent effect on the thermal transitions measured by DSC. This unequivocal lack of dependence of the thermal transitions on protein concentration indicates that aggregation is not part of the rate‐limiting, irreversible reaction,33, 34 but must be a subsequent step following the irreversible first‐order reactions, with its own temperature dependence.

Figure 1.

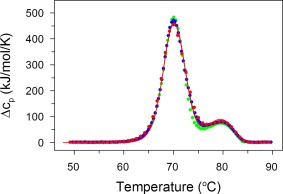
DSC reveals that thermal transitions are concentration‐independent: IgG6B3 at concentrations of 0.5 mg/ml (green), 5.0 (blue), and 15.0 mg/ml (red) in PBS pH 7.4 were recorded at a scan rate of 0.5 K/min. Experimental data (every forth point) are shown as symbols and the fits according to the kinetic model described by Eq. (4) are shown as solid lines

Subsequently, we monitored IgG6B3 thermal denaturation at non‐denaturing urea concentrations to determine the thermodynamic and kinetic parameters of the individual kinetic steps over an extended range of temperatures. The underlying idea is that urea, as an intensively characterized chaotropic agent, affects the conformational stability of proteins in a qualitatively predictive manner and that recorded parameters thus can be compared with a reference set of proteins.35

Thermal denaturation of IgG6B3 measured by DSC consists of two apparent peaks with transition temperatures of 71.3°C and 81.1°C, respectively (at a scan rate of 1 K/min). As we showed previously, the first peak consists of an overlay of two transitions—the reversible thermal transition of the C_H2 domain followed by the irreversible unfolding of the Fab domain [Eq. (4)].13 Figure 2A shows that increasing urea concentrations led to the shift of both apparent thermal transitions to lower temperatures and at the same time to a decrease in the calorimetric enthalpy of the transitions.

Figure 2.

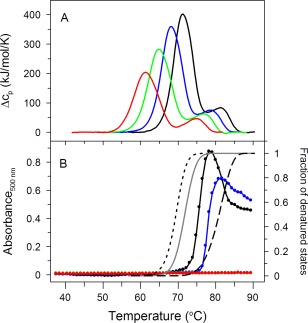
(A) Effect of increasing urea concentration (0 M—black solid line, 1 M—blue solid line, 2 M—green solid line, and 3 M—red solid line) on DSC transitions, and (B) light scattering of IgG6B3 as a function of temperature. The addition of urea follows the same color code as in (A). Addition of urea can be seen to delay or completely prevent aggregation. Using the model of eq. 4 (derived in Sedlak et al.13) the molar fraction of either the U + D+F states (dotted black line), the D + F states (gray solid line), or just the F state (dashed black line) as a function of temperatures are also shown. No correlation is apparent between the onset of IgG6B3 aggregation (black line with symbols, absence of urea) and the temperature dependence of the molar fraction of any particular domain. DSC scans as well as light scattering experiments were performed with an IgG6B3 concentration of 0.75 mg/ml (5 μM) in PBS at pH 7.4 and a scan rate of 1.0 K/min

Aggregation rates at high temperatures show no apparent correlation with the irreversible steps

The absence of a dependence of IgG thermal transitions on protein concentration turned our interest toward the direct monitoring of the aggregation kinetics as a function of temperature. Therefore, aggregation of the IgG was monitored by light scattering using absorbance spectroscopy at 500 nm under several conditions (Fig. 2B). The aggregation of IgG6B3 is concentration‐dependent; when the IgG6B3 concentration increased from 0.2 mg/ml to 2.0 mg/ml, the temperature at which the aggregation starts, decreased by ∼5°C in a concentration‐dependent manner (Supporting Information Fig. S2). In the absence of urea, IgG6B3 aggregation started at a temperature of ∼74°C, which did not correlate with any apparent transition observed in DSC (see black line in Fig. 2B). Interestingly, the presence of urea in the buffer (chaotropic formulation) efficiently suppressed the aggregation of thermally‐denatured IgG6B3 (Fig. 2B). While in the presence of 1 M urea aggregation is shifted to higher temperature (∼ 78°C, blue line), even higher urea concentrations caused the temperature‐induced aggregation to disappear altogether and to not be detectable anymore (green and red line in Fig. 2B), indicating that urea interferes with the aggregation step itself. In contrast, urea facilitates the reversible and irreversible first‐order denaturation steps (Fig. 2A).

Taken together, there does not seem to be a simple correlation between the molar fraction of any of the denaturation intermediates (U, D, and F) as a function of temperature and the onset of aggregation in the absence of urea (see gray and dashed lines in Fig 2B), and aggregation is a separate process, even if it may use these intermediates as starting points.

The IgG native state is unaffected by the different formulations used in this study

To analyze whether the non‐denaturing urea concentrations used here affect the native state of IgG6B3 and hence if the used conditions allow the usage of the three‐step model, both the ellipticity in the far‐UV spectral region measured by a CD spectrometer, the intrinsic tryptophan fluorescence as well as the fluorescence of the dye 8‐anilinonaphthalene‐1‐sulfonate (ANS) were investigated (Supporting Information Fig. S3). The ellipticity in the far‐UV region sensitively reflects changes in the secondary structure of proteins,36 while the intrinsic tryptophan fluorescence sensitively reacts to the polarity and dynamics of the tryptophan environment.37 Finally, ANS binds to exposed hydrophobic patches or cavities which normally should be hidden within the protein core.38 The spectral properties of IgG6B3, remaining basically identical in the absence and presence of up to 3 M urea, strongly indicate that the native state of IgG6B3 is nearly unaffected by urea at the concentrations used in our experiments (Supporting Information Fig. S3). This allowed us to apply the proposed model for thermal denaturation of IgG6B3 under all the conditions studied.

IgG kinetic stability deduced from the analysis of the three‐step model over an extended temperature range

The absence of a concentration dependence in the rate‐limiting steps of IgG thermal unfolding as well as the lack of any significant effect of urea on the native conformation substantiate the application of our three‐step model, which involves only first‐order reactions. Figure 3 summarizes the parameters characterizing the individual steps as defined in the model of IgG thermal denaturation [Eq. (4)] obtained from fitting the experimental data by the function expressed in Eq. (5). These values were obtained as the average of the fitted parameters (with corresponding standard deviations) at four different scan rates (Supporting Information Table S2). The parameters characterizing the first (reversible) transition (i.e., the transition temperature T _trs and the calorimetric enthalpy ΔH _cal1) both decrease in a linear fashion with increasing urea concentrations (Fig. 3A). This is in agreement with the generally observed effects of non‐denaturing urea concentrations on the thermal transitions of proteins.39 The linear dependence is broken at higher urea concentrations (> 3 M) (data not shown), indicating a significant effect of such high concentrations of urea on the native state of IgG, again as expected from the measurements of urea‐induced unfolding at room temperature. In fact, from the slope of the linear dependence of ΔH _cal1 vs. T _trs, one can obtain the value of the heat capacity, Δc _p, where the increase of ΔH _cal1 is due to an increased exposure of hydrophobic residues upon thermal denaturation. In our case, we calculated a Δc _p value of 17.5 ± 3.2 kJ/mol/K (correlation coefficient R = 0.9678) (Fig. 3A, inset).

Figure 3.

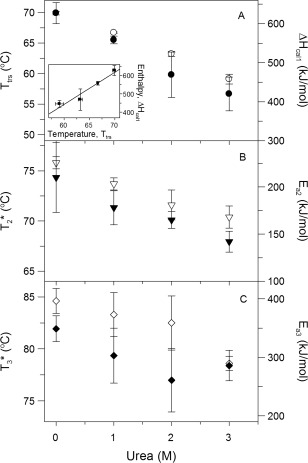
Effect of urea concentration (0, 1, 2, and 3 M) on DSC transition temperatures (black symbols) and enthalpies (white symbols) of IgG6B3, according to the kinetic model described by Eq. (4). In panel A, the inset shows the calorimetric enthalpy of the first (reversible) transition as a function of transition temperature at the studied urea concentration. The line represents a linear fit (correlation coefficient R = 0.9678). DSC scans were performed with an IgG6B3 concentration of 0.75 mg/ml (5 μM) in PBS pH 7.4 and a scan rate of 1.0 K/min

The parameters characterizing the irreversible steps are the activation energy E _a and the temperature T ^*, i.e., the temperature at which the rate constant k equals 1 min⁻¹ (ref. 33). These two parameters define the rate constant k in the following way:

$$k({\min }^{-1})=\exp \left[-\frac{E_a}{R}\left(\frac{1}{T}-\frac{1}{T^{\ast }}\right)\right]$$ (6)

where R is the gas constant with R = 8.314 J/mol/K.

The parameters for the first irreversible step, as shown in Eq. (4), depend on the urea concentration in a linear way (Fig. 3B). The analysis of these dependences indicates that both the enthalpic part (E _a2) as well as the entropic part ( $\frac{E_{a2}}{T^{\ast }}$) of the first irreversible step decrease with higher urea concentration.

The parameters characterizing the second irreversible (final) step in Eq. (4) also depend on the urea concentration in an analogous way as the parameters of the preceding irreversible step. The parameters E _a3 and $T_3^{\ast }$ also decrease with increasing urea concentration in a linear way in the range 0–2 M, however this linearity breaks at around 3 M urea (Fig. 3C).

Binding of ANS as an orthogonal method for monitoring partially unfolded states

To obtain the IgG kinetics for the irreversible steps by an independent approach, we employed an orthogonal, fluorescence‐based method using ANS as an extrinsic fluorescence probe.

ANS fluorescence significantly depends on the polarity of its environment; the very weak ANS fluorescence in polar solvents such as water significantly increases and shifts to shorter wavelengths in hydrophobic environments.31, 38, 40 This feature of ANS fluorescence enables the detection of partially unfolded conformational states with exposed hydrophobic patches or cavities. Interestingly, ANS has a low affinity to extended unfolded states, pointing towards a certain residual amount of protein tertiary structure being required for protein‐ANS interactions.38

Previous findings from isothermal denaturation of IgG6B3 indicated that ANS binds only to the Fab domain in the process of chemical denaturant‐induced unfolding of IgG.13 Based on this observation, we applied ANS now as a probe for monitoring temperature‐induced unfolding of the Fab domain, i.e., the first irreversible step of the IgG thermal denaturation as shown in Eq. (4). To allow an objective analysis, we ruled out that ANS binding to the protein affects the process of the thermal denaturation of IgG as measured by DSC, since the binding of ANS and its analogs had been shown to stabilize intermediate states for some other proteins.41, 42 DSC scans of IgG in the presence and in the absence of ANS showed that the effect of ANS on the thermal denaturation of IgG is insignificant (Supporting Information Fig. S4). In fact, the apparent transition temperatures of both peaks were nearly unaffected—the analysis of the individual steps of IgG transition showed that the transition temperature of the first step was only slightly shifted to lower temperatures by ∼1°C (Supporting Information Fig. S4 and Table S1).

Kinetics of ANS binding to IgG

The ability of ANS to solely bind to the Fab domains of IgG6B3 provided us with the unique opportunity to experimentally determine the rate constant of the second step, i.e., the first irreversible reaction in Eq. (4). Figure 4 shows the time dependence of the ANS fluorescence in the temperature range of the first peak (i.e., 59.5–74.5°C) corresponding to the first (reversible) and the second (irreversible) transitions [Eq. (4)] in the model of the thermal denaturation of IgG. The presence of a lag phase indicated that the kinetics of the ANS fluorescence is more complex than one would expect from a first order irreversible step, and thus cannot be described by a single exponential function. We could rule out effects of slow temperature equilibration, and in fact, similar ANS kinetics had been observed previously.43 Such a lag phase is generally typical for two consecutive reactions; therefore, we used either Eq. (1) or (2) for the analysis of the measured kinetics. In fact, the experimental data of the kinetics of the ANS fluorescence are very well fitted by these equations (see solid lines in Fig. 4). Interestingly, the observed kinetics at higher temperatures are better fitted by Eq. (2) while for the kinetics at lower temperatures Eq. (1) performed superior (Supporting Information Table S3), however, it is also possible to use one single equation [Eq. (1) or (2)] for the whole temperature range without significant effects on the derived rate constants as shown in Figure 5. An important observation from the ANS fluorescence kinetics at various temperatures is that its amplitude significantly depends on the temperature. When plotting the amplitudes of ANS fluorescence versus temperature, this curve is seen to correlate with the temperature dependence of the molar fraction of the combined U and D states, derived from Eq. (5) (Supporting Information Fig. S5), suggesting that the ANS amplitude monitors indeed their population.

Figure 4.

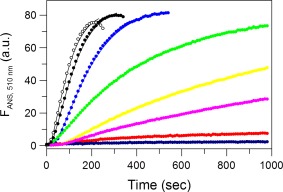
Kinetics of ANS binding to IgG6B3 at 0 M urea monitored by ANS fluorescence at 510 nm (excitation at 395 nm) and different temperatures: 74.5°C (white), 72.3°C (black), 70.0°C (blue), 67.0°C (green), 65.3°C (yellow), 64.0°C (magenta), 61.4°C (red), and 59.5°C (dark blue). Experimental data are shown as symbols and the fits according to Eq. (1) (single pseudo‐first‐order reaction) (59.5°C‐61.4°C) or Eq. (2) (consecutive pseudo‐first‐order reactions) (64.0°C‐74.5°C) are shown as solid lines. The protein and ANS concentrations were 5 μM and 500 μM, respectively. The buffer was PBS at pH 7.4.

Figure 5.

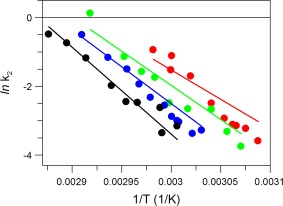
Dependence of the rate constants of ANS binding to IgG as a function of temperature (shown as symbols) at different urea concentrations (indicated by color): 0 M (black), 1 M (blue), 2 M (green), and 3 M (red). Note that the lines are not the fit to the shown experimental data but depict the k ₂ values derived from independent DSC measurements as a function of temperature, obtained from Eq. (5), describing the first irreversible step in IgG thermal unfolding in Eq. (4). The buffer was PBS at pH 7.4.

Comparison of the results obtained by the ANS fluorescence assay, DSC profiles and predictions from the three‐step model

A comparison of the DSC scans with the temperature dependence of ANS fluorescence shows consistency between the temperatures of the maxima of the excess heat capacity (corresponding to apparent temperature maxima of the first peaks) and that of the temperature dependence of ANS fluorescence (Supporting Information Fig. S6). The good correlation of the temperature dependence of the combined molar fractions of both the U and D states, calculated in Eq. (5) (Supporting Information Fig. S5) from our DSC model [Eq. (4)], with the ANS fluorescence indicates that ANS binds both to the state U and state D during IgG6B3 thermal denaturation. This binding to state D is in agreement with the conclusion obtained from isothermal denaturations of IgG6B3. However, in its thermal denaturation, ANS apparently also binds to the thermally denatured C_H2 domain, corresponding to the U state.13

A comparison of the rate constants for ANS binding to IgG6B3 at different temperatures (obtained by using Eqs. (1), (2), (3); symbols in Fig. 5) and the rate constant of the first irreversible step in the thermal denaturation of IgG6B3 (obtained from Eq. (4); lines in Fig. 5) indicates a good agreement between the values obtained from these orthogonal methods.

Discussion

IgGs are multi‐domain glycosylated proteins with a rather complex structure, consisting of twelve domains that form pair‐wise arranged “super‐domains”: two homodimeric domains C_H2 and C_H3 forming the F_c fragment of IgGs, and four heterodimeric domains that are organized into two identical Fab fragments. Moreover, the C_H2 domains are glycosylated, which adds an additional layer of complexity to the analysis of structural properties of IgGs. This structural composition is well‐reflected in the thermal denaturation of IgGs. Typically, this denaturation consists of three apparent transitions: one reversible transition of the C_H2 domain and two consecutive irreversible transitions, reflecting the denaturation of the C_H3 and Fab domains, respectively. The order of these transitions is usually C_H2 < Fab < C_H3 (in agreement with conclusions of the work of Ionescu and coworkers8) and can be schematically described by Eq. (4). In highly engineered antibodies, the stability of the Fab can reach that of C_H3. This model is mathematically described by the equations derived in our previous work.13 In the present work, we analyzed in detail particularly the first two transitions, in an effort to address two critical questions regarding our model: (i) whether it correctly describes the observed thermal transitions and can thus be cross‐validated by other methods, and (ii) whether it is possible from parameters obtained by DSC measurements to predict the shelf‐life of IgG and/or rank stabilities of different IgGs. To address these issues, we investigated the properties of a model IgG called 6B3 in a gradually destabilizing environment created by increasing concentrations of urea, and we used orthogonal methods to observe partial unfolding.

Validity of the three‐step model

The first question, regarding the correctness of our model, was addressed by two different approaches. In the case of the reversible transition of the C_H2 domain of IgG6B3, the obtained parameters (Fig. 3A) were compared to corresponding parameters of reversible thermal transitions of (mostly) single domain proteins, summarized in the work of Robertson and Murphy.35 The linear dependence of ΔH _cal1 vs. T _trs at different urea concentrations enabled us to determine the Δc_p value from the slope, Δc _p = (δΔH _cal1/δT _trs)_p, which equals 17.5 ± 3.2 kJ/mol/K. This value is somewhat higher than the 13.1 kJ/mol/K obtained from a regression analysis of Δc_p vs. the size of proteins (represented by the number of residues) obtained from the aforementioned dataset of 49 different proteins.35 The difference between these two Δc_p values might result from the fact that (i) the C_H2 domain is glycosylated, while the protein dataset did not contain any glycosylated protein, and that (ii) the C_H2 domain is localized between two other domains in the intact IgG, while the previously analyzed dataset contained only individual, mono‐domain proteins which were not part of any larger, multi‐domain proteins or complexes. In fact, one can hypothesize that glycosylation protects hydrophobic residues in the native state from their interaction with polar solvent and, on the other hand, increases the solubility and thus exposure of hydrophobic residues in the thermally denatured state of C_H2 in comparison with its non‐glycosylated form and thus contributes to the increased values of Δc_p of this domain. Nonetheless, the explanation how the localization of C_H2 domain within the context of the full‐length IgG affects the value of Δc _p will require further investigations. From the linearity of a plot of ΔH _cal1 vs. T _trs and the obtained value of Δc _p, comparable with values of proteins with similar size, one may nonetheless hypothesize that our model appropriately describes the parameters of the reversible step of thermal denaturation of an IgG.

The correctness of the parameters derived for the second step in Eq. (4), (i.e., the first irreversible step) was concluded from a comparison with the rate constants of this step obtained by an orthogonal approach, i.e., calculated independently from the DSC profile and from the kinetics of ANS binding to the IgG at denaturing temperatures (Fig. 5).

The agreement of the parameters describing the first (reversible) transition with parameters obtained from a dataset for proteins of similar size,35 consistency of rate constants of the second (irreversible) transition obtained by two orthogonal methods—even though there is no suitable assay to unequivocally assess the rate constant of the third step—suggest that our mathematical model correctly describes all individual transitions in the thermal denaturation of the studied IgG.

Prediction of IgG denaturation at low temperatures from accelerated stability studies

The correct determination of the kinetics of the first irreversible step in the multistep reaction scheme of protein thermal denaturation is critical for predicting its kinetic conformational stability, also referred to as the shelf‐life. In fact, at least theoretically, the shelf‐life (or half‐life) of a reversibly unfolding protein is unlimited, since the removal of denaturing conditions should result in the recovery of the native state. However, the situation changes if the reversible transition is followed by an additional irreversible transition, as in the case for IgGs [Eq. (4)]. In such cases, the apparent rate constant describing the decay of the native state in the first two steps [as shown in Eq. (4)] is k_2,app and can be expressed (under the assumption of a fast pre‐equilibrium) as: $k_{2,\text{app}}=k_2\frac{K}{1+K}$, where K is the equilibrium constant of the first step and k₂ is the rate constant of the second step. The ratio $\frac{K}{1+K}$ thus expresses the molar fraction of the U state, in equilibrium with the N state, at any given temperature. The agreement of the values of the rate constants obtained by an independent experimental method (ANS fluorescence, points in Fig. 5) with those calculated from our model of DSC data (lines in Fig. 5) indicates that the formation of the U state is too fast to be detected by our technique, but that conversely the assumption of a fast pre‐equilibrium is justified. In our experiments, we do not directly detect the amount of native state of IgG, and therefore we cannot extract the factor $\frac{K}{1+K}$ from the rate constant of the native state decay kinetics. Nonetheless, the effect of this factor is apparent in the kinetics of ANS fluorescence with decreasing temperature (Fig. 4), since the molar fraction of the U state determines the amplitude of the ANS fluorescence. As we cannot attribute ANS fluorescence to the individual states, the combined molar fraction of the U and D states (state F does not bind ANS) determines the measured amplitude of the ANS fluorescence at a given temperature, as shown in Supporting Information Figure S5.

A plot of ln(k_2,app) vs. temperature clearly shows how the multistate denaturation affects the temperature dependence of the kinetic conformational stability of the IgG (Fig. 6). While the values of k₂ predict the overall kinetic conformational stability of IgG very well at high denaturation temperatures (>70°C), the curved nature of the plot and the long extrapolation will make a prediction of kinetic stability at low temperature (i.e., the typical accelerated stability assumption) from measurements at high temperatures very uncertain (Fig. 6). However, we believe that the comparison of k_2,app values can still be a suitable parameter for ranking stabilities of various IgGs that differ either structurally or in formulation (manuscript in preparation).

Figure 6.

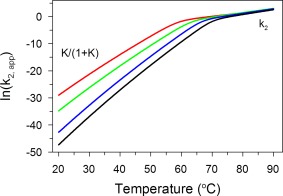
Temperature dependence of $\ln \left(k_{2,\text{app}}\right)$, i.e., $\ln \left(k_2\frac{K}{1+K}\right)$, at increasing urea concentrations: 0 M (black), 1 M (blue), 2 M (green), and 3 M (red). The values of the rate constants k ₂ and equilibrium constants K at different temperatures were obtained from the model described in Eqs. (4) and (5). The plot of $\ln \left(k_{2,\text{app}}\right)$ vs. temperature is nonlinear with a break point at the transition temperature, T _trs, of the reversible transition. At lower temperatures, the plot is ruled by the temperature dependence of $\frac{K}{1+K}$, while at higher temperatures by the temperature dependence of k ₂.

Conclusions

The presented model provides a practical tool for assessing the kinetic conformational stability and/or ranking the conformational stability of different variants or formulations of IgGs, or in general, any proteins obeying our multistate model of thermal denaturation. However, prediction of colloidal stability is a more complex task since the models need to take into account, next to modeling the conformational stability, also the protein concentration, the absolute rate of aggregate formation, possibly even parallel processes for different aggregates, and their individual temperature dependences. Even though aggregation is a step subsequent to irreversible denaturation, the pharmaceutically relevant shelf life will indeed be influenced by aggregation, since the loss of a few percent of active drug may be tolerable, while the formation of aggregates is clearly not. Nonetheless, we believe that our model, which enables one to calculate the temperature dependence of molar fractions of individual intermediates in the process of thermal denaturation, may be of great importance and a foundation for future models attempting to address colloidal stability of proteins, particularly of IgGs.28

Supporting information

Supporting Information 1