Abstract
The helical flagella that are attached to the cell body of bacteria such as Escherichia coli and Salmonella typhimurium allow the cell to swim in a fluid environment. These flagella are capable of polymorphic transformation in that they take on various helical shapes that differ in helical pitch, radius, and chirality. We present a mathematical model of a single flagellum described by Kirchhoff rod theory that is immersed in a fluid governed by Stokes equations. We perform numerical simulations to demonstrate two mechanisms by which polymorphic transformation can occur, as observed in experiments. First, we consider a flagellar filament attached to a rotary motor in which transformations are triggered by a reversal of the direction of motor rotation [L. Turner et al., J. Bacteriol. 182, 2793 (2000)]. We then consider a filament that is fixed on one end and immersed in an external fluid flow [H. Hotani, J. Mol. Biol. 156, 791 (1982)]. The detailed dynamics of the helical flagellum interacting with a viscous fluid is discussed and comparisons with experimental and theoretical results are provided.
I. INTRODUCTION
Single-celled organisms employ a wide range of techniques to swim and maneuver in an aqueous environment [1–4]. Of the motile organisms, peritrichous bacteria such as Escherichia coli and Salmonella typhimurium utilize rotating flagellar filaments, each of which is connected to a motor through a short flexible hook as illustrated in Fig. 1 [5,6]. The swimming modes of E. coli or S. typhimurium are characterized by two phases; a run and a tumble [7]. In the run phase, all of the flagellar motors on the cell spin counterclockwise (CCW), during which each flagellum is in a left-handed helical shape. The hydrodynamic interactions between the flagella will cause the filaments to bundle together to form a superflagellum, which propels the bacterium forward. In the tumble phase, one or more flagellar motors will reverse its motor rotation to spin clockwise (CW) and initiate a transformation that changes the chirality of the helical flagella from left-handed to right-handed. Furthermore, the helical pitch and radius of the flagella changes in sequence from a normal left-handed state to a semi-coiled state (right-handed), then finally to a curly-1 state (right-handed) before going back to the normal form [6]. The ability for the flagella to take on these various states is what is referred to as polymorphism. The right-handed flagella will leave the bundle and cause the cell to change its course of swimming. Eventually, all motors return to CCW rotation, and the cell runs again at full speed. Alternating runs and tumbles are essential in bacterial chemotaxis and allow the cell to move in a favorable direction in response to a spatial gradient of a chemical attractant [6,8].
FIG. 1.
A schematic showing the physiology of an E. coli cell. The flagellar filaments are randomly distributed along the cell body. Each filament is attached to a rotary motor via a flexible hook.
Bistable flagella exhibit coexistence of left- and right-handed helical forms as polymorphic transition is progressed along the filament. Pijper [9] observed polymorphic forms of bacterial flagella in his experiments. Polymorphism was then studied by Asakura [10], where he developed a structural model based on flagellin subunits. Later, Calladine [11] proposed a geometric model with 12 helical polymorphic forms of the bacterial flagellum based on the state of 11 protofilaments. Turner et al. [6] visualized the motion of individual flagella in real time in which E. coli cells are fluorescently labeled, and revealed a sequence of polymorphic transformations initiated by a motor reversal. It has been also reported that perturbations in environmental conditions trigger transformations from one polymorphic form to another. Changes in the pH or salt concentration [12,13] of the solution and the addition of alcohols [14] or certain sugars [15] cause polymorphic transformations. Polymorphic transformations of flagella are also observed in the temperature change in the solution [16]. Applying mechanical forces or torques to the filament is another way to generate transitions between different helical forms [17,18].
Elastic helical flagella are often modeled using Kirchhoff rod theory because the flagellum is a long (~20 µm) but thin (~20 nm) structure. Goldstein et al. [19] introduced a Kirchhoff free-energy functional with a double-well potential to permit two stable helical configurations. Darnton and Berg [20] used Kirchhoff rod theory to estimate the bending rigidity of a flagellum and the required force to transition between polymorphic states by fitting the model to force-extension data. This work was then extended by Vogel and Stark [21] who calculated an upper bound on the ratio of torsional and bending rigidities using a nonsmooth double-well energy potential. Later, they showed that a motor-induced torque can alter the energy state of a flagellum of a monotrichous bacterium and therefore initiate a polymorphic transformation [22]. Recently, Adhyapak and Stark [23] demonstrated that the ground-state energies of a Kirchhoff free-energy function influence the dynamics of a rotating flagellum undergoing polymorphic transformation. There are other approaches to model polymorphic transformations of an elastic filament besides Kirchhoff rod theory, such as the work by Gebremichael et al. [24], who described the filament using a network of springs coupled to a smooth-particle hydrodynamic model. Moreover, their model includes the 11-protofilament structure of a real flagellum. They investigated the flow field and propulsive dynamics generated by a rotating flagellum and the influence of the aqueous environment on filament deformations. However, the smooth-particle hydrodynamic model utilizes an artificial viscosity and thus direct comparisons to theoretical and experimental work cannot be made. Wada and Netz [25] discretized the elastic filament with a sequence of spherical beads combined with a Kirchhoff-type free energy. Each bead has a “spin” variable to keep track of its local polymorphic state. They performed Monte Carlo simulations showing polymorphic transformations due to an external force pulling on the filament.
To incorporate hydrodynamic effects in cellular locomotion, resistive-force theory has been used to approximate the local drag on a short segment of the filament due to the fluid [26,27]. However, this theory does not accurately resolve the fluid flow resulting from the flagellum [28,29]. For a more accurate description of the fluid dynamics, slender-body theory [30–33] employs a superposition of stokeslets along the centerline of a rigid filament. A similar approach is to use regularized stokeslets [34,35], which yields a similar result to slender-body theory for rigid helices [36] but can be extended to elastic filaments [34]. Recent studies have used full three-dimensional numerical computations of the Navier–Stokes equations in an immersed boundary framework to capture the two-way fluid-structure interaction between the filament and the aqueous environment [37,38]. In particular, Lim and Peskin [38] incorporated the Kirchhoff rod theory to describe the flagellar dynamics of a pair of monostable helical filaments interacting with the surrounding viscous fluid. Large-scale physical models have also been developed to study hydrodynamic interactions of rotating helices. Kim et al. [39,40] constructed a macroscopic model demonstrating that flagellar bundling depends on the direction of motor rotation and the chirality of the helical filaments. More recently, Rodenborn et al. [36] used rigid metal helices attached to a stepper motor to test various hydrodynamic theories.
In this paper, we present a fluid-structure interaction model that describes a single helical flagellum capable of polymorphic transformations in a viscous fluid. The elastic energy functional for the helical flagellum includes a double-well potential in the twist energy that allows two stable helical configurations with opposite chirality [19]. The structural properties of the flagellum are described by the Kirchhoff rod theory and the surrounding fluid is governed by the Stokes equations. In this work we focus on two mechanisms by which a bacterial flagellum undergoes transformation. The first mechanism to switch helical shapes is by reversing the motor rotation, which has been observed in experiments [6,18] and occurs during the tumble swimming phase. The other means of polymorphic transformation that we consider is motivated by Hotani’s experiments [17], in which a filament anchored at one end is subject to a viscous fluid flow. Hotani observed that a sufficiently high flow velocity using a methylcellulose solution can produce periodic transformations in a S. typhimurium filament. Goldstein et al. [19] and Coombs et al. [41] examined the dynamics in Hotani’s experiments and developed a theory that relates the transformation front speed to the flow velocity and the geometric properties of the helical filament. Unlike their analysis, which simplifies the hydrodynamic forces acting on the filament, our model incorporates fluid-structure interaction. The detailed flagellar dynamics in a viscous fluid will be discussed in both mechanisms. Our simulation results will be compared to experimental and theoretical data, which may provide physical insight into the mechanisms of polymorphic transformations.
II. MATHEMATICAL MODEL
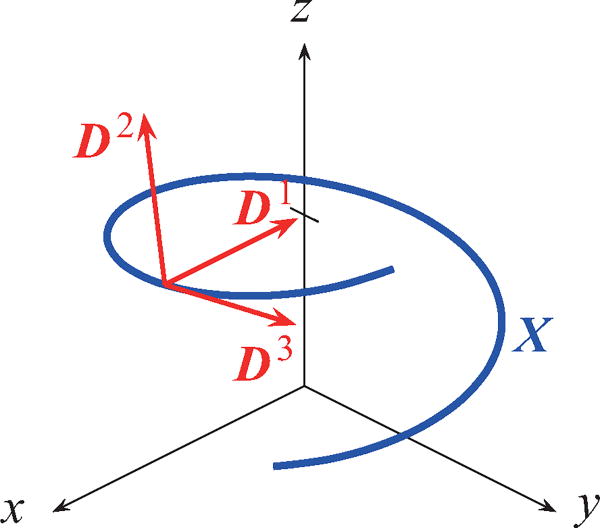
We consider a model of a single helical flagellum immersed in a viscous fluid. The flagellar filament is described by Kirchhoff rod theory in which we assume that the flagellum is a long thin rod and that stresses are applied to each cross-section along the filament. The configuration and orientation of the flagellum is determined by its centerline X(s,t) and an orthonormal triad of direction vectors {D1(s,t), D2(s,t), D3(s,t)} (see Fig. 2), where s is a Lagrangian parameter with 0 ≤ s ≤ L, t is time, and L is the contour length of the filament. The shape of the flagellum at rest can be defined by the minimum of the energy functional [19,38]:
| (1) |
The first two energy terms are defined by
| (2) |
| (3) |
Here, a1 and a2 are bending moduli, a3 is the twist modulus, γ is the twist-gradient coefficient, and for any (i, j, k) that is a cyclic permutation of (1,2,3). The twist energy contains two stable states Ω3 = τ1 and Ω3 = τ2. The coefficient γ controls the width of the front as the filament transitions from one stable state to the other. The intrinsic curvature is defined by , and τ1 and τ2 determine the intrinsic twist (or torsion). The intrinsic strain vector (κ1, κ2, τ) (where τ = τ1 or τ = τ2) determines the equilibrium shape of the helical filament characterized by the radius R and pitch P,
| (4) |
| (5) |
In general, the values of κ1, κ2, τ1, and τ2 need not be constant along the flagellum. The last two terms in Eq. (1) describe how the filament resists shearing and stretching as follows:
| (6) |
| (7) |
where b1 and b2 are shear force constants and b3 is the stretch force constant.
FIG. 2.
An illustration of the parametrization of the flagellar filament. The centerline of the flagellum is parameterized by X(s,t) and its orientation is determined by an orthonormal triad {D1(s,t), D2(s,t), D3(s,t)}.
Let f (s,t) and n(s,t) be the applied force and moment densities acting on the rod, respectively, and let F(s,t) and N(s,t) be the internal force and moment transmitted across a section of the filament, respectively. The balance equations for the momentum and angular momentum are then described as follows:
| (8) |
| (9) |
where , and , and the constitutive relations are given by
| (10) |
| (11) |
| (12) |
| (13) |
where δ3i is the Kronecker δ. The above relations can be derived by taking variational derivatives of the energy functionals given by Eqs. (2) and (3) and Eqs. (6) and (7) (see Appendix in Ref. [42]).
Bacterial motility involves very small length scales (20 µm or smaller), so we assume that the fluid is governed by the Stokes equations [43,44]:
| (14) |
| (15) |
Here, u(x,t) is the fluid velocity, p(x,t) is the fluid pressure, μ is fluid viscosity, and g(x,t) is the body force in which the force and torque exerted by the rod are applied to the fluid through a smoothed δ function δc(x) with unbounded support
| (16) |
where
| (17) |
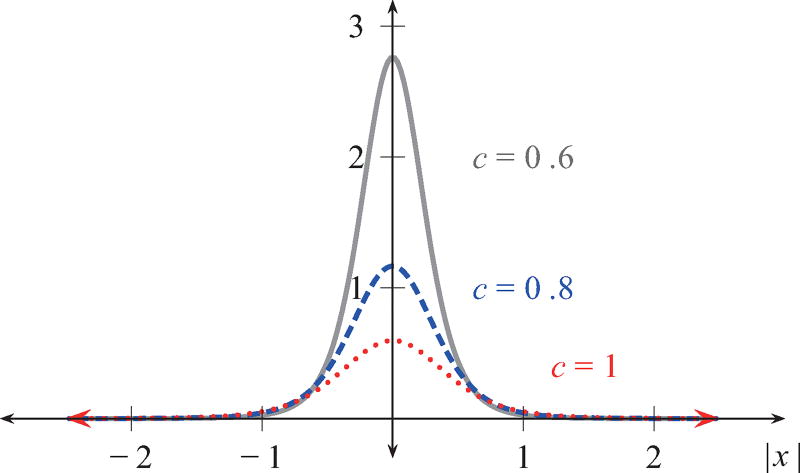
The regularization parameter c controls how the force is distributed on the fluid near the filament, as shown in Fig. 3 for various values of c. This function is a widely used choice for the regularized δ function [34,44,45] due to its simplicity in deriving an analytical formula for the fluid velocity, while satisfying ∫ δc(x) dx = 1 and the first moment condition ∫ x δc(x) dx = 0 [34]. In the limit c → 0, the Dirac δ function is recovered. The linear and angular velocities at the filament are computed using regularized stokeslets and rotlets [43,44], and the filament evolves according to
| (18) |
| (19) |
where is the angular fluid velocity.
FIG. 3.
The regularized δ function for various smoothing parameter values of c.
The numerical method can be summarized as follows. For a given configuration of the flagellum with M material points, we compute a point force fi and torque ni via Eqs. (8)–(13) at each material point s = iΔs, where is the filament grid size and i is the index for the material points. From the regularized point forces and point torques given in Eq. (16), we use the fundamental solutions to find the regularized stokeslet uS, rotlet uR, and dipole uD. The velocity and angular velocity can then be computed by
| (20) |
and
| (21) |
respectively, after which the new position of the flagellum and the orientation of the directional triad can be found by Eqs. (18) and (19). More details of the numerical method can be found in Ref. [44].
In our simulations, the filament at s = 0 is fixed in space and the flagellum is initialized with a Higdon helix [46],
| (22) |
where we choose k = 2 µm−2, so that the helical axis is aligned with the fixed point. Table I lists the physical and computational parameters used in our simulations. These values pertain to E. coli and S. typhimurium and are taken from the experimental literature [5–7] and other modeling studies of bacterial flagella [38].
TABLE I.
Physical and computational parameters.
| Parameter | Symbol | Value |
|---|---|---|
| Length | L | 6 µm |
| Shear modulus | b1, b2 | 8.0×10−1 gµm/s2 |
| Stretch modulus | b3 | 8.0×10−1 gµm/s2 |
| Bending modulus | a1, a2 | 3.5×10−3 gµm3/s2 |
| Twist modulus | a3 | 1.0×10−4 gµm5/s2 |
| Twist-gradient coefficient | γ | 1.0×10−3 g1/2 µm3/2/s |
| Intrinsic curvature | κ | 1.3055 µm−1 |
| Right-handed intrinsic twist | τ1 | −2.1472 µm−1 |
| Left-handed intrinsic twist | τ2 | 2.1472 µm−1 or 1.4310 µm−1 |
| Fluid viscosity | μ | 0.01×10−4 g/(µm · s) |
| Time step | Δt | 1.0×10−7 s |
| Filament grid size | Δs | 3.0×10−2 µm |
| Regularization parameter | c | 5Δs |
III. RESULTS AND DISCUSSION
A. Motor-driven polymorphic transformation of a single flagellum
We present numerical simulations of a single flagellum that is driven by a rotary motor. At s = 0, we fix the point on the filament to act as the motor that is capable of rotating CW or CCW with a prescribed angular frequency ω. The directional triad at s = 0 is initially set to
| (23) |
| (24) |
| (25) |
and rotates about the axis of the helical filament according to
| (26) |
for i = 1,2,3, where Q is a rotation matrix defined by
| (27) |
where t2 ≥ t1. The motor spins CCW if ω > 0 and CW if ω < 0. We then reverse the motor at a later time t0, so that
| (28) |
for t > t0 and i = 1,2,3. Although experiments show that a bacterial motor rotates CW and CCW asymmetrically [47], in this work we assume the motor rotates CW and CCW at the same rate for simplicity.
The filament is attached to the motor through a flexible hook, which is also governed by the Kirchhoff rod theory. The length of a hook for an E. coli bacterium ranges from 50 to 80 nm [48–50]. In our simulations, we simply choose the hook length to be 2Δs = 60 nm. The hook is known to be much more flexible than the filament, hence we take its bending modulus to be two orders of magnitude smaller than that of the filament. We assume that the hook is intrinsically straight (τ = 0, κ = 0); however, as the name suggests, the hook is actually highly curved [48,50]. We have performed simulations of a rotating flagellum with curved hooks (data not shown) and we found that the hook curvature has little effect on the dynamics of a motor-driven flagellum.
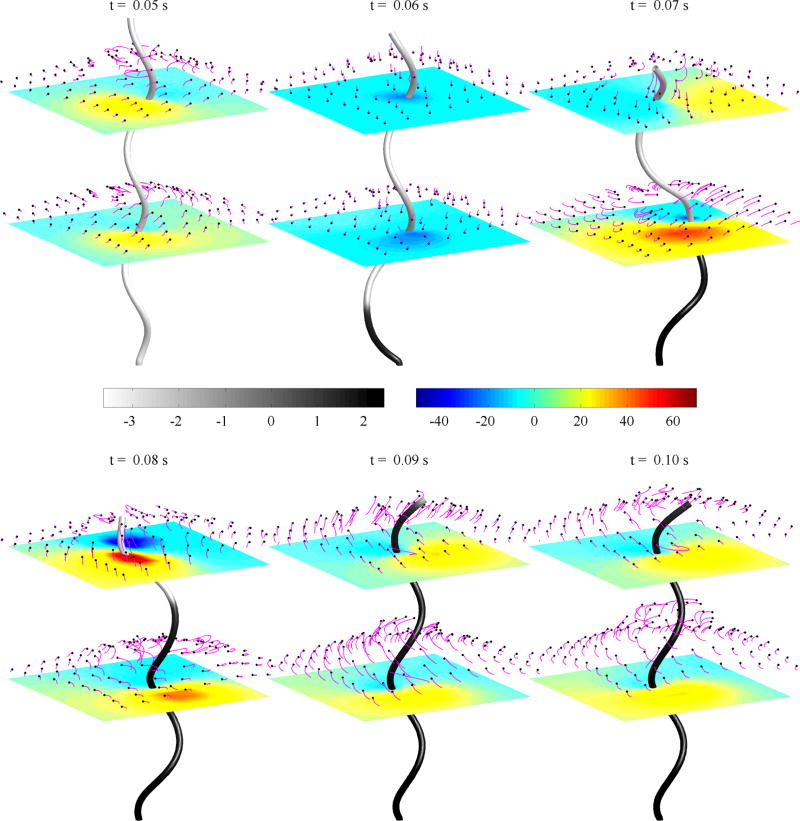
Figure 4 shows snapshots of a simulation of a motor-driven flagellum where a filament is undergoing a polymorphic transformation from the left-handed helix (gray) to the right-handed helix (black) as the motor reverses from CCW to CW (see Movie 1 in the Supplemental Material [51]). In each panel, the horizontal plane shows the vertical component of fluid velocity and the fluid is tracked by passive markers with their trajectories indicated using tails (magenta). Initially, the filament is a normal left-handed helix and the motor is rotating CCW at 100 Hz. The helix remains left-handed and the fluid flows upward away from the motor. At time t0 = 0.05 s, the motor switches to CW rotation but at the same frequency. The motor reversal initiates a change in chirality from left-handed to right, which forms a kink in the filament. This simulation shows qualitatively similar behavior to experiments in Ref. [6, Fig. 6], where they record a single rotating filament undergoing polymorphic transformation. The CW rotation causes the filament to drive fluid downward briefly as the kink appears from the motor. However, as the filament kink propagates toward the free end, the fluid flow is directed upwards again. This is consistent with previous studies of rotating flagella [38], in which the left-handed helix turning CCW and right-handed helix turning CW pump the fluid upward, and these are the only combinations that push the cell body forward. Hence, bistable flagella have the advantage of unbundling its superflagellum while continuing to drive fluid away from the cell body and swim forward. Although two monostable left-handed helices can unbundle when their motors rotate in different directions, the helices would push fluid in opposing directions [38].
FIG. 4.
Snapshots of a bistable helix with τ1 = −2.1472 µm−1 and τ2 = 1.4310 µm−1, rotating at 100 Hz. The shade of the rod indicates the torsion value where gray is negative (left-handed) and black is positive (right-handed). The horizontal planes show the vertical velocity of the fluid and the markers shown in magenta are passive fluid tracers.
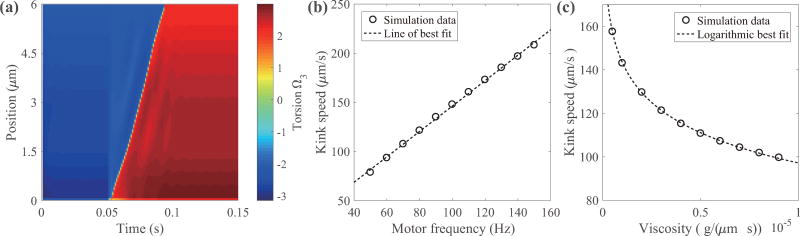
FIG. 6.
Torsion along the filament over time (left) and kink propagation speed plotted against motor rotation frequency (middle) and fluid viscosity (right). The intrinsic twist values are given as τ1 = −2.1472 µm−1 and τ2 = 2.1472 µm−1. The left panel illustrates how torsion changes over time at the rotating frequency of 100 Hz. The negative value (blue) of torsion corresponds to the left-handed helix and the positive value (red) corresponds to the right-handed helix. The kink speed is estimated as the slope of the curve where the filament is torsion-free. The middle and right panels show that the kink speed is approximately proportional to the motor frequency and decreases logarithmically with increasing fluid viscosity, respectively.
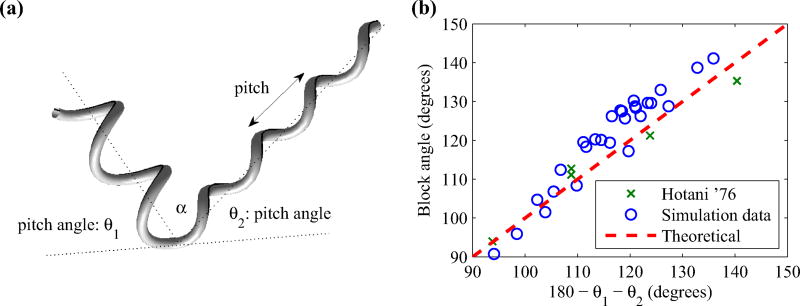
As the kink in the filament propagates from the motor to the free end, the helical axes of the left- and right-handed form a block angle at the point of transition as illustrated in Fig. 5(a). This block angle α is found theoretically [19] by
| (29) |
where θ1 and θ2 are the pitch angles of the helix that is formed near the point of transition. The pitch angle is estimated by [11]
| (30) |
where i = 1,2. Here R1 and P1 are the apparent pitch and radius of the helix below the kink and, similarly, R2 and P2 are the helical properties above the kink. Figure 5(b) plots the block angles that are estimated in our simulations along with experimental measurements by Hotani [52], which shows that our simulations are in good agreement with block angles observed in experiments.
FIG. 5.
A schematic diagram of the block angle α formed by a kink in the helical filament (left) and estimated block angles from our simulations for various helical shapes (right). Simulation results and experimental data from Hotani [52] are in good agreement.
Figure 6(a) illustrates how the torsion value along the filament changes over time when the motor rotates at the rate of 100 Hz and switches from CCW to CW at the time t = 0.05 s. The torsion is calculated by . The filament is initially left-handed (blue) and deforms into a right-handed (red) helix following the kink propagation. The sharp transition appearing in the figure corresponds to the location at which the filament is torsion-free and shows how fast the kink travels along the filament, from which we estimate the propagation speed of the kink as the slope of this torsion-free curve. For frequencies from 50 to 150 Hz, there is a clear linear relationship between the motor frequency and the kink propagation speed; see Fig. 6(b). An E. coli cell typically rotates its filaments around 100 Hz which results in a propagation speed of approximately 147.9 µm/s. At this frequency, two transformations complete in about 0.081 s for a 6 µm filament which is consistent with typical time scale of 0.1 s for the tumble phase [6]. In addition, we also investigate the kink speed as a function of fluid viscosity in the absence of the hook; see Fig. 6(c). As fluid viscosity increases, the kink speed decreases logarithmically. These simulations are done without a hook because the filament with a hook buckles at higher viscosity. We also examine the effect of the regularization parameter c on filament dynamics for c ∈ [2Δs,6Δs], and for the same range of rotation frequencies and fluid viscosities as in Fig. 6. We find that decreasing the value of c will slightly increase the kink propagation speed (see Appendix); however, the qualitative behavior of the filament does not change.
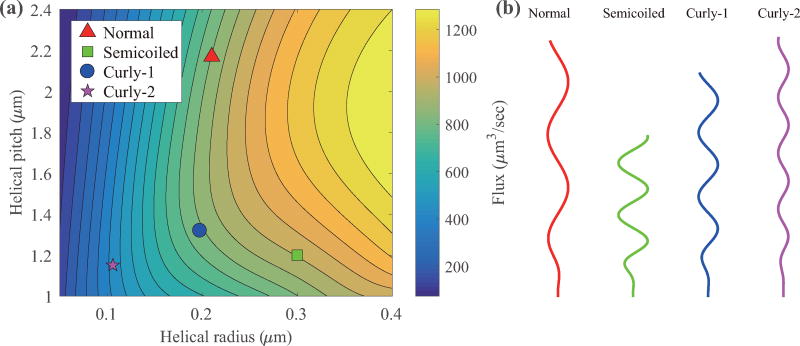
Next we perform simulations of a filament with various helical properties as it is known that flagella can attain various helical shapes [11]. In Fig. 7, we plot the mean fluid flux that is driven by a rotating helical filament at 100 Hz for various helical pitches and radii. The markers denote normal, semi-coiled, curly-1, and curly-2 helical shapes. The fluid flux depends more strongly on the helical radius than the helical pitch. Moreover, the semicoiled shape has the highest fluid flux among the four common states.
FIG. 7.
Mean fluid flux driven by a helical flagellum rotating at 100 Hz for various pitches and radii. The markers on the left panel denote the mean flux for four helical shapes commonly observed in nature [11,17], which are shown on the right.
B. Dynamics of a single flagellum in a steady viscous flow
In this section, we investigate the dynamics of a flagellum that is subject to a steady fluid flow. This is motivated by the experiments performed by Hotani [17], wherein a single flagellum derived from S. typhimurium attaches at one end to a glass surface and is subject to a viscous fluid flow. Note that this flagellum has no motor, and also has no hook. The steady flow generates a hydrodynamic torque on the filament and produces polymorphic transformations that propagate along the filament from the anchored end toward the free end. Hotani used a methylcellulose (400 cps) solution to apply a fluid flow and found that polymorphic transformation occurred when fluid speed was 6–8 µm/s.
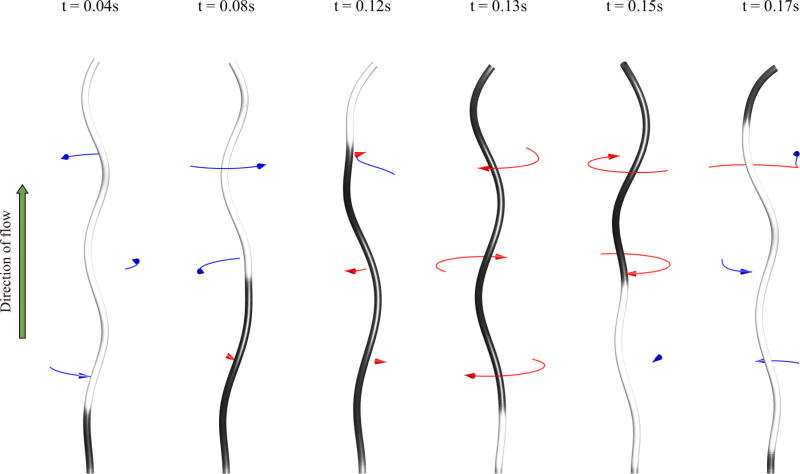
In our simulations, the flagellum (without a hook) is clamped at its motor end so that the triad at the motor end is unable to rotate. To include the background fluid flow, we simply add on the desired velocity u0 onto our computed velocity field. Figure 8 shows snapshots of a simulation showing the transformation from left-handed (gray) to right-handed (black) helical forms, and vice versa (see Movie 2 in the Supplemental Material [51]). In this figure, the lowest point on the filament is held in space and the fluid is flowing vertically upward at the speed of 2000 µm/s. The fluid flow applies a torque at the bottom of the filament and if a sufficient torque is generated, the filament will change its chirality. As the handedness changes first from left to right, the free-end of the filament rotates CCW (blue arrow). However, the portion of the filament below the kink tends to remain nearly stationary. As the first kink nears the free-end, a new transformation occurs at the fixed-end and the filament rotates CW (red arrow). As the filament transforms from right-handed to left-handed, the filament rotates much faster than during the first transformation. This asymmetry is caused by the two different values of the intrinsic twist, i.e., τ1 = −2.1472 µm−1 for the left-handed helix and τ2 = 1.4310 µm−1 for the right-handed helix. When τ1 = −τ2, the rotational speeds during chiral transformations are the same (data not shown).
FIG. 8.
Simulation of an experiment by Hotani [17] using intrinsic torsion values τ1 = −2.1472 µm−1 and τ2 = 1.4310 µm−1. Fluid (water) is flowing upward at 2000 µm/s. The shade of the rod indicates the torsion value where gray is negative (left-handed) and black is positive (right-handed). The arrows indicate CW (red) or CCW (blue) rotation and their length is proportional to the motion over the previous 0.008 s.
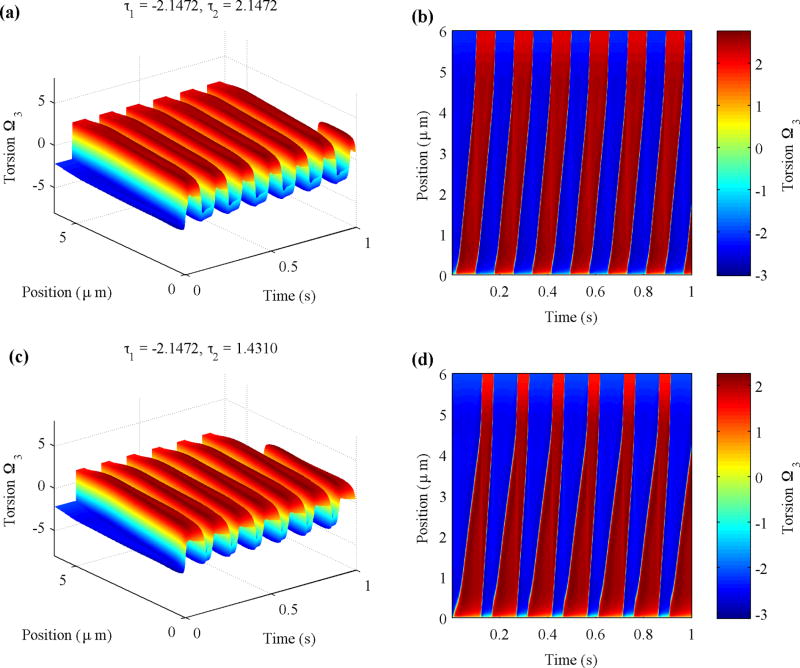
The simulations based on Hotani’s experiment can be further analyzed by evaluating torsion Ω3. Figure 9 compares the torsion along the filament over time (left column) and its projection (right column) for two cases. The top panels illustrate a symmetric case with τ1 = −2.1472 µm−1 and τ2 = 2.1472 µm−1, and the bottom panels illustrate an asymmetric case with τ1 = −2.1472 µm−1 and τ2 = 1.4310 µm−1 (see Movie 3 for a symmetric case and Movie 4 for an asymmetric case in the Supplemental Material [51]). The simulation quickly settles into a stable periodic motion. The sign of the torsion indicates the chirality of the helical filament, in which the negative value corresponds to the left-handed helix and the positive value corresponds to the right-handed helix. The slopes of the sharp changes in the plot show how fast the kink propagates along the filament. A polymorphic transformation begins at s = 0 as indicated by the transition from blue to red. Torsion builds up as the background steady flow causes the helix to turn and eventually results in handedness reversal, which relieves the torsion, but then torsion starts to build up with the opposite sign, alternating two helical forms periodically. For a symmetric case, the kink speed of the left-handed form is approximately the same as that of the right-handed form [Figs. 9(a) and 9(b)]. However, the asymmetry of the two types of handedness shows up as different propagation speeds of the two types of transitions [Figs. 9(c) and 9(d)]. In both cases, the constant speed of propagation ends rather abruptly by accelerating to essentially infinity (vertical lines in the figure) when the transition zone gets close enough to the free end of the flagellum. Increasing the flow velocity will increase the kink propagation speed (data not shown).
FIG. 9.
Values of torsion Ω3 from simulations of Hotani’s experiment plotted against time t and filament position s. The negative value (blue) of torsion corresponds to the left-handed helix and the positive value (red) corresponds to the right-handed helix. The intrinsic torsion values used are τ1 = −2.1472 µm−1, τ2 = 2.1472 µm−1 (top) and τ1 = −2.1472 µm−1, τ2 = 1.4310 µm−1 (bottom). The fluid viscosity is 0.01 × 10−4 g/(µm · s). The background flow speed is set to 2000 µm/s.
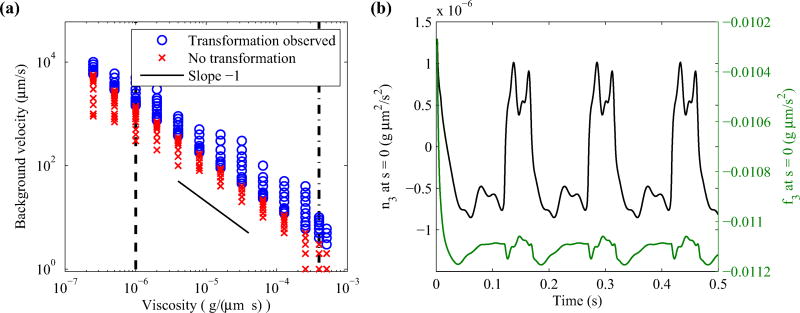
Hotani found in his experiment that no transformations occurred when the flow velocity was lowered to 1 µm/s [17]. In our simulations, we learn that there is a minimum flow velocity at which polymorphic transformation occurs and that it is inversely proportional to fluid viscosity, as shown in Fig. 10(a). In the case of water, the filament reaches an equilibrium configuration when the flow speed is less than 1425 µm/s. For methylcellulose [μ = 4 × 10−4g/(µm · s)], polymorphic transformation occurs when the flow speed is 4 µm/s or higher, which is in good agreement with Hotani’s experiment (we use the viscosity for Hotani’s stock solution, since the exact viscosity of the diluted methylcellulose solution is not known). Furthermore, Hotani showed that chirality change is primarily caused by periodic changes in torque at the fixed end, rather than tension. Our simulations show qualitatively similar behavior in that n3 at the motor periodically changes signs, while there is little variation in f3 at the motor (see Fig. 10(b) and Ref. [17, Fig. 5]).
FIG. 10.
(Left) Observed handedness change for various background flow velocity and fluid viscosity. The vertical dashed line and the dashed-dot line denote the viscosity of water and methylcellulose, respectively. Both axes are plotted on a log scale. (Right) Time evolution of n3 and f3 at the motor for flow speed 2000 µm/s. In both plots, the intrinsic torsion is set to τ1 = −2.1472 µm−1 and τ2 = 1.4310 µm−1.
The twist energy barrier to switch helical forms is crucial for the chirality change in Hotani’s experiment and also for the tumble phase during locomotion. Coombs et al. [41] analyzed the symmetric double-well twist energy in Ref. [19] and found that the critical velocity U* at which chirality changes in Hotani’s experiment is related to the twist energy barrier H by
| (31) |
The coefficient σ measures the local drag due to the fluid derived from resistive-force theory [41,53] and is given by
| (32) |
where ζ‖ is the drag coefficient parallel to the filament and is proportional to fluid viscosity. Note that Eq. (31) implies that the critical velocity is inversely proportional to fluid viscosity when all other parameters are held fixed, which we observe in Fig. 10(a) for an asymmetric twist energy. We also observe this relationship in the symmetric case (data not shown). The height of the energy barrier in our double-well twist energy for the symmetric case (−τ1 = τ2 = τ) is
| (33) |
Together with Eqs. (4) and (5) for the helical radius and pitch, we find the critical flow velocity follows
| (34) |
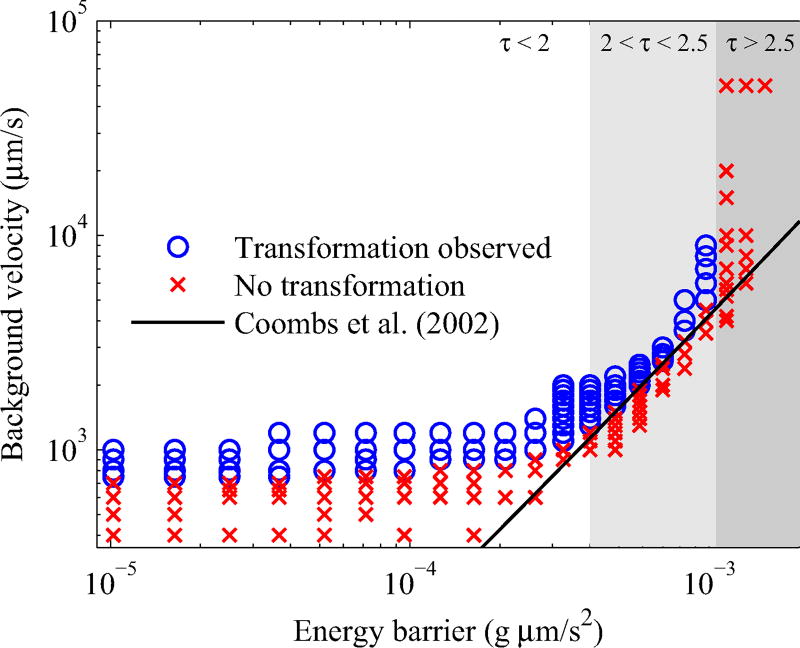
Figure 11 plots the background flow velocity against the energy barrier corresponding to 0.8 ≤ τ ≤ 2.7 on a log-log scale. In our simulations, we find the critical velocity at which the helical filament changes handedness follows Eq. (34) for a limited range of torsion values 2.0 < τ < 2.5. If we decrease τ below 2.0, where the helical radius is sufficiently large, the critical threshold plateaus and becomes independent of H. Although the energy barrier is low, the critical velocity remains high. When τ > 2.5, the helical radius decreases and the filament straightens out and cannot generate enough torque, and thus we do not observe a handedness change even for very high flow velocities.
FIG. 11.
Background flow velocity plotted against the energy barrier for the symmetric twist energy τ = −τ1 = τ2. The result by Coombs et al. (solid curve) was scaled to fit the data. Both axes are plotted on a log scale.
IV. SUMMARY AND CONCLUSIONS
This paper presents a fluid-structure interaction model of a bacterial flagellum capable of polymorphic transformation. The structural properties of the flagellum are described by the Kirchhoff rod theory that incorporates two stable helical configurations of opposite handedness. The flagellum is coupled to the fluid through a regularized stokeslet and rotlet formulation. We performed numerical simulations that are motivated by experiments in which polymorphic transformations are observed. Two mechanisms causing shape transitions were considered: a motor-driven flagellum and a flagellum under a steady viscous fluid flow.
In our motor-driven simulations, we showed that a reversal in the motor rotation can initiate a polymorphic transformation of the flagellar filament between different helical shapes. Our model assumes the hook to be intrinsically straight and its length to be fixed at 60 nm. Although the hook is actually curved and can have different lengths, we found that the hook curvature has little effect on the dynamics of a flagellum. We have shown that a bistable helical filament implemented with a double-well energy functional induces polymorphic transformations by switching the direction of motor rotation from CCW to CW or vice versa, resulting in reversible transformations. Previous studies of rotating helices show that the bundling of flagella and the direction of fluid pumping depends on the direction of motor rotation and the chirality of the helices [38,39]. It is reported that the only combinations that push the cell forward, or pump the fluid away from the cell body, are that when the flagellar filament is either the left-handed helix with its motor turning CCW or the right-handed helix with its motor turning CW. Hence, one immediate advantage of a bistable helix is that flagella can unbundle while continuing to drive fluid away from the cell body. This in turn will allow a bacterium to disband its superflagellum while continuing to swim in a forward direction. Although two monostable left-handed helices can unbundle when rotating in opposite directions, the helices would push fluid in opposing directions [38]. As shown in Fig. 4, the fluid is driven away from the motor for the majority of the transformation period. Furthermore, our simulations show that the speed at which the kink propagates along filament is proportional to the motor rotation frequency but decreases logarithmically with fluid viscosity. Hence, the rapid rotary motor (~100 Hz) of an E. coli bacterium enables the cell to quickly tumble and begin a new run.
In the case of a single flagellum in a steady viscous flow, we simulated the filament dynamics subject to a viscous flow when one end of the filament is tethered in place and showed that a sufficiently large flow velocity can produce a periodic transformation of helical flagella that is consistent with experiments performed by Hotani [17]. The passing fluid applies torque to the filament and torsion builds up until the filament flips the handedness to release it, resulting in the kink propagation from the fixed end to the free end. It is intriguing to see that the constant kink speed changes suddenly to infinite speed when the kink reaches the free end zone. As observed in experiments by Hotani [17], we also observed that the portion of the filament that has not yet changed handedness tends to rotate as the kink propagates, whereas the filament portion below the kink has a tendency to remain motionless. The filament rotates CCW as the chirality changes from left to right, and rotates CW as it changes from right to left. Moreover, having an asymmetric twist energy (τ1 ≠ −τ2) causes different CW and CCW rotation speed. Finally, we studied the critical flow velocity required for chirality change for various cases. We found that the minimum velocity required for transformations to occur is inversely proportional to fluid viscosity and therefore highly viscous fluids (such as methylcellulose used by Hotani) require low flow velocities (≈ 4 µm/s). Furthermore, we examined the case of a symmetric double-well twist energy and found that for an intermediate range of intrinsic torsion values (2 ≤ τ ≤ 2.5) our simulations agree with the analysis in Ref. [41].
Future work includes simulating the bundling and unbundling behavior of two or more bistable flagella. This will be an extension of Ref. [38], in which the two flagella that were considered each had only a single stable helical configuration. Simulating multiple bistable flagella can provide insight into the advantage bistable helices have over monostable helices. Another topic to consider in future investigation is the role of the hook in bacterial motility. Recent experiments show that lower hook compliance makes it more difficult for flagella to bundle [54]. Furthermore, a modeling study of a monotrichous bacterium by Shum and Gaffney [55] shows that the hook’s length and rigidity considerably affects swimming motion. Taking into account various properties of the hook, such as length and stiffness, and their role in flagellar bundling is an interesting topic for further study.
Acknowledgments
We thank Boyce Griffith for useful discussion. S.L. was supported by National Science Foundation Grant No. DMS-1410886 and the Charles Phelps Taft Research Center at University of Cincinnati, USA. Y.K. was supported by the National Research Foundation of Korea Grant funded by the Korean Government (Grant No. 2015R1A2A2A01005420). W.L. was supported by the National Institute for Mathematical Sciences (NIMS) Grant funded by the Korean government (Grant No. A21300000). H.C.B. was supported by the U.S. National Institutes of Health (NIAID), the National Science Foundation (Physics of Living Systems), and the Rowland Institute at Harvard.
APPENDIX
REGULARIZATION PARAMETER
The interaction between the flagellar filament and the surrounding fluid is mediated by the regularized δ function,
| (A1) |
where c controls how the force is spread near the filament. Although a precise relationship between the regularization parameter c and the filament thickness is not known, a general rule-of-thumb is to set c to be the filament radius. This means that c = 0.01 µm is a more suitable choice in our simulations. However, a small value of c requires a small time step Δt. Since δc(x) behaves like O(c−3) at the location of the filament, we find that Δt = O(c3), which enforces a severe time step restriction. A value of c = 0.01 µm would require a time step that is 153 = 3375 times smaller than the time step used for c = 5Δs = 0.15 µm, and this would be impractical even for a simulation running in parallel. For this reason, we choose c = 5Δs in our simulations and yet we obtain results that are qualitatively similar to those found in experiments.
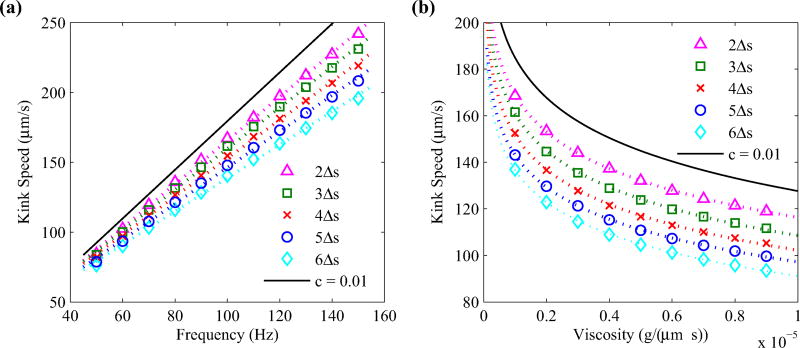
Decreasing the value of the regularization parameter does show some quantitative differences in our simulations, however, the overall dynamics tends to stay the same. Figure 12 shows the kink propagation speed of a motor-driven rotating filament for various rotation frequencies [Fig. 12(a)] and fluid viscosities [Fig. 12(b)], where we vary the regularization parameter c = 2Δs, …, 6Δs. In each case, decreasing the regularization parameter tends to increase the propagation speed. This is primarily due to the increased magnitude of the force applied at the location of the filament.
FIG. 12.
Kink propagation speed plotted against motor rotation frequency (left) and fluid viscosity (right) for various regularization parameters c = 2Δs, …, 6Δs. Here, Δs = 0.03 µm, and intrinsic twist values are set to τ1 = −2.1472 µm−1 and τ2 = 2.1472 µm−1. The dotted lines on the left panel denote the lines of best fit, and the dotted curves on the right panel denote a logarithmic best fit curves. The solid curve in each panel estimates the result for c = 0.01 µm based on the best fit parameters.
We find that the kink speed υ approximately depends on the frequency ω and the regularization parameter by
| (A2) |
where
| (A3) |
| (A4) |
and Δs = 0.03 µm. Moreover, the υ depends logarithmically on the fluid viscosity by
| (A5) |
where
| (A6) |
| (A7) |
Using the above best fit results, we estimate the kink speed for c = 0.01 µm to follow
| (A8) |
| (A9) |
as shown in Fig. 12.
Contributor Information
William Ko, Department of Mathematical Sciences, University of Cincinnati, 4199 French Hall West, Cincinnati, Ohio 45221, USA.
Sookkyung Lim, Department of Mathematical Sciences, University of Cincinnati, 4199 French Hall West, Cincinnati, Ohio 45221, USA.
Wanho Lee, National Institute for Mathematical Sciences, KT Daeduk 2 Research Center, 70, Yuseong-daero 1689-gil, Yuseong-gu, Daejeon 305-811, Republic of Korea.
Yongsam Kim, Department of Mathematics, Chung-Ang University, Dongjakgu, Heukseokdong, Seoul 156-756, Republic of Korea.
Howard C. Berg, Rowland Institute at Harvard, 100 Edwin H. Land Boulevard, Cambridge, Massachusetts 02142, USA
Charles S. Peskin, Courant Institute of Mathematical Sciences, New York University, 251 Mercer Street, New York, New York 10012, USA
References
- 1.Lauga E. Annu. Rev. Fluid Mech. 2016;48:105. [Google Scholar]
- 2.Li C, Motaleb A, Sal M, Goldstein SF, Charon NW. J. Mol. Microbiol. Biotechnol. 2000;2:345. [PubMed] [Google Scholar]
- 3.McBride MJ. Annu. Rev. Microbiol. 2001;55:49. doi: 10.1146/annurev.micro.55.1.49. [DOI] [PubMed] [Google Scholar]
- 4.Weibull C. In: The Bacteria: A Treatise on Structure and Function. Gunsalus IC, Stanier RY, editors. Vol. 1. Academic Press; New York: 1960. pp. 153–205. [Google Scholar]
- 5.Berg HC. Annu. Rev. Biochem. 2003;72:19. doi: 10.1146/annurev.biochem.72.121801.161737. [DOI] [PubMed] [Google Scholar]
- 6.Turner L, Ryu WS, Berg HC. J. Bacteriol. 2000;182:2793. doi: 10.1128/jb.182.10.2793-2801.2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Darnton NC, Turner L, Rojevsky S, Berg HC. J. Bacteriol. 2007;189:1756. doi: 10.1128/JB.01501-06. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Berg HC, Brown DA. Nature. 1972;239:500. doi: 10.1038/239500a0. [DOI] [PubMed] [Google Scholar]
- 9.Pijper A. In: Ergeb. Mikrobiol. Immunitatsforsch. Exp. Ther. Kikuth W, Meyer KF, Nauck EG, Pappenheimer AM Jr, Tomcsik J, editors. Springer; Berlin: 1957. pp. 37–95. [DOI] [PubMed] [Google Scholar]
- 10.Asakura S. Adv. Biophys. 1970;1:99. [PubMed] [Google Scholar]
- 11.Calladine CR. J. Mol. Biol. 1978;118:457. [Google Scholar]
- 12.Kamiya R, Asakura S. J. Mol. Biol. 1976;106:167. doi: 10.1016/0022-2836(76)90306-5. [DOI] [PubMed] [Google Scholar]
- 13.Shimada K, Kamiya R, Asakura S. Nature. 1975;254:332. doi: 10.1038/254332a0. [DOI] [PubMed] [Google Scholar]
- 14.Hotani H. BioSystems. 1980;12:325. doi: 10.1016/0303-2647(80)90030-1. [DOI] [PubMed] [Google Scholar]
- 15.Seville M, Ikeda T, Hotani H. FEBS Lett. 1993;332:260. doi: 10.1016/0014-5793(93)80645-b. [DOI] [PubMed] [Google Scholar]
- 16.Hasegawa E, Kamiya R, Asakura S. J. Mol. Biol. 1982;160:609. doi: 10.1016/0022-2836(82)90318-7. [DOI] [PubMed] [Google Scholar]
- 17.Hotani H. J. Mol. Biol. 1982;156:791. doi: 10.1016/0022-2836(82)90142-5. [DOI] [PubMed] [Google Scholar]
- 18.Macnab RM, Ornston MK. J. Mol. Biol. 1977;112:1. doi: 10.1016/s0022-2836(77)80153-8. [DOI] [PubMed] [Google Scholar]
- 19.Goldstein RE, Goriely A, Huber G, Wolgemuth CW. Phys. Rev. Lett. 2000;84:1631. doi: 10.1103/PhysRevLett.84.1631. [DOI] [PubMed] [Google Scholar]
- 20.Darnton NC, Berg HC. Biophys. J. 2007;92:2230. doi: 10.1529/biophysj.106.094037. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Vogel R, Stark H. Eur. Phys. J. E. 2010;33:259. doi: 10.1140/epje/i2010-10664-5. [DOI] [PubMed] [Google Scholar]
- 22.Vogel R, Stark H. Phys. Rev. Lett. 2013;110:158104. doi: 10.1103/PhysRevLett.110.158104. [DOI] [PubMed] [Google Scholar]
- 23.Adhyapak TC, Stark H. Soft Matter. 2016;12:5621. doi: 10.1039/c6sm00443a. [DOI] [PubMed] [Google Scholar]
- 24.Gebremichael Y, Ayton GS, Voth GA. Biophys. J. 2006;91:3640. doi: 10.1529/biophysj.106.091314. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Wada H, Netz RR. Europhys. Lett. 2008;82:28001. [Google Scholar]
- 26.Gray J, Hancock GJ. J. Exp. Biol. 1955;32:802. [Google Scholar]
- 27.Lighthill J. SIAM Rev. 1976;18:161. [Google Scholar]
- 28.Chattopadhyay S, Wu XL. Biophys. J. 2009;96:2023. doi: 10.1016/j.bpj.2008.11.046. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Johnson RE, Brokaw CJ. Biophys. J. 1979;25:113. doi: 10.1016/S0006-3495(79)85281-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Higdon JJL. J. Fluid Mech. 1979;94:305. [Google Scholar]
- 31.Johnson RE. J. Fluid Mech. 1980;99:411. [Google Scholar]
- 32.Kim MJ, Powers TR. Phys. Rev. E. 2004;69:061910. doi: 10.1103/PhysRevE.69.061910. [DOI] [PubMed] [Google Scholar]
- 33.Lighthill J. J. Eng. Math. 1996;30:35. [Google Scholar]
- 34.Cortez R, Fauci L, Medovikov A. Phys. Fluids. 2005;17:031504. [Google Scholar]
- 35.Flores H, Lobaton E, Méndez-Diez S, Tlupova S, Cortez R. Bull. Math. Biol. 2005;67:137. doi: 10.1016/j.bulm.2004.06.006. [DOI] [PubMed] [Google Scholar]
- 36.Rodenborn B, Chen C-H, Swinney HL, Liu B, Zhang HP. Proc. Natl. Acad. Sci. USA. 2013;110:1574. doi: 10.1073/pnas.1219831110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Hsu CY, Dillon R. Bull. Math. Biol. 2009;71:1228. doi: 10.1007/s11538-009-9400-3. [DOI] [PubMed] [Google Scholar]
- 38.Lim S, Peskin CS. Phys. Rev. E. 2012;85:036307. doi: 10.1103/PhysRevE.85.036307. [DOI] [PubMed] [Google Scholar]
- 39.Kim MJ, Bird JC, Van Parys AJ, Breuer KS, Powers TR. Proc. Natl. Acad. Sci. USA. 2003;100:15481. doi: 10.1073/pnas.2633596100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Kim MJ, Kim MJ, Bird JC, Park J, Powers TR, Breuer KS. Exp. Fluids. 2004;37:782. [Google Scholar]
- 41.Coombs D, Huber G, Kessler JO, Goldstein RE. Phys. Rev. Lett. 2002;89:118102. doi: 10.1103/PhysRevLett.89.118102. [DOI] [PubMed] [Google Scholar]
- 42.Lim S, Ferent A, Wang XS, Peskin CS. SIAM J. Sci. Comput. 2008;31:273. [Google Scholar]
- 43.Cortez R. SIAM J. Sci. Comput. 2001;23:1204. [Google Scholar]
- 44.Olson SD, Lim S, Cortez R. J. Comput. Phys. 2013;238:169. [Google Scholar]
- 45.Smith DJ. Proc. R. Soc. London A. 2009;465:3605. [Google Scholar]
- 46.Higdon JJL. J. Fluid Mech. 1979;94:331. [Google Scholar]
- 47.Yuan J, Fahrner KA, Turner L, Berg HC. Proc. Natl. Acad. Sci. USA. 2010;107:12846. doi: 10.1073/pnas.1007333107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Block SM, Blair DF, Berg HC. Nature. 1989;338:514. doi: 10.1038/338514a0. [DOI] [PubMed] [Google Scholar]
- 49.Flynn TC, Ma J. Biophys. J. 2004;86:3204. doi: 10.1016/S0006-3495(04)74368-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Sen A, Nandy RK, Ghosh AN. J. Electron Microsc. 2004;53:305. doi: 10.1093/jmicro/53.3.305. [DOI] [PubMed] [Google Scholar]
- 51.See Supplemental Material at http://link.aps.org/supplemental/10.1103/PhysRevE.95.063106 for simulation movies.
- 52.Hotani H. J. Mol. Biol. 1976;106:151. doi: 10.1016/0022-2836(76)90305-3. [DOI] [PubMed] [Google Scholar]
- 53.Holwill ME, Burge RE. Arch. Biochem. Biophys. 1963;101:249. doi: 10.1016/s0003-9861(63)80010-7. [DOI] [PubMed] [Google Scholar]
- 54.Brown MT, Steel BC, Silvestrin C, Wilkinson DA, Delalez NJ, Lumb CN, Obara B, Armitage JP, Berry RM. J. Bacteriol. 2012;194:3495. doi: 10.1128/JB.00209-12. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Shum H, Gaffney EA. Phys. Fluids. 2012;24:061901. [Google Scholar]