A Bayesian model for quantifying the change in mortality associated with future ozone exposures under climate change

Summary

Climate change is expected to have many impacts on the environment, including changes in ozone concentrations at the surface level. A key public health concern is the potential increase in ozone-related summertime mortality if surface ozone concentrations rise in response to climate change. Although ozone formation depends partly on summertime weather, which exhibits considerable inter-annual variability, previous health impact studies have not incorporated the variability of ozone into their prediction models. A major source of uncertainty in the health impacts is the variability of the modeled ozone concentrations. We propose a Bayesian model and Monte Carlo estimation method for quantifying health effects of future ozone. An advantage of this approach is that we include the uncertainty in both the health effect association and the modeled ozone concentrations. Using our proposed approach, we quantify the expected change in ozone-related summertime mortality in the contiguous United States between 2000 and 2050 under a changing climate. The mortality estimates show regional patterns in the expected degree of impact. We also illustrate the results when using a common technique in previous work that averages ozone to reduce the size of the data, and contrast these findings with our own. Our analysis yields more realistic inferences, providing clearer interpretation for decision making regarding the impacts of climate change.

1. Introduction

The environmental effects of climate change may have an impact on risks to human health. One concern is that concentrations of outdoor air pollutants could increase as a consequence of climate change. In particular, surface ozone concentrations may rise because of the photochemical formation of ozone (IPCC, 2007). Numerous epidemiological studies and meta-analyses have reported positive associations between short-term changes in ozone exposure and daily mortality rates (Stieb et al., 2002; Bell et al., 2005; Ito et al., 2005; Levy et al., 2005). Based on an overall synthesis of evidence from several scientific disciplines, the most recent U.S. EPA integrated science assessment has concluded that “there is likely to be a causal relationship between short-term exposures to O₃ and total mortality” (U.S. EPA, 2013). This scientific evidence raises concern over the health impacts on daily mortality if surface ozone levels increase in the future.

Interventions to reduce ground level air pollution emissions have also been proposed to mitigate the possible effects of climate change (van Vuuren et al., 2011). Understanding how surface ozone will change in the future is difficult because of the influences of multiple competing factors, including a warming climate, changes in humidity, natural ozone sources, increasing methane levels, and potential reductions in emissions of ozone precursors (Lam et al., 2011; Chen et al., 2009; Murazaki and Hess, 2006). Thus, climate model simulations with detailed atmospheric chemistry are needed to investigate the complex interactions and estimate future surface ozone concentrations. Statistical analyses should account for the features of this type of data when using these modeled ozone concentrations to quantify future health impacts.

The expected future mortality attributable to changes in ozone levels has been estimated in several recent studies under different climate change scenarios (Post et al., 2012; Bell et al., 2007; Tagaris et al., 2009). However, the statistical methodology used to estimate these changes and their uncertainty is incomplete. For example, Post et al. (2012) reports only point estimates with no measure of uncertainty, and Bell et al. (2007) only accounts for the uncertainty in the health effect association. Future ozone projections are inherently variable because they are influenced by the high inter-annual variability of weather. Yet no statistical methodology has been proposed to account for the uncertainty in the climate model simulations. This drawback severely limits the interpretation and inferences that can be made using these mortality estimates.

We present a Bayesian approach for quantifying health effects of future ozone concentrations under climate change. An important contribution of this approach is that we account for both the uncertainty in the health effect association and the inter-annual variability of the modeled ozone projections. We demonstrate this approach by quantifying the expected change in ozone-related summer mortality in the contiguous United States between 2000 and 2050 under a changing climate with two different emission control scenarios.

2. Data Structure of Climate Change Model Output

2.1 Ozone projections for present and future

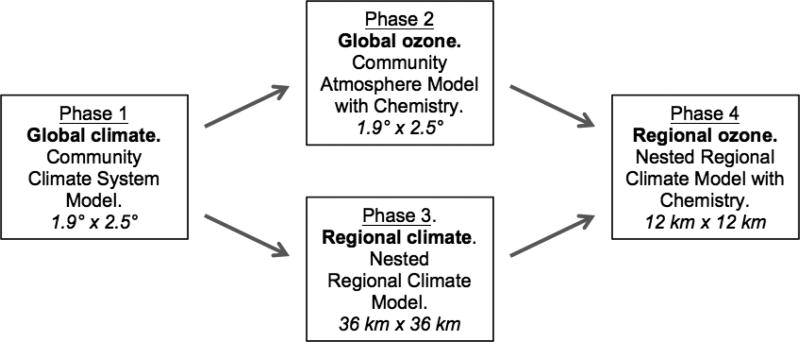
Here, we describe a project to study changes in surface ozone over the contiguous U.S. in the next 50 years, which proceeded in four phases of modeling as summarized in Figure 1. Each phase of modeling requires extensive supercomputing resources to generate the projections of present and future ozone concentrations using climate and chemical transport models.

Figure 1.

Summary of the coupled modeling phases needed to generate simulated 12km × 12km regional ozone concentrations over the contiguous U.S. states.

Global climate projections were generated in phase 1 by the Community Climate System Model run under the IPCC SRES A2 scenario, a high climate impact scenario which includes rapid increases in global methane and nitrous oxide and radiative forcing of 8Wm⁻² by 2100 (Meehl et al., 2007). In phase 2, the global Community Atmosphere Model with Chemistry generated global ozone projections at 1.9 degrees Latitude by 2.5 degrees Longitude using the Representative Concentration Pathway (RCP) 8.5 scenario, which is comparable to the SRES A2 scenario (Lamarque et al., 2011). In phase 3, the global climate projections of phase 1 were dynamically downscaled using the Nested Regional Climate Model to a 36 km × 36 km domain over the larger North America region (Done et al., 2015). The results of phases 2 and 3 provided initial conditions and boundary conditions for the Nested Regional Climate Model with Chemistry, a fully coupled chemical transport model. In Phase 4, this model generated hourly ozone concentrations during summertime over the contiguous U.S. for the present (ca. 2000) and future (ca. 2050) at a 12 km × 12 km resolution. The Nested Regional Climate Model with Chemistry has been extensively evaluated and compared with monitoring data, with details found in Kim et al. (2009) and Pfister et al. (2014). The supercomputing resources needed for Phase 4 alone totaled 6.2 million processor core hours.

Using this coupling of physical models, ozone concentrations were simulated for 13 years during summertime months of June, July, and August for the present and future time periods. Present time anthropogenic emissions were computed from the year 2000 emissions inventory. For the future, two anthropogenic emissions scenarios for the U.S. were considered: Future S, for “same emissions,” where U.S. emissions continue at the present levels into the future and Future R, for “reduced emissions,” where U.S. emissions are reduced in the future based on the RCP 8.5 emissions inventory. All RCPs assume a more stringent air pollution control policy in the future, and emissions of many ozone precursors such as NOx are assumed to decrease (van Vuuren et al., 2011). Further details of the aerosol emissions inventory can be found in Lamarque et al. (2011) and details of the ozone projections can be found in Pfister et al. (2014).

2.2 Change of support problem for ozone model output

Spatial data often arise at different spatial resolutions, causing a spatial misalignment problem. In our setting, climate-chemistry simulations produce ozone model output on a 12km × 12km grid, while Census data for population sizes occur in sets of areal units. Thus, a method is needed to estimate the average ozone exposure over each of the areal polygon regions, starting with the point data of the modeled ozone concentrations. This type of spatial misalignment, using points to predict at polygons, is called a change of support problem.

Banerjee et al. (2014) describe several solutions to the points to polygons change of support problem, pointing out the advantages of kriging over ad hoc approaches such as averaging over the observations of points that fall within each polygon boundary. Gotway and Young (2002) suggest block kriging to predict the average process by minimizing the prediction mean squared error over the block region as in point kriging. Banerjee et al. (2014) point out that approximation by Monte Carlo integration is well-suited to handle irregularly shaped regions: a set of locations is drawn uniformly over the irregular region, kriging predictions are made at each point, and the average of those predictions is computed.

We follow an approach similar to that suggested by Banerjee et al. (2014) to compute the county-level daily ozone concentrations for each of the 3,219 counties in the contiguous U.S. For the kriging step, we interpolate to a 2km mesh using the fields package in R, fitting a thin plate spline approximation to kriging, and interpolating without a nugget effect. An example of this interpolation is illustrated in Web Figure 1. From a computational perspective, this is an expensive step because the kriging involves a matrix inversion step and the processing involves thousands of spatial fields. Specifically, our daily ozone data totals tens of gigabytes, which includes 3,588 daily spatial fields each with 242,208 points. Web Appendix C includes the R code, implemented in parallel over a computer cluster.

Although the change of support problem is well defined in the statistical literature, previous climate and health studies do not document how this aspect is handled. Yet all climate and health studies require the creation of area level averages from the original climate model output to link with population data. Additionally, previous studies have averaged the ozone concentrations into a single summertime average to avoid the computational demands of creating areal averages for every daily ozone field. In this study, we use spatial statistics methodology to estimate ozone concentrations to give a transparent treatment of the change of support problem. Our computational approach allows implementation of this procedure for every daily ozone field to preserve the daily ozone information and its inter-annual and intra-annual variability.

3. Modeling Approach

This section provides details of our proposed statistical approach for quantifying climate change-induced health effects. The first two subsections define our Bayesian framework for the distributions the health effect parameter and of ozone in the present and future. Next, we outline inference procedures for two quantities: the change in the total summertime mortality and the percent change in the total summertime mortality. Finally, we contrast our proposed model with the double averaging approach used in previous studies.

3.1 Prior and Posterior distributions for β

The goal of this paper is to study how best to quantify predictions of future ozone-related mortality. For that reason, we focus on finding the distributions of posterior summaries of the ozone mortality association, and we take advantage of the fact that the first step of the Bayesian analysis is already in hand from previously published work. Accordingly, we use the Bayesian meta-analysis of Bell et al. (2005) to provide the posterior distribution of the health effect parameter, β. The posterior distribution is given by $\beta ~N({\mu }_{\beta },{\sigma }_{\beta }^2)$, where μ_β and ${\sigma }_{\beta }^2$ are taken from the U.S.-specific meta-analysis results in Bell et al. (2005). Specifically, the authors report that the posterior distribution of the pooled log-relative rate of total daily mortality has mean μ_β = 0.0084 per 10-ppb increase in 24-hr ozone, with standard deviation σ_β = 0.00183. Although the statistical framework outlined below assumes Normality of the posterior, our approach can be generalized to any posterior distribution for β, as long as samples can be generated from the posterior.

3.2 Health Effect Model for Ozone and Mortality

Suppose we have a region consisting of locations i = (1, …, N) and consider days t = (1, …, T). Let Y_it denote the number of deaths for location i on day t. Let X_it denote the surface ozone concentration for location i on day t, and let X be a N × T length random vector of these surface ozone concentrations for all locations in the region and all days of summer. Assume that X follows a multivariate spatio-temporal distribution, X ~ F_X. For each geographic location, i, let the population be denoted by P_i and the baseline mortality rate be denoted by R_i, and assume both are known, either from observation or prescribed for a future scenario. Assume $\beta ~N({\mu }_{\beta },{\sigma }_{\beta }^2)$ is the posterior distribution of the health effect parameter as defined above. Let the expected mortality follow

$$E(Y_{\mathit{\text{it}}}|\beta ,X_{\mathit{\text{it}}};P_i,R_i)=P_i{R}_i\text{ exp }(\beta X_{\mathit{\text{it}}}),$$ (1)

based on the Poisson regression model with a log link function commonly used to model daily mortality counts or rates (Frome, 1983; Woodward, 2014). Air pollution mortality studies typically use a Poisson regression model and report inferences for the quantity exp(β), interpreted as the relative rate of mortality for a one-unit increase in X, or for the quantity exp(β) − 1, interpreted as the percent change in expected mortality for a one-unit increase in X (Zeghnoun et al., 2001; Dockery and Pope, 1994; Dominici et al., 2002). The inferences may also be scaled for a particular increase in X, such as the inter-quartile range. We now extend this concept to a multivariate random variable rather than a scalar fixed quantity.

Equation (1) gives an expression for the expected daily mortality for each location i given a particular β and X. We now construct a Bayesian hierarchical model where mortality is a random variable whose distribution depends on the joint distribution of β and X. Let the scalar random variable η(β, X) represent the regional expected total summertime mortality,

$$\eta (\beta ,\mathit{X})=\sum _i\sum _t{P}_i{R}_i\text{ exp }(\beta {\mathit{X}}_{\mathit{\text{it}}}).$$ (2)

The posterior distribution of β depends on the distribution of observed ozone, however, our X represents simulated ozone concentrations generated from climate-chemistry models. Thus, these two ozone space-time records can be considered independent, and furthermore β and X are independent random variables. Conceptually, the distribution of η(β, X) has similarities to computing a posterior predictive distribution, except that instead of a prediction interval given one new observation X̃, we are interested in the distribution of this mean function given all possible values of X from its distribution F_X.

3.3 Inference for percent change in expected total summertime mortality

The distribution of percent change in mortality facilitates comparison of regional effects when regions have different population sizes. Let ζ denote the percent change, defined as $\zeta (\beta ,{\mathit{X}}^P,{\mathit{X}}^F)=\frac{\eta (\beta ,{\mathit{X}}^F)}{\eta (\beta ,{\mathit{X}}^P)}-1$. The posterior mean and the c.d.f. of ζ (β, X^P, X^F), respectively, are given by

$$E\{\zeta (\beta ,{\mathit{X}}^P,{\mathit{X}}^F)\}=\int \{\frac{\eta (\beta ,\mathit{x})}{\eta (\beta ,\mathit{u})}-1\}{f}_{\beta }(\beta )f_{{\mathit{X}}^F}(\mathit{x})f_{{\mathit{X}}^P}(\mathit{u})d\mathit{x}d\mathit{u}d\beta$$ (3)

$${\mathrm{\Phi }}_{\zeta }(a)={\int }_{\{A:\frac{\eta (\beta ,\mathit{x})}{\eta (\beta ,\mathit{u})}-1\le a\}}{f}_{\beta }(\beta )f_{{\mathit{X}}^F}(\mathit{x})f_{{\mathit{X}}^P}(\mathit{u})d\mathit{x}d\mathit{u}d\beta .$$ (4)

To obtain the central 95% credible interval (CI) for ζ, we find the inverse of the c.d.f ${\mathrm{\Phi }}_{\zeta }^{-1}(p)$ for percentiles p = 0.025, 0.975. The integrals in equations (3) and (4) can be approximated by Monte Carlo simulation, with details given in Web Appendix A and R code given in Web Appendix C. A key innovation of our study is to use the empirical distribution for ozone by treating the different years within a climate simulation as independent realizations of X. This exploits the natural variability inherent in the climate-chemistry simulations to characterize the uncertainty of the mortality estimates w.r.t. X without making distributional assumptions about the underlying space-time process.

Now consider the influence of the fixed population size and mortality rate in computing the percent change in expected total mortality attributable to ozone. For a single county, the percent change does not depend on the mortality rate or the population size when assuming the same population and mortality rate in the present and future because these terms cancel in the fraction. For the percent change over a larger region which aggregates multiple counties, the population and mortality rate act as weights in a weighted average of the percent change in each county. In addition, the population will act as a more influential weight than the mortality rate because the variation in county population size is much greater than the variation of mortality rates.

The 95% CI for ζ (β, X^P, X^F) includes both uncertainty in the health effect parameter and variability of summertime ozone concentrations by modeling β, X^P, and X^F as random variables. Also of interest is the marginal distribution of ζ (β), defined as

$$\zeta (\beta )=\int \{\frac{\eta (\beta ,\mathit{x})}{\eta (\beta ,\mathit{u})}-1\}{f}_{{\mathit{X}}^F}(\mathit{x})f_{{\mathit{X}}^P}(\mathit{u})d\mathit{x}d\mathit{u}.$$ (5)

This nested distribution represents the uncertainty in the health association for the average summertime effect. The 95% CI for ζ (β) includes uncertainty in the health effect averaged over the distributions of present and future ozone.

3.4 Inference for change in expected total summertime mortality

Denote the difference in expected total summertime mortality by δ, defined as δ (β, X^P, X^F) = η (β, X^F) − η (β, X^P). The statistical summaries needed for inference around this difference are the posterior mean and the c.d.f., given respectively by

$$E\{\delta (\beta ,{\mathit{X}}^P,{\mathit{X}}^F)\}=\int \eta (\beta ,\mathit{x})f_{\beta }(\beta )f_{{\mathit{X}}^F}(\mathit{x})d\mathit{x}d\beta -\int \eta (\beta ,\mathit{x})f_{\beta }(\beta )f_{{\mathit{X}}^P}(\mathit{x})d\mathit{x}d\beta$$ (6)

$${\mathrm{\Phi }}_{\delta }(a)={\int }_{\{A:\eta (\beta ,\mathit{x})-\eta (\beta ,\mathit{u})\le a\}}{f}_{\beta }(\beta )f_{{\mathit{X}}^F}(\mathit{x})f_{{\mathit{X}}^P}(\mathit{u})d\mathit{x}d\mathit{u}d\beta .$$ (7)

The c.d.f. is then used to construct the central 95% posterior probability credible interval, such that 2.5% of the posterior probability lies above and below the interval. To obtain the bounds for the central 95% CI, we find the inverse of the c.d.f ${\mathrm{\Phi }}_{\delta }^{-1}(p)$ for percentiles p = 0.025, 0.975.

These integrations are then approximated using a Monte Carlo algorithm as described in Web Appendix A. The Monte Carlo simulation method can be simplified under the assumption of Section 3 that β has a normal distribution. Specifically, we obtain an exact solution to the integrals for the E {η(β, X)} and Var {η(β, X)} over the distribution of β (Lemma 1, Web Appendix A). This solution can be generalized to compute the mean and variance integrals for the difference δ (β, X^P, X^F) where the two random variables are correlated through their dependence on β (Corollary 1, Web Appendix A). The exact integral solution eliminates the need for Monte Carlo simulation over realizations of β, thereby improving precision and reducing computational time. However, to use the mean and variance to construct credible intervals requires assumptions about the form of the posterior distributions. Observing that X is only moderately correlated over space and time, it may be reasonable to assume a Normal distribution.

To decompose the overall variability in expected mortality into the contributions of the health parameter and the ozone concentrations, we also consider the nested marginal distribution of δ (β), defined as

$$\delta (\beta )=\int \{\eta (\beta ,\mathit{x})-\eta (\beta ,\mathit{u})\}{f}_{{\mathit{X}}^F}(\mathit{x})f_{{\mathit{X}}^P}(\mathit{u})d\mathit{x}d\mathit{u}.$$ (8)

The 95% CI for δ (β) measures the uncertainty in the health effect averaged over the distributions of present and future ozone. This interval lies within the 95% CI for δ (β, X^P, X^F), which includes the additional summer to summer variability in ozone concentrations.

3.5 Comparison to the double averaging method

The key difference between our study and previous studies estimating future ozone-related mortality (Post et al., 2012; Bell et al., 2007; Tagaris et al., 2009) is the modeling of the ozone concentrations. Ozone-related mortality changes due to climate change have previously been estimates using an approach that we will call the double averaging method. Specifically, the double averaging method first averages ozone over T days of summer and M years of simulated ozone, $\overline{X}=\frac{1}{T}\frac{1}{M}{\sum }_{t=1}^T{\sum }_{m=1}^M{X}_{\mathit{\text{tm}}}$, and then treats X̅ as a representative daily ozone value. This averaging eliminates both the inter-annual and intra-annual variability of ozone, and has several consequences when quantifying future ozone mortality.

Inferences for the double averaging method can be compared directly to inferences based on the marginal distributions for ζ(β) and δ(β) given in equations (5) and (8) respectively. The double averaging method yields biased estimates of the posterior mean and 95% CI bounds for these distributions. The double averaging method will underestimate the expected total summertime mortality for each time period because ${\sum }_{t=1}^T{\sum }_{m=1}^M\text{exp}(\beta X_{\mathit{\text{tm}}})>\mathit{\text{TM}}\text{exp}(\beta \overline{X})$ by Jensen’s inequality. Post et al. (2012) argue that double averaging of ozone is a good approximation “because the health impact functions are nearly linear,” although clearly these are log-linear functions. The double averaging approximation will be more accurate for lower ozone concentrations when exp(βX̅) is closer to one. Since the estimates of expected mortality for the present and future will both have bias, the combined estimates of the total difference or the percent change in mortality will have bias that depends on the magnitudes of each biased estimate.

Conceptually, the double averaging method is a simple extension of the interpretation of the health association parameter in a Poisson regression model. Inferences are often reported for the quantity exp(β) − 1, interpreted as the percent change in expected mortality for a one-unit increase in ozone exposure, or the 95% CIs may also be rescaled for a particular unit increase in ozone exposure. The double averaging method considers the particular unit increase of the average increase in daily ozone concentrations between present and future summers. However, this rescaling of CI of the health association is limited when the goal is to make inferences across a region where the average ozone change varies from county to county. This limitation has caused previous studies to not report 95% CIs for aggregated regions. For example, Post et al. (2012) reports aggregated point estimates with no CIs, and Bell et al. (2007) reports the percent change for each city and the overall average of the city-wide percent changes.

Our Bayesian framework has several clear advantages in comparison to the double averaging method. By modeling the ozone concentrations as random variables, we define two CIs of interest: one that includes both the variability in the health association parameter and the inter-annual ozone variability, and a second that reflects the uncertainty in the health association parameter by appropriately computing the marginal distribution over summertime ozone. By construction, this inner interval will be narrower and nested within the first interval. Because the integration is done explicitly through our Monte Carlo scheme, this interval (a) avoids bias and (b) may be aggregated spatially to any region of interest.

4. Application Results: Quantification of future mortality in 2050 under climate change for two emissions scenarios

We apply our methodology to the climate change study described in Section 2. County-level population data was obtained from the U.S. 2000 Census (U.S. Census Bureau, 2011). We computed average daily mortality rates during the summertime months for each state using the population data and mortality data for year 2000 obtained from the Center for Disease Control (CDC, 2011). For the entire contiguous U.S., we estimate an increase of 1, 212 ozone-related deaths in summertime (95%CI: −816 to 3, 247) under Future S compared to the present, and a change of −2, 543 ozone-related deaths in summertime (95%CI: −4, 473 to −794) under Future R compared to the present.

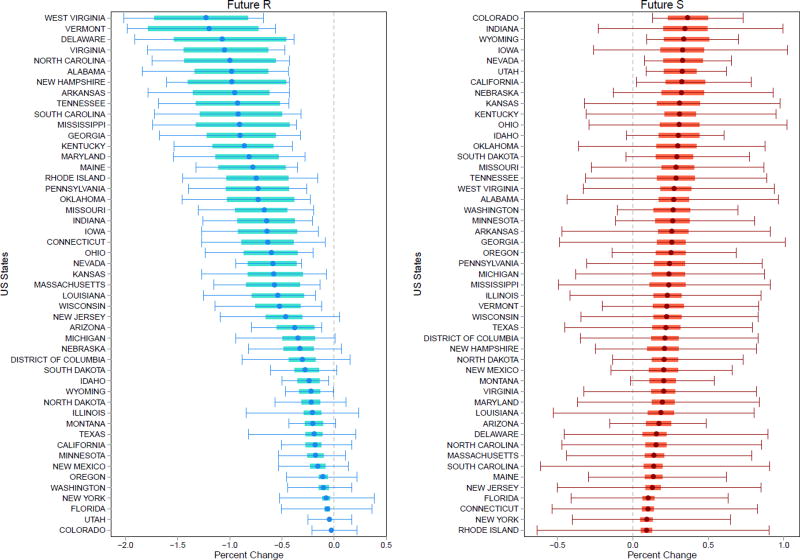
Figure 2 shows the percent change in expected total summertime mortality attributable to ozone for each U.S. state, sorted by effect size. The outer CI includes both the variability in the health parameter and the variability of ozone. The nested inner CI is the average change over the possible summertime ozone concentrations and reflects the variability in the health parameter, as described in Section 3.3. The width of the inner CI is roughly proportional to the effect size, whereas the width of the outer CI also depends on the variability of ozone from summer to summer and across all counties within the state.

Figure 2.

Percent change in expected total non-accidental summertime mortality attributable to changing ozone concentrations in U.S. states under two future emissions scenarios.

To interpret the outer CIs, first consider the states with the largest average percent change in mortality under Future S: Colorado, Indiana, Wyoming, Iowa, and Nevada. The outer CIs for Colorado, Wyoming, and Nevada are narrower than those of Indiana and Iowa, and they do not include zero. This implies that there is less summer-to-summer ozone variability both in the present and in the future; the result is a more consistent change in ozone-related mortality between present and future. A possible interpretation is that these states are usually sunny, hot, and dry during each summer. In contrast, Indiana and Iowa have much wider outer CIs. Although ozone is increasing on average, a few present-day summers have higher ozone levels than a few of the summers in Future S. This effect may be due to the influence of weather factors which contribute to a few hot and sunny summers in the present (yielding higher ozone levels) and a few cloudy and mild summers in the future (yielding lower ozone levels). Web Tables 1 and 2 of Web Appendix B list the numerical estimates in each state for the number of deaths and the percent change in mortality.

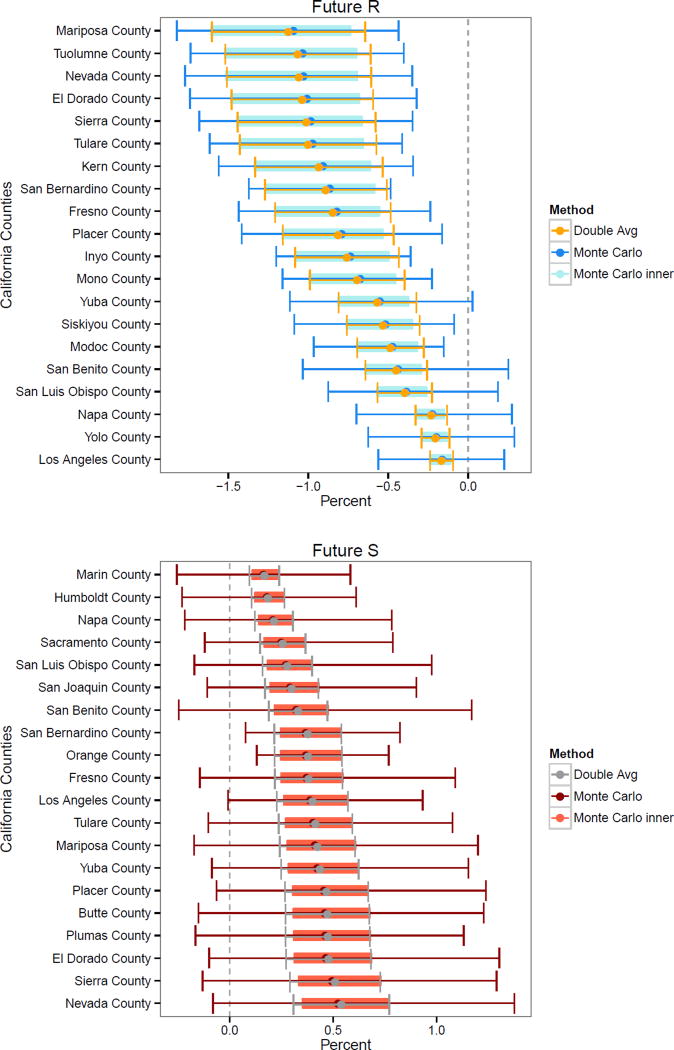
We also contrast the results of our Bayesian model with the results of the double averaging method. The results for twenty counties in the state of California using our approach of Bayesian model with Monte Carlo estimation as well as using the double averaging approach are shown in Figure 3 (all California counties are shown in Web Figures 2 and 3 in Web Appendix B). Figure 3 illustrates the relationship between the double averaging method and the inner CI representing the marginal distribution of percent change, ζ(β). The double averaging method yields a biased approximation of the both the posterior mean and the inner CI endpoints. The degree of bias in the posterior mean estimate is small and is most pronounced when the impact of climate change is greater (farther away from zero), consistent with the nonlinear nature of the exponential function. The double averaging CIs and the inner CIs are much narrower than the outer CIs because they do not reflect the additional inter-annual variation in ozone concentrations. Since the double averaging estimates use only the average daily ozone level, the estimate actually represents mortality change for a summer when every day has that average ozone concentration. In contrast, our inner credible intervals reflect the variability in the daily ozone projections and computes mortality changes for each day in each simulated summer.

Figure 3.

Percent change in expected total summertime mortality attributable to ozone under Future S and Future R for twenty counties in California, comparing our Monte Carlo method to the double averaging method.

We also consider estimating the difference in summertime mortality using the Monte Carlo simplification based on the exact integral solution with respect to β, as described in Section 4.2. To create a credible interval using these exact solutions for the mean and variance, we assume a Normal distribution for the difference in deaths. As an example, we computed the mean and variance for one state and consider the Normal distribution. The exact mean and variance match the Monte Carlo mean and variance extremely well, however the Monte Carlo posterior looks slightly skewed, perhaps more like a log-normal distribution. Thus, the Normal distribution provides a reasonable credible interval, but may differ slightly from the Monte Carlo-based interval. Figure 4 in Web Appendix B shows a histogram of the Monte Carlo samples versus the Normal distribution with the exact mean and variance.

5. Discussion and Conclusions

We developed a Bayesian framework and a Monte Carlo simulation method to estimate expected summertime mortality attributable to change in ozone between 2000 and 2050. The key features of our methodology are (i) the propagation of uncertainty in both the health effect and the ozone projections and (ii) use of the empirical distribution of the daily ozone projections to account for their variation. Overall, this approach yields statistical inferences that give us new scientific insights into a key public health concern. We showed that if U.S. emissions stay at their current levels under a warming climate, ozone mortality will stay the same or increase, depending on location. In contrast, we found that U.S. emission reduction strategies may benefit human health by reducing ozone mortality even in the face of a warming climate, with clear benefits in most states.

This work is an example of the new perspective of the potential for large volumes of data, i.e. Big Data, to be harnessed for scientific advances. By carefully staging our computations and using efficient and parallel data analysis tools we are able to handle a very large volume of climate model output and still do relevant computations on a daily time scale. The use of interpolation to improve the accuracy of averaging over irregular shaped regions helps to derive average exposure for the regions where mortality and demographic information is reported. These choices yield an unbiased evaluation of the posterior of expected mortality and also utilize the climate model simulations as fully as possible, which is important with respect to the significant investment of scientific staff and supercomputing resources to produce the geophysical simulations. A companion statistical statistical analysis should exploit the detail produced from these state-of-the-art simulations rather than averaging out all the inter-annual and intra-annual variation in ozone to reducing the size of the dataset.

We also derive an analytic expression for the mean and variance integrals with respect to the mortality parameter. This expression is useful to reduce the Monte Carlo computational burden, but constructing a confidence interval using these moments requires that one assume a particular form for the posterior distribution. For seasonal totals of mortality, the Gaussian assumption is reasonable and provides a close approximation of the Monte Carlo intervals of ozone-related mortality presented in this work. Because the log link function is commonly used in health studies, we believe this approximation will be useful in future work.

The results of our study have several improvements over the results of recent studies of climate change and ozone-related mortality. The key methodological advantages discussed in Section 3.5 allow inference via 95% credible intervals at the county, state, and entire contiguous US, with nested intervals representing the components of variability in health and ozone. Previously reported average US estimates of summertime ozone mortality without changing population are within our credible interval for Future S; Specifically, Tagaris et al. (2009) estimate an increase of 300 deaths, and the estimates in Post et al. (2012) range from an increase of 780 deaths to a decrease of 100 deaths. Post et al. (2012) reports mean estimates with no confidence intervals and considers ozone projections produced by varying combinations of global climate scenarios and global and regional models. In contrast, our study examines two emissions scenarios under the same global and regional climate model, highlighting the strong influence of emissions in the ozone projections and providing a clear comparison for intervention. Tagaris et al. (2009) uses the global climate scenario of IPCC-A1B, a scenario in which in the global warming effects are more gradual than the effects in the IPCC-A2 scenario used in our study. Although Tagaris et al. (2009) attempts to account for climate model uncertainty in its ozone projections, a key limitation is the use of only one year of ozone model output, which is insufficient to approximate the mean for a given climate scenario, given that studies of the variability of climate models have shown considerable variability for these shorter time scales (Hawkins and Sutton, 2009). Instead of total deaths, Bell et al. (2007) reports only the percent change in ozone-related mortality for 50 eastern US cities, without aggregating estimates to any larger scale because no population or mortality data was incorporated into the estimates.

Our study application results are limited by our assumptions about the population and mortality rate. First, we assume that population and mortality rates do not change in the future, whereas population is expected to increase and mortality rate is expected to decrease (Ortman and Guarneri, 2009). Spatially resolved estimates of the changes in population and mortality rates across demographics were not readily available to incorporate into this analysis. Second, we assume that current population and mortality rates are fixed and known, with no additional variability incorporated. Alternatively, if posterior samples for the present and future spatial distributions of population and mortality rate across the US were available, we could extend our Bayesian hierarchical model by treating each quantity as a random variable with some uncertainty distribution. Specifically, we would characterize the distribution of η(X, β, R, P) by sampling over the distributions of all four random variables, where sampling over the spatial distributions of population and mortality would be similar to our sampling over the spatio-temporal distribution of ozone, except that the distribution of mortality rate may be dependent on the population distribution. The methodology proposed in this paper can be viewed as a step toward that model.

There are additional sources of uncertainty not included in this study. In particular, variability across global climate models and regional climate models is not included nor is the uncertainty of the climate model relative to actual ozone concentrations. The largest component of variability not included in our model is the additional variability of the daily mortality counts around the mean mortality rate function. This additional variability corresponds to the variance of the Poisson distribution, possibly over-dispersed, in the health studies comprising the health effect meta-analysis. Rather than constructing a prediction interval seeking to represent all possible summertime mortality counts, our model characterizes the uncertainty around the mean rate function for mortality to understand how changes in the distribution of future ozone will affect the mean mortality counts and rates.

Our approach offers a Bayesian statistical framework where posterior mean estimates and credible intervals can be reported that reflect the statistical uncertainty given the modeling assumptions. Overall, this approach offers useful interpretations and can be used to gain better quantitative insight into pressing health impact questions involving climate change.