Sex-based differences in the determinants of old age life expectancy: The influence of perimenopause

Abstract

Studies using the sensitive periods framework typically examine the effects of early life exposures on later life health, due to the significant growth and development occurring during the first few years of life. The menopausal transition (i.e., perimenopause) is similarly characterized by rapid physiological change, yet rarely has been tested as a sensitive window in adulthood. Cohort mortality data drawn from three historic populations, Sweden (1751–1919), France (1816–1919), and England and Wales (1841–1919), was analyzed using time series methods to assess whether conditions at midlife significantly influenced or “programmed” later life longevity. Results indicated a significant inverse association between mortality at ages 45–49, the average age range in which perimenopause occurred, and life expectancy at age 60 among females in all three countries. Study findings suggest a degree of plasticity associated with women’s aging, and in particular, the age group correlated with perimenopause.

Introduction

Health development and health trajectories are the consequence of various biological and social factors operating throughout the life span, according to life course epidemiology (Kuh et al. 2003). Certain windows of time, however, represent critical or sensitive periods, during which environmental stimuli or threats can have particularly enduring effects on health and development (Cameron and Demerath 2002). An exposure occurring during a discrete window of time may have lasting effects on the structure or function of organs, tissues, and body systems during a critical period. Such changes cannot be modified in any significant way later in life (Ben-Shlomo and Kuh 2002). Sensitive periods are classified as windows during which exposures have a stronger effect than they would have at other times. Outside these windows, excess disease risk associated with exposure is weaker (Kuh et al. 2003; Halfon and Hochstein 2002).

Studies testing the critical periods hypothesis have predominantly focused on the effects of early life exposures on later life health—pioneered by Barker’s work on the fetal programming of cardiovascular disease (Kuh et al. 2003; Barker 1995). Much work since then has linked the fetal environment with various other morbidities, including diabetes mellitus, stroke, lung abnormalities, depression, and immune dysfunction, as well as with life expectancy (Bengtsson and Lindstrom 2000; Costa and Lahey 2005; Calkins and Devaskar 2011). These studies show that conditions in prenatal and early postnatal life play an important role in the etiology of these diseases (Cameron and Demerath 2002; Ben-Shlomo and Kuh 2002). Researchers increasingly are finding that childhood and adolescence are critical periods for adult health outcomes as well. Studies show, for example, that environmental conditions and behaviors during childhood and adolescence can profoundly affect the risk for obesity and osteoporosis, as well as influence later life longevity (Myrskyla 2010; Catalano and Bruckner 2006; Falconi et al. 2014; Horiuchi 1983).

A relatively scant body of literature—in comparison to that on infancy and youth—has reported on the role of critical and sensitive periods in adulthood. Data from clinical trials, however, suggests that hormone replacement therapy initiated during perimenopause, the transition period between regular pre-menopausal menstruation and the last menstrual period—but not post-menopause—may prevent or delay cognitive decline in aging women (Sherwin 2009).

The significance of the sensitive periods model in adulthood was tested in this paper through an exploratory analysis of the relationship between women’s environmental conditions at mid-life and longevity. Although no study, to my knowledge, has tested whether the presence of sensitive periods for longevity occur in adulthood, evidence suggests that changes in risk for numerous diseases and health conditions—including cancer and cardiovascular disease—occurs during perimenopause (Hoyt and Falconi 2015). Hormones, moreover, have been considered “programming agents” that can alter functional pathways (Halfon and Hochstein 2002). The immense—and often erratic—hormonal changes occurring during perimenopause, therefore, may incite a period of vulnerability as women transition to a post-reproductive state. This paper used the sensitive periods model as conceptual framework to test whether elevated mortality rates occurring at mid-life (i.e. ages 45–49, the age range at which perimenopause approximately occurs in populations), was significantly related to longevity, defined as life expectancy at age 60.

A significant association between women’s mortality rates at midlife and life expectancy at age 60 would imply a sensitive period for women during perimenopause. An association in which higher mortality at age 45–49 was linked with lower life expectancy at age 60, more specifically, would suggest the occurrence of cohort “scarring.” Under this scenario, adverse conditions or exposures at mid-life would permanently damage or impair survivors in the cohort (Elo and Preston 1992; Preston et al. 1998). An association in which higher mortality at age 45–49 was linked with higher life expectancy at age 60 would suggest the occurrence of cohort selection. In this situation, conditions or exposures at mid-life would “cull” frail individuals from the cohort, selecting the hardier individuals for survival to older ages (Preston et al. 1998). If, however, no sensitive periods existed over and above the general effect of a given cohort’s frailty (i.e., a cohort’s susceptibility to mortality), then no statistically significant associations would be expected between women’s mortality rates at ages 45–49 and life expectancy at 60.

Most existing life course studies are limited in that they examine the effect of exposures within one cohort at a single time, and therefore may have low external validity (Ben-Shlomo and Kuh 2002). This study examined 169 different cohorts in Sweden (1751–1919), 104 cohorts in France (1816 and 1919), and 79 cohorts in England and Wales (1841 and 1919), testing whether perimenopause represented a sensitive period for women with respect to longevity. Implications about population health, therefore, can be drawn from the experience of a multitude of cohorts.

Data

Sex-specific cohort mortality and life expectancy data from the civilian populations in Sweden (cohorts born between 1751–1919), France (1816–1919) and England and Wales (1841–1919) were drawn from the Human Mortality Database (HMD) (“Human mortality database” Available at www.mortality.org or www.humanmortality.de). The HMD is a collection of high-quality death rates and life tables for countries where death registration and census data are virtually complete. Only 37 countries—spanning various lengths of time—provide data that meet the standards of the HMD. The longest spans of reliable cohort data belong to Sweden, France, and England and Wales, which differ with respect to the frequency and severity of societal disruptions (e.g., epidemics, wars, etc.) that could influence cohort mortality rates. Whereas Sweden experienced relatively few population-level perturbations, France’s history is marked with many more epidemics and hostilities, and England and Wales falls somewhere in between these two countries.

Dependent Variable

Longevity was assessed through female cohort life expectancy at age 60, given evidence suggesting a postmenopausal acceleration of female physiological dysregulation and mortality peaking around age 60 (Yang and Kozloski 2011; Horiuchi 1997), as well as an increase, on average, of late life mortality acceleration (Li et al. 2013). Together, such findings suggest that age 60 is a particularly vulnerable age for women’s health, at which earlier shocks to health might be more readily apparent or detectable. Age 60 is commonly used in aging research, moreover, to demarcate the beginning of old age in populations (Lutz et al. 2008; Roebuck 1979).

Analysis of mortality patterns shows an increase in the life table aging rate (LAR) in females occurring at middle and old age (at ages 50 and 70), due to “intrinsic forces” (i.e., the gradual degeneration of physiological function), and “extrinsic forces” (i.e., the result of external challenges overcoming remaining vitality). Without knowing the cause of death of women in the populations included in the present analysis—and because increases in LAR drift away from age 70 and closer toward age 50 dating further back into the 19^th Century—age 60 captures the average effects on mortality from intrinsic and extrinsic forces.

Because cohort life expectancy can only be calculated among closed birth cohorts whose members have virtually all died, the time series end in 1919. Life expectancy at age 60 gradually increased over the time series analyzed, although was interrupted by a few major events. In Sweden, for example, the population was heavily affected by dysentery outbreaks in 1772–73, 1808–09, and 1857) that elevated mortality rates in those years. In France, epidemics of cholera (1832, 1849, 1854) and the Franco-Prussian War (1870–1871) temporarily decreased life expectancy. Likewise, in England and Wales, outbreaks of typhoid and flu (1846–1848) and cholera (1832, 1849, and 1865–1866) caused temporary spikes in mortality that affected life expectancy. General trends of increasing life expectancy, as well as exogenous shocks affecting birth cohort death rates, such as those caused by war and epidemics, were controlled in analysis.

Independent Variables

Female cohort mortality rates at ages 45–49 were used to indicate the conditions or circumstances to which a given cohort was exposed during perimenopause. Elevated mortality rates that occurred significantly above what would be statistically expected implied the presence of adverse conditions affecting the population. Cohort mortality rates at infancy (age 0) and five-year intervals which prior literature has indicated as critical or sensitive periods (i.e., early childhood (ages 1–4) and puberty (ages 10–14)) were tested for significance as potential predictors of female longevity. (Studies on pubertal duration in historical populations in Europe show the age range 10–14 encompasses the start and progression of pubertal events for most girls in Sweden, France, and England & Wales during the mid-19^th Century (Parent et al. 2003; Mishra and Cooper 2009; Marshall and Tanner 1969).) The mortality rate for ages 55–59 was also included in the models to control for recency or period effects on life expectancy at age 60.

The age classification designated to represent perimenopause is indicative of the average female in Sweden, France, and England and Wales during the mid- to late 1800s. Research indicates the average age of menopause occurs between 49 and 52 years of age in westernized countries (e.g., Europe, United States of America) (Gold 2011; Collaborative Group on Hormonal Factors in Breast Cancer 2012; Burger et al. 2002) and has not changed significantly over time (McKinlay 1996; Boldsen and Jeune 1990; Sievert 2001). Studies also indicate that perimenopause lasts approximately 4–5 years and begins on average between the ages of 45 and 47.5 (McKinlay 1996; Leidy 1994). The age range of 45–49, therefore, would have encompassed the start and progression for most of perimenopause.

As with life expectancy, mortality rates improved over the 19^th and 20^th centuries. This general decreasing trend for all age groups is controlled for in analysis.

Methods

This test assessed whether life expectancy at age 60 changed from its statistically expected value given increases in mortality rates between the ages 45–49, controlling for cohort mortality rates in other presumed sensitive periods for female longevity, as well for endogenous cohort frailty. Several studies have provided evidence showing that a cohort’s life expectancy is most significantly influenced by the environmental conditions or exposures at certain ages. These sensitive windows for longevity include infancy (age 0), early childhood (ages 1–4), and puberty (ages 10–14) (Beltran-Sanchez et al. 2012; Catalano and Bruckner 2006; Myrskyla 2010; Falconi et al. 2014). Cohort mortality rates from these age groups, therefore, were included as covariates. Because phenomena that would cause a cohort to die more frequently at midlife and at age 60 would be expected to manifest at other ages throughout the life course, cohort frailty was controlled with the inclusion of cohort mortality rates for the presumed sensitive windows as well for cohort mortality at ages 55–59. Cohort mortality at ages 55–59, in particular, captured the closest measure of cohort frailty prior to the count of remaining life (i.e., life expectancy at age 60).

Significant (i.e., p < 0.05, two-tailed test) derivations from the expected value in the independent variable that were associated with deviations from the expected value in the dependent variable signaled the presence of a sensitive window. Mortality and life expectancy data exhibited autocorrelation (e.g., trends, cycles, tendencies to remain elevated or depressed, oscillations after higher or low values), which caused the expected value to deviate from the mean of the series. In order to estimate the expected values, autocorrelation was identified and removed from the dependent and independent variables using autoregressive integrated moving average (ARIMA) modeling, developed by Box and Jenkins (Box et al. 1994). The ARIMA procedure involves applying numerous filters to a time series in order to predict values from past values and shocks in the series. This process yields a time series of residuals that are statistically independent of one another, exhibit no temporal patterns, and have an expected value of zero. ARIMA modeling provides significant benefits in the analysis of mortality and life expectancy data because it takes into account the temporal interdependence of the data.

Following the procedural strategy developed by Box and Jenkins for modeling time series, I identified and removed autocorrelation in the values for life expectancy and for cohort mortality for each year. This procedure identifies any non-stationarity or seasonality present in the data. The Box and Jenkins routines model these patterns as well as the tendency of a series to remain elevated or depressed after high or low values. Trends were then removed or differenced (i.e., the values of each year were subtracted from those of the following year). Other forms of autocorrelation were modeled with autoregressive or moving average parameters. I proceeded through the following analytical steps using software from the Scientific Computing Associates Statistical System.

Identification and Modeling of Autocorrelation in the Dependent and Independent Variables

1) I used Box-Jenkins routines to identify and model autocorrelation in the dependent variable (i.e., life expectancy at age 60) for Sweden, France, and England and Wales. In order to achieve stationarity, the series was differenced, and any other regularly occurring behavior the series shared with the original regression was removed. The residuals created from this process represent the degree to which life expectancy at 60 deviated from its expected value.

2) The same Box-Jenkins techniques were applied from the first step to identify and model autocorrelation in female cohort mortality rates at ages 45–49, as well as at infancy, ages 1 through 4, and the remaining five-year age groups (e.g., 10–14, 55–59) in each country.

Estimation

3) I ran a preliminary test of the bivariate association to examine first whether cohort mortality rates at ages 45–49 were significantly correlated with cohort life expectancy at age 60. This step involved adding the residuals of the age 45–49 mortality series to the equation formed from modeling female cohort life expectancy.

4) The parameters for the full Box-Jenkins models for each country were estimated using maximum likelihood estimation. In this step, the residuals of the other age-specific mortality series generated from the second step were added to the model generated in step 3. The test equations that emerged from this process are as follows:

$$\mathit{\nabla }{Y}_{\mathit{tSweden}}=C\mathit{+}{\omega }_{\mathit{1}}{X}_{\mathit{0}t}\mathit{+}{\omega }_{\mathit{2}}\mathit{\nabla }{X}_{\mathit{1}-\mathit{4}t}\mathit{+}{\omega }_{\mathit{3}}\mathit{\nabla }{X}_{\mathit{10}-\mathit{14}t}\mathit{+}{\omega }_{\mathit{4}}\mathit{\nabla }{X}_{\mathit{45}-\mathit{49}t}\mathit{+}{\omega }_{\mathit{5}}\mathit{\nabla }{X}_{\mathit{55}-\mathit{59}t}\mathit{+}\frac{(1-{\theta }_{1}B-{\theta }_2{B}^2\dots -{\theta }_q{B}^q)}{(1-{\varphi }_{1}B-\varphi 2B^{\mathit{2}}\dots -{\varphi }_p{B}^p)}{a}_t$$

$$\mathit{\nabla }{Y}_{\mathit{tFrance}}=C\mathit{+}{\omega }_{\mathit{1}}\mathit{\nabla }{X}_{\mathit{0}t}\mathit{+}{\omega }_{\mathit{2}}\mathit{\nabla }{X}_{\mathit{1}-\mathit{4}t}\mathit{+}{\omega }_{\mathit{3}}\mathit{\nabla }{X}_{\mathit{10}-\mathit{14}t}\mathit{+}{\omega }_{\mathit{4}}\mathit{\nabla }{X}_{\mathit{45}-\mathit{49}t}\mathit{+}{\omega }_{\mathit{5}}\mathit{\nabla }{X}_{\mathit{55}-\mathit{59}t}\mathit{+}(1-{\theta }_{1}B-{\theta }_2{B}^2\dots -{\theta }_q{B}^q)a_t$$

$$\mathit{\nabla }{Y}_{\mathit{tEngland}\mathit{\&}\mathit{Wales}}=C\mathit{+}{\omega }_{\mathit{1}}{X}_{\mathit{0}t}\mathit{+}{\omega }_{\mathit{2}}\mathit{\nabla }{X}_{\mathit{1}-\mathit{4}t}\mathit{+}{\omega }_{\mathit{3}}\mathit{\nabla }{X}_{\mathit{10}-\mathit{14}t}\mathit{+}{\omega }_{\mathit{4}}\mathit{\nabla }{X}_{\mathit{45}-\mathit{49}t}\mathit{+}{\omega }_{\mathit{5}}\mathit{\nabla }{X}_{\mathit{55}-\mathit{59}t}\mathit{+}\frac{(1-{\theta }_{1}B-{\theta }_2{B}^2\dots -{\theta }_q{B}^q)}{(1-{\varphi }_{1}B-\varphi 2B^2-{\varphi }_p{B}^p)}{a}_t$$

∇ is the difference operator indicating that Y has been differenced from Y_t−1 to remove trends and cycles from the series and render stationarity in its mean.

Y_t equals female cohort life expectancy at age 60 at year t.

C is a constant.

ω₁ through ω₅ is the estimated parameters for the residuals of the age-specific cohort mortality rates.

X_0t through X_55–59t are the residuals of the best fitting models of cohort mortality rate for each age group.

Bⁿ is the backshift operator that either θ or ϕ acts on the value of the error term ‘a’ at year t-q or t-p.

θ is the moving average parameter.

ϕ is the autoregressive parameter a_t is the error term at year t.

5) The equations resulting from Step 4 were estimated for the time series in each of the countries (i.e., Sweden: 1751–1919, France: 1816–1919, and England and Wales: 1841–1919) using the methods described in Steps 1 and 2 to ensure the error terms were free of autocorrelation. The final forms of the models were derived by applying the Ljung-Box test to the autocorrelation and partial autocorrelation functions of the residuals.

Results

Cohort life expectancy at age 60 increased for Swedish females between 1751 and 1919, rising 11.3 years—from 12.62 (age 72.6) to 23.93 (age 83.9) remaining life years (see Figure 1). Similarly, cohort life expectancy also rose for French females, increasing 11 years—from 14.2 (age 74.2) to 25.2 (age 85.2) remaining years of life between 1816 and 1919 (see Figure 2). Cohort life expectancy at age 60 also increased for females in England and Wales during the time series (1841–1919), rising 7.4 years, from 15.3 (age 75.3) to 22.7 (age 82.7) remaining years of life (see Figure 3). Table 1 shows the equations modeling cohort life expectancy at age 60 for these countries. The difference operator, ∇, in the equations for Sweden, France and England and Wales indicates there was a general increasing trend in life expectancy at age 60 throughout the series. The autoregressive parameters (i.e., 0.387, standard error = 0.095; and 0.536, standard error = 0.079) in the model of French life expectancy, for example, suggests that high or low values carried into succeeding years, with “echoes” of such values appearing 1 and 10 years later, but decreased geometrically. The positive, albeit small, coefficient (0.090, standard error = 0.018) in the model for England and Wales indicates that life expectancy slightly drifted above the general upward trend during many of the years between 1841 and 1919.

Figure 1. Observed and expected values of life expectancy at age 60 among women in Sweden, 1751–1919.

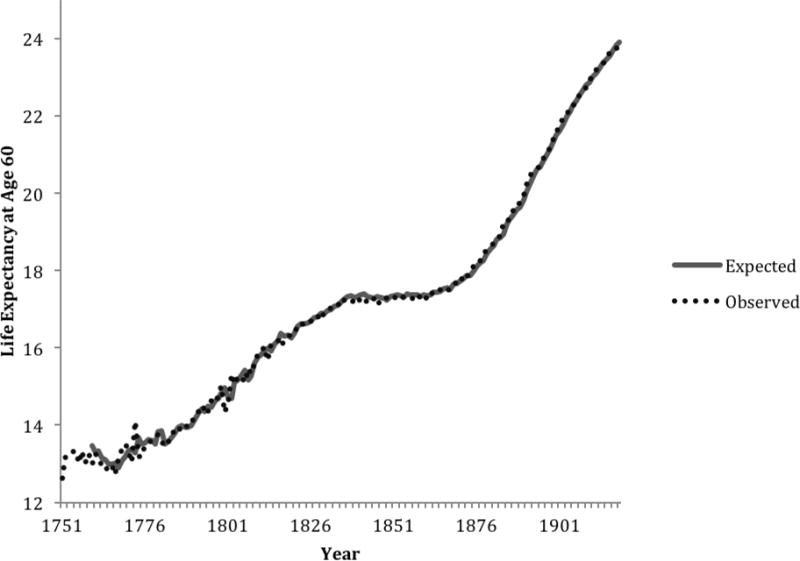
Note: The first 9 years of expected values were lost due to modeling

Figure 2. Observed and expected values of life expectancy at age 60 among women in France, 1816–1919.

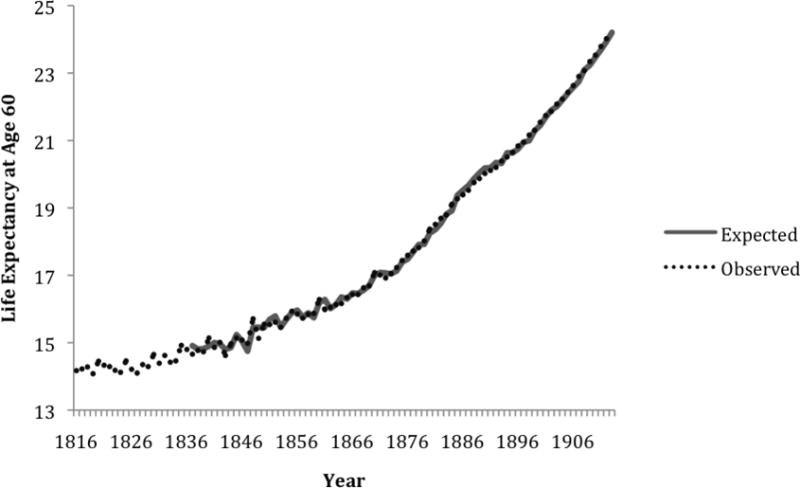
Note: The first 21 years of expected values were lost due to modeling

Figure 3. Observed and expected values of life expectancy at age 60 among women in England and Wales, 1841–1919.

Note: The first 17 years of expected values were lost due to modeling

Table 1.

Box-Jenkins equations for female cohort life expectancy at age 60 for Sweden (1751 through 1919), France (1816 through 1919) and England and Wales (1841 through 1919).

Country	Box-Jenkins Equation
Sweden	$\nabla Z_t=0.0716+\frac{\left(1+0.4908\right)}{\left(1+0.2743B^7\right)\left(1+0.2567B^8\right)}{a}_t$
France	$\nabla Z_t=0.1428+\frac{1}{\left(1-0.3869\mathrm{B}\right)\left(1+0.5362{\mathrm{B}}^{10}\right)}{a}_t$
England and Wales	$\nabla Z_t=0.0899+a_t$

Table 2 shows the equations that modeled cohort mortality rates in Sweden, France, and England and Wales. A decreasing trend in female mortality rates in nearly all age groups was observed in all three countries. This trend was removed by taking the first differences of the series. Each of the age groups also exhibited various moving average and autoregressive patterns, which were subtracted from the cohort mortality series. The negatively signed constant values for several of the equations indicate the rates drifted below the general downward trend for many of the years in the series.

Table 2.

Box-Jenkins equations for female cohort mortality rates at ages 0, 1–4, 10–14, 45–49, and 55–59 for Sweden, (1751 through 1919), France (1816 through 1919) and England and Wales (1841 through 1919).

	Sweden	France	England and Wales
Age 0	$Z_t=-0.0011+(1+0.4609B^2)(1+0.2905B^3) a_t$	$\nabla Z_t=\frac{(1+0.3720B)(1+0.2352B^4)}{(1+0.2540B^5)}{a}_t$	$Z_t=0.1318+ \frac{1}{(1+0.9097B)(1+0.3390B^6)}{a}_t$
Ages 1–4	$\nabla Z_t=-0.0002+(1-0.2414B^{ })(1+0.2761B^4) a_t$	$\nabla Z_t=\frac{(1-0.2516B)(1+0.3206B^4)}{(1+0.3987B^5)}{a}_t$	$\nabla Z_t=-0.0003+ \frac{1}{(1-0.3088B^3)}{a}_t$
Ages 10–14	$\nabla Z_t=-0.3832+ \frac{1}{(1-0.1693B^5)(1-0.2991B^6)}{a}_t$	$\nabla Z_t=\frac{(1+0.3506B^6)}{(1+0.2596B)}{a}_t$	$\nabla Z_t=-0.00005+ a_t$
Ages 45–49	$\nabla Z_t= \frac{1}{(1-0.1548B^5)(1-0.2943B^6)}{a}_t$	$\nabla Z_t=-0.0001+\frac{(1+0.2859B^9)}{(1+0.2214B^{10})}{a}_t$	$\nabla Z_t=-0.0001+ \frac{1}{(1-0.2828B)}{a}_t$
Ages 55–59	$\nabla Z_t=-0.0001+ \frac{1}{(1-0.2131B^6)}{a}_t$	$\nabla Z_t=-0.0001+\frac{(1+0.4230B)}{(1-0.3730B^5)}{a}_t$	$\nabla Z_t=-0.0002+ \frac{1}{(1-0.0730B^2)(1+0.1615B^{20})}{a}_t$

The results in Table 3 show that cohort mortality at ages 45–49 was predictive of life expectancy at age 60 in the test of bivariate association in Sweden and France (p<0.01) after autocorrelation was removed from both variables. In England and Wales, the association approached significance (p=0.053). Cohort mortality at ages 45–49 was significant (p<0.01) for all three countries in the full models that controlled for cohort mortality in the other presumed sensitive windows. Results indicate that life expectancy at age 60 among females in Sweden between 1751 and 1919, France between 1816 and 1919, and in England and Wales between 1841 and 1919 varied inversely with female cohort mortality rates between the ages 45–49.

Table 3a.

Coefficients and standard errors for predictors of female cohort life expectancy at age 60 in Sweden (1751–1919), France (1816–1919) and England and Wales (1841–1919)

	Sweden
	Model of bivariate association		Model with covariates
Variable	Coefficient	Standard Error	Coefficient	Standard Error
Constant	0.0808***	0.0161	0.0715***	0.0111
Cohort death rate age 0			0.1193	1.1983
Cohort death rate age 1–4			2.6179	4.9219
Cohort death rate age 10–14			−44.6081	34.0159
Cohort death rate age 45–49	−101.0414**	25.1945	−78.1612**	22.0632
Cohort death rate age 55–59			−81.6520***	18.3305
Box Jenkins parameters	θB12 = 0.3590*** ϕB8 = 0.3317***	0.0922 0.0851	θB12 = 0.2912*** ϕB8 = 0.2099***	0.0889 0.0756

^*p<0.05, 2-tailed test

^**p<0.01, 2-tailed test

^***p<0.001, 2-tailed test

Cohort mortality rates for ages 55–59 were also significantly associated with life expectancy at age 60 in all three countries, along with cohort mortality at infancy—but only in England and Wales. The coefficient for cohort mortality at ages 55–59 was the most significant variable in the models for all of the countries, suggesting that conditions immediately preceding the measure of life expectancy have the greatest predictive power on life expectancy at age 60. The coefficient for cohort mortality at ages 45–49 was the next most significant covariate for all countries, followed lastly by the covariate for infancy in England and Wales.

The coefficients shown in Table 3 indicate that life expectancy at age 60 among female cohorts decreased by 0.0782 (0.94 months) in Sweden, 0.1292 years (1.55 months) in France and 0.2029 years (2.43 months) in England and Wales, for each increase of 1 per thousand in the age 45–49 mortality rate. To translate into a more interpretable context, mortality rates for age 45–49 were transformed from a continuous variable to a binary variable equal to 1 for cohorts exhibiting greater than expected death rates during ages 45–49 and 0 otherwise. The test equations were run again, with results of the coefficient for the binary variable revealing that life expectancy at age 60 decreased 0.0451 years (0.54 months) on average for Swedish female cohorts that experienced higher than expected mortality at ages 45–49. Among similarly aged females in France, life expectancy at age 60 decreased 0.0454 years (0.54 months) on average for French female cohorts that experienced higher than expected mortality at ages 45–49. Among females in England and Wales, life expectancy at age 60 decreased 0.059 years (0.71 months).

As a frame of reference, cohort life expectancy at age 60 for Swedish and French females increased approximately 11 years, or an average of 0.78 months over the 170 years of analysis for Sweden and 1.27 months per year over the 104 years included in the time series for France. Female cohort life expectancy in England and Wales increased 7.4 years, or an average of 1.12 months, over the 79 years in this study. These findings suggest that “threatened” perimenopausal females lost roughly half (69 percent in Sweden, 43 percent in France and 63 percent in England and Wales) of the gains in life expectancy that females in this age group acquired due to general improvements in health, modernization, etc. that occurred during the 19^th Century.

Sensitivity Analyses

As a robustness test for the female-specific findings, additional models were run in which cohort mortality for infancy and all five-year age groups leading up to 60 (e.g., age 0, 1–4, 5–9….55–59) were included as covariates. These analyses did not yield significantly different outcomes from the results of the original models, with the age 45–49 category remaining the most statistically significant predictor of life expectancy at age 60 (after cohort mortality at age 55–59) for all three countries. Models also were run in which the dependent variable was transformed to a natural logarithm in order to reduce any bias induced by variation in variability over time. The results remained robust to the transformation and did not change the findings appreciably.

Because certain extreme events, such as a war, could cause ‘shocks’ to life expectancy at age 60, the methods of Alwan and Roberts (1988) were used to correct for outlying sequences of values in the cohort life expectancy variable. This correction adjusted for single-year ‘spikes’ (i.e., temporary changes occurring due to outlying values that then regress back to the average or expected value) and sequences that begin with an outlying value but do not regress back to the expected value. The results of the test did not change upon adjusting for outliers, however.

The analyses described above for modeling cohort life expectancy and cohort mortality rates was also repeated for males, for whom theory would predict no significant association, given that they do not experience an equivalent—and abrupt—shift in hormone concentrations at mid-life (Gould et al. 2000). The results in Table 4 show there was no significant bivariate association between male cohort mortality at ages 45–49 and male cohort life expectancy at age 60 for both France and England and Wales, although there was a significant (p<0.05) bivariate association among Swedish males for this age group. When models were fitted that included the five age groups included in the equivalent female models, however, the age 45–49 category appeared significantly associated with life expectancy at age 60 for males in Sweden and in England and Wales. Only the age 55–59 group was significantly associated with life expectancy at age 60 among males in France.

Table 4a.

Coefficients and standard errors for predictors of male cohort life expectancy at age 60 in Sweden (1751–1919), France (1816–1919) and England and Wales (1841–1919)

	Sweden
	Model of bivariate association		Model with covariates
Variable	Coefficient	Standard Error	Coefficient	Standard Error
Constant	0.0570**	0.0103	0.0393***	0.0089
Cohort death rate age 0			−1.1654	1.0409
Cohort death rate age 1–4			−2.1290	4.9436
Cohort death rate age 10–14			−32.5942	29.1608
Cohort death rate age 45–49	−49.662*	20.3515	−43.7815***	16.8103
Cohort death rate age 55–59			−49.6513***	13.5108
Box Jenkins parameters	θB = 0.3430***	0.0827	θB = 0.3225***	0.0864

^*p<0.05, 2-tailed test

^**p<0.01, 2-tailed test

^***p<0.001, 2-tailed test

Discussion

Results of analyses showed a significant, inverse association between conditions at mid-life and later life longevity among females. Mortality rates among females ages 45–49 were predictive of life expectancy at age 60, such that unexpected increases in mortality at ages 45–49 were related to decreases in life expectancy at age 60.

This test is not the first attempt to estimate the effects of mortality at one age on mortality in later years. Indeed, much work has connected early and later life cohort mortality, with study findings showing a strong relationship between mortality in youth (especially during infancy) and old-age mortality across varying countries and disease environments (Finch and Crimmins 2004; Crimmins and Finch 2006a; Crimmins and Finch 2006b). The present analysis adds to this growing body of literature by controlling for the well-documented effects of early life experiences on later life health and showing the independent association between circumstances occurring during the perimenopausal years and later life mortality. Importantly, the non-significant findings in Tables 3a–3c for the association between circumstances in infancy and childhood and later life longevity should not be interpreted to suggest that experiences in youth bear minimal influence on adult mortality. These results instead indicate that the impact of early life influences on later life health is captured by mortality occurring at ages 55–59 (and perhaps supportive of the “cohort morbidity phenotype” hypothesis (Finch and Crimmins 2004). More broadly, these results support the “scarring” or “damaged cohort” hypothesis, where adverse conditions appear to permanently damage or impair survivors of the cohort.

Table 3c.

Coefficients and standard errors for predictors of female cohort life expectancy at age 60 in Sweden (1751–1919), France (1816–1919) and England and Wales (1841–1919)

	England and Wales
	Model of bivariate association		Model with covariates
Variable	Coefficient	Standard Error	Coefficient	Standard Error
Constant	0.0967***	0.0161	0.1054***	0.0096
Cohort death rate age 0			−5.4115**	1.8838
Cohort death rate age 1–4			−14.2032	11.6961
Cohort death rate age 10–14			−147.4615	102.0756
Cohort death rate age 45–49	−87.1607	44.5225	−202.8933***	58.6037
Cohort death rate age 55–59			−191.3639***	50.5740
Box Jenkins parameters	θB12 = 0.3564** ϕB5 = 0.4051***	0.1268 0.1109	θB12 = 0.1044 ϕB5 = 0.0191	0.1718 0.1316

^*p<0.05, 2-tailed test

^**p<0.01, 2-tailed test

^***p<0.001, 2-tailed test

It is unlikely that these results occurred due to frailty associated with some cohorts that happened to die more frequently at ages 45–49 as well as in later life, given that endogenous cohort frailty was controlled with the inclusion of cohort mortality at infancy, childhood, adolescence, and ages 55–59. The remaining variance in mortality at ages 45–49 therefore, was unique and significant above and beyond any variance that mortality rates in this age group shared with mortality rates in other age groups. The finding of a significant association between mortality rates at ages 55–59 and life expectancy was somewhat expected, given that conditions occurring in this window immediately precede the measure of the dependent variable.

The mechanism(s) underlying the significant association between mortality at ages 45–49 and life expectancy at age 60 remains unclear, although perimenopause is plausibly implicated as a possible explanation. Perimenopause represents a time of physiological reorganization in a woman’s life, during which rapid changes occur in hormonal levels (Hill 1996; Cook 1993). This physiological restructuring may leave women particularly vulnerable to both environmental threats and stimuli as they transition from a reproductive to non-reproductive state (Hoyt and Falconi 2015). These changes are consistent with the notion of critical and sensitive periods, during which intrinsic changes in the organization of an organism occur rapidly and when regulatory pathways are being constructed or modified (Halfon and Hochstein 2002; Kuh et al. 2003).

Although the lack of an analogous relationship among French males lends further support to the proposed explanation of perimenopause as a significant period for longevity, the significant association among males in Sweden and in England and Wales weakens this inference. The age at which perimenopause occurs in populations, however, coincides with major social changes that could have increased women’s and men’s vulnerability and affected their longevity. In contemporary society, for example, women and men experience (often differentially) increased stress at midlife due to their children leaving home, increased caregiving for elderly parents, relationship changes, or changes occurring in the workplace (Mishra 2013). It is possible, therefore, that some psychosocial mechanism (as opposed to the biological mechanism proposed by the onset of perimenopause) explains the significant association between ages 45–49 and life expectancy at age 60 among women.

According to other life course models for health and disease, such as the model for accumulation of risk, this study’s findings could also potentially be explained by the accumulation of adverse exposures over the life course that may have been “triggered” at ages 45–49. Circumstances occurring when women were 45–49, in other words, may have acted as the final link in a chain of events that subsequently affected life expectancy at age 60 (Kuh et al. 2003; Ben-Shlomo and Kuh 2002). Results supporting this model of causality would have been expected to show a direct relationship between cohort mortality and life expectancy, such that an increase in mortality at ages 45–49 would winnow or cull the relatively frail members from the cohort. The results of this study do not support this explanation, given the inverse association between cohort mortality and life expectancy. Elevated mortality at ages 45–49 appeared to damage or weaken cohort survivors, resulting in a lower life expectancy at age 60.

These findings corroborate other studies that have found that adverse conditions in adulthood are often more influential on later life health than biological programming that may have occurred earlier in youth. The association between early life socioeconomic position and adult mortality rates, for example, is significantly reduced after controlling for adult socioeconomic position (SEP). Adult SEP, moreover, significantly affects mortality rates independent of early life SEP. These findings have proven robust across multiple populations, including Sweden, England and Wales, and Japan (Ben-Shlomo and Smith 1991; Rosvall et al. 2006; Engelaer et al. 2013).

An empirical challenge of this study, reflective of observational cohort analysis more generally, is the inability to definitively determine the causal mechanism(s) that led to the associations between cohort mortality at midlife and life expectancy at age 60. Significant findings found in aggregate, moreover, may not apply at the individual level. Some literature has, however, previously documented the importance of environmental exposures or circumstances during perimenopause to aging women’s health at the individual level (Hoyt and Falconi 2015). No study, to my knowledge, has tested the sensitive periods model among perimenopausal women at the population level. This study addressed this research gap by showing how conditions at midlife similarly impacted women across two historic populations in Europe, at least with respect life expectancy at age 60.

Study findings yield important insight for assessing population health risk. The results of this study indicate the importance of analyzing the relatively narrow—yet profound—window between the ages of 45 and 49 for women in terms of their later life health. Such information could be particularly relevant with respect to large cohorts of women, who by virtue of their number, can exert significant effects on the financing of and demand for health and social services. The height of the baby boom in the United States, for example, occurred in 1957. As the largest cohort of women in the U.S. history approaches 60 in the year 2017, it may be useful to factor into forecasts how their health status affects the demand for and costs of services. Assessing the health of these women during the not-too-distant past (i.e., between 2002–2006) could provide insight on what is to come for aging women.

Conclusion

In sum, results from this study suggest a degree of plasticity associated with women’s aging. The period of perimenopause may indicate a sensitive period for women in terms of the development or modification of health trajectories into old age. Although women’s reproductive health is integral to their overall health and wellbeing, little is known about the interrelationship between social and lifestyle factors and reproductive health and how these vary across populations and cultures (Mishra 2013). Assessing the health of women during this window could provide insight for the timing and targeting of preventive health interventions.

Table 3b.

Coefficients and standard errors for predictors of female cohort life expectancy at age 60 in Sweden (1751–1919), France (1816–1919) and England and Wales (1841–1919)

	France
	Model of bivariate association		Model with covariates
Variable	Coefficient	Standard Error	Coefficient	Standard Error
Constant	0.1408***	0.0197	0.1347***	0.0187
Cohort death rate age 0			−0.8920	1.1891
Cohort death rate age 1–4			9.5157	11.3851
Cohort death rate age 10–14			−68.6985	64.9568
Cohort death rate age 45–49	−141.0330**	47.3646	−129.2326**	46.5874
Cohort death rate age 55–59			−133.2267***	25.6761
Box Jenkins parameters	ϕB = −0.3590*** ϕB10 = 0.4418***	0.1036 0.0920	ϕB = −0.0729 ϕB10 = 0.3385**	0.1144 0.1018

^*p<0.05, 2-tailed test

^**p<0.01, 2-tailed test

^***p<0.001, 2-tailed test

Table 4b.

Coefficients and standard errors for predictors of male cohort life expectancy at age 60 in Sweden (1751–1919), France (1816–1919) and England and Wales (1841–1919)

	France
	Model of bivariate association		Model with covariates
Variable	Coefficient	Standard Error	Coefficient	Standard Error
Constant	0.1038*	0.0464	0.1007*	0.0448
Cohort death rate age 0			−0.0791	0.5957
Cohort death rate age 1–4			10.1492	6.7549
Cohort death rate age 10–14			14.0645	47.2611
Cohort death rate age 45–49	−7.6010	8.1314	−13.8859	8.9075
Cohort death rate age 55–59			−35.5029*	14.0658
Box Jenkins parameters	ϕB2 = 0.4509*** ϕB10 = 0.5987***	0.0967 0.0814	0.4600*** 0.5898***	0.9866 0.0849

^*p<0.05, 2-tailed test

^**p<0.01, 2-tailed test

^***p<0.001, 2-tailed test

Table 4c.

Coefficients and standard errors for predictors of male cohort life expectancy at age 60 in Sweden (1751–1919), France (1816–1919) and England and Wales (1841–1919)

	England and Wales
	Model of bivariate association		Model with covariates
Variable	Coefficient	Standard Error	Coefficient	Standard Error
Constant	0.0439**	0.0142	0.0273*	0.0136
Cohort death rate age 0			−4.9726*	1.9729
Cohort death rate age 1–4			2.3160	10.7743
Cohort death rate age 10–14			−122.6822	141.4054
Cohort death rate age 45–49	−56.1752	29.7463	−105.5038***	28.7543
Cohort death rate age 55–59			−104.2389***	23.7755
Box Jenkins parameters	θB12 = 0.4024** ϕB = 0.3555**	0.1283 0.1101

^*p<0.05, 2-tailed test

^**p<0.01, 2-tailed test

^***p<0.001, 2-tailed test