Inference of cell type specific regulatory networks on mammalian lineages

Abstract

Transcriptional regulatory networks are at the core of establishing cell type specific gene expression programs. In mammalian systems, such regulatory networks are determined by multiple levels of regulation, including by transcription factors, chromatin environment, and three-dimensional organization of the genome. Recent efforts to measure diverse regulatory genomic datasets across multiple cell types and tissues offer unprecedented opportunities to examine the context-specificity and dynamics of regulatory networks at a greater resolution and scale than before. In parallel, numerous computational approaches to analyze these data have emerged that serve as important tools for understanding mammalian cell type specific regulation. In this article, we review recent computational approaches to predict the expression and sequence-based regulators of a gene’s expression level and examine long-range gene regulation. We highlight promising approaches, insights gained, and open challenges that need to be overcome to build a comprehensive picture of cell type specific transcriptional regulatory networks.

Graphical abstract

Introduction

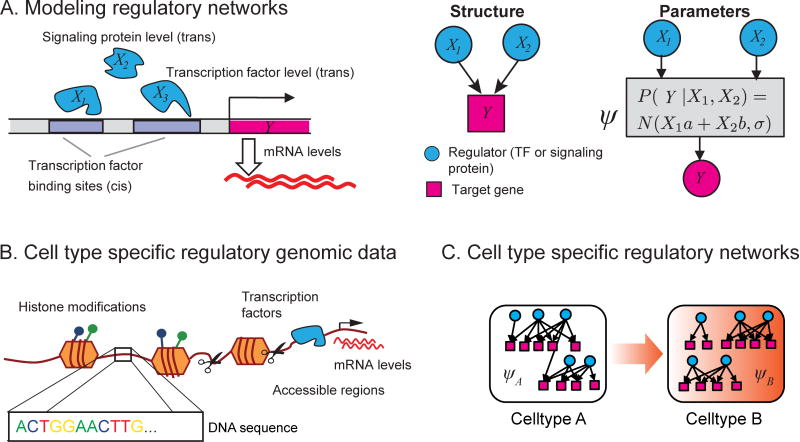
Cell type specific gene expression patterns are outputs of transcriptional regulatory networks connecting regulatory proteins such as transcription factors (TFs) and signaling proteins to target genes. These networks are defined by two components (Figure 1A): structure, specifying the regulators for a gene, and, parameters, specifying how the regulator activities drive a gene’s expression level. These networks control the spatial and temporal gene expression patterns, which are important for establishing cell type identity and function (Figure 1C). Hence, the ability to infer regulatory networks of different cell types is critical for understanding gene regulation and its role in dynamic processes such as cell fate specification. Inference of genome-scale mammalian regulatory networks is challenging because multiple factors influence which regulators can regulate the expression of a gene, including TF sequence affinity, chromatin state and three-dimensional genome organization. Advances in single cell genomics, coupled with large-scale measurements of transcriptomes, epigenomes, chromatin accessibility, TF binding, and chromosome conformation, are providing new opportunities to understand mammalian gene regulation. Here we review recent computational approaches to answer three major questions in the analysis of mammalian developmental regulatory networks (Table S1): (a) what TFs regulate the expression level of a gene? (b) what is the full complement of sequence elements that regulate a gene? (c) how does the regulatory network change between cell types?

Figure 1.

Regulatory network concepts. (A) Regulatory networks have two components: structure and parameters. The structure provides the wiring diagram of the network, specifying the regulators of each gene. The parameters (ψ) model the target gene expression level as a function of the combined activities of its regulators. Cis-regulatory elements are regulatory DNA sequence elements and include genomic regions such as transcription factor binding sites. Distal cis-elements have been called enhancers, and are brought into proximity of a gene through three-dimensional looping. Trans-regulatory elements are regulatory proteins that interact directly or indirectly with the gene’s cis-regulatory elements. (B) The context-specific regulatory environment of a cell is measured using various omics technologies. Transcriptomic and proteomic assays measure activity levels of trans-regulators and target genes. Different sequencing technologies, e.g., ChIP-seq, ATAC-seq, DNAse I-seq, are used to measure binding profiles of specific transcription factors, histone modifications, and DNA accessibility. C Cell type specific networks for two cell types A and B. The regulatory networks in each cell type can differ at the structure or at the parameter level. Cell type A can transition to cell type B by appropriate activation of B’s network.

Expression-based regulatory network inference

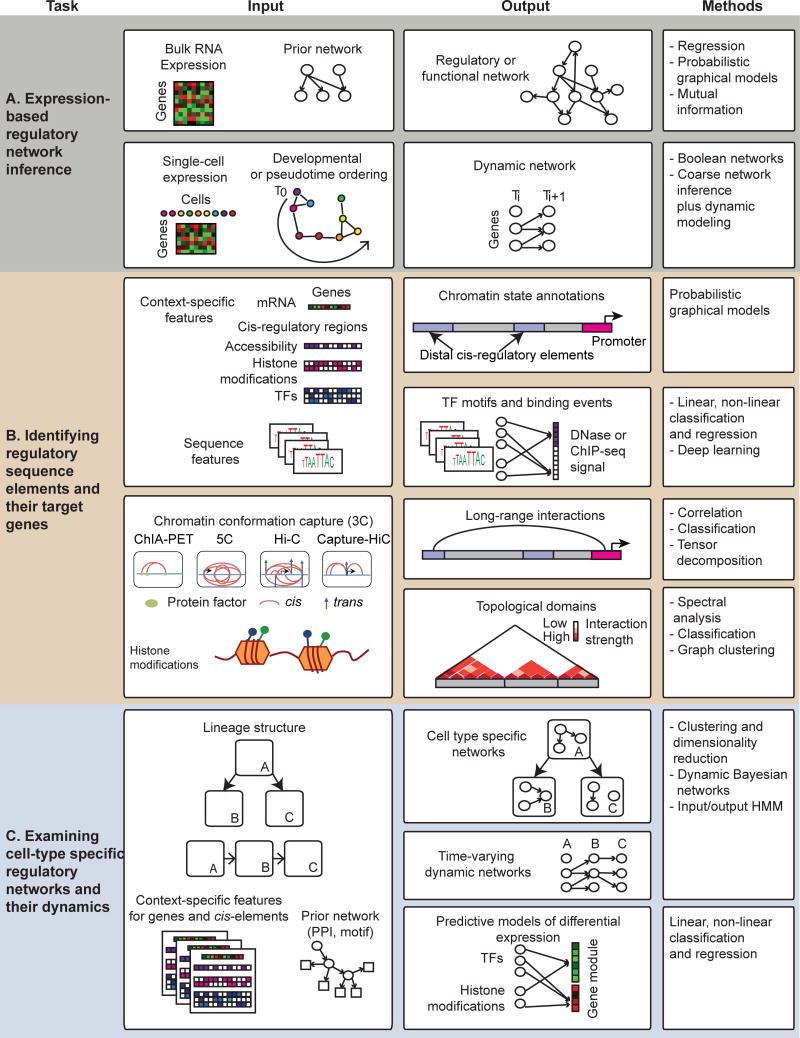
Expression-based network inference (Figure 2A) is a popular approach to infer genome-scale regulatory networks [1–10] and seeks to infer both the network structure and parameters (Figure 1A). Such methods can be especially useful to predict targets of less studied regulators or regulators with unknown sequence specificity. This class of approaches leverages large number of genome-wide measurements for a given cell type where each measurement profiles a perturbed version of the cell type. Several successful reconstructions have been undertaken for a single cell type, including Th17 cells [11, 12], germ cell tumor [13], glioblastoma multiforme (GBM) [14]. New expression-based network inference methods are either integrating auxiliary non-expression datasets, or inferring regulatory networks from single cell transcriptome data.

Figure 2.

Inference of cell type specific regulatory networks can be addressed using tools for three main types of problems. Shown are the inputs, outputs and the popular types of computational approaches used for addressing these problems. (A) Expression-based network inference uses bulk or single-cell transcriptome profiles to infer dependencies between regulators and targets. Methods can infer a single static regulatory network or infer a dynamic network that describes the change in network structure over time or between cell types. (B) Identification of regulatory elements and predicting their targets via long-range interactions. Methods can either segment the genome based on measured combinations of different regulatory signals (e.g., chromatin marks, TF binding) or predict binding sites of different TFs. Long-range gene regulation is studied using different Chromosome Conformation Capture (3C) technologies, which measure the 3D proximity of two genomic regions. 3C technologies differ in the resolution (genomic region size) and the number of regions they can interrogate. These data can be analyzed to find topological units of organization like TADs, or be used to build classifiers for predicting interactions for new loci. (C) Examining cell type specific regulatory networks that integrate expression and sequence-based regulators of target gene expression. Methods use clustering or dimensionality reduction to study relationships among cell types and loci, predictive models of expression to identify regulatory features explaining expression variation, and probabilistic graphical models. Methods based on Dynamic Bayesian networks and Hidden Markov models provide principled frameworks for modeling networks at each time point and their dynamics.

Inferring constrained networks from bulk transcriptomic data

One direction of research, motivated by the poor agreement of expression-inferred networks and physical regulatory networks (e.g., derived from ChIP-chip/seq experiments) [8], integrates context-agnostic information, such as sequence-specific motifs, to constrain the structure of the inferred network (Table S1). Such constraints are imposed using a penalized linear regression framework [15], or with graph structure priors [16, 17]. In the penalized regression framework (e.g., Inferelator [15]), the penalty of a regulatory edge is reduced if there is previous knowledge supporting this edge. In the graph structure prior approach (e.g, MERLIN-P [16]), the prior probability of an edge with regulatory evidence is higher than other edges. Extending linear regression to a non-linear setting, iRafNet [18] incorporated priors by extending GENIE3 [7], an established state-of-the-art purely expression-based network inference approach, which learns an ensemble of trees to provide a ranking on candidate regulatory edges. All these approaches have shown that adding additional constraints in the network generally improves the agreement with ChIP-chip/seq networks. In addition to requiring sufficient number of samples, these methods assume that the regulator’s expression level is predictive of its target’s expression level. Some approaches are relaxing this assumption by modeling the TF activity as a hidden variable [19–22] however, the only context-specific information here are mRNA levels.

Inferring networks from single cell transcriptomic data

While expression-based network inference from bulk expression measurements is useful, population averages from bulk data can obscure cell-to-cell variability of regulatory networks [23]. Therefore, a recent direction of expression-based network inference has been to infer dynamic regulatory networks from single cell transcriptomic data (Figure 2B, Table S1). Inference of dynamic regulatory networks requires an ordering among the samples, which may be available or can be inferred computationally using cellular trajectory finding algorithms (reviewed in [23, 24]). Once an order is established, a dynamic network is inferred by learning a Boolean network [25, 26], or more complex models, such as dynamic Bayesian networks [27] and Gaussian Processes [28]. Ocone et al. [28] operated on each branch of the inferred trajectory separately. For each branch, a coarse skeleton regulatory network is inferred using GENIE3 [7], followed by detailed regulatory program learning using Gaussian Processes. While many of these approaches use single cell expression data alone, some approaches have integrated other sources of data, e.g., TF ChIP-seq [29] or TF knockdown assays [29, 30] to establish a network structure [29].

So far, single cell network inference has been applied to a relatively small number of manually chosen genes (≤100) in up to 4000 cells [25–29, 31]. Recent single cell RNA-seq measurements of thousands of cells could be used to infer genome-scale networks [32, 33], currently possible only from bulk transcriptomes. However, several technical challenges first need to be addressed including normalization and missing values due to dropout of genes [24, 34, 35].

Identification of regulatory sequence elements and their genomic targets

The regulatory network structure of a cell type depends on the regulatory sequence elements active in the cell type, as well as the three-dimensional proximity of such elements to genes. Accordingly, in addition to mRNA levels, several studies have measured genome-wide binding profiles of transcription factors [36], histone modifications [36–48], and chromatin accessibility [49–51] to identify sequence elements, as well as high-throughput chromosome conformation capture (3C) assays to examine the three-dimensional organization of the genome [51–54]. In parallel, several new computational tools have emerged that use these data to both identify regulatory sequence elements and predict gene targets of these elements.

Identifying regulatory sequence elements

One approach to identify regulatory sequence elements is genome segmentation using one-dimensional regulatory genomic signals, e.g., genome-wide chromatin marks, chromatin accessibility and TF binding (Table S1, [55–62]). These methods assign a state annotation to genomic regions based on combinations of these regulatory signals. A state is a concise description of a region’s regulatory status and can often be mapped to known regulatory elements, including enhancers. Among the earliest approaches for genome segmentation were ChromHMM [55] (a Hidden Markov Model) and Segway [56] (a Dynamic Bayesian Network). More recently, EpiCSeg [59], extended ChromHMM to model count data as negative binomial distributions rather than discretized values. jMOSAiCS [58] also uses count values and considers all possible combinatorial enrichment patterns of different regulatory signals. These methods differ based on the statistical model of the count data, and how they model data from multiple cell types, e.g., either by concatenating the data from multiple cell types [55], or by jointly modeling cell-type [61] or time point specific [57] chromatin mark data. While most of these approaches use one-dimensional regulatory genomic signals, one exception is Graph-based Regularization (GBR) [62], which extended Segway to use high-throughput 3C data as a prior graph to encourage regions that are nearby in 3D space to share the same annotation.

While genome annotation methods identify general sequence elements, another set of methods identify binding events of transcription factors from TF ChIP-seq, DNase I-seq [63, 64] or ATAC-seq [65]. Computational footprinting methods using DNase I-seq data (Table S1, [66]) are specifically geared towards finding footprints of TFs defined as “protected regions” of DNA where a TF might bind. Footprints may be identified using only accessibility data [67–69], or by integrating information of known sequence-specific motifs (see methods reviewed by Gusmao et al.[66]). An alternative is to perform de novo motif discovery on accessible regions using machine learning frameworks that identify sequence features that are predictive of accessibility or ChIP-seq data. In particular, SeqGL [70] and gkm-SVM [71, 72] use a binary classification framework to discriminate peak from non-peak or flanking regions using k-mer features, while the Synergistic Chromatin Model (SCM) [73] performs L1-regularized Poisson regression to predict quantitative accessibility signal. These approaches can identify sequence specific motifs based on the selected k-mers. SeqGL aims to improve the interpretability of the resulting motifs by clustering similar k-mers to account for redundancy and using a Group Lasso penalty to select groups of k-mers. SCM’s regression approach bypasses the need to call peaks and models synergistic relationships among nearby k-mers to directly predict the accessibility of a region. More recently, several deep learning methods [74, 75] aim to predict chromatin features including accessibility [76–78] (Table S1). A recent approach is Basset [78], which uses convolutional neural networks to learn context-specific sequence predictors of DNA accessibility. An advantage of deep learning approaches comes from using convolutional filters to automatically learn informative sequence features from the data, in contrast to manual feature engineering.

Identifying long-range regulatory interactions between enhancers and target genes

Any given cell type can have thousands of active regulatory elements, e.g., enhancers [48, 79], many of which regulate a gene’s expression through long-range interactions by being in three-dimensional proximity to their targets [80–83]. Therefore, a key problem in understanding mammalian regulation is to identify the target genes of enhancers (Figure 2B).

Several approaches have been developed to predict long-range interactions either from statistical analysis of Hi-C data [84], inferring statistical correlation among pairs of genomic loci [49], or by integrating 3C datasets with one-dimensional regulatory signals (Table S1). A correlation-based approach, first proposed by Thurman et al. [49], relied on the correlation of open chromatin profiles of pairs of genomic loci across hundreds of cell types. More recently, the EpiTensor method [85] used tensor decomposition of one-dimensional signals for multiple marks from multiple cell types. This approach uses a tensor to represent three dimensions: cell type, region and signal. PRESTIGE incorporates CTCF domain information with H3k4me1 and RNA-seq expression from multiple cell types to compute a pairwise information theoretic score that is predictive of these interactions [86]. A similar approach developed by Marbach et al. [87] relied on CAGE-seq data from multiple cell types (measured by the FANTOM consortium). Both enhancers and promoters are defined by CAGE-seq expression in a tissue, although CAGE might not identify all enhancers due to its restriction to 5′ capped transcripts from transcription start sites. Enhancers are matched to nearest promoters and filtered based on joint expression in the tissue type. By applying this approach to hundreds of cell types, the authors provided a comprehensive collection of interactions of CAGE-detected enhancers to promoters.

A complementary set of methods use supervised learning, e.g., IM-PET [88], RIPPLE [89], TargetFinder [90], CITD [91]. These methods differ based on the 3C technology used for training, which can be ChIA-PET (IM-PET), 5C (RIPPLE), or Hi-C (TargetFinder, RIPPLE, CITD), input regulatory signals, and whether the methods use data from multiple cell types. TargetFinder and RIPPLE were both trained in a per-cell type manner, while IM-PET combined data from multiple cell types. Beyond chromatin features, IM-PET used sequence conservation as well, while TargetFinder used features associated with regions between the enhancer and promoter.

Both classes of methods are useful. While correlation based methods do not need 3C data and instead rely on the statistical dependencies inferred from one-dimensional signals, the supervised methods combine both 3C data and one-dimensional signals to more directly predict these interactions and identify informative datasets that can predict these interactions.

Analysis of Hi-C data from different cell types has shown that the genome is organized into higher order organizational units, such as A/B compartments, topologically associated domains (TADs) and sub-TADs [92]. TADs are ∼1 megabase in size and remain largely stable across cell types, while A/B compartments partition entire chromosomes into active (A) and inactive regions (B) [92]. Compartments can be identified from a spectral or clustering analysis of the Hi-C interaction matrix [93–95]. TADs can be identified by quantifying the tendency of a region to interact more with its upstream or downstream neighborhood, termed the Directionality Index (DI, [96]), and modeling DI with a Hidden Markov model. Newer TAD finding methods attempt to identify more fine-grained domains (e.g., sub-TADs) that can reveal a hierarchical organization among the domains that could vary across cell types. Both Armatus [97] and TADtree [98] use dynamic programming to identify TADs as well other types of domains. Armatus finds non-overlapping domains by examining the interaction matrix at different resolutions and selecting those that persist across multiple resolutions. In contrast, TADtree identifies a nested hierarchy of TADs, where TADs and sub-TADs can overlap. Computational methods have also been developed to predict TAD boundaries from one-dimensional regulatory signals by training a classifier (e.g., Bayesian Additive Regression Trees (BART) [99]) with examples of TAD boundaries.

The three-dimensional organization of the genome can change substantially during development [51–54, 92, 100]. Relatively few computational approaches have been developed to examine dynamics of Hi-C data across different cell types. One approach constructed meta-TADs by hierarchical clustering of TADs in three cell types from neuronal development [54], and found that while TAD boundaries were conserved across cell types, there were changes at the meta-TAD levels that corresponded with mRNA level changes. Another approach, Arboretum-Hi-C [101], used multi-task graph clustering to identify topological units in multiple cell types and species and concluded that chromosome organization at a coarse megabase scale is largely conserved between cell types and species.

Integrative approaches to examine cell-type specific regulatory networks

With increasing availability of genome-scale measurements for multiple cell types, approaches to identify and compare cell type specific regulatory networks are needed to provide insights into the dynamics of cell type specific behavior. A straightforward way to combine information across multiple cell types is clustering and dimensionality reduction [36, 39, 41, 42, 44, 48, 50, 102]. Such approaches can be used to group cell types based on their genome-wide profiles or group genomic loci based on their signal across multiple cell types. Approaches to examine cell type specific networks and their dynamics are in their infancy; below we summarize two main themes (Figure 2C).

Predictive models of gene expression

Predictive models of gene expression have been powerful to identify regulatory elements driving gene expression programs [103–106] (Figure 2C, Table S1). These approaches model expression level or change in expression as a function of features capturing the chromatin state, TF occupancy, and sequence composition in proximal and distal regions [40, 42, 107]. These approaches differ in whether they predict change in expression level (e.g., [42, 107]) or differential expression status for a gene [40], as well as how they handle distal elements. For example, Gonzalez et al. [107] initially assign distal regions to the nearest gene followed by reassignment based on prediction error, whereas Hagey et al. [42] assign a distal region to all genes within a 500kb window. In all cases, a linear or logistic regression model learns feature weights, which can identify important cis-regulatory elements for cell type specific expression. When profiling multiple cell types using a single active mark (e.g., H3K27ac), one can use the MARGE framework [108] to identify a set of cis-regulatory elements associated with differentially expressed genes. However, these approaches do not infer regulatory connections for individual genes.

Dynamic Bayesian Networks and extensions

Probabilistic graphical models, specifically, Dynamic Bayesian Networks (DBNs) and Hidden Markov Models (HMMs), can model dynamics of networks [27, 109–112] (Figure 2C, Table S1). Early promising work in this area has extended DBNs to capture time-point specific regulatory networks. In particular, Gong et al. [109] used Time-varying Dynamic Bayesian networks (TVDBN) [113] to model regulatory relationships between ∼70 TFs and target genes at four steps of mouse cardiac cell differentiation (ESC, mesoderm, cardiac progenitors and cardiomyocytes). The TVDBN model allows the parameters to change smoothly over time, which overcomes the stationarity assumption of DBNs. Gong et al. integrated 17 TF ChIP-seq data from either ES or the cardiac cell type, stage-specific RNA-seq and histone marks at all four developmental stages in mouse. In addition to modeling the dynamics in the cardiac differentiation network over time, this approach predicted the relevant cis-regulatory regions up to 20kb from a TSS, and identified several known enhancer regions. TVDBNs learn a rich model of regulation for each gene’s expression level as a function of a gene’s cis-regulatory elements, but requires careful regularization that makes each gene’s regulatory program similar between time points to avoid overfitting.

Conclusions

Here we reviewed recent computational approaches to examine mammalian gene regulation with a focus on cell lineages. Prior-constrained, expression-based network inference methods leverage a large number of genome-wide measurements for the same cell type to predict the regulators of a given gene. However, these predictions are a first approximation and need to be experimentally validated with ChIP-seq binding experiments, when possible, and by targeted perturbation experiments of regulators and transcriptome profiling [114, 115]. Genome annotation and TF binding prediction methods use histone modification, accessibility, and TF ChIP-seq profiles to predict the sequence elements that are active in a cell type. However, to construct a regulatory network, we need to infer regulatory connections among sequence elements, target genes and TFs, many of which have yet unknown sequence specificities. Hence, methods to measure sequence specificity of TFs will be key to build a complete picture of a regulatory network. A current open problem is to examine the dynamics and context-specificity of these networks. Early work in this area using predictive models of gene expression and dynamic probabilistic graphical models are promising. However, inferring detailed regulatory mechanisms for multiple cell types in complex lineages will require systematic measurements of transcriptomic, proteomic and epigenomic signals and computational methods to integrate these measurements. We envision that integrative iterative approaches combining experimental measurements and computational modeling will be essential to construct cell type specific networks and identify the regulatory sub-circuits that establish and change cell fates.

Highlights.

• Transcription factors and chromatin state together determine regulatory networks.

• Cell type specific network inference must integrate mRNA and epigenomic datasets.

• Expression-based network inference is useful to map genome-wide regulatory networks.

• Regulatory sequence element identification helps determine network structure.

• Predictive models of expression and graphical models can examine network dynamics.