DYNAMIC PREDICTION FOR MULTIPLE REPEATED MEASURES AND EVENT TIME DATA: AN APPLICATION TO PARKINSON’S DISEASE

Abstract

In many clinical trials studying neurodegenerative diseases such as Parkinson’s disease (PD), multiple longitudinal outcomes are collected to fully explore the multidimensional impairment caused by this disease. If the outcomes deteriorate rapidly, patients may reach a level of functional disability sufficient to initiate levodopa therapy for ameliorating disease symptoms. An accurate prediction of the time to functional disability is helpful for clinicians to monitor patients’ disease progression and make informative medical decisions. In this article, we first propose a joint model that consists of a semiparametric multilevel latent trait model (MLLTM) for the multiple longitudinal outcomes, and a survival model for event time. The two submodels are linked together by an underlying latent variable. We develop a Bayesian approach for parameter estimation and a dynamic prediction framework for predicting target patients’ future outcome trajectories and risk of a survival event, based on their multivariate longitudinal measurements. Our proposed model is evaluated by simulation studies and is applied to the DATATOP study, a motivating clinical trial assessing the effect of deprenyl among patients with early PD.

1. Introduction

Joint models of longitudinal outcomes and survival data have been an increasingly productive research area in the last two decades (e.g., Tsiatis and Davidian, 2004). The common formulation of joint models consists of a mixed effects submodel for the longitudinal outcomes and a semiparametric Cox submodel (Wulfsohn and Tsiatis, 1997) or accelerated failure time (AFT) submodel for the event time (Tseng, Hsieh and Wang, 2005). Subject-specific shared random effects (Vonesh, Greene and Schluchter, 2006) or latent classes (Proust-Lima et al., 2014) are adopted to link these two submodels. Many extensions have been proposed, e.g., relaxing the normality assumption of random effects (Brown and Ibrahim, 2003), replacing random effects by a general latent stochastic Gaussian process (Xu and Zeger, 2001), incorporating multivariate longitudinal variables (Chi and Ibrahim, 2006), and extending single survival event to competing risks (Elashoff, Li and Li, 2007) or recurrent events (Sun et al., 2005; Liu and Huang, 2009).

Joint models are commonly used to provide an efficient framework to model correlated longitudinal and survival data and to understand their correlation. A novel use of joint models, which gains increasing interest in recent years, is to obtain dynamic personalized prediction of future longitudinal outcome trajectories and risks of survival events at any time, given the subject-specific outcome profiles up to the time of prediction. For example, Rizopoulos (2011) proposed a Monte Carlo approach to estimate risk of a target event and illustrated how it can be dynamically updated. Taylor et al. (2013) developed a Bayesian approach using a Markov chain Monte Carlo (MCMC) algorithm to dynamically predict both the continuous longitudinal outcome and survival event probability. Blanche et al. (2015) extended the survival submodel to account for competing events. Rizopoulos et al. (2013) compared dynamic prediction using joint models v.s. landmark analysis (van Houwelingen, 2007), an alternative approach for dynamically updating survival probabilities. A key feature of these dynamic prediction frameworks is that the predictive measures can be dynamically updated as additional longitudinal measurements become available for the target subjects, providing instantaneous risk assessment.

Most dynamic predictions via joint models developed in the literature have been restricted to one or two longitudinal outcomes. However, impairment caused by the neurodegenerative diseases such as Parkinson’s disease (PD) affects multiple domains (e.g., motor, cognitive, and behavioral). The heterogeneous nature of the disease makes it impossible to use a single outcome to reliably reflect disease severity and progression. Consequently, many clinical trials of PD collect multiple longitudinal outcomes of mixed types (categorical and continuous). To properly analyze these longitudinal data, one has to account for three sources of correlation, i.e., inter-source (different measures at the same visit), longitudinal (same measure at different visits), and cross correlation (different measures at different visits) (O’Brien and Fitzmaurice, 2004). Hence, a joint modeling framework for analyzing all longitudinal outcomes simultaneously is essential. There is a large number of joint modeling approaches for mixed type outcomes. Multivariate marginal models (e.g., likelihood-based (Molenberghs and Verbeke, 2005), copula-based (Lambert and Vandenhende, 2002), and GEE-based (O’Brien and Fitzmaurice, 2004)), provide direct inference for marginal treatment effects, but handling unbalanced data and more than two response variables remain open problems. Multivariate random effects models (Verbeke et al., 2014) have severe computational difficulties when the number of random effects is large. In comparison, mixed effects models focused on dimensionality reduction (using latent variables) provide an excellent and balanced approach to modeling multivariate longitudinal data. To this end, He and Luo (2016) developed a joint model for multiple longitudinal outcomes of mixed types, subject to an outcome-dependent terminal event. Luo and Wang (2014) proposed a hierarchical joint model accounting for multiple levels of correlation among multivariate longitudinal outcomes and survival data. Proust-Lima, Dartigues and Jacqmin-Gadda (2016) developed a joint model for multiple longitudinal outcomes and multiple time-to-events using shared latent classes.

In this article, we propose a novel joint model that consists of: (1) a semiparametric multilevel latent trait model (MLLTM) for the multiple longitudinal outcomes with a univariate latent variable representing the underlying disease severity, and (2) a survival submodel for the event time data. We adopt penalized splines using the truncated power series spline basis expansion in modeling the effects of some covariates and the baseline hazard function. This spline basis expansion results in tractable integration in the survival function, which significantly improves computational efficiency. We develop a Bayesian approach via Markov chain Monte Carlo (MCMC) algorithm for statistical inference and a dynamic prediction framework for the predictions of target patients’ future outcome trajectories and risks of survival event. These important predictive measures offer unique insight into the dynamic nature of each patient’s disease progression and they are highly relevant for patient targeting, management, prognosis, and treatment selection. Moreover, accurate prediction can advance design of future studies, experimental trials, and clinical care through improved prognosis and earlier intervention.

The rest of the article is organized as follows. In Section 2, we describe a motivating clinical trial and the data structure. In Section 3, we discuss the joint model, Bayesian inference, and subject-specific prediction. In Section 4, we apply the proposed method to the motivating clinical trial dataset. In Section 5, we conduct simulation studies to assess the prediction accuracy. Concluding remarks and discussions are given in Section 6.

2. A motivating clinical trial

The methodological development is motivated by the DATATOP study, a double-blind, placebo-controlled multicenter randomized clinical trial with 800 patients to determine if deprenyl and/or tocopherol administered to patients with early Parkinson’s disease (PD) will slow the progression of PD. We refer to as placebo group the patients who did not receive deprenyl and refer to as treatment group the patients who received deprenyl. The detailed description of the design of the DATATOP study can be found in Shoulson (1998).

In the DATATOP study, the multiple outcomes collected include Unified PD Rating Scale (UPDRS) total score, modified Hoehn and Yahr (HY) scale, Schwab and England activities of daily living (SEADL), measured at 10 visits (baseline, month 1, and every 3 months starting from month 3 to month 24). UPDRS is the sum of 44 questions each measured on a 5-point scale (0–4), and it is approximated by a continuous variable with integer value from 0 (not affected) to 176 (most severely affected). HY is a scale describing how the symptoms of PD progresses. It is an ordinal variable with possible values at 1, 1.5, 2, 2.5, 3, 4, and 5, with higher values being clinically worse outcome. However, the DATATOP study consists of only patients with early mild PD and the worst observed HY is 3. SEADL is a measurement of activities of daily living, and it is an ordinal variable with integer values from 0 to 100 incrementing by 5, with larger values reflecting better clinical outcomes. We have recoded SEADL variable so that higher values in all outcomes correspond to worse clinical conditions and we have combined some categories with zero or small counts so that SEADL has eight categories.

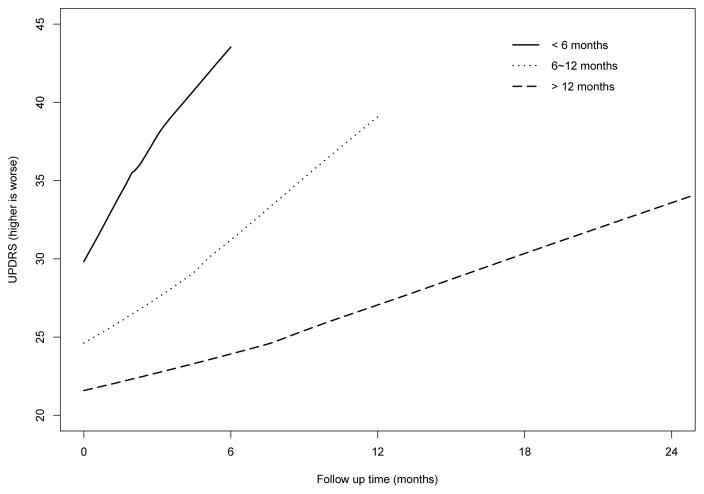
Among the 800 patients in the DATATOP study, 44 did not have disease duration recorded and one had no UPDRS measurements. We exclude them (5.6%) from our analysis and the data analysis is based on the remaining 755 patients. The mean age of patients is 61.0 years (standard deviation, 9.5 years). 375 patients are in the placebo group and 380 are in the treatment group. About 65.8% of patients are male and the average disease duration is 1.1 years (standard deviation, 1.1 years). Before the end of the study, some patients (207 in placebo and 146 in treatment) reached a pre-defined level of functional disability, which is considered to be a terminal event because these patients would then initiate symptomatic treatment of levodopa, which can ameliorate the clinical outcomes. Figure 1 displays the mean UPDRS measurements over time for DATATOP patients with follow-up time less than 6 months (96 patients, solid line), 6–12 months (215 patients, dotted line), and more than 12 months (444 patients, dashed line). Figure 1 suggests that patients with shorter follow-up had higher UPDRS measurements, manifesting the strong correlation between the PD symptoms and terminal event. Similar patterns are observed in HY and SEADL measurements. Such a dependent terminal event time, if not properly accounted for, may lead to biased estimates (Henderson, Diggle and Dobson, 2000).

Fig 1.

Mean UPDRS values over time.

Because levodopa is associated with possible motor complications (Brooks, 2008), clinicians tend to provide more targeted interventions to delay their initiation of levodopa use. To this end, in the context of DATATOP study and similar PD studies, there is an important clinically relevant prediction question: for a new patient (not included in the DATATOP study) with one or multiple visits, what are his/her most likely future outcome trajectories (e.g., UPDRS, HY, and SEADL) and risk of functional disability within the next year, given the outcome histories and the covariate information? These important predictive measures are highly relevant for PD patient targeting, management, prognosis, and treatment selection. In this article, we propose to develop a Bayesian personalized prediction approach based on a joint modeling framework consisting of a semiparametric multilevel latent trait model (MLLTM) for multivariate longitudinal outcomes and a survival model for the event time data (time to functional disability).

3. Methods

3.1. Joint modeling framework

In the context of clinical trials with multiple outcomes, the data structure is often of the type {y_ik(t_ij), t_i, δ_i}, where y_ik(t_ij) is the kth (k = 1, . . . ,K) outcome, which can be binary, ordinal, or continuous, for patient i (i = 1, . . . , I) at visit j (j = 1, . . . , J_i) recorded at time t_ij from the study onset, $t_i=\mathit{min}(T_i^{\ast },C_i)$ is the observed event time to functional disability, as the minimum between the true event time $T_i^{\ast }$ and the censoring time C_i which are assumed to be independent of $T_i^{\ast }$, and δ_i is the censoring indicator (1 if the event is observed, and 0 otherwise). We propose to use a semiparametric multilevel latent trait model (MLLTM) for the multiple longitudinal outcomes and a survival model for the event time.

To start building the semiparametric MLLTM framework, we assume that there is a latent variable representing the underlying disease severity score and denote it as θ_i(t) for patient i at time t with a higher value for more severe status. We introduce the first level model for continuous outcomes,

$$y_{ik}(t)=a_k+b_k{\theta }_i(t)+{\epsilon }_{ik}(t),$$ (1)

where a_k and b_k (positive) are the outcome-specific parameters, and the random errors ${\epsilon }_{ik}(t)~N(0,{\sigma }_{{\epsilon }_k}^2)$. Note that a_k = E[y_ik(t)|θ_i(t) = 0] is the mean of the kth outcome if the disease severity score is 0 and b_k is the expected increase in the kth outcome for one unit increase in the disease severity score. The parameter b_k also plays the role of bringing up the disease severity score to the scale of the kth outcome. The models for outcomes that are binary (e.g., the presence of adverse events) and ordinal (e.g., HY and SEADL) are as follows (Fox, 2005):

$$\begin{array}{l}\text{logit}\{p(y_{ik}(t)=1\mid {\theta }_i(t))\}=a_k+b_k{\theta }_i(t)\\ \text{logit}\{p(y_{ik}(t)\le l\mid {\theta }_i(t))\}=a_{kl}-b_k{\theta }_i(t),\end{array}$$ (2)

where l = 1, 2, . . . , n_k − 1 is the lth level of the kth ordinal variable with n_k levels. Note that the negative sign for b_k in the ordinal outcome model is to ensure that worse disease severity (higher θ_i(t)) is associated with a more severe outcome (higher y_ik(t)). Interpretation of parameters is similar for continuous outcomes, except that modeling is on the log-odds, not the native scale, of the data. We have selected logit link function in model (2), while other link functions (e.g., probit and complementary log-log) can be adopted. A major feature of models (1) and (2) is that they all incorporate θ_i(t) and explicitly combine longitudinal information from all outcomes.

To model the dependence of severity score θ_i(t) on covariates, we propose the second level semiparametric model

$${\theta }_i(t)={\mathit{X}}_i(t)\mathit{\beta }+{\mathit{Z}}_i(t){\mathit{u}}_i+{\mathit{V}}_R(t)\mathit{\zeta },$$ (3)

where vectors X_i(t) and Z_i(t) are p and q dimensional covariates corresponding to fixed and random effects, respectively. They can include covariates of interest such as treatment and time. To allow additional flexibility and smoothness in modeling the effects of some covariates, we adopt a smooth time function ${\mathit{V}}_R(t)\mathit{\zeta }={\sum }_{r=1}^R{\zeta }_r{(t-{\kappa }_r)}_{+}$ using the truncated power series spline basis expansion V_R(t) = {(t − κ₁)₊, . . . , (t − κ_R)₊}, where κ = {κ₁, . . . , κ_R} are the knots, and (t − κ_r)₊ = t − κ_r if t > κ_r and 0 otherwise. Following Ruppert (2002), we consider a large number of knots (typically 5 to 20) that can ensure the desired flexibility and we select the knot location to have sufficient subjects between adjacent knots. To avoid overfitting, we explicitly introduce smoothing by assuming that $\mathit{\zeta }={({\zeta }_1,\dots ,{\zeta }_R)}^{\prime }~N(0,{\sigma }_{\zeta }^R\mathit{I})$ (Ruppert, Wand and Carroll, 2003; Crainiceanu, Ruppert and Wand, 2005). The choice of knots is important to obtain a well fitted model and should be selected with caution to avoid overfitting. Several approaches of automatic knot selection based on stepwise model selection have been proposed (Friedman and Silverman, 1989; Stone et al., 1997; Denison, Mallick and Smith, 1998; DiMatteo, Genovese and Kass, 2001). Wand (2000) gives a good review and comparison of some of these approaches. Penalizing the spline coefficients to constrain their influence also helps to avoid overfitting (Ruppert, Wand and Carroll, 2003), as in our model. Moreover, in clinical studies with same scheduled follow-up visits, the frequency of study visits needs to be accounted for in the selection of knots. For the ease of illustration, we include the nonparametric smooth function for the time variable, although our model can be extended to accommodate more nonparametric smooth functions. The vector u_i = (u_i1, . . . , u_iq)′ contains the random effects for patient i’s latent disease severity score and it is distributed as N(0,Σ). Equations (1), (2) and (3) consist of the semiparametric MLLTM model, which provides a nature framework for defining the overall effects of treatment and other covariates. Indeed, if ${\theta }_i(t)={\beta }_0+{\beta }_1{x}_i+{\beta }_{2}t+{\beta }_3{x}_{i}t+{\sum }_{r=1}^R{\zeta }_r{(t-{\kappa }_r)}_{+}+u_{i0}+u_{i1}t$, where x_i is treatment indicator (1 if treatment and 0 otherwise), then β₁ is the main treatment effect and β₃ is the time-dependent treatment effect. In this context, the null hypothesis of no overall treatment effect is H₀ : β₁ = β₃ = 0. Because the number of outcomes (K) has been reduced to one latent disease severity score, models are quite parsimonious in terms of number of random effects, which improves computational feasibility and model interpretability.

Because the semiparametric MLLTM model is over-parameterized, additional constraints are required to make it identifiable. Specifically, we set a_k1 = 0 and b_k = 1 for one ordinal outcome. For the ordinal outcome k with n_k categories, the order constraint a_k1 < . . . < a_kl < . . . < a_knk−1 must be satisfied, and the probability of being in a particular category is p(Y_ik(t) = l) = p(Y_ik(t) ≤ l|θ_i(t))−p(Y_ik(t) ≤ l−1|θ_i(t)). With these assumptions, the conditional log-likelihood of observing the patient i data {y_ik(t_ij)} given u_i and ζ is $l_y({\mathbf{\Theta }}_y;{\mathit{y}}_i,{\mathit{u}}_i,\mathit{\zeta })={\sum }_{j=1}^{J_i}{\sum }_{k=1}^{K}logp(y_{ik}(t_{ij})\mid {\mathit{u}}_i,\mathit{\zeta })$. For notational convenience, we let $\mathit{a}={({\mathit{a}}_1^{\prime },\dots ,{\mathit{a}}_k^{\prime },\dots ,{\mathit{a}}_K^{\prime })}^{\prime }$, with a_k being numeric for binary and continuous outcomes and a_k = (a_k1, . . . , a_knk−1)′ for ordinal outcomes. We let b = (b₁, . . . , b_K)′ and y_i(t) = {y_ik(t), k = 1, . . . ,K}′ be the vector of measurements for patient i at time t and let y_i = {y_i(t_ij), j = 1, . . . , J_i} be the outcome vector across J_i visit times. The parameter vector for the longitudinal process is Θ_y = (a′, b′,β′,Σ, σ_εk, σ_ζ )′.

To model the survival process, we use the proportional hazard model

$$h_i(t)=h_0(t)\text{exp}\{{\mathit{W}}_i\mathit{\gamma }+\nu {\theta }_i(t)\},$$ (4)

where γ is the coefficient for time-independent covariates W_i and h₀(·) is the baseline hazard function. Some covariates in W_i can overlap with vector X_i(t) in model (3). Ibrahim, Chu and Chen (2010) gave an excellent explanation of the coefficients for those overlapped covariates. In the current context, if we denote β_o and γ_o as the coefficients for the overlapped covariates in vectors X_i(t) and W_i, respectively, we have: (1) β_o is the covariate effect on the longitudinal latent variable; (2) γ_o is the direct covariate effect on the time to event; (3) νβ_o+γ_o is the overall covariate effect on the time to event. The association parameter ν quantifies the strength of correlation between the latent variable θ_i(t) and the hazard for a terminal event at the same time point (refer to as ‘Model 1: shared latent variable model’). Specifically, a value of ν = 0 indicates that there is no association between the latent variable and the event time while a positive association parameter ν implies that patients with worse disease severity tend to have a terminal event earlier, e.g., a value of ν = 0.5 indicates that the hazard rate of having the terminal event increases by 65% (i.e., exp(0.5) −1) for every unit increase in the latent variable. For prediction of subject-specific survival probabilities, a specified and smooth baseline hazard function is desired. To this end, we again adopt a truncated power series spline basis expansion $h_0(t)=\text{exp}\{{\eta }_0+{\eta }_{1}t+{\sum }_{r=1}^R{\xi }_r{(t-{\kappa }_r)}_{+}\}$ and assume $\mathit{\xi }={({\xi }_1,\dots ,{\xi }_R)}^{\prime }~N(0,{\sigma }_{\xi }^2\mathit{I})$ to introduce smoothing. The knot locations can be the same or different from those in equation (3).

In equation (4), different formulations can be used to postulate how the risk for a terminal event depends on the unobserved disease severity score at time t. For example, one can add to equation (4) a time-dependent slope ${\theta }_i^{\prime }(t)$, so that the risk depends on both the current severity score and the slope of the severity trajectory at time t (refer to as ‘Model 2: time-dependent slope model’):

$$h_i(t)=h_0(t)\text{exp}\{{\mathit{W}}_i\mathit{\gamma }+{\nu }_1{\theta }_i(t)+{\nu }_2{\theta }_i^{\prime }(t)\}.$$ (5)

Alternatively, one can consider the standard formulations of joint models that include only the random effects in the Cox model (refer to as ‘Model 3: shared random effects model’):

$$h_i(t)=h_0(t)\text{exp}\{{\mathit{W}}_i\mathit{\gamma }+{\mathit{\nu }}^{\prime }{\mathit{u}}_i\}.$$ (6)

A good summary of these various formulations in the joint modeling framework can be found in Rizopoulos et al. (2014) and Yang, Yu and Gao (2016).

The log-likelihood of observing event outcome t_i and δ_i for patient i is l_s(Θ_s; t_i, δ_i,u_i, ζ, ξ) = log{h_i(t_i)^δ_iS_i(t_i)}, where the survival function $S_i(t_i)=\text{exp}\{-{\int }_0^{t_i}{h}_i(s)ds\}$ and the parameter vector for the survival process is Θ_s = (γ′, ν, η₀, η₁, σ_ξ)′. Note that the truncated power series spline basis expansion in modeling the smooth time function in equation (3) and in modeling the baseline hazard function is linear function of time, which results in tractable integration in the survival function S_i(t_i), and consequently, significant gain in computing efficiency. Conditional on the random effect vector u_i, y_i is assumed to be independent of t_i. The penalized log-likelihood of the joint model for patient i given random effects u_i and smoothing parameters σ_ζ, σ_ξ is

$$l(\mathbf{\Theta },\mathit{\zeta },\mathit{\xi };·)=l_y({\mathbf{\Theta }}_y;{\mathit{y}}_i,{\mathit{u}}_i,\mathit{\zeta })+l_s({\mathbf{\Theta }}_s;t_i,{\delta }_i,{\mathit{u}}_i,\mathit{\zeta },\mathit{\xi })-\frac{1}{{\sigma }_{\zeta }^2}{\mathit{\zeta }}^{\prime }\mathit{\zeta }-\frac{1}{{\sigma }_{\xi }^2}{\mathit{\xi }}^{\prime }\mathit{\xi },$$ (7)

where the unknown parameter vector $\mathbf{\Theta }={({\mathbf{\Theta }}_y^{\prime },{\mathbf{\Theta }}_s^{\prime })}^{\prime }$.

3.2. Bayesian inference

To infer the unknown parameter vector Θ, we use Bayesian inference based on Markov chain Monte Carlo (MCMC) posterior simulations. The fully Bayesian inference has many advantages. First, MCMC algorithms can be used to estimate exact posterior distributions of the parameters, while likelihood-based estimation only produces a point estimate of the parameters, with asymptotic standard errors (Dunson, 2007). Second, Bayesian inference provides better performance in small samples compared to likelihood-based estimation (Lee and Song, 2004). In addition, it is more straightforward to deal with more complicated models using Bayesian inference via MCMC. We use vague priors on all elements in Θ. Specifically, the prior distributions of parameters ν, η₀, η₁, and all elements in vectors β and γ are N(0, 100). We use the prior distribution b_k ~ Uniform(0, 10), k = 2, . . . ,K, to ensure positivity. The prior distribution for the difficulty parameter a_k of the continuous outcomes is a_k ~ N(0, 100). To obtain the prior distributions for the threshold parameters of ordinal outcome k, we let a_k1 ~ N(0, 100), and a_kl = a_k,l−1 +Δ_l for l = 2, . . . , n_k − 1, with Δ_l ~ N(0, 100)I(0, ), i.e., normal distribution left truncated at 0. We use the prior distribution Uniform[−1, 1] for all the correlation coefficients ρ in the covariance matrix Σ, and Inverse-Gamma(0.01, 0.01) for all variance parameters. We have investigated other selections of vague prior distributions with various hyper-parameters and obtained very similar results.

The posterior samples are obtained from the full conditional of each unknown parameter using Hamiltonian Monte Carlo (HMC) (Duane et al., 1987) and No-U-Turn Sampler (NUTS, a variant of HMC) (Hoffman and Gelman, 2014). Compared with the Metropolis-Hastings algorithm, HMC and NUTS reduce the correlation between successive sampled states by using a Hamiltonian evolution between states and by targeting states with a higher acceptance criteria than the observed probability distribution, leading to faster convergence to the target distribution. Both HMC and NUTS samplers are implemented in Stan, which is a probabilistic programming language implementing statistical inference. The model fitting is performed in Stan (version 2.14.0) (Stan Development Team, 2016) by specifying the full likelihood function and the prior distributions of all unknown parameters. For large datasets, Stan may be more efficient than BUGS language (Lunn et al., 2000) in achieving faster convergence and requiring smaller number of samples (Hoffman and Gelman, 2014). To monitor Markov chain convergence, we use the history plots and view the absence of apparent trends in the plot as evidence of convergence. In addition, we use the Gelman-Rubin diagnostic to ensure the scale reduction R̂ of all parameters are smaller than 1.1 as well as a suite of convergence diagnosis criteria to ensure convergence (Gelman et al., 2013). After fitting the model to the training dataset (the dataset used to build the model) using Bayesian approaches via MCMC, we obtain M (e.g., M = 2, 000 after burn-in) samples for the parameter vector Θ₀ = (Θ′, ζ′, ξ′)′. To facilitate easy reading and implementation of the proposed joint model, a Stan code has been posted in the Web Supplement. Note that Stan requires variable types to be declared prior to modeling. The declaration of matrix Σ as a covariance matrix ensures it to be positive-definite by rejecting the samples that cannot produce positive-definite matrix Σ. Please refer to the Stan code in the Web Supplement for details.

3.3. Dynamic prediction framework

We illustrate how to make prediction for a new subject N, based on the available outcome histories ${\mathit{y}}_N^{\{t\}}=\{{\mathit{y}}_N(t_{Nj});0\le t_{Nj}\le t\}$ and the covariate historry ${\mathit{X}}_N^{(t)}=\{{\mathit{X}}_N(t_{Nj}),{\mathit{Z}}_N(t_{Nj}),{\mathit{W}}_N;0\le t_{Nj}\le t\}$ up to time t, and δ_N = 0 (no event). We want to obtain two personalized predictive measures: the longitudinal trajectories y_Nk(t′), for k = 1, . . . ,K, at a future time point t′ > t (e.g., t′ = t + Δt), and the probability of functional disability before time t′, denoted by ${\pi }_N(t^{\prime }\mid t)=p(T_N^{\ast }\le t^{\prime }\mid T_N^{\ast }>t,{\mathit{y}}_N^{\{t\}},{\mathit{X}}_N^{\{t\}})$. To do this, the key step is to obtain samples for patient N’s random effects vector u_N from its posterior distribution $p({\mathit{u}}_N\mid T_N^{\ast }>t,{\mathit{y}}_N^{\{t\}},{\mathbf{\Theta }}_0)$. Specifically, conditional on the mth posterior sample ${\mathbf{\Theta }}_0^{(m)}$, we draw the mth sample of the random effects vector u_N from its posterior distribution

$$\begin{array}{l}p({\mathit{u}}_N\mid T_N^{\ast }>t,{\mathit{y}}_N^{(t)},{\mathbf{\Theta }}_0^{(m)})=\frac{p({\mathit{y}}_N^{\{t\}},T_N^{\ast }>t,{\mathit{u}}_N\mid {\mathbf{\Theta }}_0^{(m)})}{p({\mathit{y}}_N^{\{t\}},T_N^{\ast }>t\mid {\mathbf{\Theta }}_0^{(m)})}\propto p({\mathit{y}}_N^{\{t\}},T_N^{\ast }>t,{\mathit{u}}_N\mid {\mathbf{\Theta }}_0^{(m)})\\ =p({\mathit{y}}_N^{\{t\}}\mid {\mathit{u}}_N,{\mathbf{\Theta }}_0^{(m)})p(T_N^{\ast }>t\mid {\mathit{u}}_N,{\mathbf{\Theta }}_0^{(m)})p({\mathit{u}}_N\mid {\mathbf{\Theta }}_0^{(m)}),\end{array}$$

where the first equality is from Bayes theorem.

For each of ${\mathbf{\Theta }}_0^{(m)}$, m = 1, . . .,M, we use adaptive rejection Metropolis sampling (Gilks, Best and Tan, 1995) to draw 50 samples of random effects vector u_N and retain the final sample. This process is repeated for the M saved values of Θ₀. Suppose that patient N does not develop functional disability by time t′, then the outcome histories are updated to ${\mathit{y}}_N^{\{t^{\prime }\}}$. We can dynamically update the posterior distribution to $p({\mathit{u}}_N\mid T_N^{\ast }>t^{\prime },{\mathit{y}}_N^{(t^{\prime })},{\mathbf{\Theta }}_0^{(m)})$, draw new samples, and obtain the updated predictions.

With the M samples for patient N’s random effects vector u_N, predictions can be obtained by simply plugging in realizations of the parameter vector and random effects vector { ${\mathbf{\Theta }}_0^{(m)},{\mathit{u}}_N^{(m)}$, m = 1, . . .,M}. For example, the mth sample of continuous outcome y_Nk(t′) is obtained from equations (1) and (3):

$$y_{Nk}^{(m)}(t^{\prime })=a_k^{(m)}+b_k^{(m)}\left\{{\mathit{X}}_N(t^{\prime }){\mathit{\beta }}^{(m)}+{\mathit{Z}}_N(t^{\prime }){\mathit{u}}_N^{(m)}+{\mathit{V}}_R(t^{\prime }){\mathit{\zeta }}^{(m)}\right\}+{\epsilon }_{Nk}^{(m)}(t^{\prime }),$$

where the random errors ${\epsilon }_{Nk}^{(m)}(t^{\prime })~N(0,{\sigma }_{{\epsilon }_k}^{2(m)})$, and each parameter is replaced by the corresponding element in the mth sample { ${\mathbf{\Theta }}_0^{(m)},{\mathit{u}}_N^{(m)}$}.

Similarly, the mth sample of ordinal outcome y_Nk(t′) = l with l = 1, 2, . . . , n_k is

$$\text{logit}\{p(y_{Nk}^{(m)}(t^{\prime })\le l)\}=a_{kl}^{(m)}-b_k^{(m)}\{{\mathit{X}}_N(t^{\prime }){\mathit{\beta }}^{(m)}+{\mathit{Z}}_N(t^{\prime }){\mathit{u}}_N^{(m)}+{\mathit{V}}_R(t^{\prime }){\mathit{\zeta }}^{(m)}\}.$$

The probability of being in category l is $p(y_{ik}^{(m)}(t^{\prime })=l)=p(y_{ik}^{(m)}(t^{\prime })\le l)-p(y_{ik}^{(m)}(t^{\prime })\le l-1)$. The mth sample of the hazard of patient i at time t′ is

$$h_N^{(m)}(t^{\prime }\mid {\mathit{u}}_N^{(m)})=h_0^{(m)}(t^{\prime })\text{exp}\{{\mathit{W}}_N{\mathit{\gamma }}^{(m)}+{\nu }^{(m)}[{\mathit{X}}_N(t^{\prime }){\mathit{\beta }}^{(m)}+{\mathit{Z}}_N(t^{\prime }){\mathit{u}}_N^{(m)}+{\mathit{V}}_R(t^{\prime }){\mathit{\zeta }}^{(m)}]\}.$$

Thus, the conditional probability of functional disability before time t′ is

$$\begin{array}{l}{\widehat{\pi }}_N(t^{\prime }\mid t)=\int p(T_N^{\ast }\le t^{\prime }\mid T_N^{\ast }>t,{\mathit{y}}_N^{\{t\}},{\mathit{X}}_N^{\{t\}},{\mathit{u}}_N)p({\mathit{u}}_N\mid T_N^{\ast }>t,{\mathit{y}}_N^{\{t\}},{\mathit{X}}_N^{\{t\}})d{\mathit{u}}_N\\ \approx \frac{1}{M}\sum _{m=1}^{M}p\left(T_N^{\ast }\le t^{\prime }\mid T_N^{\ast }>t,{\mathit{y}}_N^{\{t\}},{\mathit{X}}_N^{\{t\}},{\mathit{u}}_N^{(m)}\right)\\ =\frac{1}{M}\sum _{m=1}^M\left\{1-\frac{p(T_N^{\ast }>t^{\prime }\mid {\mathit{y}}_N^{\{t\}},{\mathit{X}}_N^{(t)},{\mathit{u}}_N^{(m)})}{p(T_N^{\ast }>t\mid {\mathit{y}}_N^{\{t\}},{\mathit{X}}_N^{\{t\}},{\mathit{u}}_N^{(m)})}\right\}\\ =\frac{1}{M}\sum _{m=1}^M\left\{1-\text{exp}\left(-{\int }_t^{t^{\prime }}{h}_N^{(m)}(s\mid {\mathit{u}}_N^{(m)})ds\right)\right\},\end{array}$$

where the integration with respect to u_N in the first equality is approximated using Monte Carlo method. Note that the truncated power series spline basis expansion in modeling the smooth time function in equation (3) and in modeling the baseline hazard function results in tractable integration not only in the survival function S_N(t_N), but also in the integration of hazard function in the last equality. All prediction results can then be obtained by calculating simple summaries (e.g., mean, variance, quantiles) of the posterior distributions of M samples { $y_{Nk}^{(m)}(t^{\prime })$, m = 1, . . .,M}. Note that although it may take a few hours to obtain enough posterior samples for the parameter vector Θ₀, it only takes a few seconds to obtain the prediction results for a new subject. Hence, the dynamic prediction framework and the web-based calculator (detailed in Section 4) can provide instantaneous supplemental information for PD clinicians to monitor disease progression.

3.4. Assessing predictive performance

It is essential to assess the performance of the proposed predictive measures. Here, we focus on the probability π(t′|t). Specifically, we assess the discrimination (how well the models discriminate between patients who had the event from patients who did not) using the receiver operating characteristic (ROC) curve and the area under the ROC curves (AUC) and assess the validation (how well the models predict the observed data) using the expected Brier score (BS).

3.4.1. Area under the ROC curves

Following the notation in Section 3.3, for any given cut point c ∈ (0, 1), the time-dependent sensitivity and specificity are defined as $\text{sensitivity}(c,t,t^{\prime }):P\{{\pi }_i(t^{\prime }\mid t)>c\mid N_i(t,t^{\prime })=1,T_i^{\ast }>t\}$ and $\text{specificity}(c,t,t^{\prime }):P\{{\pi }_i(t^{\prime }\mid t)\le c\mid N_i(t,t^{\prime })=0,T_i^{\ast }>t\}$, respectively, where $N_i(t,t^{\prime })=I(t<T_i^{\ast }\le t^{\prime })$, indicating whether there is an event (case) or no event (control) observed for subject i during the time interval (t, t′]. In the absence of censoring, sensitivity and specificity can be simply estimated from the empirical distribution of the predicted risk among either cases or controls. To handle censored event times, Li, Greene and Hu (2016) proposed an estimator for the sensitivity and specificity based on the predictive distribution of the censored survival time:

$$\begin{array}{r}\widehat{P}\{{\pi }_i(t^{\prime }\mid t)>c\mid N_i(t,t^{\prime })=1,T_i^{\ast }>t\}=\frac{{\sum }_{i=1}^n{\widehat{W}}_i(t,t^{\prime })I\{{\widehat{\pi }}_i(t^{\prime }\mid t)>c\}}{{\sum }_{i=1}^n{\widehat{W}}_i(t,t^{\prime })}\\ \widehat{P}\{{\pi }_i(t^{\prime }\mid t)\le c\mid N_i(t,t^{\prime })=0,T_i^{\ast }>t\}=\frac{{\sum }_{i=1}^n[1-{\widehat{W}}_i(t,t^{\prime })]I\{{\widehat{\pi }}_i(t^{\prime }\mid t)\le c\}}{{\sum }_{i=1}^n[1-{\widehat{W}}_i(t,t^{\prime })]},\end{array}$$ (8)

where Ŵ_i(t, t′) is the weight to account for censoring and it is defined as

$$\begin{array}{l}{\widehat{W}}_i(t,t^{\prime })=I(t<t_i\le t^{\prime }){\delta }_i+I(t<t_i\le t^{\prime })(1-{\delta }_i)P\{T_i^{\ast }<t^{\prime }\mid T_i^{\ast }\ge t_i,{\widehat{\pi }}_i(t^{\prime }\mid t)\}\\ =I(t<t_i\le t^{\prime }){\delta }_i+I(t<t_i\le t^{\prime })(1-{\delta }_i)\left[1-\frac{P\{T_i^{\ast }\ge t^{\prime }\mid {\widehat{\pi }}_i(t^{\prime }\mid t)\}}{P\{T_i^{\ast }\ge t_i\mid {\widehat{\pi }}_i(t^{\prime }\mid t)\}}\right].\end{array}$$

Note that the subjects who have the survival event before time t (i.e., t_i < t) have their estimated weight Ŵ_i(t, t′) = 0 and thus they play no role in equation (8). The conditional survival distribution $P\{T_i^{\ast }\ge \stackrel{\sim }{t}\mid {\widehat{\pi }}_i(t^{\prime }\mid t)\}$, where t̃ can be either t′ or t_i, can be estimated using kernel weighted Kaplan-Meier method with a bandwidth d, which can be easily implemented in standard survival analysis software accommodating weighted data:

$$P\{T_i^{\ast }\ge \stackrel{\sim }{t}\mid {\widehat{\pi }}_i(t^{\prime }\mid t)\}=\prod _{s\in \mathrm{\Omega },s\le \stackrel{\sim }{t}}\left[1-\frac{{\sum }_{i^{\prime }\ne i}{K}_d\{{\widehat{\pi }}_{i^{\prime }}(t^{\prime }\mid t),{\widehat{\pi }}_i(t^{\prime }\mid t)\}I(T_{i^{\prime }}=s){\delta }_{i^{\prime }}}{{\sum }_{i^{\prime }\ne i}{K}_d\{{\widehat{\pi }}_{i^{\prime }}(t^{\prime }\mid t),{\widehat{\pi }}_i(t^{\prime }\mid t)\}I(T_{i^{\prime }}\ge s)}\right],$$

where Ω is the set of distinct t_i’s with δ_i = 1 and K_d is the kernel function, e.g., uniform and Gaussian kernels. Specifically, we use uniform kernel in this article.

With the estimation of sensitivity and specificity, the time-dependent ROC curve can be constructed for all possible cut points c ∈ (0, 1) and the corresponding time-dependent AUC(t, t′) can be estimated using standard numerical integration methods such as Simpson’s rule.

3.4.2. Dynamic Brier score

The Brier score (BS) developed in survival models can be extended to joint models for prediction validation (Sène et al., 2016; Proust-Lima et al., 2014). The dynamic expected BS is defined as E[(D(t′|t) − π(t′|t))²], where the observed failure status D(t′|t) equals to 1 if the subject experiences the terminal event within the time interval (t, t′] and 0 if the subject is event free until t′. An estimator of BS is

$$\widehat{\text{BS}}(t,t^{\prime })=\frac{1}{N_t}\sum _{i=1}^{N_t}{\widehat{G}}_i(t,t^{\prime }){(D_i(t,t^{\prime })-{\pi }_i(t^{\prime }\mid t))}^2,$$

where N_t is the number of subjects at risk at time t, and the weight ${\widehat{G}}_i(t,t^{\prime })=\frac{I(t_i>t^{\prime })}{{\widehat{S}}_0(t^{\prime })/{\widehat{S}}_0(t)}+\frac{I(t<t_i\le t^{\prime }){\delta }_i}{{\widehat{S}}_0(t_i)/{\widehat{S}}_0(t)}$ is to account for censoring with Ŝ₀ denoting the Kaplan-Meier estimate (Sène et al., 2016).

AUC and BS complement each other by assessing different aspects of the prediction. AUC has a simple interpretation as a concordance index, while BS accounts for the bias between the predicted and true risks. In general, AUC = 1 indicates perfect discrimination and AUC = 0.5 means no better than random guess, while BS = 0 indicates perfect prediction and BS = 0.25 means no better than random guess. Blanche et al. (2015) provides excellent illustration of AUC and BS.

4. Application to the DATATOP study

In this section, we apply the proposed joint model and prediction process to the motivating DATATOP study. For all results in this section, we run two parallel MCMC chains with overdispersed initial values and run each chain for 2, 000 iterations. The first 1, 000 iterations are discarded as burn-in and the inference is based on the remaining 1, 000 iterations from each chain. Good mixing properties of the MCMC chains for all model parameters are observed in the trace plots. The scale reduction R̂ of all parameters are smaller than 1.1.

In order to validate the prediction and compare the performance of candidate models, we conduct a 5-fold cross-validation, where 4 partitions of the data are used to train the model and the left-out partition is used for validation and model selection. Then we fit the final selected model to the whole dataset, except that 2 patients are set aside for subject-specific prediction purpose. The covariates of interest included in equation (3) are baseline disease duration, baseline age, treatment (active deprenyl only), time, and the interaction term of treatment and time. We allow a flexible and smooth disease progression along time by using penalized truncated power series splines with 7 knots at the location κ = (1.2, 3, 6, 9, 12, 15, 18) in months, to ensure sufficient patients within each interval. Specifically, euqation (3) is

$${\theta }_i(t_{ij})={\beta }_0+{\beta }_1{\text{duration}}_i+{\beta }_2{\text{age}}_i+{\beta }_3{\text{trt}}_i+{\beta }_4{t}_{ij}+{\beta }_5({\text{trt}}_i\times t_{ij})+\sum _{r=1}^7{\zeta }_r{(t_{ij}-{\kappa }_r)}_{+}+u_{i0}+u_{i1}{t}_{ij},$$

where the random effects (u_i0, u_i1)′ ~ N₂(0,Σ) with $\mathbf{\sum }=\{({\sigma }_1^2,\rho {\sigma }_1{\sigma }_2),(\rho {\sigma }_1{\sigma }_2,{\sigma }_2^2)\}$ and $\mathit{\zeta }~N(0,{\sigma }_{\zeta }^2\mathit{I})$ to avoid overfitting.

For the survival part, three different formulations are considered as discussed in Section 3.1. For instance, the shared latent variable model (Model 1) is h_i(t) = h₀(t) exp(γ₁duration_i + γ₂age_i + γ₃trt_i + νθ_i(t)). The proposed time-dependent slope model (Model 2) and shared random effects model (Model 3) can be obtained by replacing νθ_i(t) with ${\nu }_1{\theta }_i(t)+{\nu }_2{\theta }_i^{\prime }(t)$ and ν′u_i, respectively. The baseline hazard h₀(t) is similarly approximated by penalized splines $h_0(t)=\text{exp}\{{\eta }_0+{\eta }_{1}t+{\sum }_{r=1}^7{\xi }_r{(t-{\kappa }_r)}_{+}\}$ and $\mathit{\xi }~N(0,{\sigma }_{\xi }^2\mathit{I})$. In addition, we compared the proposed model with two standard predictive models for time to event data, (1) a widely used univariate joint model (refer to as Model JM), where the continuous UPDRS is used as the longitudinal outcome regressing on same covariates of interest and the survival part is constructed in the same structure, and (2) a naive Cox model adjusted for time-independent covariates including all baseline characteristics as well as UPDRS, HY and SEADL scores.

We compare the performance of all candidate models in terms of discrimination and validation using 5-fold cross-validation and present AUC and BS score in Table 1 and Web Table 1. All of the three formulations of the proposed MLLTM joint model outperform the univariate Model JM (except AUC(t = 3, t′ = 9)) and naive Cox model with larger AUC and smaller BS in most of the scenarios, suggesting that the MLLTM model accounting for multivariate longitudinal outcomes are preferable in terms of prediction. The three formulations have very similar performance with close AUC and BS. Model 1 is selected as our final model, because it leads to a straightforward interpretation of the overall covariate effect described in Section 3.1 and it is more intuitive to use the trajectory of latent variable θ_i(t) to predict the time to event as in Model 1, instead of using time-dependent slope ${\theta }_i^{\prime }(t)$ or random effects u_i as in Models 2 and 3. The results also suggest that AUC increases by using more follow up measurements, e.g., in Model 1, conditional on the the measurement history up to month 3 (i.e., t = 3), when t′ = 15, AUC(t = 3, t′ = 15) = 0.744, while AUC increase to AUC(t = 12, t′ = 15) = 0.766, indicating that conditional on the measurement history up to month 12, our model has 0.766 probabilities to correctly assign higher probability of functional disability by month 15 to more severe patients (who had functional disability earlier) than less severe patients (who had functional disability later). Meanwhile, BS decreases from BS(3, 15) = 0.216 to BS(12, 15) = 0.108, i.e., the mean square error of prediction decreases from 0.216 to 0.108, suggesting better prediction in terms of validation.

Table 1.

Area under the ROC curve and Brier score (BS) for the DATATOP study.

t	t′	Model 1		Model 2		Model 3		Model JM		Cox
		AUC	BS	AUC	BS	AUC	BS	AUC	BS	AUC	BS
3	9	0.754	0.136	0.759	0.138	0.761	0.139	0.757	0.140	0.736	0.139
	12	0.744	0.204	0.744	0.200	0.744	0.200	0.739	0.203	0.725	0.203
	15	0.744	0.216	0.742	0.212	0.744	0.211	0.726	0.218	0.719	0.212
	18	0.775	0.171	0.766	0.163	0.772	0.167	0.728	0.186	0.720	0.185
6	9	0.789	0.078	0.806	0.078	0.806	0.078	0.770	0.081	0.721	0.094
	12	0.764	0.159	0.778	0.154	0.775	0.154	0.732	0.164	0.705	0.173
	15	0.763	0.183	0.771	0.178	0.771	0.178	0.725	0.194	0.697	0.194
	18	0.786	0.158	0.773	0.154	0.769	0.159	0.726	0.175	0.701	0.175
12	15	0.766	0.108	0.787	0.103	0.782	0.102	0.695	0.124	0.647	0.155
	18	0.758	0.149	0.739	0.147	0.723	0.153	0.700	0.161	0.663	0.163

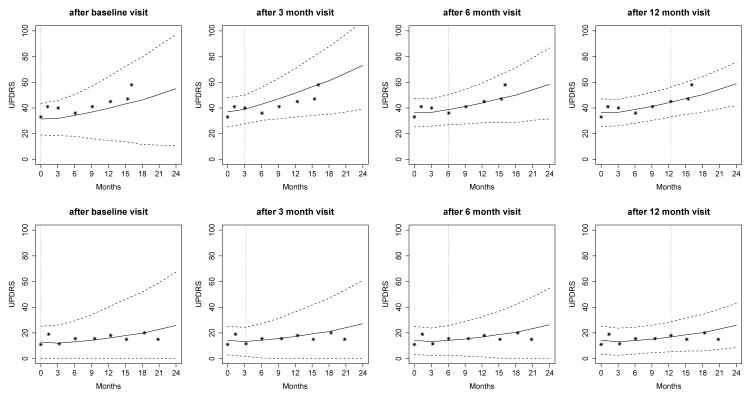
Parameter estimates based on Model 1 are presented in Table 2 and Web Table 2 (outcome-specific parameters only). To illustrate the subject-specific predictions, we set aside two patients from the DATATOP study and predict their longitudinal trajectories as well as the probability of functional disability at a clinically relevant future time point, conditional on their available measurements. A more severe Patient 169 with clinically worse longitudinal measures and earlier development of functional disability as well as a less severe Patient 718 are selected. Patient 169 had 8 visits with mean UPDRS 42.6 (SD 7.7), median HY 2, median SEADL 80, and developed functional disability at month 16. In contrast, Patient 718 had 9 visits with mean UPDRS 15.6 (SD 3.1), median HY 1, median SEADL 95, and was censored at month 21. Figure 2 displays the predicted UPDRS trajectories for these two patients, based on different amounts of data. When only baseline measurements are used for prediction, the predicted UPDRS trajectory is biased with wide uncertainty band. For example, Patient 169 had a relatively low baseline UPDRS value of 33 and our model based only on baseline measurements tends to underpredict the future UPDRS trajectory (t_i = 0, the first plot in upper panels). However, Patient 169’s higher UPDRS values of 41 and 40 at months 1 and 3, respectively, subsequently shift up the prediction and tend to overpredict the future trajectory (t_i = 3 months, the second plot in upper panels). By using more follow-up data, predictions are closer to the true observed values and the 95% uncertainty band is narrower (t_i = 6 or 12 months, the last two plots in upper panels). Patient 169’s predicted UPDRS values after 12 months are above 40 and increase rapidly, indicating a higher risk of functional disability in the near future. In comparison, the predicted UPDRS values for Patient 718 are relatively stable because his/her observed UPDRS values are relatively stable.

Table 2.

Parameter estimates for the DATATOP study from Model 1.

	Mean	SD	95%	CI
For latent disease severity
Int	−0.738	0.338	−1.385	−0.081
Duration (months)	0.021	0.004	0.014	0.028
Age (years)	0.024	0.005	0.014	0.035
Trt (deprenyl)	−0.108	0.099	−0.304	0.099
Time (months)	0.021	0.025	−0.028	0.070
Trt × Time	−0.089	0.010	−0.109	−0.071
ρ	0.310	0.044	0.226	0.393
σ1	1.328	0.051	1.230	1.430
σ2	0.116	0.006	0.104	0.128
σε	5.081	0.074	4.933	5.226
For survival process
Duration (months)	−0.009	0.004	−0.017	−0.002
Age (years)	−0.034	0.006	−0.045	−0.024
Trt (deprenyl)	−0.608	0.118	−0.846	−0.375
ν	0.692	0.039	0.618	0.769

Fig 2.

Predicted UPDRS for Patient 169 (upper panels) and Patient 718 (lower panels). Solid line is the mean of 2000 MCMC samples. Dashed lines are the 2.5% and 97.5% percentiles range of the 2000 MCMC samples. The dotted vertical line represents the time of prediction t.

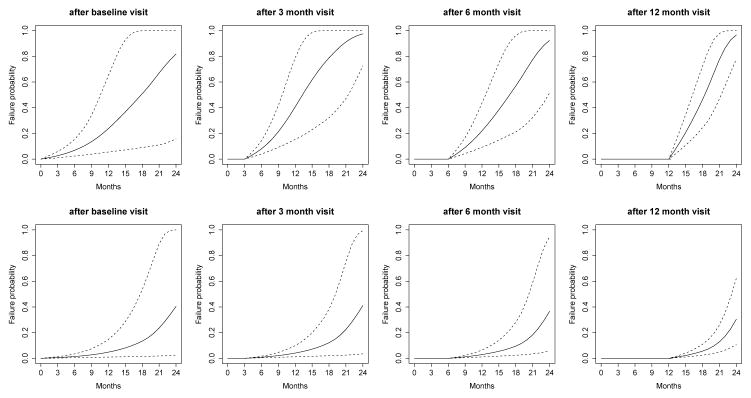
The predicted probability being in each category for outcomes HY and SEADL are presented in Web Figures 1 and 2, respectively. Please refer to the Web Supplement for the interpretation. Besides the predictions of longitudinal trajectories, it is more of clinical interest for patients and clinicians to know the probability of functional disability before time t′ > t: π_i(t′|t), conditional on the patient’s longitudinal profiles up to time t and the fact that he/she did not have functional disability up to time t. The predicted probabilities for Patients 169 and 718 based on various amount of data are presented in Figure 3. A similar pattern is that the prediction becomes more accurate if more data are used. With such predictions, clinicians are able to precisely track the health condition of each patient and make better informed decisions individually. For example, based on the first 12 months’ data, for Patient 169, the predicted probabilities in the next 3, 6, 9 and 12 months are 0.21, 0.46, 0.78 and 0.97 (the last plot of upper panels), while for Patient 718, the probabilities are 0.02, 0.06, 0.13 and 0.30 (the last plot of lower panels). Patient 169 has higher risk of functional disability in the next few months and clinicians may consider more invasive treatments to control the disease symptoms before the functional disability is developed.

Fig 3.

Predicted conditional failure probability for Patient 169 (upper panels) and Patient 718 (lower panels). Solid line is the mean of 2000 MCMC samples. Dashed lines are the 2.5% and 97.5% percentiles range of the MCMC samples.

To facilitate the personalized dynamic predictions in clinical setting, we develop a web-based calculator available at https://kingjue.shinyapps.io/dynPred_PD. A screenshot of the user interface is presented in Web Figure 3. The calculator requires as input the PD patients’ baseline characteristics and their longitudinal outcome values up to the present time. The online calculator will then produce time-dependent predictions of future health outcomes trajectories and the probability of functional disability, in addition to the 95% uncertainty bands. Moreover, additional data generated from more follow-up visits can be input to obtain updated predictions. The calculator is a user friendly and easily accessible tool to provide clinicians with dynamically-updated patient-specific future health outcome trajectories, risk predictions, and the associated uncertainty. Such a translational tool would be relevant both for clinicians to make informed decisions on therapy selection and for patients to better manage risks.

5. Simulation studies

In this section, we conduct an extensive simulation study to investigate the prediction performance of the probability π(t′|t) using the proposed Model 1. We generate 200 datasets with samples size n = 800 subjects and six visits, i.e., baseline and five follow-up visits (J_i = 6), with the time vector t_i = (t_i1, t_i2, . . . , t_i6)′ = (0, 3, 6, 12, 18, 24). The simulated data structure is similar to the motivating DATATOP study, and it includes one continuous outcome and two ordinal outcomes (each with 7 categories).

Data are generated from the following models: θ_i(t_ij) = β₀+β₁x_i1+β₂t_ij+ β₃x_i1t_ij+u_i0+u_i1t_ij and h_i(t) = h₀ exp{γx_i2+νθ_i(t)}, where the longitudinal and survival submodels share the latent variable as in proposed Model 1. Covariate x_i1 takes value 0 or 1 each with probability 0.5 to mimic treatment assignment and covariate x_i2 is randomly sampled integer from 30 to 80 to mimic age. We set coefficients β = (β₀, β₁, β₂, β₃)′ = (−1,−0.2, 0.8,−0.2)′, γ = −0.12 and ν = 0.75. For simplicity, baseline hazard is assumed to be constant with h₀ = 0.1. Parameters for the continuous outcome are a₁ = 15, b₁ = 7 and σ_ε = 5. Parameters for the ordinal outcomes are a₂ = (0, 1, 2, 4, 5, 6), a₃ = (−1, 1, 3, 4, 6, 8), b₂ = 1 and b₃ = 1.2. We assume that random effects vector u_i = (u_i0, u_i1)′ follows a multivariate normal distribution N₂(0,Σ), where $\mathbf{\sum }=\{({\sigma }_1^2,\rho {\sigma }_1{\sigma }_2),(\rho {\sigma }_1{\sigma }_2,{\sigma }_2^2)\}$ with σ₁ = 1.5, σ₂ = 0.15 and ρ = 0.4. The independent censoring time is sampled from Uniform(10, 24).

From each simulated dataset, we randomly select 600 subjects as the training dataset and set aside the remaining 200 subjects as the validation dataset. Web Table 3 displays bias (the average of the posterior means minus the true values), standard deviation (SD, the standard deviation of the posterior means), coverage probabilities (CP) of 95% equal tail credible intervals (CI), and root mean squared error (RMSE) of model inference based on the training dataset. The results suggest that the model fitting based on the training dataset provides parameter estimates with very small biases and RMSE and the CP being close to the nominal level 0.95. Using MCMC samples from the fitted model and available measurements up to time t, we make prediction of π_i(t′|t) for each subject in the validation dataset.

Web Table 4 compares the time-dependent AUC based on various amount of data from Model 1, Model JM and naive Cox model. When 3 or 6 months data are available, Model 1 outperforms Model JM and Cox with high discriminating capability and higher AUC values above 0.9. In general, AUC is increasing with more available data, e.g., AUC(3, 12) = 0.920 and AUC(6, 12) = 0.930.

From each of the 200 simulation datasets, we randomly select 20 subjects to plot the bias between the predicted event probability π(t′|t) from Model 1 and the true event probability with t′ = 9 (upper panels) and t′ = 12 (lower panels) in Web Figure 4. When more data are available, bias is decreasing as more bias is within the region of [−0.2, 0.2]. For example, with only baseline data, 5.8% and 21.7% of bias for the predictions of π(t′ = 9|t = 0) and π(t′ = 12|t = 0), respectively, are outside the range. With up to three months’ data, 3.4% and 13.7% of bias for the predictions of π(t′ = 9|t = 3) and π(t′ = 12|t = 3), respectively, are outside the range. With up to six months’ data, the prediction is precise with only 1.2% and 7.7% of bias for the prediction of π(t′ = 9|t = 6) and π(t′ = 12|t = 6), respectively, being outside the range.

6. Discussion

Multiple longitudinal outcomes are often collected in clinical trials of complex diseases such as Parkinson’s disease (PD) to better measure different aspects of disease impairment. However, both theoretical and computational complexity in modeling multiple longitudinal outcomes often restrict researchers to a univariate longitudinal outcome. Without careful analysis of the entire data, pace of treatment discovery can be dramatically slowed down.

In this article, we first propose a joint model that consists of a semiparametric multilevel latent trait model (MLLTM) for the multiple longitudinal outcomes by introducing a continuous latent variable to represent patients’ underlying disease severity, and a survival submodel for the event time data. The latent variable modeling effectively reduces the number of outcomes and has improved computational feasibility and model interpretability. Next we develop the process of making personalized dynamic predictions of future outcome trajectories and risks of target event. Extensive simulation studies suggest that the predictions are accurate with high AUC and small bias. We apply the method to the motivating DATATOP study. The proposed joint models can efficiently utilize the multivariate longitudinal outcomes of mixed types, as well as the survival process to make correct predictions for new subjects. When new measurements are available, predictions can be dynamically updated and become more accurate and efficient. A web-based calculator is developed as a supplemental tool for PD clinicians to monitor their patients’ disease progression. For subjects with high predicted risk of functional disability in the near future, clinicians may consider more targeted treatment to defer the initiation of levodopa therapy because of its association with motor complications and notable adverse events (Brooks, 2008). Although the dynamic prediction framework has utilized only three longitudinal outcomes in the DATATOP study, it can be broadly applied to similar studies with more longitudinal outcomes.

There are some limitations in our proposed dynamic prediction framework that we will address in the future study. First, the semiparametric MLLTM submodel assumes a univariate latent variable (unidimensional assumption), which may be reasonable for small number of outcomes. However, for large number of longitudinal outcomes, multiple latent variables may be required to fully represent the true disease severity across different domains impaired by PD. We will develop a multidimensional latent trait model that allows multiple latent variables. Second, Proust-Lima, Amieva and Jacqmin-Gadda (2013) and Proust-Lima, Dartigues and Jacqmin-Gadda (2016) proposed a flexible multivariate longitudinal model that can handle mixed outcomes, including bounded and non-Gaussian continuous outcomes. In contrast, our model (1) only applied to normally distributed continuous outcomes. In our future research, we would like to extend the dynamic prediction framework to accommodate more general continuous outcomes including bounded and non-Gaussian variables. Third, we have chosen multivariate normal distribution for the random effects vector because it is flexible in modeling the covariance structure within and between longitudinal measures of patients and it has meaningful interpretation on correlation. In fact, misspecification of random effects and residuals has little impact on the parameters that are not associated with the random effects (Jacqmin-Gadda et al., 2007; Rizopoulos, Verbeke and Molenberghs, 2008; McCulloch et al., 2011). The impact of misspecification in the proposed modeling framework warrants further investigation. Alternatively, we will relax the normality assumption by considering Bayesian non-parametric (BNP) framework based on Dirichlet process mixture (Escobar, 1994).

Equation (2) for ordinal outcome requires the proportional odds assumption. Statistical tests to evaluate this assumption in the traditional ordinal logistic regression have been criticized for having a tendency to reject the null hypothesis, when the assumption holds (Harrell, 2015). Tests of the proportional odds assumption in the longitudinal latent variable setting are not well established, and the consequence of violating the assumption is unclear and is worth future examination. Three different functional forms of joint models that allow various association between the longitudinal and event time responses are examined and they provide comparable predictions in the DATATOP study. Instead of selecting a final model in terms of simplicity and easy interpretation, a Bayesian model averaging (BMA) approach to combine joint models with different association structures (Rizopoulos et al., 2014) will be investigated in future study. In addition, missed visits and missing covariates exist in the DATATOP study. In this article, we assume that they are missing at random (MAR). However, the missing data issue becomes more complicated in prediction model framework because it can impact both the model inference (missing data in the training dataset) and dynamic prediction process (e.g., the new subject only has measurements of UPDRS and HY, but not SEADL). How to address this issue in the proposed prediction framework is an important direction of future research. Moreover, the online calculator is based on the DATATOP study, which may not represent PD patients at all stages and from all populations. Nonetheless, the large and carefully studied group of patients provides an important resource to study the clinical expression of PD. We will continue to improve the calculator by including more heterogeneous PD patients from different studies.