Inversed-planned Respiratory Phase Gating in Lung Conformal Radiotherapy

Abstract

Background and Purpose

Respiratory gating is a frequently-used clinical motion-management strategy in lung radiotherapy. In conventional gating, the beam is turned on during a pre-determined window; typically, around end-exhalation (EE). In this work, we postulate that the optimal gating window for each beam will be dependent on a variety of patient-specific factors, such as tumor size and location, and the extent of relative tumor and organ motion.

Material and Methods

In order to create optimal gating treatment plans, we started from an optimized clinical plan, created a plan per respiratory phase using the same beam arrangements, and used an inverse planning optimization approach to determine the optimal gating window for each beam and optimal beam weights, i.e., monitor units (MUs). Two pieces of information were used for optimization: (i) the state of the anatomy at each phase, extracted from 4D CT scans, and (ii) the time spent in each state, estimated from a 2-minute monitoring of the patient’s breathing motion. We retrospectively studied 15 lung cancer patients clinically treated by hypofractionated conformal radiation therapy, where 45 – 60 Gy was administered over 3 – 15 fractions using 7 – 13 beams. Mean gross tumor volume and respiratory-induced tumor motion was 82.5 cc and 1.0 cm, respectively.

Results

Although patients spent most of their respiratory cycle in EE, our optimal gating plans used EE for only 34% of the beams. Using optimal gating, maximum and mean doses to esophagus, heart and spinal cord were reduced by an average of 15 – 26% and the beam-on times were reduced by an average of 23% compared to equivalent single-phase EE gated plans (p < 0.034, paired, two – tailed T – test).

Conclusions

We introduce a personalized respiratory-gating technique where inverse planning optimization is used to determine patient- and beam-specific gating phases towards enhancing dosimetric quality of radiotherapy treatment plans.

Introduction

Managing respiratory motion is one of the major challenges in modern thoracic and abdominal radiation therapy [1, 2]. Motion-induced uncertainties can cause significant geometric and dosimetric errors in lung radiotherapy [3, 4]. In hypofractionated regimens, where higher doses are delivered in fewer fractions, the impact of such errors is further amplified [5]. In this work, we focus on respiratory gating which is one of the most frequently-used techniques for managing respiratory motion uncertainties. According to Pan et al.’s survey on stereotactic body radiation therapy (SBRT) usage in the US, 54.2% of the lung and 57.9% of the liver radiotherapy physicians reported using respiratory gating [6].

In conventional respiratory-gated treatment planning, irradiation is triggered during pre-decided fixed intervals (called gating windows) in the patient’s respiratory cycle. The percentage of one period of the respiratory cycle during which the beam is actually “on” is called the duty cycle. Ideally, the consideration of a gating window within the respiratory cycle leads to a reduced motion-induced uncertainty, and hence, results in an improved tumor conformity and OAR sparing. Therefore, respiratory gating has been shown to yield an enhanced overall local control and survival [7, 8]. In a gated treatment plan, the efficiency of completing the treatment delivery is variable relative to the gating duty cycle, while the treatment accuracy is dependent on the stability and reproducibility of the target during the chosen gating window. Therefore, although lung volume is the largest during end-inhalation (EI), giving higher chances to reduce OAR and normal tissue irradiation, EE is the most preferred gating phase due to the stability and reproducibility of target position as well as a longer duty cycle [9–12]. This preference for EE gating window, however, constitutes a perceived benefit that has not been fully and objectively quantified.

Our goal in this study is to individualize respiratory gating using the facts that (i) breathing patterns are patient-specific [13] and (ii) respiratory-induced anatomical changes seen at beams’ eye views are beam-specific and dependent on tumor location and size. To this end we use the core idea used in phase-adaptive 4D treatment planning using inverse plan optimization [14]. Wink et al. have studied an individualized gating technique, where tumor motion extent was used to determine the optimal length for the gating window [12]. Other researchers studied image guidance and internal markers for creating an adaptive or dynamic gating window [15–17]. In these personalized gating studies, the gating phase was predetermined and kept fixed on either EI or EE, as in standard gating, while the window length was changed. In our work, however, we use patient-specific 4D CT images and patient-specific breathing patterns to determine the optimal gating phase for each beam and for each patient while keeping the gating window length fixed to a single phase. The 4D CT scans in our study are phase-binned and a 2-min breathing record is acquired during the 4D CT acquisition. This work is limited to conformal radiation therapy (CRT) as this is the most commonly used technique for hypofractionated non-small-cell lung cancer (NSCLC) radiotherapy [6, 18–21]. We use the same beam arrangements as the clinically delivered plan, define planning target volumes (PTVs) on each phase, and calculate 3D CRT plans on each phase using the clinical treatment planning system to generate N_phases × N_beams apertures, where N_phases and N_beams are the number of phases and beams. We use an inverse planning approach that employs a metaheuristic global optimization algorithm, particle swarm optimization (PSO [22]), to determine the optimal MUs per beam and identify an optimal gating phase for each beam. Similar approach has previously been demonstrated by Modiri et al. for 4D treatment planning in [23]. For evaluation, we compare the resulting optimal plans with their equivalent single-phase EE-gated plans in terms of dosimetric quality and beam-on time.

Methods and Materials

We chose fifteen early stage NSCLC patients treated with hypofractionation (3–15 fractions), giving preference to patients exhibiting significant motion (≥ 5 mm). This was a retrospective study using de-identified patient data, under an umbrella IRB protocol for retrospective studies in our institution. The chosen patients were clinically treated by CRT. The clinical plans were composed of 7 – 13 beams. Tumors ranged from 3.9 to 479.4 cc in gross tumor volume (GTV) and exhibited motion from 0.5 to 1.5 cm. The prescribed doses (45 – 60 Gy) were administered over 3 – 15 fractions (see TABLE I). Target 3D motions were measured as the distance between tumor centroids at EI and EE in treatment planning system.

TABLE I.

Target and prescription details for the 15 patients of this study

Patient	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
GTV volume (cc)	129	61	5	9	25	110	41	113	479	104	28	100	4	16	14
Abdominal Compression	No	Yes	Yes	Yes	Yes	Yes	No	No	No	No	No	Yes	Yes	Yes	Yes
Target motion (cm)	1.5	1.5	1.5	1.0	1.0	0.8	1.0	0.7	0.5	0.6	1.3	0.5	0.9	1.0	1.1
Tumor location	RLL1	RLL	RML2	LLL3	LUL4	RUL5	RUL	LUL/C6	RUL/C	LUL/C	LLL	LLL	LUL	LLL	LLL
Prescription Gy × fx	12 × 5	10 × 5	12 × 5	12 × 5	18 × 3	12 × 5	18 × 3	10 × 5	3 × 15	12 × 5	18 × 3	12 × 5	18 × 3	10 × 5	18 × 3

¹Right lower

²Right middle lobe

³Left lower lobe

⁴Left upper lobe

⁵Right upper lobe

⁶Central: within 2cm proximity of tracheobronchial tree

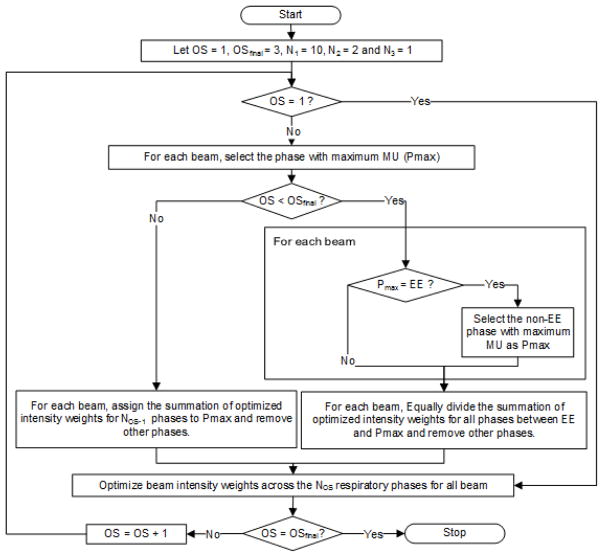
For each patient, the target and normal structures were manually contoured on the EE volume of 4D CT by a dosimetrist and deformably propagated across phases using Velocity V3.0.1, a commercial deformable-image-registration tool (Varian Medical Systems, Palo Alto, CA). The quality of contour propagation was inspected visually by a clinician and modifications were made where required. Ten respiratory phases were considered and the corresponding ten individual-phase CRT plans were created in the Eclipse treatment planning system (Research Eclipse V13.6). Dose deposition matrices per beam were then exported for MU weight optimization. Our in-house PSO engine was used to perform a multistage optimization for inverse planning (See FIG 1). The optimization goal was to find only one optimal phase per beam for gating while improving the dosimetric quality of the plans; i.e., reducing OAR dose while maintaining tumor coverage. In the first optimization stage (OS1), the algorithm iteratively optimized the MU weights for all beams across all ten phases (N₁=10). Then, keeping the EE phase, one other candidate respiratory phase per beam was identified and the beam intensities were re-optimized (OS=2, N₂=2). The non-EE candidate phase (P_max) was the phase with the largest MU (after scaling beam MUs by their optimized weights). In the final stage (OS=3), for each beam, the algorithm chose one phase (N₃=1) as optimal phase (either EE or the candidate phase) and re-optimized the MU weights.

FIG. 1.

The three-stage optimization for optimal gating inverse planning, where the number of gating windows per beam gradually reduces from N1=10 to N3=1 over the three optimization stages (OSs). At OS3, a candidate non-EE phase (Pmax) competes with the EE phase.

We used 20 particles and 30 iterations (10 iterations per OS) for all optimization runs and employed the same objective function as in [23]. In each iteration cycle, the total dose (D_Total) was calculated as

$$\begin{array}{l}{D}_{\mathit{Total}}={\sum }_{j=1}^{N_{\mathit{phase}}}\mathit{DIR}\{{\sum }_{i=1}^{N_{\mathit{beams}}}{D}_{ij}\times w_{ij}\}\\ w_{ij}=p_j\times x_{ij}{x}_{ij}\ge 0\end{array}$$ (1)

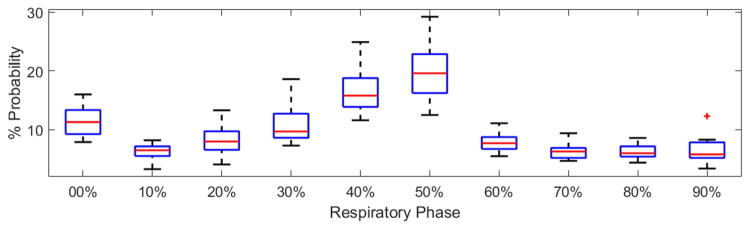
where N_phases and N_beams are the number of phases and beams, respectively. DIR denotes the deformable image registration operator (we integrated NiftyReg, an open source package [24], into our optimization code). The structure contours, previously approved by a clinician, were used to validate DIR performance using dice coefficients. D_ij and x_ij are the dose deposition matrix and MU weight for beam i at respiratory phase j, and p_j is the probability of respiratory phase j. To have a fair comparison, same optimization engine and objective function were used to optimize EE-gated plans (Single-stage optimization using 20 particles and 30 iterations). For each patient, respiratory phase probabilities (indicative of the time duration of respiratory phases) were estimated from a 2-minute recording, which was previously captured using Philips bellows pneumatic belt (FIG 2).

FIG. 2.

Box-whisker illustration of the respiratory phase probabilities for 15 patients, where the central mark indicates the median, and the bottom and top edges of the box indicate the 25th and 75th percentiles, respectively. The outliers are shown using ‘+’. See Appendix A for a detailed quantification of the respiratory phase probabilities per patient.

Our in-house PSO algorithm minimized summation of normalized weighted squared errors for (i) maximum and volume-based doses to esophagus, heart and spinal cord, (ii) the 95% tumor coverage with 100% prescribed dose, and (iii) lung V₁₃ (the percentage lung volume receiving ≥ 13 Gy). We used the objective function introduced by Modiri et al. in [23], where dose-volume constraints were included, and therefore, the problem was non-convex in nature. PSO’s global search and parallelizability were its key features for being chosen as our solver. PSO has been successfully used in radiotherapy inverse planning of non-convex solution space in previous studies such as [23]. Our MATLAB prototype took ≤1.5 hrs to optimize each case; however, this process time may potentially be significantly reduced using compiled language platforms.

Our inverse planning process allowed the possibility of having MU weights equal to zero, so that the optimization algorithm could eliminate some beams toward achieving better dosimetric results. Nonetheless, to have a fair comparison, for each patient, the same beam sets were used for inverse planning optimization of both optimal gating and EE gating. Percentage dose reduction in OARs (dosimetric gains) achieved from optimal gating (OG) versus single-phase EE gating (EG) were calculated as

$$\mathrm{\Delta }=100\times (OG-EG)/EG.$$ (4)

Also, the total beam-on time was calculated as

$$T_{\mathit{BeamON}}={\sum }_{i=1}^{N_{\mathit{beams}}}\frac{M{U}_i}{S}\times {\sum }_{j=1}^{N_{\mathit{phase}}}\frac{w_{ij}}{p_j}={\sum }_{i=1}^{N_{\mathit{beams}}}\frac{M{U}_i}{S}\times x_i$$ (5)

where S is the treatment machine dose rate. Note that each beam is delivered during one phase only; therefore, the summation over phases (sigma over j) is removed, and x_i is used instead of x_ij.

Results

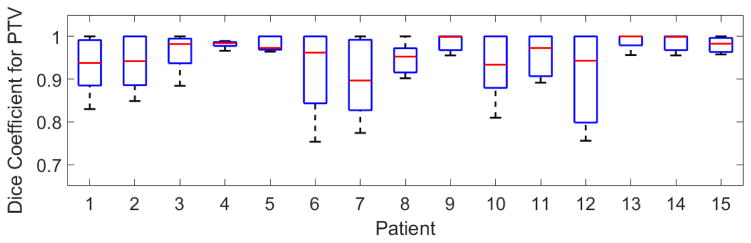
FIG 3 shows dice coefficients calculated for NiftyReg registration for the fifteen patients in this study.

FIG. 3.

Dice coefficient variation for PTV over nine floating respiratory phases, registered on one reference phase (EE), for the 15 patients of this study

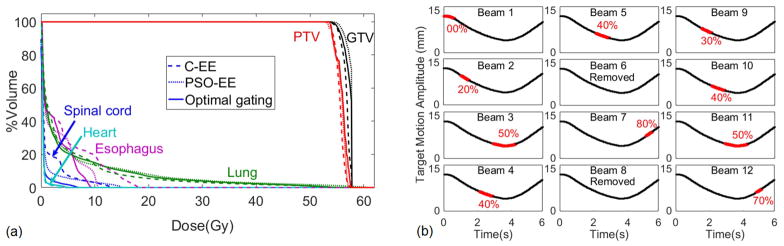
We compared the dose volume histograms of (i) the clinical EE (C-EE) plans, which were created in our clinical treatment planning system (Eclipse) using clinically assigned beam arrangement and conforming beam apertures to PTV at EE, (ii) EE optimized plans (PSO-EE), which were the C-EE plans after being optimized by our in-house PSO, and (iii) our proposed optimal gating plans, which were created using our in-house PSO to identify optimal beam MUs and optimal gating phases per beam. As shown in the example case in FIG 4(a), PSO-EE plans were superior to C-EE plans in terms of OAR sparing while maintaining PTV coverage. Therefore, we considered it a fair comparison to compare the proposed optimal gating plans with their optimized EE equivalents (PSO-EE plans). The dosimetric comparison of the three above-mentioned plans for all patients are included in Appendix B.

FIG. 4.

(a) Dose volume histogram comparison of the clinical EE (C-EE) plan (dashed line), the optimized EE (PSO-EE) plan (dotted line), and our proposed optimal gating plan (solid line) are shown for one of the patients of this study (patient 5). (b) For the 12 clinical beams of this case study, the beam-specific optimal gating windows are shown in red over one respiratory cycle. Two out of twelve beams (6 and 8) were removed by the optimizer. The beam-on time for this patient was 31 minutes (Appendix C).

FIG 4(b) shows the beam-specific gating windows for the 12 clinical beams of the corresponding plan (patient 5). The optimization algorithm eliminated two beams (beams 6 and 8) and adjusted the weights of the remained ten (see TABLE I for tumor specifications).

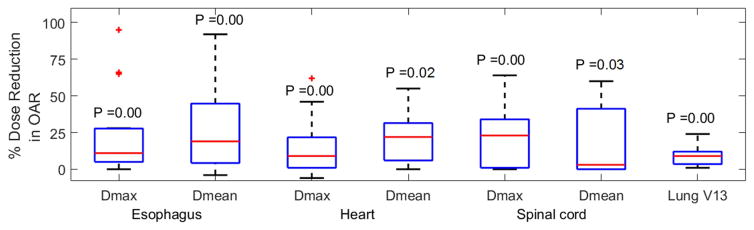
Dose reduction to OARs achieved through optimal gating is summarized in FIG 5. Detailed quantification of dose comparisons is given in Appendix C. We found statistically significant results for 15 patients (paired two-tailed T-test p ≤ 0.034), where, on average, [maximum and mean] doses given to esophagus, heart and spinal cord were reduced by [23% and 26%], [15% and 22%] and [23% and 19%], respectively, as compared to equivalent optimized EE-gated plans. Lung V₁₃ was reduced by 9%.

FIG. 5.

Percentage dose reduction in OARs achieved from optimal gating versus PSO-EE are shown. P (paired two-tailed T-test) values are added to the figure for each dosimetric quantity. Box whisker graphs have the same specification as FIG 2.

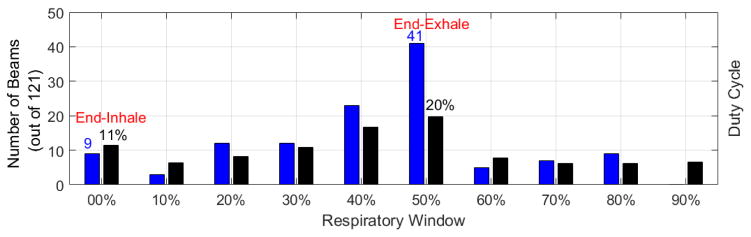
In FIG 6, the optimal gating windows chosen by our optimization algorithm are depicted. The duty cycles for the ten respiratory windows were not identical because respiratory phase lengths were not equal. All beams for all patients, 121 beams, are shown in this figure. Note that some beams were eliminated during the optimization process. Although patients were spending most of their respiratory cycles in EE phase, the optimization algorithm chose EE for no more than 34% of beam-patient cases. Only for one patient (patient 10), out of 15, the optimization algorithm chose EE for gating all beams. These results present a significant contrast to the conventional clinical gating paradigm, where typically EE is used for gating all beams. In FIG 6, the probability of a phase being chosen by the algorithm well follows the probability of that phase happening in the patient respiratory cycle.

FIG. 6.

The number of beams (out of 121) which were chosen by our optimization process to be gated at different gating windows are shown with blue bars and the duty cycles, corresponding to each phase, averaged over 15 patients, are shown with black bars.

We observed that, on average, optimal gating could decrease the total beam-on time by 23%. To calculate the beam-on time per fraction (T_BeamON), treatment machine dose rate (S = 600 MU/minute) and respiratory cycle length (6 seconds) were considered to be constant (see Appendix C).

Discussion

In this work, we investigated the idea of inverse-planned optimal beam-specific and patient-specific respiratory gating, where the states of anatomy and respiratory phase lengths were used to determine optimal gating windows. We showed statistically significant results for 15 patients (p ≤ 0.034), where, on average, dose to esophagus, heart and spinal cord were reduced by ≥ 19%. The magnitude of dosimetric improvements were dependent on tumor location as well as respiratory-induced motion range and tumor size. For instance, we observed that percentage dose reduction for esophagus D_max was highly correlated with the ratio of tumor motion to tumor volume. However, for heart D_max or spinal cord D_max, percentage dose reduction was highly dependent on tumor location. In this study, 9 out of 15 patients had abdominal compression, which was a limiting factor in the level of improvements we could achieve using our optimal gating method. In 10 out of 15 cases, the PSO-EE plans already satisfied the clinical constraints. However, it was seen that in 14 out of 15 cases optimal gating technique reduced dose to OARs and for the remaining case, OAR dose was the same with both techniques. This result proves that inverse optimized gating is a potential technique for dosimetrically superior treatment plans in lung hypofractionation.

We also showed that our optimal gating technique decreased the total beam-on time, on average, by 23%, while in 3 cases, the beam-on times were not shortened. Mainly, the beam-on times changed because MU weights and gating windows were being adjusted. Furthermore, the algorithm was allowed to remove some of the clinically assigned beams by giving them a zero weight, and therefore, the number of beams were optimized (reduced) along with the MU weights. As a future work, this study can be extended to include variable gating window lengths, and thus, variable delivery efficiencies.

This work was focused on CRT which has been reported to be used 2.3 times more frequently than IMRT in NSCLC radiation therapy [25]. Prior to our optimization, beam intensities and aperture shapes were calculated in Eclipse treatment planning system for each respiratory phase, creating deliverable plans. Our optimization algorithm adjusted beam MU weights, without changing aperture shapes, and identified optimal gating phases per beam. This way, the optimized plans stayed deliverable while beam-on times varied. Our technique provides an inverse-optimization-based framework for improving the quality of respiratory-gated dose delivery, where the specific solution (i.e, gating window and MU per beam) will depend on the choice and prioritization of clinical objectives such as target coverage and OAR dose constraints.

While non-trivial, the basic concept described in this study is extendible to more complex delivery techniques such as IMRT, where each beam has hundreds of apertures (control points). For example, for an optimally gated IMRT delivery, Eq. (1) changes to

$$\begin{array}{l}{D}_{\mathit{Total}}={\sum }_{j=1}^{N_{\mathit{phase}}}\mathit{DIR}\{{\sum }_{i=1}^{N_{\mathit{beams}}}{\sum }_{k=1}^{N_{\mathit{apertures}}}{D}_{\mathit{ijk}}\times w_{\mathit{ijk}}\}\\ w_{\mathit{ijk}}=p_j\times x_{\mathit{ijk}}{x}_{\mathit{ijk}}\ge 0\end{array}$$ (6)

where N_apertures is the number of apertures per beam. Assuming that we are gating per beam, Eq. (5) changes to

$$T_{\mathit{BeamON}}={\sum }_{i=1}^{N_{\mathit{beams}}}\frac{M{U}_i}{S}\times \{{\sum }_{j=1}^{N_{\mathit{phases}}}\{\frac{1}{p_j}\times {\sum }_{k=1}^{N_{\mathit{apertures}}}{w}_{\mathit{ijk}}\}\}={\sum }_{i=1}^{N_{\mathit{beams}}}\frac{M{U}_i}{S}\times {\sum }_{k=1}^{N_{\mathit{apertures}}}{x}_{ik}$$ (7)

Eq. (6) and (7) show that extending our technique to IMRT involves optimizing for a large number of variables (aperture MU weights), thereby significantly increasing the computational complexity. Using graphics processing units (GPUs) is a strong solution for handling the added computational complexity [26].

Extension to other complex radiotherapy techniques may need substantial change in the problem modeling and formulation. For example, in volumetric modulated arc therapy (VMAT), in addition to the parameters considered herein, several additional issues need to be considered for optimally gated VMAT, such as gantry movement (e.g., mechanical constraints for stops and re-starts and dose rate ramp-up times), patient-specific synchronization of the gantry speed with the breathing pattern, etc. The mathematical formulation for such treatment planning is beyond the scope of the present study.

One limitation of our study is that gating and dose delivery over non-EE and non-EI phases, chosen by our optimizer, is challenging because these phases are short in length and hard to reproduce at the presence of breathing variation. Breathing irregularities can affect our proposed method in two ways: 1- incorrect estimation of anatomy (organ and tissue shapes and positions), and 2- incorrect estimation of the time duration of each respiratory phase. Our planning technique is vulnerable to the first uncertainty, because our proposed method relies on 4D CT scans as a priori knowledge of the anatomy at each respiratory phase. However, the second uncertainty can be managed by changing beam-on time. For example, let’s assume that the optimal gating technique chooses 40% as the gating window for one beam. Let’s also assume that the estimated duration of phase 40%, based on a 2-minute respiration recording, is 0.8 seconds. If the patient breaths irregularly and the time duration of phase 40% changes to 0.4 seconds, the dosimetric results won’t vary; however, the beam-on time for that beam will be doubled and the plan delivery efficiency will be affected accordingly. Nevertheless, our planning technique is vulnerable to situations where, for example, due to breathing irregularity, phase 40% completely disappears from patient’s breathing cycle over the course of treatment. In such situations, the dosimetric results of our planning technique will be affected. This limitation may be overcome by introduction of improved techniques in real-time monitoring of patient respiration and adaptive radiotherapy [27, 28].

CONCLUSION

The standard method of using a fixed respiratory phase, typically end-of-exhale, for respiratory gating does not necessarily result in the best OAR sparing. We used an inverse planning optimization approach to identify the optimal gating window for each beam. Our optimization algorithm chose end of exhale for 34% of beams (46 out of 121 beams); i.e., for 66% of beams, end of exhale was not chosen as optimal gating window. We also showed that although optimal gating can decrease dose to OARs by 15% to 26% and total beam-on time by 23% compared to equivalent end-exhale gating. These results mean that although optimal gating introduces a more complex planning strategy and may likely involve more effort for quality assurance (QA), it results in an enhanced dosimetric quality compared to conventional, forward-planned gating without compromising treatment delivery efficiency.

Summary.

The standard method of using a fixed respiratory phase, typically end-of-exhale, for respiratory gating does not necessarily result in the best OAR sparing. We use an inverse planning optimization approach and identify the patient-specific optimal gating phase for each beam considering (i) the state of the anatomy at each respiratory phase and (ii) the time spent in each phase.