Abstract
The concept of motifs provides a fresh perspective for studying local patterns, which is useful for understanding the essence of a network structure. However, few previous studies have focused on the evolutionary characteristics of weighted motifs while further considering participants’ differences. We study how information connections differ among multiple investors. The evolutionary 10-year trend of weighted 3-motifs in China’s energy stock markets is explored for the networks of co-holding behaviors among shareholders, who are classified as companies, funds and individuals. Our works allow us to detect the preferential local patterns distributed among different agents as their fluctuate involvement in networks. We find that the diversity of shareholders contributes to the statistical significance of local patterns, while homophily always exist among individuals. Modules of information connections are stable among reserved investors, which is especially apparent among companies. Individuals prefer to keep their connections with companies and funds. Unsteady modules happen owing to strengthen links among funds during the time that they are main participants in stock markets. More details about multiple investors informationally connected in evolutionary local patterns can be detected by our work.
Introduction
How does one complete a puzzle? Apart from knowing the whole picture at first glance of the general graphical structure, the task requires much more attention to the blocks. In fact, although the information from each block is different, the shape of them normally can be classified into a limited number of types, which promotes the reconstruction of the whole puzzle. Similarly, motifs, which are defined as ‘recurring and significant patterns of interconnections’1, are the simple structural blocks of complex networks. It has been proven that motifs play essential roles in network evolution2 and optimization3. Considering multi agents into one unit, motifs are suitable for understanding financial behaviors among diverse investors, which is a long-standing issue for explaining herding effects in stock markets4–6. Theoretical analysis has approved the importance of information connections in diffusing signals about stocks that traders receive for making financial behaviors7,8. As a result, how investors are informationally connected has drawn large attention from researchers. To identify information links from realized trades8, common shareholdings have been widely adopted as a structural perspective to describe information connections among investors9,10. Since the necessity of considering investor heterogeneity11 into the studies of trading activities has been recognized, the problem of characterizing the distribution of information connections among diverse investors remains open. In this paper, we study how information connections differ among multiple investors, which is revealed by evolutionary weighted motifs.
The concept of motifs provides a platform to study local network patterns12, especially the interactions among agents. Since it was first proposed by Milo et al.1, the concept of motifs has grown in its importance13–15, and has been widely applied to international trade16,17, the internet3, transportation18, social contagion19, and biological systems20,21. Latent variable modeling22, which includes Gaussian process latent variable model23, t-distributed stochastic neighbor embedding24, locally linear embedding and so on, are introduced for motif-finding with quick speed and high quality. Graph-theories are combined for financial analysis on time series to reveal underlying connectivity structure25,26. These studies approve motifs’ function in different application fields. Instead of requiring the statistical significance, recent studies extend the definition of motifs as a class of equivalent sub-graphs27. Based on this more general concept, both for communication networks, Li et al.28 explore motifs’ temporal characteristics, while Kovanen et al.29 consider attributes such as sex and age to classify agents in motifs. They approve that more structural features can be revealed by the motifs with the classification of components. However, not much is known about evolving weighted motifs among multiple investors. In our study, evolutionary characteristics would be explored for the motifs with the classification of both agents and links.
Components classified motifs provide a microscopic perspective for understanding local information connections among multiple investors. In one aspect, investors with different financial attributes always have specific investment preferences11. Previous works have manifested their differences in responses to the stock information30, and financial interactions among a certain type of investors are studied31,32. In another aspect, there are significant differences in closeness among investors based on their investment similarities7 and geological closeness33. The weak tie theory34 makes the interaction among investors much more complex because of the tendency of receiving information signals beyond neighbors. Apart from social connections4,35,36, co-holding behaviors in the same listed companies’ stock are widely adopted to describe information connections in recent works7–9. It reflects investor shareholding similarities37, which leads to the formation of paths for information diffusion in a local pattern38. Pareek8 examined its effect on investors’ trading behaviors, which approves the networks feasibility. Li et al.9 measured the evolutionary stability for China’s listed energy companies by associated maximal connected sub-graphs from the perspective of global pattern. Apart from these valuable works with a global perspective, more details need to be explored by exploring local patterns. In this paper, we introduce weighted motifs to model investors of different types into one unit with consideration of their co-holding strength.
In our study, evolutionary weighted motifs and agents’ financial attributes are both considered to explore local co-holding patterns among shareholders. Considering the importance to stable society and economic development, Chinese listed companies and shareholders whose main business is energy are selected as the case, and the evolution period is from 2006 to 2015. After knowing the components in co-holding networks, we first detect weighted motifs and their involved multiple investors in 10 years. Correlative characteristics of motifs’ proportional fluctuation with the changes of network structures are also measured in this part. Further, quantitative researches with more economic interpretations are provided. Statistical importance of local patterns are gauged with the financial classification for agents to discover typical groups of information connected traders. At last, the evolving motifs among multiple investors are detected in both short and long term. This work aims at indicating the dynamic connecting modules as the constitutional fluctuation of different investors.
The remainder of this paper is organized as follows. The next section include the data source and models. Section 3 shows the results classified into six parts: network components, evolutionary motifs, their reflection on network structure, preferential local pattern, motifs’ significance and the local structural evolution. Finally, we discuss interesting findings and conclude the paper in Section 4.
Data and Modeling
Investment data
The source of our data is the Wind financial database (http://www.wind.com.cn/), which provides a professional platform for researchers with various statistical data for the Chinese financial market. Data of stock market can be divided according to the major business run by the listed companies. As a result, we downloaded the data from the Chinese energy stock market on September 14, 2016, including the code and name of Chinese energy listed companies. At the same time, the name of their top 10 circulation shareholders are obtained, which are the only ones that can be disclosed. Circulation shareholders are more fluctuant than un-circulation ones are. We select the time period from 2006 to 2015 to see the evolutionary trend of the basic structural units constructing co-shareholding relations among investors. For convenience, we give each shareholder a unique number following the letter ‘H’.
Based on the information about investors in our data, we classify shareholders into three categories: companies, funds and individuals39. Companies are the institutions which include both energy-related companies, such as Yanzhou Coal Mining Company Limited, and financial investment-related companies, such as Central Huijin Investment Limited. Shareholders, which are classified as funds, are always published by banks. Individuals are the retails actively joining the investment in stock markets.
Co-holding networks and motifs
The motifs are applied to explore the local pattern characteristics based on co-holding behaviors among shareholders. As a result, in this section, we show our methodology from four parts. First, the construction of the complex network is described, which provides a measurement for the basic relations among shareholders. Second, the motifs in our work are introduced, showing all types of local patterns that we can explore from the complex network. Third, to explore the correlations between motifs and the network structure, statistical indicators for the network structure and their corresponding meanings are provided. Further, to quantify these correlations, the Pearson correlation coefficient is adopted for the measurement.
Network modeling
A complex network is used to describe the relations among investors. The original data show the relations between Chinese energy listed companies and their corresponding top 10 circulation shareholders. In our studies, relations among investors are derived from the original data. As Li et al.9 did in their previous studies, we take shareholders as nodes, whether they take a stock share in the same listed company as the edge, and the number of listed companies they co-shareholding as the weight of the edge. That is, we construct a weighted but undirected network to describe the co-holding behaviors among investors. Using to represent shareholders, the matrix A describes the co-holding relations as follows:
| 1 |
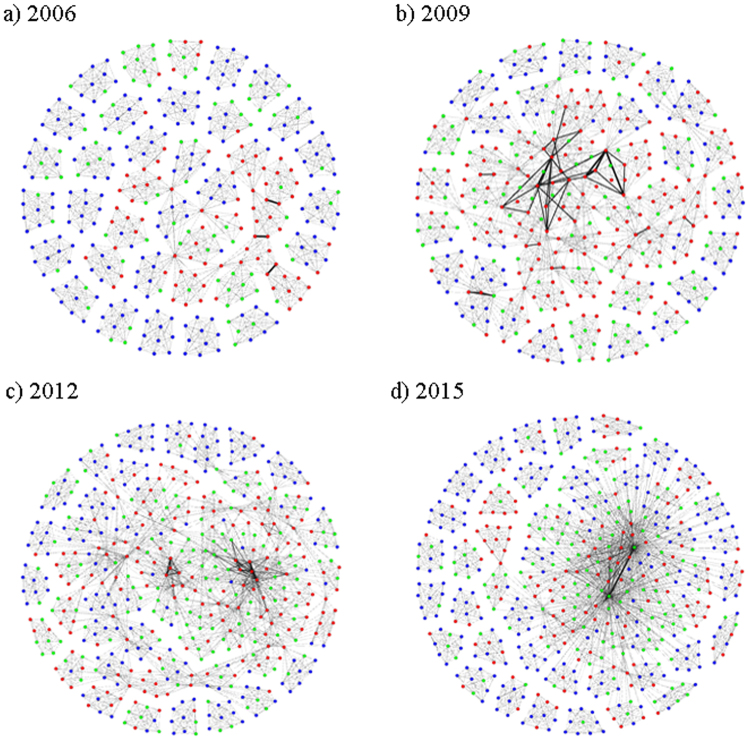
where w ij is the number of listed energy companies that shareholders H i and H j co-hold. Based on this definition, we construct 10 networks for each data unit from 2006 to 2015. Figure 1 shows the example networks for 2006, 2009, 2012 and 2015, where the nodes are shareholders and the links are the co-holding behaviors among them.
Figure 1.
Networks for co-holding behaviors among shareholders in four years. Nodes are colored into three types: Greens are companies, reds are funds and blues are individuals.
Motifs in co-holding networks
Motifs are the basic units of a network, so the recurrence of them contributes to the whole network40. Fluctuations of the number of motifs affect the network structure, whereas structural changes of the network pattern reflect changes in the motif constitutions. Studies on motifs in networks help us better understand the essence of the network structure1. According to the basic definition introduced by Milo et al.1, the recurring patterns of interconnections occurring in the real network at numbers that are significantly higher than in corresponding random network are called motifs1. That is, the subgraphes with low statistical significances always receive less attention from researchers. However, consideration of agents’ attribute into motifs need complete information extraction. As a result, in our study, the extended definition from Onnela et al.41 is adopted, and ‘motifs’ denote to equivalent subgraphes with independence of their statistical significance. 3-motifs are studied since they can model at most three different types of shareholders into one unit, which corresponds to our classification for investors. Each motif involves paths connecting three investors.
Here, two levels of classification for links and nodes in 3-motifs are involved in this paper. First, the weight of connections are classified for 3-motifs, which are shown in Fig. 2(a). For the Chinese energy stock market, a very small number of shareholders co-hold shares in more than two of the same energy listed companies. Therefore, we classify links into two types: strong ones and weak ones41. Thick links in the figure indicate that there are many same listed companies held by two related shareholders, whereas light ones indicate that two shareholders co-hold only one common listed company. Among these bipartite weighted 3-motifs, motif 1, motif 2, motif 3 and motif 7 are the ones with triadic closure. Motif 4 are the open ones with only two connections among three agents. Further, the classification of investors are considered for each weighted 3-motif, and Fig. 2(b) shows an example based on the weighted motif 1 in Fig. 2(a).
Figure 2.
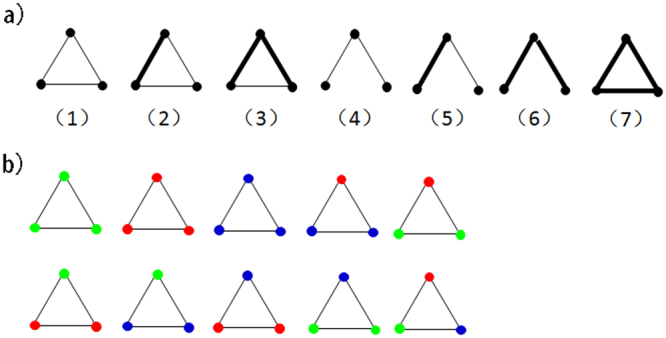
(a) Seven types of weighted triangle motifs. Thick lines as strong co-holding relations and thin lines as weak co-holding relations. (b) Motif 1 with colored investors: Greens are companies, reds are funds and blues are individuals.
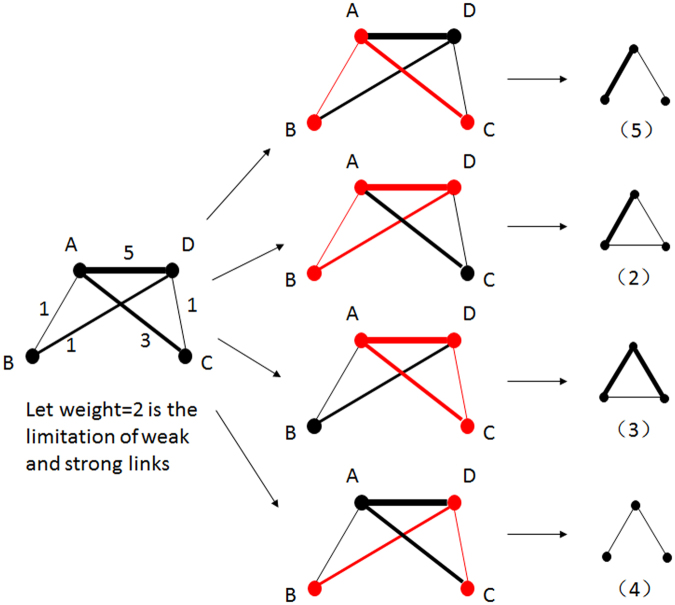
These two levels of classification are used to explore local structural characteristics from different perspectives. Weighted 3-motifs provide general understanding for answering how investors are connected in co-holding networks. Further classification of nodes in 3-motifs provide specific exploration on information connections among multiple investors. It helps to answer how certain types of shareholders are connected. A schematic view of motif calculation is shown in Fig. 3.
Figure 3.
Schematic figure of the motif calculation.
Motifs with statistical significance
Detection of 3-motifs helps to explore information connections among multiple investors. In our study, we introduce Z-score42,43 into our study to measure the importance of 3-motifs in networks. It compares the statistical significance of certain motif in real networks than in the random networks. The basic definition of Z-score, which is widely used in undirected networks, is as follows,
| 2 |
where is the number of motif i in real network. is the number of motif i in random networks, is its average, and is its standard deviation. The motif with higher Z-score value is more important to the network.
For weighted networks, Z-score is promoted with the combination of motifs’ intensity27,44, coherence27,44, entropy45, within-module degree46,47 and so on. According to Onnela et al.27, the Z-score definitions for unweighted network and weighted network coincide for binary weights. Considering the fact that links’ weight in 3-motifs are classified into two types in this work, basic definition of Z-score is adopted to measure structural importance.
Indicators for measuring network structure
The constitution of triangle motifs is a significant reflection of the network structure. As a result, we calculate the indicator values for the global network pattern to see whether there are correlated characteristics between the evolution of network structure and motif composition. To measure the global network pattern, in addition to the number of nodes and edges, we select the following indicators: average weighted degree, network diameter, network density, modularity and average weighted clustering coefficient.
The average weighted degree (AWD) is used to describe each node’s connection with other nodes. A higher value of this indicator infers that most nodes in the network have a high correlation with other nodes with many strong links. The definition is as follows48:
| 3 |
where H denotes the set of shareholders, t represents a shareholder belonging to H, and S WD(t) is t’s weighted degree, which is further defined in this equation. N t is the set of t’s neighbor nodes, k is t’s neighbor, and w tk is the weight of link between t and k.
The network diameter (NDia) is the maximum of all of the nearest routes from one investor to another. Normally, if a network has a relatively low diameter, the relations among agents will be close, and information can be spread among investors over a small amount of time. The definition of network diameter is as follows49:
| 4 |
where t, v are all shareholders belonging to H and L min (t, v) is the smallest number of paths connecting t and v.
The network density (NDen) describes the scale of co-holding behaviors among shareholders. If the network density is large, the co-holding behavior will be a common phenomenon for investors. The measurement of these extensive relations is as follows50:
| 5 |
where m is is the number of shareholders, and n is the number of real edges.
The average weighted clustering coefficient (AWCC) is used to measure the local connection density. It describes whether each node’s neighbor nodes are closely connected with each other. Its definition is as follows27:
| 6 |
where n t is the number of real links among shareholder t’s neighbor investors.
Modularity is an indicator that classifies nodes into different communities according to their closeness. Normally, it is used to measure the linking density inside communities compared with the links between communities. The partition results are better when the modularity value is higher. As a result, this indicator helps determine whether agents have apparent differences in closeness with each other. The definition of modularity is as follows51:
| 7 |
where wij is the weight of the link between i and j, Ai is the weighted degree of i, ci is the community to which i is assigned, δ(ci, cj) is 1 if ci=cj and 0 otherwise, and .
Correlation measurement
To answer whether there is correlative characteristics between the network structure and local patterns, we measure correlations between two fluctuation trends, which is motifs’ percentage and network indicators’ value over ten years. Here, we do not concern how motifs’ constitution contribute to the network structure. As a result, we try to grasp the significant characteristics by correlation coefficient. Previous studies have applied Pearson correlation, Kendall correlation52 and Spearman rank correlation53 for various research fields. These indexes have different consideration for data. Considering our low data size and the focus on correlative features, we adopt Pearson correlation in this work. As one of the most commonly used indicator, we select the Pearson correlation coefficient54 to study the evolution similarities between the network structures and the constitution of motifs from 2006 to 2015. That is, this indicator provides a general perspective to measure how two fluctuation trends are correlated. The coefficient is between −1 and 1, where 1 represents total positive correlation, 0 means no correlation, and −1 indicates total negative correlation.
In our work, the percentages of the seven weighted triangle motifs and seven global network indicators (the number of nodes, the number of edges, average weighted degree, network diameter, network density, modularity and average weighted clustering coefficient) are calculated for each data unit from 2006 to 2015. As a result, the evolutionary trend over 10 years for each motif and indicator can be obtained. The matrix of the Pearson correlation coefficient, R, is defined as follows:
| 8 |
where M is the number of motifs and N is the number of global structural indicators. Thus, M=N=7.
The equation for the Pearson correlation coefficient is as follows:
| 9 |
where r m, n is the Pearson correlation coefficient between motif m and indicator n and t is the number of spot data for each variable. In our study, t=10 is the number of years. is the average percentage value of motif m, which is the same as .
Results and Analysis
Components in co-holding networks
In this part, we explore basic components for co-holding networks to understand who are participating in the China energy stock market, and how they are connected. This work helps to interpret our results economically, and have basic knowledge of the market with consideration of investors’ financial attributes.
We track the scale of different investors for 10 networks respectively, and their percentages are shown in Table 1. Generally, in most years, the percentage of companies is around 30 with a relative steady trend. However, constitutions for funds and individuals are always opposite during these 10 years. From 2006 to 2009, although there is fluctuation, the percentage of funds is increasing while that for individuals is decreasing. Afterwards, both trends reversed, and changed their prominence in 2012. As a result, the scale fluctuation of three types of investors can be typically classified into three phases by the year 2009 and 2012.
Table 1.
Percentage of each type of investors in each year (Unit: %).
| 2006 | 2007 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | |
|---|---|---|---|---|---|---|---|---|---|---|
| Companies | 22.28 | 28.65 | 27.36 | 27.66 | 27.80 | 26.49 | 29.90 | 28.60 | 28.47 | 26.19 |
| Funds | 22.55 | 36.34 | 34.43 | 44.21 | 39.69 | 40.04 | 34.46 | 28.79 | 27.43 | 26.19 |
| Individuals | 55.17 | 35.01 | 38.21 | 28.13 | 32.51 | 33.47 | 35.64 | 42.62 | 44.10 | 47.62 |
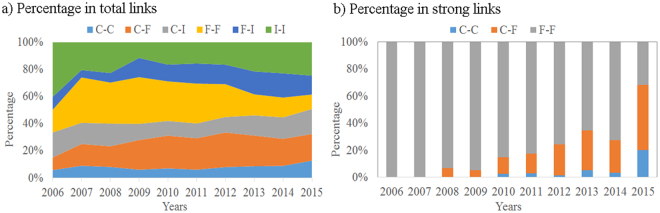
Further, we detect the distribution of co-holding relations among shareholders with different classified financial types. It helps to understand how shareholders are linked with each other based on their investment similarities. Figure 4(a) shows the percentage of co-holding links between shareholders with certain financial’ types in each year. With the consideration of linking strength, for each year, we further count the percentage of these shareholder pairs in the strong links, which is shown in Fig. 4(b).
Figure 4.
Percentage of links between pairs of shareholders with certain types. The percentage of shareholder pairs in certain financial types with (a) co-holding links or (b) thick links.
From Fig. 4(a), we find that the distribution of co-holding relations has been equalized in recent two years. During the early times, there are high percentage of funds co-holding stocks with themselves. This trend has been decreased as the increase of co-holding relations between companies and funds. However, although strong links account a very little proportion in total co-holding links (the highest proportion is 2.78% in 2015), the distribution of them has apparent preference. Figure 4(b) approves that most strong links happen among funds, and it is relieved only in recent years as the rising participation of companies. For companies, our results show that they have expansion investment on energy listed companies. These results also reveal the investment limitation of individuals. Although they are always the main participants, their stocks always in a low number of limited companies. On the contrary, funds in the Chinese stock market come from certain number of banks. As a result, the funds from same banks would perform the overlap of their investment.
The constitution of components shows a fluctuant stock market. The involvement of multiple investors differs in each year, and their co-holding behaviors are unevenly distributed. This situation asks for an evolutionary perspective to study the local information connections among multiple investors. At the same time, considering the close relations between motifs and network structure, the works in this part provide references for explaining motif-related results in latter sections.
Constitution of 3-motifs
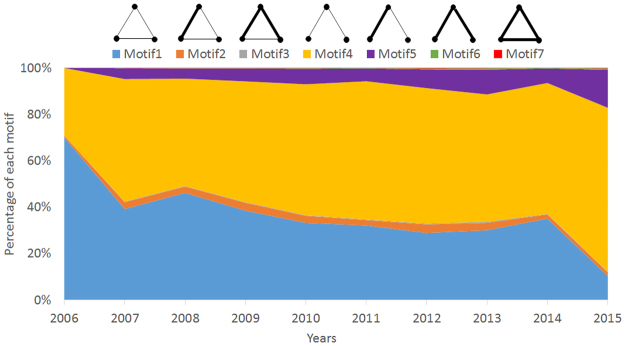
Constitution of motifs help to reveal the basic local co-holding patterns among shareholders. In this part, without the consideration of statistical significance, we explore all seven weighted triangle motifs for the Chinese energy stock market from 2006 to 2015. Here, investors are not classified in order to know general existence of motifs in co-holding networks. To compare the evolution of each type of motifs, we calculate their percentages in a total of seven types of motifs but not the numbers. Figure 5 provides the results.
Figure 5.
Evolution of each type of weighted triangle motif measured by their percentage in co-holding networks, from 2006 to 2015.
The results show an apparent trend of the motif constitution over these 10 years in Chinese energy stock market. Networks are mainly composed by motif 1 and motif 4. As the steady increasing proportion of motif 4, motif 1 counts a decreasing percentage. The constitution reveals that the relations based on co-holding behaviors widely exist, but the connections are weak. However, in recent years, more couples of investors appear stronger shareholding overlaps. The more distinct rising trend of motif 5 than motif 2 approves that limited strong links always happen in the local pattern with less closely connections. In general, nodes in motif 1 can reach each other within one path. However, in motif 4, its structure looks like a tree being rooted with an intermediate agent, and two leaf-like nodes have to reach each other through 2 paths. Since the average linking cost for open motifs is higher than closed motifs, the proportional growth of motif 4 means a more scattered network structure over years, and the interaction of investment behavior would be slower.
Based on the above results, the local patterns for Chinese energy stock market exhibit apparent changes and fluctuation. In recent years, the co-holding behavior has gotten stronger, but stable relations have decreased, which has led to much higher indirect and long spreading paths.
Associative characteristics with network patterns
The changes of network structure is the reflection of the fluctuation of local co-holding patterns. It is hard to quantitatively describe their bilateral correlations, but the correlation of their fluctuation trend can reveal their associated characteristics. Patterns of co-holding networks are described by statistical indicators from different perspectives. The results have been shown in Fig. 6. Each block represents the Pearson correlation coefficient between the motif proportion and the indicator value during 10 years. The colors provide intuition for our results, and their meanings are shown in the legend. Dark red is a fully positive correlation, and dark blue represents a fully negative correlation.
Figure 6.
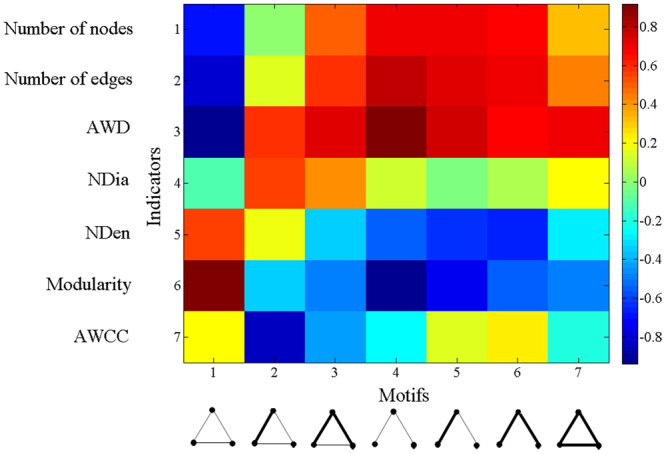
Pearson correlation coefficient (in each block) between the 10-years percentage fluctuation of each motif and the value fluctuation of each structural indicator.
Corresponding to the motif constitution, network scales show a negative correlation with motif 1, but a positive relation with all four motifs from 3 to 6. Conversely, the modularity of networks appear to show opposite reactions. Although motif 3 is also a closed one with two stronger links than motif 1, its reflection on networks are closer with open motifs but not motif 1.
Results are correlated with the characteristics of stock market, depending on where these local patterns occur in networks. We find that motif 1 exists in every cluster, while motif 4 tends to occur in ‘core’ and across clusters. Taken the network structures shown in Fig. 1 as references, networks are composed by separate clusters and the ‘core’. Separate clusters show co-holding behaviors happen among the ten disclosed shareholders who hold stocks in the same listed company. ‘Core’ is the subgraph involving connected clusters, which means at least one associate shareholder holds stocks in more than two listed companies. However, there are always limited shareholders bridging the cross-cluster correlations. As a result, other agents in two clusters, together with the bridge-like nodes as the intermediate, form large numbers of open local patterns.
Networks in recent years show much denser cores than in 20069. It means that shareholders tend to expand their investment to more selections with rising investment similarities, which is reflected by the positive correlation with network scales. In addition, the integration with more clusters means weakening boundaries among them, which leads to the negative correlation with network modularity.
As a result, increasing shareholders in Chinese energy stock market have investment expansion. There are higher investment similarities in local patterns, promoting higher global network scale and lower classification among them.
Multiple investors in 3-motifs
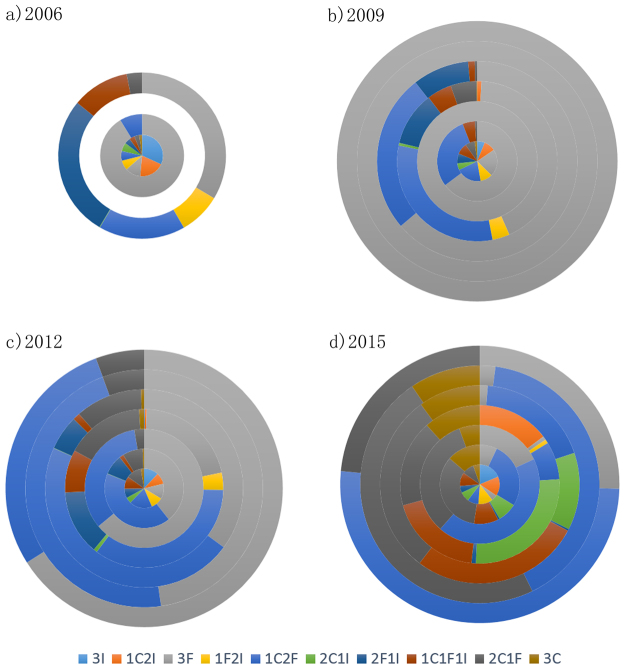
To understand how groups of different shareholders join in 3-motifs, we track the percentage of motifs with different combination of three shareholders’ financial types. Based on the three categories that we have classified for investors, there are normally 10 combinations for each motif, as shown in the legend of Fig. 7, where C represents companies, F is funds and I is individuals. The results in 2006, 2009 2012 and 2015 are selected as examples to show the evolution characteristics, which are shown as doughnuts in Fig. 7. The innermost circle is motif 1, whereas the outer donuts are sequentially from motif 2 to motif 7.
Figure 7.
Combinations of three shareholders’ categories in each motifs (C: Companies; F: Funds; I: Individuals).
In 2006, only motifs 1, 2 and 4 are found in the network, and all seven motifs can be found in three other years.
For motif 1 and motif 4, the combination of multiple investors are much more abundant than other motifs. Especially, investors involved in motif 3, motif 6 and motif 7 are mainly from certain groups of investors with certain financial types. For example, in 2009 and 2012, funds are the main participants in these three motifs. However, in 2015, companies involved in the local connections with at least two strong co-holding relations. Except motif 1, the changing of main participants around 2015 also happen to three other motifs. In particular, individual join in motif 4 and motif 5 with companies or funds together. In comparison, combinations of multiple investors contribute more evenly in recent years.
These results help to explain how investors in three different types informationally connected with local structural characteristics. Moreover, how investors involve in different types of motifs are also answered.
Statistical significance of 3-motifs
Although some motifs are high detected in networks, whether they are specific local patterns in the empirical stock market still need measurement. As a result, in this part, statistical significance are measured for each 3-motifs with multiple investors. Here, investors’ location differences in each weighted 3-motif are considered to classify their roles in connections.
We calculate the Z-score for each classified motif, rank them from the maximum to the minimum, and select the top 10 motifs in each year. Figure 8 shows the results. Black circles specify the motifs among agents with total different types, while colored squares are used to highlight the ones among same type shareholders. The color of the square represent a certain type of shareholder: Greens are companies, reds are funds, and blues are individuals.
Figure 8.
Top 10 motifs with highest Z-scores in each year, from 2006 to 2015. Green nodes are companies, red ones are funds, and blue ones are individuals. Black circles specify the motifs among agents with total different types. Squares specifies the motifs with three same type shareholders.
Whether shareholders tend to appear investment similarities with those who have similar financial attributes is answered by results with homophily and heterology characteristics. Results show that there are both homophily and heterology in motifs. In most years, heterology plays more significant roles than homophily. For the heterology, shareholders in motifs always appear with relative heterology (two agents with same type and the third one with different type) or with total heterology (agents with three different types). Especially, totally heterogeneous motifs experience fluctuations, but increasing importance in networks. In comparison, homophily exists in networks, but perform high uncertainty. What is more, the importance of homophily always appear among individuals. Although homogenous motifs exist among companies and funds, their importance in networks are much lower than the ones among individuals.
In conclusion, motifs show both homophily and heterology among shareholders in the Chinese energy stock market. Heterology contributes more to the networks than homophily. In addition, homophily always appear among individuals with higher importance.
Evolution of local co-holding behaviors
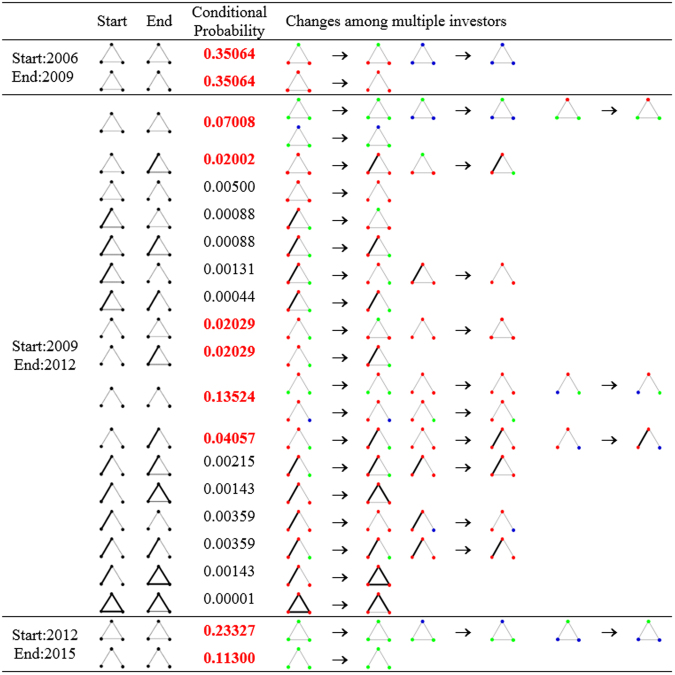
In this part, we explore the dynamic changes of motif structure for each groups of agents. For Chinese energy stock market, the set of shareholders has high uncertainty, so there are limited investors reserved from each previous year. As a result, we find the overlap shareholders in the start year and the end year firstly, and then follow the motif structure changes among each group of three overlapped shareholders. Short term (1-year) and long term (3-years) are taken as the time expansion, and results are shown in Table 2 and Fig. 9 respectively.
Table 2.
Changes of 3-motifs from the start module to the end module among overlap shareholders, 1-year term from the start year to the end year. Conditional probabilities over 0.05 is highlighted with boldface. Motif 1 is  ; motif 2 is
; motif 2 is  ; motif 4 is
; motif 4 is  ; motif 5 is
; motif 5 is  .
.
| Start | 2006 | 2007 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 | 2014 | |
|---|---|---|---|---|---|---|---|---|---|---|
| End | 2007 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | |
| Start | End | |||||||||
| 1 | 1 | 0.52596 | 0.33265 | 0.33400 | 0.35131 | 0.29899 | 0.29218 | 0.26711 | 0.28796 | 0.34987 |
| 1 | 2 | 0.00000 | 0.02132 | 0.01066 | 0.00803 | 0.01260 | 0.01133 | 0.00959 | 0.00532 | 0.00122 |
| 1 | 4 | 0.17532 | 0.02843 | 0.08883 | 0.02008 | 0.01856 | 0.01670 | 0.00664 | 0.00760 | 0.00000 |
| 1 | 5 | 0.00000 | 0.00569 | 0.02843 | 0.00602 | 0.00265 | 0.00060 | 0.00443 | 0.00000 | 0.00000 |
| 2 | 1 | 0.00000 | 0.01882 | 0.00175 | 0.00644 | 0.00312 | 0.00176 | 0.00532 | 0.00413 | 0.00597 |
| 2 | 2 | 0.00360 | 0.00099 | 0.00962 | 0.01041 | 0.01585 | 0.01055 | 0.01452 | 0.01593 | 0.00597 |
| 2 | 4 | 0.00000 | 0.00793 | 0.01049 | 0.00793 | 0.00338 | 0.00477 | 0.00871 | 0.00767 | 0.00299 |
| 2 | 5 | 0.00360 | 0.00000 | 0.00262 | 0.00595 | 0.00572 | 0.00427 | 0.00750 | 0.00383 | 0.00000 |
| 4 | 1 | 0.00000 | 0.04224 | 0.04804 | 0.03893 | 0.01502 | 0.01706 | 0.00612 | 0.00707 | 0.02880 |
| 4 | 2 | 0.00000 | 0.03989 | 0.01747 | 0.01946 | 0.01567 | 0.03344 | 0.01311 | 0.00809 | 0.00000 |
| 4 | 4 | 0.29152 | 0.36137 | 0.33189 | 0.38686 | 0.49174 | 0.47640 | 0.50516 | 0.50633 | 0.52984 |
| 4 | 5 | 0.00000 | 0.07978 | 0.06114 | 0.06813 | 0.03918 | 0.06143 | 0.05681 | 0.02729 | 0.00576 |
| 5 | 1 | 0.00000 | 0.00000 | 0.00406 | 0.00316 | 0.00155 | 0.00229 | 0.00149 | 0.00303 | 0.00000 |
| 5 | 2 | 0.00000 | 0.00000 | 0.00947 | 0.00394 | 0.00802 | 0.00719 | 0.00298 | 0.00692 | 0.00522 |
| 5 | 4 | 0.00000 | 0.03048 | 0.01623 | 0.02603 | 0.01603 | 0.01602 | 0.02892 | 0.04626 | 0.04174 |
| 5 | 5 | 0.00000 | 0.01255 | 0.01217 | 0.01578 | 0.03776 | 0.02550 | 0.04084 | 0.04798 | 0.01565 |
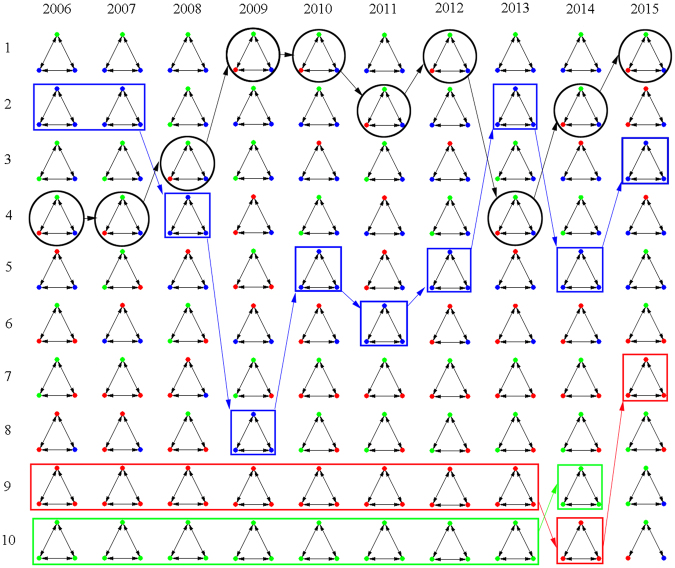
Figure 9.
Changes of 3-motifs among overlap shareholders, 3-years term. Green nodes are companies, reds are funds, and blues are individuals. Red boldface are the conditional probabilities over 0.01.
Reserved local pattern refers to the condition that the motif established among certain three shareholders in the start year still exist in the end year without the consideration of their structural changes. Over these 10 years, we find that increasing connections among certain three shareholders can still be found in the next years. For example, almost 50% of the groups of shareholders from 2014 resolved their local pattern in 2015. Among these reserved local patterns, we calculate the conditional probabilities for each structural change, which is also shown in Table 2. Because the percentage of motif 3, 6 and 7 are too low to be counted, we only provide the changes among motif 1, 2, 4 and 5 here, which are also main motifs in 10 co-holding networks. The highlighted numbers with boldface are the relative high possibilities with the threshold of 0.05.
Results reveal that most motifs keep their style in a new year. However, we can find that, in early years, closed motifs with fully connections decomposed to open ones. In recent years, weak open motifs has involved more strong links. As a result, the decomposition of motifs do not mainly come from the closed ones which existed in networks. The increasing of co-holding strength contributes to the network fluctuation.
We further prolong the term for detecting motif changes. 3-years expansion is considered for the reason that companies, funds and individuals show three phases of proportional evolution in a longer term (as shown in Table 1). As the increasing of the time period, there are few triadic connections existent among limited overlap investors. Figure 9 shows all detected changes from the former motif at the start year to the latter motif at the end year. Involved investors are colored to show their position in each motif.
In a longer term, local patterns among companies are always steady, keeping their original connections. Stable structures are also reserved if a fund or an individual connects with two companies. At the same time, from 2009 to 2012, many motifs tend to get strengthened, which is mainly from the strong links established among funds. In comparison, as the decreasing proportion of individuals in the stock market, connections among themselves have turned to with companies. Increasing percentage of funds doesn’t contributes to steady structural evolution, but promote motifs being strengthened ones.
In this part, we demonstrate how local patterns are evolving among multiple shareholders. Multiple investors participate in the motif changes with their own roles with dynamic stock market in different time periods.
Discussion and Conclusion
The evolutionary 3-motifs with classified agents reveal that information connections differ among multiple investors in the stock markets. In this paper, networks are modeled based on common holding behaviors among shareholders, who are classified into three categories: companies, funds and individuals. Weighted 3-motifs are detected from networks. Their statistical significance and dynamics are further measured. Main conclusions and discussions are as follows:
First, the detection on motifs is able to reveal preferential local patterns among diverse agents. In China energy stock market, individuals and funds appear opposite involvements, and high shareholding similarities mainly distribute among companies and funds. During 10 years, increasing proportions of shareholders are linked indirectly in local patterns without fully connections. At the same time, network structure shows a growth of network scale but lower modularity. Although motifs distribute more evenly among different groups of shareholders, companies and funds are main contributors for the motifs involving strengthen links.
Second, our study approves that heterology exists among traders in stock markets. Homophily shows its limit existence among individuals. It provides the research support for previous studies that focus on the social, geological and professional similarities among individuals. This paper shows the heterology with higher statistical significance than homophily in stock markets. Information would be more diverse from traders with different types. As a result, companies, funds and individuals tend to be informationally connected with each other as small groups.
Third, motif evolution reflect agents’ roles in dynamic local connections. Among the investors who have relative steady shareholdings, they tend to keep local patterns in both short and long terms. It is more common among companies, and individuals also tend to be steadily connected with companies. Unsteady local structure mainly come from funds because of strengthen connections established among themselves.
Our work is essential for understanding the relations between investors’ behaviors and the co-holding network structure. In particular, the results help to make the network reconstruction possible. As a result, our study will be of interest to researchers or stock managers who are interested in knowing more about investors’ behaviors. In the present work, we classify the weak and strong links based on a simple baseline, which will become a more precise classification in our future work.
Acknowledgements
This research is supported by grants from the National Natural Science Foundation of China (Grant No. 71173199), the open project of Key Laboratory of Carrying Capacity Assessment for Resource and the Environment, Ministry of Land and Resources (No. CCA2017.01), and the State Scholarship Fund from China Scholarship Council (CSC) (Grant No. 201606400005). The authors would like to express their gratitude to Xiangyun Gao, Huajiao Li, Shupei Huang and Wei Fang who helped a lot during this work. In addition, authors would like to thank for FANMOD software, which helps to get statistical results and related figures in this paper.
Author Contributions
An, H. and Guan, Q. designed research; Guan, Q., An, F. and Jiang. M performed research and analyzed results; Guan, Q. and Liu, N. extract the conclusions. All authors reviewed the manuscript.
Competing Interests
The authors declare that they have no competing interests.
Footnotes
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
- 1.Milo R, et al. Network motifs: Simple building blocks of complex networks. Science. 2002;298:824–827. doi: 10.1126/science.298.5594.824. [DOI] [PubMed] [Google Scholar]
- 2.Barabasi AL, Oltvai ZN. Network biology: Understanding the cell’s functional organization. Nat Rev Genet. 2004;5:101–U115. doi: 10.1038/nrg1272. [DOI] [PubMed] [Google Scholar]
- 3.Krumov, L. Local Structures Determine Performance within ComplexNetworks. Technische Universität, Darmstadt, 54 (2010).
- 4.Fu R, Gupta-Mukherjee S. Geography, Informal Information Flows and Mutual Fund Portfolios. Financial Management. 2014;43:181–214. doi: 10.1111/fima.12042. [DOI] [Google Scholar]
- 5.Han B, Yang LY. Social Networks, Information Acquisition, and Asset Prices. Management Science. 2013;59:1444–1457. doi: 10.1287/mnsc.1120.1678. [DOI] [Google Scholar]
- 6.Liu, C., Tian, L., Huangfu, Y. T. & Chen, L. L. Stock Price fluctuation under Asymmetric Information. 2015 International Conference on Logistics, Informatics and Service Sciences (Liss) (2015).
- 7.Ozsoylev HN, Walden J, Yavuz MD, Bildik R. Investor Networks in the Stock Market. Review of Financial Studies. 2014;27:1323–1366. doi: 10.1093/rfs/hht065. [DOI] [Google Scholar]
- 8.Pareek, A. Information Networks: Implications for Mutual Fund Trading Behavior and Stock Returns. AFA 2010 Atlanta Meetings Paper (2012).
- 9.Li H, et al. The evolutionary stability of shareholders’ co-holding behavior for China’s listed energy companies based on associated maximal connected sub-graphs of derivative holding-based networks. Applied Energy. 2016;162:1601–1607. doi: 10.1016/j.apenergy.2015.04.049. [DOI] [Google Scholar]
- 10.Barber BM, Odean T. Trading is hazardous to your wealth: The common stock investment performance of individual investors. Journal of Finance. 2000;55:773–806. doi: 10.1111/0022-1082.00226. [DOI] [Google Scholar]
- 11.Pan D, Shi J, Wu F, Zhang BH. Investor heterogeneity and commonality in stock return and liquidity. Economic Systems. 2015;39:458–473. doi: 10.1016/j.ecosys.2015.07.001. [DOI] [Google Scholar]
- 12.Han, H., Liu, W.-L. & Wu, L.-Y. The measurement of complex network based on motif. Acta Phys Sin-Ch Ed62, 168904 (168909 pp.)-168904 (168909 pp.), 10.7498/aps.62.168904 (2013).
- 13.Azpeitia, E. et al. The combination of the functionalities of feedback circuits is determinant for the attractors’ number and size in pathway-like Boolean networks. Sci Rep-Uk7, 10.1038/srep42023 (2017). [DOI] [PMC free article] [PubMed]
- 14.Costa LDF, Rodrigues FA, Travieso G, Boas PRV. Characterization of complex networks: A survey of measurements. Advances in Physics. 2007;56:167–242. doi: 10.1080/00018730601170527. [DOI] [Google Scholar]
- 15.Kotorowicz, M. & Kozitsky, Y. Motif based hierarchical random graphs: structural properties and critical points of an Ising model. Condensed Matter Physics14, 10.5488/cmp.14.13801 (2011).
- 16.Sarajlic, A., Malod-Dognin, N., Yaveroglu, O. N. & Przulj, N. Graphlet-based Characterization of Directed Networks. Sci Rep-Uk6, 10.1038/srep35098 (2016). [DOI] [PMC free article] [PubMed]
- 17.Squartini, T. & Garlaschelli, D. Triadic motifs and dyadic self-organization in the world trade network. (2012).
- 18.Liu L, Xu WS, Han CF. Motif and Superfamily in National Critical Transportation Networks. Journal of Tongji University (Nature and Science) 2013;1:53–59. [Google Scholar]
- 19.Harrigan N, Achananuparp P, Lim E-P. Influentials, novelty, and social contagion The viral power of average friends, close communities, and old news. Soc Networks. 2012;34:470–480. doi: 10.1016/j.socnet.2012.02.005. [DOI] [Google Scholar]
- 20.Geard N, Bullock S, Lohaus R, Azevedo RBR, Wiles J. Developmental Motifs Reveal Complex Structure in Cell Lineages. Complexity. 2011;16:48–57. doi: 10.1002/cplx.20341. [DOI] [Google Scholar]
- 21.Niemyska, W. et al. Complex lasso: new entangled motifs in proteins. Sci Rep-Uk6, 10.1038/srep36895 (2016). [DOI] [PMC free article] [PubMed]
- 22.Yu, C.-N. J. & Joachims, T. Learning structural SVMs with latent variables. (2009).
- 23.Chao, W., Xiangrui, C., Zhenguo, Z. & Yanlong, W. Purchase and Redemption Prediction Based on Multi-task Gaussian Process and Dimensionality Reduction. (2016).
- 24.Berman, G. J., Choi, D. M., Bialek, W. & Shaevitz, J. W. Mapping the stereotyped behaviour of freely moving fruit flies. J R Soc Interface11, 10.1098/rsif.2014.0672 (2014). [DOI] [PMC free article] [PubMed]
- 25.Dong Z, Li X. The study of network motifs induced from discrete time series. Acta Phys Sin-Ch Ed. 2010;59:1600–1607. [Google Scholar]
- 26.Cheng, Y., Wilson, R. C. & Hancock, E. R. Analyzing graph time series using a generative model. (2016).
- 27.Onnela, J. P., Saramaki, J., Kertesz, J. & Kaski, K. Intensity and coherence of motifs in weighted complex networks. Phys Rev E71, 10.1103/PhysRevE.71.065103 (2005). [DOI] [PubMed]
- 28.Li, M. X. et al. Statistically validated mobile communication networks: the evolution of motifs in European and Chinese data. New Journal of Physics16, 10.1088/1367-2630/16/8/083038 (2014).
- 29.Kovanen L, Kaski K, Kertesz J, Saramaki J. Temporal motifs reveal homophily, gender-specific patterns, and group talk in call sequences. P Natl Acad Sci USA. 2013;110:18070–18075. doi: 10.1073/pnas.1307941110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Jaggi B, Li W, Wang SS. Individual and Institutional Investors’ Response to Earnings Reported by Conservative and Non-Conservative Firms: Evidence from Chinese Financial Markets. Journal of International Financial Management & Accounting. 2016;27:158–207. doi: 10.1111/jifm.12047. [DOI] [Google Scholar]
- 31.Li, H.-J., An, H.-Z., Huang, J.-C., Gao, X.-Y. & Shi, Y.-L. Correlation of the holding behaviour of the holding-based network of Chinese fund management companies based on the node topological characteristics. Acta Phys Sin-Ch Ed63, 10.7498/aps.63.048901 (2014).
- 32.Chung CY, Wang KN. Short-term trading by individual investors in the Korean stock market. Journal of the Asia Pacific Economy. 2016;21:599–611. doi: 10.1080/13547860.2016.1187798. [DOI] [Google Scholar]
- 33.Ivkovic Z, Weisbenner S. Information diffusion effects in individual investors’ common stock purchases: Covet thy neighbors’ investment choices. Review of Financial Studies. 2007;20:1327–1357. doi: 10.1093/revfin/hhm009. [DOI] [Google Scholar]
- 34.Granovetter MS. The Strength of Weak Ties. American Journal of Sociology. 1973;78:1360–1380. doi: 10.1086/225469. [DOI] [Google Scholar]
- 35.Hong H, Kubik JD, Stein JC. Thy neighbor’s portfolio: Word-of-mouth effects in the holdings and trades of money managers. Journal of Finance. 2005;60:2801–2824. doi: 10.1111/j.1540-6261.2005.00817.x. [DOI] [Google Scholar]
- 36.Pool VK, Stoffman N, Yonker SE. The People in Your Neighborhood: Social Interactions and Mutual Fund Portfolios. Journal of Finance. 2015;70:2679–2732. doi: 10.1111/jofi.12208. [DOI] [Google Scholar]
- 37.Li H, Fang W, An H, Yan L. The shareholding similarity of the shareholders of the worldwide listed energy companies based on a two-mode primitive network and a one-mode derivative holding-based network. Physica A. 2014;415:525–532. doi: 10.1016/j.physa.2014.08.035. [DOI] [Google Scholar]
- 38.Buskens V, Yamaguchi K. A new model for information diffusion in heterogeneous social networks. Sociological Methodology 1999. 1999;29(29):281–325. [Google Scholar]
- 39.Xing, H. Q. & Zhan, H. Investor Relations of Listed Company. Law Press (2007).
- 40.Antiqueira, L. & Costa, L. d. F. Characterization of subgraph relationships and distribution in complex networks. New Journal of Physics11, 10.1088/1367-2630/11/1/013058 (2009).
- 41.Lue, L. & Zhou, T. Link prediction in weighted networks: The role of weak ties. Epl-Europhys Lett89, 10.1209/0295-5075/89/18001 (2010).
- 42.Li SS, Rousseau R, Ye FY. Motifs in weighted networks and their Hirsch subgraphs. Malays J Libr Inf Sc. 2016;21:21–34. [Google Scholar]
- 43.Milo R, et al. Superfamilies of evolved and designed networks. Science. 2004;303:1538–1542. doi: 10.1126/science.1089167. [DOI] [PubMed] [Google Scholar]
- 44.Saramaki, J., Onnela, J. P., Kertesz, J. & Kaski, K. In Science of Complex Networks: From Biology to the Internet and WWW Vol. 776 Aip Conference Proceedings (eds J. F. F. Mendes et al.)108–117 (2005).
- 45.Choobdar, S., Ribeiro, P. & Silva, F. In 12th Ieee International Conference on Data Mining Workshops International Conference on Data Mining Workshops (eds J. Vreeken et al.) 210–217 (2012).
- 46.Rubinov M, Sporns O. Complex network measures of brain connectivity: Uses and interpretations. Neuroimage. 2010;52:1059–1069. doi: 10.1016/j.neuroimage.2009.10.003. [DOI] [PubMed] [Google Scholar]
- 47.Guimera, R. & Amaral, L. A. N. Cartography of complex networks: modules and universal roles. J Stat Mech-Theory E, 10.1088/1742-5468/2005/02/p02001 (2005). [DOI] [PMC free article] [PubMed]
- 48.LC. F. Centrality in social networks: conceptual clarification. Soc Networks. 1979;1:215–239. [Google Scholar]
- 49.Watts DJ, Strogatz SH. Collective dynamics of ‘small-world’ networks. Nature. 1998;393:440–442. doi: 10.1038/30918. [DOI] [PubMed] [Google Scholar]
- 50.Wasserman, S. & Faust, K. Social Network Analysis: Methods and Applications. Cambridge: Cambridge University Press (1994).
- 51.Blondel, V. D., Guillaume, J.-L., Lambiotte, R. & Lefebvre, E. Fast unfolding of communities in large networks. J Stat Mech-Theory E, 10.1088/1742-5468/2008/10/p10008 (2008).
- 52.Liu, X. F., Liu, Y. L., Lu, X. H., Wang, Q. X. & Wang, T. X. The Anatomy of the Global Football Player Transfer Network: Club Functionalities versus Network Properties. Plos One11, 10.1371/journal.pone.0156504 (2016). [DOI] [PMC free article] [PubMed]
- 53.Tan, C. M., Tan, B. L. & Liu, B. S. Investigation of the relationship between the air pollution and solar activity. Astrophysics and Space Science362, 10.1007/s10509-017-3121-0 (2017).
- 54.Piao, L. & Fu, Z. Quantifying distinct associations on different temporal scales: comparison of DCCA and Pearson methods. Sci Rep-Uk6, 10.1038/srep36759 (2016). [DOI] [PMC free article] [PubMed]