Statistical properties of radio-frequency and envelope-detected signals with applications to medical ultrasound

Abstract

Both radio-frequency (rf) and envelope-detected signal analyses have lead to successful tissue discrimination in medical ultrasound. The extrapolation from tissue discrimination to a description of the tissue structure requires an analysis of the statistics of complex signals. To that end, first- and second-order statistics of complex random signals are reviewed, and an example is taken from rf signal analysis of the backscattered echoes from diffuse scatterers. In this case the scattering form factor of small scatterers can be easily separated from long-range structure and corrected for the transducer characteristics, thereby yielding an instrument-independent tissue signature. The statistics of the more economical envelope- and square-law-detected signals are derived next and found to be almost identical when normalized autocorrelation functions are used. Of the two nonlinear methods of detection, the square-law or intensity scheme gives rise to statistics that are more transparent to physical insight. Moreover, an analysis of the intensity-correlation structure indicates that the contributions to the total echo signal from the diffuse scatter and from the steady and variable components of coherent scatter can still be separated and used for tissue characterization. However, this analysis is not system independent. Finally, the statistical methods of this paper may be applied directly to envelope signals in nuclear-magnetic-resonance imaging because of the approximate equivalence of second-order statistics for magnitude and intensity.

Introduction

Radio-frequency (rf) signals are the source of information in two major medical imaging modalities today, namely, ultrasonic imaging and magnetic resonance imaging (MRI). These signals have a random character that is due, in the first case, to the coherent interference at the detector of the backscattered signals from a diffuse collection of scatterers and, in the second case, to thermal currents in the body and the detection system. The details of the random character depend on whether one uses the complex rf signal, referred to here as the complex amplitude, or the envelope of this signal, referred to here as the magnitude signal. In the latter case one might alternatively use the square of the magnitude signal, referred to as the intensity signal.

The random signals may include a component with some long-range organization or order. In MRI this might be the presence of either a steady or an amplitude-modulated signal, and in ultrasound the presence of a regular scattering structure. Separation of the ordered from the random components is desirable in MRI to improve signal detectablity, and in ultrasound to distinguish features of the scattering for the purpose of tissue characterization or discrimination.

In principle, this separation task is more straightforward when the rf signal is analyzed directly, and, in fact, tissue discrimination using this approach has been quite successful in the eye and in the liver.^1–7 However, it is often more convenient or economical to work with the envelope-detected signal that may be obtained and stored with less sampling and memory. Also, it is the envelope-detected signal that is displayed in the conventional ultrasound B-scan image. Tissue discrimination using only envelope signals has also been successful in the liver.^8-10 The purpose of the present paper is to examine the connection between the rf and envelope signals and the underlying tissue structure. In the course of this examination we shall uncover the stronger points of each approach.

The probability-density functions (pdf's) required to characterize the first-order properties of these random phenomena include the circular complex Gaussian pdf, the Ray-leigh and Rician pdf's, and their generalizations to the case of organized structure. There is already a wealth of literature on these first-order properties, but the material available on second-order properties is sparse, and the mathematics is generally not transparent to physical insight; also, in one important case reviewed in Appendix A, the previously published mathematics is typographically inaccurate. In this paper we concentrate on these second-order properties, beginning with the rf analysis and ending with the intensity analysis. Although our examples will be drawn entirely from ultrasonic imaging, the formalism contained here is immediately applicable to MRI.

Complex Gaussian Statistics

The random character of ultrasonic images of human tissue results from the phase-sensitive detection of the scatter from many sites randomly distributed in the resolution cell of the transducer, together with the scanning of this cell through the tissue. The process of interference can be described geometrically as a random walk of component phasors. When the number of scatterers within one resolution cell is large, and the phases of the scattered waves are independent and distributed uniformly betwen 0 and 2π, the phasor or complex field amplitude a, which is the result of the random walk, has real and imaginary components a_r and a_i whose joint pdf in the narrow-band approximation is¹¹

$$p(a_r,a_i)={(2\pi {\sigma }^2)}^{-1}exp[-({a_r}^2+{a_i}^2)/2{\sigma }^2].$$ (1)

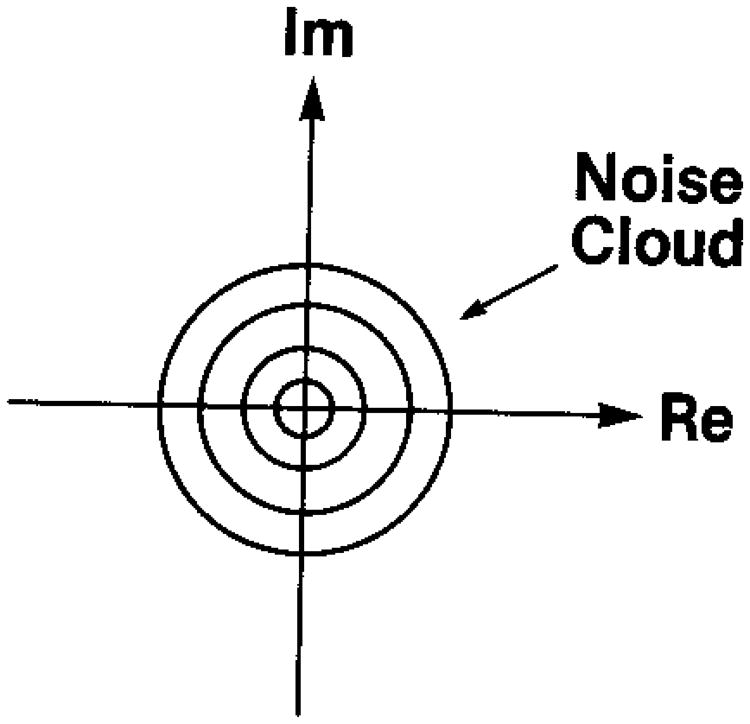
This is simply the product of two independent Gaussian density functions with zero mean and variance σ² and is referred to as a circular Gaussian pdf. Figure 1 gives a schematic representation of this pdf as a noise cloud,¹² centered on the origin of the complex coordinates. The variance σ² depends on the mean-square scattering amplitude of the particles in the scattering medium.¹¹ The resultant mean (absolute) square of the complex amplitude of Eq. (1) is easily seen to be

Fig. 1.

Schematic representation of the noise cloud that results from the random walk in the complex plane (from Goodman¹²).

$$\langle a{a}^{\ast }\rangle =\langle {a_r}^2+{a_i}^2\rangle =2{\sigma }^2=I_d$$ (2)

and will be referred to as the mean diffuse intensity I_d. We shall consider this parameter to be the average value over the bandwidth and to be constant with position.

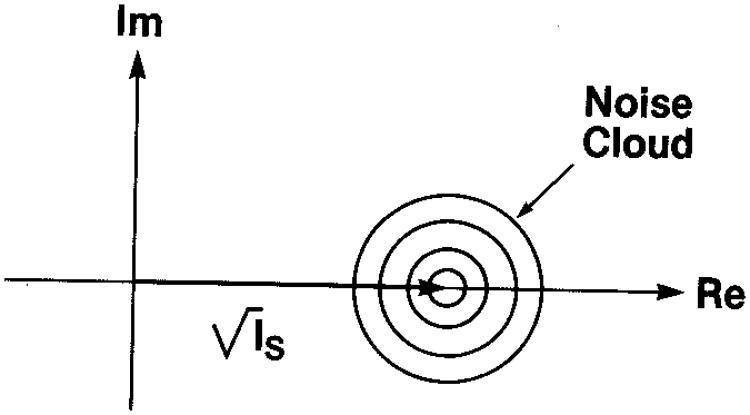
If we add a constant amplitude signal to this random accumulation, designated by a constant phasor of magnitude $\sqrt{I_s}$ and fixed phase (which can be taken to be 0 deg without loss of generality), this simply changes the mean value of the real part of the circular Gaussian statistics. This could represent a coherent signal in MRI or coherent scattering in ultrasound. The noise cloud of Fig. 1 is then just shifted along the real axis, as shown in Fig. 2. The joint pdf then becomes

Fig. 2.

Schematic representation of the noise cloud that results from a constant phasor (or coherent signal) plus a random walk in the complex plane (from Goodman¹²).

$$p(a_r,a_i)={(2\pi {\sigma }^2)}^{-1}exp\{-[{(a_r-\sqrt{I_s})}^2+{a_i}^2]/2{\sigma }^2\}.$$ (3)

The squared magnitude of the constant phasor of Eq. (3), I_s, is referred to as the specular intensity and will be allowed to vary with position in our examples below. Since this specular contribution is distributed over a region of the tissue or source of scattering, that is, it is not localized (as, e.g., at the surface of a mirror), we refer to it as “distributed specularity.” Examples will be given presently. A fundamental parameter in our analysis will be the ratio of the average specular intensity Ī_s to the diffuse intensity I_d, i.e., r = Ī_s/I_d. Other authors¹³ have used the parameter $\underset{¯}{k}=\sqrt{I_s}/\sigma$ for the analysis of envelope or magnitude signals. The relationship between r and k is then r = k²/2.

Second-Order Statistics for Complex Amplitude

We consider first a complex random process, e.g., a rf wave or a scattered pressure field. We are interested in the correlation between its values at two positions in the field, x₁ and x₂. At position x₁, we write

$$a({\mathbf{x}}_1)=a_{1r}+i{a}_{1i}.$$ (4)

The random process is taken to have zero mean and to have the variance of the real part equal to that of the imaginary part, σ², as in the complex Gaussian case introduced above. The statistical character at position x₂ is the same but may be correlated with that at position x₁. At x₂ we write

$$a({\mathbf{x}}_2)=a_{2r}+i{a}_{2i}.$$ (5)

The autocorrelation of this process, e.g., the wave or field values, is given by

$$R_a({\mathbf{x}}_1,{\mathbf{x}}_2)=\langle a({\mathbf{x}}_1)a^{\ast }({\mathbf{x}}_2)\rangle .$$ (6)

If this field is simply read out or scanned by an imaging process with a point-spread function (psf) h(x), the resulting complex signal 𝒜 is related to the original field a by^14,15

$$\mathcal{A}(\mathbf{x})=h(\mathbf{x})\ast a(\mathbf{x}),$$ (7)

where * is the convolution operator (see, e.g., Refs. 14 and 15). The autocorrelation of the resulting process 𝒜 is then given directly by

$$R_{\mathcal{A}}(\mathrm{\Delta }\mathbf{x})=h(-\mathrm{\Delta }\mathbf{x})\ast R_a(\mathrm{\Delta }\mathbf{x})\ast h^{\ast }(\mathrm{\Delta }\mathbf{x}),$$ (8)

where Δx = x₂ − x₁.

A commonly realized example is the acoustic scattering from a random collection of N point targets in a resolution cell or volume. Then

$$a({\mathbf{x}}_1)=\sum _{i=1}^N|a_i|e^{i{\varphi }_i}$$

and

$$a({\mathbf{x}}_2)=\sum _{j=1}^N|a_j|e^{i{\varphi }_j},$$ (9)

where |a_i| is the magnitude of the scattering amplitude of the ith target and there is correlation neither among the target phases ϕ_i, in the first scattering volume nor among those in the second scattering volume ϕ_j nor between the scattering volumes. Then the autocorrelation of a is

$$\langle a({\mathbf{x}}_1)a^{\ast }({\mathbf{x}}_2)\rangle =\sum _{i=1}^N\sum _{j=1}^N\langle |a_i||a_j|exp[i({\varphi }_i-{\varphi }_j)]\rangle =N\langle {|a_i|}^2\rangle \delta (\mathrm{\Delta }\mathbf{x})=I_d\delta (\mathrm{\Delta }\mathbf{x}),$$ (10)

since all phases average out unless they match up identically. Here δ(Δx) is the Dirac delta function.¹⁴ This condition is referred to as diffuse scattering, and the total diffuse intensity is N times as great as the average scattering intensity per particle. We shall consider these average properties to be independent of position. The autocorrelation of the readout or scanned process is then simply

$$R_{\mathcal{A}}(\mathrm{\Delta }\mathbf{x})=I_d[h(-\mathrm{\Delta }\mathbf{x})\ast h^{\ast }(\mathrm{\Delta }\mathbf{x})].$$ (11)

In practice, there is always a finite readout, as in this equation, and the infinite variance implied by Eq. (10) is not encountered.

In the frequency domain conjugate to x—in the conjugate coordinate k—Eq. (8) becomes

$$W_{\mathcal{A}}(\mathbf{k})={|H(\mathbf{k})|}^2{W}_a(\mathbf{k}).$$ (12)

W_𝒜 and W_a are the power spectra for the respective processes, and

$$H(\mathbf{k})\stackrel{\text{FT}}{\iff }h(\mathrm{\Delta }\mathbf{x})$$ (13)

are a Fourier-transform (FT) pair. For the uncorrelated limit,

$$\begin{array}{l}{W}_a(\mathbf{k})=I_d,\hfill \\ W_{\mathcal{A}}(\mathbf{k})=I_d{|H(\mathbf{k})|}^2.\hfill \end{array}$$ (14)

The power spectral relationships are the well-known frequency-domain representations of the autocorrelation function relationships^14,15 involving the transforms

$$\begin{array}{l}{W}_{\mathcal{A}}(\mathbf{k})\stackrel{\text{FT}}{\iff }{R}_{\mathcal{A}}(\mathrm{\Delta }\mathbf{x}),\hfill \\ W_a(\mathbf{k})\iff R_a(\mathrm{\Delta }\mathbf{x}),\hfill \\ {|H(\mathbf{k})|}^2\iff h(-\mathrm{\Delta }\mathbf{x})\ast h^{\ast }(\mathrm{\Delta }\mathbf{x}).\hfill \end{array}$$ (15)

They indicate that the power spectrum of the rf signal is given by the squared modulus of the system frequency response weighted by a factor proportional to the incoherent backscattered intensity I_d in that channel. The latter, in turn, is given by the product of the number of scatterers and the average scattering intensity per particle [Eq. (10)].

We now consider a physical realization of ultrasound pulse echo or backscatter imaging, where the process a is a more general scattering mechanism to be characterized below and the psf is due to the readout mechanisms of the pulse used to probe the scatterers and the diffraction pattern of the beam. In the far field, to a good approximation, the psf can be separated into the transverse component h_t due to diffraction and the range component h_r due to the pulse:

$$\begin{array}{c}h(\mathbf{x},k_0)=h_t(x,y,k_0)h_r(z,k_0),\\ k_0=|{\mathbf{k}}_0|.\end{array}$$ (16)

All psf's are functions of temporal frequency through the wave number k₀ = 2π/λ₀ = ω₀/c, where λ₀ is the corresponding wavelength, ω₀ is the corresponding angular frequency, and c is the velocity of sound in the medium. Since ultrasonic images are generally scans in the x–z plane, the diffraction pattern may be considered to be effectively one dimensional¹⁵:

$$h_t(x,y,k_0)={h^{\prime }}_t(x,k_0).$$

In the range direction the psf is the pulse given by

$$h_r(z,k_0)=Aexp(-z^2/2{{\sigma }_0}^2)exp(i{k}_{0}z),$$ (17)

that is, a carrier at a frequency corresponding to k₀ and an overall Gaussian envelope characterized by rms radius σ₀. In the frequency domain

$$\begin{array}{c}{H}_r(k)\stackrel{\text{FT}}{\iff }{h}_r(z,k_0),\\ H_r(k)=exp[-{{\sigma }_0}^2{(k-k_0)}^2/2].\end{array}$$ (18)

The process a is described by the coupling of an incoming wave and a source of acoustic scattering, the coupling being governed by the acoustic wave equation for inhomogeneous media.^5,6,16 We assume that we have a continuous medium or matrix with embedded discrete scatterers, i.e., changes in acoustic impedance (ρc) or compressibility κ. Since the contribution of changes in density ρ to the scattering is small,¹⁷ we have the following relations between the descriptors of the scattering¹⁶;

$$\begin{array}{c}\kappa \equiv 1/\rho c^2\\ \rho c=1/\kappa c\\ \mathrm{\Delta }(\rho c)/\rho c=-\mathrm{\Delta }(\kappa c)/\kappa c\end{array}\},\mathrm{\Delta }\rho \to 0\Rightarrow \{-\mathrm{\Delta }\kappa /\kappa =2\mathrm{\Delta }c/c\equiv -{\gamma }_{\kappa }.$$ (19)

The fractional change in compressibility is referred to as γ_κ. The description of the coupling of the incident wave and the scattering targets depends on which of the following three conditions prevails:

(1) Independent Scatterers Whose Structure Is on a Scale Smaller Than a Wavelength. At the focal plane of the source, an incident wave directed along the z direction— effectively a plane wave in the commonly encountered weak-focusing geometry—senses the change in compressibility κ or impedance ρc at the scattering site. The scattering site removes energy from the plane wave and reradiates spherical waves whose amplitude is a function of frequency and the size of the scatterer. For the weak-scattering condition₁₃ the Born approximation is valid,¹⁶ and the amplitude Φ_b(2k) for scattering waves of wave number k in the backward direction is

$$\begin{array}{c}{\mathrm{\Phi }}_b(2k)=2{\pi }^2{k}^2{\mathrm{\Gamma }}_{\kappa }(2k),\\ {\mathrm{\Gamma }}_{\kappa }(2k)=\frac{1}{{(2\pi )}^3}\int d\mathbf{x}{\gamma }_{\kappa }(\mathbf{x})exp(-2i\mathbf{k}\cdot \mathbf{x}),\end{array}$$ (20)

where Γ_κ(2k) is the FT in the variable 2k of the distribution of fluctuation in compressibility γ_κ. The variable 2k is the difference in wave vector between incoming and backscattered waves. Assuming spherical symmetry,¹⁶

$${\mathrm{\Phi }}_b(2k)=k^2{\int }_0^{a_0}d{r}^{\prime }{\gamma }_{\kappa }(r^{\prime })sin(2k{r}^{\prime })r^{\prime 2}/(2k{r}^{\prime }).$$ (21)

In the small-scatterer or long-wavelength limit this becomes

$${\mathrm{\Phi }}_b(2k)\Rightarrow {\mathrm{\Phi }}_0(2k)=\frac{1}{3}{k}^2{a_0}^3{\overline{\gamma }}_{\kappa },2k{a}_0\ll 1,$$ (22)

where a₀ is the radius of the scatterer and γ̄_κ is the average value of γ_κ over the scatterer. The differential scattering cross section in the backward direction is just

$$\mathrm{d}{\sigma }_0={|{\mathrm{\Phi }}_0|}^2=\frac{1}{9}{k}^4{a_0}^6{{\overline{\gamma }}_{\kappa }}^2=\ge \langle {|a|}^2\rangle ,$$ (23)

and this limit is referred to as Rayleigh scattering.

The function Γ is often referred to as the form factor in studies of scattering phenomena.¹⁸ The negative of the second derivative of the form factor at the origin (the inverse of the radius of curvature) is equal to the rms radius of the scattering distribution γ_κ, That is,

$$-{{\nabla }_{2\mathbf{k}}}^2{\mathrm{\Gamma }}_{\kappa }(2\mathbf{k})=\frac{1}{{(2\pi )}^3}\int \mathrm{d}\mathbf{x}{\gamma }_{\kappa }(\mathbf{x})(\mathbf{x}\cdot \mathbf{x})exp(-2i\mathbf{k}\cdot \mathbf{x})\stackrel{\mathbf{k}\to 0}{\to }\langle {|\mathbf{x}|}^2\rangle .$$ (24)

Therefore, if only the effect of size or scale—as opposed to structure—is important, then it is reasonable to model Γ_κ as any originally zero-slope function with the correct curvature corresponding to the characteristic or rms radius. That is, any simple low-pass filter function will be adequate. Gaussian and other elementary functions have been used,^1–7 and the details are unimportant until 2ka₀ ∼ 1, where a more elaborate understanding and description are required. More on this presently.

The autocorrelation of the scattering process is

$$R_{\gamma }({\mathbf{x}}_1{\mathbf{x}}_2)=\langle {\gamma }_{\kappa }({\mathbf{x}}_1){\gamma }_{\kappa }({\mathbf{x}}_2)\rangle .$$ (25)

By Eq. (8), then, the autocorrelation of the scanned pulse-echo process becomes

$${R^{\prime }}_{\gamma }({\mathbf{x}}_1{\mathbf{x}}_2)=Aexp(-\mathrm{\Delta }{z}^2/2{{\sigma }_0}^2)exp(i{k}_0\mathrm{\Delta }z)\ast \langle {\gamma }_{\kappa }({\mathbf{x}}_1){\gamma }_{\kappa }({\mathbf{x}}_2)\rangle \ast exp(-\mathrm{\Delta }{z}^2/2{{\sigma }_0}^2)exp(-i{k}_0\mathrm{\Delta }z).$$ (26)

The transverse or diffraction-pattern psf may be absorbed into the normalization A in this small-scatterer regime and be calibrated out by measurement of a signal scattered from a perfectly reflecting surface^5,6,19 or a strong point reflector. In these applications there is no scanning in the transverse or diffraction direction. For imaging applications in which transverse scanning is used, or for the large-scatterer case, the diffraction psf must be included.

The expected measured power spectrum corresponding to Eq. (26) is

$$W_b(k)=d{\sigma }_0{{\mathrm{\Gamma }}_0}^2(2k){|H_r(k)|}^2=\langle {|a_i|}^2\rangle {|H_r(k)|}^2$$ (27)

and is proportional to the product of k⁴a₀⁶, the system response |H_r(k)|², and a normalized form factor

$${{\mathrm{\Gamma }}_0}^2(2k)=(9/16{\pi }^2{a_0}^6{{\overline{\gamma }}_{\kappa }}^2)\times \int \mathrm{d}{\mathbf{x}}_1\int \mathrm{d}{\mathbf{x}}_2\langle {\gamma }_{\kappa }({\mathbf{x}}_1){\gamma }_{\kappa }({\mathbf{x}}_2)\rangle exp(-2i\mathbf{k}\cdot \mathrm{\Delta }\mathbf{x}),$$ (28)

again in the variable 2k corresponding to the forward-and-back trip of the probing waves in backscatter measurements.

In practice, this expression [Eq. (27)] is further simplified by measuring |H_r(k)|², here modeled or approximated by expressions (18) and dividing it out from the measured spectrum, thus leaving the simple expression dσ₀Γ₀². This means that the form factor for scatterers with small-scale structure can be deduced by dividing out k⁴ from the normalized rf power spectra. When there is acoustic attenuation, an additional factor must be considered. This will be included in the examples to be given presently.

(2) Structure on a Scale Larger Than a Wavelength. A realization of this is a collection of small targets that are organized into a quasi-periodic structure on a scale greater than the wavelength, i.e., about one millimeter or greater. A number of investigators have reported observing such structure in abdominal organ tissue.^20–23 The pulse in diagnostic ultrasound is usually about three wavelengths long—about 1–2 mm. This means that these regular structures are partially resolved and therefore produce a line spectrum corresponding to this spacing (scaled by c/2) that will be directly superimposed upon the measured diffuse-scatterer rf power spectrum. It may be difficult to detect in the low-frequency region (just below 1 MHz in the case of several abdominal organs) but can stand out after some signal processing, as we indicate later. A near-zero-frequency component is also possible since the pulse can embrace several scatterers and return a coherent or distributed specular scatter. We refer to this as the unresolvable component, which—being a specular scatter—will vary more slowly with frequency and have significant power only at low frequencies.⁵

If the structure is due to large-scale scattering targets, the resolvable component is a more complex function of k. For ka ≫ 1, the scattered intensity is mirrorlike or specular and approximately independent of k. Examples of large scattering targets in ultrasound imaging are major blood vessels and organ surfaces. In our analysis such structures are eliminated by preprocessing the data.²³

(3) Structure on a Scale Comparable with a Wavelength. In this regime there are just a few scatterers per resolution cell, and both the physics and the statistics are much less transparent to a straightforward analysis. Since there are many common examples of structure from categories (1) and (2) in the body, most work has concentrated on these regimes, and category (3) has been neglected. Also, for most applications in this category the statistics are non-Gaussian (the few-scatterer case). While we have been developing the formalism for this case, we have attempted to screen out this category in the second-order statistics of intensity, as mentioned below. Again, for the case of isolated blood vessels and other specular scatterers, we have used a straightforward cross-correlation or matched-filter technique to identify such structures and eliminate them from the data before further analysis.²³

Examples of Radio-Frequency Spectra

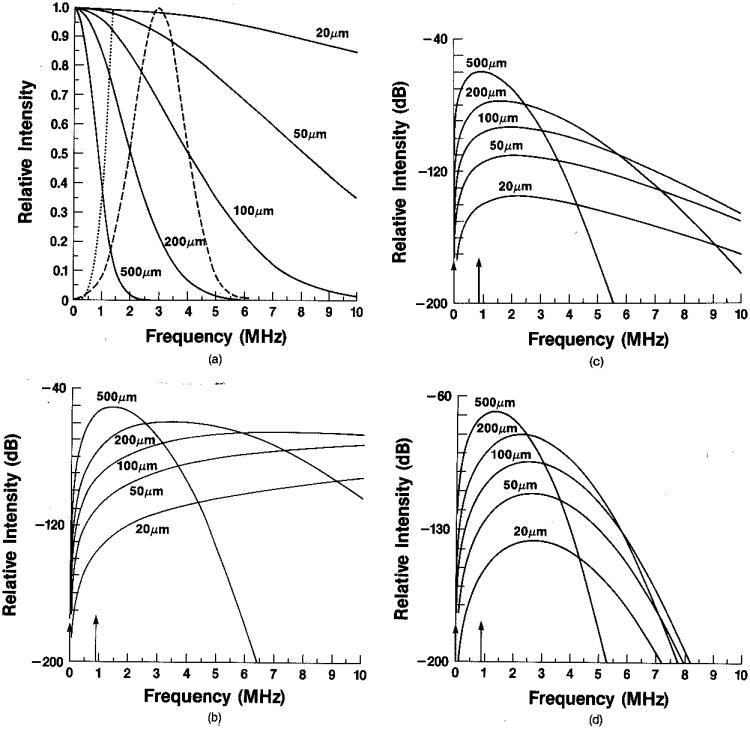
In Fig. 3 we include a set of examples of expected power spectra for category (1) and category (2) scales of structure in the ultrasound rf case. In Fig. 3(a) we show typical Gaussian form factors for particle diameters 20–500 μm (4 standard deviations), the k⁴ weighting factor, and a Gaussian probing pulse with a 3-MHz center frequency. In Fig. 3(b) the squared normalized form factor Γ₀² (2k) has been multiplied by the k⁴a₀⁶ weighting to give theoretical rf power spectra from such fuzzy spherical scatterers. Figure 3(c) is a modification of the spectra in Fig. 3(b) to include attenuation. Typical values for liver tissue have been used: α₀ = 0.5 dB/cm MHz and a depth z = 8 cm. Finally, Fig. 3(d) shows the expected measured rf power spectra in this model using a 3-MHz Gaussian pulse with a 2-MHz FWHM bandwidth. Resolvable semiperiodic structure of dimension 1.15 mm, such as that found for normal liver,^20,21,23 will be seen as superimposed narrow-band spectra. The resolvable and nonresolvable components are indicated by arrows in Figs. 3(b)–3(d).

Fig. 3.

(a) Rayleigh backscattered intensity as a function of frequency (dotted curve, f⁴); normalized squared form factors for Gaussian shapes with diameters (four standard deviations) shown (solid curve); typical 3-MHz pulse with PWHM equal to 2 MHz (dashed curve), (b) Product of f⁴ and squared form factors from (a); vertical arrows indicate location of specular scattering strength, (c) Product of functions from (b) and attenuation factor (see text), (d) Product of functions from (c) and pulse from (a).

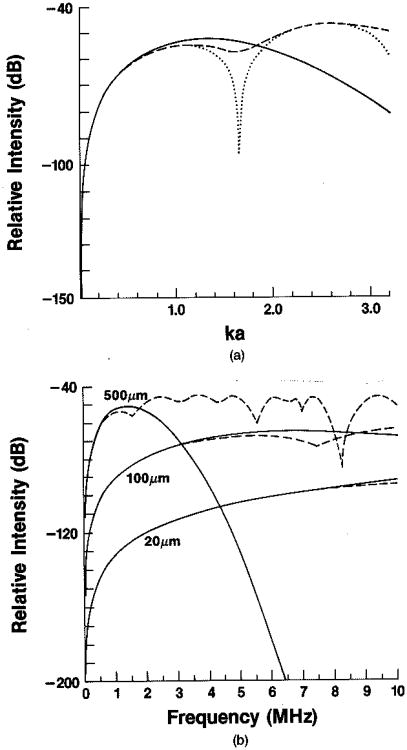
This model, in which scattering is described as the product of dσ₀ and the square of a simple form factor, has been formulated for small ka₀. In Figs. 4(a) and 4(b) we compare this simple treatment with an exact scattering theory from Faran²⁴ to see when the approximation breaks down. The solid curve is the simple Gaussian model, the dotted line is the simple hard-sphere model, and the dashed line is the theory of Faran. The last-named model was calculated for a scattering phantom composed of spherical glass targets embedded in gelatin. Relevant physical properties of the scatterers and the surrounding gelatin are, respectively, longitudinal speed of sound, 5571.9 and 1540.0 m/sec; densities, 2.38 and 1.00 g/cm³; and Poisson's ratio, 0.21.²⁵ This example clearly pushes the limits of the simple model because of the density difference.

Fig. 4.

(a) Solid curve, f⁴ weighted by squared Gaussian form factor; dotted curve, f⁴ weighted by squared hard-sphere form factor; dashed curve, expected backscattered intensity for scattering from glass spheres in gelatin, using the exact method of calculation derived by Faran²⁴ (see text for parameters). All results are plotted as a function of the product of wave number k and particle radius a. (b) Solid curves, same as (a) with particle diameter as a parameter; dashed curves, same as (a) with particle diameter as a parameter.

Figure 4(a) shows that the Gaussian and spherical models are good approximations to the exact calculation for values of ka₀ < 1. Figure 4(b) illustrates the same point for the Gaussian model and target sizes of interest in the diagnostic ultrasound frequency range. For 100-μm particles the model works well up to 6 MHz, where the disagreement with the exact calculation is 2 dB. The agreement is quite good, even though γ_κ and γ_ρ are relatively large: γ_κ = 0.97 and γ_ρ = 0.68. The resonances in the calculated curve will not be present in soft-tissue scattering.²⁶

This has been a summary outline of the simple model that has been evolving for ultrasound rf analysis over the past 5–10 years. Evidence for the applicability of the model has been offerred by Lizzi et al.,⁵ Feleppa et al.,⁷ Sommer et al.,²⁰ Fellingham and Sommer,²¹ and Waag,⁶ among others. It has been speculated that difficulties in applying the model are due to isolated large scatterers with the structure discussed in class (3) above, namely, the intermediate-size domain in the order of a few wavelengths.^2,27 However, this is just the kind of structure that can be detected and deleted from the signal by matched filtering,²³ leaving the possibility that class (1) (diffuse scatterers) and class (2) (resolvable and nonresolvable distributed specular scattering) may lead to unambiguous tissue signatures. This does not rule out the possibility that class (3) scatterers may also be calibrated and used as a tissue signature. In fact, we shall see in the next section that the presence of just a few scatterers per resolution cell—the class (3) regime—manifests itself through non-Gaussian intensity statistics. The latter raises a flag that may itself be used as a tissue signature.

In the second half of this paper, then, we show how the rf signals that we have been discussing get mixed together when the envelope or intensity signal is used and to what extent the mixing may be undone.

Second-Order Statistics of Intensity

The autocovariance of a process a is defined by analogy with the variance as

$$C_a(\mathrm{\Delta }\mathbf{x})=R_a(\mathrm{\Delta }\mathbf{x})-{|\langle a\rangle |}^2,$$ (29)

where 〈a〉² is the square of the mean of the process. The normalized autocovariance of a complex field is referred to as the complex coherence factor ρ(Δx)^11,12:

$$\rho (\mathrm{\Delta }\mathbf{x})=C_a(\mathrm{\Delta }\mathbf{x})/C_a(0).$$ (30)

The autocorrelation of detected signal intensities or their magnitudes can be expressed in terms of ρ. In the magnitude case the results are found as generalized hypergeometric functions in ρ. This treatment is relegated to Appendix A since it is not so transparent to intuition as is the intensity case and is not so directly useful. In the intensity case the results are found to be simple algebraic expressions in ρ, which—when reduced to autocovariance functions and normalized to their value at the origin—are good approximations to the results for magnitude. We shall comment further on this point after deriving the autocorrelation function for intensities.

The autocorrelation of intensities for the purely random case—e.g., the diffusely scattering case—can be derived from the autocorrelation of the rf signals by using straightforward algebra and a well-known theorem for higher-order statistics of Gaussian signals. We shall first derive the well-known result for the diffuse case and expand the treatment to include specular scatter or long-range order. We seek the autocorrelation 〈I₁I₂〉, where

$$I_1={a_{1r}}^2+{a_{1i}}^2,I_2={a_{2r}}^2+{a_{2i}}^2,\langle I\rangle =2{\sigma }^2.$$ (31)

So

$$\langle I_1{I}_2\rangle =\langle ({a_{1r}}^2+{a_{1i}}^2)({a_{2r}}^2+{a_{2i}}^2)\rangle .$$ (32)

This can be simplified by using the moment theorem for jointly normal, zero-mean, Gaussian random variables X₁,X₂,X₃,X₄ (Ref. 28)

$$\langle X_1{X}_2{X}_3{X}_4\rangle =\langle X_1{X}_2\rangle \langle X_3{X}_4\rangle +\langle X_1{X}_3\rangle \langle X_2{X}_4\rangle +\langle X_1{X}_4\rangle \langle X_2{X}_3\rangle$$ (33)

since the real and imaginary parts of a are zero-mean Gaussian random variables. The variances of a_1r and a_1i were given above as 〈a_1r²〉 = σ² and 〈a_1i²〉 = σ². Assuming that the real and imaginary parts of a are uncorrelated,

$$\langle a_{1r}{a}_{2i}\rangle =\langle a_{1i}{a}_{2r}\rangle =0,$$

we may write

$$\langle I_1{I}_2\rangle =2\langle {a_{1r}}^2\rangle \langle {a_{2r}}^2\rangle +4{\langle a_{1r}{a}_{2r}\rangle }^2+2\langle {a_{1i}}^2\rangle \langle {a_{2r}}^2\rangle$$ (34)

and use the symmetry of ρ,

$$\rho =\langle a_1{a_2}^{\ast }\rangle /\langle I\rangle =(\langle a_{1r}{a}_{2r}\rangle +\langle a_{1i}{a}_{2i}\rangle )/2{\sigma }^2=\langle a_{1r}{a}_{2r}\rangle /{\sigma }^2=\langle a_{1i}{a}_{2i}\rangle /{\sigma }^2,$$ (35)

to obtain simply

$$\langle I_1{I}_2\rangle ={(2{\sigma }^2)}^2(1+{\rho }^2),={I_d}^2(1+{\rho }^2).$$ (36)

(When there are phase errors it cannot be assumed that ρ is real as we have done here. In that case the result is given in terms of the squared magnitude of ρ. cf. also Appendix A.)

We proceed next to the case of diffuse scattering with intensity I_d, in the presence of a constant level of distributed specular scattering Ī_s, which is analogous to a carrier with additive thermal noise in the rf case. This may also be the steady, dc, or unresolved average component of the more general case to be considered presently. Then, as above,

$$\begin{array}{c}{a}_1=a_{1r}+\mathcal{R}+i{a}_{1i},\\ a_2=a_{2r}+\mathcal{R}+i{a}_{2i},\end{array}$$ (37)

where ℛ = (Ī_s)^1/2. We then have for the autocorrelation function

$$\langle I_1{I}_2\rangle =\langle ({a_1}^2+2a_{1r}\mathcal{R}+{\mathcal{R}}^2)({a_2}^2+2a_{2r}\mathcal{R}+{\mathcal{R}}^2)\rangle ,$$ (38)

where

$$\begin{array}{c}{a_1}^2={a_{1r}}^2+{a_{1i}}^2,\\ {a_2}^2={a_{2r}}^2+{a_{2i}}^2.\end{array}$$ (39)

The first terms in each set of parentheses generate the Rayleigh- or diffuse-scattering autocorrelation function as just given in Eq. (36). The remaining terms are simple to average since ℛ is constant. We get the final result by using the properties of the a's that are distributed according to the complex Gaussian pdf given above together with

$$\langle {a_1}^2{a}_{2r}\rangle =\langle a_{1r}{a_2}^2\rangle =0,$$ (40)

which follows from the random phase of the a's, obtaining

$$\langle I_1{I}_2\rangle ={I^{\prime 2}}_d(1+{\rho }^2)+2{I^{\prime }}_d{\overline{I}}_s+{{\overline{I}}_s}^2+2{I^{\prime }}_d{\overline{I}}_s\rho .$$ (41)

We shall use I′_d to refer to the measured value of the diffusely scattered intensity. It is the area under the power spectrum, considered as the average value over the band, I_d, weighted and summed over the pulse response [Eqs. (14)]:

$${I^{\prime }}_d=\int \mathrm{d}k{I}_d{|H(k)|}^2.$$ (42)

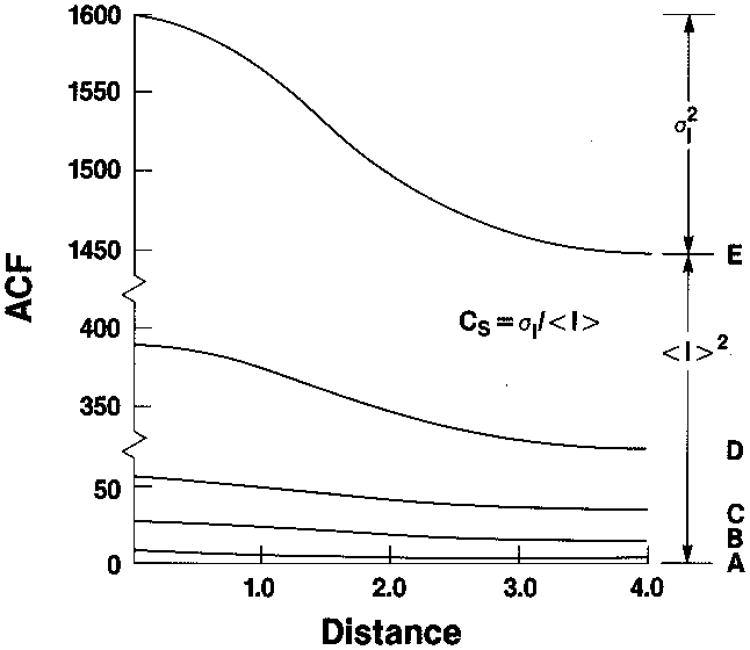
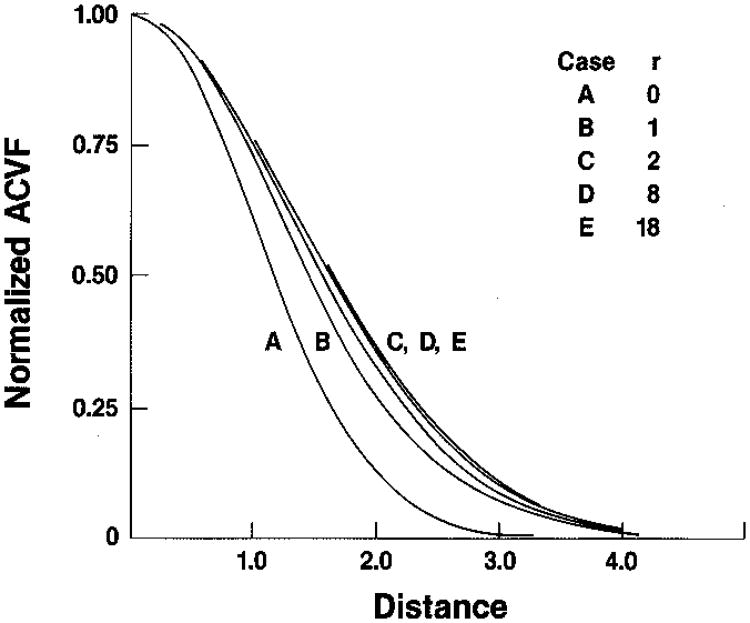
We show examples of the autocorrelation function of Eq. (41) in Fig. 5 for various values of the ratio r = Ī_s/I′_d, on an absolute scale, and in Fig. 6 on a scale normalized to unity after removing the squared mean, i.e., the conventional correlation function. We have taken ρ to be the coherence factor corresponding to a Gaussian psf, as in Eq. (17) above (envelope only),

Fig. 5.

Autocorrelation functions for intensity as a function of distance, in units of the standard deviation of the underlying Gaussian spread function. The curve parameter, from bottom to top, is r = Ī_s/I′_d = 0, 1, 2, 8, 18. The absolute units are determined by the value of I′_d = 2 [cf.Eq. (2)].

Fig. 6.

Normalized autocovariance functions for intensity corresponding to absolute curves of Fig. 5. When the autocovariance functions for magnitude (derived in Appendix A) are plotted on the same scale, they are almost indistinguishable from these functions, except for the case r = 0 in which the greatest difference is between 0.03 and 0.04 (see Ref. 15).

$$\rho ={(\pi {{\sigma }_0}^2)}^{-1/2}exp(-z^2/2{{\sigma }_0}^2)\ast exp(-z^2/2{{\sigma }_0}^2).$$ (43)

The squared mean-intensity level is the value of this function [Eq. (41)] at infinity, where ρ = 0, and the mean-square level is the value at the origin, where ρ = 1,

$$\begin{array}{c}{\langle I\rangle }^2={I^{\prime 2}}_d+2{I^{\prime }}_d{\overline{I}}_s+{{\overline{I}}_s}^2={({I^{\prime }}_d+{\stackrel{\sim }{I}}_s)}^2,\\ \langle I^2\rangle =2{I^{\prime 2}}_d+4{I^{\prime }}_d{\overline{I}}_s+{{\overline{I}}_s}^2,\end{array}$$ (44)

from which the variance is seen to be

$$\langle I^2\rangle -{\langle I\rangle }^2={I^{\prime 2}}_d+2{I^{\prime }}_d{\overline{I}}_s={{\sigma }_R}^2,$$ (45)

in agreement with Middleton.²⁹ We refer to this as the Rician variance, σ_R², after Rice,³⁰ who was one of the first to study this problem (as was North³¹). When Ī_s ⇒ 0, we recover the result for Rayleigh scattering given above. The Rician variance therefore contains the Rayleigh variance plus an interaction term that couples the diffuse and specular scattering. Notice that the total scattered intensity is the sum of the average diffuse-scattering intensity and the average specular-scattering intensity. As the ratio r increases, the average total intensity increases faster than its standard deviation, with the result that the point signal-to-noise ratio SNR₀ = 〈I〉/σ_I > 1, increasing monotonically with r.

In Appendix A we derive the autocorrelation functions for the envelope-detected or magnitude signal. The results are sums of hypergeometric functions and, in general, are not transparent to intuition. However, when these functions have their squared mean values subtracted off and the reamining autocovariance portion is normalized to unity at the origin, the results as a function of r are almost identical to the results for the intensity signal given in Fig. 6. For r = 0 the greatest difference between the normalized magnitude and normalized intensity functions is about 0.03–0.04. As r increases, this difference decreases. This means that if one keeps track of the overall normalization, the intensity and the magnitude autocovariance functions may be used interchangeably for most practical purposes.

Finally, if the distributed specular scattering is a function of position, we may obtain the general case by letting

$$\begin{array}{c}{a}_1=a_{1r}+{\mathcal{R}}_1+i(a_{1i}+{\mathcal{I}}_1),\\ a_2=a_{2r}+{\mathcal{R}}_2+i(a_{2i}+{\mathcal{I}}_2),\end{array}$$ (46)

where (a_1r, a_1i) represents the diffuse scattering, constant with position, and (ℛ₁, ℐ₁) the specular scattering, a function of position. Again, as above, we obtain

$$\langle I_1{I}_2\rangle ={I^{\prime 2}}_d(1+{\rho }^2)+{I^{\prime }}_d(I_{s1}+I_{s2})+\langle ({{\mathcal{R}}_1}^2+{{\mathcal{I}}_1}^2)({{\mathcal{R}}_2}^2+{{\mathcal{I}}_2}^2)\rangle +2{I^{\prime }}_d\rho \langle ({\mathcal{R}}_1{\mathcal{R}}_2+{\mathcal{I}}_1{\mathcal{I}}_2)\rangle .$$ (47)

If we now set position x₂ = x₁ + Δx and average the result for a fixed Δx over position x₁, we obtain

$$\langle I(\mathbf{x})I(\mathbf{x}+\mathrm{\Delta }\mathbf{x})\rangle ={I^{\prime 2}}_d(1+{\rho }^2)+2{I^{\prime }}_d{\overline{I}}_s+I_{s1}{\otimes }^{\prime }{I}_{s2}+2{I^{\prime }}_d\rho ({\mathcal{R}}_1{\otimes }^{\prime }{\mathcal{R}}_2+{\mathcal{I}}_1{\otimes }^{\prime }{\mathcal{I}}_2).$$ (48)

Here we use the symbol ⊗ for the conventional correlation operation, and we now adopt the symbol ⊗′ to mean that this operation is averaged over the record length X of the position of the x₁ variable:

$$I_{s1}{\otimes }^{\prime }{I}_{s2}=X^{-1}{I}_{s1}\otimes I_{s2}={(X)}^{-1}\sum _{{\mathbf{x}}_1}{I}_s({\mathbf{x}}_1)I_s({\mathbf{x}}_1+\mathrm{\Delta }\mathbf{x}).$$ (49)

It is the average autocorrelation function that is measured in practice, and some of its properties are discussed in Ref. 32.

It is straightforward to write Eq. (48) in the frequency domain. We first separate out the steady or dc contributions by writing

$$\begin{array}{c}{I}_s={\overline{I}}_s+\mathrm{\Delta }{I}_s,\\ \mathcal{R}=\overline{\mathcal{R}}+\mathrm{\Delta }\mathcal{R},\\ \mathcal{I}=\overline{\mathcal{I}}+\mathrm{\Delta }\mathcal{I}.\end{array}$$ (50)

Then we have

$$I_s{\otimes }^{\prime }{I}_s={{\overline{I}}_s}^2+\mathrm{\Delta }{I}_s{\otimes }^{\prime }\mathrm{\Delta }{I}_s.$$ (51)

If we write

$$\begin{array}{c}{I}_s{\otimes }^{\prime }{I}_s\stackrel{\text{FT}}{\iff }{{\overline{I}}_s}^2\delta (f)+{|\stackrel{\sim }{{\mathrm{\Delta }I}_s}(f^{\prime })|}^2/X,\\ \mathrm{P}\stackrel{\text{FT}}{\iff }\rho ,\text{etc}.,\end{array}$$ (52)

where f′ means all f ≠ 0, we obtain for the Fourier-domain equivalent of Eq. (48)

$$W(f)=\delta (f)({I^{\prime 2}}_d+2{I^{\prime }}_d{\overline{I}}_s)+\delta (f){{\overline{I}}_s}^2+{I^{\prime 2}}_d\mathrm{P}\ast \mathrm{P}+{|\stackrel{\sim }{{\mathrm{\Delta }I}_s}(f^{\prime })|}^2/X+2{I^{\prime }}_d\mathrm{P}[{\overline{\mathcal{R}}}^2+{\overline{\mathcal{I}}}^2]+2{I^{\prime }}_{d}P\ast [{|\stackrel{\sim }{\mathrm{\Delta }\mathcal{R}}(f^{\prime })|}^2+{|\stackrel{\sim }{\mathrm{\Delta }\mathcal{I}}(f^{\prime })|}^2]/X.$$ (53)

We note that the actual level of the power spectrum of a sinusoidal component with a fixed reference phase increases with the record length studied,³³ whereas the power spectrum of a random phase process is independent of record length. This ambiguity is removed, however, if the area under the power spectrum or variance is measured; as the height of the corresponding line spectrum increases, its width decreases. We shall see this effect below. These expressions suggest, then, a method for obtaining a tissue scattering signature that we present in the next section.

Analysis of the Intensity Variance

If one were to work only with the first-order statistics of the intensity signal to estimate the value of r = Ī_s/I′_d, without accounting for the variable part of the ordered or coherent component, the result would suggest non-Gaussian statistics. This can be seen from the following considerations. In the non-Gaussian case there are few diffuse scatterers per resolution cell. When this number is a random variable, one finds that the variance is greater than the squared mean³⁴

$$\text{Var}(I)=\langle I^2\rangle -{\langle I\rangle }^2>{\langle I\rangle }^2(\text{non}-\text{Gaussian statistics})$$ (54)

often, referred to as enhanced fluctuations. This condition can be taken as a cue that scattering structure (3) listed above is present and may serve as a tissue signature. In the Gaussian case—many scatterers per resolution cell—when there is no variable component, the inequality is always

$$\text{Var}(I)={I^{\prime 2}}_d+2{I^{\prime }}_d{\overline{I}}_s={{\sigma }_R}^2\le {({I^{\prime }}_d+{\overline{I}}_s)}^2={\langle I\rangle }^2(\text{Gaussian statistics}),$$ (55)

as indicated above in Eqs. (44) and (45). This may be seen graphically in Fig. 5. The presence of a variable component will inflate the variance, driving it in the direction of the inequality described in Eq. (54). If one then attempts to solve Eqs. (44) for Ī_s and I′_d or, in effect, r, the result will be imaginary solutions. This might be interpreted as the few-scatterer or non-Gaussian case if the variable component is ignored—as might happen if only first-order statistics are considered. We next indicate a simple procedure for avoiding this ambiguity through the use of the second-order expressions given above.

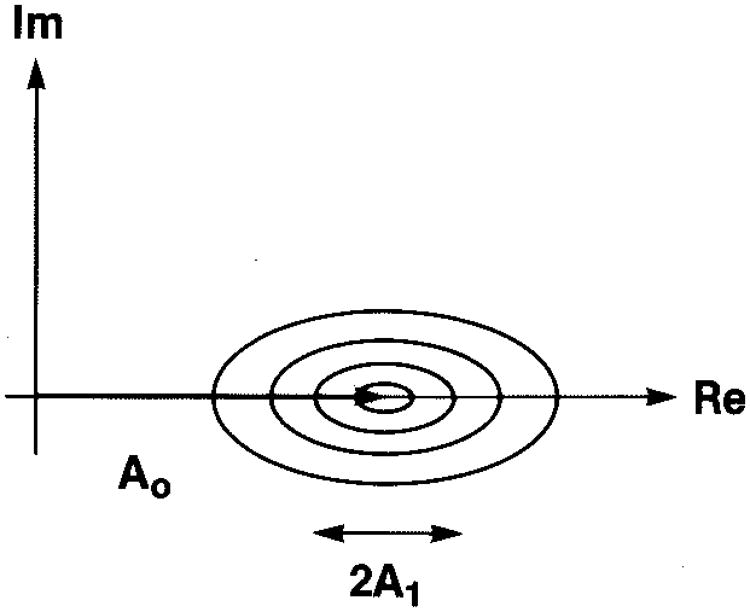
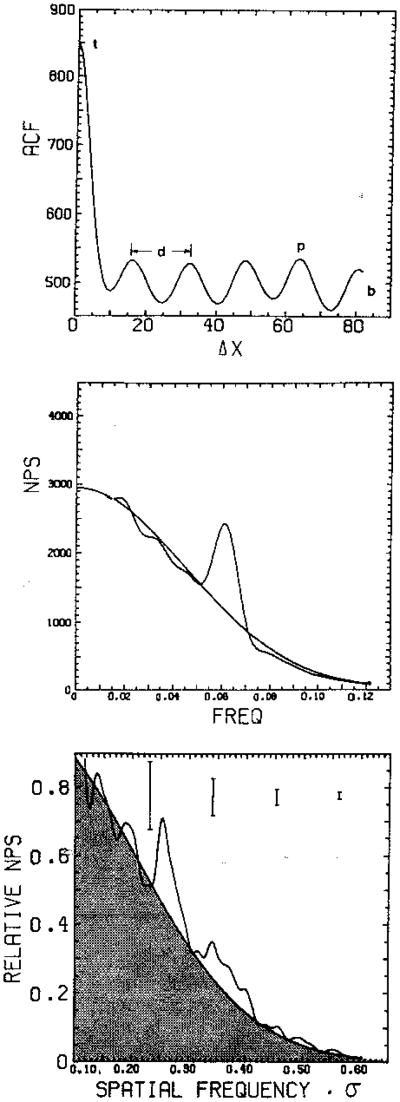
We consider the autocorrelation function and power spectrum from a region of tissue with diffuse-scattering intensity I′_d, mean specular intensity Ī_s, and a sinusoidally varying component of specular intensity to be characterized by its total contribution to the variance of I_s. We label this last contribution Σ_s². The effect on the noise cloud is shown in Fig. 7. We may deduce the form of the autocorrelation function from Eq. (48), and this is shown schematically in the top panel of Fig. 8; the corresponding theoretical power spectrum is shown in the middle panel of Fig. 8; a sample of a measured intensity power spectrum from a normal liver is shown in the bottom panel. From three values labeled t, b, and p that can be read from the autocorrelation function, we are able to calculate the values of I′_d, Ī_s, and Σ_s. This requires calculating the autocorrelation function at Δx = 0, where ρ = 1 (i.e., the mean square); at Δx = ∞, where ρ = 0 (i.e., the squared mean); and at Δx, where the sinusoidal structure has been shifted one cycle. In practice, the square of the measured mean intensity is used rather than a value of b read from the autocorrelation function. From Eq. (48) we have, for a sufficiently low-frequency sinusoid with wavelength greater than the range of ρ,

Fig. 7.

Effect of a sinusoidal variation in coherent signal strength on the noise cloud of Fig. 2 (cf. Goodman¹²).

Fig. 8.

Top panel, autocorrelation function in intensity for simulated Rician speckle with single-frequency structured specularity of period d (other parameters defined in text). Middle panel, corresponding speckle power spectrum showing Gaussian fit to Rician noise, which integrates to the Rician variance, and peak corresponding to structured specularity, which integrates to var (I_s) = Σ_S². Bottom panel, measured power spectrum for human liver in vivo. Error bars are ±1 standard error. Darkened area is Rician variance. (After Refs. 22 and 23.)

$$\begin{array}{c}t=2{I^{\prime 2}}_d+4{I^{\prime }}_d{\overline{I}}_s+\langle {I_s}^2\rangle ,\\ p={I^{\prime 2}}_d+2{I^{\prime }}_d{\overline{I}}_s+\langle {I_s}^2\rangle ,\\ b={({I^{\prime }}_d+{\overline{I}}_s)}^2,\end{array}$$ (56)

which combine to yield

$$\begin{array}{c}t-p={I^{\prime 2}}_d+2{I^{\prime }}_d{\overline{I}}_s={{\sigma }_R}^2,\\ p-b=\langle {I_s}^2\rangle -{{\overline{I}}_s}^2={{\sum }_s}^2,\\ b^{1/2}={I^{\prime }}_d+{\overline{I}}_s.\end{array}$$ (57)

The first and third of these relations combine to give a simple quadratic for Ī_s (or I′_d) and a trivial expression for I′_d (or Ī_s). This procedure may also be illustrated in the frequency domain by using the middle panel of Fig. 8, and we have found this to be more robust in practice.²³ In this case the lengths along the autocorrelation ordinate become areas under portions of the power spectrum. The variance due to the structure is stripped from the Rician noise cloud by fitting the latter with a Gaussian function.²³ A typical example of the application of this algorithm to measurements on normal human liver is given in the bottom panel of Fig. 8.

If the structure is not exactly periodic, i.e., if it is irregular, the above procedure will still properly yield the variance of this structure. The success of this procedure may, however, be extremely sensitive to the curve fitting that is used to strip out the Rician variance from the structured variance. In practice, it has been found to be essential to preprocess the intensity image: (1) to remove the low-frequency trends from the image and (2) to remove large isolated specular scatterers such as blood vessels by matched filtering.²³ Otherwise the sample heterogeneity leads to an ambiguous interpretation.

As an example of the working of Eq. (53), we consider the case in which the specular scattering has a steady or dc component and a single sinusoidal component at frequency f₀. That is, we take ℐ(f) = 0 and

$$\stackrel{\sim }{\mathcal{R}}(f)=(A_1/2)[\delta (f-f_0)+\delta (f+f_0)]+A_0\delta (f),$$ (58)

where δ(f) is the Dirac delta function. Now, since I_s = ℛ², we shall require Ĩ_s(f) = ℛ̃ * ℛ̃, |Ĩ_s(f)|² = |ℛ̃ * ℛ̃|², and, for the decomposition of variance, their integrals over frequency.

First,

$$\stackrel{\sim }{\mathcal{R}}(f)\ast \stackrel{\sim }{\mathcal{R}}(f)=\int \mathrm{d}{f}^{\prime }\stackrel{\sim }{\mathcal{R}}(f^{\prime })\stackrel{\sim }{\mathcal{R}}(f-f^{\prime })=\delta (f)({A_1}^2/2+{A_0}^2)+A_1{A}_0[\delta (f-f_0)+\delta (f+f_0)]+({A_1}^2/4)[\delta (f-2f_0)+\delta (f+2f_0)],$$ (59)

and so the first required integral over frequency is

$$X^{-1}\int \mathrm{d}f{|\stackrel{\sim }{\mathcal{R}}(f)\ast \stackrel{\sim }{\mathcal{R}}(f)|}^2={A_0}^4+{A_0}^2{A_1}^2+{A_1}^4/4+2{A_0}^2{A_1}^2+{A_1}^4/8,$$ (60)

where the first three terms are the contribution from f = 0, the fourth from f = ±f₀, and the fifth from f = ±2f, and we have used the identity under integration, δ²(f) = Xδ(f).³⁵

Note that since

$$\begin{array}{c}{\overline{I}}_s=\langle R^2\rangle ={A_0}^2+{A_1}^2/2,\\ \langle {I_s}^2\rangle =\langle R^4\rangle ={A_0}^4+3{A_0}^2{A_1}^2+3{A_1}^4/8,\end{array}$$ (61)

and

$${{\sum }_s}^2=\langle {I_s}^2\rangle -{{\overline{I}}_s}^2=2{A_0}^2{A_1}^2+{A_1}^4/8,$$ (62)

we have

$$X^{-1}\int \mathrm{d}f{|\stackrel{\sim }{\mathcal{R}}(f)\ast \stackrel{\sim }{\mathcal{R}}(f)|}^2={{\overline{I}}_s}^2+{{\sum }_s}^2$$ (63)

or

$$X^{-1}\int \mathrm{d}f{|\stackrel{\sim }{{\mathrm{\Delta }I}_s}(f^{\prime })|}^2={{\sum }_s}^2.$$ (64)

This can be identified with p – b in Eqs. (57) above, i.e., the variance in the structure or the area under the line portions of the power spectrum.

For the final step we also require |ℛ̃(f)|² and its integral over frequency. Using the expression from Eq. (58), we find immediately, as above, that

$$\int \mathrm{d}f{|\stackrel{\sim }{\mathcal{R}}(f)|}^2={A_0}^2+{A_1}^2/2={\overline{I}}_s.$$ (65)

Now, since the integral of a convolution is the product of the individual integrals

$$\int \mathrm{d}x(a\ast b)=(\int \mathrm{d}xa)(\int \mathrm{d}xb),$$ (66)

we obtain for the cross term

$$2{I^{\prime }}_d\int \mathrm{d}f\mathrm{P}\ast {|\stackrel{\sim }{\mathcal{R}}(f)|}^2=2{I^{\prime }}_d{\overline{I}}_s$$ (67)

since the integral under P is the value of ρ at the origin, unity.

We see from the last two results that, if one takes the intensity signal to be a tissue signature, with features I′_d, Ī_s, and Σ_s, these features can be determined according to the paradigm just presented and perhaps with less ambiguity than available in the pure rf signal. However, if one thinks of the rf signal as the fundamental tissue signature, with features A₀, A₁, and I′_d, where I′_d is approximately the average diffuse power in the backscattered rf sampled by the pulse [see Fig. 3 and Eq. (42)], the intensity signal mixes together the A₀ and the A₁ contributions to this signature. Furthermore, the quantities ℛ, ℐ, A₀, A₁ here refer to signals after the detection stage, i.e., after degradation by the system psf or transfer function. A₀ and A₁ are degraded differently by this function, and, since the analysis does not yield them separately, corrections for the system cannot be applied unambiguously. The problem is even more difficult in practice since there may be components present at other frequencies. Moreover, recalling that [Eqs. (11) and (30)]

$$\begin{array}{c}\rho =h(-\mathrm{\Delta }\mathbf{x})\ast h^{\ast }(\mathrm{\Delta }\mathbf{x})/{[h\ast h^{\ast }]}_{\mathrm{\Delta }\mathbf{x}=0},\\ \rho \stackrel{\text{FT}}{\iff }\mathrm{P}={|H(f)|}^2\end{array}$$ (68)

for the diffuse-scattering case, for example, one sees that the correction for the system transfer function |H(f)|² is different for each term of Eq. (53). One needs to have solved the decomposition of the variance, as indicated above—but free of system effects—in order to correct for the system effects: so the best that can be hoped for is an iterative solution to obtain results that are independent of the system. Finally, it would be possible to invert Eqs (61) to obtain A₀ and A₁ if one had a calibration or a priori information on the correct branch of the solution to choose.

The diffuse contribution is separated from the specular contribution unambiguously in this scheme if the diffuse scatterers are point scatterers. If they have a nontrivial form factor, this will narrow the shaded region of Fig. 8 [see expressions (27) and (68)]. In principle, this bandwidth can be compared with the bandwidth expected from the calculated value of r = Ī_s/I′_d and the curves of Fig. 6. The difference can then be ascribed to the nontrivial form factor. In general, however, this will be a small effect that, in practice, will be harder to see in the intensity power spectrum than in the rf analysis since the system transfer function enters to four powers in the former and only to two in the latter [formulas (27), (53), and (68)].

In spite of the limitations to the approach of analyzing the intensity correlations instead of the rf correlations or power spectra, the intensity analysis has been shown to yield excellent tissue discrimination in liver scans. It allows for the separation of the diffuse- from the specular-scattering contributions and yields the period of the regular specular structure. It might also be calibrated to give a measure of the diffuse-scatterer form factor, but this remains to be seen. Since this analysis can be achieved with less sampling and data storage, it remains an attractive approach.

Finally, we point out that the problem addressed in this paper is the analog of many important problems in statistical optics.¹² The approximate equivalence of the magnitude and the intensity statistics means that the analysis of intensity variance given here is also directly applicable to MRI when the magnitude is the quantity of interest.

Summary

The fundamental properties of second-order statistical measures, namely, the autocorrelation function and the signal power spectrum, have been presented for the case of coherent detection of rf signals. Direct analysis of the rf suggests the possibility of separating the diffuse-scattering strength from the distributed specular-scattering strength., However, the rf power spectrum as conventionally used does not directly yield this information.

A principal benefit of rf analysis is the opportunity to study the backscatter as a function of frequency and thereby to identify the form factor that characterizes the size of the diffuse scatterers. An exact calculation indicates that a simple low-pass function works well as an approximate form factor for values of ka₀ up to the neighborhood of about 2.

Analysis of the envelope or magnitude of the rf is equivalent, to a good approximation, to analysis of the intensity of the rf. The latter is preferred for its mathematical simplicity and physical transparency. A straightforward procedure for separating the specular- from the diffuse-scattering intensities based on second-order statistics was presented. Any method based on first-order statistics will be biased toward inferring non-Gaussian statistics, i.e., few scatterers per resolution cell. The intensity analysis may require calibration techniques, however, to get to the form factor of the diffuse scatterers and also requires much larger correction factors than with the rf analysis. It also mixes together components of the distributed specular-scattering strength at different frequencies. Nevertheless, the features that result from intensity autocorrelation analysis have offerred good to excellent discriminating power in abdominal organ scans.

The results obtained here are summarized in Tables 1 and 2.

Table 1. Rf Tissue Signature.

Scattering Regime	Scatterer Size	Particle-Size Signature
Rayleigh	ka ≪ 1 (small)	None/weak
	ka ∼ 1 (intermediate)	Form factor: low-f curvature (rms size only)
Mie	ka > 1 (large)	Form factor: higher frequencies (size and shape)

Table 2. Intensity Tissue Structure Signature^a.

Distribution Function	First-Order Signature (Ambiguous)	First- and Second-Order Structure Analysis
Sub-Rayleigh	σI2 > 〈I〉2	Non-Gaussian/few diffuse scatterers
Rayleigh	σI2 = 〈I〉2	Gaussian/many diffuse scatterers
Rician	σI2 ≤ 〈I〉2	Unresolved coherent component (spacing < pulse width)
Generalized Rician	σI2 > 〈I〉2	Resolved coherent component (spacing > pulse width)

^aTrends and heterogeneities (e.g., large vessels) must be removed.

Many analogs of this problem exist in the field of statistical optics and MRI when magnitude or intensity signals are detected.

Appendix A: Gaussian Statistics

When there are a large number of scatterers contributing magnitude a_i and phase ϕ_i to the resultant field a,

$$a=\sum _i|a_i|e^{i{\varphi }_i},$$ (A1)

and the magnitudes and phases of the individual scatterers are statistically independent of one another and among scatterers, then the field has real and imaginary parts a_r, a_i that are distributed according to circular Gaussian statistics

$$p_2(a_r,a_i)={(2\pi {\sigma }^2)}^{-1}exp[-({a_r}^2+{a_i}^2)/2{\sigma }^2]$$ (A2)

by the central limit theorem.¹¹ We shall write p₁ whenever we refer to a pdf that has a one-dimensional argument and p₂ when referring to a pdf that has a two-dimensional argument. The two-dimensional Gaussian function is simply the product of two independent one-dimensional Gaussian pdf's with zero mean and variance σ². The laws of conservation of probability then yield a two-dimensional pdf in magnitude V = (a_r² + a_i²)^1/2 and phase ϑ, which when integrated over ϑ yields the one-dimensional pdf

$$p_1(V)=(V/{\sigma }^2)exp(-V^2/2{\sigma }^2)V\ge 0=0\text{otherwise}.$$ (A3)

This is referred to as the Rayleigh distribution. Similarly, for the intensity I = V², the pdf

$$p_1(I)={(2{\sigma }^2)}^{-1}exp(-I/2{\sigma }^2)I\ge 0=0\text{otherwise}$$ (A4)

is obtained. This is the exponential or χ₂² pdf. The parameter σ², written often as ψ = σ² in the papers by Middleton,^29,36 depends on the mean-square magnitude or mean intensity of the scattering strength of the particles in the scattering medium.¹¹

The second-order statistics will require the joint pdf at two positions x₁, x₂ in the field. We can construct this as a four-dimensional Gaussian pdf in the variable a = (a_1r, a_1i, a_2r, a_2i):

$$p_4(a)=\frac{exp[-\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.(a^t{{\mathbf{k}}_0}^{-1}a)]}{{(2\pi )}^2{\Vert {\mathbf{k}}_0\Vert }^{1/2}},$$ (A5)

if we have the covariance matrix K₀. When the power spectrum of the underlying process is symmetric about its center frequency, the covariance matrix K₀ can be written as

$${\mathbf{k}}_0={\sigma }^2\left[\begin{array}{cccc}1& 0& \rho & 0\\ 0& 1& 0& \rho \\ \rho & 0& 1& 0\\ 0& \rho & 0& 1\end{array}\right];\text{det}{\mathbf{k}}_0=\Vert {\mathbf{k}}_0\Vert ={\sigma }^8{(1-{\sigma }^2)}^2.$$ (A6)

(Unsymmetric spectra generate additional off-diagonal contributions,²⁹ but we have not detected these in experiments.¹⁵) Thus the real and imaginary parts remain independent normal processes but are individually correlated according to the complex coherence factor ρ:

$$\rho \equiv \frac{\langle a_1{a_2}^{\ast }\rangle }{{(I_1{I}_2)}^{1/2}}=\frac{\langle a_{1r}{a}_{2r}\rangle }{{\sigma }_1{\sigma }_2}=\frac{\langle a_{1i}{a}_{2i}\rangle }{{\sigma }_1{\sigma }_2}.$$ (A7)

The first equality is the definition of ρ, and the remaining equalities hold under the assumption of symmetry between the real and imaginary parts.

As above, when this expression for p₄ is written in terms of magnitudes and phase and integrated over phase, the joint pdf in magnitudes becomes

$$p_2(V_1,V_2)=\frac{V_1{V}_2}{{\psi }^2(1-{\rho }^2)}exp[-({V_1}^2+{V_2}^2)/2\psi (1-{\rho }^2)]\times I_0(\rho V_1{V}_2/\psi [1-{\rho }^2]),$$ (A8)

where V_i = (a_ir² + a_ii²)^1/2 and I₀ is the modified Bessel function of the first kind, zeroth order.

The autocorrelation function that arises in the analysis of physical systems is the joint second moment of the second-order pdf. That is,

$$R_{\nu }(\mathrm{\Delta }x)=\langle {V_1}^{\nu }{V_2}^{\nu }\rangle ={\int }_0^{\infty }\mathrm{d}{V}_1\mathrm{d}{V}_2{V_1}^{\nu +1}{V_2}^{\nu +1}{p}_2(V_1{V}_2),$$ (A9)

where Δx = x₂ − x₁; in the magnitude case ν = 1, and in the intensity case ν = 2.

The integration may be carried out, using p₂(V₁, V₂) of Eq. (A8), by expanding the Bessel function, as indicated by Middleton,²⁹ with the result

$$\langle {V_1}^{\nu }{V_2}^{\nu }\rangle ={(2\psi )}^{\nu }{\mathrm{\Gamma }}^2(\frac{\nu }{2}+1)\{\begin{array}{c}{{(1-{\rho }^2)}^{\nu }}_2{F}_1(\frac{\nu }{2}+1,\frac{\nu }{2}+1;1;{\rho }^2)\\ \text{or}\\ {}_{2}F{}_1(-\frac{\nu }{2},\frac{-\nu }{2};1;{\rho }^2)\end{array}.$$ (A10)

The hypergeometric functions ₂F₁ are defined according to common convention (see, e.g., Middleton³⁶ and Abramowitz and Stegun³⁷), and the alternative results are a consequence of Kummer's theorem.^36,37 For the intensity case ν = 2, the hypergeometric series terminates, giving the simple result

$$\langle {V_1}^2{V_2}^2\rangle =\langle I_1{I}_2\rangle ={(2\psi )}^2(1+{\rho }^2),$$ (A11)

which is obtained more directly in the text by using the Gaussian moment theorem.

We next allow for the presence of a coherent background signal that adds to the random fluctuations of the Gaussian-distributed components. That is, we consider there to be a constant level of spatially distributed specular scattering I_s = ℛ² added to the previous constant level of diffuse scattering. This simply moves the origin of the circular Gaussian statistics of Eq. (A2):

$$p_2(a_r,a_i)={(2\pi {\sigma }^2)}^{-1}exp\{-[{(a_r-\mathcal{R})}^2+{a_i}^2]/2{\sigma }^2\}.$$ (A12)

The joint pdf in magnitude can now be found by using the multidimensional Gaussian and integrating over angles²⁹

$$\begin{gathered} p_2(V_1{V}_2)=\frac{V_1{V}_2}{{\psi }^2(1-{\rho }^2)}exp[-({V_1}^2+{V_2}^2)/2\psi (1-{\rho }^2)] \\ \times exp[-{\mathcal{R}}^2/2\psi (1+\rho )]\times \sum _{m=0}^{\infty }{\epsilon }_m{I}_m\left[\frac{\rho V_1{V}_2}{\psi (1-{\rho }^2)}\right]\times I_m\left[\frac{\mathcal{R}{V}_1}{\psi (1+\rho )}\right]I_m\left[\frac{\mathcal{R}{V}_2}{\psi (1+\rho )}\right], \end{gathered}$$ (A13)

where ε₀ = 1, ε_m = 2, m ≥ 1, and all orders, m, of modified Bessel functions of the first kind are required. This reduces to Eq. (A8) when ℛ → 0 since I₀(0) = 1 and I_m(0) =0, m ≥ 1.

The integration required for the autocorrelation function [Eq. (A9)] is somewhat more involved than for the ℛ = 0 case. Several routes have been indicated by Middleton³⁶; we have used the direct power-series expansion of the Bessel functions and termwise integration to obtain

$$R_{\nu }(\mathrm{\Delta }x)=\langle {V_1}^{\nu }{V_2}^{\nu }\rangle ={(2\psi )}^{\nu }{(1-{\rho }^2)}^{\nu +1}\times exp[-{\mathcal{R}}^2\rho /\psi (1+\rho )]\times \sum _{m=0}^{\infty }\frac{{\epsilon }_m{\rho }^m}{{(m!)}^2}{\left(\frac{1-\rho }{1+\rho }\right)}^m{p}^m\times \sum _{n=0}^{\infty }\frac{{\rho }^{2n}{\mathrm{\Gamma }}^2(m+n+1+\raisebox{1ex}{$\nu $}\!\left/ \!\raisebox{-1ex}{$2$}\right.)}{n!(n+m)!}\times {}_{1}F{}_1{[-n-\raisebox{1ex}{$\nu $}\!\left/ \!\raisebox{-1ex}{$2$}\right.;m+1;\frac{-p(1-\rho )}{1+\rho }]}^2,$$ (A14)

where p = ℛ²/2ψ. The exponential factor represents a correction to the result given by Middleton.³⁶ When ℛ = 0, only the m = 0 term will contribute, the confluent hypergeometric functions ₁F₁ reduce to unity, the sum over n can be identified as a hypergeometric function, and the first form of Eq. (A10) is recovered.