Abstract
Distributed Lag Models (DLMs) are used in environmental health studies to analyze the time-delayed effect of an exposure on an outcome of interest. Given the increasing need for analytical tools for evaluation of the effects of exposure to multi-pollutant mixtures, this study attempts to extend the classical DLM framework to accommodate and evaluate multiple longitudinally observed exposures. We introduce 2 techniques for quantifying the time-varying mixture effect of multiple exposures on an outcome of interest. Lagged WQS, the first technique, is based on Weighted Quantile Sum (WQS) regression, a penalized regression method that estimates mixture effects using a weighted index. We also introduce Tree-based DLMs, a nonparametric alternative for assessment of lagged mixture effects. This technique is based on the Random Forest (RF) algorithm, a nonparametric, tree-based estimation technique that has shown excellent performance in a wide variety of domains. In a simulation study, we tested the feasibility of these techniques and evaluated their performance in comparison to standard methodology. Both methods exhibited relatively robust performance, accurately capturing pre-defined non-linear functional relationships in different simulation settings. Further, we applied these techniques to data on perinatal exposure to environmental metal toxicants, with the goal of evaluating the effects of exposure on neurodevelopment. Our methods identified critical neurodevelopmental windows showing significant sensitivity to metal mixtures.
Keywords: distributed lag models, chemical mixtures, weighted quantile sum regression, random forests
INTRODUCTION
Originally developed in the field of econometrics, distributed lag models (DLMs) have in recent years been applied extensively to environmental health research [1–7]. They are regression models for time series data in which the effects of some independent variables are distributed across time [1]. In environmental epidemiology, they are particularly useful to study the effect of an exposure at a certain time point while adjusting for all the past (lagged) values of that exposure. While useful, classical DLMs have a number of shortcomings; most importantly, the inability to model complex mixture effects of multiple exposures. Modeling of time-dependent chemical mixture effects is an increasingly relevant problem in environmental health. Most individuals are exposed to a complex cocktail of environmental pollutants which, over time, interact in elaborate ways to shape the trajectory of biological and health outcomes. To properly model these multivariate associations, it is essential that analytical approaches for time-lagged effects are extended to accommodate chemical mixtures.
In this paper, we introduce two novel approaches for modeling longitudinal chemical mixture effects. We emphasize one particular application: identifying time periods with the largest and most potentially biologically relevant mixture effects. One particular problem for which such an application could be useful is in identifying critical windows of development wherein exposure to multi-pollutant mixtures could increase risk of a health outcome at a later life stage. As a motivating example, we consider a study that uses teeth as a biomarker of past chemical exposure in children. For each child, biochemical analyses of baby teeth produce precise measures of intensity and timing of exposure to multiple metals (e.g. zinc, manganese, lead, barium, lithium) throughout the perinatal period. As the brain develops in utero and during the early years after birth, there are certain critical periods that are particularly sensitive to environmental insults [8]. Further, exposure to metals is known to influence neurodevelopment in children. At a physiological level, multiple metals may interact in unknown ways to shape neurodevelopment, so the goal is to identify critical periods where the cumulative mixture effect among a set of metals appears to significantly influence development. The spectrometric technique used for the biochemical analysis of teeth (Laser Ablation-Inductively Coupled Plasma-Mass Spectrometry [LA-ICP-MS]) permits a high degree of temporal resolution in the metal exposure measurements. This produces a set of very fine-scale longitudinal exposure measurements (on the order of a few days apart) over a period of a few months before birth to a year or so after birth. However, the timing of the measurements is irregular, in the sense that they vary from subject to subject. Some subjects may also have missing measurements within a certain span of time (e.g. a few weeks), for reasons that will be discussed later. This heterogeneity in exposure measurement timing across subjects presents some analytical challenges. The techniques we propose for modeling longitudinal mixture effects deal with these challenges using different strategies.
While the 2 techniques we present here share a number of similarities, they utilize very different modeling paradigms and have distinct but partly complementary sets of strengths and weaknesses. The first approach is a flexible, parametric technique that is based on Weighted Quantile Sum (WQS) regression [9–12]. This is a penalized regression technique similar to ridge regression [13] and Lasso [14]. Weighted Quantile Sum regression utilizes a non-negative, unit-sum constraint that groups variables into a unidimensional index. We extend this technique to handle lagged exposures and term the extension Lagged Weighted Quantile Sum Regression (henceforth referred to as Lagged WQS). As we will show, this method is particularly ideal for the motivating example described above, a data set where a large number of repeated measures are taken on multiple pollutants, and the timing of measurements is not necessary uniform across subjects. Lagged WQS attempts to model the complex longitudinal exposure trajectory as a continuous function of time. It is also robust to missing data in exposure measurements. The second approach is based on Random Forests [15]. This nonparametric approach uses the extensible framework of decision tree ensembles to model complex interactions among exposure variables with respect to their cumulative effect on an outcome of interest. We refer to this approach as Tree-based DLMs. Unlike Lagged WQS, it is more ideal for data where exposures are measured at discrete, well-defined time points that are similar or identical across subjects. Therefore, for data with complex longitudinal exposure measurements and heterogeneity in the timing of measurements across individuals (such as the motivating example described above), the use of tree-based DLMs often requires a preprocessing step which bins the exposure measurements into a series of discrete time windows that are uniform across all subjects. As will be discussed, the tree-based DLM approach is also more sensitive to missing exposure measurements.
METHODS
DLMs yield an estimate of the effect of exposure incurred at specific time windows while adjusting for exposures at other times, under the assumption that the effect of exposure varies smoothly over time. Let Yi denote a quantitative outcome value for a subject i (where i = 1,…,n) at a fixed time. Here, Yi could represent some health outcome, e.g. forced expiratory volume in the span of 1 second (FEV1), a measure of lung function. Further, for each subject i, let Xi,t (t = 1,2,3,…,T) denote a series of measurements of a single environmental chemical/pollutant/risk factor at discrete time points prior to the measurement of Yi. In other words, the Xi,t represent subject i’s history of exposure to the chemical at discrete time points prior to the time at which Yi was measured. A brief point regarding notation: we have chosen not to index Yi by time since it is only measured once (at a time point subsequent to all the Xi,t measurements). Across all subjects, we assume that the timing of the measurements of Yi and Xi,t (t = 1,….,T) are roughly identical. The key idea underlying DLMs is that the value of outcome Yi taken at a fixed time point is influenced by prior exposure to the chemical at preceding time points t = 1, 2, 3,....,T. This functional relationship between the outcome and lagged exposure values can be expressed as:
| (1) |
In the above model, we have also adjusted for a covariate z (multiple covariates can be included but for ease of presentation we include only one here). The term λ represents the coefficient of covariate z. Each of the coefficients αt (t=1,…,T) represents the effect of exposure at time point t on the subsequent outcome Y. The ei represent subject-specific error terms with distributions that depends on the nature of Yi. Here, we have assumed that Yi is a continuous measure following a normal distribution, therefore Equation (1) is a linear regression model and the ei are assumed to be normally distributed. Note, however, that DLMs can work with other outcome types (e.g. Bernoulli-, Poisson-distributed outcomes), as long as the appropriate model is used, e.g. if Yi is binary, then a logistic regression model can be used in lieu of the linear model in Equation (1). While DLMs are useful, parameter estimation is complicated by the fact that the Xi,t (t=1,…,T) are usually highly correlated. This is expected since they represent measurements of the same chemical/pollutant at different time points. Therefore in practice, different techniques are employed to reduce the effect of multicollinearity. One popular method introduced by Almon (1965) [16] imposes a constraint on the lag coefficients αt (t = 1,.., T) by assuming a functional relationship among them, i.e. αt = f(t). Here, f is typically a simple polynomial of degree q (q < T), but could also be modeled as a spline-based function.
Before introducing the first of our proposed methods (Lagged WQS), we begin by describing a useful reparameterization of the classic distributed lag modeling framework described above. First introduced by Chen et al (2015) [17], this reparameterization forms the basis for the Lagged WQS technique. It involves recasting Equation (1) by interchanging the role of the outcome and exposure as follows:
| (2) |
In the model above, Yi, which was the dependent variable in the DLM in Equation (1) is now an independent/explanatory variable, while the dependent variable is now the exposure Xi(t) (originally represented as Xi,t in Equation (1)). The model in Equation (2) has the form of a mixed model since the dependent variable Xi(t) is a time-varying longitudinally observed measure. Recall that the original DLM formulation (in Equation (1)) has a cross-sectional (i.e. time-invariant) outcome Yi and a longitudinally-measured exposure, but by switching the roles of the latter and the former, we arrive at the more familiar mixed model structure given in Equation (2). Also, we use time-varying coefficients represented by smooth functions constructed using splines, which makes this a generalized additive mixed model (GAMM). The time-varying coefficients are: β0(t), the intercept term, β1(t), representing the time-varying correlation between X and Y, and γ(t), the covariate (zi) coefficient. The random effect term, u, permits the assumption of a specified correlation pattern for intra-subject observations. In our studies, we use a simple compound symmetry structure. The εi(t) is the error term and is assumed independent of the random effect term. The model in Equation (2) is fit using nonlinear mixed model estimation techniques with spline structure for the coefficients. Details on this are provided in the next section.
Chen et al (2015) [17] refer to the model in Equation (2) as a reverse temporal model. As they point out, the model is somewhat counterintuitive from a temporal standpoint, i.e. X(t), our dependent variable, is actually measured prior to the measurement of Y, the explanatory variable. However the coefficient β1(t) has a relatively straightforward interpretation. When Y is a continuous variable, β1(t) simply represents the time-varying correlation/association between Y and the levels of exposure to X. Time points wherein β1(t) is significantly positive are seen as periods in which higher exposure to X predisposes individuals to higher levels of the outcome Y, and vice versa. Note that while the time-varying coefficient β1(t) in Equation (2) and the αt (t=1,…,T) coefficients in Equation (1) have somewhat analogous interpretations (generally representing the relationship between exposures and the outcome), a key difference in their formulations is worth highlighting here. In Equation (1), each αt coefficient represents the conditional association between exposure at a specific time and the outcome, adjusted for exposures at other time points. In Equation (2), β1(t) represents the time-varying association between the outcome and the lagged exposures.
To assess significance of β1(t) across time points (various values of t), time-varying Holm-Bonferroni-adjusted [18] 95% confidence intervals are constructed for β1(t) assuming regularly timed comparisons. This procedure produces a series of evenly-spaced confidence intervals across the entire observation period. Portions of the observation period in which the confidence intervals are significant (i.e. do not include 0) are denoted as critical windows, i.e. time windows where the level of exposure X has a statistically significant impact on the level of the response variable Y observed at a later time.
As mentioned in the Introduction, the Lagged WQS technique works particularly well for complex longitudinal exposure data, i.e. where a large number of measurements are taken over time, and the timing of these measurements might be irregular within and/or across subjects. The reverse temporal model described above recasts the problem into a GAMM framework wherein the longitudinal exposure data is modeled as the dependent variable. With this setup, we can then estimate the time-varying effect of the pollutant on the outcome. We will now demonstrate how to extend this model to accommodate situations where densely sampled longitudinal exposure measurements are taken not just on one, but multiple chemicals/pollutants. The goal of the Lagged WQS technique is to be able construct a smoothly-varying (over time) function that represents the time-varying effect of the mixture of chemicals on the health outcome of interest.
1.1 Extension to mixtures–Lagged WQS
We now describe the extension of this methodology for evaluating chemical mixture concentrations and evaluating their effects on an outcome of interest. Assume we have a mixture of C chemicals, the levels of which are denoted by Xc (c=1,…,C). First, we define a time-varying weighted sum as: with constraints 0 < wc (t) <1, where the weights are assumed to vary smoothly over time. The time-varying weights are modeled using a cubic spline regression function embedded within a nonlinear logistic function: , where Sc(t) is a cubic spline with knots, say, at K = (k1, k2, k3) for each of c = 1,…,C. Knots are typically chosen as quantiles of observation time, e.g. quartiles. Mutual independence across subjects is assumed.
The Lagged WQS technique is implemented via the following steps:
STEP 1: Initialize WQS(t) with equal weights over time.
-
STEP 2: Conditional on WQS(t), use the reversed DLM in the equation below to estimate a time-varying association between WQS(t) and the variables Y and z, resulting in estimates for β0(t), β1(t), and γ(t):
(2b) Note that in the case where we have just 1 exposure variable, WQSi(t) in Equation (2b) can simply be replaced by Xi(t), and this reduces to Equation (2) (a single exposure DLM).
STEP 3: Improve the working estimates for the weights in WQS(t) conditional on the current estimates for β0(t), β1(t), and γ(t); i.e., define Ri(t) = β̂0(t) + β̂1(t)Yi + γ̂(t)zi and then regress Ri(t) onto WQSi(t) via the following model: . Recall that the weighted sum on the right hand side is WQSi(t). Note that since the weights wc(t) are composite parameters constructed from splines (see above), the parameters estimated in this step are not actually the weights themselves, but rather the spline coefficients used to construct the weights. Note also that this step is conducted assuming independence over subjects and time.
STEP 4: Repeat step 2 conditional on the weights in step 3. This is the final step.
Note that this procedure is not iterative; Steps 1–4 only need to be carried out once to derive β1(t) estimates of the time-varying mixture effect. Confidence intervals are constructed for β1(t) in the final STEP 2. At time points where the estimate of β1(t) is positive and significant, we claim that the mixture is associated with an increase in the response variable; when the estimate of β1(t) is negative and significant, we claim the mixture is associated with a decrease in the response variable, i.e. the overall mixture effect leads to a decrease in levels of the response variable. As per our definition, both significant positive and negative associations are deemed exposure-related critical windows for the health outcome (denoted here by Y). The contributions of individual components relative to the time-varying overall mixture effect are demonstrated graphically by multiplying the time-varying weights byβ̂1(t). The approach is thus limited to either an overall negative or positive association and is not able to detect opposing effects at a given time point.
The model in Step 2 is fitted as a mixed model with spline structure for coefficients. In Step 3, model estimates were also obtained using this approach. We carried out these computations using the SAS (Cary, NC) procedure NLMIXED [19].
1.2 Tree-based DLM
Unlike the Lagged WQS approach, this technique is based on the traditional formulation of classical DLMs given in Equation (1), which examines the effect of the exposure at a set of discrete time points (presumably identically timed across subjects). The key innovation of this method is the use of random forests (RF) in place of regression models. RF offers a fully non-parametric tree-based approach that has multiple strengths which will be discussed below.
We revert to the classical DLM formulation given in Equation (1). But we extend this linear model to a more general functional form that can accommodate multiple chemicals in addition to multiple time points of exposure, and is fully non-parametric:
| (3) |
Here, represents the measured exposure level of chemical c (c=1,…,C) at time t (t = 1,…,T). Note the slight switch in notation from Section 1.1, where we denoted exposures by Xc(t) since the Lagged WQS method treats exposures and model parameters as smooth functions of time. The new notation is more suited to the current method which, like the classical DLM formulation, uses a discrete time structure where exposures are indexed by lag indices. Note also that X in the expectation expression in Equation (3) above is a vector of all the exposure values across all lags and all chemicals, i.e. . The term z represents a covariate (note that more than one covariate can be included). Similar to Equation (1), Equation (3) expresses a general form for the underlying functional relationship existing between the outcome at a certain time (Y) and measured values of the C chemicals at various time windows prior to (and potentially leading up to) the time at which Y is measured. What we propose herein is approximating the function f using random forests (RF). Note that the classical DLM formulation (shown in Equation (1)) assumes a linear functional form for f. RF is a simple, effective, non-parametric tree-based learning algorithm that is generally considered to be one of the most powerful statistical modeling and prediction methods [20]. It is particularly effective for modeling complex, nonlinear relationships in high dimensional settings [21]. Trying to model such complex relationships using parametric modeling techniques is often difficult since a functional form has to be assumed, in the face of little prior knowledge. Due to its appealing characteristics, RF is a promising methodology for use in estimating f above. It allows flexible modeling of the joint effect of chemical mixtures at each time point on the outcome.
1.2.1 Random Forest Algorithm
Assume that we have data on n subjects: 𝓓n = {(Xi,Yi)}1≤ i ≤ n. For each subject i, . The data on each subject i consists of the longitudinal (lagged) exposure measures for each of the C chemicals, and a single outcome Yi measured subsequently. Here, just as in Equation (1), we have chosen not to index Yi by time since it is only measured once (at a time point subsequent to all the exposure measurements).
The random forest (RF) algorithm involves generating M bootstrap samples (each of size n) of this data and recursively partitioning each bootstrap sample using a series of binary splits determined by values of the individual predictor variables. The predictor variables chosen at each split (and the corresponding split points) are determined by optimization of loss functions related to the outcome. By recursively bisecting the predictor space in this manner, a hierarchical tree-like structure is formed which functions as a piecewise approximation of the underlying relationship between the predictors and the outcome.
Let the M bootstrap samples be denoted by . We represent the trees built on each of these samples by f̂1,......, f̂M. These can be seen as individual functional estimators of the outcome Y. If the outcome is continuous, the final step of the RF algorithm involves averaging these estimators. Therefore in equation (3) above, we can estimate f (X) by:
| (4) |
Since RF is non-parametric, there is no inherent mechanism for formal inference on the strength of association of each predictor variable with the outcome. However, the RF approach allows us to obtain heuristic measures of the ‘importance’ of individual variables [22]. Likewise, the importance of arbitrarily defined groups of variables can be estimated. The distribution of these Variable Importance (VI) measures is not easily determined, which means attaching statistical significance to them is not straightforward. However, nonparametric estimates of p-value can be obtained by using permutation tests to estimate the null distribution of the VI measures. Below, we show how to estimate the VI for a single variable, i.e. the measured exposure for a particular chemical c at a particular time t. We then show how to estimate the VI for a set of C chemicals all measured at a particular time t.
VI measures require the use of what are referred to as ‘out-of-bag’ samples. As mentioned above, the RF algorithm generates M bootstrap samples (each of size n, the total number of unique subjects/observations in the dataset) and fits separate trees on each of these bootstrap samples. Each bootstrap sample m (m ∈{1,..., M}) is generated by taking n random draws (with replacement) from the original data. This approach guarantees that in almost all bootstrap samples taken from the data, some observations will not make it into the bootstrap sample. It can be shown mathematically that on average, ~37 % of the observations from the original data will not make it into the bootstrap sample. These leftover observations are referred to as out-of-bag (OOB). The OOB subset from each bootstrap sample m can be used as an independent validation set for testing the generalization error of the tree constructed on m. Let represent the OOB samples corresponding to the bootstrap samples m=1,…,M. Then for each bootstrap sample m, we can estimate the generalization error of the tree built on m by using its corresponding OOB sample. The form of the generalization error will differ depending on the type of outcome. For continuous outcomes, a popular metric is the Mean Squared Error (MSE). Therefore,
| (5) |
As the equation shows, for each observation/individual i in the OOB sample, we compute the squared difference between i’s observed outcome Yi and their predicted outcome f̂m(Xi) (recall that ). We then average these squared residuals over all the subjects to obtain the MSE for the tree built using the mth bootstrap sample. To estimate the VI for a single variable , we randomly permute the variable in each OOB sample. Note that all other variables in the dataset (including the outcome) are left intact–only is randomly permuted. The random permutation breaks any association that may exist between and the outcome Y. We then re-estimate the MSE of these permuted datasets and compare to the MSE computed from the original data (equation (5)). If variable has a strong association with Y, then the new MSE should be substantially greater than that of the original MSE (in the original unpermuted data). To express this difference symbolically, let be the modified version of OOB sample that is obtained by randomly permuting within the sample. Then the VI of variable can then be expressed as:
| (6) |
In a similar fashion to the single-variable case, we can define the VI for a group of variables, as outlined in Gregorutti et al. (2014) [23]. Let XJ represent a subset of the vector of exposure variables . So XJ could, for example, be the subset of variables representing exposure to all the chemicals (c=1,…,C) at one specific time/lag t=t′. As in the single-variable case, we randomly permute group XJ by jointly permuting every individual variable in the group. This is done by using the same permutation pattern for each variable, i.e. we do not permute each variable separately but rather, as a group. This groupwise permutation approach preserves the empirical joint distribution among the variables comprising XJ but abolishes any associations that these variables have with the outcome Y. If the joint effect of these variables on the outcome is substantial, then it can be surmised that the MSE of a sample produced by jointly permuting these variables will increase (compared to the original, unpermuted data). Similar to equation (6), we can express the joint VI for group XJ as:
| (7) |
In Equation (7), J represents the index set for XJ. And is the modified version of OOB sample that is obtained by joint random permutation of the group of variables XJ within the sample. Note that the group VI is normalized via division by |J| (the cardinality of index set J), to account for differing group sizes.
1.2.2 Evaluating mixture effects using Tree-based DLMs
Having described the random forests algorithm, we now demonstrate how it can be adapted for use in multi-exposure DLMs.
To illustrate, we restate the original extended, generalized DLM given in Equation (3):
The RF algorithm estimates f, thereby producing a model-free approximation of the functional relationship between the multiple pollutants/chemicals (c = 1,…,C) measured at multiple time points (t = 1, 2, …., T). As described in the prior section, the RF framework also includes a mechanism for computing variable importance (VI) measures for single variables and, more importantly, groups of variables. For example, to determine the time-dependent joint effect of chemicals c = 1,…,C at a certain time t = t′ we compute the group VI for the corresponding set of variables, i.e. the set { }. This set represents the measurements of the levels of exposure to each of the C chemicals at one specific, fixed time point t = t′. We may be interested in assessing how exposure to this set of chemicals at this specific time point influences values of the outcome Y at a later time. The group VI measure provided by random forests allows estimation of the group/cumulative effect of these C chemicals (at a fixed time point) on the outcome. For each time point (t = 1, 2, ….,T), group VI can be computed. Together, these group VI measures provide a way of delineating the time-varying effect of the mixture of chemicals on the outcome.
Additionally, the statistical significance of the VI measures can be estimated through a permutation testing procedure described below:
Compute the VI of the variable(s) of interest in the current dataset
In the original data, randomly permute the outcome to produce a new dataset
Carry out Step 1 on the new dataset from Step 2 and record the new VI
Repeat Steps 2–3 H times (where H is typically a large number, e.g. 500).
- Estimate the empirical p-value of the VI as the number of iterations in which the VI derived from permuted data exceeded the VI computed from the original (unpermuted) data:
(8)
1.2.3 Interpretation of importance measures produced by Tree-based DLMs
For a combination of chemicals/pollutants measured at a specific time point, the group VI measure defined above quantifies the overall mixture effect at that time point. Note that this measure conveys no information about the directionality of the mixture effect. Group VI measures only quantify the combined explanatory power of the chemical mixtures for the outcome. In other words, each component of the mixture might have positive or negative effects, and the overall effect might have a complex response surface, but the group VI only measures the cumulative magnitude of this effect. Note that this limitation is shared also by the Lagged WQS approach. Both techniques proposed in this paper are designed primarily to quantify the magnitude of the time-varying joint effect of multiple exposures on an outcome. They characterize the overall, combined effect of multiple exposures on the outcome, but neither is able to provide a more nuanced delineation of the mixture effect, e.g. disentangling which exposure alters the effect of other exposure(s) on the outcome. This level of detail likely requires mapping out the multidimensional exposure-response surface, a challenging undertaking particularly in light of the time-varying nature of the mixture effects.
Note that unlike Lagged WQS which attempts to model a series of longitudinal exposure measurements using a smooth function of time, tree-based DLM approach requires a series of measurements at discrete time points that are the same (or roughly so) across all subjects. Many environmental exposure designs adhere to this discrete time structure. However, for the application of tree-based DLMs to exposure measurements with complex and/or irregular timing patterns (such as the motivating example described in the Introduction), binning the measurements into a series time windows (that are identical across subjects) is a prerequisite step. This allows conversion from a continuous time structure to a discrete time structure more suitable for the tree-based DLM approach.
1.3 Simulation studies
Using simulated datasets, we demonstrate the application of each technique and we compare their performance with respect to the ability to identify time windows harboring significant mixture effects. Simulations were based on a relatively simple scenario with 3 exposure variables and 5 time windows. In this scenario, no effects (additive or otherwise) exist at the 1st, 2nd and 5th time windows. But at the 3rd and 4th time windows, non-zero mixture effects exist that are nonlinear. Also, we do not include any covariates, although either technique naturally accommodates auxiliary variables of this sort. So overall, our simulation scenario describes a simple setting wherein the 3 exposure variables (e.g. chemicals) have no effect at the 1st and 2nd time windows, exhibit a non-zero and nonlinear mixture effect at the 3rd and 4th time windows, and have no effect at the 5th. A real-life situation similar in spirit to this simulation scenario could easily be conceived, e.g. during fetal development, exposure to a group of 3 chemicals throughout the prenatal period might shape neurodevelopment. Further, the cumulative neurobiological effects of this 3-chemical mixture might vary over the prenatal period. Say we divide this period into 5 epochs (time windows), one can imagine a scenario where neurological development is particularly vulnerable to the deleterious effects of these chemicals at the 3rd and 4th epochs, but significantly less so at the others.
In our simulation scenario, we assume that the effects at the 3rd and 4th epochs are non-additive, i.e. they involve synergistic relationships among the chemicals that cannot be adequately modeled by approaches assuming additivity (e.g. the classical DLM formulation). The relationship between the exposure levels of the 3 chemicals at the 5 time windows was assumed to follow the model below:
| (9) |
Equation (9) shows the basic generative model for our simulations. Here, represents the measured level of chemical c (c=1,2,3) at time window t (t=1,..,5). For each of the 5 time windows, we define a function representing the mixture effect within that window. These functions are given by f1, f2,…, f5 in Equation (9) and their functional forms are explicitly specified. So in our simulation setup, we are modeling Y (the outcome of interest) as a function of exposure to chemicals c = 1,2,3 over the 5 time points, and a residual component ε due to random individual variation (noise).
The mixture effect functions ft (t = 1,…,5) are given below:
| (10) |
| (11) |
| (12) |
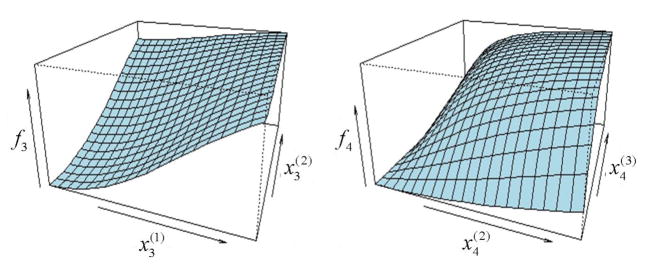
As the equations show (and as noted earlier), time windows t = 1, 2 and 5 have zero/null effects. And at time windows 3 and 4, the non-additive, nonlinear mixture effects are defined using the logistic and arctangent functions, respectively. A close inspection of the above definitions for f3 and f4 reveal that these functions involve only two of the three chemicals (though not the same two), i.e. f3 involves only chemicals 1 and 2, while f4 involves only chemicals 2 and 3. This was assumed for simplicity and ease of visualization. The figures below show a visual depiction of functions f3 and f4 :
Below, we show how the exposure variables ( ) were randomly generated. The goal was to simulate 100 datasets each with a sample size of 200. Each exposure-time variable (i.e. representing the measured level of chemical c (c=1,2,3) at time window t (t=1,..,5)), was generated from a standard normal distribution, i.e.
| (13) |
For each of the 100 datasets, values of (c=1 to 3; t=1 to 5) were generated for each of the 200 individuals/samples. Since, in practice, exposure levels are generally nonnegative, in each of the 100 datasets, we added a constant offset value to each to produce exposure measures that were, at minimum, zero. Note that a viable alternative approach would be to generate the from a log-normal distribution, which various pollutant exposures have been observed to follow [24]. However, taking the natural logarithm of log-normally distributed exposure values will simply yield the normally-distributed variables used in our simulation scenario. Also, in practice, correlations are expected to exist among the exposure variables , therefore our simulations incorporated a correlation structure among these variables. For the sake of simplicity, we specified a very simple correlation structure wherein correlations exist only within lagged measures of each chemical, but not between lagged measures of different chemicals, i.e.:
| (13a) |
The above is the formulation of a block-diagonal first order autoregressive (AR(1)) correlation structure, with ρ = 0.2 in our simulations. As is evident from the definition, for any pair of lagged values of different chemicals (c ≠ c′), the correlation is zero. However, among any pair of lagged exposure values of the same chemical (c = c′), a correlation exists which decays exponentially as a function of lag difference, i.e. exposure levels closer in time tend to be more correlated than those measured further apart. To impose this correlation structure on the simulated exposure values, we use a Cholesky decomposition (see Appendix for full details). This transformation is carried out on the lagged exposure values for each individual/case across the 100 datasets. Having generated exposures with the desired correlation structure, we use these values to generate Y (outcome) values. This was done by plugging the values into the simulation model given in Equation (9) (reproduced below):
| (14) |
As discussed earlier, in our simulation setup, we are modeling Y (the outcome of interest) as an explicitly defined function of exposure to chemicals c = 1,2,3 over the 5 time points, and a residual component ε due to random individual variation (noise). In each of the 100 simulated datasets, the residual ε is independently and identically distributed across the 200 individuals, with a common standard deviation σ. It is straightforward to see that the magnitude of σ controls the signal-to-noise ratio in our simulated data, e.g. a very high value of σ (relative to the variation in the signal [the summation term in Equation (14)]) will make it more difficult to detect the true underlying exposure-response relationship. The value of σ can be chosen by pre-selecting a desired signal-to-noise ratio (SNR) and using the following relationship:
| (15) |
We carried out simulations for two SNR values: 0.5 and 1.
To summarize, we simulated data corresponding to a simple exposure-response scenario wherein longitudinal exposure to a 3-chemical mixture affects an outcome Y (Equation (9)). Among the exposure values, we defined the simple correlation structure given in (13a) using a value of ρ = 0.2. We carried out simulations for two settings of the signal-to-noise ratio: SNR = 0.5 and SNR=1.
Data structure
The simulation steps outlined above result in a simple, discrete-time data structure, i.e. in each of the 100 simulated datasets, each row represents a unique individual/subject, with columns representing the outcome and also the exposure levels of each chemical at each time point. Specifically, each row represents data for individual i, given by {Yi, Xi}, where . As discussed earlier, this discrete time structure is ideal for tree-based DLMs. Because the Lagged WQS method is based on a mixed modeling framework, the simulated data had to be transformed from the ‘wide’ data format shown above (1 row per subject) into a longitudinal data structure (i.e. ‘long’ format). In this format, rows are indexed by time and subject, i.e. each row takes the form of: {t, Yi, }. Here, t denotes time (t=1,2,3,4 or 5), Yi is the outcome for subject i, and the X variables represents levels of the 3 chemicals for subject i at time t. Since there are 5 time points, this ‘long’ format represents each individual’s data as 5 rows. Next, to mimic the continuous time structure seen in longitudinal exposure measurements such as in the motivating study described in the Introduction, we made simple modifications to the time value across subjects (described below). As discussed earlier, Lagged WQS is especially suitable for scenarios where the timing of measurements is not necessary uniform across subjects, such as the motivating example described in the Introduction. This is because the technique models the longitudinal exposure trajectory as a continuous function of time. Therefore, to accommodate this feature, we modified the time measures in our simulated data from a discrete time structure to a continuous time structure. For each time point t ∈ {1, 2,3, 4,5}, let τ ~ Uniform[t −0.5, t + 0.5]. For each individual, we replace each of the integer time points t ∈{1, 2,3, 4,5} with a real number time point τ randomly generated from a uniform distribution centered at each t. For example, for time point t=1, we replace this with a real number τ that is randomly sampled from a uniform distribution with range 0.5 to 1.5; for time point t=2, we replace this with a real number τ randomly sampled from a uniform distribution with range 1.5 to 2.5, and so on. These modifications produce an irregular timing pattern across subjects, resulting in a temporal distribution akin to a continuous time structure. Note that each subject would still have 5 measurements of the 3 chemicals, but the timing of each measurement will vary across all subjects.
Comparison of techniques
The performance of Lagged WQS and Tree-based DLMs were compared for these simulations. For the purpose of comparison, we also used Generalized Additive Models (GAM) with multivariate thin-plate splines [25] (implemented in the R package mgcv [26]). This is one of the few established techniques for testing the statistical significance of mixture effects. It allows modeling of mixture effects among multiple variables using multivariate (high-dimensional) smooth splines. Statistical significance of these smooth terms can also be derived. Therefore, just like Lagged WQS and Tree-based DLMs, this implementation of GAM also has the capability to produce significance measures for mixture effects. For Tree-based DLM and GAM, we used the raw simulated data in wide format (i.e. each row represents data for individual i and is given by {Yi, Xi}, where the vector ). On the other hand, for Lagged WQS, we used the long format (with continuous time structure) described in the previous paragraph. With these simulations, we evaluated the performance of Lagged WQS, Tree-based DLMs and GAMs in terms of their ability to correctly detect the pre-defined association patterns across the 100 simulated datasets. For each of the simulated datasets, we obtained p-values representing the significance of the mixture effect at the 5 time windows. Across all 100 simulated datasets, we recorded, for each time window, the proportion of datasets wherein the mixture effect was statistically significant. The goal of this approach is to assess the extent to which each method is able to correctly detect (and attribute statistical significance to) important mixture effects within critical time windows. Based on our simulation model (Equation (9)), we know that mixture effects exist only at time points 3 and 4, and at the other time points the effect is zero. We compared the 3 methods on their ability to correctly identify these predefined effect patterns.
Note that due to the nonlinear mixture effects in our simulations (specified in Equations (11) and (12)), using the classical DLM formulation would be inadequate since it assumes a simple linear (additive) association model between lagged exposures and response. Further, it does not provide a method for evaluating the joint (mixture) effect of multiple chemicals (or other types of exposure). The 3 methods tested in our simulations (Lagged WQS, Tree-based DLMs, and GAM) all provide a means for assessing the significance of the mixture effect of a group of chemicals at multiple time points. On the other hand, using classical DLMs, we would only be able to assess significance for individual chemicals (at various lags), but not for groups of chemicals. Therefore, classical DLMs are not ideal for the current application because they do not have an in-built feature for assessing the statistical significance of joint/combined effects from a group of pollutants/chemicals at various time points.
1.4 Real data application
We assessed the performance of Lagged WQS and Tree-based DLMs on data from the Early Life Exposures in Mexico to ENvironmental Toxicants (ELEMENT) study. Detailed information on the study (including study design and data collection) has been published previously [27, 28]. To demonstrate the feasibility of our statistical methods, we used time-series measures of perinatal (pre-birth and post-birth) exposure to manganese, lead and zinc, and a standardized validated childhood neurobehavioral measure. The methods we describe here can be readily applied to a larger set of exposures (> 3) as well. Our goal was to test for the existence of windows of vulnerability–phases during the perinatal period wherein neurological development of children is strongly influenced by levels of exposure to manganese, lead and zinc. The key assumption here is that exposure to this multi-pollutant mixture during these crucial developmental phases leads to alterations in behavioral and emotional functioning that is different to the effect of any single metal exposure alone. We used both Lagged WQS and Tree-based DLMs to analyze metal mixture and behavioral assessment data, with the aim of identifying putative neurodevelopmental critical windows. These models were adjusted for covariates believed to influence childhood behavior: sex of child and total schooling of child’s mother, a measure of maternal education level. Metal level exposure levels in the children were estimated using a recently developed and validated spectrometric technique that analyzes teeth collected from children in the study cohort.
Analysis was carried out using SAS (Cary, NC) [19] and R [29]. Lagged WQS models were fit using PROC NLMIXED in SAS, and tree-based DLMs were constructed using the R packages randomForest and RFgroove.
RESULTS
2.1 Simulation results
We examined the rate at which each technique reported statistically significant mixture effects in each time window. As outlined in the Methods section, we carried out this evaluation by summarizing, for each time window, the proportion of the 100 simulated datasets in which a statistically significant mixture effect was identified (at the α = 0.05 significance level). Recall that, based on the simulation configuration, the expectation is that the 3rd and 4th time windows harbor statistically significant mixture effects, while the 1st, 2nd and 5th do not. As discussed in the Methods section, the tree-based DLM and GAM techniques were applied to the raw simulated data, which had a discrete time structure (i.e. discrete time points t=1,2,3,4 & 5). These methods were used to estimate the mixture effects (and corresponding statistical significance) of the 3 pollutants at these 5 time points. For these methods, we summarized, for each time window, the proportion of the 100 simulated datasets in which a statistically significant mixture effect was identified. On the other hand, the Lagged WQS was fitted on the longitudinal version of the simulated data, which had a continuous time structure generated from uniform distributions. Recall that Lagged WQS technique models the longitudinal mixture effect as a smooth function of time. Specifically, it estimates a time-varying regression coefficient representing the mixture effect. Confidence intervals for this time-varying coefficient are constructed and the significance of the mixture effect at various time points can be evaluated. This was carried out across the 100 simulated datasets.
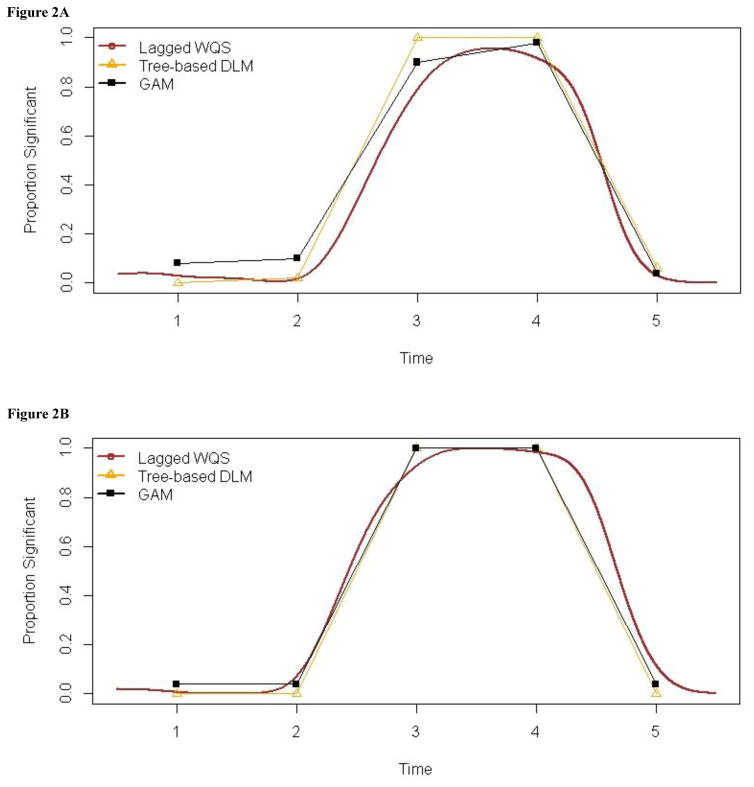
Results are summarized in Figures 2A and 2B. Note that the plot for Lagged WQS (denoted in brown) extends from time 0.5 to 5.5 because of the way the raw simulation data was transformed to a continuous time structure (see Methods section). On the other hand, for Tree-based DLMs and GAM which used the raw simulation data (which had a discrete, uniform time structure), the plots (denoted in yellow and black, respectively) are line segments connecting summary estimates at each of the 5 time points. Overall, the results for the 3 methods show good mutual agreement, with weak mixture effects at time windows 1,2 & 5, and overwhelmingly significant mixture effects at time windows 3 & 4.
Figure 2.
Figure 2A: Summary of simulation results for SNR=0.5. The plot shows, for each time point, the proportion of simulated datasets wherein significant mixture effects were found.
Figure 2B. Summary of simulation results for SNR=1.0. The plot shows, for each time point, the proportion of simulated datasets wherein significant mixture effects were found.
In Figure 2A (SNR=0.5), we see that all 3 techniques perform reasonably well across the 5 time points. At the 3rd and 4th time windows, all 3 techniques identified significant effects in a majority of the 100 simulated datasets, though Lagged WQS showed lower success rates for these periods than the other techniques. At the other time windows, the proportion of the 100 simulated datasets in which significant effects were (incorrectly) found is generally low, with the highest rate observed for GAM at time points 1 & 2.
In Figure 2B (SNR =1), all 3 techniques show higher success rates (relative to the SNR=0.5 case) at identifying significant mixture effects for time points 3 and 4. For the other time points, the rate at which significant effects are (erroneously) found is overall lower (compared with the SNR=0.5 case). However, for Lagged WQS, the error rates appear to be higher for the last time point.
2.2 Results for analysis of ELEMENT Data
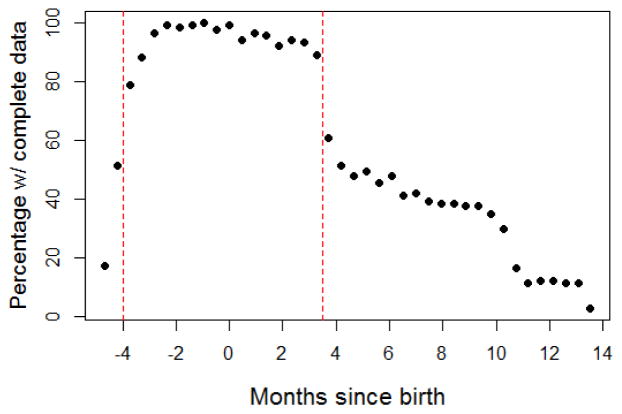
In total, n=133 children had non-missing values for the behavioral measure used as an outcome in our analysis. This outcome (a neurobehavioral assessment score) was measured once in each child roughly around age 8. Exposures, on the other hand, were measured longitudinally. Collectively, measures of manganese, lead and zinc levels spanned the pre- and post-natal period, from 4 months pre-birth up to 12 months post-birth. The exposure measures are not evenly distributed throughout this period. Certain periods were more densely sampled (particularly the last trimester and first 3 months after birth) across the cohort. Time periods at the extremes (early in the second trimester and after the first year postnatally) have missing values because only certain teeth type undergo primary dentinal mineralization during this period. We had mostly incisors analyzed, which capture the period of approximately 3 months postnatally – this led to a drop in sample size around this period. The plot below (Figure 3) provides a visual summary of the longitudinal variation in missingness rates.
Figure 3.
ELEMENT Study -The entire perinatal period was divided into a series of contiguous 2-week bins, and the percentage of children with at least one Mn/Pb/Zn exposure measurement within each bin is depicted below. The dashed red lines demarcate the restricted time frame used in the Tree-based DLMs
As discussed earlier, Lagged WQS uses a mixed model framework, a versatile methodology that is relatively robust to missing values in the observations, i.e. inference can proceed and estimates can be produced without having to explicitly account for the missing values (e.g. through imputation). As a result, Lagged WQS can provide reliable and largely bias-free estimates of the longitudinal mixture effect across the entire perinatal period despite the fact that not all subjects in the data have complete measurements throughout this period. The Tree-based DLM methodology, on the other hand, utilizes the familiar classical DLM framework, wherein the entire observation period is divided into a sequence of discrete segments (lags) at which measurements of the exposure variable(s) are taken (see Equation (3)). For this analysis, we chose time windows/bins of 2 weeks, averaging measurements of each metal within each bin. This produced a data structure where each row represented an individual and each column contained the 2-week average exposure level of a specific metal (manganese, lead or zinc). Every subject in the sample must have a complete set of measurements across all columns since this modeling framework does not naturally accommodate missing values. So due to the missing values in our data, inference via Tree-based DLMs could only proceed via imputation or complete-case analysis. The low number of subjects with complete data across the entire observation period precluded the use of complete-case analysis. Therefore, we chose the strategy of confining our analysis to the most densely sampled span of time within the perinatal period (depicted in Figure 3 as the region bounded by the dashed red lines [126 days pre-birth to 112 days post-birth]). For individuals with at least some measurements within this restricted time frame, we carried out imputations of missing measurements using kernel regression [30] with bandwidth specification via the method of Racine and Li (2004) [31].
Using this scheme, we were able to retain a large proportion of the original sample of subjects (n=130) for the tree-based DLM analysis. This scheme was not needed for the Lagged WQS, i.e. we were able to implement this technique on the raw (unimputed) data across the full observation period (4 months pre-birth to 12 months post-birth).
To get a sense of the correlation structure among the 3 metals, we computed Spearman correlations between each pair and averaged over time. The highest correlation was observed between lead and zinc (mean=0.47, SD=0.039). The correlation between manganese and zinc was 0.34 (SD=0.057), while the manganese-lead correlation was 0.17 (SD=0.051).
Both Lagged WQS and Tree-based DLM techniques were able to identify time windows/bins wherein mixture effects (of manganese, lead and zinc) where significantly associated with the neurobehavioral outcome. The results are summarized in Figures 4A (for Lagged WQS) and 4B (for Tree-based DLM).
Figure 4.
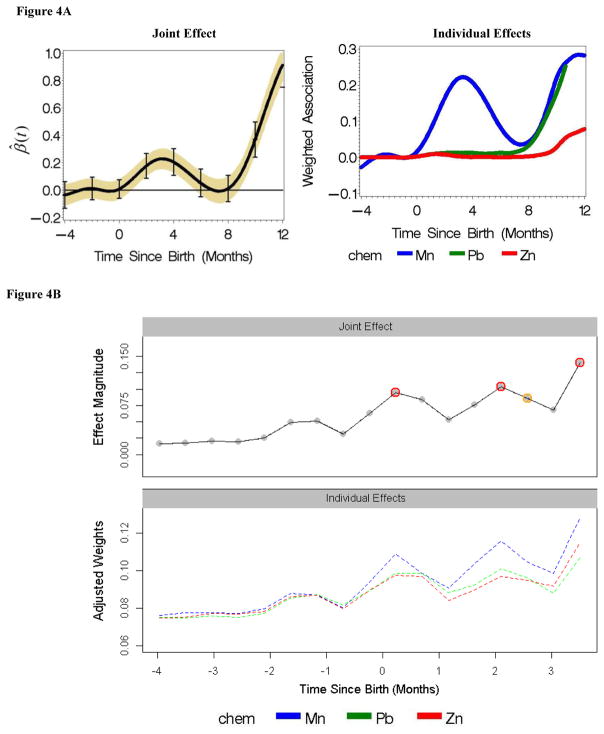
Figure 4A. Lagged WQS: Time-varying joint/mixture and individual effects of Mn, Pb and Zn on behavioral outcome. On the first plot, the y-axis represents the time-varying coefficient of the mixture effect. Yellow: 95% CIs unadjusted for multiple testing, adjusted for intra-subject correlations; bars: Holm-Bonferroni adjustment for multiple testing
Figure 4B. Tree-based DLMs - Time-varying individual and joint/mixture effects of Mn, Pb and Zn on neuro-behavioral outcome. In the upper panel, time windows with significant mixture/joint effects are denoted by red circles. Orange circles denote marginally significant (at the 10% significance level) mixture effects. The lower panel plot shows the contributions of each chemical over time.
For Lagged WQS, the first plot in Figure 4A shows the time-varying mixture effects. The second plot in Figure 4A shows the contributions of the individual metals to the observed mixture effect in the first plot. We observe significant mixture effects from 0–6 months post birth, and then again after the 8-month mark. From the second plot in Figure 4A, it can be surmised that the effect at the first critical window (0–6 months) appears to be largely driven by manganese while both lead and manganese are dominant drivers after the 8-month point.
For the Tree-based DLM approach, the upper panel of Figure 4B summarizes the longitudinal joint effect within the restricted time frame chosen for this method (4 months pre-birth to nearly 4 months post-birth). We see significant mixture effects at/around birth, and also at 2 and 3–4 months post-birth. This shows some agreement with the Lagged WQS results, despite the different time frames in each analysis. The lower panel in Figure 4B shows the effects of each individual metal, revealing the greater contribution of Mn to the effect detected at the critical periods. Note that the units on the y-axis in both plots are arbitrary units of single and group Variable Importance measures produced by the RF algorithm–they do not have any particular interpretation.
DISCUSSION
While useful, classical DLMs have a number of shortcomings, one of which is that they assume linear associations between lagged exposure measures and the outcome of interest; this may not accurately represent the true underlying association structure. This shortcoming also means that the complex, potentially non-linear effects of multi-chemical mixtures on an outcome of interest cannot be properly estimated. Further, as we mention in the Methods section, classical DLMs do not have a built-in feature for assessing the statistical significance of joint/combined effects of a group of variables (representing pollutants/chemicals) at various time points. One standard method that does is based on generalized additive models (GAMs) that allow construction of multi-dimensional splines. In this study, we compared our 2 novel techniques to this standard methodology. GAMs were used to model the mixture effect of 3 chemicals (at discrete time points) using thin-plate splines. Thin-plate splines result from the extension of one-dimensional smoothing splines to multivariate settings. This allows modeling of non-linear, high-dimensional surfaces, such as those estimating the multi-pollutant mixture effects. We found that our 2 novel techniques showed comparable performance to GAMs for the 3-chemical, 5 time-point simulations. However, we found that GAMs break down when we attempted to model mixture effects for more than 3 chemicals (or for several time points) – most models failed to converge due to issues with overparameterization. Because of the curse of dimensionality, the computational complexity of estimating parameters associated with multivariate thin-plate splines increases substantially with each additional dimension. In our studies, we have found that both Lagged WQS and tree-based DLM techniques are able to handle larger sets of pollutants. Lagged WQS constructs a weighted sum of chemical exposure levels (see Equation (2b)) which it uses as an index, thereby reducing the dimensionality of the pollutant/chemical mixture. This makes it relatively more robust to the curse of dimensionality. Tree-based DLMs utilize random forests, a nonparametric approach that is well-known for its ability to handle high-dimensional data. Another issue with the GAM approach is that, in addition to being limited by the number of pollutants, its feasibility is also constrained by number of time points. For example, for the ELEMENT study analysis described earlier, we found that GAM was overparameterized when applied to the binned version of the data (consisting of averaged measures of manganese, lead and zinc over seventeen 2-week time windows, for 130 children). Recall that this version of the data resulted from binning the irregular, fine-scale longitudinal metal exposure measurements into a series of seventeen 2-week time windows. The tree-based DLM approach was applied to this data, and the significance of the multi-pollutant effect at each of the 17 time points was readily estimated (see Figure 4B). However, this was not feasible using GAMs, as our attempt to construct 17 separate three-dimensional thin-plate splines (each one estimating the multi-pollutant effect among the 3 chemicals at each time point) failed due to overparameterization. One solution would be to decrease the number of time points by using larger time windows, however since the goal of our analysis was to identify perinatal periods of vulnerability, using larger time windows would likely reduce the power to detect such periods.
A key motivation underlying the decision to present these 2 techniques in the same communication is their complementary nature. The main strength of the Lagged WQS approach is its reliance on the mixed modeling framework, which makes it ideal for analysis of longitudinal mixture effects. Moreover, missing values in the exposure data do not need to be explicitly accounted for. The use of the WQS index allows the mixture effect to be summarized via a unidimensional construct and enables the variation of this effect over time to be quantified. These features facilitate the identification of critical periods wherein the mixture effect size is significant. In addition, the method provides information about which individual exposure components are driving this effect. The contribution of each exposure variable to the overall mixture effect size can be delineated by using the time-varying WQS weight estimates. An important consideration here is the direction of effect for each exposure, i.e. whether each exposure is positively or negatively correlated with the outcome. Because of the way the WQS method aggregates exposure variables to form an index [32], individual exposure effects should be homogeneous with respect to directionality of the relationship with the outcome. A degree of signal attenuation is expected at time points wherein some exposure variables are positively associated with the outcome and others are negatively associated.
The tree-based DLM technique provides an extension to the classical DLM framework by using random forests in lieu of parametric regression methodology. This provides a flexible nonparametric alternative that can model nonlinear exposure-response relationships and handle high-dimensional data (e.g. where the number of lagged exposure variables exceeds the sample size [the p > n case]). Just like in classic DLMs, each independent variable in the model represents the measured level of an exposure at a certain time point/window [33]. The key improvement over classic DLMs that is offered by Tree-based DLMs is that they can evaluate the statistical significance of the joint effect of a group of variables on the outcome, at various time points. Tree-based DLMs estimate the mixture effect size at each time window by assessing the ‘group importance’ of the variables representing measured levels of all chemicals under consideration at that time window. As discussed earlier, this group importance measure at each time window quantifies the joint explanatory power of the chemicals/exposures measured in that period. Recall that the group importance of a set of variables is derived by measuring the loss of predictive/explanatory power (for the outcome) incurred by the removal (via permutation) of those variables from the random forest model. The inherent benefit of this approach is that it does not require all exposure variables to have the same direction of association (all positive or all negative) with the outcome, unlike the Lagged WQS approach. Since the focus is on explanatory power, a chemical/exposure that is strongly predictive of the outcome (in a certain time window) will contribute to the overall group importance measure regardless of whether the direction of association is positive or negative. This mode of mixture effect size assessment is, however, limited. In any conceivable application of multi-exposure DLMs, the direction of effect for each exposure would be a highly important piece of information. Another limiting feature of tree-based DLM is that it cannot handle missing values in exposure levels. Its implementation requires that all observations have complete data within all time windows. This makes tree-based DLMs less tenable for exposure data with incomplete measurements in certain time windows. In the real data application described in this study (ELEMENT data), we handled this issue by restricting our analysis to the largest contiguous block of time containing complete exposure measurements across all the chemicals.
Here, we provide a few recommendations for researchers interested in implementing these methods. The first issue is the type of data and the longitudinal lag structure. The tree-based DLM technique uses a discrete-time modeling structure, so it requires exposure data to be structured as a series of lagged exposure measures, each one representing a discrete time point or window. Further, the lag times should be identical (or close to identical) for all subjects. This means that for datasets with irregularly-timed exposure measures distributed non-uniformly across subjects (such as the ELEMENT data used in this study), the use of Tree-based DLM requires binning of irregularly timed exposure measurements into a series of discrete time windows that are uniform across all subjects. If there are multiple measures within a time window/bin, the average (or another suitable summary statistic) of these measures can be taken. Each subject’s exposure data is thus represented as a series of variables, each one of which represents the mean level of exposure to a specific pollutant/chemical within a specific time window. A potential downside of this approach is that depending on the chosen size of these time bins/windows and the number of pollutants/chemicals in the mixture, the dimensionality of the data could increase due to the large number of variables. However, random forests are well-suited to handle high-dimensional problems, so this does not pose a serious limitation in most practical scenarios. Another potential limitation of this approach is that missing values are not permitted in any of the time windows/bins. The Random Forest algorithm by default does not permit missing values, so subjects with one or more missing values typically cannot be included in the analysis. Hence tree-based DLM approach is not well-suited for data with missing values of lagged exposures. We note, however, that the classical DLM approach is also not equipped to handle data with missingness in the lagged exposure measures. Such data could, however, be analyzed using Lagged WQS. Unlike Tree-based DLM which uses a discrete lag structure and requires continuous, non-uniform measures to be binned, Lagged WQS is more flexible. Because Lagged WQS is based on the mixed model framework, it is more robust to missing values at certain time points. Therefore, Lagged WQS is a particularly attractive option for datasets with irregularly-timed exposure measures, i.e. where the timing of the lagged measures varies from subject to subject. One additional consideration, in the choice of which approach to use, is computational expense. Tree-based DLM, compared to Lagged WQS, is a computationally intensive technique. It relies on random forests, which use a heuristic/greedy top-down recursive partitioning approach with thousands of iterations. In addition, to determine significance of mixture effects within each time window/bin, the tree-based DLM approach relies on permutation tests, and this further increases the computational burden.
In this study, we have introduced two techniques for evaluating the effect of longitudinal multi-pollutant exposure on a health outcome. We examined the feasibility and performance of both proposed techniques using simulated data generated from a simple 3-pollutant model with non-additive, time-varying mixture effects. Based on encouraging results from these simulations, and also from the ELEMENT study analysis, future work will focus on further assessment of the performance of our multi-exposure DLM techniques in more complex settings featuring a larger set of chemicals/exposures and more elaborate longitudinal patterns of non-additive mixture effects. The work presented herein represents a crucial first step towards characterization, validation and refinement of these techniques.
Figure 1.
Figure 1A. 3D plots of functions f3 and f4 in the simulation model (Equation 9). These plots show the response surfaces of the mixture effects within time windows 3 and 4
Acknowledgments
Funding
This research is funded by the Icahn School of Medicine at Mount Sinai, and National Institute of Environmental Health Scienes (R01ES026033 and DP2ES02545)
APPENDIX
In the simulation studies described in Section 1.3, we impose a block-diagonal first order autoregressive on the simulated exposure data. Below, we outline each step in this procedure:
| (13b) |
| (13c) |
| (13d) |
The 1 × 15 matrix X represents a vector of exposure values for 1 individual/case. The 5 × 5 matrix A represents the desired correlation structure among lagged values of each chemical over the 5 time points. The full correlation matrix across all 3 chemicals and all 5 time points is given by Q, a 15 × 15 correlation matrix. Next, we carry out a Cholesky decomposition of Q to produce the 15 × 15 lower-triangular matrix L which has the following relationship with Q:
| (13e) |
L is known as the Cholesky factor of correlation matrix Q, and may be interpreted as the ‘square root’ of Q. Note that this decomposition is possible because Q, as defined above, is positive-definite. L is then used to transform X so that it exhibits the desired correlation structure:
| (13f) |
Footnotes
Competing Interests
The authors declared no potential conflicts of interest with respect to the research, authorship, and/or publication of this article
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- 1.Wyzga R. The effect of air pollution upon mortality: a consideration of distributed lag models. J Am Stat Assoc. 1978;73(363):463–72. doi: 10.1080/01621459.1978.10480035. [DOI] [PubMed] [Google Scholar]
- 2.Gasparrini A, Armstrong B, Kenward M. Distributed lag non-linear models. Statistics in Medicine. 2010;29(21):2224–2234. doi: 10.1002/sim.3940. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Baek J, et al. Distributed Lag Models: Examining Associations between the Built Environment and Health. Epidemiology. 2016;27(1):116–124. doi: 10.1097/EDE.0000000000000396. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Baek J, Sanchez-Vaznaugh E, Sanchez B. Hierarchical Distributed-Lag Models: Exploring Varying Geographic Scale and Magnitude in Associations Between the Built Environment and Health. Am J Epidemiol. 2016;183(6):583–592. doi: 10.1093/aje/kwv230. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Zhao X, et al. Characterizing the effect of temperature fluctuation on the incidence of malaria: an epidemiological study in south-west China using the varying coefficient distributed lag nonlinear model. Malar J. 2014:13. doi: 10.1186/1475-2875-13-192. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Heaton M, Peng R. Flexible Distributed Lag Models using Random Functions with Application to Estimating Mortality Displacement from Heat-Related Deaths. J Agric Biol Environ Stat. 2012;17(3):313–331. doi: 10.1007/s13253-012-0097-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Lall R, Ito K, Thurston G. Distributed Lag Analyses of Daily Hospital Admissions and Source-Apportioned Fine Particle Air Pollution. Environ Health Perspect. 2011;119(4):455–460. doi: 10.1289/ehp.1002638. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Rice D, Barone SJ. Critical periods of vulnerability for the developing nervous system: evidence from humans and animal models. Environ Health Perspect. 2000;108(Suppl 3):511–533. doi: 10.1289/ehp.00108s3511. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Bello G, Dumancas G, Gennings C. Development and Validation of a Clinical Risk-Assessment Tool Predictive of All-Cause Mortality. Bioinformatics and Biology Insights. 2015;9(3):1–10. doi: 10.4137/BBI.S30172. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Christensen K, et al. Multiple classes of environmental chemicals are associated with liver disease: NHANES 2003–2004. Int J Hyg Environ Health. 2013;216(6):703–709. doi: 10.1016/j.ijheh.2013.01.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Gennings C, Sabo R, Carney E. Identifying Subsets of Complex Mixtures Most Associated With Complex Diseases: Polychlorinated Biphenyls and Endometriosis as a Case Study. Epidemiology. 2010;21(4):S77–S84. doi: 10.1097/EDE.0b013e3181ce946c. [DOI] [PubMed] [Google Scholar]
- 12.Carrico C. Biostatistics. Virginia Commonwealth University; Richmond, VA: 2013. Characterization of a Weighted Quantile Score Approach for Highly Correlated Data in Risk Analysis Scenarios. [Google Scholar]
- 13.Tibshirani R. Regression shrinkage and selection via the lasso. J Royal Stat Soc. 1996;58(1):267–288. [Google Scholar]
- 14.Hoerl A, Kennard R. Ridge Regression: Biased Estimation for Nonorthogonal Problems. Technometrics. 1970;12(1):55–67. [Google Scholar]
- 15.Breiman L. Random Forests. Machine Learning. 2001;45(1):5–32. [Google Scholar]
- 16.Almon S. The Distributed Lag Between Capital Appropriations and Expenditures. Econometrica. 1965;33(1):178–196. [Google Scholar]
- 17.Chen Y, et al. Statistical methods for modeling repeated measures of maternal environmental exposure biomarkers during pregnancy in association with preterm birth. Environ Health. 2015;14(9):1–13. doi: 10.1186/1476-069X-14-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Holm S. A simple sequentially rejective multiple test procedure. Scandinavian Journal of Statistics. 1979;6(2):65–70. [Google Scholar]
- 19.SAS Institute. Release 9.4. SAS Inst; Cary, NC: 2014. [Google Scholar]
- 20.Sun Y. Multigenic modeling of complex disease by random forests. Adv Genet. 2010;72:73–99. doi: 10.1016/B978-0-12-380862-2.00004-7. [DOI] [PubMed] [Google Scholar]
- 21.Winham S, et al. SNP interaction detection with Random Forests in high-dimensional genetic data. BMC Bioinformatics. 2012:13. doi: 10.1186/1471-2105-13-164. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Genuer R, Poggi JM, Tuleau-Malot C. Variable selection using random forests. Pattern Recognition Letters. 2010;31:2225–2236. [Google Scholar]
- 23.Gregorutti B, Michel B, Saint-Pierre P. Grouped variable importance with random forests and application to multiple functional data analysis. Computational Statistics & Data Analysis. 2015;90:15–35. [Google Scholar]
- 24.Limpert E, Stahel W, Abbt M. Log-normal distributions across the sciences: Keys and cues. BioScience. 2001;51:5. [Google Scholar]
- 25.Wood S. Stable and efficient multiple smoothing parameter estimation for generalized additive models. J Amer Statist Ass. 2004;99:673–686. [Google Scholar]
- 26.Wood S. R Package mgcv. 2012 Available from: https://cran.r-project.org/web/packages/mgcv/mgcv.pdf.
- 27.González-Cossío T, et al. Decrease in birth weight in relation to maternal bone-lead burden. Pediatrics. 1997;100(5):856–862. doi: 10.1542/peds.100.5.856. [DOI] [PubMed] [Google Scholar]
- 28.Hernandez-Avila M, et al. Effect of maternal bone lead on length and head circumference of newborns and 1-month-old infants. Arch Environ Health. 2002;57(5):482–488. doi: 10.1080/00039890209601441. [DOI] [PubMed] [Google Scholar]
- 29.R Core Team. R: A Language and Environment for Statistical Computing. R Foundation for Statistical Computing; Vienna, Austria: 2015. [Google Scholar]
- 30.Hayfield T, Racine J. Nonparametric Econometrics: The np Package. J Stat Software. 2008;27(5):1–32. [Google Scholar]
- 31.Racine J, Li Q. Nonparametric estimation of regression functions with both categorical and continuous data. Journal of Econometrics. 2004;119:99–130. [Google Scholar]
- 32.Czarnota J, Gennings C, Wheeler D. Assessment of weighted quantile sum regression for modeling chemical mixtures and cancer risk. Cancer Informatics. 2015;14(Suppl 2):159–171. doi: 10.4137/CIN.S17295. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Peng R, Dominici F. Statistical Methods for Environmental Epidemiology in R: A Case Study in Air Pollution and Health. In: Gentleman R, Hornik K, Parmigiani G, editors. Use R! Baltimore, Maryland: Springer; 2008. [Google Scholar]