Rapid Deployment Aortic Valves Deliver Superior Hemodynamic Performance In Vitro

Abstract

Objective

Clinical studies have demonstrated excellent hemodynamic performance of rapid deployment aortic valves; however, few studies have directly compared the performance of these valves with conventional bioprosthetic valves. Thus, the hemodynamic function of the EDWARDS INTUITY valve (rapid deployment valve) was compared with the Edwards Magna Ease valve in vitro (Edwards Lifesciences Corp, Irvine, CA USA).

Methods

Elastomeric material was used to create an aortic root model that included a left ventricular outflow tract and aortic annulus. The model was based on reconstructions from 3-dimensional multislice computed tomography images in patients with aortic stenosis; the aortic root was scaled to a 21-mm effective annulus diameter. EDWARDS INTUITY valves (21-mm diameter) were deployed by stent frame expansion within the aortic root; Edwards Magna Ease valves (21-mm diameter) were sutured to the annulus. The left ventricular outflow tract area index (left ventricular outflow tract area/baseline area) and ellipticity or noncircularity as indexed by D_max/D_min were measured under a video microscope after valve placement. Hemodynamic data were collected under pulsatile flow with saline (70 beats per minute, 5 L/min, 100 mm Hg aortic pressure).

Results

Compared with the Edwards Magna Ease valve (n = 4), the EDWARDS INTUITY valve (n = 4) had a greater effective orifice area (1.56 ± 0.01 vs 1.85 ± 0.06 cm², P < 0.001) and a lower transvalvular pressure gradient (23.4 ± 0.51 vs 16.8 ± 1.3 mm Hg, P < 0.001). Multiple regression analysis showed that 93% of the variation in the effective orifice area and transvalvular pressure gradient was due to variation in the left ventricular outflow tract area index and ellipticity index.

Conclusions

A clinically relevant aortic root model was developed to evaluate aortic valve performance. The superior performance of the EDWARDS INTUITY valve seemed to be related to both a greater inflow area and a more circular left ventricular outflow tract.

The enhancement of aortic valve hemodynamic performance has several important clinical benefits including a regression of left ventricular (LV) mass and improved long-term survival and functional status after surgical aortic valve replacement.^1–5 Sutureless and rapid deployment aortic valve prostheses have recently been introduced into clinical practice in Europe and Asia, and several studies have demonstrated their short-term safety and efficacy.^6–8 A rapid deployment aortic valve, the EDWARDS INTUITY (EI) valve (Edwards Lifesciences Corp, Irvine, CA USA), has been developed with a subannular balloon-expandable stent frame (Fig. 1). The implantation of this valve could lead to widening of the LV outflow tract (LVOT), resulting in a larger effective orifice area (EOA) compared with conventional surgical valves.

FIGURE 1.

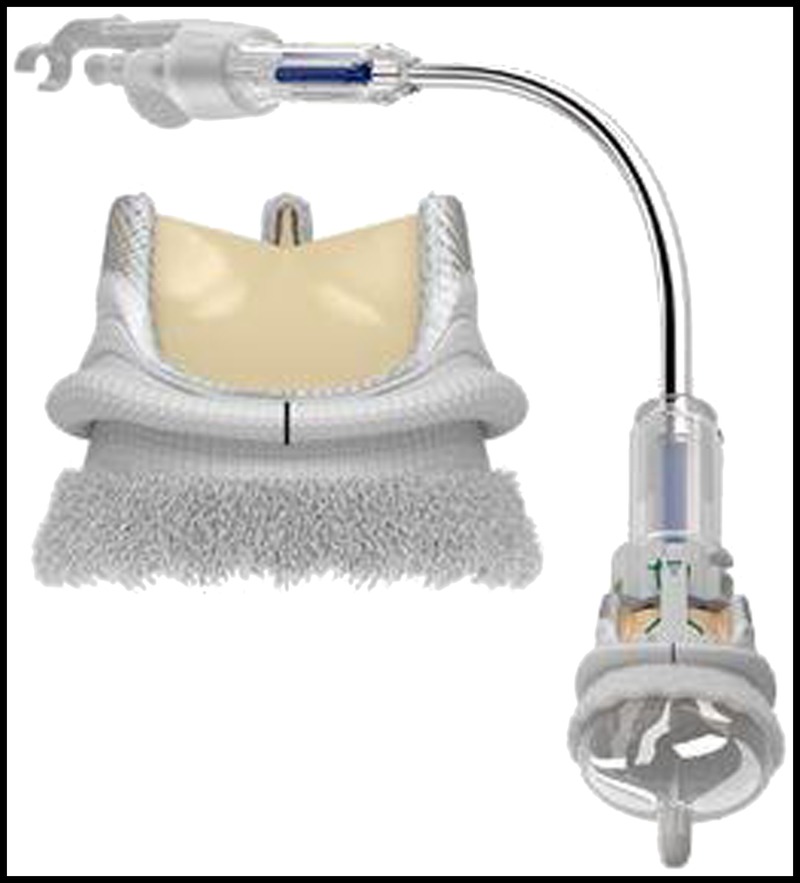
Images of the EI valve. The back vertical mark on valve sewing ring is for placement of 1 of 3 guiding sutures that holds the valve ring in the annulus while the balloon is inflated to a pressure of 4.5 atm for 10 s to expand the stent frame.

Although the EI valve has been shown to perform well in early clinical trials,^9–11 few studies have directly compared the hemodynamic performance of this valve to more conventional bioprosthetic valves to account for its superior performance. Therefore, the purposes of this study were to first develop a clinically relevant aortic root model and then to compare the hemodynamic performance of the EI valve with the Edwards Magna Ease (ME) valve (Edwards Lifesciences Corp, Irvine, CA USA) using a pulsatile flow system in vitro. The ME valve is a conventional bioprosthetic valve that is sutured to the aortic annulus and has been shown to perform well in several clinical studies.^12–14

METHODS

The Young modulus was derived to be approximately 0.5 MPa at low strain (10%–15%) and 1.5 MPa at moderate strain (15%–20%) from the least compliant stress-strain curve of mechanical properties measured on the aortic root tissue of 13 fresh human cadaver hearts. Rubber-like PolyJet photopolymers were used to 3-dimensional (3D) print the aortic root model. Shore 27A material was selected because it approximates a Young modulus of 0.6 to 1.0 MPa,^15,16 which closely simulates the elasticity of LVOT within the low-to-moderate strain range. The model was based on the representative anatomic dimensions of the aortic annulus and LVOT and the distance between them reported by Buellesfeld et al¹⁷ based on clinical 3D multislice computed tomography (MSCT) reconstructions in patients with aortic stenosis (Fig. 2). The “Swept Blend” function in CREO 3.0 (PTC, Inc., Needham, MA USA) was used to connect the derived annulus and LVOT sections and create transition surface of LVOT wall. The final model was scaled so that perimeter-derived effective diameter of the aortic annulus was 21 mm and Model 1133 sizers (sizes 21 and 23 mm) were also used to verify the size. Because both the native aortic valve annulus and LVOT are elliptical and the major-minor diameter ratio or the ellipticity index (D_max/D_min), as defined by Buellesfeld et al¹⁷ to describe the ovality of the valve, could greatly affect the valve hemodynamic performance along with the area,¹⁸ the ellipticity index (D_max/D_min) and the area index (normalized by the area of a 21-mm-diameter circle) were selected as the measurements in this study. In the final model, the aortic annulus area was 3.38 cm,² the LVOT area was 3.01 cm,² the ellipticity index (D_max/D_min) of the LVOT was 1.44, and the ellipticity index of the aortic annulus was 1.21. Multiple copies of the model were printed at the same time to ensure that all valves would be mounted on models with the same dimensions and an indentation was created in the annulus region of the model to prevent the valve from sinking into the model LVOT (Fig. 3D). Figures 3A to C show the deployment of the valves in the aortic root model, whereas Figures 3E to F show the deployment of the valves in the human cadaver heart. All valves were positioned within the aortic root using the commissure orientation from the MSCT images (Fig. 2).¹⁷

FIGURE 2.

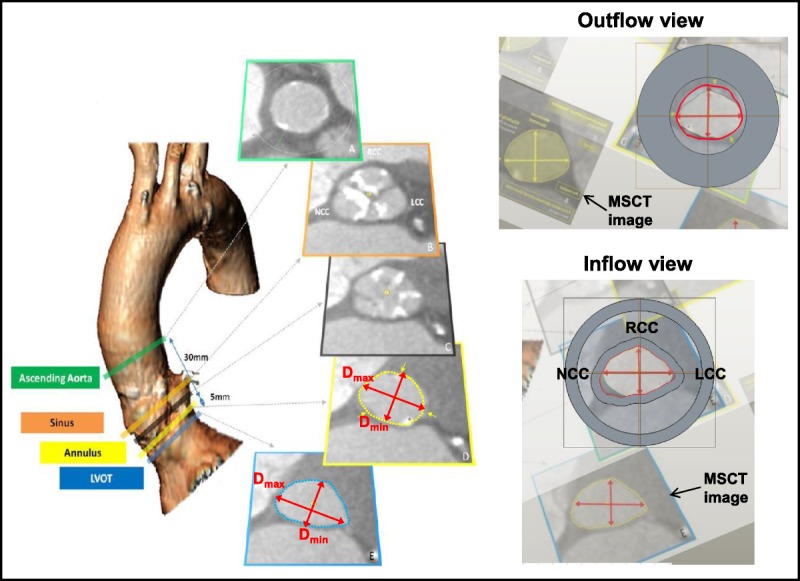
The construction of the rubber gasket aortic root model was based on MSCT images obtained from patients with aortic stenosis. The upper panel shows the outflow side of the aortic root model, and the lower panel shows the inflow side. The MSCT images shown in the bottom half of each panel that were used to scale the model were adapted with permission from Buellesfeld et al.¹⁷ NCC, noncoronary cusp; LCC, left coronary cusp; LVOT, left ventricular outflow tract; MSCT, multislice computed tomography; RCC right coronary cusp.

FIGURE 3.

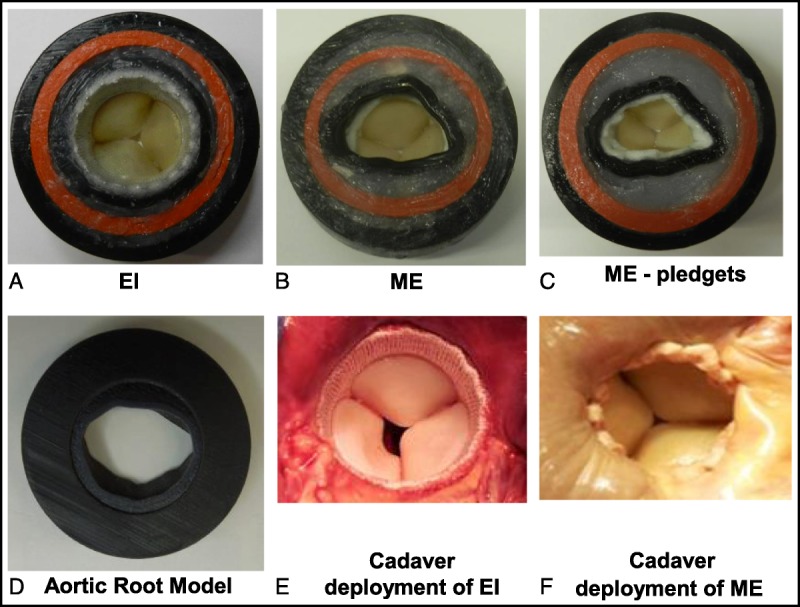
A view of the LVOT in the rubber gasket aortic root model vs. in the Cadaver heart with valve deployment. A, EI valve in the model. B, ME valve in the model without pledgets. C, ME valve in the model with pledgets. D, The outflow view of aortic root model. E, EI valve in human cadaver heart. F, ME valve in human cadaver heart with pledgets. A larger LVOT area and more circular geometry is clearly visible with the EI valve compared with the ME valve with and without pledgets. EI, EDWARDS INTUITY; ME, Edwards Magna Ease.

At first, the ME valves were sutured to the annulus of the aortic root model with 12 (2–0 braided Polyester) sutures. Because conventional aortic valves are typically sutured to the annulus using pledgets, the ME valves were evaluated with and without the use of TFE polymer (Ethicon) pledgets (Fig. 3). These sutures were evenly spaced around the circumference of the annulus. Once hemodynamic data were obtained using this configuration, 6 additional evenly spaced sutures (2–0 braided polyester) were placed with precut pledgets (7.0 × 3.0 × 1.5 mm), so that the pledgets covered the entire circumference of the annulus.

For deployment of the EI valves, three 2–0 polyester guiding sutures were first placed through the aortic annulus and then passed through the black vertical lines on the valve suture ring (Fig. 1). The EI valves were then seated and secured in the aortic annulus (Fig. 3) by balloon inflation to a pressure of 4.5 atm for 10 seconds. This inflation procedure results in expansion of the inflow end of the stent frame to a nominal diameter that ranges from 22 to 25 mm within the LVOT of the aortic root model. After hemodynamic testing of valves with frames expanded using the nominal balloon inflation pressure, the stent was crimped and additional hemodynamic testing was performed on valves with frames that were expanded using a series of rigid cylinders to expand the stent frame to diameters of 22, 23, 24, and 25 mm. As part of this test sequence, the frames at 2 different diameters (22 and 24 mm) were manually compressed in 1 dimension to create a more elliptical shape.

For each valve type or configuration, the aortic root-valve assembly was placed under a Nikon Video Measuring System (in the absence of flow) to measure the LVOT area (inflow area) and ellipticity index (Fig. 4). To perform these measurements, 20 evenly spaced points on the perimeter were selected and the software was used to fit the opening to an ellipse. The area and minimum and maximum diameters of the fitted ellipse were calculated, and the diameters were used to calculate the ellipticity index (D_max/D_min). The LVOT area index was calculated by dividing the measured LVOT area by the baseline area (3.46 cm²). The baseline valve area was considered to be the area of a circle with a diameter of 21 mm.

FIGURE 4.

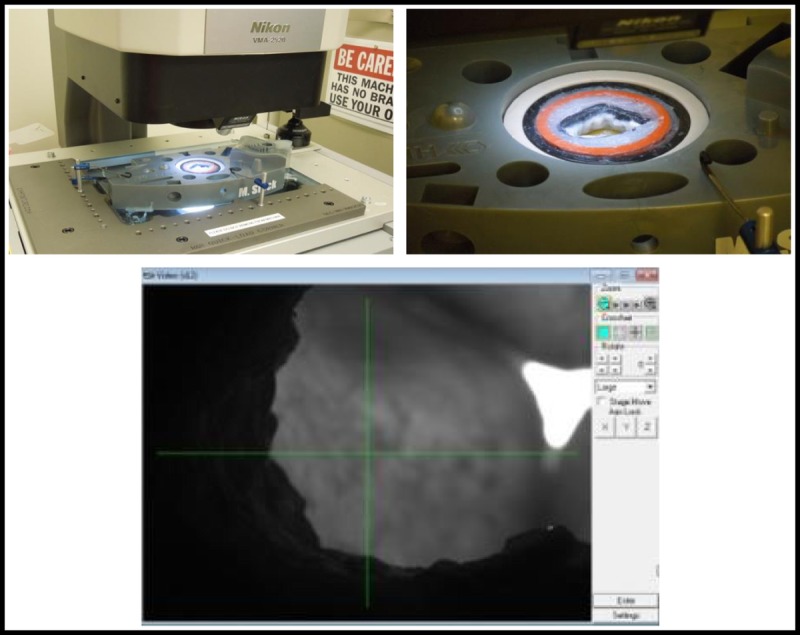
The Nikon Video Imaging system that was used to measure the area of the LVOT and the ellipticity for each valve type or configuration. The panels on the top show a valve mounted on the XY stage of the imaging system, and the bottom panel shows a screen shot of the program used to collect 20 discrete XY points and fit the data to an ellipse. The LVOT area and ellipticity index were calculated from the fitted ellipse.

In accordance with the official valve testing standards for cardiac valve prostheses (ISO 5840-1:2015), the aortic root-valve assembly was placed in a standard pulse duplicator and subjected to a nominal pulsatile flow with 0.9% saline at room temperature (70 beats per minute, 5 L/min, 100 mm Hg mean aortic pressure). All valves were sealed at least 24 hours before hemodynamic testing by placing silicone glue around the circumference of the annulus to minimize any paravalvular leak. A block diagram of the pulsatile flow system is shown in Figure 5. Pressure and flow data were collected continuously during the cardiac cycle and used to determine the transvalvular pressure gradient (TPG) and the EOA. The TPG was calculated as the mean pressure gradient across the valve during systole, whereas the EOA was calculated using the root mean square of the measured flow (qv_RMS) as shown in the following equation per ISO-5840:

FIGURE 5.

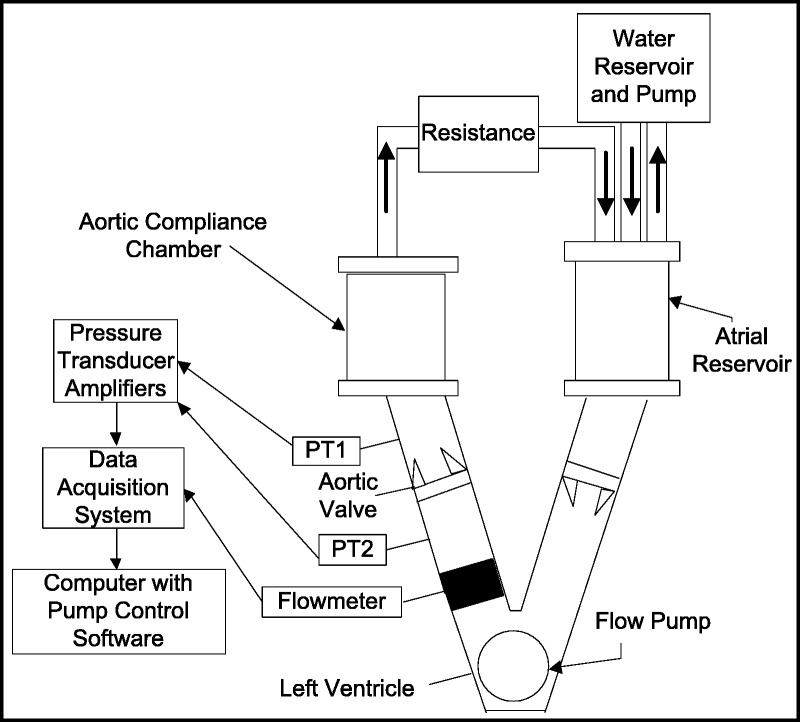
A block diagram of the pulsatile flow system used to evaluate hemodynamic performance of aortic valves. Edwards TruWave disposable pressure transducers (PT1 and PT2) were used to measure the TPG, and a Transonic TS410 Flowmeter was used to monitor flow. The analog signals were digitized, stored, and analyzed using custom software. The linear actuator generated a pulsation rate of 70 beats per minute.

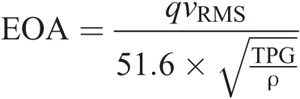
where EOA is the effective orifice area (cm²); qv_RMS is the root mean square forward flow (mL/s) during the positive differential pressure period; TPG is the mean pressure difference (measured during the positive differential pressure period) (mm Hg); ρ is the density of the test fluid (g/cm³). The values obtained for TPG and EOA were averaged for 10 consecutive cardiac cycles.

To gain further insight into the function of the EI and ME valves, studies were performed using particle imaging velocimetry (PIV). Particle imaging velocimetry is a quantitative, optical-based method of flow visualization, which has been extensively used to study velocity and shear stress fields of valves under pulsatile flow in vitro.^18–20 The PIV system consisted of a Nd:YAG pulsed laser (532 nm) that was used to illuminate silicon dioxide particles (9–13 μm) added to the saline in the pulsatile flow system. A CCD camera with a Micro-Nikkor 60-mm f/2.8 lens was placed above the outflow portion of the aortic root assembly to record the velocity profile. The camera was synchronized with the pulsatile flow pump so that images were obtained during peak systole. At least 3 to 4 images were obtained at 10-millisecond intervals to capture the highest flow velocity during systole. Based on the velocity profiles, the following parameters were automatically calculated using DaVis software Version 8.1 (LaVision Inc, Ypsilanti, MI USA): maximum velocity (m/s), turbulent shear stress (m²/s²), and turbulent kinetic energy (m²/s²). Because the camera could only obtain a velocity profile in a single 2D plane at any given camera position, data were obtained with the laser sheet illuminating the major and minor axis planes, respectively, and a single value of each parameter that represented the spatial and temporal maximum was used for further analysis.

RESULTS

Figure 6 shows a comparison of the hemodynamic performance of the EI valve (nominal frame expansion) and the ME valves with and without pledgets. The EOAs (mean ± SD) for the EI valve, ME without pledgets, and ME with pledgets were 1.85 ± 0.06, 1.56 ± 0.01, and 1.24 ± 0.08 cm², respectively (n = 4 for each valve). The difference in EOA between the EI and the ME valves without pledgets was significant (unpaired t test, P < 0.002), and the difference in EOA between the ME valves with and without pledgets was also significant (paired t test, P < 0.002). The TPGs for the EI, ME without pledgets, and ME with pledgets were 16.8 ± 1.3, 23.4 ± 0.05, and 37.1 ± 3.2 mm Hg, respectively (n = 4 for each valve). The difference in TPG between the EI and ME valves without pledgets was significant (unpaired t test, P < 0.001), and the difference between the ME valves with and without pledgets was also significant (paired t test, P < 0.002).

FIGURE 6.

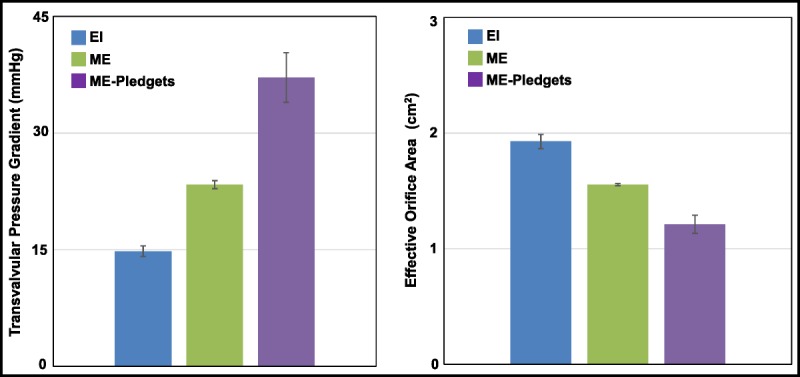
A bar graph showing the TPG (left) and EOA (right) for the EI valves with nominal frame expansion, ME valves without pledgets, and ME valves with pledgets. The bars show the mean ± SD for 4 different valves. The mean TPG and EOA were significantly different comparing the EI valves with the ME valves without pledgets (unpaired t test, P < 0.001). The mean TPG and EOA were significantly different comparing the ME valves without pledgets with the ME valves with pledgets (paired t test, P < 0.001). EI, EDWARDS INTUITY; ME, Edwards Magna Ease.

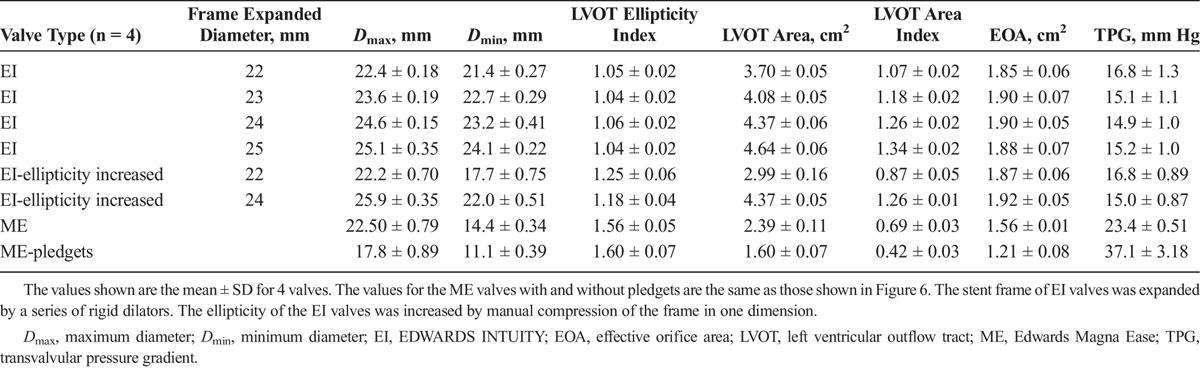
Table 1 shows a summary of the data on LVOT area, ellipticity, and hemodynamic performance of the EI and ME valves. For the EI valves, increasing the frame diameter from 22 to 25 mm in 1-mm increments resulted in a graded increase in the average LVOT area index from 1.02 (22-mm frame expansion) to 1.34 (25-mm frame expansion), but there was little effect on the average EOA or TPG. Furthermore, deployment of EI valves created a more circular geometry of the LVOT, because the ellipticity index of the LVOT fell from 1.44 without any valve mounted to 1.04 to 1.06 with EI frame expansion of 22 to 25 mm. Increasing the ellipticity of the EI valves at 22 mm of frame expansion increased the ellipticity index from 1.04 to 1.25 and decreased the LVOT area index from 1.04 to 0.87, but these changes had little impact on the EOA or TPG. When the ME valve was sutured to the annulus, the average LVOT area index was only 0.69, and the addition of pledgets further decreased the index to 0.42. Furthermore, the average LVOT ellipticity index with the ME valve was 1.56 without pledgets and 1.60 with pledgets, and these values were slightly greater than the ellipticity index of the LVOT (1.44) without any valve mounted.

TABLE 1.

The LVOT Geometry, EOA, and TPG With Different Valve Types and Configurations

To gain insight into the association between the EOA or TPG and the LVOT area index and ellipticity index, multiple linear regression analysis was performed on the EOA and TPG data listed in Table 1 in MiniTab 17 against the following 3 variables: LVOT area index, LVOT ellipticity index, and the multiple of LVOT area index and LVOT ellipticity index. For the EOA, the following regression equation was found to provide the best fit of the raw data:

EOA (cm²) = 3.784 − 1.963 LVOT area index − 1.900 LVOT ellipticity + 1.942 LVOT area index × LVOT ellipticity

The regression coefficients in the model were all significant (P < 0.001). A plot of the residuals against the predicted EOA (not shown) showed that they had a symmetrical distribution near 0. The regression analysis indicated that 93% (r² = 0.93) of the variation in EOA was due to variation in the LVOT area index and ellipticity index. For the TPG, the following regression equation was found to provide the best fit of the raw data:

TPG (mm Hg) = −40.0 + 62.5 LVOT area index + 57.57 LVOT ellipticity − 63.17 LVOT area index × LVOT ellipticity

The regression coefficients in the model were all significant (P < 0.001). A plot of the residuals against the predicted TPG (not shown) showed that they had a symmetrical distribution near 0. The regression analysis indicated that 93% (r² = 0.93) of the variation in EOA was due to variation in the LVOT area index and ellipticity index.

To directly examine the flow patterns developed across the EI and ME valves, PIV was performed on both major and minor axes planes during peak systole with silicon dioxide particles added to the saline (Fig. 7). The average maximum velocity (m/s) was 4.24 ± 0.14 m/s with the EI valve and 4.64 ± 0.10 m/s with the ME valve without pledgets, and these were values were significantly different (n = 4, unpaired t test, P < 0.003). The average maximum turbulent shear stress was 0.92 ± 0.08 m²/s² with the EI valve and 2.57 ± 0.08 m²/s² with the ME valves without pledgets, and these values were also significantly different (n = 4, P < 0.02). In addition, the average maximum turbulent kinetic energy was 1.57 ± 0.36 m²/s² with the EI valve, and this was significantly less than the average maximum turbulent kinetic energy with the ME valve without pledgets (4.33 ± 0.84 m²/s², n = 4, P < 0.002).

FIGURE 7.

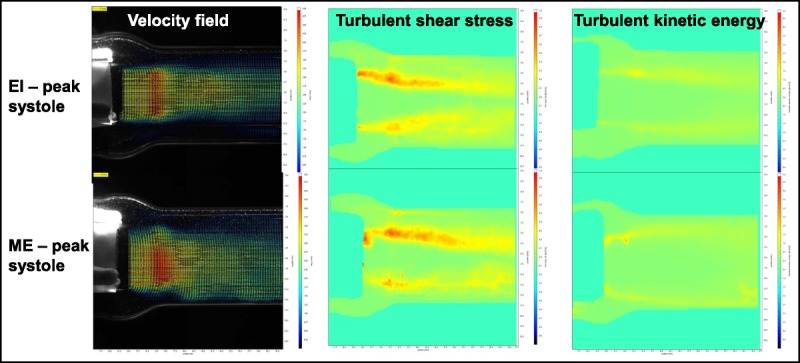
Flow velocity images across the aortic valves during peak systole obtained by particle image velocimetry. The top images are for an EI valve with nominal frame expansion, and the lower images are for a ME valve without pledgets. EI, EDWARDS INTUITY; ME, Edwards Magna Ease.

DISCUSSION

An important objective of the present study was to develop a clinically relevant aortic root model that could be used to evaluate the hemodynamic performance of aortic valves in vitro. Our rubber gasket model of the aortic root had dimensions that were obtained from MSCT images in patients with aortic stenosis and then scaled down to an effective annulus diameter of 21 mm. The ellipticity index of the LOVT (1.44) and aortic annulus (1.21) in the model were very similar to the average values reported by Buellesfeld et al¹⁷ in 177 patients with aortic stenosis (1.49 ± 0.02 and 1.29 ± 0.1, respectively).

A key finding of the present study is that the hemodynamic performance of the EI valve was superior to that of the conventional ME valve, despite that the EI valve was built on the platform of ME valve by employing a balloon-expandable frame to anchor the valve. Compared with the ME valve sutured to the aortic annulus without pledgets, the EI valve with nominal frame expansion had a significantly lower TPG and significantly higher EOA (Fig. 6), a hemodynamic advantage of approximately 2 valve sizes. Furthermore, PIV analysis showed that peak systolic flow across the EI valve was accompanied by a significantly lower maximum velocity, less turbulent shear stress, and less turbulent kinetic energy than flow across the ME valve (Fig. 7).

Although the sizes and supra-annular design of the EI and ME valves were the same (21 mm), balloon expansion of the stent frame of the EI valve results in a nominal valve frame diameter that ranges from 22 to 25 mm. The increase in diameter beyond 21 mm did not seem to account for the superior hemodynamic performance of the EI valve compared with the ME valve in our aortic root model. This was evident from the results obtained on valves with expanded diameters of 22, 23, 24, and 25 mm. Although increasing the expanded diameter from 22 to 25 mm resulted in an increase in the LVOT area, there were only minor changes in the EOA and TPG (Table 1). At least part of the reason that valve performance did not change much as the stent frame diameter varied from 22 to 25 mm is that the LVOT area (3.70–4.64 cm²) under these conditions was greater than the aortic annulus area (3.38 cm²). Once the LVOT area exceeds the aortic annulus area (i.e., inflow area exceeds outflow area), the LVOT may no longer be flow limiting.

Expansion of the EI valve frame also resulted in a more circular geometry of the LVOT, because the ellipticity index remained 1.06 or less, regardless of the frame diameter (Table 1). Compression of the stent frame of the expanded EI valve in 1 dimension at an expanded diameter of 22 mm increased the average ellipticity index to 1.25. Despite this increase in ellipticity, there was little change in the TPG or EOA. However, when the ME valve was sutured to the aortic annulus, the average LVOT ellipticity index was 1.56, and the LVOT area index was 0.69. Thus, attachment of ME valve to the aortic annulus resulted in marked increase in ellipticity and a marked decrease in LVOT area compared with the EI valve. These changes in ellipticity and LVOT area were associated with a significant decrease in the EOA and increase in the TPG.

Another important finding was that the use of pledgets significantly impaired the hemodynamic performance of the ME valve. The addition of pledgets to the sewing ring of the ME valve significantly reduced the EOA and increased the TPG (Fig. 6). The pledgets increased the average ellipticity index of the LVOT from 1.56 to 1.60 and further decreased the average LVOT area index from 0.69 to 0.42 (Table 1). The reduction in LVOT area index was due at least in part to the area occupied by the pledgets, and this probably contributed to the reduced EOA and increased TPG. Because the pledgets were sutured to the annulus using 6 additional sutures after the valve had already been sutured to the annulus (with 12 sutures), the use of these additional sutures might have played a role in reducing the LVOT area.

Because the EOA and TPG seemed to be influenced by both the LVOT area and ellipticity, we performed multiple linear regression analysis to determine how the EOA and TPG were influenced by changes in the LVOT area index and ellipticity index. Our regression models indicated that 93% of the variation in both the EOA and TPG could be explained by variation in the LVOT area index and ellipticity index.

The terms in the regression models can be rearranged to give the following 2 equations:

EOA (cm²) = 1.86 − 1.94 (0.98 − LVOT area index) × (LVOT ellipticity index − 1.01)

TPG (mm Hg) = 16.9 + 63.17 (0.91 − LVOT area index) × (LVOT ellipticity index − 0.99)

Our regression model for the EOA also predicted that the ellipticity index needed to be much greater than 1.01 along with an LVOT area index that was much lower than 0.98 for these 2 variables to have an important impact on the EOA. Likewise, our regression model for the TPG predicted that the ellipticity index needed to be much greater than 0.99 along with an LVOT area index that was much lower than 0.91 for these variables to have an important effect on the TPG. Thus, a change in the ellipticity index or LVOT area index by itself would have little impact on the EOA or TPG. Our models predicted that a large simultaneous change in both parameters is necessary to produce a clinically relevant change in the EOA and TPG. Because the balloon-expanded frame of the EI valve leads to a more circular LVOT, making the LVOT ellipticity index of the EI valve close to 1, the impact of LVOT area or frame expansion on the EOA and TPG of the EI valve is small as predicted by the regression models.

A recent study by Gunning et al¹⁸ evaluated the effect of eccentric deployment of transcatheter aortic valves in vitro using an acrylic model of the aortic root. When the eccentric index (1 − D_min/D_max) of the deployed valve was increased to 28% (= 1 − 18.7 mm/25.8 mm, equivalent to ellipticity index of D_max/D_min = 25.8 mm/18.7 mm = 1.38), there was little change in the TPG or EOA. Based on the diameters that they reported for their circular (22 mm) and elliptical valves (D_max, 25.8 mm; D_min, 18.7 mm), the calculated areas are 380 and 378 mm², respectively. Furthermore, assuming a baseline area of 380 mm², the inflow area index would have been 0.99 for the elliptical valve. Based on our regression models, an increase in the ellipticity index to 1.38 with a decrease in the inflow (LVOT) area index to 0.99 would have little impact on either the EOA or TPG. Thus, their experimental results seem to be consistent with our model predictions.

Limitations

It is important to note that the present study has some limitations. Although the dimensions of the aortic root model were based on dimensions obtained from MSCT images in patients, the images were reconstructed at approximately 60% of the RR interval, the aortic root model was not attached to a left ventricle, and no attempt was made to precisely replicate all of the mechanical properties of the aortic annulus and LVOT due to the scope of this study. Thus, the dynamic contraction of the LVOT in the absence of expanded stent frame was not captured in this model, and the LVOT geometry that we observed with deployment of the ME and EI valves may not be the same that would occur in patients undergoing aortic valve replacement. Pathological changes in the aortic root of patients such as atherosclerosis, medial hyperplasia, and calcification may limit the ability of EI frame expansion to alter both the area and geometry of the LVOT in vivo. Furthermore, pathological changes in the aortic root may alter the contraction and relaxation of LVOT tissue, and this could impact ME and valve performance in vivo. An additional study limitation was that all hemodynamic testing in vitro was done with saline rather than blood or a blood substitute, and this may have slightly affected valve performance. Furthermore, all hemodynamic data were obtained under normotensive condition with constant heart rate and cardiac output, and dynamic variation in these parameters would be expected to alter valve performance. The PIV study was performed on nominal EI stent frame expansion configurations, and representative measurements were obtained in only 2 planes that represented the major and minor axes. It is also possible that flow dynamics across the valve may have been altered by changes in area and/or ellipticity even when there was no change in the EOA or TPG.¹⁸ The 21-mm effective annulus diameter valve size was selected because the range of INTUITY frame expansion specification has greater impacts on the inflow (LVOT) area index on the smaller valves than on the larger valves. Due to the fact that the leaflets of size of 19-mm valves could cause potential flow restriction, size 21 valve was selected to exclude the influence of flow restriction due to the leaflet opening. Certainly, the findings of the current in vitro comparative study require validation with more valve sizes and will require confirmation in vivo.

CONCLUSIONS

A clinically relevant rubber gasket model of the aortic root was developed to evaluate the hemodynamic performance of aortic valves in vitro. When pulsatile flow was applied to the aortic root-valve assembly, the EOA was significantly higher and the TPG was significantly lower with the EI valve than with the ME valve sutured to the annulus without pledgets. The addition of pledgets further impaired the performance of the ME valve. Particle imaging velocimetry analysis showed that peak systolic flow across the EI valve was accompanied by a significantly lower maximum velocity, less turbulent shear stress, and less turbulent kinetic energy than flow across the ME valve. The hemodynamic advantages of EI valve may result in the superior clinical performance of the EI valve compared with conventional surgical valves. Particle imaging velocimetry demonstrated that this superior performance may be attributed to the ability of rapid deployment valves to transform an elliptical LVOT into circular one, unlike conventional surgical valves, which are associated with an abrupt transition from the elliptical LVOT to circular valve flow area.

CLINICAL PERSPECTIVE

This interesting in vitro study compared the hemodynamic function of the rapid-deployment EDWARDS INTUITY (EI) valve with a standard Edwards Magna Ease (ME) valve. An elastomeric model was developed based on reconstructions from three-dimensional multislice computed tomography images from patients with aortic stenosis; the aortic root was scaled to a 21-mm effective annulus diameter. The EI valve was deployed by stent frame expansion within the aortic root, whereas the ME valve was sutured to the annulus. The EI valve had a greater effective orifice area and a lower transvalvular pressure gradient. Interestingly, the superior performance of this valve seemed to be related to a greater inflow area and a more circular left ventricular outflow tract. Also, the authors found that the use of pledgets significantly impaired the hemodynamic performance of the ME valve. This was a well-performed in vitro study, which demonstrated the advantages of the EI rapid deployment valve.

This study did have significant limitations. Although the aortic root was based on dimensions obtained from computed tomography scans, there was no attempt made to precisely replicate all of the mechanical properties of the aortic annulus and the left ventricular outflow tract. It may be inaccurate to extrapolate these findings in an in vitro model to the in vivo situation. An additional shortcoming was that the testing was done with saline rather than blood, and this may have had an impact on valve performance. However, you would have expected this to have impacted both valves in a similar fashion. Finally, the authors only studied one valve size.With these limitations in mind, this important study provides evidence to support the potential advantages of rapid-deployment valves compared with our traditional stented bioprostheses.