Exploring the Development of Ground-State Destabilization and Transition-State Stabilization in Two Directed Evolution Paths of Kemp Eliminases

Abstract

Computer-aided enzyme design presents a major challenge since in most cases it has not resulted in an impressive catalytic power. The reasons for the problems with computational design include the use of nonquantitative approaches, but they may also reflect other difficulties that are not completely obvious. Thus, it is very useful to try to learn from the trend in directed evolution experiments. Here we explore the nature of the refinement of Kemp eliminases by directed evolution, trying to gain an understanding of related requirements from computational design. The observed trend in the directed evolution refinement of KE07 and HG3 are reproduced, showing that in the case of KE07 the directed evolution leads to ground-state destabilization, whereas in the case of HG3 the directed evolution leads to transition-state stabilization. The nature of the different paths of the directed evolution is examined and discussed. The present study seems to indicate that computer-aided enzyme design may require more than calculations of the effect of single mutations and should be extended to calculations of the effect of simultaneous multiple mutations (that make a few residues preorganized effectively). However, the analysis of two known evolution paths can still be accomplished using the relevant sequences and structures. Thus, by comparing two directed evolution paths of Kemp eliminases we reached the important conclusion that the more effective path leads to transition-state stabilization.

Graphical Abstract

INTRODUCTION

The design of improved or new enzymes by computational approaches is a problem of significant current interest.^1–6 However, the progress in this field has been disappointedly slow, and most of the actual progress has involved directed evolution rather than prediction using computational studies.⁷

Basically, the challenge is to generate active sites with a large catalytic effect which resembles that of real enzymes, and this challenge has not been accomplished yet.⁷ As we argued before, a part of the problem is the fact that many of the computational approaches used have not been validated by reproducing the catalytic effect of known enzymes. However, even much more rigorous approaches have not yet led to the design of efficient enzymes.

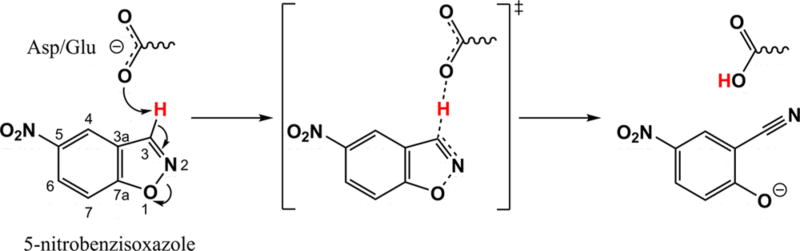
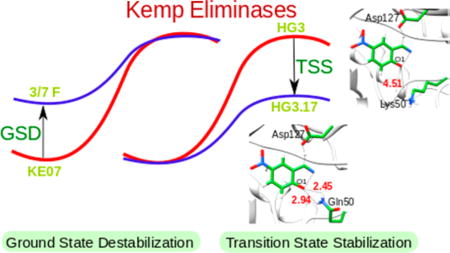
As a step in addressing the above problems, we try here to explore the effect of directed evolution in Kemp eliminases, where the corresponding chemical reaction is described in Scheme 1. The design of these systems has been one of the most active directions in enzyme design,^8–14 including several computational studies.^15–20

Scheme 1.

Schematic Representation of the Kemp Elimination Reaction

Our previous studies, which reproduced the observed experimental trend, predicted that transition-state stabilization (TSS) should result from electrostatic stabilization of the charge developed on O1.^18,19 However, attempts to use this computational insight in the refinement of Kemp eliminases have not been successful, and the progress in actual catalytic refinement has been obtained almost exclusively by directed evolution. Furthermore, we have found that most of the effect of directed evolution has resulted in ground-state destabilization(GSD),¹⁸ rather than TSS, which operates in naturally evolved enzymes.²¹ However, a recent study of Hilvert and co-workers²² found what is likely TSS.

In this work, we focus on the move from GSD to TSS in Kemp eliminases. Our study reproduces the trend in the two different directed evolution paths and allows analyzing the corresponding trend. Furthermore, our analysis seems to indicate that effective refinements of an inactive enzyme may require calculations of several mutational steps rather than calculations of mutations of single residues.

COMPUTATIONAL METHODS

The catalytic effects were calculated using the empirical valence bond (EVB) methods.^23–25 The corresponding activation free energies were calculated by the free energy perturbation/umbrella sampling (FEP/US).²⁶ The EVB and the FEP/US approaches have been described and used in many previous works and are reviewed briefly in the Supporting Information and in part below.

The center of the reactive species was taken as the center of the system which was immersed in a water sphere of 18 Å and solvated using the surface constrained all atom solvent (SCAAS) model.²⁷ The long-range effects were treated using the local reaction field (LRF) method.²⁸ The system was first relaxed for at least 100 ps using a step size of 1 fs, and then 3 different starting structures were generated.²⁹ The FEP simulation was divided into 41 mapping frames, and each frame was simulated for 20 ps with a step size of 1 fs, resulting in a total simulation time of around 1 ns. The linear response approximation (LRA) approach^30,31 was used to calculate the solvation free energies (which include the electrostatic effect of the protein and the solvent) and analyze the nature of the catalytic effect. The corresponding free energies were calculated on moving from the charged state to the uncharged state at both the reactant and transition-states. The calculations were performed using the MOLARIS-XG package.^32,33 The specific EVB parameters used in the current calculations are given in the Supporting Information, where we also asses the stability of the EVB.

The starting structure for the EVB calculations was taken from the X-ray crystal structures (KE07 (PDB: 2RKX),⁸ R6 3/7 F (PDB: 3IIP),⁹ HG3 (PDB: 3NYD, S265T),¹⁰ and HG3.17 (PDB: 4BS0)).²² Two conformations were reported in the 4BS0 PDB entry, and on the basis of previous studies, we started our calculations using conformer B.¹⁷ The EVB calculations were carried out using the MOLARIS-XG package with the ENZYMIX force field.^32,33 The ESP charges for the two diabatic states that represent the reactant and a specialized product were taken from a previous study, with specialized product state charges that account for the complex three state feature (see the Supporting Information of ref 18). The EVB region was taken as the carboxylate group of the ASP/GLU residue and the ligand 5-nitrobenzisoxazole (see Supporting Information).

We would like to note that the EVB calculations are expected to give reliable results in studies of catalytic effects. That is, the EVB force field has been calibrated on observed solvation free energies rather than on less-relevant properties and has been validated repeatedly on highly relevant properties such as pK_as (see a review in ref 34). Overall, we believe that the accuracy of MOLARIS (with the SCAAS and LRF) in reproducing activation free energies is a well-established fact (e.g., see our study of the ketosteroid isomerase³⁵ and B₁₂ enzymes³⁶). Furthermore, our studies of enzyme design have provided stable and reliable results for well-defined benchmarks.³⁷ Nevertheless, other modern simulation programs with properly parametrized force fields would probably give similar results once they implement the full EVB treatment and repeat the procedure used here.

RESULTS AND DISCUSSION

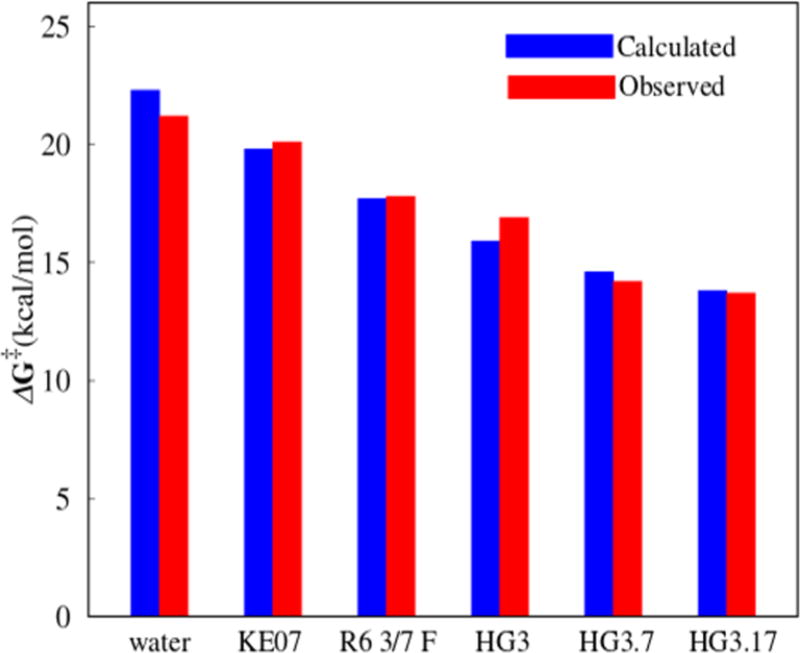
We started by exploring the catalytic effect of the KE07, R6 3/7 F, HG3, HG3.7, and HG3.17 systems. The first system (KE07) was designed by Baker and co-workers and was further improved using directed evolution to give R6 3/7 F.⁸ HG3 was developed by Houk, Mayo, and co-workers¹⁰ and was improved by Hilvert and co-workers²² to yield the most effective systems (HG3.7 and HG3.17) (Table 1). Overall, we reproduce the observed experimental trend (Figure 1 and Table 1).

Table 1.

Calculated and Observed Activation Free Energies (kcal/mol) for Different Systems^a

system	ΔG‡cal	ΔG‡obs
KE07 (wt, PDB: 2RKX)	19.8	20.1
R6 3/7 F (PDB: 3IIP)	17.7	17.8
HG3 (PDB: 3NYD, S265T	15.9	16.9
HG3.17 (PDB: 4BS0)	13.8	13.7
HG3.3b	16.1	16.0
HG3.7	14.6	14.2
water (cage)	22.3	21.2

^aOur activation barriers that are evaluated (as in all of our previous works (e.g., see ref 18)) are referred to the chemical barriers. Namely, the barrier that corresponds to k_cat in the enzyme and k_cage in water. The observed result for k_cage is taken when the format ion is used rather than when acetate ion was used as a base (extrapolation of the concentration to 55M). This point is discussed in detail in ref 18.

Figure 1.

Comparison of calculated and observed^8–10,22 activation free energies for different systems.

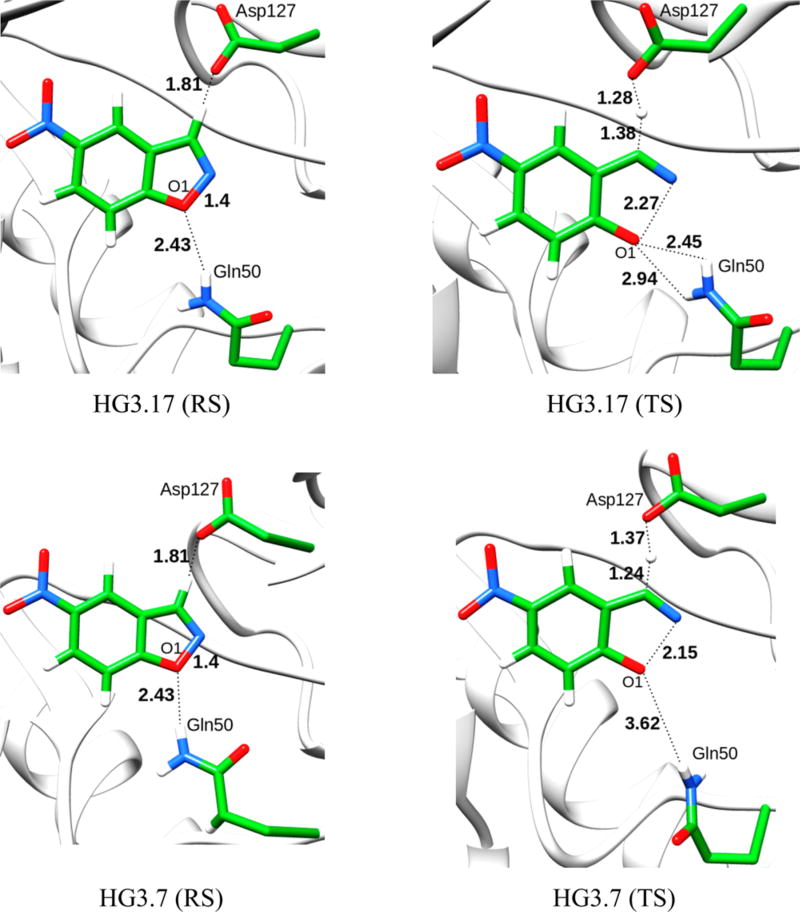
Encouraged by the above results, we tried to examine the origin of the difference between the evolution of the KE07 system and the HG3 systems in terms of the origin of the catalytic effect. Toward this aim, we started first with the HG3.3b system, which involves 6 mutations from the wt; HG3. Next we studied the HG3.7 systems wherein there are 7 mutations and K50 is mutated to Q50. Because the crystal structures of both HG3.3b and HG3.7 were not reported, we obtained the starting geometries by manually mutating residues in the wt; HG3. The starting structures were then subjected to a 1.5 ns relaxation runs before performing the actual EVB simulations. Even though, in the starting structure of HG3.7, Q50 forms H-bonds with O1 of the ligand, this interaction is not observed in the TS (Figure 2). On the contrary in HG3.17, Q50 forms H-bonds both at the reactant and transition state, which consequently renders stabilization.

Figure 2.

Reactant and transition-state geometries for the HG3.17 and HG3.7 systems. Distances are given in Å.

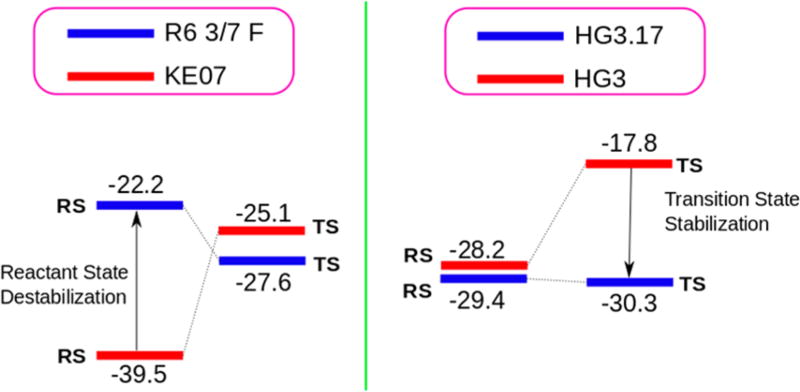
As seen from Table 2 (and the Supporting Information), when one moves from KE07 to the mutant (R6 3/7 F), the major catalysis comes from GSD (as clarified in the caption of Table 2, the GSD is not equal to the change in binding energy since a protein residue (i.e., the Asp residue) is a part of the substrate). To demonstrate this point, we performed PDLD/SLRA calculations to study the individual effect of the GLU residue and the ligand for the KE07 and R6 3/7 F systems. It was found that while the electrostatic contribution to the solvation free energy from the ligand remains the same on moving from the reactant state of KE07 to R6 3/7 F, the GLU residue becomes destabilized (see Table S6 in the Supporting Information). On the other hand, on going from HG3 to the mutant (HG3.17), the effect is due to TSS. This is clearly interesting since enzymes that where designed by regular (natural) evolution work by TSS. As can be seen from Figure 3, there is a huge GSD for the KE07 systems which is not compensated by TSS.

Table 2.

LRA Contributions (kcal/mol) of the Solvation Free Energies for Different Systems^a

	KE07		R6 3/7 F
	RS	TS	RS	TS
${<U_Q-U_0>}_Q^{W+P}$	−78.8	−55.9	−56.6	−63.0
${<U_Q-U_0>}_0^{W+P}$	−0.2	5.7	12.2	7.8
ΔGsolv	−39.5	−25.1	−22.2	−27.6

	HG3		HG3.3b		HG3.7		HG3.17
	RS	TS	RS	TS	RS	TS	RS	TS
${<U_Q-U_0>}_Q^{W+P}$	−56.7	−35.5	−77.9	−42.2	−50.8	−48.4	−46.9	−48.3
${<U_Q-U_0>}_0^{W+P}$	0.4	−0.1	17.0	4.2	−2.2	−0.3	−11.9	−12.2
ΔGsolv	−28.2	−17.8	−30.5	−19.0	−26.5	−24.4	−29.4	−30.3

^aU_Q and U₀ represent the charged and uncharged states, respectively. W and P represent water and protein, respectively. An important point to note here is that the difference in the K_M values does not reflect the true change in binding energy as a protein residue (ASP/GLU) is part of the substrate. We also like to note that the LRA is much less quantitative that the FEP/US approach, but it still provides reliable qualitative information about the difference between GSD and TSS. Note that that as established in our earlier papers the LRA electrostatic contribution is a very good marker for the magnitude of the GSD and TSS.³⁸

Figure 3.

LRA contributions of the solvation free energies (protein + water) for the evolution of the KE07 and HG3 systems.

Another interesting feature emerges from the comparison of the electrostatic contributions of the reactant states of different systems. That is, as seen from Table 3, on going from HG3 to HG3.17 via intermediate stages of the directed evolution, one does not see a very large destabilization of the reactant state. On the contrary, the directed evolution from KE07 to R6 3/7 F results in a considerable destabilization of the reactant state. In the initial KE07 enzyme, the Glu101 residue is stabilized by Lys222 in the reactant state. However, in the evolved enzymes, this stabilization is lost which leads to reactant state destabilization.⁹ This further shows the different routes adopted by KE07 and HG3 during directed evolution.

Table 3.

LRA Contributions (kcal/mol) of the Solvation Free Energies for the Reactant State of Different Systems

	HG3	HG3.3b	HG3.7	HG3.17
ΔGsolv	−28.2	−30.5	−26.5	−29.4
	KE07	R3 I3/10 A		R6 3/7 F
ΔGsolv	−39.5	−33.87		−22.7

An important residue which is found in the best mutant (HG3.17) is Q50 (Figure 2). This residue stabilizes the TS by forming oxyanion hole type H-bonding interactions with the developing negative charge on O1. It has been shown experimentally that the Q50A mutation in HG3.17 leads to a 50 fold decrease in k_cat/K_M (and probably to a significant reduction in k_cat). We tried to study the effect of this residue in the absence of any other mutations and thus mutated K50 to Q50 in the wt HG3 system. However, this mutation failed to yield any improvements, establishing the importance of the additional mutations that occur in the evolution of HG3.17 and make Q50 so effective. An important point to note here is that on mutating K50 to Q50 in HG3, the orientation of Q50 is of prime importance. For structures where the Q50 was within H-bonding distance to the ligand, the activation energy showed a slight decrease in comparison to the wt (15.9 kcal/mol). However, in the majority of the obtained structures, the position of Q50 was far away from the substrate. Such simulations gave a much higher activation barrier (21.1 kcal/mol). These results show that mutations other than Q50 are essential to improve catalysis. The finding that Q50A becomes crucial to catalysis only after many other mutations is very instructive.

We also studied the H50Q mutation in HG3.3b and found a 0.3 kcal/mol decrease in the activation energy from HG3.3b, suggesting that this mutation might not be very effective at this stage. To study the Q50A mutation in HG3.17, the ALA residue was constrained by a weak force. This was done to avoid the entrance of water molecules in the extra space created during the mutation. The results show a 1 kcal/mol increase in the activation energy from HG3.17, which is in the right direction (50 fold decrease in the value of k_cat/K_M).²² It should be noted that even our previous attempts to stabilize the negative charge on O1 by a single mutation in KE07 did not yield TSS,¹⁸ and thus, it becomes clearer that it is difficult to achieve TSS with a single point mutation alone.

CONCLUDING REMARKS

This work explored the nature of the refinement of Kemp eliminases by directed evolution, trying to learn about the requirements from computational design. The trend in the directed evolution refinement of KE07 and HG3 were reproduced, showing that in the case of KE07 the directed evolution leads to GSD, whereas in the case of HG3 the directed evolution leads to TSS.

As stated above, our previous study¹⁸ attempted to generate a single mutant to stabilize the O1 charge in KE07 but did not yield TSS. That is, as discussed at length in ref 18, our attempt to stabilize O1 by mutating residue 9 to polar residues (that was supposed to help in TSS) did not help in producing the expected effect (as was judged by subsequent unpublished experiment). This led us to realize that the EVB charge distribution should be modified (see ref 18 and the discussion on moving from set B to set A charges), where we found that the TS delocalized charges make it hard to create an effective oxyanion hole, particularly when we already have a polar group (namely, Ser 48). Problems such as these can lead to difficulties in the design of new enzymes, and thus, a thorough study that can reproduce the experimental values is of utmost importance. Similarly, it was shown experimentally that the Q50A mutation in HG3.17 leads to a 50-fold decrease in k_cat/K_M (and probably a reduction in k_cat).²² Significantly, in HG3 it is hard to get correct preorganization for Q50 due to the position of other residues. The change in the effectiveness of Q50 from the wt to HG3.17 provides a remarkable demonstration of the fact that the evolution to TSS requires more than one mutant. If this finding is general, then it might mean that computer-aided enzyme design requires more than the evaluation of the effect of single mutations. The requirement of several refinement steps should be considered in estimating the effort of computational design.

We would like to clarify that in most native enzymes, one can find a single residue whose mutation will destroy the catalysis and inversely restoring such a single residue will restore catalysis. However, reaching such a stage where a single residue leads to catalysis has required many steps in the neutral evolution.

It is useful to elaborate here more on the issue of computer-aided enzyme design. That is, we agree that it is important to be able to generate the structures of the mutants considered and that one may be trapped in incorrect local conformations. However, our long relaxation before the EVB mapping and the relatively long simulation, while obtaining the TS free energy, guarantees that we are sampling a relatively large region. This is further supported by repeating the simulations from different starting points in the region of the initial structure. Thus, an approach that considers several starting conformers should be enough to explore the effects of single mutations. To move in this direction, we took the initial HG3 and manually mutated it to HG3.17 followed by superimposing it on the crystal structure of HG3.17. This resulted in a RMSD of 0.43, indicating that the backbone structure does not change much during the directed evolution, and therefore, our approach of manually mutating residues to generate HG3.3b and HG3.7 seems to be justified.

At this point, it might be useful to clarify that in general we do not use the RMSD from observed structure in judging whether we can reproduce the correct reorganization energy and activation barrier (in particularly not the RMSD to the initial structure). Different force field will always have nonzero RMSD from their minima to the exact structure of the RS, but yet the free energy of moving from the RS to the TS can be very reliable.³⁹ In fact, one should never use the observed structure in attempting to obtain the correct reorganization energy,⁴⁰ but rather calculate the reorganization free energy in the landscape of the given model. Thus, the real question is not so much what is the RMSD but how far can be the initial guess structure from the correct minimum configuration of the model used with the given sequence, and still give (after long relaxation) the correct reorganization energy and activation barrier. This issue is best explored in cases with accurate structural information on the enzyme substrate complex, and thus, we provide in the Supporting Information a partial analysis based on our current study of dehalogenase.

With the above point in mind, we note that some workers may give too much weight to the availability of well-defined mutant structures, perhaps being mainly familiar with screening approaches that simply cannot give the activation barriers, even if they could use the exact X-ray structure of the TS. We believe that this is not the most crucial problem once one uses the EVB or related approaches. On the other hand, the search for mutations that increase the catalytic activity (with approaches that can give the correct barriers with correct starting structures) can be very challenging if it requires changes in several residues. In this case, one would need more computer power for generating multiple mutants and structures and evaluating the corresponding catalytic effects.

At this point, we would like to clarify that our work does not try to provide better design for Kemp eliminases (although we point out that a rational design cannot be obtained by approaches that cannot predict the catalytic effect). Instead the focus was placed on understanding the origin of the catalytic effects in two directed evolution paths. Finding that the more effective path leads to TSS is very encouraging, in view of our long-standing observation that enzymes that evolved by natural evolution do not use GSD. Fortunately, while looking at the above problem we found what is perhaps the main problem in rational enzyme design, namely the effect of other residues on the preorganization of the key preorganized residues.