Phase i trials in melanoma: A framework to translate preclinical findings to the clinic

Abstract

Background

One of major issues in clinical trials in oncology is their high failure rate, despite the fact that the trials were designed based on the data from successful equivalent preclinical studies. This is in part due to the intrinsic homogeneity of preclinical model systems and the contrasting heterogeneity of actual patient responses.

Methods

We present a mathematical model driven framework, phase i (virtual/imaginary) trials, that integrates the heterogeneity of actual patient responses and preclinical studies through a cohort of virtual patients. The framework includes an experimentally calibrated mathematical model, a cohort of heterogeneous virtual patients, an assessment of stratification factors, and treatment optimization. We show the detailed process through the lens of melanoma combination therapy (chemotherapy and an AKT inhibitor), using both preclinical and clinical data.

Results

The mathematical model predicts melanoma treatment response and resistance to mono and combination therapies and was calibrated and then validated with in vitro experimental data. The validated model and a genetic algorithm were used to generate virtual patients whose tumor volume responses to the combination therapy matched statistically the actual heterogeneous patient responses in the clinical trial. Analyses on simulated cohorts revealed key model parameters such as a tumor volume doubling rate and a therapy-induced phenotypic switch rate that may have clinical correlates. Finally, our approach predicts optimal AKT inhibitor scheduling suggesting more effective but less toxic treatment strategies.

Conclusion

Our proposed computational framework to implement phase i trials in cancer can readily capture observed heterogeneous clinical outcomes and predict patient survival. Importantly, phase i trials can be used to optimize future clinical trial design.

Introduction

Significant advances have been made in understanding mechanisms that provoke tumor initiation and progression, and often this knowledge has been translated into the development of targeted agents that selectively disable the mutated, activated and/or overexpressed oncoproteins manifest in tumor cells (1). Most of these targeted agents have been tested in clinical trials either alone or in combination with other treatments (2), and though some are clinically effective (e.g., small molecule BRAF kinase inhibitors (3)), the majority are not (4-6) despite the fact that such agents have potent activity in preclinical cancer cell and animal model studies. The leading cause of failure tends to be lack of efficacy, in part due to lack of robust predictive models that consider patient heterogeneity, and poorly designed clinical trials (6-9). This inconsistency is also partly due to difficulties in predicting the long-term effectiveness of a cancer therapy using time-limited in vitro (typically < 1 month) or in vivo (often < 3 months) model systems.

We reasoned that an appropriately defined and parameterized mathematical model, based on observations in cell and animal studies and clinical trials, might reveal insights regarding the design of improved and informed therapeutic approaches for treating cancer patients. We consider the recently completed multi-arm phase 1 trial of the MK2206 AKT inhibitor in combination with standard chemotherapy with advanced solid tumors, including melanomas (ClinicalTrials.gov, trial number: NCT00848718) (10). To investigate potential mechanisms of treatment efficacy, a mathematical model comprised of a system of ordinary differential equations was developed to describe the dynamics of melanoma cells exposed to four treatment conditions, no treatment, chemo, AKTi and combination of chemo and AKTi. Cell culture experiments were then used to parameterize the model. The calibrated model was further validated using results from an extensive series of cell culture experiments that consider twelve different drug combinations and timings. This validated model was then used to predict the long-term effects of the twelve treatments on melanoma cells, which revealed that all treatments eventually fail, but do so at significantly different rates.

To investigate the long-term effects of therapy in a more clinically relevant setting, we varied model parameters to generate virtual patients that had a heterogeneous mix of responses similar to typical clinical trial outcomes. We employed a genetic algorithm (GA) to generate a diverse virtual patient cohort consisting of over 3,000 patients. Statistical analyses of the simulated cohort showed that the treatment responses of 300 virtual patients sampled from the cohort matched actual patient responses in the trial (10). Analyses of complete virtual patient cohort defined parameters that discriminated virtual patients having more favorable versus less favorable outcomes. Finally, the model predicts optimal therapeutic approaches across all virtual patients. This strategy allowed implementation of a “virtual clinical trial” (phase i trial) (11). Similar virtual clinical trials have been developed to simulate clinical trials of cardiovascular disease, hypertension, diabetes (www.entelos.com), and acute inflammatory diseases (12). There have also been some previous studies that employed modeling approaches to predict outcomes of clinical trials (13, 14). Statistical approaches based on clinical drug metabolism (e.g., dose-concentration relationships) have also been developed to design virtual clinical trials (reviewed in (15)) that detect significant differences between treatments (for example, placebo vs. treatment). Here we rather sought to translate biological mechanism coming from in vitro experiments with clinical studies on melanoma combination therapy, into a phase i trial.

Results

Mathematical Modeling and Underlying Assumptions

We reported unexpectedly long-term responses (of up to 15 months) to the combination therapy of chemotherapy (chemo) and AKT inhibitor (AKTi, MK2206) in two BRAF-wild type melanoma patients in the trial (16). Although little was known regarding why this combination therapy was successful, we reasoned this reflected differential effects on inducing autophagy (16). Autophagy represents a cancer cell-intrinsic mechanism of resistance that allows cells to survive times of drug-induced stress (17, 18) or, if uncontrolled, can deplete key cellular components and provoke tumor cell death (19, 20). Differential autophagic responses to the chemo plus AKTi combination and accompanying effects on tumor cell growth and survival were manifest in melanoma cells (16).

Motivated by these experimental results, we formulated a mathematical model comprised of three phenotypic compartments (Fig. 1), a non-autophagy compartment (N) and two autophagy compartments (P and Q). We divided the autophagy compartment into two, physiological autophagy (P) and quiescent autophagy (Q) compartments, based on studies showing that some cells where autophagy is manifest continue to maintain normal cell homeostasis whereas others did not (21-24) (See supplementary text and Figure S1 for further explanation). Figure 1 and Figure S2 show the interactions between the N, P and Q compartments within the four different environments: no-treatment, three treatment conditions (chemo, AKTi, and combination therapy (chemo+AKTi)).

Figure 1.

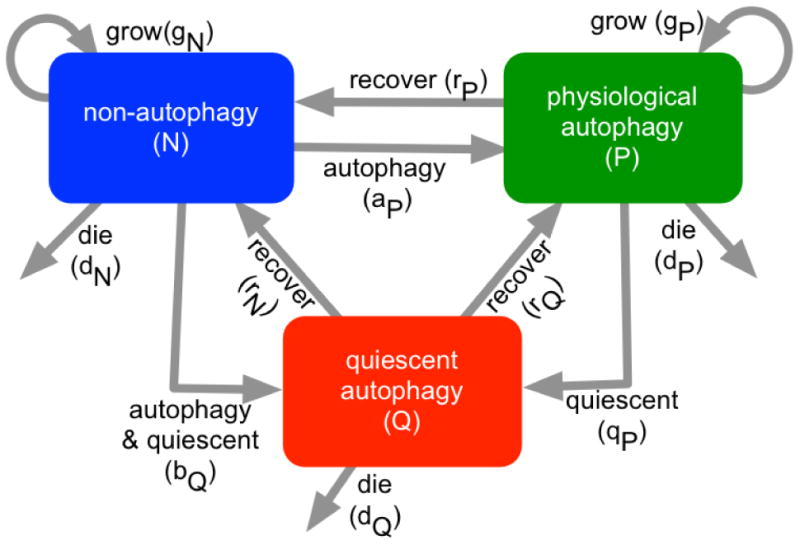
Mathematical model development. Schematic of a compartmental model composed of three compartments, non-autophagy (blue), physiological autophagy (green), and quiescent autophagy (red).

Untreated melanoma cells proliferate (rate: g_N), and following treatment can acquire either a physiological autophagy phenotype (transition rate: a_P) or a quiescent autophagy phenotype (transition rate: b_Q). Physiological autophagy cells grow (rate: g_P) and can revert to non-autophagy cells (returning rate: r_P), or enter a quiescent/senescent state (rate: q_P). Tumor cells having the quiescent autophagy phenotype do not divide, but can either reacquire a physiological autophagy phenotype (rate: r_Q) or a non-autophagy phenotype (rate: r_N) state. Cells in each compartment die at some rate (d_N,P,Q). To model increased cell deaths on days 6-9 (16), we included the delayed cell deaths of quiescent/senescent autophagy cells (τ).

The effects of chemo, AKTi and their combination were incorporated into the model (Fig. S2). As cell culture experiments showed that chemo triggered cell death with negligible effects on autophagy (16), we augmented cell death to model effects of chemo. Further, as chemo is effective only in proliferating melanoma populations, the therapy increases the death rate of the two proliferating phenotypes, non-autophagy (d_N) and physiological autophagy cells (d_P)(Fig. S2, black arrows) in the model. The frequency with which cells became quiescent/senescent (q_P) increased with chemo (Fig. S2, black lines). Our in vitro studies showed that while AKTi did not augment cell deaths or effectively inhibit melanoma cell growth (16), it did induce autophagy; thus, we assumed that AKTi increases the rate of transitioning to the autophagy phenotypes, a_P and b_Q (Fig. S2, black arrows). As combination therapy does not augment cell death compared with chemo, nor significantly increase autophagy relative to AKTi, the combination of the two treatments was modeled by adding the effects of chemo and AKTi (16) (Fig. S2, black arrows and crosses). Finally, no cells with a given phenotype can revert to their original states in the model while any treatment is being applied. The schematic representation of this compartment model (Fig. 1 and Fig. S2) converts readily into a system of ordinary differential equations:

$$\begin{array}{l}\dot{N}=(g_N-d_N)N-(a_P+b_Q)N+(1-A)r_{P}P+[(1-A)(1-C(t)]r_{N}Q\hfill \\ \dot{P}=(g_P-d_P)P+a_{P}N-(1-A)r_{P}P-q_{P}P+[(1-A)(1-C)]r_{Q}Q\hfill \\ \dot{Q}=-\left(d_Q+\frac{d_{\tau }}{1+e^{-(t-\tau )}}\right)Q-[(1-A)(1-C)](r_N+r_Q)Q+b_{Q}N+q_{P}P\hfill \end{array}$$ (1)

where d_N = d₀ + c_NC, d_P = d₀ +c_PC, q_P =q₀ + c_QC, a_P = a₀ + a_NA, and b_Q = b₀ + b_PA. In equation (1), A and C are defined by

$$A,C=\{\begin{array}{ll}0& \text{drug is off},\\ 1& \text{drug is on}.\end{array}$$

Note that the drug is assumed to reach its maximum concentration immediately after administration and remains at that level until the beginning of the treatment break. Although the chemotherapeutic agents (paclitaxel and carboplatin) are detectable in patients for 24 hours, the half-life in serum is relatively short, in the range of 5.6 – 11.1 hours (25, 26); the concentration of chemotherapeutic agents in the model was maintained for only 1 day after administration and became zero at the beginning of the treatment break. As the plasma concentration of AKTi (MK2206) is known to be constant for approximately 48 hours (with a long terminal elimination half-life of 40-100 hours) (27), a 1-day application of AKTi to cells or patients corresponds to a 2-day application to cells or patients in the model. A fixed dose was considered for both chemo and AKTi.

Model calibration with preclinical data

To calibrate model parameters, two melanoma cell lines (M257 and WM3918) were treated with chemo on the first four days (day 0-4) and with AKTi on every other day (days 0, 2, 4, and 6). We quantified the number of melanoma cells from images taken at days 4, 6 and 8 (Matlab Image Toolbox). We employed an optimization algorithm called implicit filtering (28), a steepest descent algorithm for problems with bound constraints, to determine the parameter set that minimized the difference between predicted number of cells and experimental results (See Supplementary Methods for a detailed explanation). A list of parameters and their ranges are summarized in Table S1. For each parameter set, we tested goodness of fit using R², root mean squared error, and normalized root mean squared error, and Kolmogorov-Smirnov test. The parameters produced good fits (R² ≥ 0.8, for all cases) for the growth of each cell line (Fig. 2). The maximal root mean squared error was 68.7 and the normalized error was 13.5%. The two sample Kolmogorov-Smirnov test doesn't reject null hypothesis that the predictions using estimated parameter and experimental data are from a same distribution. (See Supplementary Parameter Estimation Section for a detailed explanation) Chemo reduced growth rates of both WM3918 and M257 (Fig. 2, Chemo panels) and continuous application of AKTi increased the proportion of the non-autophagy (N) to physiological autophagy (P) phenotype (Fig. 2, AKTi panels, increasing green lines). The combination of AKTi and chemo generally induced the quiescent autophagy (Q) phenotype (Fig. 2, combination panels, increase of red lines), which arose following the rapid transition of a non-autophagy to physiological autophagy phenotype (Fig. 2, combination panels, a sharp increase in the green line < day 1). The number of cells in the total cell population treated with the combination therapy continued to decrease as a result of cell death of the Q phenotype (Fig. 2, combination panels, decreasing red lines).

Figure 2.

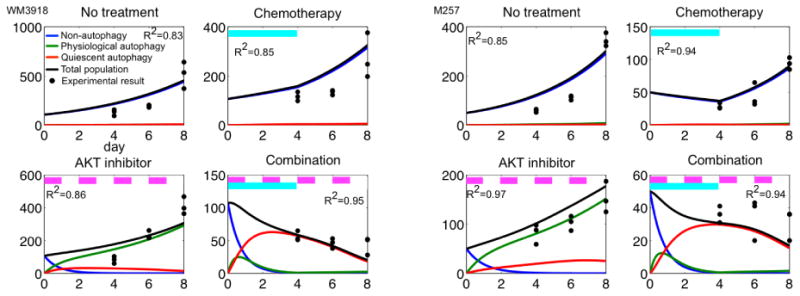
Model calibration. Predicted non-autophagy (blue), physiological autophagy (green), quiescent autophagy (red), total population (black line), and experimental cell counts (black dots) on days 4, 6 and 8, under four conditions: no treatment; chemo (day 0-4, cyan bars), AKTi (days 0, 2, 4 and 6, pink bars) and combination therapy (chemo on days 0-4 and AKTi on days 0, 2, 4 and 6) in cell lines WM 3918 (left) and M257 (right) melanoma cells. R²-values are reported for each case.

Model prediction and validation with preclinical data

Our calibrated model was used to predict the effects of twelve treatment schedules that differed in the timing and order of chemo, AKTi and combination therapy across a 16-day period (Supplementary Methods and Fig. S3 for a description of the schedules). The expected treatment responses are summarized in Fig. 3 (red bars). Compared with the untreated tumor cell population (#1), one application of chemo decreased the tumor cell population by 30-65% (#1 vs. #2) and two applications reduced the population by 50-90% (#1 vs. #3). One application of AKTi had limited impact on tumor cell growth (approximately 20% reduction from #1, untreated to #4, AKTi therapy). Continuous application of the AKTi reduced the tumor cell population size by 40-70% (#1 vs. #5). The M257 melanoma cell line was more sensitive to both chemo and AKTi than WM3918 melanoma cells. Combination therapies were substantially more effective than mono-therapies. In general, concurrent therapies with chemo and AKTi (#6 and #7) were more successful than all sequential therapies (#8-#12). Concurrent therapy #6 reduced the tumor cell population size by up to 90%, and concurrent therapy #7 nearly eradicated all of the tumor cells (Fig. 3, #7, nearly invisible red bars). Sequential therapy decreased the tumor cell population size by 50-90% (Fig. 3, #1 vs. #8-#12).

Figure 3.

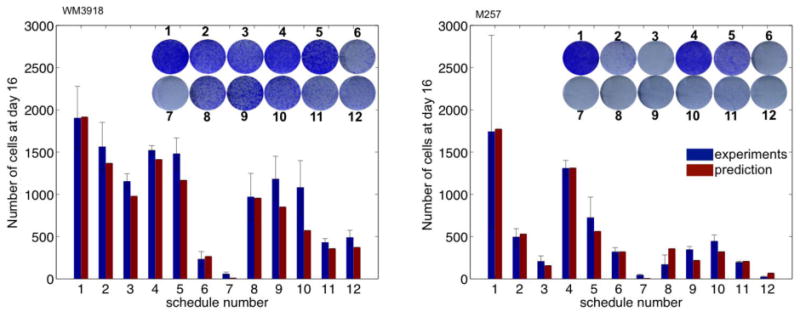
Mathematical model validation. In a total of 12 different conditions, predicted total populations (red bars) are compared with of the each experimental results (blue bars). Inset: Photographs of fixed colonies on day 16.

To validate these predictions, an extensive series of in vitro experiments were performed and the numbers of viable tumor cells were quantified on day 16 (Fig. S3B). We then compared the total experimental melanoma cell numbers with those predicted by the models (Fig. 3, blue vs. red bars). In general, the predictions matched well with the experimental results, as all predicted values (red bars) were within one standard error deviation from the mean value of the experimental results (blue bars). Thus, this mathematical model accurately describes and predicts treatment outcomes obtained in vitro.

Long-term response of treatments

Having established a successfully validated model, the longer-term effects of the therapies were assessed. Surprisingly, the best proposed strategy (#7) failed by day 40 (WM3918 cells) or day 50 (M257 cells), where the physiological autophagy phenotype developed resistance to the therapy population (green lines, Fig. S4). This finding highlights a key shortcoming of in vitro experiments; i.e., the limited timescale. To test this prediction long-term cell culture studies were performed. Unsurprisingly, as the model predicted, a 30-day treatment of strategy (#7) failed to eradicate some of the melanoma cell lines in colony formation assay experiments (16).

Phase i trial

To investigate the long-term effects of therapy beyond homogeneous cell lines (or preclinical data in general) to a more clinically relevant setting, where heterogeneous treatment responses are typically observed, we propose a virtual clinical trial, termed Phase i trial (11). The trial consists of three steps, i) model development, ii) cohort generation, iii) stratification of simulated cohort response and factors, and treatment optimization (Fig. 4).

Figure 4. Phase i trial flowchart.

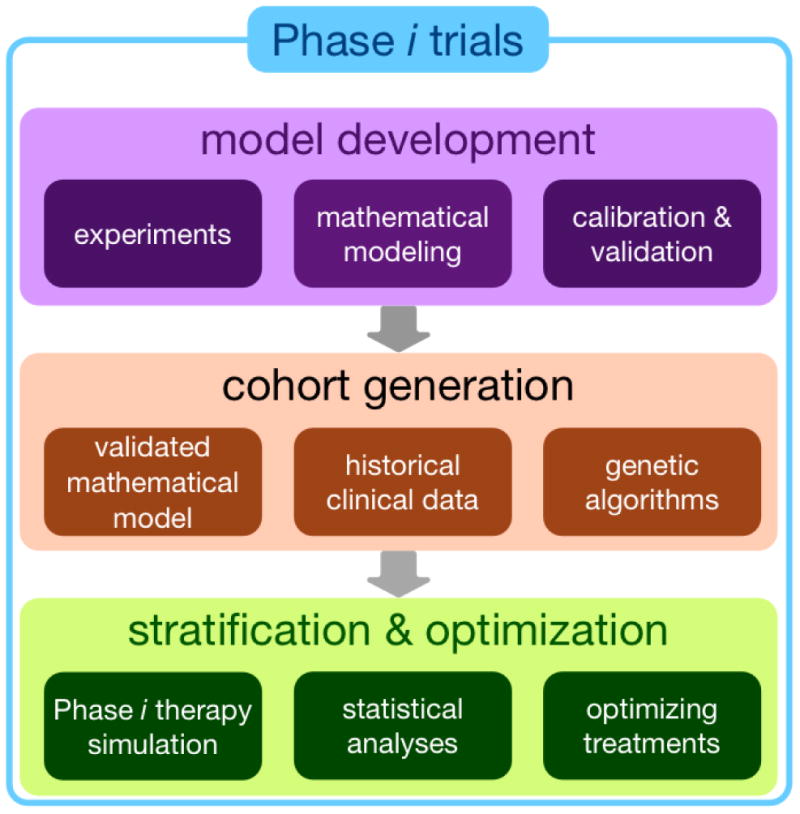
Model development: a mathematical model is developed based on experimental data. Then the model is calibrated and validated by comparing model predictions and experimental results. Cohort generation: the validated model and genetic algorithms are used to generate virtual cohort that statically matched historical clinical data. Stratification & optimization: Phase i therapy assuming the same schedules in a clinical trial is simulated using the cohort. The virtual cohort is analyzed to predict stratification factors. Optimization approaches are employed to propose optimal therapy, which may guide better patient selection and treatment strategies in subsequent clinical trials.

Virtual cohort generation

Under the assumption that our underlying resistance mechanism is relevant to the clinic, and there is some evidence to support this (29), we will use our framework to investigate the long-term treatment responses in a more clinically relevant scenario. Specifically, we consider model parameters that are more representative of real patients to generate a virtual patient cohort. The same treatment schedules as in the clinical trial (10) were used, with five cycles of first-day chemo in a 21-day cycle, and two different treatment arms of AKTi schedules (arm1, 2). In the first AKTi schedule (arm 1: Q3W), the drug is administered on the first day of the 21-day cycle for five cycles, and thereafter is given on the first day of every week (weekly maintenance therapy). In the second schedule (arm 2: QOD), the drug is administered on days 1, 3, 5 and 7 of the 21-day cycle, and is then given weekly as maintenance therapy. The total treatment time was set to be 15 months.

To generate virtual patients that exhibit the diversity of responses observed in the clinic, adaptive heuristic search Genetic Algorithms (GA, built in Matlab) were used (30, 31). We employed genetic algorithms as they are less dependent on initial conditions and allow a wider search space than classical optimization techniques. A solution (P = [g_N, g_P, d_Q, d_τ, r_P, r_N, b_P, c_P, c_Q, a_N, c_N]) was searched that minimized the difference between tumor volume with a parameter and the target tumor volume, which was randomly selected from three categories: complete response (CR; whose tumor diameter < 1 mm), partial response (PR; at least 30% reduction in tumor diameter), and stable disease (SD; up to 20% increase in tumor diameter) based on response criteria (32). Our GA found 3391 matched virtual patients, 1293 sets of parameters in the case of arm 1 and 2098 sets of parameters for arm 2 (See Supplementary Methods for a detailed explanation).

In comparing the parameter range of patients and cell lines we strikingly note that they barely intersect with each other (Fig 5A-B). Growth rates (g_N, g_P) of patients were much lower than those of cell lines (Fig 5B, top histograms). Death rates (d_Q, d_τ, c_P, c_N) and transition rates (r_P, r_N, b_P, c_Q, a_N) overlapped somewhat (Fig 5B, middle and bottom histograms). This might partially explain why preclinical results fail to translate clinically. We then compared the maximum tumor diameter changes of the 24 patients in the trial with those of 300 patients sampled from our virtual cohort (Fig. 5C, upper vs. lower waterfall plots). To test if the distributions of maximum diameter changes are from the same continuous distribution, we performed a two-sample Kolmogorov-Smirnov test (Matlab statistics toolbox) (33). The test does not reject the null hypothesis at 5% significance (test statistic = 0.12). In addition, empirical cumulative distribution functions of the two overlap each other (Fig. 5D).

Figure 5. Virtual cohort generation.

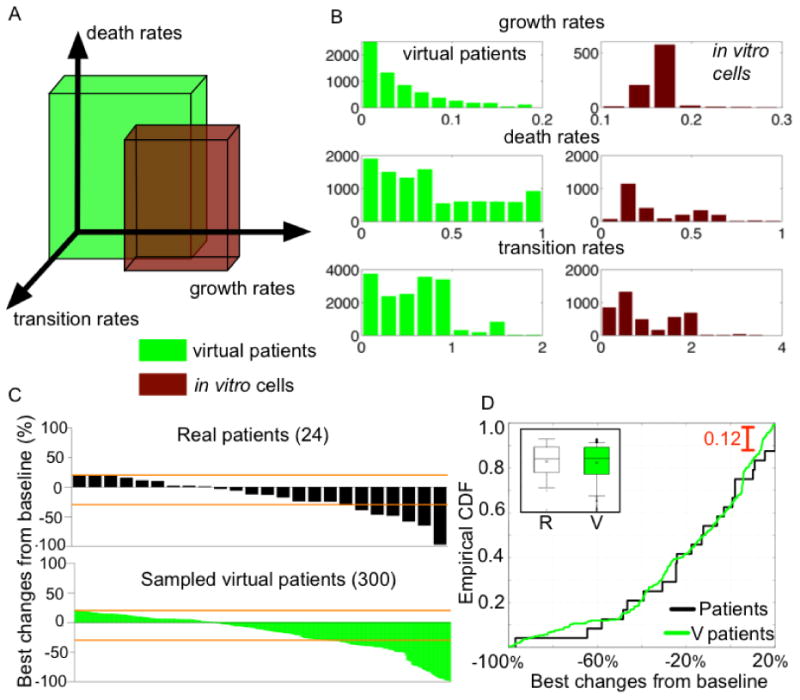
A, Parameter range of virtual patients (green) and in vitro cell lines (red). The boxes represent ranges of growth rates (g_N, g_P), death rates (d_Q, d_τ, c_P, c_N), and transition rates (r_P, r_N, b_P, c_Q, a_N) of patients and cell lines.

B, Histograms of the parameters of patients (green) and the cell lines (red), first: growth rates, second: death rates, and third: transition rates.

C, Waterfall plots representing the distribution of the maximum percentage changes of tumor diameter from baseline (initial diameter). Upper, 24 real patient tumors (Fig.1). Lower, 300 sampled virtual patient tumors (initial diameter, 1cm). Orange lines indicate -30% (PR) and 20% (SD) tumor diameter changes.

D, Empirical cumulative distribution functions of patients (black line) and 300 sampled virtual patients (green line). The maximum difference between two distributions is 0.12. Inset: Box-Whisker plots of patients (R, left) and the virtual patients (V, right). x: mean, -: median, box: 25% - 75%, upper and lower horizontal bar (-): 91-9%.

Virtual cohort stratification

Phase i combination therapy was simulated for 6 months with the two arms to predict treatment responses in the virtual patients. We randomly assigned a treatment arm (either arm 1 or arm 2) to all virtual patients. Then, all eleven parameters that were varied to generate VP were assessed to characterize this virtual cohort. We divided the patient group into CR, PR, SD, and PD (progressive disease, more than 20% increase in tumor diameter) using their tumor volumes at 6 months. Each parameter value from each group was compared and the Student's t-test was used to determine if the mean values of a parameter differed between two groups (CR vs. PR, PR vs. SD, and SD vs. PD) (Fig. S5). Our analysis identified the key parameters, growth rate of non-autophagy cells (g_N) and quiescent autophagy phenotype (b_P), as potential predictive factors of the treatment outcomes (Fig. S5). We divided all virtual patients into four sub-cohorts based on these parameter values (Fig. 6A, C_1-4) and compared tumor volume changes less than 300% at 6 months (3000 patients). Each sub-cohort showed significantly different mean (p value < 0.01, Student's t test) and median (p value < 0.01, Wilcoxon rank sum test, Matlab statistics toolbox) response to therapy (Fig. 6B). The sub-cohort C₁ (cyan) is most likely to benefit from the treatment, while the likelihood decreased gradually in C₂ (blue), and C₃ (yellow) or C₄ (red). There is also a clear shift in the distribution of treatment response from C₁ to C₄ (Fig. 6C). Patients had diverse responses to the therapy, where CR, PR, SD, and PD were observed in 40 randomly selected subjects (Fig. 6C). For example, some patients in C₄ were expected to be complete responders (CR, red bars of nearly -100%), while others in the same cohort were expected to be in PD (red bars of > 20%). In addition, a hierarchical clustering with Pearson correlation distance selected g_N and c_N as potential predictive factors of tumor volume changes (Fig. S6, A) although c_N was less effective in separating treatment outcomes (Fig. S6, B-C, unclear separations between C₁ and C₂ and between C₃ and C₄). In summary, these statistical analyses allow one to select potential stratification factors for a treatment strategy, which could be used to guide patient specific selection criteria for future therapies and trials.

Figure 6. Virtual cohort stratification and optimization.

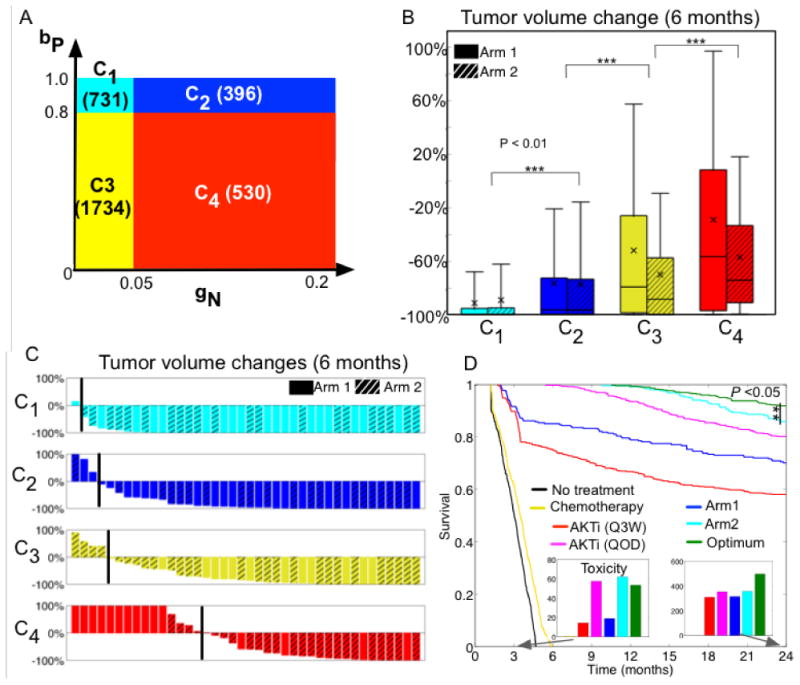
A, Partitioning of all virtual patients based on the growth rate of non-autophagy tumor cells (g_N) and the transition rate from non-autophagy to quiescent autophagy phenotype (b_P) based on the sensitivity analysis (Fig. S5). g_N was low (<0.05) but b_P was high (>0.5) in C₁ (cyan color, 731 patients). Both rates were high in patients in C₂ (dark blue, 396 patients). Both rates were low in patients in C₃ (yellow, 1734 patients)_. The tumor cells in patients in C₄ (red, 530 patients) had a higher rate of g_N (>0.05) but a lower rate of b_P (<0.8).

B, Box whisker plot of the expected 6-month treatment outcomes in the new sub-cohorts C₁-C₄.

C, Waterfall plots of the tumor volumes in randomly selected 40 patients from each sub-cohort C₁: cyan bars, C₂: blue bars, C₃: yellow bars, and C₄: red bars, black line indicates no-change of tumor volume.

D, Treatment optimization and predicted 2-year survival analysis.

Kaplan-Meier curves in patients from cohort C₄ when seven different treatments were applied for 2 years, no treatment (black), five cycles of chemo only (yellow), AKTi monotherapy following the Q3W schedule (red), AKTi monotherapy following the QOD schedule (pink), combination therapy with arm 1 (blue) or arm 2 (cyan), and the optimum therapy (green). Inset bars, sum of cumulative drug (both AKTi and chemo) concentrations at day 105 (first bar graph, same color scheme as in the survival curves) and year 2 (second bar graph).

Optimizing AKTi treatment to minimize toxicity for each sub-cohort

For the virtual sub-cohorts (C₁-C₄) optimal therapy recommendations were derived using implicit filtering (28). Notably, the schedule of chemo was fixed, as it was in the clinical trial (10), with the goals of identifying the AKTi schedule that reduced the initial tumor volume by at least 30% after 6 months of therapy (Supplementary Methods for a detailed description of AKTi treatment optimization). Optimized schedules of AKTi are summarized in Table S2. To understand the relative impact of these alternate therapies we compared the 2-year survival probability of patients on the different therapies. The therapies included optimized therapy, treatment arm 1 and arm 2, and two mono-therapies of AKTi only (i.e., AKTi treatment only from either arm 1 or arm 2), and chemo. The initial number of tumor cells was set at one billion and the melanoma was considered fatal when the number of tumor cells reached 10¹³ cells. We also compared the cumulative drug concentration of each therapy at two time points, immediately after the five-cycles of combination therapy of AKTi with chemo (105 days) and at the completion of therapy (2 years) (See Supplementary Methods for a detailed explanation of toxicity calculation).

For patient cohorts C_1-3, optimum scheduling improved the survival slightly but reduced the cumulative concentration of drugs (both AKTi and chemo) significantly. The maximum reduction was approximately 83% (Fig. S7). Here we focus on the probability of 2-year survival of the C₄ subcohort because their expected tumor volume responses were the worst (Fig. 6B, red box plots) and because their untreated survival is the poorest of the group showing a rapid decrease after 6 months (Fig. 6D, black line). Survival of the chemo-alone had only minimal improvement (Fig. 6D, yellow line). The AKTi monotherapies improved survival (Fig. 6D, red line (Q3W), and pink line (QOD)). Both treatment arm 1 and arm 2 also increased the probability of survival (Fig. 6D, blue line: arm 1 and cyan line: arm 2). Notably, the optimized therapy significantly improved the probability of survival (Fig. 6D, green line) compared to arm 2 (p value < 0.05), and the cumulative doses were also lower than arm 2 at day 105 right after the five cycles of combination of chemo with AKTi, although they became higher at year 2 (Fig. 6D bar graphs).

Discussion

The integrated approach applied herein shows that treatment-induced autophagy phenotypes are certainly one factor driving the long-term effects of treating patients with chemo in combination with AKTi. The mathematical model hypothesizes that two distinct states of autophagy exists (physiological and quiescent states), and indicates that improved patient outcomes are associated with the quiescent autophagy phenotype. The model also predicts that therapy drives the transition from the non-autophagy to the physiological autophagy phenotype, which provides a transient escape route from treatments. In contrast, the model indicates that a persistent quiescent autophagy state is detrimental to overall fitness and thus this represents a desired outcome of therapy.

Implementing a phase i trial allows one to translate models to a clinically relevant setting (Fig. 4). The key components of such a trial are an experimentally calibrated mathematical model and a cohort of virtual patients that mirror responses observed in an actual clinical trial. The model presented herein is constructed by integrating experimental results on melanoma combination therapy. Using a GA and employing standard clinical response criteria, one can easily generate a relatively large cohort of diverse virtual patients who are treated using the same treatments given to patients in a clinical trial and statistically reproduce the same responses. Our statistical analyses of the simulated cohort defined predictive factors, which discriminated between CR, PR and SD. The transition to the quiescent autophagy phenotype and the growth rate of non-autophagy cells discriminated outcomes significantly. This is in agreement with a previous clinical melanoma study, using different treatments, where increased autophagy response was associated with resistance to BRAF inhibitors (29). An important outcome of this analysis is our ability to define key stratification parameters for a given treatment, that differentiate cases having more or less favorable outcomes, demonstrating the utility of phase i trials in aiding patient selection for future therapies and trials.

Optimizing the AKTi schedule for each cohort provided the most benefit. Notably, mathematically informed drug scheduling can positively impact overall outcome, including using a lower drug dose in some cohorts. Indeed, changing the temporal protocol influenced the dynamics of the system significantly. Interestingly, another melanoma study showed that using unconventional (discontinuous) dosing schedules with BRAF inhibitors could prevent resistance (34). This idea is now being explored in a phase II clinical trial of BRAF-mutant melanoma patients (SWOG: 1320, ClinicalTrials.gov Registry Number: NCT02199730). We submit that the simulation of optimized schedules and comparing outcomes across virtual patients can assist clinical treatment planning to improve overall outcomes (10).

The underlining mechanisms, parameterization and validation of our model were based on data from a preclinical in vitro study. However, as demonstrated by Leder and colleagues, a similar integrated modeling approach can also be achieved using in vivo preclinical studies (35). By assuming that the same mechanisms of therapy response and resistance apply, this study bridged the divide between our in vitro study and the clinic. Although there are a many more potential response and resistance mechanisms in patients, we consider only one (autophagy) that we characterized using our integrated approach of mathematical modeling with in vitro experiments. We also assume that the variability in patients' responses to treatment can be characterized by variability in this autophagy mechanism, although there are certainly more sources of variability including but not limited to the variation in patient age, size and the genetic composition of an individual tumor, and immune responses. Whilst it would certainly be possible to incorporate both additional resistance mechanisms and sources of variability into our model, and given appropriate experimental controls to calibrate and validate our model, ultimately the methodology would be the same, albeit with many more parameters to generate virtual cohorts. What is clear, regardless of the model complexity or cancer system, is that using a validated mathematical model to generate a virtual patient cohort allows us to carry out phase i trials that may improve the safety and efficacy of future phase I-IV trials, as well as patient outcomes.