Abstract
High efficiency isolation of cells or particles from a heterogeneous mixture is a critical processing step in lab-on-a-chip devices. Acoustic techniques offer contactless and label-free manipulation, preserve viability of biological cells, and provide versatility as the applied electrical signal can be adapted to various scenarios. Conventional acoustic separation methods use time-of-flight and achieve separation up to distances of quarter wavelength with limited separation power due to slow gradients in the force. The method proposed here allows separation by half of the wavelength and can be extended by repeating the modulation pattern and can ensure maximum force acting on the particles. In this work, we propose an optimised phase modulation scheme for particle separation in a surface acoustic wave microfluidic device. An expression for the acoustic radiation force arising from the interaction between acoustic waves in the fluid was derived. We demonstrated, for the first time, that the expression of the acoustic radiation force differs in surface acoustic wave and bulk devices, due to the presence of a geometric scaling factor. Two phase modulation schemes are investigated theoretically and experimentally. Theoretical findings were experimentally validated for different mixtures of polystyrene particles confirming that the method offers high selectivity. A Monte-Carlo simulation enabled us to assess performance in real situations, including the effects of particle size variation and non-uniform acoustic field on sorting efficiency and purity, validating the ability to separate particles with high purity and high resolution.
I. INTRODUCTION
Acoustic manipulation can be used in a label-free, non-contact, and non-invasive manner to concentrate,1 assemble in patterns,2–5 and sort6–11 microparticles and living biological cells. This type of manipulation relies on the acoustic radiation force12–15 to drive particles towards the pressure nodes or antinodes of a standing wave acoustic field. Numerous strategies are available to acoustically manipulate and sort microparticles and cells.1,2,4,5,8,11,16–20 For instance, single transducer half-wavelength resonator devices are employed to focus and enrich particles, but are limited to trapping in a fixed defined location within a device.1 Multiple frequencies excitation of a single transducer alleviates the problem of single patterns at the expense of reduced focusing efficiency.21 In multi-transducer bulk devices, the control of the trapping position can either be achieved by a carefully designed matching layer2,4,22 or by calculations of the required phase and amplitude of the transducers' signals,23,24 providing thereby the possibility to pattern any user-specified pattern in 2D25 or even in 3D.26 Surface acoustic wave (SAW) devices offer flexibility, as no matching layer or complex design is required to achieve patterning by frequency or phase control, and such devices can produce one-dimensional,3,5,18,27–32 two-dimensional,3,5,33,34 or three-dimensional35 patterns.
Microparticles introduced in an acoustic field act as scatterers. The incident and scattered acoustic fields result in a second-order time-averaged primary radiation force.12–15,36 The analysis of the acoustic radiation force dates back to the work of King,12 where the treatment of both standing and traveling acoustic fields was carried out on incompressible spheres, much smaller in size than the wavelength of the field, at the Rayleigh scattering limit.15 Yosioka and Kawasima13 extended this discussion by introducing compressibility of the spheres. These results were summarized and reformulated by Gorkov14 and a compact equation for the acoustic radiation force in standing wave fields was provided as a gradient of the acoustic potential. Recently, Settnes and Bruus15 included viscosity of the surrounding media in the analytical treatment and found this contributed significantly to the magnitude of forces arising from travelling waves. Particles generally have positive acoustic contrast factor, and therefore, when subjected to an acoustic standing wave, they experience a force that steers them towards the pressure node.11,15,36 Some materials such as air bubbles and lipid vesicles have density and compressibility values that result in a negative contrast factor, which means that these objects agglomerate at the pressure antinodes.17 Thus, a separation occurs if particles with acoustic contrast factors of different signs are present.16,17
Many acoustic sorting methods achieve particle or cell separation either by travelling waves37,38 or by generating a standing wave field inside the active area of the device.9,39,40 The difference in time-of-flight of particles due to the acoustic-viscous force balance has been utilized for continuous sorting first by the group of Feke41,42 for size-based separation, followed by compressibility-based sorting of particles.43 Increasing the frequency of the field, transducer dimensions and therefore the device size can be reduced and successful sorting can be achieved in microfluidic devices.11,39,44 The Huang group showed that the efficiency of sorting can be increased by inclining the transducer at a specific angle to the flow direction9 and the method was applied for the isolation of circulating tumor cells.45 In recent years, dynamic acoustic approaches, where the time-averaged radiation force changes with time, have gained increasing interest for particle manipulation, and specifically for sorting.46 In its simplest form, the transducers can be switched on/off providing actuation for fluorescence-activated cell sorting (FACS) techniques.47–50 Switching the frequency between normal modes of resonance within a device allows sorting of particles.51,52 This frequency mode switching technique has been further extended from binary separation to multichannel sorting in a surface acoustic wave device.8,53
Phase modulation has been used to align particles at different locations within a microchannel in 1D,27,54 to ultimately achieve cell coculture55 or to move them in a programmable manner in 2D trajectories, such as circular patterns.56 Bernard et al. utilised acoustic streaming combined with phase shifting to obtain translation and rotation of particles and cells.57 Controlling both the transducer power and phase, 3D trapping and translation of cells could be achieved.58 Selective spatial trapping was obtained by pulsed surface waves, where the trap location can be translated using frequency modulation or phase shift.59
The separation of heterogeneous mixtures using phase patterns has been presented for a bulk device,20 by cycling a linear phase modulation to achieve sorting. Initially, the particles are trapped at the pressure nodes before the phase of one transducer is linearly modulated, resulting in a lateral (perpendicular to the flow) movement of the pressure nodes. The particles follow the movement of the nodes, against the viscous force.23 An optimal choice of the rate of phase shift provides separation for particles of different size or density.20 In this way, the time-of-flight of particles can be exploited in phase-modulated fields and the patterning technique27,54 can be extended into sorting. Our method allows the particles to be located at different nodes after separation. The separation distance is half of the wavelength, double that of the quarter wavelength separation distance usually demonstrated by standing SAW or resonator systems.10,16 Furthermore, in these time-of-flight systems, the force distribution varies sinusoidally within the channel, therefore limiting separation power. We demonstrate that by applying a specific phase pattern, the force can be kept maximum for a longer time, promoting sorting. Finally, the terminal particle position can be selected,27 allowing greater flexibility in recovery.
In this paper, we investigate and compare two phase modulation schemes for particle manipulation using an on-chip microfluidic surface acoustic wave (SAW) device. The first modulation scheme straightforwardly cycles the phase linearly from 0° to −360°, while the second method introduces phase jumps at the beginning and the end of the cycle. A novel analytical approach has specifically been developed, which provides the acoustic radiation force and particle trajectories in a surface acoustic wave device. This shows a different form of contrast factor compared with the one in bulk acoustic wave devices due to the combination of the two inclined travelling waves inside the channel. Finally, particle sorting efficiency and purity are computed and compared by investigating how the particle trajectories are affected by the acoustic pressure variations in the microchannel and the tolerance in particle size.
II. MATERIALS AND METHODS
A. Working mechanism for particle manipulation and experimental setup
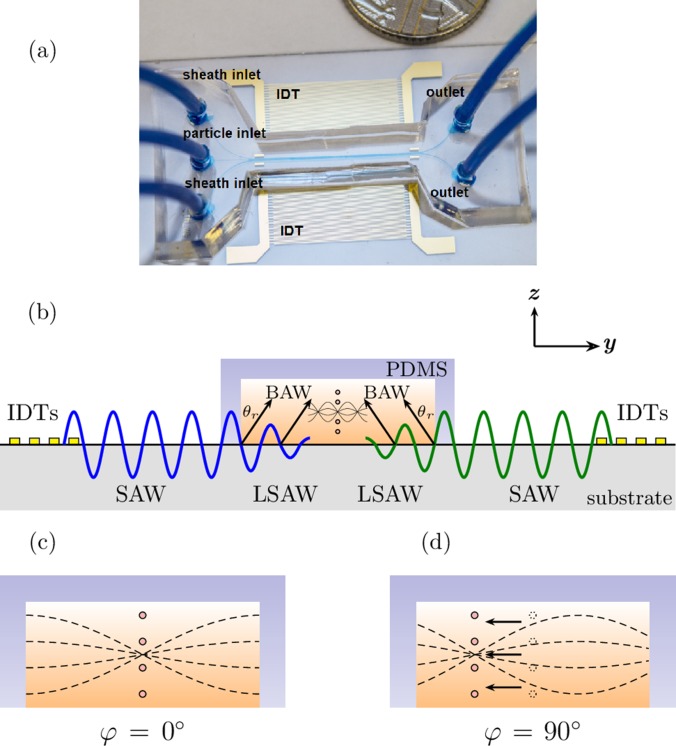
The particle manipulation device using SAWs is shown in Fig. 1(a). The device is built from two identical interdigital transducers (IDTs) with a polydimethylsiloxane (PDMS) microchannel located symmetrically between them.8,11,44,60,61 The mechanism of particle manipulation based on phase-shifting of an acoustic standing wave is illustrated in Figs. 1(b)–1(d). Two sinusoidal electrical signals of the same frequency are applied on the IDTs but they are phase shifted from each other. This configuration generates two counter propagating travelling SAWs on the piezoelectric substrate,18 as shown in Fig. 1(b). When the travelling waves reach the PDMS microchannel filled with a liquid (water), the SAW waves are converted to leaky SAWs (LSAWs) along the surface18,62–66 and two beams of bulk acoustic (longitudinal) waves (BAWs) are thus created in the fluid.18 The horizontal component ky of the BAW wave vector k must be equal to the wavenumber of the surface acoustic wave in order to satisfy the boundary condition at the lithium niobate-water interface.18 Consequently, the BAW propagates with an angle of radiation with respect to the wall, as , called the Rayleigh angle, where cf. and cs are the speed of sound in the fluid and on the surface of the substrate. The two inclined BAW travelling waves interfere with each other and form an acoustic standing wave along the horizontal direction inside the fluid [Fig. 1(b)]. The resulting standing wave field has been utilised to trap microparticles suspended in the medium as illustrated in Fig. 1(c). When the phase of one IDT is changed, the standing wave pattern shifts laterally and microparticles can be translated as shown in Fig. 1(d).
FIG. 1.
(a) The microfluidic manipulation device used in the experiments comprising the lithium niobate substrate with the IDTs and the PDMS microchannel. (b) Schematic showing the operating principle of a SAW device. The transducers create two counter travelling surface acoustic waves that convert into LSAW at the liquid-substrate interface and radiate into the liquid as inclined longitudinal waves. (c) When the phase difference between the two transducers is zero, particles agglomerate at the node. (d) When the phase difference between transducers is changed, the pressure node moves and the particles move along with it. Here, the case for 90° phase difference is shown.
The experimental setup is comprised of the device mounted on printed circuit board, syringe pumps (World Precision Instruments, Sarasota, USA), a signal generator (TG5012A; Aim-TTi, UK), and power amplifiers (ZHL-1-2W+; Mini-Circuits, UK). The appropriate phase pattern and signal parameters were uploaded to the signal generator via a general-purpose interface bus connection using LabView (National Instruments, UK). The device was mounted on a microscope (Olympus BX51; Olympus, UK), and the particle trajectories were recorded with a camera (Orca Flash 2.8; Hamamatsu, UK) at a rate of 80 fps.
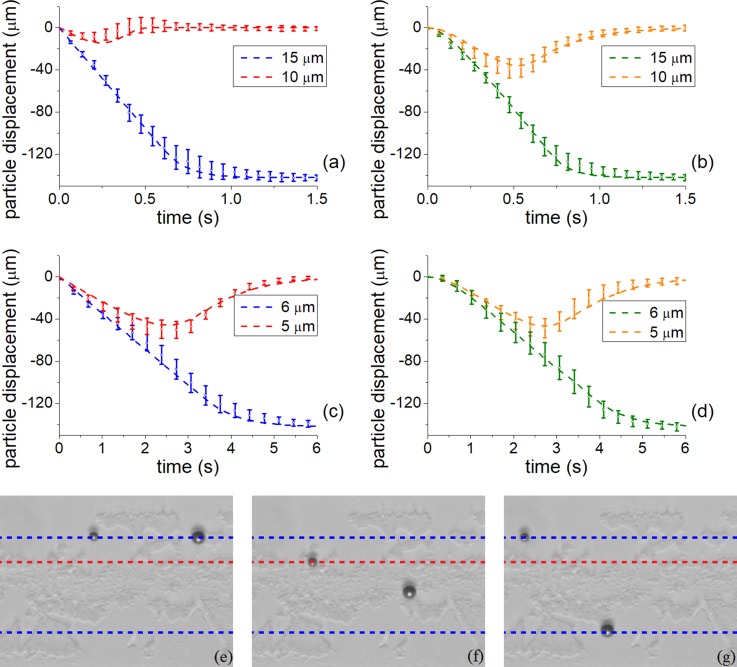
For all the experiments and force measurements, the following initial protocol was performed. The two transducers were activated using a 13.3 MHz, 23 Vpp sinusoidal signal with a phase difference that results in two nodal lines located symmetrically with respect to the center of the channel. The channel had a width of 240 μm, height of 50 μm, and a length of 2 cm, trapping the particles in a single layer in the z direction. The flow was only used to drive the particles into the PDMS channel and to align them at the upper nodal line. The flow was then stopped and the particles stayed trapped at the pressure node. Particle trajectories experiments were carried out for 3 mixtures of two sets of polystyrene particles of diameter 15 and 10, 6 and 4.5, and 6 and 5 μm, respectively, at the concentration of 106 particles/ml. This concentration was chosen to avoid the formation of particle clumps and to have sufficient distance between particles to neglect interparticle forces. Experiments were repeated 10 times for each mixture.
Details concerning the device fabrication and additional geometrical parameters can be found in the supplementary material.
B. Phase-modulated waveform for particle separation
To separate particles by dynamic acoustic phase modulation, the nodes are swept along one direction by a cyclic repetition of the phase shifted excitation pattern applied to the transducers or IDTs.20 The moving nodes generate forces on the particles that are opposed by inertia and viscous forces. This interplay of forces induces different trajectories on different particles and leads, under suitable conditions, to particle fractionation.20,67 In a system where particles agglomerate at the acoustic nodes, only the large particles experience a strong enough acoustic force and will follow the nodes shifting via the modification in phase.
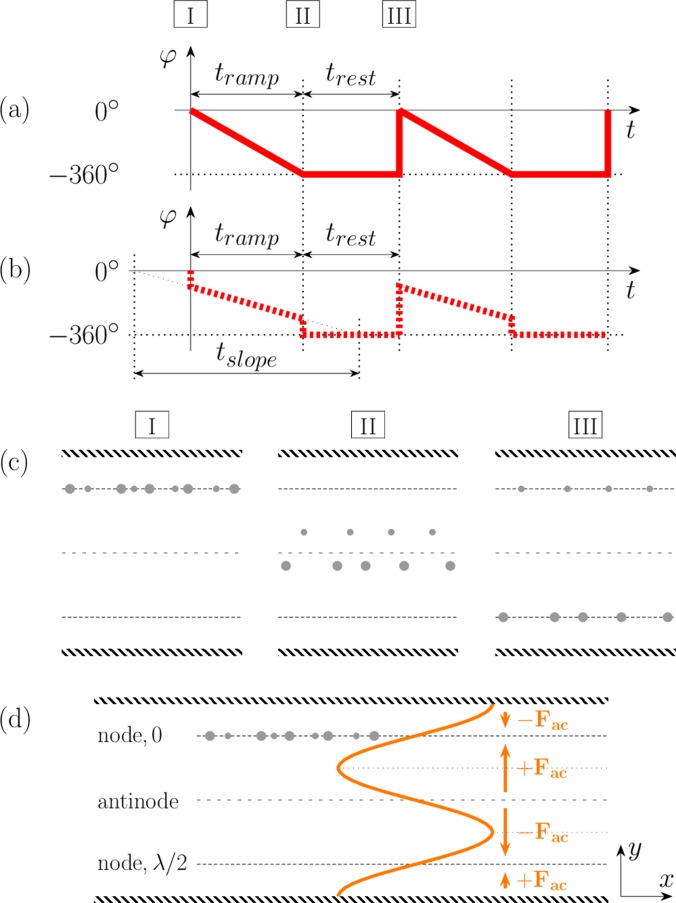
Figure 2 shows two phase modulated signals that are used to separate particles by size. Figure 2(a) shows the case where the phase varies linearly from 0° to −360°, while, in Fig. 2(b), the phase changes from −90° to −270°, during a period denoted by tramp. Changes up to −360° or −450° can also be induced in the second case. A steady zero phase shift period follows for a time duration defined as trest, allowing the particles to relax towards the nearest nodes. In Fig. 2(b), we exploit the sinusoidal spatial variation (of period λ/2) of the acoustic radiation force.5 As illustrated in Fig. 2(c), the acoustic radiation force is zero at the acoustic nodes and antinodes placed at 0, λ/4, λ/2, and 3λ/4, with maximum force amplitudes at λ/8 and 3λ/8. From this, we deduce that a faster sorting can therefore be envisaged by forcing the particles to lag the force pattern by λ/8, experience maximum force, and move at maximum velocity at all times. Since a λ/8 distance corresponds to a 90° phase lag, the phase should be modulated from −90° to at least −270° [Fig. 2(b)]. The time tslope defines the rate of phase shift as .
FIG. 2.
Phase pattern with a modulation (a) from 0° to −360° and (b) from −90° to −270°, illustrating the method as well as the different characteristic times involved. (c) Position of the particles corresponding to time instants I, II, and III in subfigure (a) or (b). (c)/I. Particle trapping at the beginning of sorting. (c)/II. At the end of ramping period, small particles and large particles are located above and below the antinode, respectively. (c)/III. The two types of particles relax to different nodal lines by the end of the resting period. (d) The distribution of the acoustic radiation force (orange curve and arrows) in the microchannel at phase 0°.
C. Analytical particle trajectories
The acoustic radiation force, Fac,y, which is exerted in the direction perpendicular to the axis of the channel, in a surface acoustic wave device due to phase modulated acoustic fields, can be expressed as follows15,27,68 (see details in the supplementary material):
| (1a) |
| (1b) |
| (1c) |
where is the acoustic energy density and ϕ the acoustic contrast factor. R is the particle radius, and ρ0 is the density; p0 is the pressure amplitude; c0 is the speed of sound in the medium, s is the rate of phase shift, and ky and kz are the wavenumbers in the horizontal and vertical direction, . The terms refer to the real part of the constant f1 or f2, respectively.15 The particle size is much greater than the viscous boundary layer thickness;15 therefore, and with and being the compressibility and density ratios of the particle and the fluid. Constants were collected in a single variable cac. Particles with positive contrast factor (1b) agglomerate at the pressure nodes while the particles with negative contrast factor accumulate at the antinodes of the standing wave field.
Importantly, the presence in Fac,y of the scale factor, which is the second term of contrast factor (1b), is the result of the standing wave formed as a combination of the two inclined traveling waves within the PDMS channel. This term does not appear in the expression of the force for a bulk device (details in supplementary material). From the angle of propagation due to the lithium niobate/water interface, this scale factor is . Since the phase modulation is much smaller than the frequency, , the phase directly appears in the force pattern (1a), as shown in supplementary material.
In addition to the acoustic radiation force, the moving microparticles are also subjected to Stokes' drag force,69,70 , where ηmedium is the dynamic viscosity of the fluid and is the relative velocity between the particle and the fluid in the transverse y direction. Solving the differential equation of motion using the inertial approximation,71 the particle trajectories can be described by the exact analytical equation27 (details in the supplementary material)
| (2) |
with and . The constant c1 can be determined from the initial position of the particle. The inverse tangent function is taken to be monotonic during the ramping time, tramp. For the constant phase shift from 0° to −360°, the start of the phase shift is zero (ts = 0). For the phase shift starting from −90°, the start of the phase shift is .
The particle trajectories during the resting time can be described by the simpler equation36
| (3) |
where c2 can be obtained from initial conditions. Since we defined the origin at the position of the pressure nodes, the equation has a negative exponential. Using (2) and (3) appropriately, any particle trajectory can be anticipated for either the continuous phase shift (0° to −360°) or for the −90° phase jump modulations. Wall effects were included in the analytical trajectories by the use of a viscosity correction factor.72
D. Monte-Carlo simulation of particle sorting efficiency and purity
The analytical expression of the particle trajectories allows for fast simulation of particle behaviour in the device as a function of particle size and acoustic energy density. Using a Monte-Carlo simulation, these particle trajectories can be used to calculate a theoretical sorting efficiency and purity within the device.73,74 The number of small and large particles at the upper and lower node is counted at the final point of the trajectories. The sorting efficiency20 and purity20 are defined as
| (4) |
| (5) |
For the energy density, the mean value and standard deviation are taken from the force measurement (technique similar to an already published method,22 details in the supplementary material) results. Particle size mean value and standard deviation are provided in the datasheet. Gaussian distributions are assumed for both energy density and particle size. Particle trajectories are calculated ten thousand times for both the small and large particles. For each case, a new random acoustic pressure and particle radius are chosen according to the Gaussian distributions.
III. RESULTS AND DISCUSSION
A. Analytical simulation and experiments on particle trajectories
The particle trajectories are investigated analytically and experimentally with the two different phase modulation schemes outlined in IIb above. The acoustic radiation force (1) scales with the volume of the particle (R3) and the fluid drag force depends linearly on the particle radius (R). Larger particles experience a higher acoustic radiation force Fac,y, than smaller ones, but only a linear increase in drag force; therefore, under suitable conditions, particles of different sizes can be sorted.75
1. Linear phase modulation: 0° to 360°
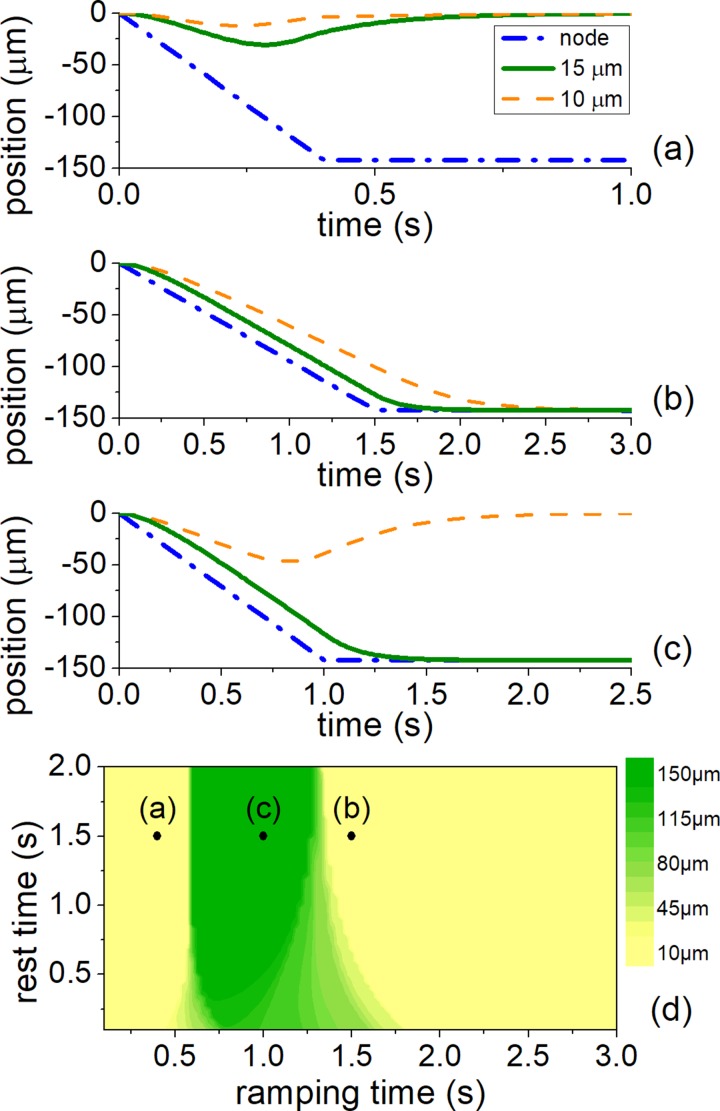
The effect of the ramping time, tramp, was first investigated, as it controls the translational speed of the nodes and therefore has a direct effect on the radiation-viscous force balance and the particle trajectories (Fig. 3). Short ramping times result in fast movement of the nodes. Consequently, the viscous force is high and prevents the particles from following the moving nodes. At the rest time, trest, they have time to relax towards their initial positions [Fig. 3(a)]. For long ramping times, all the particles experience less drag force, follow the slow movement of the nodes and are translated to the next pressure node [Fig. 3(b)]. Only with an intermediate value of the ramping time will the particles of different diameters reach different pressure nodes and be separated [Fig. 3(c)].
FIG. 3.
Effect of different ramping and resting time parameters on 15 and 10 μm polystyrene beads for separation in the linear phase modulation regime. Green solid line and orange dashed line denotes 15 μm and 10 μm particle trajectories, respectively. Blue dash-dot line corresponds to the position of the pressure node. (a) The ramping is fast, resulting in the particles staying at their initial position, (b) The ramping is slow, resulting in the particles translating to the next node, (c) The ramping time is appropriate to achieve sorting, (d) Quality of the sorting for different ramping and resting time for 15 and 10 μm particles, illustrating the three different modulation schemes: fast modulation (a), slow modulation (b), and time modulation allowing separation (c). Yellow color denotes no difference in final particle position (no separation), green color corresponds to λ/2 difference (separation). Intermediate colors correspond to separation distances as shown by the color bar.
The combined effect of ramping and resting times on particle sorting was analysed by simulating the particle trajectories as in Figs. 3(a)–3(c), and the measure of separation was taken as the distance between the two particle trajectories at the end of trest. The main parameter influencing separation is the ramping time. The resting time has no significant effect on particle motion except at small values (<0.7 s).
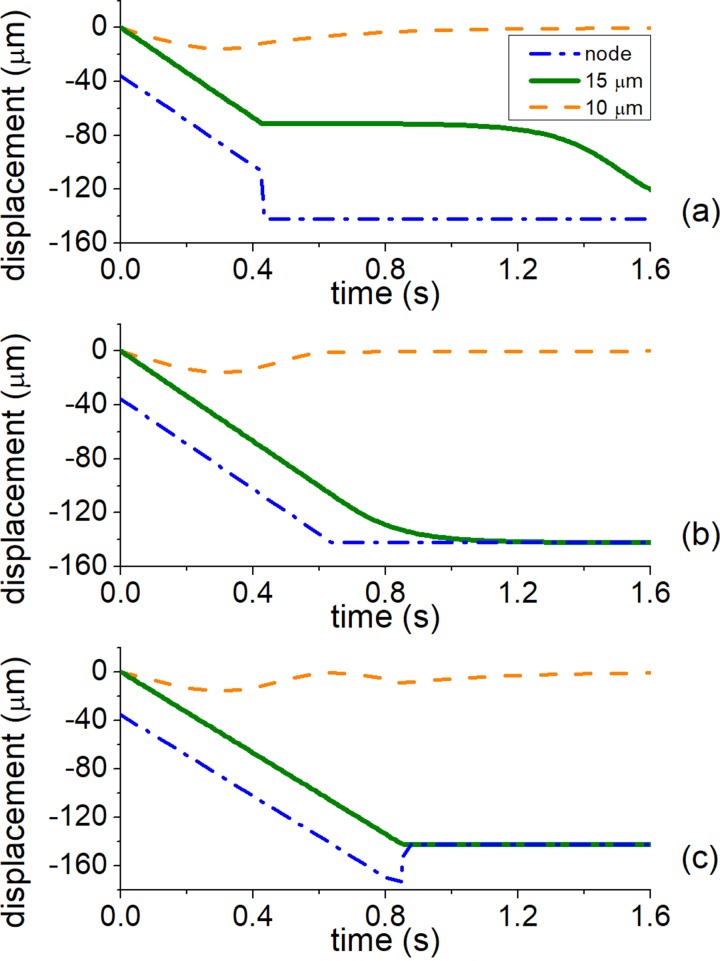
2. Phase jump modulation: −90° to at least −270°
For the phase jump modulation scheme starting at −90° [Fig. 3(b)], the large particles entirely determine tslope. The balance of radiation and viscous forces gives the maximum particle velocity as . Since half-wavelength displacement would happen after phase shift, the slope time can be readily obtained as , where both cvisc and cac are calculated for the large particle. Figure 4 shows the effect of stopping the phase ramp at different phase values, ranging from −270° to −450°, and therefore duration times. For the phase modulation −90° to −270° [Fig. 4(a)], tramp is half of tslope, and therefore, the large particles travel exactly one quarter of the wavelength and are in an unstable state at the antinodes [Fig. 2(c)]. For modulations stopping at −450° or more [Fig. 4(c)], when tramp is at least tslope, although the large particles travel to the next node rapidly (0.85 s), the small particles get displaced by a further 15 μm and require additional time to settle at the node (1.3 s). For a modulation pattern from −90° to −360° [Fig. 4(b)], with ramping time , the sorting is slightly longer (1.1 s) but the small displacement of smaller particles should lead to higher purity.
FIG. 4.
Effect of different modulation times on sorting for 90° phase jump method. (a) The phase is modulated from −90° to −270°, (b) from −90° to −360°, and (c) from −90° to −450°.
3. Experimental particle trajectories and comparison of the two phase modulation schemes
To obtain comparable experimental results, the same value of tramp was used in both phase modulation schemes. Figure 5 compares the analytical and experimental particle trajectories for particles of different diameters and includes micrographs of the separation process. After the particle movement had been recorded, the Tracker software76 was used to obtain the individual particle trajectories. Each data point in Fig. 5 is the average of at least 5 experiments, and the error bars correspond to the standard deviation. We note the excellent agreement between analytical and experimental results for all experiments and particle sizes. When the particle diameter ratio is 1.5 [Figs. 5(a) and 5(b)], the maximum displacement of small particles with the −90° to −360° phase modulation method is up to 60% less than for the 0° to −360° modulation, offering more stable separation. Moreover, the small particles reach their equilibrium position in 0.5 s (instead of 1.3 s), therefore providing shorter possible time scales for sorting applications. Even at a smaller diameter difference (5 and 6 μm), the particles can still be differentiated by both modulation schemes with similar performance [Figs. 5(c) and 5(d)].
FIG. 5.
Experimental and analytically derived particle trajectories for (a) and (b) 15 and 10 μm, and (c) and (d) 6 and 5 μm diameter polystyrene particles. Left column (a), (c) corresponds to jump modulation (−90° to ° to −360°), right column (b), (d) is the continuous linear modulation scheme. Dashed line denotes analytical trajectories, and dots and error bars denote experimental results. (e)–(g) Micrographs showing the separation process for continuous linear modulation scheme for 10 and 15 μm particles, (e) at t = 0 s, (f) after the ramping period, at t = 0.64 s, and (g) at the end of the sorting cycle, t = 1.64 s. Dashed blue lines denote the position of the nodes, and dashed red line shows the maximum displacement of the small particle. Supplementary material video M1 available online.
B. Validation of the analytical equation for particle trajectories
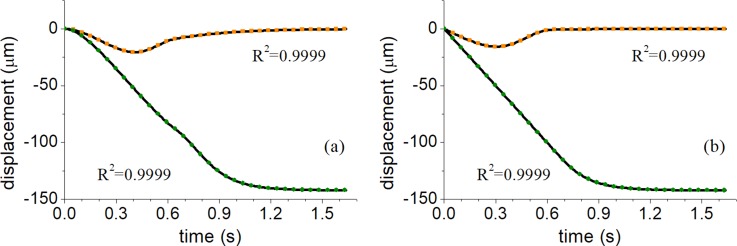
To confirm the validity of the inertial approximation () and the analytical equation of particle trajectories, a comparison with a direct numerical solution was performed. The numerical model implements the Euler-method (details in the supplementary material text) for solving the original differential equation of motion containing also the inertial term . Both the 0° to −360° and the −90° to −360° phase modulations were investigated. The numerical and analytical particle trajectories were generated using the frequency 13.3 MHz and the pressure amplitude 96 kPa, an exhaustive list of used parameters is presented in Table I in supplementary material.
The results of this comparison for 15 and 10 μm polystyrene particles trajectories under linear and jump phase modulations are shown in Fig. 6. Excellent agreement between the numerical and analytical models can be observed (all R2 values above 0.9999), and the difference in position is less than 0.2 μm at any given time, validating the inertial approximation () for phase modulated fields. Therefore, the analytical equations of motion (2) and (3) can be used to generate particle trajectories for phase modulated acoustic fields at high computational speed.
FIG. 6.
Comparison between analytical and numerical models for particle trajectories of 10 and 15 μm diameter polystyrene particles for (a) continuous phase modulation (0° to −360°) and (b) the −90° to −360° phase modulation. Black lines denote the direct numerical solution, and green circles and orange squares correspond to 15 and 10 μm analytical particle trajectories, respectively. List of simulation parameters can be found in supplementary material.
C. Efficiency and purity in particle sorting applications
Making use of the previous validation of the analytical equations and their high computational speed, particle efficiency and purity in sorting applications were further investigated using Monte-Carlo simulations. These simulations attempt to describe real-life experiments in which the particle sizes are not all exactly equal to their normal value. The particle mean sizes and standard deviations are given in Table I.
TABLE I.
Particle properties used in Monte-Carlo simulations.
| Nominal diameter (μm) | Mean diameter (μm) | Standard deviation of diameter (μm) |
|---|---|---|
| 4.5 | 4.52 | 0.15 |
| 5 | 4.97 | 0.06 |
| 6 | 5.9 | 0.29 |
| 10 | 10.1 | 0.7 |
| 15 | 15 | 1.05 |
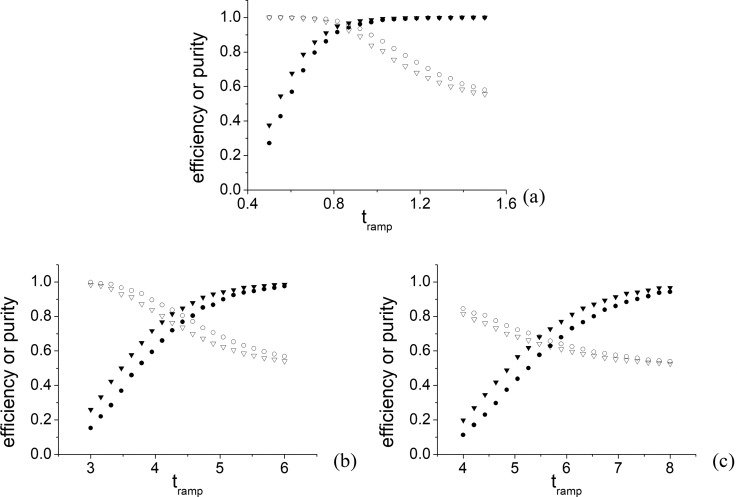
Based on the acoustic radiation force measurements for 23 Vpp input voltage, the mean value of the acoustic pressure amplitude was found to be 96 kPa with a standard deviation of 10 kPa. The simulations were performed for 3 sets of polystyrene particles: 10–15, 5–6, and 4.5–5 μm with particle ratios of 1.5, 1.2, and 1.11, respectively. Ten thousand small and large particle trajectories were analysed for 20 different possible tramp values. Figure 7 shows that with increasing ramping time, efficiency increases, but purity decreases, which is due to an increased number of small particles being transported together with the large particles. Comparing the 0° to −360° and −90° to −360° methods, for lower tramp times (faster sorting), the jump method offers up to 10% better sorting efficiency, with the purity being comparable. For higher tramp times (slower sorting), the linear phase modulation method offers up to 5% better purity while the efficiency remains similar for all particle mixtures. Generally, higher efficiency and faster sorting can be achieved using the −90° to −360° method while the linear phase modulation offers better purity. We can use the value of equal efficiency and purity as an overall figure of merit for establishing sorting. Both 10–15 and 5–6 μm sorting return high values, around 90% and 75%, respectively. Figure 7(c) shows that when the difference is less than 1 μm, the sorting becomes inefficient, as the purity drops significantly compared with the 5–6 μm mixture [Fig. 7(b)]. The overall figure of merit in this case is 65%.
FIG. 7.
Efficiency (filled shapes) and purity (empty shapes) values plotted as a result of a Monte-Carlo simulation of separation via the two modulation methods (continuous – disks, jump – triangles) for particle sets (a) 10 and 15 μm, (b) 5 and 6 μm, and (c) 4.5 and 5 μm.
IV. CONCLUSIONS
In this paper, the primary radiation force and resulting particle trajectories were first investigated theoretically for phase modulated acoustic standing wave fields in surface acoustic wave devices. It was revealed that although behaving similarly to situations in a bulk device, a scale factor appears in the contrast factor of the acoustic force. An inertial approximation allowed the solving analytically of the differential equation of motion opening the way to very fast computational simulations.
Guided by this analytical model for particle trajectories, we devised sorting strategies that allowed efficient separation for differences in particle sizes as small as 1 μm. Interestingly, this approach can enable particle translation over long distances by iterating the shift patterns along a microfluidic channel, in a manner similar to the tilted angle SAW.9 However, in this latter method, the maximum displacement is limited by IDT designs, whereas in our case, it will be limited by the dissipation of the waves within the channel, thus potentially providing a wider capability. These approaches could be used successfully for the fast separation of target entities, such as neuron cells, stem cells, or cancer cells in many areas of research. Due to the tunability of our method, separation of multiple targets present within the same sample could also be performed. This can be enabled either by using different phase shift cycles, including directional control by the sign of the phase shift, or by varying the input power intensity. We are currently investigating separation of sensory neuron cells from heterogeneous biological cell mixture for regenerative medicine.
V. SUPPLEMENTARY MATERIAL
See supplementary material for details on device fabrication, analytical derivations, methodology for numerical integration, and force measurement procedures. The supplementary video shows recordings of particle movements, side-by-side for the two methods, allowing for comparison.
ACKNOWLEDGMENTS
The authors would like to thank Mr. Neil Ross for his help with the cleanroom device fabrication processes. We also would like to thank Dr. William N. MacPherson for access to thermal evaporator equipment.
A.B. acknowledges the support from Heriot-Watt University. J.C. acknowledges the support from an EPSRC Personal Fellowship (EP/K027611/1) and an ERC Advanced Grant Bio Phononics (340117). J.R. acknowledges the University of Glasgow Lord Kelvin and Adam Smith Research Fellowship.
References
- 1. Lenshof A., Ahmad-Tajudin A., Jaras K., Sward-Nilsson A. M., Aberg L., Marko-Varga G., Malm J., Lilja H., and Laurell T., Anal. Chem. 81, 6030 (2009). 10.1021/ac9013572 [DOI] [PubMed] [Google Scholar]
- 2. Bernassau A. L., Gesellchen F., Macpherson P. G., Riehle M., and Cumming D. R., Biomed. Microdevices 14, 559 (2012). 10.1007/s10544-012-9633-z [DOI] [PubMed] [Google Scholar]
- 3. Ding X., Shi J., Lin S. C., Yazdi S., Kiraly B., and Huang T. J., Lab Chip 12, 2491 (2012). 10.1039/c2lc21021e [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4. Gesellchen F., Bernassau A. L., Dejardin T., Cumming D. R., and Riehle M. O., Lab Chip 14, 2266 (2014). 10.1039/C4LC00436A [DOI] [PubMed] [Google Scholar]
- 5. Shi J., Ahmed D., Mao X., Lin S. C., Lawit A., and Huang T. J., Lab Chip 9, 2890 (2009). 10.1039/b910595f [DOI] [PubMed] [Google Scholar]
- 6. Adams J. D. and Soh H. T., Appl. Phys. Lett. 97, 064103 (2010). 10.1063/1.3467259 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7. Agarwal G. and Livermore C., Lab Chip 11, 2204 (2011). 10.1039/c1lc20050j [DOI] [PubMed] [Google Scholar]
- 8. Ding X., Lin S. C., Lapsley M. I., Li S., Guo X., Chan C. Y., Chiang I. K., Wang L., McCoy J. P., and Huang T. J., Lab Chip 12, 4228 (2012). 10.1039/c2lc40751e [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9. Ding X., Peng Z., Lin S.-C. S., Geri M., Li S., Li P., Chen Y., Dao M., Suresh S., and Huang T. J., Proc. Natl. Acad. Sci. U.S.A. 111, 12992 (2014). 10.1073/pnas.1413325111 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10. Ren L., Chen Y., Li P., Mao Z., Huang P. H., Rufo J., Guo F., Wang L., McCoy J. P., Levine S. J., and Huang T. J., Lab Chip 15, 3870 (2015). 10.1039/C5LC00706B [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11. Shi J., Huang H., Stratton Z., Huang Y., and Huang T. J., Lab Chip 9, 3354 (2009). 10.1039/b915113c [DOI] [PubMed] [Google Scholar]
- 12. King L. V., Proc. R. Soc. London, Ser. A 147, 212 (1934). 10.1098/rspa.1934.0215 [DOI] [Google Scholar]
- 13. Yosioka K. and Kawasima Y., Acta Acust united Ac. 5, 167 (1955). [Google Scholar]
- 14. Gor'kov L. P., Sov. Phys. Dokl. 6, 773 (1962). [Google Scholar]
- 15. Settnes M. and Bruus H., Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys. 85, 016327 (2012). 10.1103/PhysRevE.85.016327 [DOI] [PubMed] [Google Scholar]
- 16. Petersson F., Nilsson A., Holm C., Jonsson H., and Laurell T., Analyst 129, 938 (2004). 10.1039/B409139F [DOI] [PubMed] [Google Scholar]
- 17. Petersson F., Nilsson A., Holm C., Jönsson H., and Laurell T., Lab Chip 5, 20 (2005). 10.1039/B405748C [DOI] [PubMed] [Google Scholar]
- 18. Shi J., Mao X., Ahmed D., Colletti A., and Huang T. J., Lab Chip 8, 221 (2008). 10.1039/B716321E [DOI] [PubMed] [Google Scholar]
- 19. Bernassau A. L., Courtney C. R. P., Beeley J., Drinkwater B. W., and Cumming D. R. S., Appl. Phys. Lett. 102, 164101 (2013). 10.1063/1.4802754 [DOI] [Google Scholar]
- 20. Skotis G. D., Cumming D. R., Roberts J. N., Riehle M. O., and Bernassau A. L., Lab Chip 15, 802 (2015). 10.1039/C4LC01153H [DOI] [PubMed] [Google Scholar]
- 21. Glynne-Jones P., Boltryk R. J., Harris N. R., Cranny A. W., and Hill M., Ultrasonics 50, 68 (2010). 10.1016/j.ultras.2009.07.010 [DOI] [PubMed] [Google Scholar]
- 22. Courtney C. R. P., Ong C. K., Drinkwater B. W., Bernassau A. L., Wilcox P. D., and Cumming D. R. S., Proc. R. Soc. A: Math., Phys. Eng. Sci. 468, 337 (2011). 10.1098/rspa.2011.0269 [DOI] [Google Scholar]
- 23. Raeymaekers B., Pantea C., and Sinha D. N., J. Appl. Phys. 109, 014317 (2011). 10.1063/1.3530670 [DOI] [Google Scholar]
- 24. Greenhall J., Guevara Vasquez F., and Raeymaekers B., Appl. Phys. Lett. 103, 074103 (2013). 10.1063/1.4819031 [DOI] [Google Scholar]
- 25. Greenhall J., Guevara Vasquez F., and Raeymaekers B., Appl. Phys. Lett. 108, 103103 (2016). 10.1063/1.4943634 [DOI] [Google Scholar]
- 26. Prisbrey M., Greenhall J., Guevara Vasquez F., and Raeymaekers B., J. Appl. Phys. 121, 014302 (2017). 10.1063/1.4973190 [DOI] [Google Scholar]
- 27. Orloff N. D., Dennis J. R., Cecchini M., Schonbrun E., Rocas E., Wang Y., Novotny D., Simmonds R. W., Moreland J., Takeuchi I., and Booth J. C., Biomicrofluidics 5, 44107 (2011). 10.1063/1.3661129 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28. Wood C. D., Evans S. D., Cunningham J. E., O'Rorke R., Wälti C., and Davies A. G., Appl. Phys. Lett. 92, 044104 (2008). 10.1063/1.2838748 [DOI] [Google Scholar]
- 29. Zhou W., Niu L., Cai F., Li F., Wang C., Huang X., Wang J., Wu J., Meng L., and Zheng H., Biomicrofluidics 10, 034121 (2016). 10.1063/1.4954934 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30. Tan M. K., Tjeung R., Ervin H., Yeo L. Y., and Friend J., Appl. Phys. Lett. 95, 134101 (2009). 10.1063/1.3238313 [DOI] [Google Scholar]
- 31. Brunet P., Baudoin M., Matar O. B., and Zoueshtiagh F., Phys. Rev. E: Stat. Nonlinear Soft Matter Phys. 81, 036315 (2010). 10.1103/PhysRevE.81.036315 [DOI] [PubMed] [Google Scholar]
- 32. Ma Z., Guo J., Liu Y. J., and Ai Y., Nanoscale 7, 14047 (2015). 10.1039/C5NR04272K [DOI] [PubMed] [Google Scholar]
- 33. Ding X., Lin S. C., Kiraly B., Yue H., Li S., Chiang I. K., Shi J., Benkovic S. J., and Huang T. J., Proc. Natl. Acad. Sci. U.S.A. 109, 11105 (2012). 10.1073/pnas.1209288109 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34. Wood C. D., Cunningham J. E., O'Rorke R., Wälti C., Linfield E. H., Davies A. G., and Evans S. D., Appl. Phys. Lett. 94, 054101 (2009). 10.1063/1.3076127 [DOI] [Google Scholar]
- 35. Shi J., Yazdi S., Lin S. C., Ding X., Chiang I. K., Sharp K., and Huang T. J., Lab Chip 11, 2319 (2011). 10.1039/c1lc20042a [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36. Bruus H., Lab Chip 12, 1014 (2012). 10.1039/c2lc21068a [DOI] [PubMed] [Google Scholar]
- 37. Cheng I. F., Froude V. E., Zhu Y., Chang H. C., and Chang H. C., Lab Chip 9, 3193 (2009). 10.1039/b910587e [DOI] [PubMed] [Google Scholar]
- 38. Ma Z., Collins D. J., Guo J., and Ai Y., Anal. Chem. 88, 11844 (2016). 10.1021/acs.analchem.6b03580 [DOI] [PubMed] [Google Scholar]
- 39. Jo M. C. and Guldiken R., Sens. Actuators, A 187, 22 (2012). 10.1016/j.sna.2012.08.020 [DOI] [Google Scholar]
- 40. Skowronek V., Rambach R. W., and Franke T., Microfluid. Nanofluid. 19, 335 (2015). 10.1007/s10404-015-1559-3 [DOI] [Google Scholar]
- 41. Tolt T. L. and Feke D. L., Chem. Eng. Sci. 48, 527 (1993). 10.1016/0009-2509(93)80307-C [DOI] [Google Scholar]
- 42. Mandralis Z., Bolek W., Burger W., Benes E., and Feke D. L., Ultrasonics 32, 113 (1994). 10.1016/0041-624X(94)90019-1 [DOI] [Google Scholar]
- 43. Gupta S., Feke D. L., and Manas-Zloczower I., Chem. Eng. Sci. 50, 3275 (1995). 10.1016/0009-2509(95)00154-W [DOI] [Google Scholar]
- 44. Guldiken R., Jo M. C., Gallant N. D., Demirci U., and Zhe J., Sensors 12, 905 (2012). 10.3390/s120100905 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45. Li P., Mao Z., Peng Z., Zhou L., Chen Y., Huang P.-H., Truica C. I., Drabick J. J., El-Deiry W. S., Dao M., Suresh S., and Huang T. J., Proc. Natl. Acad. Sci. U.S.A. 112, 4970 (2015). 10.1073/pnas.1504484112 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46. Drinkwater B. W., Lab Chip 16, 2360 (2016). 10.1039/C6LC00502K [DOI] [PubMed] [Google Scholar]
- 47. Franke T., Braunmuller S., Schmid L., Wixforth A., and Weitz D. A., Lab Chip 10, 789 (2010). 10.1039/b915522h [DOI] [PubMed] [Google Scholar]
- 48. Franke T., Hoppe R., Linsenmann C., and Zeleke K., Open Math. 11, 760–778 (2013). 10.2478/s11533-012-0165-9 [DOI] [Google Scholar]
- 49. Ma Z., Zhou Y., Collins D. J., and Ai Y., Lab Chip 17, 3176 (2017). 10.1039/C7LC00678K [DOI] [PubMed] [Google Scholar]
- 50. Nawaz A. A., Chen Y., Nama N., Nissly R. H., Ren L., Ozcelik A., Wang L., McCoy J. P., Levine S. J., and Huang T. J., Anal. Chem. 87, 12051 (2015). 10.1021/acs.analchem.5b02398 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51. Harris N., Boltryk R., Glynne-Jones P., and Hill M., Phys. Proc. 3, 277 (2010). 10.1016/j.phpro.2010.01.037 [DOI] [Google Scholar]
- 52. Liu Y. and Lim K. M., Lab Chip 11, 3167 (2011). 10.1039/c1lc20481e [DOI] [PubMed] [Google Scholar]
- 53. Li S., Ding X., Guo F., Chen Y., Lapsley M. I., Lin S. C., Wang L., McCoy J. P., Cameron C. E., and Huang T. J., Anal. Chem. 85, 5468 (2013). 10.1021/ac400548d [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54. Jo M. C. and Guldiken R., Sens. Actuators, A 207, 39 (2014). 10.1016/j.sna.2013.12.020 [DOI] [Google Scholar]
- 55. Li S., Guo F., Chen Y., Ding X., Li P., Wang L., Cameron C. E., and Huang T. J., Anal. Chem. 86, 9853 (2014). 10.1021/ac502453z [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56. Meng L., Cai F., Chen J., Niu L., Li Y., Wu J., and Zheng H., Appl. Phys. Lett. 100, 173701 (2012). 10.1063/1.4704922 [DOI] [Google Scholar]
- 57. Bernard I., Doinikov A. A., Marmottant P., Rabaud D., Poulain C., and Thibault P., Lab Chip 17, 2470 (2017). 10.1039/C7LC00084G [DOI] [PubMed] [Google Scholar]
- 58. Guo F., Mao Z., Chen Y., Xie Z., Lata J. P., Li P., Ren L., Liu J., Yang J., Dao M., Suresh S., and Huang T. J., Proc. Natl. Acad. Sci. U.S.A. 113, 1522 (2016). 10.1073/pnas.1524813113 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59. Collins D. J., Devendran C., Ma Z., Ng J. W., Neild A., and Ai Y., Sci. Adv. 2, e1600089 (2016). 10.1126/sciadv.1600089 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60. Nam J., Lim H., Kim C., Kang J. Y., and Shin S., Biomicrofluidics 6, 024120 (2012). 10.1063/1.4718719 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61. Ai Y. and Marrone B. L., Proc. SPIE 8976, 89760O (2014). 10.1117/12.2035952 [DOI] [Google Scholar]
- 62. Frommelt T., Kostur M., Wenzel-Schafer M., Talkner P., Hanggi P., and Wixforth A., Phys. Rev. Lett. 100, 034502 (2008). 10.1103/PhysRevLett.100.034502 [DOI] [PubMed] [Google Scholar]
- 63. Guttenberg Z., Muller H., Habermuller H., Geisbauer A., Pipper J., Felbel J., Kielpinski M., Scriba J., and Wixforth A., Lab Chip 5, 308 (2005). 10.1039/B412712A [DOI] [PubMed] [Google Scholar]
- 64. Tan M. K., Friend J. R., and Yeo L. Y., Lab Chip 7, 618 (2007). 10.1039/b618044b [DOI] [PubMed] [Google Scholar]
- 65. Chen Y., Nawaz A. A., Zhao Y., Huang P. H., McCoy J. P., Levine S. J., Wang L., and Huang T. J., Lab Chip 14, 916 (2014). 10.1039/C3LC51139A [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66. Nilsson A., Petersson F., Jonsson H., and Laurell T., Lab Chip 4, 131 (2004). 10.1039/B313493H [DOI] [PubMed] [Google Scholar]
- 67. Andrade M. A. B., Skotis G. D., Ritchie S., Cuming D. R. S., Riehle M. O., and Bernassau A. L., IEEE Trans. Ultrason., Ferroelectr. Freq. Control 63, 1593 (2016). 10.1109/TUFFC.2016.2608759 [DOI] [PubMed] [Google Scholar]
- 68. Kinsler L. E., Frey A. R., Coppens A. B., and Sanders J. V., Fundamentals of Acoustics ( Wiley, 1999). [Google Scholar]
- 69. Whitworth G., Grundy M. A., and Coakley W. T., Ultrasonics 29, 439 (1991). 10.1016/0041-624X(91)90073-H [DOI] [PubMed] [Google Scholar]
- 70. Woodside S. M., Bowen B. D., and Piret J. M., AIChE J. 43, 1727 (1997). 10.1002/aic.690430710 [DOI] [Google Scholar]
- 71. Bruus H., Lab Chip 12, 1578 (2012). 10.1039/c2lc21261g [DOI] [PubMed] [Google Scholar]
- 72. Leach J., Mushfique H., Keen S., Di Leonardo R., Ruocco G., Cooper J. M., and Padgett M. J., Phys. Rev. E: Stat. Nonlinear Soft Matter Phys. 79, 026301 (2009). 10.1103/PhysRevE.79.026301 [DOI] [PubMed] [Google Scholar]
- 73. Dodson B., Hammett P. C., and Klerx R., Monte Carlo Simulation ( John Wiley & Sons, Ltd, Chichester, UK, 2014). [Google Scholar]
- 74. Prieto J. L., Lu J., Nourse J. L., Flanagan L. A., and Lee A. P., Lab Chip 12, 2182 (2012). 10.1039/c2lc21184j [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75. Rogers P. R., Friend J. R., and Yeo L. Y., Lab Chip 10, 2979 (2010). 10.1039/c004822d [DOI] [PubMed] [Google Scholar]
- 76. Brown D., see http://physlets.org/tracker/ for Tracker, 2017.
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
See supplementary material for details on device fabrication, analytical derivations, methodology for numerical integration, and force measurement procedures. The supplementary video shows recordings of particle movements, side-by-side for the two methods, allowing for comparison.