An Open Benchmark Challenge for Motion Correction of Myocardial Perfusion MRI

Abstract

Cardiac magnetic resonance perfusion examinations enable non-invasive quantification of myocardial blood flow. However, motion between frames due to breathing must be corrected for quantitative analysis. Although several methods have been proposed, there is a lack of widely available benchmarks to compare different algorithms. We sought to compare many algorithms from several groups in an open benchmark challenge. Nine clinical studies from two different centers comprising normal and diseased myocardium at both rest and stress were made available for this study. The primary validation measure was regional myocardial blood flow based on the transfer coefficient (K^trans), which was computed using a compartment model and the myocardial perfusion reserve (MPR) index. The ground truth was calculated using contours drawn manually on all frames by a single observer, and visually inspected by a second observer. Six groups participated and 19 different motion correction algorithms were compared. Each method used one of three different motion models: rigid, global affine or local deformation. The similarity metric also varied with methods employing either sum-of-squared differences, mutual information or cross-correlation. There were no significant differences in K^trans or MPR compared across different motion models or similarity metrics. Compared with the ground truth, only K^trans for the sum of squared differences metric, and for local deformation motion models, had significant bias. In conclusion, the open benchmark enabled evaluation of clinical perfusion indices over a wide range of methods. In particular, there was no benefit of non-rigid registration techniques over the other methods evaluated in this study. The benchmark data and results are available from the Cardiac Atlas Project (www.cardiacatlas.org).

I. Introduction

CARDIAC magnetic resonance (CMR) of perfusion is an accurate diagnostic tool for the quantification of coronary artery disease, with excellent prognostic value [1]. First-pass perfusion MRI measurements typically use a low-weight gadolinium-based contrast agent, which is injected intravenously into the bloodstream. The bolus of contrast agent passes through the right ventricle of the heart, mixing with blood, and after passing through the lungs, arrives in the myocardium via the coronary arteries. These agents have the effect of shortening T1 resulting in higher signal intensity on T1-weighted images. Blood flow can be quantified in absolute units of ml/g/min using indicator dilution theory [2], [3]. For early detection of coronary disease, a pharmacologically induced stress perfusion measurement is required to characterize myocardial perfusion defects. This is typically performed by the administration of adenosine, regadenoson or dipyramidole to induce vasodilation. The myocardial perfusion reserve (MPR), calculated as the ratio of myocardial blood flow at stress versus rest, provides prognostic value in the assessment of suspected cardiovascular disease [4]–[6].

To maximize the contrast between the tissues with and without contrast agent, pulse sequences commonly use magnetization preparation strategies based on either inversion recovery or saturation recovery techniques. While inversion recovery based sequences provide enhanced contrast-to-noise ratio, saturation recovery based sequences enable faster image acquisition [7]. The magnetization preparation is combined with fast imaging sequences such as steady-state free precession or gradient-recalled echo sequences, to ensure that the first-pass of the contrast agent through the myocardium is captured with sufficient temporal resolution. The temporal resolution is often improved further through the use of segmented acquisitions and parallel imaging.

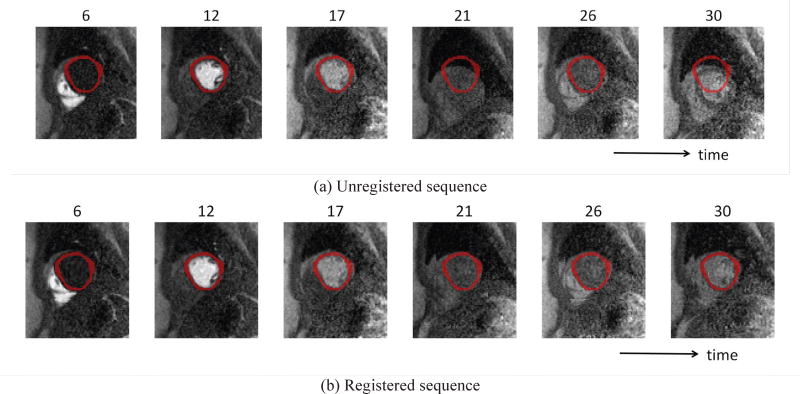
CMR of perfusion is often performed during a single breath-hold (typically up to 40 seconds) to limit movement of the heart within and through the imaging plane. However, patients are often not able to hold their breath for this period of time and involuntary motion of the diaphragm often occurs [8], [9]. Long breath-holds can also cause changes in heart rate, leading to images being acquired at slightly different cardiac phases [10]. Fig. 1a shows examples of motion artifacts caused by breathing.

Fig. 1.

Two sequences of cardiac MR perfusion images: (a) unregistered sequence before motion correction and (b) ground truth registered sequence after manually-based motion correction. Reference masks are shown as an overlay (top: unregistered, bottom: registered). After the 17th frame, motion artifacts caused by breathing start to appear, resulting in contamination of the signal for determination of K^trans.

Motion correction must therefore be performed on the resulting images for accurate and robust quantification of myocardial blood flow. Small changes in the heart location can lead to the region of interest being contaminated by blood in the left ventricle (LV) cavity, resulting in potentially large differences in average myocardial signal intensity. Manually contouring large image sets is a tedious and error-prone process, which can lead to large inter-observer differences. Image registration methods have therefore been proposed to remove this source of error.

Many registration methods assume that the transformation between images is rigid in nature [11]–[13]. While rigid transformations (translation and rotation) are computationally more efficient, robust to noise and provide better consistency, they are limited when capturing the effects of more complex transformations. Motion during these scans is not limited to motion within the plane of the image. Through-plane motion is problematic in 2D scans where the slice thickness is relatively large and the myocardium is undersampled along the long axis of the heart [7]. Three-dimensional sequences are increasingly being investigated to correct these issues [14]. Aside from through-plane motion, rigid techniques do not consider deformations that can occur in the myocardium throughout the first-pass image acquisition. Registration methods that use a global (affine) motions model [15] account for some aspects of the more complex deformations. Non-rigid motion models that account for local deformations [16]–[18] provide better alignment if there is deformation of the heart during breathing, but they are more susceptible to noise and are more computationally intensive.

The performance of a registration technique is not solely dependent on the assumed motion model. Other features such as the interpolation algorithm, the strategy for reference frame selection, and the similarity metric used can all influence the performance. Many registration techniques use similarity metrics based on intensities in the images. Techniques by Bidaut and Vallé [11], and Gupta et al. [12] are based on the sum-of-squared differences metric, which is well-suited to correcting for rotations [19]. Other groups have employed metrics based on normalized mutual information [15], and cross-correlation [12]. Other methods move away from the intensity-based approach and use metrics that assess spatial gradients [20] or independent component analysis [21]. Further, Cordero-Grande et al. [19] have proposed a method using a metric that exploits the variations in the temporal curves.

Despite the wide variety of methods available for motion correction of perfusion CMR, they are still limited in clinical acceptance. Widespread adoption of any technique in the clinical environment requires thorough validation. Xue et al. [15] did a validation study on two registration techniques across a multi-center dataset. They used a combination of qualitative and quantitative measures to assess the performance of the methods, but did not evaluate clinically relevant parameters on this dataset.

We present an open benchmark dataset and comparison of a large number of methods, which was performed as part of a MICCAI 2014 challenge [22]. The main hypothesis was that the use of non-rigid registration techniques on perfusion CMR datasets would yield more accurate estimates of blood flow indices than using rigid registration techniques. We describe the process of data selection and the calculation of ground truth perfusion measures. We then summarize the resulting myocardial blood flow indices generated by the challenge participants. The data and evaluation software will remain open to researchers at the Cardiac Atlas Project website. This resource is made available to allow researchers to compare motion correction methods and evaluate algorithmic improvements in the future.

II. Data and Methods

A. CMR data

Mid-ventricular short-axis first-pass contrast-enhanced CMR slices were selected from nine anonymized patients at both rest and adenosine induced stress conditions (50 frames). Seven cases were diagnosed as normal, one case had an anteroseptal infarction, and one an inferior infarction. All cases were affected to varying degrees by breathing motion. Some cases were included because they displayed significant motion indicative of problematic cases often found in practice. In the stress study of one case, a dark rim artifact along the endocardium was observed. Informed consent from the patients was obtained in accordance with the appropriate institutional review boards.

The image data were acquired at two different centers using different protocols and scanners. Four cases were acquired at the University of Auckland Centre for Advanced MRI, New Zealand, using a Siemens Avanto 1.5T scanner with a Cartesian saturation-recovery gradient-echo sequence. Readout time per slice was 203 ms, echo time 1.08 ms, saturation recovery time 110 ms, flip angle 12 degrees, using 85 phase encoding steps, iPAT factor 2. The acquisitions at rest were performed with a 4 cc/s bolus of 0.04 mmol/kg Omniscan (gadodiamide), followed by infusion of 140 µg/kg/min adenosine and another 4 cc/s bolus of 0.04 mmol/kg Omniscan for the stress acquisition. Imaging was done over approximately 70 heartbeats with the patient instructed to hold their breath for as long as possible. Five cases were acquired at the Utah Center for Advanced Imaging Research, Utah, USA, using a Siemens Verio 3T MRI scanner with a radial saturation-recovery gradient-echo sequence. Readout time per slice was 187 ms, echo time 1.1 ms, saturation recovery time ~100 ms, flip angle 14 degrees, using 72 rays. The acquisitions at rest were performed with a 5 cc/s injections of 0.02 mmol/kg Multihance (Gd-BOPTA). This was followed by an infusion of 140 µg/kg/min adenosine to induce vasodilation, after which a bolus of 5 cc/s Multihance at 0.03 mmol/kg was injected for the stress acquisition. Imaging was done over approximately 70 heartbeats with the patient instructed to breathe shallowly.

B. Reference Region of Interest

For each case, a single frame with high contrast between the myocardium and surrounding tissues was selected manually. The reference region of interest comprising left ventricular myocardium was manually drawn and verified by experts from both Utah and Auckland (see overlaid masks in Fig. 1b). Each reference region of interest was required to completely enclose the myocardium on the high-contrast image, avoid contamination from pixels in the blood pool, and have a thickness of at least 2 pixels at any given point. This frame and contours delineating the reference region of interest were provided to all challenge participants. The reference region of interest was used together with the motion corrected images from all other frames to calculate the pixel intensities at each time point, and thereby quantify myocardial blood flow as described in Section II.E.

C. Ground Truth

For the ground truth creation, a manually-based motion correction method was developed. A single observer manually segmented all frames using ImageJ (ver. 1.48, NIH). Papillary muscles were excluded from the segmented region. In all cases, the reference mask was used as a starting point, which was edited to cover the myocardium on all frames. All image masks were visually inspected for accuracy by a second independent observer.

The perfusion quantification algorithm required images to be registered, so that the pixel locations in each image correspond to the pixel location in the reference frame for each myocardial segment. To provide a ground truth myocardial perfusion estimate, registration was performed on the segmented binary images obtained from the manually drawn contours. First, a translation was performed to eliminate the largest motion caused by breathing. The center of the LV was calculated from the mask and aligned to the reference frame. The first level used nine bicubic Bezier elements, while the finer level used 25 elements.

The resulting transformations derived from this registration were then used to map the corresponding gray scale perfusion images to a common reference frame.

Since the ground-truth registration was performed on binary images from the manual segmentations, no pixels from outside the myocardium contaminated the result. Spurious misregistered boundary pixels on the blood cavity are known to cause signal intensity errors [24]. This is expected to give minimal bias since very different results are obtained from registrations without segmentations.

D. Participating algorithms

Six groups participated in this study with each using diverse motion correction approaches. There was no limitation on what types of approaches to apply. We characterised the participating motion correction algorithms based on their motion model and the choice of similarity metric (Table I). Five algorithms applied rigid transformation, which only consisted of image shifting (translation) and/or rotation. Two algorithms added global affine deformation, which included scaling, shear and stretching. Twelve other algorithms applied different local deformation techniques including B-splines, Bezier curve fitting, elastic matching, or diffeomorphic manifold registration. Two algorithms applied the normalised cross-correlation technique, two methods used mutual information and 15 methods used sum-of-squared differences. These methods are summarized in Table I, with the descriptions of each of the methods in the following sections.

Table I.

List of all methods with a short description

ID	Algorithm name	Registration Type	Similarity Metric	Description
M1	Deformable model-based fit	Local deformation	Cross-Correlation	An iterative model-based registration method based on a compartment model [25]
M2	Rigid model-based fit	Rigid	Mutual Information
M3	AllToOne scheme	Local deformation	Sum-of-squared difference	A package of linear and non-linear 2D + T motion compensation algorithms with different schemes [26]: ICA = Independent Component Analysis, PG = pseudo ground truth, QUASI-P = quasi-periodicity, SERIAL = temporal succession, AllToOne = global one image registration
M4	ICA scheme + affine	Global affine	Sum-of-squared difference
M5	PG scheme + affine	Global affine	Sum-of-squared difference
M6	ICA scheme + affine + B-splines	Local deformation	Sum-of-squared difference
M7	ICA scheme + rotation	Rigid	Sum-of-squared difference
M8	PG scheme + rotation	Rigid	Sum-of-squared difference
M9	ICA scheme + rotation + B-splines	Local deformation	Sum-of-squared difference
M10	ICA scheme + B-splines	Local deformation	Sum-of-squared difference
M11	ICA scheme + translation	Rigid	Sum-of-squared difference
M12	PG scheme + translation	Rigid	Sum-of-squared difference
M13	ICA scheme + translation + B-splines	Local deformation	Sum-of-squared difference
M14	QUASI-P scheme	Local deformation	Sum-of-squared difference
M15	SERIAL scheme	Local deformation	Sum-of-squared difference
M16	Local phase registration	Local deformation	Mutual Information	Motion correction based on local phase features combined with object-based myocardial segmentation [27]
M17	Finite element warping	Local deformation	Sum-of-squared difference	Image registration based on 2D lattice finite element grid deformation [28]
M18	B-Spline Symmetric Normalization	Local deformation	Cross-Correlation	Explicit regularization of symmetric image registration algorithm using B-splines approximation [29]
M19	Multi-level motion correction	Local deformation	Sum-of-squared difference	A joint motion and intensity correction algorithm based on multi-level Gauss-Newton minimization approach [30]

1) M1-M2: Deformable and rigid model-based image registration

In these two methods [25], knowledge about myocardial perfusion was directly applied to create reference images for each time frame, so that rather than having to register all frames to a single reference image, registration could be performed to a reference image specific to each time frame. After pre-processing the images by coarse rigid registration (shifting images between frames with a cross-correlation method), model images were generated by fitting the data to a compartment model [13]. The idea was that the model images reflect contrast changes without motion and these model images can be used as the reference images at each time frame.

A compartment model was described as follows:

$$C_{\mathit{\text{pix}}}(t)=C_{\mathit{\text{input}}}(t)K^{\mathit{\text{trans}}}{e}^{-k_{\mathit{\text{eq}}}t}+{\nu }_p{C}_{\mathit{\text{input}}}(t),$$ (1)

where C_pix(t) represented a curve of signal intensity differences and C_input (t) was the arterial input function from the right ventricle (RV) blood pool. The K^trans and k_ep were the rate constants representing the exchange of contrast agent between plasma and extra cellular space, respectively. The data at each pixel were fitted to (1) using minimization of the chi-squared error with the recorded signal difference curves. The fitted curves were then used to generate the model images.

After model images were generated, two different registration types were performed: diffeomorphic registration with normalized cross-correlation (M1) and rigid registration with mutual information (M2). Both methods were implemented using the Advanced Normalization Tools (ANTS) package [13], [31].

2) M3-M15: Linear and non-linear 2D + T motion compensation algorithms

For this family of methods, various related motion compensation schemes [26] were applied to the cardiac MR perfusion images. These schemes were based on 1) independent component analysis (ICA scheme) to segment the area of interest around myocardium, identify motion and eliminate it, 2) quasi-periodicity (QUASI-P scheme) of free breathing to identify key frames that are closely aligned, 3) temporal succession registration (SERIAL scheme), 4) global registration to a single image (AllToOne scheme) using a localized normalized cross correlation cost function, and 5) pseudo ground truth (PG scheme) where synthetic reference images are used to compensate motion. Three different linear transformation spaces were also investigated: translational (rigid), affine (global affine) and translation + rotation (rigid). Additionally, a non-linear transformation was also investigated based on B-splines.

This set of algorithms produced 13 different combinations of motion correction methods:

• AllToOne scheme (M3)

• ICA schemes:

  • Using affine transformation (M4)

  • Using translational transformation (M11)

  • Using rigid transformation (M7)

  • Using B-splines transformation (M10)

  • Using affine + B-splines transformations (M6)

  • Using rigid transformation with B-splines (M9)

  • Using translational transformation with B-splines (M13)

• QUASI-P scheme (M14)

• SERIAL scheme (M15)

• Pseudo ground truth (PG) schemes:

  • Pre-linear registration using ICA and affine transformation (M5)

  • Pre-linear registration using ICA and rigid transformation (M8)

  • Pre-linear registration using ICA and translational transformation (M12)

Complete descriptions of each scheme, transformation and cost function are detailed in [26], and the software implementation used for the challenge is available as free software [32].

3) M16: Phase-based registration for automatic perfusion analysis

This approach calculated the motion field using local phase, which represents image features such as edges and lines but is invariant to their magnitude. The local phase was calculated by using the intensity-invariant algorithm based on the Fourier Shift Theorem [16]. Spatial differences were then determined by estimating the voxel-wise difference in the local phase between two images.

For this motion correction study, a pipeline was constructed consisting of three processing steps: 1) pre-processing to remove outliers and to detect the location of the left ventricle automatically, 2) in-plane motion correction based on local phase, and 3) myocardial segmentation based on the object-base image analysis segmentation approach proposed in [33]. Motion was corrected by maximum intensity projection on the temporal perfusion series with the mutual information criteria. The result was a local deformation correction algorithm, (see details in [27]).

4) M17: Non-linear consecutive finite element model warping

This algorithm was based on a finite element model (FEM) formulation where 2D grid lattice was deformed to match image features following the movement of wall motion [23]. To avoid problems in strong intensity contrast changes during the uptake and washout of the contrast agent, the warping method was applied consecutively between successive image frames, starting from the reference frame. First, a coarse rigid registration was performed to remove the most severe breathing artifacts by using Canny edge detector and sum-of-squared difference function. A regular 2D lattice grid was then constructed by using bi-cubic Bezier basis function for the FEM. The grid deformation was performed by a non-rigid transformation by minimizing the sum-of-squared pixel intensity differences:

$$E=\sum _{p\in I_0}{w}^2(p){(I_0(p)-I_0^t(p))}^2$$ (2)

where $I_0^t(p)=I_t(p+u(p))$ denotes a registration of image I_t to I₀ at pixel p after a deformation function u. The coefficient w defines an image to locally control weighting in the image. Sobolev regularization was used to control the smoothness of the resulting deformation [28].

5) M18: B-Spline Symmetric Normalization (SyN)

This method used Symmetric Normalization (SyN), a registration method based on explicit symmetrisation of Large Deformation Diffeomorphic Metric Mapping (LDDMM) [34], which computes the geodesic solution between image pairs in the space of diffeomorphisms. A variation of SyN, which uses B-splines as smoothing kernel, was introduced in [29]. In this study, B-Splines SyN was applied for cardiac motion correction with a small adjustment in which registrations were made between successive image frames, starting from the reference frame. To improve the correction results, preprocessing steps were performed to the input images that included bias correction to minimize low frequency intensity variation artifacts, noise reduction filtering and a Laplacian-based edge-detection algorithm. The framework was made available through the Advanced Normalization Toolkit (ANTS) as described in [31], [35]. Since LDDMM is a deformable registration technique, this approach was a non-rigid correction method.

6) M19: Joint multi-level image registration and intensity correction algorithm

This method used a non-rigid joint motion and intensity correction algorithm, introduced in [36]. This algorithm integrates changes in intensity to compensate motion artifacts. Let I,I₀ ∈ ℝ^d be a template and reference image, respectively. The motion correction algorithm can be summarized as a minimization approach to the following objective function:

$$J=\underset{w}{\text{arg min}}D(T(I)+w,R)+\alpha S(I-I_0)+\beta Q(w)$$ (3)

where D : ℝ^d × ℝ^d → RRR is the sum-of-square distance function to measure dissimilarity between two images, T: ℝ → ℝ^d is an image transformation function, S: ℝ^d → ℝ and Q: ℝ → ℝ are both regularization operators on the transformed image with weight α and on parameter w with weight β, respectively. Elastic regularization [37] was used for S, while the total variation [38] penalty function was applied for Q. The key ingredient of this algorithm was to embed an intensity correction image w ∈ ℝ^d as a parameter in the minimization algorithm. Equation (3) was then solved using a Gauss-Newton approach in different levels of displacement grids. For each pair of images, this approach yielded not only a non-rigid displacement field, but also an intensity correction image simultaneously [30].

E. Evaluation Metrics

Although many evaluation metrics are possible, this study focused on clinical absolute measures of perfusion (ml/g/min), which have been shown to be more robust than relative or surrogate indices such as time-to-peak or up-slope gradient [39]. Since the calculation of perfusion only requires motion corrected images, many methods do not calculate contours on the images. Thus, contour-based distance metrics traditionally used to evaluate segmentation error, such as the Dice metric and Hausdorff distance, cannot be used in this application.

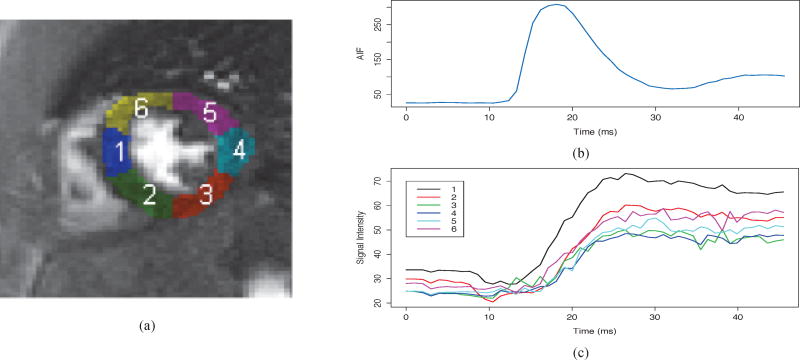
Perfusion measures were extracted using a two-compartment model, as described in [13]. The reference contour region of interest was applied to the registered dataset to create tissue intensity curves for six equiangular myocardial regions. The regions were defined using the centroid of the contours as the center of the left ventricle short-axis slice. Regions were assigned numbers in an anti-clockwise fashion with the boundary of the first region located at the manually-marked anterior insertion of the right ventricle (Fig. 2).

Fig. 2.

Figure (a) shows myocardial blood flow perfusion divided into six regions: 1) anteroseptal, 2) inferoseptal, 3) inferior, 4) inferolateral, 5) anterolateral and 6) anterior. Figure (b) shows the arterial input function and (c) shows the tissue intensity curves from each region.

An arterial input function (AIF) was required for the perfusion model to indicate the characteristics of the contrast agent bolus entering the tissues. Voxels located within the endocardial contour with signal intensity between 85–95% of the maximum were averaged to determine the AIF [40]. The use of a large contrast bolus, as was used in this study, resulted in saturation effects that cause the peak intensities of the AIF to be underestimated. Saturation correction was applied to the AIF in all cases prior to calculation of perfusion measures. The non-saturated AIFs were determined from the measured AIF using previously described techniques [40], [41].

In addition to the saturation correction, the tissue intensity curves and AIFs were corrected to more accurately represent the changes in gadolinium concentration in the tissues (see Fig. 2). The frames prior to contrast agent uptake were averaged to estimate the pre-contrast signal. The number of frames used to determine pre-contrast signal depended on whether the study was performed at stress or rest, owing to differences in the rate of contrast agent uptake The resulting signal difference curves were fit to the extended Kety-Tofts model (Equation (1)) and the K^trans parameter reported as the perfusion index (in units of ml/g/min). MPR was calculated as the ratio of K^trans at stress to rest.

In addition to the K^trans parameter, we also sought to evaluate a metric that does not rely on the pharmacokinetics of perfusion quantification. Therefore we computed the RMSE of tissue intensity curves between the manual and automated analysis from all regions of myocardium. Since some methods could shift the curves temporally, the metric was performed after matching two time intensity curves using the Dynamic Time Warping method [42], which is denoted by intensity curve dissimilarity in this paper.

F. Statistical analysis

In this study, we are interested to know if there are differences between motion correction algorithms based on their motion model and the similarity metric used to match two images. We performed the non-parametric Kruskal-Wallis tests for differences due to motion model or similarity metric.

To compare perfusion values (K^trans and MPR) with the ground truth estimates, we performed non-parametric Wilcoxon signed-rank tests between each method and the ground truth. Mauchly’s sphericity test was applied to assess the dispersion of K^trans biases between rest and stress studies. The correlations of the K^trans values for each method with the ground truth were assessed using Pearson’s correlation coefficient. We computed the root mean squared errors (RMSE) of K^trans values to assess each method’s biases. All the statistical analyses were calculated by using R [43], accompanied with the Companion to Applied Regression (CAR) package [44], the multicomp package for multiple comparison test [45] and the Dynamic Time Warping package [46].

III. Results

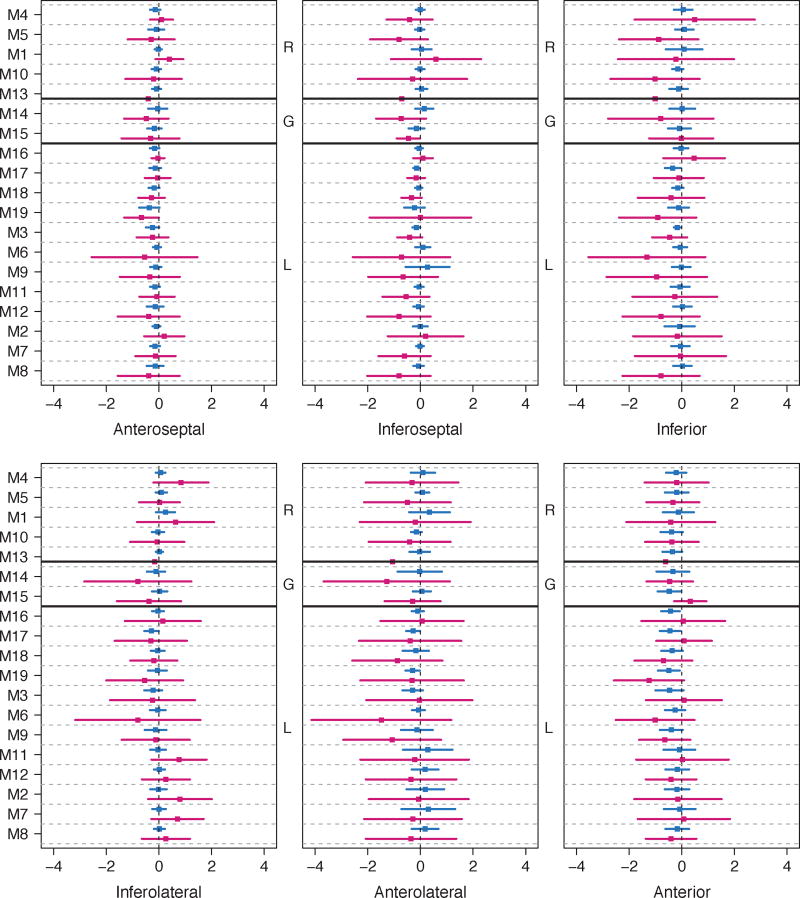
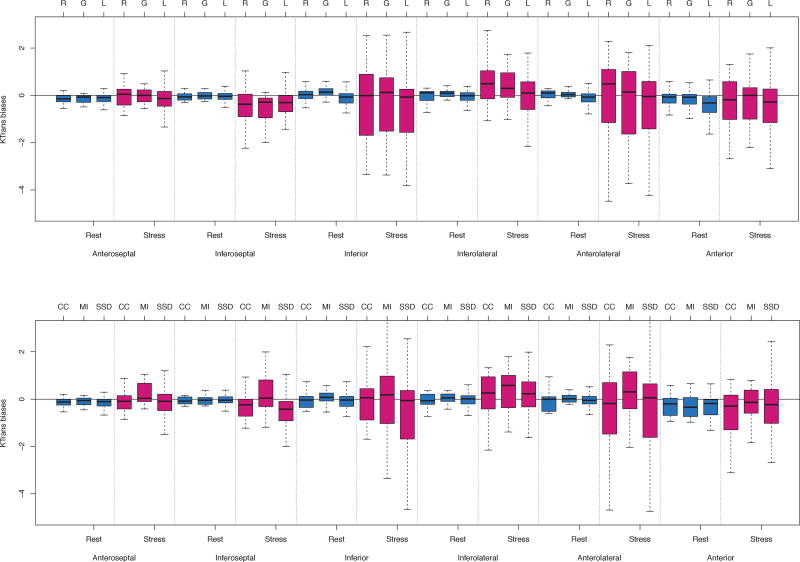
The average of K^trans, MPR, curve dissimilarity and the biases from ground truth, grouped based on motion models and similarity metrics, are shown in Table II. We found no significant differences comparing K^trans values at rest and stress, and MPR values among different motion models, or among different similarity measures. However, there were significant differences in K^trans biases for local deformation (p<0.05) and for sum-of-squared differences metric (p<0.05) in both rest and stress. For intensity curve dissimilarity, there were no significant differences. Individual performance of all methods in determining K^trans per region is shown in Fig. 3 in terms of biases, while the distributions are shown in Fig. 4. The K^trans biases for each method differed significantly with the general trend being that the methods faced more difficulty in correcting motion artifacts at stress than at rest. Mauchly’s test showed a violation of sphericity against contrasts spanned by studies (rest and stress) and the methods (W=9.1e-67, p<0.001). This means that there was a highly significant difference in the dispersion of regional K^trans biases between rest and stress. Regionally, there were no significant differences between motion model methods, except in the inferolateral region (p<0.05) for stress studies. For regional comparison between similarity metrics, we found no significant differences for either rest or stress studies.

Table II.

Comparisons of K^TRANS, MPR, intensity curve dissimilarity measured by Dynamic Time Warping, and biases from the ground truth, grouped by registration types and registration metrics; values represent the average (standard deviation)

	Ktrans		MPR	Bias			Curve dissimilarity
	Rest	Stress		KtransRest	Ktrans Stress	MPR	Rest	Stress
Ground Truth	1.39 (0.79)	3.17 (1.78)	2.56 (1.12)	NA	NA	NA	NA	NA
Methods grouped by motion model
Rigid (translation / rotation)	1.37 (0.69)	3.01 (1.63)	2.44 (1.00)	−0.02 (0.26)	−0.16 (0.91)	−0.12 (0.81)	0.31 (0.17)	0.59 (0.39)
Global deformation (affine)	1.37 (0.69)	2.97 (1.71)	2.36 (0.89)	−0.02 (0.19)	−0.19 (0.96)	−0.20 (0.69)	0.31 (0.19)	0.52 (0.35)
Local deformation (spline)	1.25 (0.68)	2.77 (1.50)	2.49 (1.04)	−0.13 (0.22) *	−0.40 (1.09) *	−0.07 (0.86)	0.40 (0.31)	0.65 (0.69)
Methods grouped by similarity metric
Sum-of-squared differences	1.29 (0.67)	2.77 (1.47)	2.43 (1.00)	−0.10 (0.24) *	−0.39 (1.05) *	−0.13 (0.85)	0.36 (0.26)	0.63 (0.62)
Cross-correlation	1.29 (0.71)	3.00 (1.70)	2.59 (1.05)	−0.10 (0.21)	−0.16 (0.90)	0.03 (0.74)	0.43 (0.38)	0.52 (0.38)
Mutual information	1.37 (0.73)	3.30 (2.00)	2.63 (1.08)	−0.02 (0.22)	0.13 (0.92)	0.07 (0.70)	0.33 (0.18)	0.72 (0.49)

^*shows significant difference at p<0.05 with the ground truth for biases.

Fig. 3.

K^trans bias distributions from each myocardial region, shown by mean (squared box) and its standard deviation. Each method shows two distributions for rest (blue) and stress (red). Methods are grouped by rigid (R), global affine (G) and local deformation (L) registration types. The group definitions are listed in Table I.

Fig. 4.

Top: The K^trans bias difference distributions (shown by Whisker’s boxplot) between rigid (R), global affine (G) and local deformation (L) registration algorithms. Bottom: The K^trans bias difference distributions between cross-correlation (CC), mutual information (MI) and sum-of-squared distance (SSD) registration metrics as minimisation criteria. Each figure was grouped by region and rest/stress. The thick horizontal lines inside each box indicate the median values; the boxplot height ranges from the first and third quartiles; and the hinges indicate interquartile ranges.

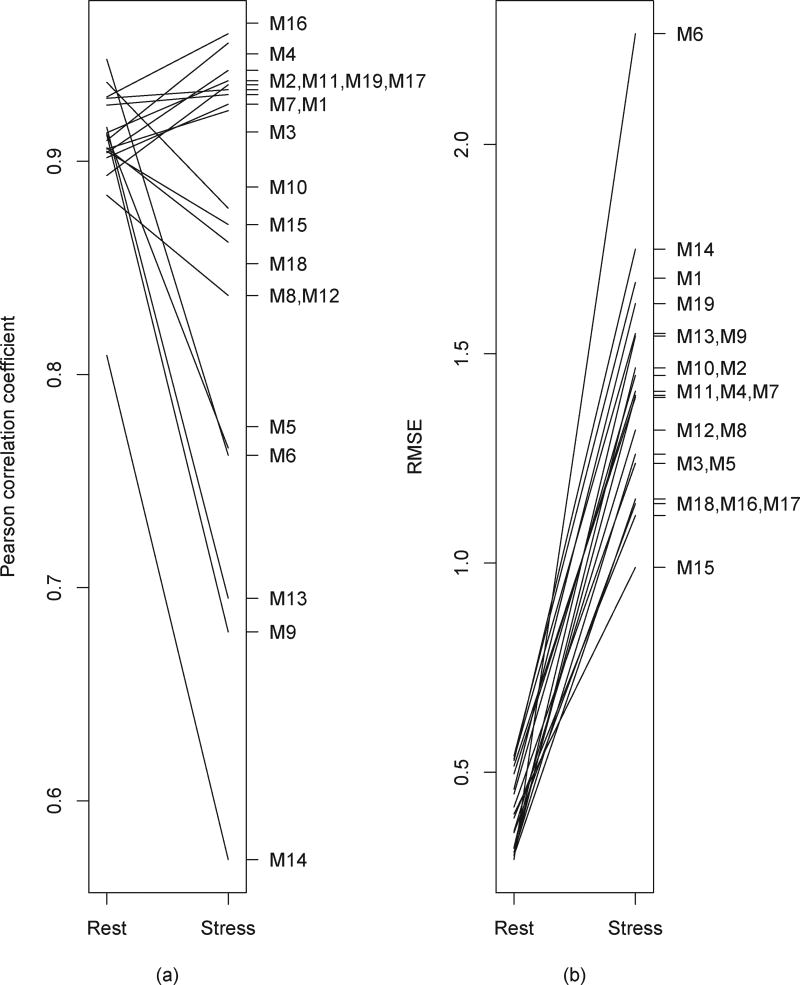
Individual correlations of K^trans determined using each method with the ground truth were all high at rest (R>0.8, all p<0.001). However, half of the methods (52.6%) did not show the same high correlation coefficients of K^trans values in the stress study (Fig. 5a). The differences observed between rest and stress affected the correlation coefficients of the MPR values, which range from 0.38 to 0.93, with an average of R=0.72 ± 0.14. All methods had lower RMSE values when correcting motion during rest as compared with stress. As shown in Fig. 5b, the range of RMSE values during rest was 0.29–0.54, while at stress the range increased to 0.99–2.23.

Fig. 5.

Comparisons of correlation coefficient (a) and RMSE values (b) between rest and stress studies for each method.

IV. DISCUSSION

Each of the cases showed some motion throughout the frames captured during the CMR acquisition. This motion was particularly problematic when the heart was under adenosine-induced stress, where the ability of the patient to breathe shallowly or to maintain a breath-hold for the duration of the first pass of contrast agent was most compromised. Image registration methods are used to correct for the misregistration resulting from motion between images acquired at different time points. Motion-corrected datasets can subsequently be used for the automated quantification of myocardial perfusion measures, such as K^trans and MPR. The registration methods used in this study should correct for the motion that is observed during a perfusion CMR acquisition. However, they act on a single slice and do not account for motion through the plane of the image, where portions of the heart outside of the slice move into the imaging slice or vice versa. Such motion will likely lead to errors in the estimated perfusion since the tissue imaged is different across time.

The small regions of interest in the myocardium, coupled with the fact that neighboring blood or lung tissues have very different properties, means that any small errors in registration could result in contamination of the signal intensity curve. Contamination with lung tissue will cause the measured signal to be hypointense, resulting in the perfusion and K^trans being underestimated. Similarly, contamination of the region of interest by hyperintense pixels in the blood pool will likely result in overestimation of tissue perfusion in the myocardium.

The accurate representation of the frame where the tracer first enters the myocardium is particularly important in quantifying K^trans [47]. In these early frames immediately following the bolus injection, accurate registration is challenging since there is little or no contrast agent in the myocardial tissue. The low signal in the myocardium makes it difficult to distinguish from neighboring regions such as the lungs and the unenhanced ventricular blood. This effect is most likely to be seen in the free wall of the LV, resulting in difficulties for algorithms to effectively track the wall motion. When the heart is under stress and the heart rate is increased, the patient will likely have a compromised ability to control their breathing throughout the duration of the scan, further exacerbating the problems with motion correction.

The results show that the RMSE for the cases at stress were consistently higher than equivalent cases at rest (Fig. 5b). The variance of biases seen in stress was much larger than at rest (p<0.001). At stress, almost all methods had difficulty in correcting motion in the inferoseptal, inferior and anterolateral regions as compared to the other regions (Fig. 4). This effect is most evident in regions of the myocardium where the image features that are exploited to register motion, such as high-contrast tissue boundaries, are not present.

A. Is non-rigid registration helpful?

Registration is likely to perform best when correcting for small changes in shape and location. Other studies have indicated that non-rigid techniques that exploit local deformations may provide more accurate quantification than other methods [7]. We did not find significant differences between motion models; however this result may be affected by confounding factors including sequential and reference based registration, the influence of interpolation and the registration metric used. We also found that local deformation methods produced small but significant biases with respect to the ground truth. There was large variation of the K^trans biases within the non-rigid methods, particularly for stress studies. As shown in Fig. 3, the methods using rigid registration and global affine techniques performed consistently better than those using local deformation in the rest cases. In the stress cases however, the distributions of the K^trans biases seen with some of the rigid methods were wider than some of the local deformation methods. The variable performance of these rigid techniques suggests that there was substantial motion in some of the stress cases. The methods that maintained high K^trans correlation coefficients for both rest and stress cases were M1–4, M7, M11, M16, M17, M19 (see Fig. 5a).

When used clinically, the purpose of perfusion CMR is to establish deficits in perfusion when the heart is under stress as compared to rest. The MPR is the index used for assessing this deficit. The MPR is the ratio of the perfusion at stress to the perfusion seen at rest over the myocardium. We found that there was no significant difference between all registration methods. The smallest MPR biases were shown by methods applying local deformation methods. Ultimately, the clinical application of any of the techniques investigated in this study will require independent validation. Animal models [48] and comparisons with invasive techniques [49] have been used for validation of MR-based cardiac perfusion techniques previously. Alternatively, the use of simulated benchmarks and phantoms would be very useful for validation [50]

B. Metrics used for image registrations

We investigated the differences of motion correction algorithms using different minimisation criteria to match two images. Three approaches were used: cross-correlation (2 methods), mutual information (2 methods) and sum-of-squared differences (15 methods). Although sum-of-squared differences is the most popular choice, methods using sum-of-squared differences produced significant biases, while cross-correlation and mutual information methods did not show any significant differences with the ground truth. K^trans values estimated using sum-of-squared differences were significantly lower in stress studies compared to cross-correlation and mutual information. Although the methods using sum-of-squared differences show a significant bias as compared to ground truth, these methods differ in the motion model used. The local deformation model used in many of these methods also shows a significant bias. Future work should include experiments designed to specifically isolate these effects.

C. The influence of reference images and interpolation

In addition to the motion model and the similarity metric used, there are number of factors which could be investigated in the future using an open benchmark. While such analyses are beyond the scope of the current paper, we note that methods could be further characterized according other aspects of the registration method, such as the interpolation strategy, and the treatment of the reference frame.

The methods evaluated in this study used different strategies for interpolation. The majority of the locally deformed models used splines to interpolate the data following registration. Other methods used techniques such as Bezier curves (M17). The choice of interpolation strategy would influence the overall accuracy of the registration, especially at the high-contrast interfaces around the myocardium. Partial volume effects may result in blurring at these interfaces, with the nature of the blurring depending on the interpolation.

For the ground truth data, the reference frame was determined manually based on a frame with high contrast between myocardium and the surrounding tissue. Most of the methods registered all other frames to this specific reference frame. However, there were two other approaches used by some methods: 1) using the pre-defined reference mask to register the adjacent frame and sequentially shifting the reference mask to register subsequent frames (M17, M18), and 2) using knowledge about the myocardial perfusion to create synthetic, knowledge-based reference images (M1, M2).

Using a sequentially adapted reference mask avoids sudden pixel intensity changes around the myocardial border when the contrast enters the left ventricle. This strategy may be particularly useful for registration of a deforming object, but there were no significant differences in both K^trans and MPR calculations between reference-based and sequential image registration (M17, M18). Also, no significant differences were found with knowledge-based reference image registration methods (M1, M2). The idea of generating reference images specific to each time frame using a compartment model is promising and could avoid the accumulated errors that are possible when using a sequential reference.

D. Regional K^trans estimations

In Table II, non-rigid and rigid methods do not show significant differences to estimate global K^trans values, except that non-rigid slightly underestimated K^trans values at rest. No significant differences were found if we compared the K^trans bias. However, regional distribution of K^trans biases show slight variations between rigid and non-rigid methods as depicted by Fig. 4. K^trans bias median values of inferolateral and anterolateral regions at stress for non-rigid methods are smaller than rigid methods. Statistically, there is only one region (inferolateral at stress) with significant difference (p<0.05) of K^trans bias distribution between rigid and non-rigid methods. In the inferoseptal region, the variance of K^trans errors of non-rigid methods is smaller than rigid methods. This indicates that non-rigid methods can be helpful to reduce the K^trans errors under stress condition in some regions.

E. Limitations

The number of cases was limited, with seven healthy subjects and two patients, acquired with two different imaging protocols. Although this was designed to test a variety of methods against a mixture of image acquisitions, more cases would be needed to evaluate benefits of different image acquisition protocols or the ability to identify disease. Each image was acquired at approximately the same time point in the cardiac cycle, and thus the motion artifacts seen in the data were only those resulting from breathing motion, which may be more severe in patients. Also, to some extent, the presence of coronary artery disease may affect the behavior of a motion correction algorithm due to regional myocardial perfusion defects. The effect of perfusion defects requires further study by expanding the benchmark data set to include additional diseased cases.

The compartment model is only one measure of perfusion, and a variety of quantification methods are possible [51]–[53]. It is possible that the conclusions could be different with different pharmacokinetic models. Further, the cases used in the study only contained a single, mid-ventricular slice. To fully assess the clinical relevance of any differences between the types of motion correction algorithms, basal and apical slices would need to be included in the analysis. Finally, ground truth from several independent observers would enable quantification of variation in the ground truth.

V. Conclusions

Motion correction is an important pre-processing step before accurate and robust quantification of myocardial perfusion analysis. The aim of this work was to provide a multi-center benchmark dataset of cardiac MR perfusion images for testing motion correction algorithms, and compare a large number of algorithms. This study shows that there was no benefit to apply local deformation to reduce bias among the methods compared, although some local deformation methods may improve precision at stress. However, all methods were able to quantify the myocardial perfusion reserve values comparable to the ground truth estimates, regardless the registration approaches or the metrics to minimise the registration process. In the future, this work can be extended into other strategies for motion correction, the inclusion of more patient data suffering perfusion defects, and a benchmarking tool to assess myocardial perfusion diagnosis, which is important to translate automated methods into clinical settings. This resource provides a valuable framework for evaluating these additional methods in the future.