Abstract
Abdominal aortic aneurysms (AAAs) typically harbour an intraluminal thrombus (ILT), yet most prior computational models neglect biochemomechanical effects of thrombus on lesion evolution. We recently proposed a growth and remodelling model of thrombus-laden AAAs that introduced a number of new constitutive relations and associated model parameters. Because values of several of these parameters have yet to be elucidated by clinical data, and could vary significantly from patient to patient, the aim of this study was to investigate the possible extent to which these parameters influence AAA evolution. Given that some of these parameters model potential effects of factors that influence the risk of rupture, this study also provides insight into possible roles of common risk factors on the natural history of AAAs. Despite geometrical limitations of a cylindrical domain, findings support current thought that smoking, hypertension, and female sex likely increase the risk of rupture. Although thrombus thickness is not a reliable risk factor for rupture, the model suggests that the presence of ILT may have a destabilizing effect on AAA evolution, consistent with histological findings from human samples. Finally, simulations support two hypotheses that should be tested on patient-specific geometries in the future. First, ILT is a potential source of the staccato enlargement observed in many AAAs. Second, ILT can influence rupture risk, positively or negatively, via competing biomechanical (e.g., stress shielding) and biochemical (i.e., proteolytic) effects. Although further computational and experimental studies are needed, the present findings highlight the importance of considering ILT when predicting aneurysmal enlargement and rupture risk.
Keywords: remodelling, discontinuous growth, rupture, smoking, hypertension, inflammation
1. Introduction
Abdominal aortic aneurysms (AAAs) are localized dilatations of the infrarenal abdominal aorta that often remain asymptomatic until rupture; they are characterized structurally by a loss of elastic fibre integrity, dysfunction or loss of smooth muscle, and remodelling of collagen. Rupture is a catastrophic endpoint in the natural history of AAAs that is associated with a high mortality rate. Unfortunately, current clinical capabilities for predicting rupture remain wanting, and clinical interventions continue to be based primarily on the maximum diameter or rate of enlargement of the lesion. Yet, many small lesions rupture while larger lesions do not [1,2], and many AAAs do not enlarge continuously. That is, radial enlargement at the apex often occurs via stepwise dilatations, with periods of stability alternating with periods of enlargement [3]. This “staccato growth” phenomenon has yet to be explained.
Most AAAs larger than 6 cm contain an ILT, as do some smaller lesions [4]. Such thrombi are typically layered structures that, unlike other blood clots, show few signs of healing. The part of the thrombus next to the blood flow, the luminal layer, is characterized by erythrocytes, leukocytes, and platelets entrapped within an evolving fibrin mesh. This layer is usually ~2 mm thick [5], which may be limited by the depth to which blood components can penetrate the fibrin mesh. Cells within the luminal layer produce enzymes (e.g., matrix metalloproteinases (MMPs) and neutrophil elastase) that degrade the aortic wall or activate those that do (e.g., by activating urokinase plasminogen activator (uPA), which increases plasmin, which activates latent MMPs). Unlike the luminal layer, the deeper parts of an ILT (i.e., medial and abluminal layers) are mostly devoid of cells [6,7]. The lack of platelets in these layers suggests little production of fibrin, hence degradation of fibrin likely dominates deposition within these layers. Whereas the biochemically active luminal layer can disrupt underlying wall structure, and thereby promote rupture of an AAA, most ILTs are much thicker than 2 mm. In these cases, the ILT may stress shield the wall mechanically [8] and may serve as a barrier to the diffusion of oxygen and proteases coming from the blood and luminal ILT. It is thus important to account for the complex and diverse biomechanical and biochemical roles of ILT when modelling AAA biomechanics [9]. It is also important to realize that the luminal layer of an ILT may contact the wall even in cases of thick ILT (e.g., at the axial shoulders of the lesion or along the posterolateral wall in cases of an eccentric deposition of thrombus). For our initial analysis and investigation of roles of rupture risk factors, however, we will focus on a simplified axisymmetric dilatation in one dimension to highlight potential effects of the constitutive descriptors and associated model parameters.
Computational growth and remodelling (G&R) models of the vasculature promise to increase our understanding of adaptations to altered hemodynamic loads as well as the progression of disease, with potential for predicting rupture risk in AAAs. Toward this end, there is first a need for reliable constitutive relations for both the aortic/aneurysmal wall and the ILT, and their interactions. We and others have adopted a “constrained mixture” framework [10] and shown that initial constitutive relations enable many salient features of arterial biomechanics to be captured well, including normal adaptations to altered pressure and flow [11] and disease progression in different cases [12,13]. It has also been shown that values of model parameters that are not easy to infer from experiments or associate with clinical data can nevertheless often be bounded to realistic ranges [14,15].
Despite overwhelming evidence that ILT is biochemically active [7,16], it has been either modelled as an inert, homogeneous material in static models that focus on the state of stress in the wall (e.g., [8]) or neglected in most G&R studies (e.g., [12,13]). To address this limitation, we recently proposed a G&R model, based on experimental data reviewed in [17], that captures evolving biochemomechanical influences of ILT on the aneurysmal wall [18]. In [18] we demonstrated the potential of the model to predict geometrical changes, diffusion of proteases, structural changes, and stresses. We also showed that ILT should be accounted for when predicting the potential enlargement or rupture risk of AAAs. We did not examine potential differences in model predictions for physiological ranges of parameter values, however. The aim of this study, therefore, is to investigate the possible extent to which these parameters influence AAA evolution and to recognize the key features of the thrombus-laden model. Given that some of these parameters model effects of commonly proposed factors that influence the risk of rupture, this study also provides some insight into possible roles of common risk factors on the natural history of AAAs.
2. Methods
We build on our prior model [18], but note salient assumptions and constitutive relations in this section for convenience. The reader well familiar with the model in [18] can proceed to section 3, however. Briefly, we assume that AAAs initiate from non-aneurysmal but aged aortas and focus on an idealized cylindrical geometry to highlight emergent effects of differences in the values of the constitutive parameters. Although this 1D model considers mechanical changes and chemical diffusion in the radial direction alone, we submit that the predictions provide new insight into the importance of and interrelationships amongst the parameters that could not be gleaned if studied within the context of complex and computationally expensive 3D geometries. That is, just as experimentalists first characterize material behaviours using simple experiments (e.g., uniaxial tension or four-point bending), so too simple boundary value problems are useful for evaluating constitutive behaviours computationally. Once evaluated, G&R models can then be used with more confidence to simulate patient-specific lesions and guide experimental studies of both the roles of ILT in AAA progression and potential therapeutic interventions.
2.1. Kinematics of AAA
The notation follows Karšaj and Humphrey [11]. Briefly, individual structurally significant constituents k, deposited at a generic G&R time τ, are incorporated within extant extracellular matrix with pre-stretch Gk (τ); in contrast, the mapping of differential position vectors defined in individual natural configurations for each constituent produced at time τ to those in a current (deformed) mixture configuration at time s is captured by deformation gradient (cf. Figure 1 in [11]). The right Cauchy-Green tensor is . Similarly, for the overall deformation gradient for the mixture F, the associated right Cauchy-Green tensor is C = FTF.
2.2. Kinetics of AAA
Elastin is not produced in maturity; it can only be mechanically damaged or proteolytically degraded as a lesion evolves [18]. In contrast, collagen and smooth muscle turnover continually, as does fibrin in the thrombus. Such turnover implies degradation and deposition, the latter at production rate ṁk (tau;). Whereas deposition is constant at a basal rate during homeostasis, it may change in response to deviations in intramural stress from a homeostatic value due to injury and disease, including inflammation. We let the current mass of each constituent k evolve as
| (1) |
where qk (s − τ) is a survival function that defines the percentage of constituent k produced at past time τ that remains at current time s, with a special case that Qk (s) = qk (s − 0). Given that Mk (0) is the initial mass of constituent k, Me (s) = Me (0)Qe (s) for elastin since there is no production in maturity.
We further let the survival function qk depend on a rate-type removal parameter , where
| (2) |
with Qk,e (s) = 1 for all constituents except muscle. To model anoikis of smooth muscle cells (i.e., apoptosis caused by a loss of attachment to surrounding matrix, including elastic fibres), the loss of smooth muscle was linked to the degradation of elastin by QSMC,e (s) = Qe (s).
2.2.1. Intraluminal thrombus
Understanding of the spatially evolving deposition of ILT remains wanting. Given that medical imaging of large AAAs suggests that the overall luminal diameter tends to be preserved, we required the luminal area to remain constant throughout our simulations as a first approximation in this qualitative study. Thus, additional ILT was deposited in every time step in which the lesion enlarged, resulting in prior portions of the luminal layer becoming medial and abluminal layers as they are buried under newer thrombus (see [17] for the naming convention of layers). Moreover, based on experimental findings [19], we considered fibrin, fibrin degradation products (FDPs), erythrocytes (RBCs), and voids to be the most significant space-filling constituents of a layered ILT. Even though leukocytes, platelets, and non-collagenous extracellular proteins were neglected as load-bearing constituents, they were nevertheless crucial for the biological activity of the thrombus.
Fibrin
Platelets release thrombin during coagulation, which helps to convert soluble fibrinogen into fibrin, which, in turn, polymerizes to form an insoluble cross-linked mesh. We modelled changes in the mass of fibrin similar to changes in wall constituents (eq. (1)), but assumed that the production rate of fibrin depended on the mass of platelets and decreased with increased fibrin density through a correlation parameter , namely
| (3) |
Fibrin is dissolved by plasmin. Moreover, since fibrinolysis has been reported to be inversely proportional to the density of the fibrin mesh and its current stretch [20–22], we considered a mass removal rate-type parameter for fibrin of the form (cf. (2))
| (4) |
where is a homeostatic value depending on the natural half-life of fibrin, is the mass of plasmin, and λi is fibrin stretch; is a weighting function.
Cells and Platelets
The majority of blood-derived cells within an ILT reside within the luminal layer [6,23], presumably because flowing blood can replenish and sustain cells only to a certain depth. Thus, we defined the boundary of the luminal layer by a depth beyond which cells could not be replenished, either because a critical fibrin mesh density was reached or because a critical distance rcrit (τ) was attained. This critical distance (in the radial direction) was defined in each instant by a critical mass of fibrin , such that
| (5) |
where is mass of fibrin in layer i, rl is luminal radius, and the quantity of platelets in the luminal layer is . We assumed a first order loss process for cells that became buried in the medial layer (with a half-life of 7 to 11 days for platelets and for erythrocytes). In summary, the mass of platelets (and similarly for leukocytes, primarily neutrophils, ) was calculated as
| (6) |
where is the time at which a critical mass of fibrin (i.e., rcrit) was achieved, thus transitioning the layer from luminal to medial. Similarly, represents the time at which the limit of the luminal layer was achieved by reaching the critical mass fraction of fibrin (i.e., mesh density). Leukocytes were assumed not to contribute significantly to the volume of the ILT; nonetheless, their presence is important for biochemical activity (e.g., production of plasmin, MMPs or other elastases). The distribution of erythrocytes within the ILT was defined similarly, except with a mass fraction used to calculate the overall stored energy of ILT instead of the mass:
| (7) |
Plasmin, EDPs, and neovascularization
Conversion of plasminogen to plasmin is a complex process catalysed by multiple enzymes, including a key step by either tissue plasminogen activator (tPA, found on endothelial cells) or urokinase plasminogen activator (uPA, coming mainly from mesenchymal and inflammatory cells). Conversely, activation may be inhibited by plasmin activation inhibitor (PAI-1) and alpha-2 antiplasmin. For our simplified model, we sought to capture phenomenologically the overall increase in activated plasmin and to model its diffusion from two primary sources: the leukocyte-rich luminal layer of the ILT and the inflamed aneurysmal wall (to which leukocytes invade via the vasa vasorum). This increased production of plasmin within the wall is consistent with immunohistological reports [24]. The mass of activated plasmin that degrades fibrin is given as
| (8) |
where is a correlation factor between plasmin and neutrophils in the thrombus, is the amount of plasmin consumed per unit of fibrin, and is the mass of plasmin in the wall, calculated as . We assumed that plasmin generated within the wall depends largely on the total mass of elastin degradation products , which are chemo-attractants for inflammatory cells and stimulate neovascularization of the wall (i.e., increase the area of vasa vasorum , [25]). Correlations between plasmin and EDPs/vasa vasorum were accounted for by and , respectively. The production rate of EDPs depended on the amount of elastin degraded per time step, while their degradation was modelled using a first-order decay with a constant half-life. The total mass of EDPs can then be calculated by eq. (1).
Due to the controversial influence of hypoxia on neovascularisation, as well as studies showing that EDPs alone can promote neovascularization [25], we modelled the development of vasa vasorum solely as a function of the mass of EDPs, such that
| (9) |
where is the area of vasa vasorum in healthy aorta and is a correlation factor that relates vasa vasorum growth per unit of EDPs per unit time.
Fibrin degradation products and voids
The luminal layer contains entrapped erythrocytes within a thick fibrin mesh. Once the luminal layer is buried deeper within the thrombus, erythrocytes cannot be replenished. Likewise, the availability of platelets necessary for fibrin deposition decreases steeply with depth, thus allowing degradation to outpace deposition. Dissolution of fibrin and haemolysis can leave small interconnected channels (“voids” or “canaliculi”) throughout the ILT [6]. We assumed that degrading fibrin was converted partly into fibrin degradation products (FDPs) and partly into canaliculi (as fibrin was removed by macrophages) in a 7:3 ratio. These canaliculi might also result from microstructural mechanical damage, as signs of thrombus fracture are occasionally seen on contrast enhanced CT imaging of larger AAAs.
2.2.2 Biochemical interaction of ILT and aneurysmal wall
Effects of the proteolytically active luminal layer were integrated via additional terms in the mass removal rate-type parameter in eq. (2). For example, the elastin present in normally aging aorta depends solely on its natural half-life , which is on the order of fifty years: . Increased degradation of elastin in an aneurysm due to inflammation was incorporated via an additional term,
| (10) |
where the amount of elastase, Melas, was modulated by a weighting factor .
In contrast, for collagen we let (cf. [11])
| (11) |
where the collagen mass removal parameter depends on the ratio of the current ( ) to the homeostatic ( ) tension, and is the rate-type removal parameter associated with the homeostatic half-life, which is on the order of 90 days; the additional terms relate to distributions of active MMPs (i.e., collagenases).
Similar to plasmin, MMPs may arise from two primary sources: the luminal layer in ILT or cells entering via the vasa vasorum in the aortic wall. A first approximation, quasi-static transport, was determined from the diffusion equation, , where D is a diffusion coefficient that can be estimated based on available data for the radial distribution of proteases [16,23]. We defined available elastase/MMPs from the luminal layer as (or for MMPs), where described how much elastase/MMP was produced per unit of leukocytes per time step, as a point source centred at radius rL, where
| (12) |
similar to a centre of mass. The concentration of elastase/MMPs available at the outer radius depended on the area of the vasa vasorum and number of inflammatory cells: . Thus, by solving the diffusion equation, the overall distribution of proteases was:
| (13) |
where k indicates elastases or collagenases. The mass of inflammatory cells in the wall, , was modelled similar to eq. (1), with degradation depending on cellular half-life and production increasing with increases in mass of EPDs and vasa vasorum, such that
| (14) |
where is a correlation factor that relates the proliferation of white blood cells with EDPs and neovascularisation, and α is power parameter.
2.3 Stress analysis
The Cauchy stress within the aortic wall was calculated as a constrained mixture,
| (15) |
with the overall stored energy function and tactive the active stress contribution from circumferentially oriented smooth muscle contraction. Similar to Valentín et al. [26], phenotypic transitioning of smooth muscle cells from a contractile to synthetic state is considered by allowing a decreasing maximal active stress Tm such that Tm (s) = Tm (0) · (βm + (1 − βm)Qe (s)).
Noting that fibres deposited within extant matrix at different times may undergo different overall deformations compared to their natural state, the total stored energy of a constituent is a combination of the unique stored energies of each fibre, namely
| (16) |
For the stored-energy form of each type of constituent (Ŵk), isotropic elastin is modelled as neo-Hookean while collagen and smooth muscle are modelled as fibre-like with an exponential constitutive response in tension but no compressive stiffness, as in [18].
Additionally, since AAAs can expand from an initial 2 cm diameter to > 7 cm, strains measured from the homeostatic configurations can be much larger than in aging healthy aorta. Elastin, which does not undergo turnover, may experience these strains fully; in contrast, ongoing turnover helps to prevent overloading of collagen and smooth muscle, particularly considering the exponential nature of their strain energy function. Nevertheless, in rapidly progressing aneurysms, collagen and smooth muscle may still be at risk of mechanical failure. Thus, failure criteria of 6 MPa for collagen and 0.15 MPa for SMC [27] were implemented. Note that this increased risk of fibres mechanically failing in the G&R model is consistent with the clinical observation that rapidly growing lesions are more likely to rupture, while slower expansion allows adequate time for ECM turnover. Thus, noting that elastin undergoes extremely large deformations during AAA evolution that can easily surpass its physical range, we modelled damage of elastin if its stretch exceeded a value of 2.2 (the estimated ultimate uniaxial elastin stretch in [28]) by decreasing its stiffness similar to [13]:
| (17) |
where ce is elastin stiffness, and is elastin stretch in circumferential direction.
Mechanically, ILT can bear stress and possibly reduce the peak wall stress. Cauchy stress in the ILT was modelled using a stored energy function for an isotropic fibrin mesh based on [19], and a neo-Hookean strain energy function was used for the FDPs.
3. Risk Factors and Therapeutics in AAA Progression
One goal of computationally modelling aneurysmal G&R is to help clinicians predict rupture risk. Although multiple risk factors have been suggested for AAA rupture [29], we consider herein a few key factors within the limitations of our model. Herein, rupture was assumed to be possible when any normal component of wall stress reached 460 kPa [30].
3.1. Smoking
Smoking has been linked to multiple vascular diseases. Among other effects, smoking elevates oxidative stress, compromises the arterial endothelium, and promotes atherogenesis [31]. It also promotes monocyte migration into the subintimal space, which promotes localized inflammation of the wall [32], and it increases the concentration of plasma fibrinogen and alters the activity of platelets, which together promote thrombosis on the dysfunctional endothelium [32]. Finally, smoking correlates strongly with increased aortic blood pressure, heart rate, and arterial stiffness [33], with smoking-induced stiffening appearing to be isotropic, as reflected by a consistent increase in an elastin-associated parameter and a marked increase in the collagen-associated parameters [34].
Many studies associate smoking with larger AAAs [4,35] and enlargement rates [36]. Some studies suggest that cessation of smoking may inhibit aneurysmal enlargement, even though two years of cessation does not reduce arterial stiffness [37]; indeed, it can take up to a decade to reduce stiffness to the level of never-smokers [38]. Similarly, five years of abstinence can reduce fibrinogen concentrations to the range of never-smokers [39].
Motivated by these studies, we investigated the natural histories of aneurysms in simulated smokers, ex-smokers, and non-smokers. Smoking was modelled by an increased elastin stiffness, collagen stiffness, inflammation, and platelet activity. Parameter values that differ between simulations are shown in Table 1. Endothelial and smooth muscle cell dysfunction are characteristic of aneurysms independent of smoking and were implicitly included in the model for both smokers and non-smokers.
Table 1.
Parameters for non-smokers and smokers: and are parameters in the stored energy functions for elastic and collagenous fibres (cf. [34]).
| [kPa] | [kPa] | [−] | [g−1 day−1] | [g−1 day−1] | [g mm−1] | |
|---|---|---|---|---|---|---|
| Non-smokers | 74.6 | 498.2 | 22 | 10 | 60 | 0.15 |
| Smokers | 148.7 | 861.3 | 44 | 20 | 120 | 0.2 |
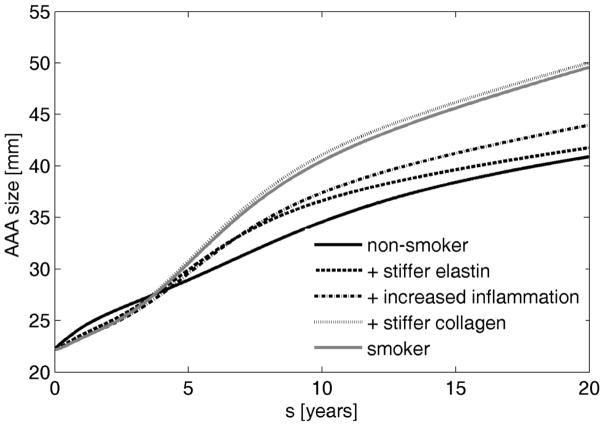
Simulated AAA diameter was greater at 20 years for smokers (4.96 cm) than non-smokers (4.09 cm), with an associated mean dilatation rate 0.043 cm/year greater than that for non-smokers (Figure 1). These results are consistent with clinical observations. Bhak et al. [35] reported that smoking associated with a 0.05±0.01 cm/year increase in linear enlargement rate. Our results suggest further that increased stiffness is a key factor that leads to large aneurysms in smokers (Figure 1). There was only a slight decrease in AAA size due to increased production of fibrin through a higher platelet activity, which resulted in a slightly stiffer but thinner luminal layer of the ILT. Note that this finding does not mean that increased platelet activity could potentially stabilize AAAs since platelets are chemotactic for neutrophils and monocytes [40] and can cause higher inflammation and enlargement rates.
Figure 1.
Simulated evolution of AAAs in a non-smoker (solid black line), in cases of increased elastin stiffness (dashed line), both an increased elastin stiffness and inflammation (dash-dotted line), an increased elastin and collagen stiffness plus elevated inflammation (dotted line), and an increased stiffness, higher inflammation, and increased platelet activity (solid grey line) – that is, full effects of smoking.
Changes in rates of dilatation after smoking cessation have not been studied well. As it has been shown that stiffness is reduced only after 10 years [38], we would not expect an immediate decrease in enlargement rate. Rather, we would expect competing effects to evolve after several years: a reduced growth due to attenuated rates of elastin degradation but increased enlargement due to a decrease in collagen stiffness. Thus, consistent with general public health guidelines, immediate cessation of smoking is recommended, preferably before AAA development.
3.2. Aneurysm stabilization factors
Numerous studies have proposed the use of anti-inflammatory drugs for reducing or arresting the enlargement of AAAs, some of which act directly on MMPs [41,42] while others reduce matrix degradation indirectly (e.g., via platelet inhibitors [43] or immunosuppressive agents [44]). For example, one study in mice showed that preserving medial elastin can attenuate aneurysmal dilatation [41] while another study in mice showed that non-specific inhibition of collagenases can lead to lesion stabilization [42]. Nevertheless, non-specific MMP inhibition has not reduced aneurysmal progression in human patients [45]. Clearly, there is a need for increased understanding of the biochemical mechanisms of aneurysm formation and evolution.
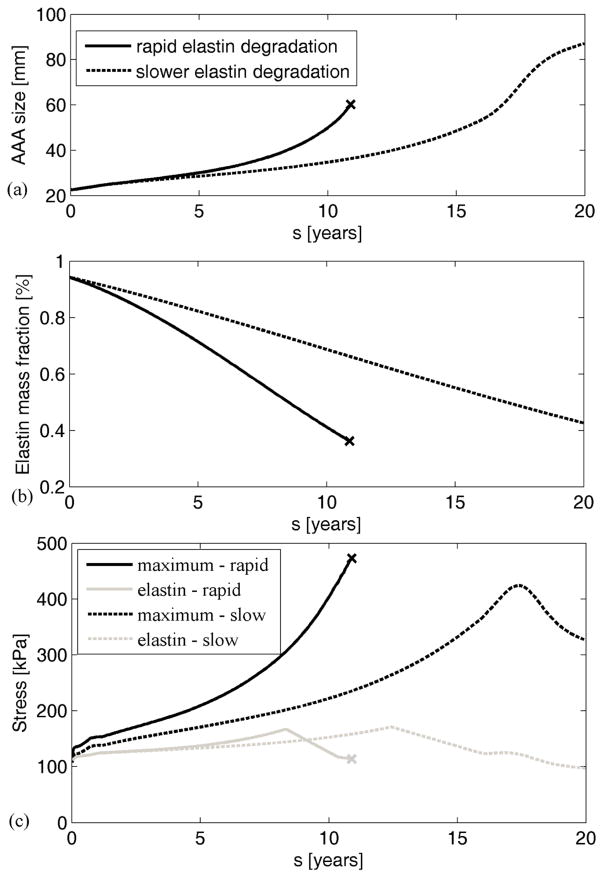
Figure 2 shows that our thrombus-laden aneurysm model supports results from [41], whereby attenuating elastase activity (i.e., decreasing the degradation of elastin from to ) helped to decrease the likelihood of rupture and to some extent led towards stabilization, independent of collagen stiffness. The decreased load carrying by elastin following its damage (after reaching a stretch of 2.2) can be seen in Figure 2(c).
Figure 2.
Simulated AAA evolution (a), corresponding degradation of elastin (b), and evolution of maximum wall stresses ||t||max (black lines) and elastin stresses ||te||max (grey lines) (c) in cases of rapid (solid line) versus normal (dashed line) elastin degradation. Note that the aneurysm was initiated by degrading only 5% of the elastin. Maximum stress is the highest normal value of the mixture stress. Expected rupture is denoted by “x”.
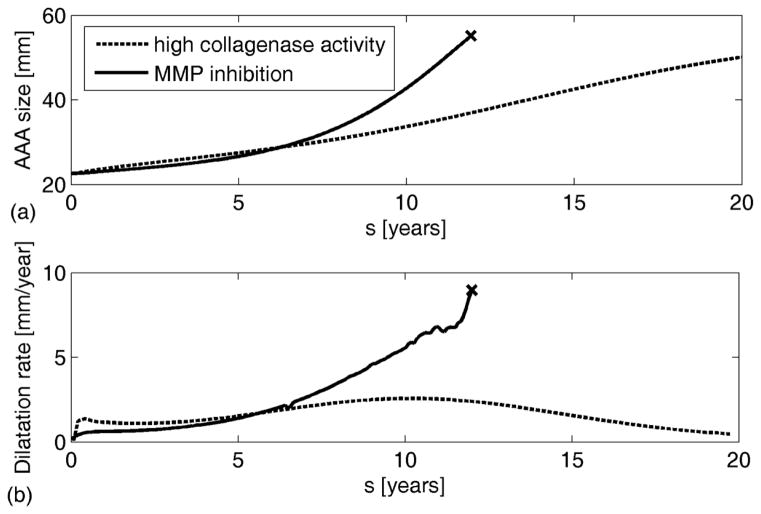
The current model similarly suggests that high rates of collagen degradation ( ) could lead to progressive enlargement (solid line in Figure 3) while reduced inflammatory driven proteolytic activity ( ) could prevent rupture despite continued enlargement (dashed line in Figure 3). Thus, the current results suggest that rates of degradation of structural constituents (governed by local concentrations of proteases, controlled by parameters and in eq. (10)) should indeed affect aneurysmal progression. Note that stiffening was modelled in these simulations by changing the exponential parameter for collagen in the stored energy function relative to both the homeostatic value and the ratio of the current to the initial stretch (i.e., ).
Figure 3.
Simulated AAA evolution (a), with associated dilatation rates (b), for different rates of collagen degradation in the case of collagen stiffening. The “oscillations” in the curve with high collagenase activity likely reflects damage of collagen fibers prior to normal controlled turnover. “x” denotes expected rupture.
3.3. Effects of sex and age
Sex differences have been identified in cardiovascular aging and in the evolution, management, and response to treatment of many cardiovascular diseases, including AAAs [46]. For example, females have stiffer large arteries pre-puberty, but more compliant ones post-puberty [47]. Additionally, age-associated endothelial function declines in men years before women [48]. These findings, among many others, could contribute to the increased prevalence of AAAs in men compared to women [49]. Yet, males have a 3–4 times lower risk of rupture than females [46], possibly due to higher strength of the AAA wall [50]. Similarly, noting that males have stiffer arteries on average [51], previous G&R models suggested that increased material stiffness and turnover of collagen decreases the likelihood of rupture [52].
Beyond the effects of sex, age may also play a role in AAA progression. Wilson et al. [13] demonstrated in a G&R model that aortic properties at the age of lesion initiation may strongly influence AAA progression. Such properties likely depend on a patient’s biological age (e.g., genetics, smoking status, comorbidities, and exercise) as opposed to simply a chronological age. For example, the observation that females who undergo open surgical repair for AAA are significantly older compared to males [51] may be reflective of their “younger” biological status as suggested by their later decline of endothelial function. Thus, we explored differences in AAA enlargement in males and females by prescribing different values of collagen stiffness (increasing collagen stiffness in males, but consistent stiffness in females) and different initial aortic microstructures. Initiation of an aneurysm at a younger age, typically in men, was taken into account by higher amounts of elastin and a thinner intima. Additionally, assuming equivalent elastin material properties, elastin in younger patients is less pre-stretched compared to the remaining elastin in older patients due to the slow increase in diameter with age and the lack of elastin turnover. Values of parameters that differ among simulations are presented in Table 2.
Table 2.
Parameters for younger and older patients: and are volume fractions for the intima and media, respectively; Ge is the initial pre-stretch of elastin; ϕe is the initial volume fraction of elastin in aortic wall.
| [%] | [%] | Ge [−] | [kPa] | ϕe [%] | |
|---|---|---|---|---|---|
| Young | 4 | 80 | 1.3 | 87.8 | 33.6 |
| Old | 16 | 52 | 1.4 | 74.6 | 27.4 |
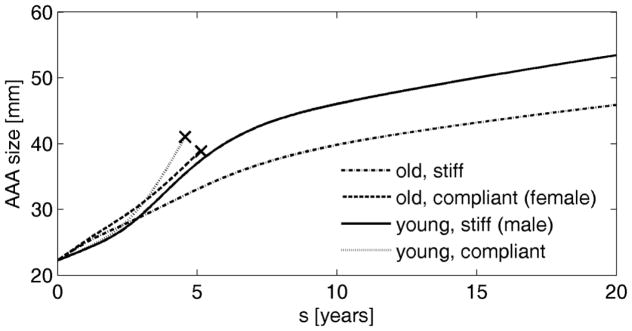
Inducing aneurysms in an initially stiffer aortic wall led to lower enlargement rates, with less likelihood of rupture (Figure 4). With regards to age, a younger aortic wall was more compliant and experienced greater dilatation (whether ruptured or unruptured). It also had greater amounts of elastin, the preservation of which may help prevent rupture (see section 3.2). Therefore, the biological age at which an aneurysm develops may have an important impact on AAA evolution, and might be an additional factor contributing to the high rupture risk in females.
Figure 4.
Simulated evolution of AAAs for males and females of varying age. “x” denotes expected rupture
3.4. Hypertension
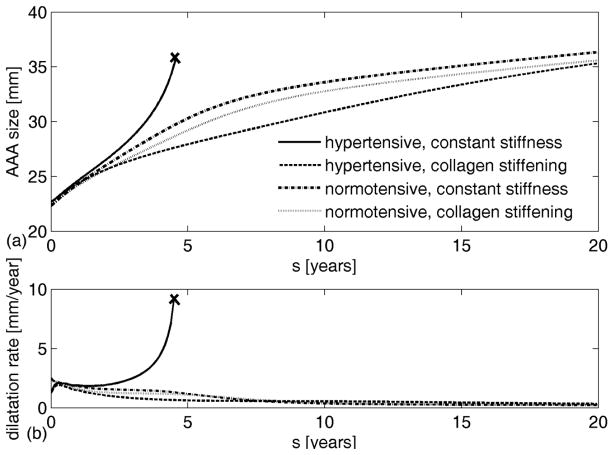
Hypertension is thought to be a key factor in AAA enlargement [35] and rupture-risk, particularly in aneurysms smaller than 5.5 cm [53]. Hypertension leads to progressive changes in vascular structure, function, and material properties that often manifest grossly as increased wall thickness, radial dilatation, and axial lengthening [54], all of which are G&R responses. To evaluate possible effects of hypertension on AAA progression, we considered two cases: patients who were hypertensive before developing an AAA and patients who developed hypertension during the progression of the lesion. In the former, we first simulated G&R of a hypertensive (but non-aneurysmal) aorta and used it as the initial state in which the aneurysm developed. Results suggested that aneurysms originating from a hypertensive wall tend either to rupture or to stabilize at smaller sizes (Figure 5(a)), depending on the properties of collagen. Furthermore, they suggested that lack of treatment of hypertension before aneurysmal development might increase the likelihood of rupture, since the aneurysms modelled as normotensive (but with otherwise the same G&R parameters) showed a tendency towards stabilization, not rupture.
Figure 5.
Evolution of AAA diameter (a) and enlargement rate (b) from an initially hypertensive aorta. Solid lines represent enlargement for constant collagen material properties; dashed lines represent enlargement during collagen stiffening; dash-dotted lines represent enlargement of normotensive aneurysm with constant collagen properties; dotted lines represent enlargement of normotensive aneurysm with collagen stiffening. ‘x’ denotes expected rupture.
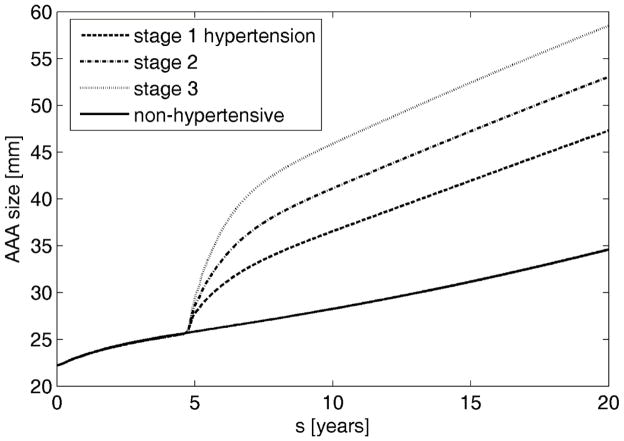
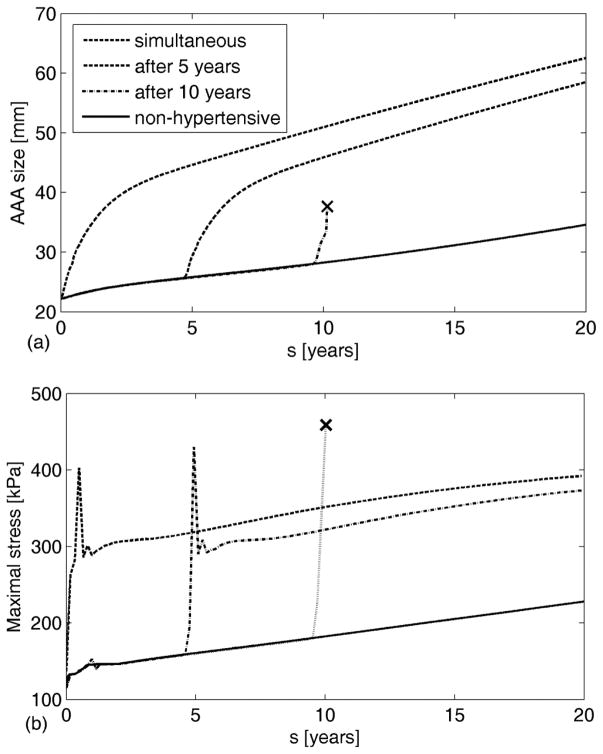
When hypertension developed during aneurysmal progression, the increased luminal load increased the inner radius further which changed the wall stresses that drive much of the G&R. We considered three degrees of hypertension [55] defined as increases in mean arterial pressure of 40% (36 mmHg), 60% (54 mmHg), and 80% (72 mmHg) as Cases 1, 2, and 3, respectively. As expected, a greater increase in blood pressure resulted in a larger evolving diameter (Figure 6). The average increase in enlargement rate of a hypertensive aneurysm over 15 years was 0.235, 0.228 and 0.221 mm/year per 10 mmHg increase (i.e., stages 1, 2 and 3, respectively). These values are in good agreement with clinical observations of 0.02 ±0.01 cm/year per 10 mmHg [35]. Interestingly, the present computational results also suggested that a later development of hypertension is more likely to lead to rupture even though earlier hypertension may lead to larger AAAs (Figure 7(a)). This finding highlights the importance of G&R compensation, for it is not strictly the diameter that determines rupture, but rather the failure of the cells to adequately respond to a perturbation (i.e., dilatation need not imply an improper response). In this case, a relatively healthier wall (i.e., earlier in AAA development) was better able to compensate for a higher blood pressure than was a wall exposed to the same pressure after being more extensively damaged via the AAA progression, as seen from evolution of stresses (Figure 7(b)).
Figure 6.
Evolution of AAAs arising from a heathy aorta after either maintaining normal blood pressure (solid) or spontaneously developing elevated blood pressure to different degrees: Cases 1 (dashed), 2 (dash-dotted), or 3 (dotted) represent, respectively, a 40% (36 mmHg), 60% (54 mmHg), or 80% (72 mmHg) increase in mean arterial pressure.
Figure 7.
Evolution of AAAs from an initially normotensive aorta following the rapid development of case 3 hypertension (72 mmHg increase in mean arterial pressure) at different times during AAA progression (a), and evolution of corresponding maximal stresses (b). “x” denotes expected rupture. Note the G&R response to restore stresses towards normal except in the case of rupture prior to G&R.
3.5. Thickness of intraluminal thrombus
Another potential risk factor that has garnered increased attention is the size of the ILT. Different measures of ILT size, including thickness [56], volume [57], and relative cross-sectional area [4], have been correlated with rapid enlargement or rupture. Yet other studies suggest that ILT volume is the same in ruptured and intact AAAs [58], and case reports of unruptured giant thrombus-laden aneurysms (e.g., 25 cm in [59]) have been described. Because of the cylindrical geometry and concentric thrombus used herein, ILT thickness, area, and volume are all a direct function of AAA diameter, and therefore, differential effects of these metrics of ILT size could not be evaluated. Moreover, we posit that it is the luminal layer of the ILT that is most active proteolytically and hence most dangerous; a 1-D model cannot address different scenarios wherein the luminal layer contacts the aneurysmal or aortic wall (e.g., at the shoulders of the lesion). Nevertheless, the distribution of proteases (e.g., Melas for neutrophil elastase and MMMP for some collagenases) in this 1D model depends on both the available proteases from each source (luminal layer of the ILT and vasa vasorum in the aortic wall) and the distance between the two sources; hence, it is proportional to ILT thickness.
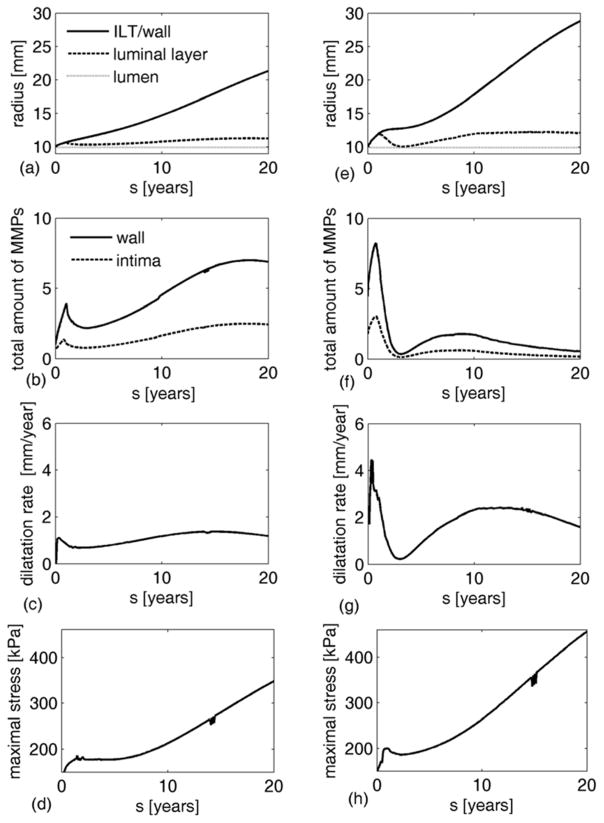
The amount of available proteases in the luminal layer varies significantly among patients, from virtually non-existent to very high (e.g., see measured MMP-9 activity in both thrombus and wall specimens from 35 patients in Figure 3 in [24]). Thus, we investigated the possible evolution of an AAA for different degrees of protease activity in the ILT (by increasing in eq. (13)). Figure 8 shows differences in predicted AAA enlargement for cases wherein the ILT and vasa vasorum have equal proteolytic activity ((a)–(d)) ( ) or the ILT is much more proteolytically active ((e)–(h)) ( ). In the latter case, the proteolytic activity in the wall increased sharply as long as the luminal layer was directly attached to the aneurysmal wall (i.e., while the solid and dashed lines in Figure 8(e) coincide), thus resulting in rapid enlargement of the aneurysm. As less proteolytically active deeper layers formed and acted as a barrier to protease diffusion, proteolytic activity decreased abruptly and the enlargement rate declined (Figure 8(c) and (g)). Note that elevated activity in the luminal layer led to a reduction in enlargement rate once the luminal layer was displaced from the wall, even causing a near cessation of enlargement temporarily (Figure 8(g)).
Figure 8.
Evolution of radius, MMPs, and enlargement rate for AAAs with low proteolytic activity in the luminal layer of ILT (a–d) versus high proteolytic activity (e–h). (a,e) Evolution of radius at the ILT/wall interface (solid line), lumen/luminal layer interface (dotted line) and luminal layer/wall (for thin ILTs) or luminal/medial layer interface (when medial layer of thrombus is developed) (dashed line). (b,f) Evolution of the normalized total amount of MMPs in the wall (solid line) and intima (dashed line). (c,g) Evolution of AAA enlargement rate. (d,h) Evolution of maximal stresses in aortic wall.
Several studies (e.g., [3]) report that the majority of AAAs dilate discontinuously, with periods of enlargement alternating with periods of quiescence. Though the precise causes of this phenomenon have not been determined, the current results suggest that ILT, specifically altering the proximity of the biologically active luminal layer to the wall, may directly influence enlargement rates and thus play a role in determining clinical outcomes. Although only one cycle of enlargement and arrest is allowed in this axisymmetric cylindrical geometry, extending this model to 3D patient-specific geometries will allow further testing of the relationship of ILT, discontinuous enlargement, and patient-specific outcomes by exploring more complex enlargement patterns due to eccentric deposition of thrombus (i.e., where one portion of the ILT remains thinner than others), non-continuous deposition of thrombus, local bulging, and multiple regions where the wall is adjacent to thin thrombus throughout AAA development.
For both levels of activity within the luminal layer, a second peak of MMP activity and enlargement rate was observed due to the increase in proteases from a developing vasa vasorum, driven (in this model) by elastin degradation products (EDPs). Interestingly, this second MMP peak is greater in the model with a lower luminal activity even though the enlargement rate is lower, perhaps due to the more consistent release of EDPs from the slower elastin degradation occurring in the case of lower luminal activity.
As expected, note from Figure 8(a) and (d) that the simulated AAA was larger after 20 years in the case of high proteolytic activity (5.5 cm vs. 4.5 cm in outer diameter). Yet, there is little indication that thrombus thickness alone increases the likelihood of AAA rupture, as seen from simulations in previous sections where expected ruptures occurred in both small and large aneurysms while some large simulated aneurysms (9 cm) remained stable. Further finite element analyses are warranted for confirmation, but we do not expect ILT thickness or other simple measures of ILT size to enable rupture predictions directly.
Limitations and proposed experiments
The current model was developed using a cylindrical geometry to focus on the importance of different constitutive assumptions and ranges of parameter values before introducing complex geometric effects that arise with local, eccentric aneurysmal dilatation. Although patient-specific models must be considered in future studies, including fluid-solid-growth (FSG) simulations, the current simple geometric model yet yielded general insights into both the important roles that ILT may play during the evolution of AAAs and the potential roles of diverse risk and stabilization factors. Given this new insight, attention should now focus on the collection of data that will render complex simulations meaningful. For example, most prior experimental findings focus solely on the radial direction for both the thrombus and AAA wall; thus, molecular distributions and heterogeneities in mechanical properties are virtually unknown in axial and circumferential directions. Full 4-D information (radial, circumferential, and axial distributions of structural constituents and biomolecules at multiple times during lesion evolution) will thus be needed to create realistic patient-specific models including the biochemomechanics associated with ILT.
Another potential limitation of the current model is the assumption that luminal area remains constant and concentric throughout the G&R process. Some clinical observations support this assumption of constant luminal diameter in thrombus-laden aneurysms (e.g., [60]), but this is not universal, especially in smaller lesions. Non-uniform thrombus deposition is undoubtedly related to the complex evolving hemodynamics [60,61], which can vary depending on the location, size, and shape of the lesion. Future studies should explore the added complexities of incorporating a hemodynamically driven evolution of thrombus deposition within a FSG model. With such a 4D model, the G&R effects of eccentric thrombus deposition and potential internal dissection of thrombus could be explored.
Additional simplifications of our model include neglect of convection-mediated transport of biomolecules through both the thrombus and wall, which could affect the morphology of the thrombus [62]. There is similarly a need to refine the constitutive relations for the production of these biomolecules. For example, we did not model explicitly the activation of plasmin or MMPs (e.g., by tPA and uPA or plasmin, respectively) or their inhibition (e.g., PAI or TIMP). For MMPs, this modelling is even more complex for the different sub-types (e.g., MMP1 vs. MMP2, and so forth) should be derived separately. In order to avoid a number of additional assumptions and associated parameters, and due to the lack of spatiotemporal experimental data, we chose to model plasmin and MMP distributions phenomenologically.
Notwithstanding the use of phenomenological relations to reduce the complexity of the modelling, this introduces numerous parameters, some of which are difficult to determine directly from experiments. Fortunately, however, the vast majority of the requisite parameters could be estimated indirectly from experimental observations: parameters describing growth of vasa vasorum (eq. (8)) were based on data in [63] that showed an approximately 7–10 fold increase in the neovascularized proportion of the aortic wall from healthy to large aneurysmal (Fig. 2C); the initial area of neovascularization was inferred from [56] (around 0.2% of initial area). Vorp et al. showed similar results for increases in the percent area of inflammatory cells [56]. Parameter in equation (8) was calibrated to fit the given bound. In the absence of human data, weighing factors in equations (9) and (10) were based on animal models. Experiments on elastase-induced aneurysms in rats showed that elastolytic activity was significantly elevated within the aortic wall of animals perfused with thioglycollate plus plasmin 9 days after perfusion (207.6± 54.8 μg elastin-rhodamine lysed/18 hr; control rats, 25.43±11.13) [64]. Similarly, an approximately 50-fold increase in type 1 collagen degradation products has been observed in aneurysms compared to controls [65], assumingly over 20–30 years. The calculated values of weighting factors for elastase and collagenase were similar, as they should be, considering their physical meaning is the amount of protein degraded per unit of protease per time. Several studies ([25,66–68]) provided insight into realistic ranges of increased inflammation, and helped us bound the parameters defining increases in inflammation (i.e., production of leukocytes). Many of the remaining equations are well-known and frequently used as G&R constitutive relations. Because some of the parameters have been shown to vary significantly among patients (e.g., proteolytic activity in the luminal layer [24]), we explored the stated range parametrically. A full parameter sensitivity study would also be useful, but was beyond the present scope given our focus on the first examination of potential effects of common risk factors.
In summary, further refinement of the model in terms of both identifying relevant pathophysiological ranges of parameters and the means to assess more exact values for patient-specific models can and should proceed as the necessary experimental and clinical data become available. As outlined in our earlier review [17], there is a pressing need for better quantification of:
Biomolecular kinetics – identify cellular sources of relevant biomolecules (e.g., plasmin, MMPs, and inflammatory chemokines and cytokines), including rates of production/degradation, activation / inhibition, and convection / diffusion, as well as their evolving circumferential and axial distributions.
Stress-strain relations motivated by microstructure – quantify the nonlinear heterogeneously distributed mechanical properties of the multi-layered ILT and aneurysmal wall, ideally with direct correlations to histological constituents and properties (e.g., collagen-content, elastic fragmentation, fibrin density, etc.).
Failure/rupture – quantify regionally, and propose constitutive relations for, the evolution of the strength of the ILT and aneurysmal wall, including models of failure that consider the propagation of dissections or frank rupture.
Out of many possible experiments, we propose some that could improve this thrombus-laden aneurysm model, assist with the calibration of the model parameters, as well as increase the understanding of the pathophysiology of the disease:
In humans, during the open surgical repairs, samples of ILT and wall could be harvested, and locations of high MMP activity or neutrophil content in the luminal ILT or wall could be determined. One could study whether these locations could be correlated with the areas of local high dilatation rate defined from prior imaging (e.g., from CT scans obtained during follow-ups).
In murine models with ILT (rat elastase model, for example), one could try to eliminate functional neutrophils and/or MMPs (in genetic mutants or with drugs). The experimental results could be compared with predictions of the presented model.
In murine models, one could try to induce AAAs in older vs younger rats to test the prediction that older rats with stiffer aortas may have less AAA expansion than young rats, as predicted here.
Conclusions
Computational biomechanics is increasingly used to investigate complex processes in vascular health and disease. Prior G&R models of aortic aneurysms (cf. [12,13]) have provided considerable insight that complement histopathological studies and clinical observations, but have heretofore neglected biochemomechanical effects of intraluminal thrombus on the aneurysmal wall. We consider these effects to be fundamental to the evolution of these lesions and therefore for predicting clinical outcomes related to AAA enlargement and rupture.
This study provides new insights into both the important roles that ILT may play during the evolution of an aneurysm and the potential roles of diverse risk factors and therapeutic strategies. That is, basic results were largely consistent with intuition, clinical observations, and previous computational G&R models having more complex geometries but without thrombus. Simulations yielded, for example, average rates of enlargement of ~2 mm/year, while rapid enlargement (10 mm/year and more) led to rupture. Smoking increased enlargement rates by ~0.43 mm/year, and hypertension increased enlargement by ~0.22 cm/year per 10 mmHg, both of which are consistent with clinical observations [35]. The model was also consistent with observations that female sex, smoking, and hypertension increase likelihood of rupture-risk. It also introduces a hypothesis that the mechanical state of an AAA (e.g., the amount of elastin remaining or the pre-stretch of the deposited collagen) significantly influences its ability to adapt to hemodynamic or other changes. While stiffening the collagen fibres could help to stabilize an enlarging aneurysm (as shown previously in models without thrombus [52]), this might not be sufficient in cases of high proteolytic activity resulting from an ILT (see Figure 8(e)-(h); stress after 20 years is at approximately 455 kPa, and rupture is expected within a year) or an abrupt change in blood pressure (e.g., see Figures 6 and 7). Limiting proteolytic activity also appears to be important because a biologically active luminal layer of thrombus could otherwise increase enlargement rates and rupture risk when in close proximity to a remodelling wall (e.g., in a thin thrombus or in posterolateral or shoulder regions where the ILT contacts the wall). Indeed, an evolving ILT may contribute in this way to clinically observed discontinuous patterns of enlargement (see Figure 8(d) and (h)). We conclude, therefore, that ILT should not be neglected in future experimental or computational models.
As noted above, due to the paucity of experimental data on biomolecular distributions and heterogeneities in mechanical properties in the axial and circumferential directions, translation of some of the modelling assumptions to 3D will not be straightforward. Therefore, we encourage experimentation that will provide the requisite data for developing and validating a FSG model, the ultimate aim of which is to enhance our ability to understand and predict the complex, biochemomechanical processes occurring during AAA progression and thus to improve patient-specific risk stratification and clinical outcome.
In conclusion, we suggest that a careful, integrated consideration of the evolving mechanical, chemical, and biological properties of biologically active, multi-layered intraluminal thrombus on the natural history of AAAs will also be needed to maximize the potential of computational models to help identify and ameliorate rupture-risk factors (or, equally important, promoting stabilization factors), provide patient-specific diagnostics and interventional planning, and ultimately improve clinical outcomes.
Acknowledgments
This work was supported, in part, by grants from the Croatian Science Foundation (project IP-2014-09-7382 and Installation Grant to I. Karšaj), an NIH T32HL007745 training grant (J. Wilson) and the US National Institutes of Health (R01 HL086418 and U01 HL116323).
References
- 1.Darling RC, Messina CR, Brewster DC, Ottinger LW. Autopsy study of unoperated abdominal aortic aneurysms. The case for early resection. Circulation. 1977;56(3 Suppl):II161–4. [PubMed] [Google Scholar]
- 2.Choksy SA, Wilmink AB, Quick CR. Ruptured abdominal aortic aneurysm in the Huntingdon district: a 10-year experience. Ann R Coll Surg Engl. 1999;81(1):27–31. [PMC free article] [PubMed] [Google Scholar]
- 3.Kurvers H, Veith FJ, Lipsitz EC, et al. Discontinuous, staccato growth of abdominal aortic aneurysms. J Am Coll Surg. 2004;199(5):709–15. doi: 10.1016/j.jamcollsurg.2004.07.031. [DOI] [PubMed] [Google Scholar]
- 4.Behr-Rasmussen C, Grøndal N, Bramsen MB, Thomsen MD, Lindholt JS. Mural thrombus and the progression of abdominal aortic aneurysms: a large population-based prospective cohort study. Eur J Vasc Endovasc Surg. 2014;48(3):301–7. doi: 10.1016/j.ejvs.2014.05.014. [DOI] [PubMed] [Google Scholar]
- 5.VandeGeest JP, Sacks MS, Vorp DA. A planar biaxial constitutive relation for the luminal layer of intra-luminal thrombus in abdominal aortic aneurysms. J Biomech. 2006;39(13):2347–54. doi: 10.1016/j.jbiomech.2006.05.011. [DOI] [PubMed] [Google Scholar]
- 6.Adolph R, Vorp DA, Steed DL, Webster MW, Kameneva MV, Watkins SC. Cellular content and permeability of intraluminal thrombus in abdominal aortic aneurysm. J Vasc Surg. 1997;25(5):916–26. doi: 10.1016/s0741-5214(97)70223-4. [DOI] [PubMed] [Google Scholar]
- 7.Houard X, Rouzet F, Touat Z, et al. Topology of the fibrinolytic system within the mural thrombus of human abdominal aortic aneurysms. J Pathol. 2007;212:20–28. doi: 10.1002/path2148. [DOI] [PubMed] [Google Scholar]
- 8.Wang DHJ, Makaroun MS, Webster MW, Vorp DA. Effect of intraluminal thrombus on wall stress in patient-specific models of abdominal aortic aneurysm. J Vasc Surg. 2002;36(3):598–604. doi: 10.1067/mva.2002.126087. [DOI] [PubMed] [Google Scholar]
- 9.Humphrey JD, Holzapfel GA. Mechanics, mechanobiology, and modeling of human abdominal aorta and aneurysms. J Biomech. 2012;45(5):805–14. doi: 10.1016/j.jbiomech.2011.11.021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Humphrey JD, Rajagopal KR. A constrained mixture model for growth and remodeling of soft tissues. Math Model Methods Appl Sci. 2002;12(3):407–430. doi: 10.1142/S0218202502001714. [DOI] [Google Scholar]
- 11.Karšaj I, Humphrey JD. A multilayered wall model of arterial growth and remodeling. Mech Mater. 2012;44:110–119. doi: 10.1016/j.mechmat.2011.05.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Watton PN, Hill NA. Evolving mechanical properties of a model of abdominal aortic aneurysm. Biomech Model Mechanobiol. 2009;8(1):25–42. doi: 10.1007/s10237-007-0115-9. [DOI] [PubMed] [Google Scholar]
- 13.Wilson JS, Baek S, Humphrey JD. Importance of initial aortic properties on the evolving regional anisotropy, stiffness and wall thickness of human abdominal aortic aneurysms. J R Soc Interface. 2012;9(74):2047–58. doi: 10.1098/rsif.2012.0097. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Valentín A, Humphrey JD. Parameter sensitivity study of a constrained mixture model of arterial growth and remodeling. J Biomech Eng. 2009;131(10):101006. doi: 10.1115/1.3192144. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Sankaran S, Humphrey JD, Marsden AL. An efficient framework for optimization and parameter sensitivity analysis in arterial growth and remodeling computations. Comput Methods Appl Mech Eng. 2013;256:200–210. doi: 10.1016/j.cma.2012.12.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Fontaine V, Touat Z, Mtairag EM, et al. Role of leukocyte elastase in preventing cellular re-colonization of the mural thrombus. Am J Pathol. 2004;164(6):2077–87. doi: 10.1016/s0002-9440(10)63766-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Wilson JS, Virag L, Di Achille P, Karšaj I, Humphrey JD. Biochemomechanics of intraluminal thrombus in abdominal aortic aneurysms. J Biomech Eng. 2013;135(2):21011-1–21011-14. doi: 10.1115/1.4023437. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Virag L, Wilson JS, Humphrey JD, Karšaj I. A computational model of biochemomechanical effects of intraluminal thrombus on the enlargement of abdominal aortic aneurysms. Ann Biomed Eng. 2015;43(12):2852–2867. doi: 10.1007/s10439-015-1354-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Tong J, Cohnert T, Regitnig P, Holzapfel GA. Effects of age on the elastic properties of the intraluminal thrombus and the thrombus-covered wall in abdominal aortic aneurysms: biaxial extension behaviour and material modelling. Eur J Vasc Endovasc Surg. 2011;42(2):207–19. doi: 10.1016/j.ejvs.2011.02.017. [DOI] [PubMed] [Google Scholar]
- 20.Scott DJA, Prasad P, Philippou H, et al. Clot architecture is altered in abdominal aortic aneurysms and correlates with aneurysm size. Arterioscler Thromb Vasc Biol. 2011;31(12):3004–10. doi: 10.1161/ATVBAHA.111.236786. [DOI] [PubMed] [Google Scholar]
- 21.Varjú I, Sótonyi P, Machovich R, et al. Hindered dissolution of fibrin formed under mechanical stress. J Thromb Haemost. 2011;9(5):979–86. doi: 10.1111/j.1538-7836.2011.04203.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Weisel JW. Stressed fibrin lysis. J Thromb Haemost. 2011;9(5):977–8. doi: 10.1111/j.1538-7836.2011.04258.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Houard X, Touat Z, Ollivier V, et al. Mediators of neutrophil recruitment in human abdominal aortic aneurysms. Cardiovasc Res. 2009;82(3):532–41. doi: 10.1093/cvr/cvp048. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Fontaine V, Jacob M-P, Houard X, et al. Involvement of the mural thrombus as a site of protease release and activation in human aortic aneurysms. Am J Pathol. 2002;161(5):1701–10. doi: 10.1016/S0002-9440(10)64447-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Nackman GB, Karkowski FJ, Halpern VJ, Gaetz HP, Tilson MD. Elastin degradation products induce adventitial angiogenesis in the Anidjar/Dobrin rat aneurysm model. Surgery. 1997;122(1):39–44. doi: 10.1016/s0039-6060(97)90262-2. [DOI] [PubMed] [Google Scholar]
- 26.Valentín A, Humphrey JD, Holzapfel GA. A multi-layered computational model of coupled elastin degradation, vasoactive dysfunction, and collagenous stiffening in aortic aging. Ann Biomed Eng. 2011;39(7):2027–2045. doi: 10.1007/s10439-011-0287-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Isenberg BC, Tranquillo RT. Long-Term Cyclic Distention Enhances the Mechanical Properties of Collagen-Based Media-Equivalents. Ann Biomed Eng. 2003;31(8):937–949. doi: 10.1114/1.1590662. [DOI] [PubMed] [Google Scholar]
- 28.Lillie MA, Gosline JM. Mechanical properties of elastin along the thoracic aorta in the pig. J Biomech. 2007;40(10):2214–2221. doi: 10.1016/j.jbiomech.2006.10.025. [DOI] [PubMed] [Google Scholar]
- 29.Choke E, Cockerill G, Wilson WRW, et al. A review of biological factors implicated in abdominal aortic aneurysm rupture. Eur J Vasc Endovasc Surg. 2005;30(3):227–44. doi: 10.1016/j.ejvs.2005.03.009. [DOI] [PubMed] [Google Scholar]
- 30.Fillinger MF, Marra SP, Raghavan ML, Kennedy FE. Prediction of rupture risk in abdominal aortic aneurysm during observation: Wall stress versus diameter. J Vasc Surg. 2003;37(4):724–732. doi: 10.1067/mva.2003.213. [DOI] [PubMed] [Google Scholar]
- 31.Burke A, Fitzgerald GA. Oxidative stress and smoking-induced vascular injury. Prog Cardiovasc Dis. 2003;46(1):79–90. doi: 10.1016/S0033-0620(03)00076-8. [DOI] [PubMed] [Google Scholar]
- 32.Powell JT. Vascular damage from smoking: disease mechanisms at the arterial wall. Vasc Med. 1998;3(1):21–28. doi: 10.1191/135886398670269973. [DOI] [PubMed] [Google Scholar]
- 33.Mahmud A, Feely J. Effect of smoking on arterial stiffness and pulse pressure amplification. Hypertension. 2003;41(1):183–187. doi: 10.1161/01.HYP.0000047464.66901.60. [DOI] [PubMed] [Google Scholar]
- 34.Enevoldsen MS, Henneberg KA, Jensen JA, Lönn L, Humphrey JD. New interpretation of arterial stiffening due to cigarette smoking using a structurally motivated constitutive model. J Biomech. 2011;44(6):1209–1211. doi: 10.1016/j.jbiomech.2011.01.032. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Bhak RH, Wininger M, Johnson GR, et al. Factors associated with small abdominal aortic aneurysm expansion rate. JAMA Surg. 2015;150(1):44–50. doi: 10.1001/jamasurg.2014.2025. [DOI] [PubMed] [Google Scholar]
- 36.Al-Barjas HS, Ariëns R, Grant P, Scott JA. Raised plasma fibrinogen concentration in patients with abdominal aortic aneurysm. Angiology. 2006;57(5):607–14. doi: 10.1177/0003319706293132. [DOI] [PubMed] [Google Scholar]
- 37.van den Berkmortel FWPJ, Wollersheim H, van Langen H, Smilde TJ, den Arend J, Thien T. Two years of smoking cessation does not reduce arterial wall thickness and stiffness. Neth J Med. 2004;62(7):235–241. [PubMed] [Google Scholar]
- 38.Jatoi NA, Jerrard-Dunne P, Feely J, Mahmud A. Impact of smoking and smoking cessation on arterial stiffness and aortic wave reflection in hypertension. Hypertension. 2007;49(5):981–985. doi: 10.1161/HYPERTENSIONAHA.107.087338. [DOI] [PubMed] [Google Scholar]
- 39.Meade TW, Imeson J, Stirling Y. Effects of changes in smoking and other characteristics on clotting factors and the risk of ischaemic heart disease. Lancet. 1987;330(8566):986–988. doi: 10.1016/s0140-6736(87)92556-6. [DOI] [PubMed] [Google Scholar]
- 40.Deuel TF, Senior RM, Chang D, Griffin GL, Heinrikson RL, Kaiser ET. Platelet factor 4 is chemotactic for neutrophils and monocytes. Proc Natl Acad Sci U S A. 1981;78(7):4584–4587. doi: 10.1073/pnas.78.7.4584. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Parodi FE, Mao D, Ennis TL, Bartoli MA, Thompson RW. Suppression of experimental abdominal aortic aneurysms in mice by treatment with pyrrolidine dithiocarbamate, an antioxidant inhibitor of nuclear factor-kB. J Vasc Surg. 2005;41(3):479–489. doi: 10.1016/j.jvs.2004.12.030. [DOI] [PubMed] [Google Scholar]
- 42.Steinmetz EF, Buckley C, Shames ML, et al. Treatment with simvastatin suppresses the development of experimental abdominal aortic aneurysms in normal and hypercholesterolemic mice. Ann Surg. 2005;241(1):92–101. doi: 10.1097/01.sla.0000150258.36236.e0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Owens AP, Edwards TL, Antoniak S, et al. Platelet inhibitors reduce rupture in a mouse model of established abdominal aortic aneurysm. Arterioscler Thromb Vasc Biol. 2015;35(9):2032–2041. doi: 10.1161/ATVBAHA.115.305537. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Lawrence DM, Singh RS, Franklin DP, Carey DJ, Elmore JR. Rapamycin suppresses experimental aortic aneurysm growth. J Vasc Surg. 2004;40(2):334–338. doi: 10.1016/j.jvs.2004.05.020. [DOI] [PubMed] [Google Scholar]
- 45.Arnoud Meijer C, Stijnen T, Wasser MNJM, Hamming JF, Van Bockel JH, Lindeman JHN. Doxycycline for stabilization of abdominal aortic aneurysms: A randomized trial. Ann Intern Med. 2013;159(12):815–823. doi: 10.1016/j.jvs.2014.02.035. [DOI] [PubMed] [Google Scholar]
- 46.Brown PM, Zelt DT, Sobolev B. The risk of rupture in untreated aneurysms: The impact of size, gender, and expansion rate. J Vasc Surg. 2003;37(2):280–284. doi: 10.1067/mva.2003.119. [DOI] [PubMed] [Google Scholar]
- 47.Ahimastos AA, Formosa M, Dart AM, Kingwell BA. Gender differences in large artery stiffness pre- and post puberty. J Clin Endocrinol Metab. 2003;88(11):5375–5380. doi: 10.1210/jc.2003-030722. [DOI] [PubMed] [Google Scholar]
- 48.Celermajer DS, Sorensen KE, Spiegelhalter DJ, Georgakopoulos D, Robinson J, Deanfield JE. Aging is associated with endothelial dysfunction in healthy men years before the age-related decline in women. J Am Coll Cardiol. 1994;24(2):471–6. doi: 10.1016/0735-1097(94)90305-0. [DOI] [PubMed] [Google Scholar]
- 49.Blanchard JF, Armenian HK, Friesen PP. Risk factors for abdominal aortic aneurysm: results of a case-control study. Am J Epidemiol. 2000;151(6):575–583. doi: 10.1093/oxfordjournals.aje.a010245. [DOI] [PubMed] [Google Scholar]
- 50.Vande Geest JP, Sacks MS, Vorp DA. The effects of aneurysm on the biaxial mechanical behavior of human abdominal aorta. J Biomech. 2006;39(7):1324–34. doi: 10.1016/j.jbiomech.2005.03.003. [DOI] [PubMed] [Google Scholar]
- 51.Tong J, Schriefl AJ, Cohnert T, Holzapfel GA. Gender differences in biomechanical properties, thrombus age, mass fraction and clinical factors of abdominal aortic aneurysms. Eur J Vasc Endovasc Surg. 2013;45(4):364–72. doi: 10.1016/j.ejvs.2013.01.003. [DOI] [PubMed] [Google Scholar]
- 52.Wilson JS, Baek S, Humphrey JD. Parametric study of effects of collagen turnover on the natural history of abdominal aortic aneurysms. Proc Math Phys Eng Sci. 2013;469(2150):20120556. doi: 10.1098/rspa.2012.0556. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Brown LC, Powell JT. Risk factors for aneurysm rupture in patients kept under ultrasound surveillance. Ann Surg. 1999;230(3):289–297. doi: 10.1097/00000658-199909000-00002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.O’Rourke MJ, McCullough JP, Kelly S. An Investigation of the relationship between hemodynamics and thrombus deposition within patient-specific models of abdominal aortic aneurysm. Proc Inst Mech Eng Part H J Eng Med. 2012;226(7):548–564. doi: 10.1177/0954411912444080. [DOI] [PubMed] [Google Scholar]
- 55.Chobanian AV, Bakris GL, Black HR, et al. Seventh report of the Joint National Committee on Prevention, Detection, Evaluation, and Treatment of High Blood Pressure. Hypertension. 2003;42(6):1206–1252. doi: 10.1161/01.HYP.0000107251.49515.c2. [DOI] [PubMed] [Google Scholar]
- 56.Vorp DA, Lee PC, Wang DH, et al. Association of intraluminal thrombus in abdominal aortic aneurysm with local hypoxia and wall weakening. J Vasc Surg. 2002;34(2):291–9. doi: 10.1067/mva.2001.114813. [DOI] [PubMed] [Google Scholar]
- 57.Parr A, McCann M, Bradshaw B, Shahzad A, Buttner P, Golledge J. Thrombus volume is associated with cardiovascular events and aneurysm growth in patients who have abdominal aortic aneurysms. J Vasc Surg. 2011;53(1):28–35. doi: 10.1016/j.jvs.2010.08.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Golledge J, Iyer V, Jenkins J, Bradshaw B, Cronin O, Walker PJ. Thrombus volume is similar in patients with ruptured and intact abdominal aortic aneurysms. J Vasc Surg. 2014;59(2):315–20. doi: 10.1016/j.jvs.2013.08.036. [DOI] [PubMed] [Google Scholar]
- 59.Krievins D, Thora S, Zarins CK. Gigantic 25-cm abdominal aortic aneurysm. J Vasc Surg. 2015;61(4):1067. doi: 10.1016/j.jvs.2014.09.005. [DOI] [PubMed] [Google Scholar]
- 60.Zambrano BA, Gharahi H, Lim C, et al. Association of intraluminal thrombus, hemodynamic forces, and abdominal aortic aneurysm expansion using longitudinal CT images. Ann Biomed Eng. 2015:1–13. doi: 10.1007/s10439-015-1461-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Basciano C, Kleinstreuer C, Hyun S, Finol EA. A relation between near-wall particle-hemodynamics and onset of thrombus formation in abdominal aortic aneurysms. Ann Biomed Eng. 2011;39(7):2010–26. doi: 10.1007/s10439-011-0285-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Touat Z, Ollivier V, Dai J, et al. Renewal of mural thrombus releases plasma markers and is involved in aortic abdominal aneurysm evolution. Am J Pathol. 2006;168(3):1022–30. doi: 10.2353/ajpath.2006.050868. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Mäyränpää MI, Trosien JA, Fontaine V, et al. Mast cells associate with neovessels in the media and adventitia of abdominal aortic aneurysms. J Vasc Surg. 2009;50(2):388–96. doi: 10.1016/j.jvs.2009.03.055. [DOI] [PubMed] [Google Scholar]
- 64.Anidjar S, Salzmann JL, Gentric D, Lagneau P, Camilleri JP, Michel JB. Elastase-induced experimental aneurysms in rats. Circulation. 1990;82(3):973–981. doi: 10.1161/01.CIR.82.3.973. [DOI] [PubMed] [Google Scholar]
- 65.Abdul-Hussien H, Soekhoe RGV, Weber E, et al. Collagen Degradation in the Abdominal Aneurysm. Am J Pathol. 2007;170(3):809–817. doi: 10.2353/ajpath.2007.060522. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Reeps C, Pelisek J, Seidl S, et al. Inflammatory infiltrates and neovessels are relevant sources of MMPs in abdominal aortic aneurysm wall. Pathobiology. 2009;76(5):243–52. doi: 10.1159/000228900. [DOI] [PubMed] [Google Scholar]
- 67.Brophy CM, Reilly JM, Smith GJ, Tilson MD. The role of inflammation in nonspecific abdominal aortic aneurysm disease. Ann Vasc Surg. 1991;5(3):229–33. doi: 10.1007/BF02329378. [DOI] [PubMed] [Google Scholar]
- 68.Treska V, Kocova J, Boudova L, et al. Inflammation in the wall of abdominal aortic aneurysm and its role in the symptomatology of aneurysm. Cytokines Cell Mol Ther. 2002;7(3):91–7. doi: 10.1080/13684730310001652. [DOI] [PubMed] [Google Scholar]