Bayesian treatment comparison using parametric mixture priors computed from elicited histograms

Abstract

A Bayesian methodology is proposed for constructing a parametric prior on two treatment effect parameters, based on graphical information elicited from a group of expert physicians. The motivating application is a 70-patient randomized trial to compare two treatments for idiopathic nephrotic syndrome in children. The methodology relies on histograms of the treatment parameters constructed manually by each physician, applying the method of Johnson et al. (2010). For each physician, a marginal prior for each treatment parameter characterized by location and precision hyperparameters is fit to the elicited histogram. A bivariate prior is obtained by averaging the marginals over a latent physician effect distribution. An overall prior is constructed as a mixture of the individual physicians’ priors. A simulation study evaluating several versions of the methodology is presented. A framework is given for performing a sensitivity analysis of posterior inferences to prior location and precision and illustrated based on the idiopathic nephrotic syndrome trial.

1 Introduction

A pervasive problem when comparing treatments based on randomized clinical trials in children, rare diseases, or important disease subgroups, is that the sample size often is too small to obtain a confirmatory conclusion using conventional statistical methods. Examples of subgroups include patients with a biomarker believed to interact with treatment, an age interval arising due to metabolic heterogeneity in children, or cancer patients who have relapsed after achieving remission with frontline therapy. In such settings, even a multi-institution trial may not obtain a sample size large enough to provide convincing comparative inferences.

Depending on the setting, the treatment parameter may be the probability of a binary response, the mean of a real-valued outcome, or mean survival time. As a toy example to illustrate the sort of settings we have in mind, suppose that one wishes to compare the response probabilities, θ₁ and θ₂, of two competing treatments. If a randomized trial of 160 patients gives 39 responses in 75 (52%) patients for treatment 1 and 54 responses in 85 (64%) patients for treatment 2, then a frequentist two-sided binomial test of the null hypothesis θ₁ = θ₂ has p value = .14, which conventionally is considered nonsignificant. From a Bayesian viewpoint, if one assumes independent $\mathit{beta}(.50,.50)$ priors for θ₁ and θ₂, then the posterior probability that treatment 2 provides at least a .15 improvement over treatment 1 is $\text{Pr}({\theta }_1+.15<{\theta }_2|\mathit{data})$ = .32, and the posterior 95% credible intervals (CIs) are .41–.63 for θ₁ and .53–.73 for θ₂, which overlap substantially. Thus, while the data suggest that treatment 2 is superior, conventional comparative inferences are far from confirmatory. Assuming the above sample response rates of 52 and 64%, for example, hypothetical data 130/250 and 185/290 having these rates but based on much larger samples would give nonoverlapping 95% posterior CIs .46–.58 and .58–69. This suggests that, if one were planning a trial using nonoverlapping posterior 95% CIs as a criterion for posterior reliability, a total sample size of roughly 540 would be required. As explained above, we are motivated by settings where a sample this large simply is not practical. Because the ultimate goal of a randomized trial is to provide a convincing basis for practicing physicians to choose between treatments, in settings where the sample size is not large and it is unlikely that a trial will be repeated, one reasonable course of action is seek expert opinion as an additional source of information. This leads naturally to a Bayesian approach wherein expert opinion is elicited and formalized by an informative prior distribution on (θ₁, θ₂).

Our proposed methodology was motivated by the desire to analyze the results of a randomized trial of two treatments for idiopathic nephrotic syndrome, which is the most common kidney disease in children. About 90% of cases are sensitive to corticosteroids, and among them about 60% have dependence on corticosteroids sufficient to justify the addition of an immunosuppressive agent to reduce the frequency of relapses and side effects.^1,2 Cyclophosphamide is an immunosuppressive agent often used as first-line therapy; and in case of failure, the second-line therapy used most often is cyclosporine. For both treatments, duration of administration is limited by toxicity, which occurs in the bone marrow and gonads with cyclophosphamide and in the kidneys with cyclosporine. The risk of toxicity is the primary reason that cyclophosphamide is administered on a short, three-month basis.³ Observational studies have shown that, if no toxicity occurs, cyclophosphamide may achieve remission at one year in 17–67% of patients. A new treatment, mycophenolate mofetil (MMF), may reduce the corticosteroid dependence and thus limit the need for cyclosporine. Observational studies have shown that continuous treatment with MMF provides remission in 42–75% of patients.^4,5 A key motivation is that MMF has been shown to be nonnephrotoxic and nongonadotoxic, so if it can be established that MMF has a response rate similar to that of cyclophosphamide, then MMF would be preferable due to its superior safety.

Motivated by these results, a randomized trial (NEPHROMYCY, NCT01092962) was conducted to compare the efficacy of cyclophosphamide (148 mg/kg during 12 weeks) versus MMF (1200 mg/m² during 18 months) in children with steroid-dependent nephrotic syndrome. The primary outcome was response, defined as relapse not occurring during the first 24 months of follow-up. The trial included 70 patients from 26 pediatric nephrology centers in France. Denoting the response probabilities by θ₁ for cyclophosphamide and θ₂ for MMF, a key posterior probability is ${\pi }_{1,2}^E(\epsilon )$ = Pr$({\theta }_1-\epsilon <{\theta }_2|\mathit{data}),$ computed for small ε = 0.05 or 0.10. A large value of ${\pi }_{1,2}^E(\epsilon )$ provides evidence that MMF is “ε-equivalent” to cyclophosphamide in terms of their response probabilities. This may motivate a practicing physician to use MMF rather than cyclophosphamide, since MMF is nontoxic.

Because idiopathic nephrotic syndrome is a rare disease, it was recognized at the start that the trial’s sample size would be small, and that 70 children could be expected to be accrued in a realistic time period. A Bayesian analysis of the trial data was planned in the protocol. To obtain prior expert opinion before the trial was begun, each of 17 physicians experienced in treating this disease was asked to construct a histogram reflecting what they believed to be the distribution of the probability of response for each of MMF and cyclophosphamide, denoted by θ₁ and θ₂. This was done by applying the so-called “bins-and-chips” graphical method of Johnson et al.,⁶ which we will describe in detail below, in Section 3.

The general issue that we address in this article is how histograms elicited in this way from a set of experts may be used to construct a parametric prior on (θ₁, θ₂) as a basis for a Bayesian analysis to compare the two parameters. Our proposed methodology for constructing a parametric prior is carried out in three stages. In the first stage, a parametric distribution for the marginal priors of the θ_j’s, with location parameter μ and precision parameter $\gamma ,$ is specified. For each expert and each ${\theta }_j,$ this model is fit to the elicited histogram to obtain a marginal parametric prior. In the second stage, a bivariate expert-specific prior for (θ₁, θ₂) is constructed by averaging the product of each expert’s two marginal parametric priors over a distribution for two correlated latent expert effects, one for μ and the other for $\gamma .$ We consider two ways to formulate this latent effect distribution, either assuming homogeneity across experts or including expert-specific covariates, if they are available. In the third stage, an overall joint prior for (θ₁, θ₂) is constructed as a discrete mixture of all the experts’ bivariate parametric priors. For this mixture prior, each expert’s weight may be a covariate-based index of their experience, or an index of the agreement between the means of the elicited histograms and corresponding model-based parameter estimates obtained from the data. A third approach is simply to weight the experts equally. Once the overall prior has been established, it may be used as a basis for Bayesian analyses of (θ₁, θ₂).

To address the issues of how prior location and precision may affect posterior inferences, we provide a formal framework for conducting a prior-to-posterior sensitivity analysis. We do this by constructing an array of alternative priors, each obtained by specifying numerical values of two quantities, one that changes the prior’s location E(θ₂–θ₁) and the other that changes its precision. Posterior quantities used to compare θ₁ to θ₂ are computed for each alternative prior. This produces an array of posterior values, one for each combination of location shift and precision transformation, including one based on the untransformed prior. This set of prior-to-posterior quantities may be used as a basis for making a conclusion about the comparative effectiveness of the two treatments, in light of both the observed data and the elicited prior opinion.

Making inferences about medical treatments based on small- to moderate-sized clinical trials while assuming informative priors constructed from elicited expert opinion is inherently controversial. While the ability to formally incorporate expert opinion a priori may be considered a major benefit of taking a Bayesian approach, it must be done carefully. Use of an informative prior constructed from elicited expert opinion may be seen as introducing bias into posterior inferences. The problems of eliciting expert opinion, constructing priors from the elicited values, and performing Bayesian analyses on that basis have been addressed by numerous authors in many different settings. Many authors have discussed methods for prior elicitation,^6–12 establishing priors for Bayesian model-based clinical trials and medical applications,^13–15 graphical methods for prior elicitation,^6,16,17 and combining priors and expert opinion.^18,19 A review is given by O’Hagan et al.²⁰ Our methodology is related to the general development for combining expert priors given by Albert et al.,²¹ who consider the somewhat different problem of using elicited probabilities and elicited quantiles to construct a prior. Their framework requires an additional parameter quantifying prior uncertainty to be elicited from each expert, which is not required by our method.

Our proposed methodology for constructing a parametric prior for (θ₁, θ₂) based on elicited histograms, and the process of solving numerically for hyperparameters, will be presented in Section 2. In Section 3, we describe how the graphical bins-and-chips method of Johnson et al.⁶ was applied to elicit histograms for the response probabilities of MMF and cyclophosphamide for the NEPHROMYCY trial, and how beta distributions were fit to the histograms. In Section 4, a simulation study is presented that compares six different versions of our proposed method, obtained from the two ways to formulate the latent physician effect distribution and the three ways to weight the experts. Section 5 describes a formal method for performing sensitivity analyses of posterior inferences to prior location and informativeness, and this is illustrated by a simulated version of the NEPHROMYCY data set. We close with a brief discussion in Section 6.

2 Parametric models for the priors

2.1 Definition of treatment parameters

For the i-th subject in the data set to be analyzed, $i=1,\dots ,n,$ denote treatment by ${\tau }_i,$ observed outcome by $Y_i,$ and covariates by $Z_i$ = $(Z_{i,1},\dots ,Z_{i,q}).$ Index treatments by $j=1,2,$ and denote ${\theta }_{j,i}$ = $E(Y_i|{\tau }_i=j,Z_i).$ As in Wahed and Thall,²² we define the overall effect of treatment j as the mean over the sample of n_j subjects

$${\overline{\theta }}_j=\int {\theta }_{j,i}(z)f_Z(z)\text{d}z=\frac{1}{n_j}\sum _{i=1}^{n_j}{\theta }_{j,i}$$ (1)

where $f_Z$ denotes the patient covariate distribution. That is, for each treatment $j=1,2,$ we define ${\overline{\theta }}_j$ by averaging over the empirical distribution of subject covariates, with subjects weighted equally within treatment groups. If subject covariates are not available and subjects are assumed to be homogeneous, then ${\theta }_{j,1}$ = $\dots$ = ${\theta }_{j,n_j}$ = ${\overline{\theta }}_j.$ Note that we have elaborated the notation by now denoting the two overall treatment parameters as ${\overline{\theta }}_1$ and ${\overline{\theta }}_2$, rather than ${\theta }_1$ and ${\theta }_2$, as done previously in Section 1.

2.2 Probability models for the physicians’ marginal priors

Let $k=1,\dots ,K$ index the expert physicians from whom the histograms for ${\overline{\theta }}_1$ and ${\overline{\theta }}_2$ are elicited. We formulate a marginal model for the k-th physician’s prior on ${\overline{\theta }}_j$ by assuming a parametric distribution $p_{j,k}({\overline{\theta }}_j|{\mu }_{j,k},{\gamma }_{j,k}),$ where ${\mu }_{j,k}$ is a location parameter and ${\gamma }_{j,k}>0$ is a precision parameter, for j = 1, 2. We formulate the marginal distributions in terms of location and precision parameters to facilitate analysis of the sensitivity of posterior inferences to prior bias and informativeness, which we will describe in Section 5 below. Association between ${\overline{\theta }}_1$ and ${\overline{\theta }}_2$ in each physician’s joint prior is induced by assuming a bivariate prior for two latent physician effects (frailties), one effect for location and a second effect for precision. The marginals of $[{\overline{\theta }}_1|{\mu }_{1,k},{\gamma }_{1,k}]$ and $[{\overline{\theta }}_2|{\mu }_{2,k},{\gamma }_{2,k}]$ are defined conditional on the k-th physician’s frailties, and a bivariate prior then is obtained by averaging the product of these conditional marginals over the frailty distribution.

Models for the marginal priors of the ${\theta }_{j,k}$’s may be chosen for their tractability, since they will be fit to the elicited histograms. We require that they are parameterized in terms of location and precision parameters, μ and $\gamma ,$ to give the structure needed for conducting prior-to-posterior sensitivity analyses. For binary Y, where the ${\theta }_{j,k}$’s are probabilities, the beta distribution is a convenient, flexible family of parametric priors. Suppressing (j, k) temporarily, the beta pdf with mean μ and variance $\mu (1-\mu )/(1+\gamma )$ is given by

$$p(x|\mu ,\gamma )=\frac{x^{\mu \gamma -1}(1-x{)}^{(1-\mu )\gamma -1}}{B(\mu \gamma ,(1-\mu )\gamma )},0<x<1$$

where B(a, b) = $\Gamma (a)\Gamma (b)/\Gamma (a+b)$ and $\Gamma (·)$ denotes the gamma function. Thus, larger γ corresponds to greater precision. For real-valued Y, the normal distribution with mean μ and precision parameter γ = 1/$\mathit{var}(\theta )$ is a natural choice for the prior family. For Y an event time or other nonnegative-valued random variable, there are several reasonable two-parameter models that may be defined in terms of location and precision parameters. For example, a flexible model for the prior of the ${\theta }_{j,k}$’s is a gamma distribution with mean μ and precision γ, with pdf

$$p(x|\mu ,\gamma )=\frac{(\mu \gamma {)}^{{\mu }^2\gamma }{x}^{{\mu }^2\gamma -1}{e}^{-\mu \gamma x}}{\Gamma ({\mu }^2\gamma )}x>0$$

To obtain priors for ${\overline{\theta }}_1$ and ${\overline{\theta }}_2,$ the parametric models $p_{1,k}({\overline{\theta }}_1|{\mu }_{1,k},{\gamma }_{1,k})$ and $p_{2,k}({\overline{\theta }}_2|{\mu }_{2,k},{\gamma }_{2,k})$ are fit to the corresponding histograms elicited from the k-th physician, which yields numerical values of the four hyperparameters ${\mu }_{1,k},{\gamma }_{1,k},{\mu }_{2,k},{\gamma }_{2,k},$ for each $k=1,\dots ,K.$ A numerical method for obtaining these fits is described below, in Section 3.2.

Since the two marginal prior distributions $p_{1,k}$ and $p_{2,k}$ both are obtained from the k-th physician, this implies that, a priori, ${\overline{\theta }}_1$ and ${\overline{\theta }}_2$ may be associated with each other for each physician. To formalize this idea, we propose two similar but different approaches for constructing a bivariate prior $p_k({\overline{\theta }}_1,{\overline{\theta }}_2)$ from the marginal priors $p_{1,k}$ and $p_{2,k}$, for each $k=1,\dots ,K.$ Both approaches rely on bivariate latent physician effects (frailties), which are conceptual variables that are not observed. The frailties are used to induce prior within-physician correlation between ${\overline{\theta }}_1$ and ${\overline{\theta }}_2,$ and thus obtain a bivariate prior on these parameters for each physician. The physician frailites are motivated by the idea that, given the two histograms and resulting beta priors obtained from the k-th physician expert, the pairs $({\mu }_{1,k},{\gamma }_{1,k})$ and $({\mu }_{2,k},{\gamma }_{2,k})$ must be associated with each other through the unobserved physician frailty, which in turn implies that ${\overline{\theta }}_1$ and ${\overline{\theta }}_2$ are associated with each other for each physician.

2.3 First method for computing prior hyperparameters

To implement Method 1 for establishing bivariate physician-specific priors on $({\overline{\theta }}_1,{\overline{\theta }}_2),$ for each $k=1,\dots ,K,$ we first link ${\mu }_{j,k}$ and ${\gamma }_{j,k}$ to linear terms, each of which is the sum of a real-valued parameter and a latent physician effect. Let ${\epsilon }_k=({\epsilon }_{k,\mu },{\epsilon }_{k,\gamma }),k=1,\dots ,K,$ be independent and identically distributed (iid) pairs of real-valued latent physician effects, following a bivariate normal distribution

$${\epsilon }_k\hspace{1em}\sim N(\mathbf{0},\mathbf{\Sigma })=N(\mathbf{0},[\begin{array}{cc}{\sigma }_{\epsilon ,\mu }^2& \hfill \rho {\sigma }_{\epsilon ,\mu }{\sigma }_{\epsilon ,\gamma }\hfill \\ \rho {\sigma }_{\epsilon ,\mu }{\sigma }_{\epsilon ,\gamma }& \hfill {\sigma }_{\epsilon ,\gamma }^2\hfill \end{array}])$$ (2)

Denote $\sigma$ = $({\sigma }_{\epsilon ,\mu },{\sigma }_{\epsilon ,\gamma },\rho ),$ and denote this bivariate normal by $p_{\epsilon }(x_{\mu },x_{\gamma }|\sigma )$ for $(x_{\mu },x_{\gamma })\in R^2.$ Let $g_{\mu }$ and $g_{\gamma }$ denote appropriate link functions. If each ${\overline{\theta }}_j$ is a probability, then $g_{\mu }$ may be the logit, probit, or complementary log–log link. The identity link or log link may be used, respectively, if ${\mu }_{j,k}$ is real-valued or positive real-valued. Since ${\gamma }_{j,k}>0$ in any case, $g_{\gamma }$ may be the log link. In our motivating application, $g_{\mu }$ is the logit link and $g_{\gamma }$ is the log link.

For Method 1, we assume that

$$\begin{array}{c}{g}_{\mu }({\mu }_{j,k})={\upsilon }_{j,k,\mu }+{\epsilon }_{k,\mu }\\ g_{\gamma }({\gamma }_{j,k})={\upsilon }_{j,k,\gamma }+{\epsilon }_{k,\gamma }\end{array}$$ (3)

where the ${\upsilon }_{j,k,\mu }$’s are real-valued location parameters and the ${\upsilon }_{j,k,\gamma }$’s are real-valued precision parameters. The joint prior of $({\overline{\theta }}_1,{\overline{\theta }}_2)$ for the k-th physician is obtained by averaging over the bivariate physician effect distribution. Denoting ${\upsilon }_k$ = $({\upsilon }_{1,k,\mu },{\upsilon }_{2,k,\mu },{\upsilon }_{1,k,\gamma },{\upsilon }_{2,k,\gamma }),$ the joint prior is

$$p_k({\overline{\theta }}_1,{\overline{\theta }}_2|{\upsilon }_k,\sigma )={\int }_{R^2}\{\underset{j=1,2}{\Pi }{p}_{j,k}({\overline{\theta }}_j|g_{\mu }^{-1}({\upsilon }_{j,k,\mu }+x_{\mu }),g_{\gamma }^{-1}({\upsilon }_{j,k,\gamma }+x_{\gamma }))\}{p}_{\epsilon }(x_{\mu },x_{\gamma }|\sigma ){\mathit{dx}}_{\mu }{\mathit{dx}}_{\gamma }$$

Under this parametric model, the hyperparameters ${\upsilon }_k$ are specific to p_k only, whereas the hyperparameters $\sigma$ that characterize Σ in the bivariate normal distribution of the ${\epsilon }_k$’s appear in all K physician’s priors. The frailty prior $p_{\epsilon }(x_{\mu },x_{\gamma }|\sigma )$ induces correlation and shrinks ${\overline{\theta }}_1$ and ${\overline{\theta }}_2$ toward each other, with the degree of shrinkage determined by the assumed numerical values of the entries of $\sigma .$

To implement our Method 1, when applying the elicitation method of Johnson et al.,⁶ there is no elicited prior information on the parameters $\sigma$ = $(\rho ,{\sigma }_{\epsilon ,\mu },{\sigma }_{\epsilon ,\gamma })$ that characterize the variance–covariance matrix Σ of the latent effect distribution that we have introduced. Thus, numerical values of these three hyperparameters must be specified. It may be argued that introduction of $({\epsilon }_{k,\mu },{\epsilon }_{k,\gamma })$ is an unnecessary complication, and a more parsimonious approach would be to assume that the two beta priors for ${\overline{\theta }}_1$ and ${\overline{\theta }}_2$ are independent. Alternatively, it may be argued that, if the latent physician effects are included in the model, then values of $\rho ,$ ${\sigma }_{\epsilon ,\mu }$, and ${\sigma }_{\epsilon ,\gamma }$ also should be elicited, that is, that our assumed model requires a more elaborate elicitation procedure. Since the meanings of these second-order parameters to a physician are not entirely straightforward, however, it is not obvious how such an additional elicitation may be carried out. As shown in Section 2.4 below, our second method for computing hyperparameters does provide numerical values of $\sigma ,$ essentially because it exploits the information in physician covariates. Thus, to complete the prior specification when implementing Method 1, we use the numerical values of $\sigma$ obtained by Method 2. Still, since in theory, any value of $\rho \in (-1,1)$ may be specified; and moreover in some applications, physician covariates may not be available. In Section 4, we will present an analysis of the sensitivity of posterior inferences to ρ when using Method 1.

2.4 Second method for computing prior hyperparameters

The second approach, Method 2, for constructing physician-specific priors on $({\overline{\theta }}_1,{\overline{\theta }}_2)$ incorporates physician covariate vectors, $X_1,\dots ,X_K,$ if they are available. Thus, for Method 2, the model for $p_{j,k}({\overline{\theta }}_j|{\mu }_{j,k},{\gamma }_{j,k})$ is extended to include regression structure. This approach is appropriate if it is desired that the prior should reflect physician covariate effects on the ${\mu }_{j,k}$’s and ${\gamma }_{j,k}$’s. Method 2 also uses the values of ${\mu }_{1,k},{\gamma }_{1,k},{\mu }_{2,k},{\gamma }_{2,k}$ obtained by fitting the parametric models $p_{1,k}({\overline{\theta }}_1|{\mu }_{1,k},{\gamma }_{1,k})$ and $p_{2,k}({\overline{\theta }}_2|{\mu }_{2,k},{\gamma }_{2,k})$ to the elicited histograms, but in a very different way than Method 1. For Method 2, the latent physician effects are as before, but for each k, we assume that

$$\begin{array}{c}{g}_{\mu }({\mu }_{j,k})={\upsilon }_{j,\mu }+{\beta }_{\mu }{X}_k+{\epsilon }_{k,\mu }+e_{\mu }\\ g_{\gamma }({\gamma }_{j,k})={\upsilon }_{j,\gamma }+{\beta }_{\gamma }{X}_k+{\epsilon }_{k,\gamma }+e_{\gamma }\end{array}$$ (4)

where $\mathbf{e}=(e_{\mu },e_{\gamma })\hspace{1em}\sim N_2(0,(\begin{array}{cc}{\sigma }_0^2& \hfill 0\hfill \\ 0& \hfill {\sigma }_0^2\hfill \end{array}))$ are general error terms associated with location and scale that do not vary with (j, k). Denoting $\beta$ = $({\beta }_{\mu },{\beta }_{\gamma }),$ with Method 2, we define the marginals of ${\overline{\theta }}_1$ and ${\overline{\theta }}_2$ conditional on both $X_k$ and ${\epsilon }_k,$ as

$$p_{j,k}({\overline{\theta }}_j|{\upsilon }_{j,\mu },{\upsilon }_{j,\gamma },\beta ,X_k,{\epsilon }_k)$$

for $j=1,2.$ In this regression formulation, there now are four intercept parameters, $\upsilon$ = $({\upsilon }_{1,\mu },{\upsilon }_{1,\gamma },{\upsilon }_{2,\mu },{\upsilon }_{2,\gamma }),$ in the linear terms, and these are identical for all physicians, since allowing them to vary with k would render the model nonidentifiable. This is a key difference from the model (3) used with Method 1, where the intercept parameters vary with physician $k=1,\dots ,K.$ Thus, for Method 2, between-physician variability is accounted for by their covariates.

For Method 2, the available physician covariate information allows numerical values of $(\upsilon ,\beta ,\sigma )$ in the physician covariate regression model to be computed. A numerical value of σ₀ must be specified, however. To implement Method 2, we obtain these hyperparameter values by treating the location and dispersion parameters, obtained from the elicited histograms, as pseudo outcomes and the hyperparameter vector $(\upsilon ,\beta ,\sigma )$ as pseudo parameters, fit regression model (4), and use the estimated pseudo parameters as the prior means of $(\upsilon ,\beta ,\sigma )$ in the marginal priors $\{p_{j,k}({\overline{\theta }}_j|X_k,\upsilon ,\beta ,\sigma ),j=1,2,k=1,\dots ,K\}.$ This fit may be done in several different ways, all of which give very similar numerical results. We did this by assuming independent N (0,100) pseudo priors for the elements of $\upsilon$ and $\beta ,$ and inverse gamma or uniform distributions for the elements of Σ. Additional details are given below, in Section 3.2. The posterior means obtained from fitting this nonlinear Bayesian regression model were used as the hyperparameters for the physician-specific marginal priors. Given these marginal priors for the k-th physician, the joint prior of $({\overline{\theta }}_1,{\overline{\theta }}_2)$ is obtained, as in Method 1, by averaging over the bivariate physician effect distribution

$$\begin{array}{c}{p}_k({\overline{\theta }}_1,{\overline{\theta }}_2|\upsilon ,\beta ,\sigma ,X_k)=\hfill \\ {\int }_{R^2}[\underset{j=1,2}{\Pi }{p}_{j,k}\{{\overline{\theta }}_j|g_{\mu }^{-1}({\upsilon }_{j,\mu }+{\beta }_{\mu }{X}_k+x_{\mu }),g_{\gamma }^{-1}({\upsilon }_{j,\gamma }+{\beta }_{\gamma }{X}_k+x_{\mu })\}]p_{\epsilon }(x_{\mu },x_{\gamma }|\sigma ){\mathit{dx}}_{\mu }{\mathit{dx}}_{\gamma }\end{array}$$

For Method 2, the K bivariate priors have identical hyperparameter vectors, $(\upsilon ,\beta ,\sigma ),$ and the prior p_k is specific to the k-th physician only through the covariate vector $X_k.$

2.5 Mixture priors

Given the K bivariate physician-specific parametric priors obtained by either Method 1 or 2, let $w$ = $(w_1,\dots ,w_K)$ denote physician weights that sum to 1. Using Method 1, the combined prior of $({\overline{\theta }}_1,{\overline{\theta }}_2)$ is defined to be the mixture

$$p({\overline{\theta }}_1,{\overline{\theta }}_2|{\upsilon }_1,\dots ,{\upsilon }_K,\sigma )=\sum _{k=1}^K{w}_k{p}_k({\overline{\theta }}_1,{\overline{\theta }}_2|{\upsilon }_k,\sigma )$$ (5)

and with Method 2 the combined prior is

$$p({\overline{\theta }}_1,{\overline{\theta }}_2|\upsilon ,\beta ,\sigma ,X_1,\dots ,X_K)=\sum _{k=1}^K{w}_k{p}_k({\overline{\theta }}_1,{\overline{\theta }}_2|\upsilon ,\beta ,\sigma ,X_k)$$ (6)

The physician weights $w$ may be determined in several different ways, three of which are described here. To construct $w$ empirically, denoting the treatment of patient i by ${\tau }_i,$ one may first fit a likelihood for $[Y_i|{\tau }_i,Z_i]$ to the data ${\mathcal{D}}_n$, and denote the maximum likelihood estimates of the parameters for each (j, i) by ${\hat{\theta }}_{j,i}^{(\mathit{like})},$ with ${\hat{\theta }}^{(\mathit{like})}$ the 2 n-vector of these estimates. Alternatively, estimates may be obtained as posterior means computed under a Bayesian model with noninformative pseudo priors. For each $j=1,2,$ we quantify the mean of θ_j obtained from the elicited histogram of physician k by its empirical mean, which we denote by ${\hat{\theta }}_{j,k}^{(\mathit{elicited})}.$ For the k-th physician, the agreement between the two mean vectors ${\hat{\theta }}_k^{(\mathit{elicited})}$ = $({\hat{\theta }}_{1,k}^{(\mathit{elicited})},{\hat{\theta }}_{2,k}^{(\mathit{elicited})})$ computed from that physician’s elicited histograms and the 2 n likelihood data-based estimated mean vectors ${\hat{\theta }}^{(\mathit{like})}$ can be quantified by the mean absolute deviation

$$\Vert {\hat{\theta }}_k^{(\mathit{elicited})}-{\hat{\theta }}^{(\mathit{like})}\Vert =\frac{1}{2n}\sum _{j=1}^2\sum _{i=1}^n|{\hat{\theta }}_{j,k}^{(\mathit{elicited})}-{\hat{\theta }}_{j,i}^{(\mathit{like})}|$$

Since smaller $\Vert {\hat{\theta }}_k^{(\mathit{elicited})}-{\hat{\theta }}^{(\mathit{like})}\Vert$ corresponds to closer agreement, we define the physician weights to be

$$w_k=\frac{\Vert {\hat{\theta }}_k^{(\mathit{elicited})}-{\hat{\theta }}^{(\mathit{like})}){\Vert }^{-1}}{\sum _{r=1}^K\Vert {\hat{\theta }}_r^{(\mathit{elicited})}-{\hat{\theta }}^{(\mathit{like})}){\Vert }^{-1}}$$

If physician covariates are available, then an alternative way to define the physician weights using the covariates is as follows. Without loss of generality, assume that each physician covariate is positive-valued and that larger $X_{k,l}$ corresponds to greater reliability of physician k, such as $X_{k,l}$ being years of experience. The weights then can be defined as

$$w_k=\frac{1}{q}\sum _{l=1}^q\frac{X_{k,l}}{\sum _{r=1}^K{X}_{r,l}}$$

A larger value of $X_{k,l}/\sum _{r=1}^K{X}_{r,l}$ corresponds to greater reliability of the opinion of physician k, relative to the other physicians, in terms of the l-th covariate. The average over $l=1,\dots ,q$ treats the covariates as being equally important. With this weighting scheme, the physician-specific priors computed using Method 2 use each physician’s covariates twice, once to obtain the prior p_k and a second time to obtain the weight $w_k.$ A third alternative is simply to weight the physicians equally by setting all w_k = $1/K.$

3 Bins and chips prior elicitation

When planning the NEPHROMYCY trial, each physician’s prior on each θ_j was elicited by applying the bins and chips method of Johnson et al.,⁶ as follows. The Bayesian approach first was explained to the group of physicians at a pretrial planning meeting. This included explanations of the primary efficacy outcome, and how a priori belief is combined with data, by application of Bayes’ theorem, to compute a posterior distribution for making inferences about key parameters. An example of Bayesian thinking was presented, in which a physician who sees a patient reporting a pain in their chest may have the prior belief that the patient’s actual illness has probability distribution Pr(anxiety) = .10, Pr(myocardiac infarction) = Pr(MI) = .30, and Pr(pneumonia) = .60. Then, after obtaining the results of a chest X-ray and electrocardiogram, this information changes the physician’s belief so that the new probabilities are Pr(anxiety) = .05, Pr(MI) = 0, and Pr(pneumonia) = .95.

It was next explained that analysis of the trial data would require each of the physicians to provide their own prior on the response probabilities with each treatment (M or C). It was then explained that each physician would receive, by mail, an envelope containing a questionnaire (given in the Supplementary Material) that, once they had filled it out, would characterize their prior. The items of the questionnaire were then explained, including how to carry out the so-called “bins and chips” construction of each prior histogram. They were told that the envelope would contain 40 colored stickers, and that 20 stickers would be used to construct each prior. It was explained that, for each treatment response probability, each sticker represented probability .05, and that they should place 20 stickers into the discrete intervals printed on the questionnaire so that the resulting histogram would represent their belief about the distribution of the response probability for that treatment. The intervals used in the questionnaire were [0, .05], [.06, .10],…, [.91, .95], [.96, 1.00]. They were told to carry out this exercise for each of the two treatments, and mail back the competed questionnaire. During this explanation, a graphical illustration was provided, including several examples of what a competed histogram might look like. This illustration was the figure with colored chips given in Appendix C of Johnson et al.⁶

3.1 Computing marginal prior hyperparameters

In this section, we explain how one may perform the computations to obtain the parameters of each marginal parametric prior from the corresponding elicited histogram. The computation is carried out in two steps, which we describe for binary outcomes. In the first step, for each physician $k=1,\dots ,,K,$ each histogram j = 1, 2 is matched with a beta distribution, $p_{j,k},$ having mean and precision parameters $({\mu }_{j,k},{\gamma }_{j,k}).$ At the end of the elicitation process, for each expert $k=1,\dots ,K,$ and treatment $j=1,2,$ the histogram gives the elicited prior probability ${\theta }_{j,k,r}^{(\mathit{elicited})}$ of $P_{j,k}(l_r<{\theta }_{j,k}<u_r)$ for each of the subintervals, used in the elicitation, that partition the domain of the ${\theta }_{j,k}$‘s. For probabilities, r indexes the 20 subintervals [0, .05], [.06, .10],…, [.96, 1.0]. In practice, some of the ${\theta }_{j,k,r}^{(\mathit{elicited})}$ values may be 0, corresponding to an elicited prior that has support in a proper subset of [0, 1]. Denote the r-vector of elicited values corresponding to the intervals by ${\theta }_{j,k}^{(\mathit{elicited})}.$ To solve for the two hyperparameters $({\mu }_{j,k},{\gamma }_{j,k})$ of the beta, we match the elicited prior probabilities with the model-based prior probabilities by minimizing

$$\sum _{r=1}^{20}\{P_{j,k}(l_r<{\theta }_{j,k}<u_r|{\mu }_{j,k},{\gamma }_{j,k})-{\theta }_{r,j,k}^{(\mathit{elicited})}{\}}^2$$

This might be done by applying the Nelder-Mead algorithm. For real or positive real-valued ${\overline{\theta }}_j$‘s, the graphical histogram elicitation method may be implemented by first determining a range $[L_{\theta },U_{\theta }]$ for the parameters, and then partitioning this range into subintervals of equal width. One then proceeds as before, by asking each physician to place 20 stickers each having probability mass .05 into the intervals to construct a prior histogram for each of the ${\overline{\theta }}_j$‘s.

In the second step, for Method 2, denoting $\mu$ = $({\mu }_1,{\mu }_2)$ and $\gamma$ = $({\gamma }_1,{\gamma }_2),$ we treat the estimates $(\mu ,\gamma )$ obtained by the above minimization as pseudo outcomes in the regression model given by (4), and treat $({\upsilon }_{1,\mu },$ ${\upsilon }_{2,\mu },$ ${\upsilon }_{1,\gamma },$ ${\upsilon }_{2,\gamma },$ ${\beta }_{\mu },{\beta }_{\gamma },{\sigma }_{\epsilon ,\mu },{\sigma }_{\epsilon ,\gamma },\rho )$ as pseudo parameters to be estimated. To fit the Bayesian regression model to estimate the hyperparameter means, described earlier, we assumed independent noninformative normal pseudo priors for the covariate effects, ${\beta }_{\mu }\hspace{1em}\sim$ $N(0,{\sigma }_{{\beta }_{\mu }}^{2}I)$ and ${\beta }_{\gamma }\hspace{1em}\sim$ $N(0,{\sigma }_{{\beta }_{\gamma }}^{2}I)$ where $I$ is the identity matrix, with both prior variances ${\sigma }_{{\beta }_{\mu }}^2$ and ${\sigma }_{{\beta }_{\gamma }}^2$ suitably large. Similarly, independent noninformative normal pseudo priors were assumed for ${\upsilon }_{j,\mu }$ and ${\upsilon }_{j,\gamma }$, denoted by ${\upsilon }_{j,\mu }\hspace{1em}\sim$ $N(0,{\sigma }_{\upsilon }^2)$ and ${\upsilon }_{j,\gamma }\hspace{1em}\sim$ $N(0,{\sigma }_{\upsilon }^2)$, with ${\sigma }_{\upsilon }^2$ one order of magnitude larger than ${\sigma }_{{\beta }_{\mu }}^2$ and ${\sigma }_{{\beta }_{\gamma }}^2$. Moreover, independent noninformative inverse gamma, denoted by IG(1, 1), pseudo priors were assumed for ${\sigma }_{\epsilon ,\mu },{\sigma }_{\epsilon ,\gamma }$, whereas a uniform distribution in the interval $(-1,1)$ was assumed for ρ. Computations were carried out in R, using a rstan package, which is available as a Supplementary file. To approximate the double integral over R² to compute $p_k({\overline{\theta }}_1,{\overline{\theta }}_2|\upsilon ,\beta ,\sigma ,X_k)$, we used Monte Carlo sampling.

To illustrate the marginal parametric priors obtained from the elicited histograms, Figure 1 gives the elicited histograms and fitted beta priors for θ₁ and θ₂ for three of the 17 physicians who participated in the elicitation process in planning the NEPHROMYCY trial. Since some physicians used less than 20 stickers for some histograms, in these cases, we normalized the histogram to have total probability mass 1 before fitting the corresponding beta distribution. Plots of the elicited histograms and fitted beta distributions for all 17 physicians are given in Supplementary Figure S1.

Figure 1.

Elicited histograms and fitted beta priors for θ₁ (left-hand side – cyclophosphamide) and θ₂ (right-hand side – MMF) for three of the 17 physicians who participated in the elicitation process in planning the NEPHROMYCY trial. MMF: mycophenolate mofetil.

Contour plots of the distributions of the estimates of (μ,γ) from the beta distributions fit to the elicited histograms of the 17 physicians are given in Figure 2 (left-hand side for cyclophosphamide and right-hand side for MMF). Histograms of the marginal distributions of the physician-specific estimates of μ (along the top) and γ (on the right side) are also given. The histograms for μ₁ and μ₂ show that, on average, the physicians believed MMF to have a higher response probability than cyclophosphamide, although there was substantial between-physician variability. The histograms for both the precision parameters γ₁ and γ₂ were highly disperse, but had remarkably similar shapes with most mass between 30 and 70.

Figure 2.

Contour plots of estimated (μ, γ) for each expert in the domain $(0,1)\times R^{+}$ for the estimate prior response probabilities of cyclophosphamide (left-hand side) and MMF (right-hand side). Marginal histograms are plotted on the top for μ and right-hand side for $\gamma .$ MMF: mycophenolate mofetil.

4 Simulation study

In this section, we summarize a simulation study using Methods 1 and 2 and each of the three ways to weight physicians in the mixture prior, for a total of six versions of the methodology. Four scenarios were considered, determined by the assumed true values of the response probabilities (p₁, p₂) = (0.5, 0.5), (0.2, 0.3), (0.2, 0.4), or (0.4, 0.2). Let ${\hat{\theta }}_j^{\mathit{est}}$ denote the median of the marginal posterior density of θ_j, for j = 1, 2. Table 1 gives the posterior ε-equivalence probabilities ${\pi }_{12}^E(.05),$ ${\pi }_{12}^E(.10),$ and the median and first and third quantiles of ${\hat{\theta }}_j^{\mathit{est}}$ obtained from 500 replications for each combination of Method and physician weighting scheme in each simulation scenario.

Table 1.

Simulations of a 70-subject trial using each combination of method for computing hyperparameters and weighting physicians.^a

True $({\overline{\theta }}_1,{\overline{\theta }}_2)$	Method	Physician weights	${\pi }_{12}^E(0.05)$	${\pi }_{12}^E(0.10)$	Posterior median (25th, 75th percentiles)
					${\overline{\theta }}_1$	${\overline{\theta }}_2$
(0.5, 0.5)	1	1	0.86 (0.74, 0.95)	0.96 (0.9, 0.99)	0.48 (0.43, 0.53)	0.52 (0.47, 0.57)
		2	0.91 (0.79, 0.97)	0.97 (0.91, 0.99)	0.46 (0.41, 0.51)	0.54 (0.49, 0.59)
		3	0.88 (0.76, 0.96)	0.96 (0.9, 0.99)	0.47 (0.42, 0.52)	0.53 (0.48, 0.58)
	2	1	0.97 (0.89, 0.99)	0.99 (0.95, 1)	0.44 (0.4, 0.49)	0.56 (0.51, 0.61)
		2	0.97 (0.91, 0.99)	0.99 (0.96, 1)	0.44 (0.39, 0.49)	0.57 (0.52, 0.61)
		3	0.96 (0.9, 0.99)	0.99 (0.95, 1)	0.44 (0.4, 0.49)	0.56 (0.51, 0.61)
(0.2, 0.3)	1	1	0.98 (0.92, 1)	1 (0.98, 1)	0.21 (0.18, 0.24)	0.32 (0.27, 0.36)
		2	0.98 (0.93, 1)	1 (0.98, 1)	0.21 (0.18, 0.24)	0.34 (0.29, 0.39)
		3	0.98 (0.92, 0.99)	1 (0.98, 1)	0.21 (0.18, 0.25)	0.33 (0.28, 0.38)
	2	1	0.99 (0.97, 1)	1 (0.99, 1)	0.20 (0.17, 0.23)	0.36 (0.31, 0.4)
		2	1 (0.98, 1)	1 (1, 1)	0.20 (0.17, 0.23)	0.36 (0.31, 0.41)
		3	0.99 (0.97, 1)	1 (0.99, 1)	0.21 (0.17, 0.23)	0.36 (0.31, 0.4)
(0.2, 0.4)	1	1	1 (0.98, 1)	1 (1, 1)	0.22 (0.18, 0.25)	0.40 (0.35, 0.47)
		2	1 (0.99, 1)	1 (1, 1)	0.22 (0.19, 0.25)	0.43 (0.37, 0.48)
		3	1 (0.98, 1)	1 (1, 1)	0.22 (0.18, 0.26)	0.41 (0.36, 0.47)
	2	1	1 (1, 1)	1 (1, 1)	0.22 (0.19, 0.26)	0.44 (0.39, 0.48)
		2	1 (1, 1)	1 (1, 1)	0.22 (0.19, 0.26)	0.44 (0.39, 0.48)
		3	1 (1, 1)	1 (1, 1)	0.22 (0.19, 0.26)	0.44 (0.39, 0.48)
(0.4, 0.2)	1	1	0.38 (0.18, 0.62)	0.60 (0.34, 0.81)	0.35 (0.31, 0.4)	0.26 (0.21, 0.31)
		2	0.39 (0.17, 0.64)	0.59 (0.33, 0.81)	0.35 (0.31, 0.4)	0.27 (0.21, 0.32)
		3	0.39 (0.18, 0.62)	0.60 (0.34, 0.81)	0.35 (0.31, 0.4)	0.27 (0.21, 0.31)
	2	1	0.51 (0.25, 0.77)	0.68 (0.41, 0.89)	0.34 (0.3, 0.39)	0.29 (0.23, 0.35)
		2	0.55 (0.27, 0.8)	0.71 (0.44, 0.9)	0.34 (0.29, 0.39)	0.3 (0.24, 0.35)
		3	0.52 (0.26, 0.76)	0.68 (0.41, 0.88)	0.34 (0.29, 0.39)	0.29 (0.23, 0.35)

^aEach entry is the simulation average median, with first and third quantiles in parentheses. ${\pi }_{1,2}(\epsilon )$ = Pr$({\theta }_1-\epsilon <{\theta }_2|\mathit{data})$ for ε = .05 or .10.

To implement Method 2 in the simulations, three physician covariates $X_k$ were selected from the questionnaires given to the physicians when planning the NEPHROMYCY trial. These were the logarithm of the number of years experience as paediatrician, the logarithm of the average number of patients consulted per year, and a binary indicator of whether the physician had training in clinical trial methodology. These covariates were also used to compute the covariate-based physician weights in that version of the mixture prior.

The computed hyperparameters were

$$\Sigma =[\begin{array}{cc}0.399& \hfill -0.003\hfill \\ -0.003& \hfill 0.634\hfill \end{array}]$$

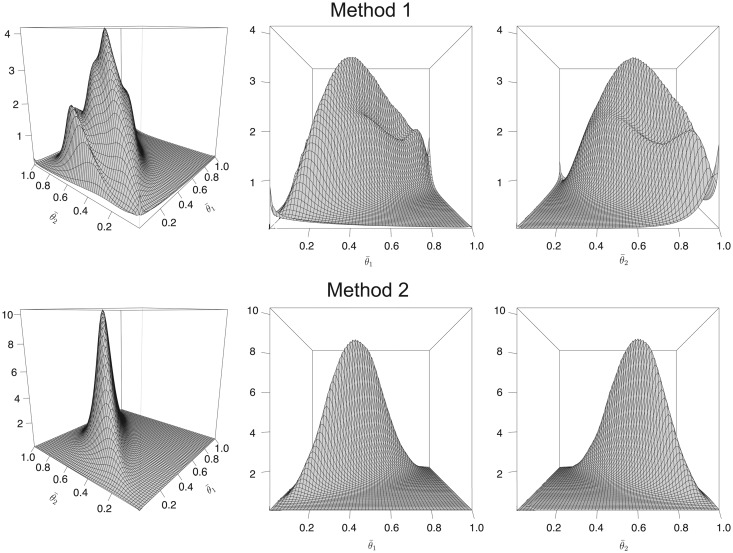
with $({\nu }_{1,\mu },{\nu }_{2,\mu },{\nu }_{1,\gamma },{\nu }_{2,\gamma })$ = (–0.708, 0.237, 3.387, 3.395), ${\beta }_{\mu }$ = (0.173, –0.049, –0.053), and ${\beta }_{\gamma }$ = (–0.185, 0.239, 0.334). Figure 3 shows the two joint prior distributions for $({\overline{\theta }}_1,{\overline{\theta }}_2)$ obtained using these values by Methods 1 and 2, using equal physician weights for the mixture. Method 2 produces a smoother surface, whereas Method 1 gives a bimodal distribution. This implies that that Method 2 is more informative than Method 1. As described earlier, the numerical $\Sigma$ given above that was obtained via Method 2 will be assumed for both methods in what follows.

Figure 3.

Three-dimensional plots of prior distributions of $({\overline{\theta }}_1,{\overline{\theta }}_2)$ using Method 1 (top row) and Method 2 (bottom row), with equal physician weights. For Method 2, the covariates $X_k$ were the logarithm of the number of year as pediatrician, the logarithm of the average number of patients consulted per year, and a binary indicator of whether the physician had training in clinical trial methodology.

The simulation results are summarized in Table 1. In all scenarios and cases, there are at most trivial differences in the effects on posterior quantities of the three different ways to compute physician weights. For the null scenario where the true response probabilities in the two treatment groups are (0.5, 0.5), Method 2, which uses physician covariates to compute the prior, produces larger values, 0.96 to 0.97, of ${\pi }_{(1,2,\phi ,\delta )}^E(.05),$ compared to the values 0.86 to 0.91 obtained using Method 1. This effect is seen for both ${\pi }_{(1,2,\phi ,\delta )}^E(.05)$ and ${\pi }_{(1,2,\phi ,\delta )}^E(.10)$ in the scenario with true response probabilities (0.4, 0.2), although in this case, the numerical values are far too small to provide convincing evidence of equivalence. The slightly greater dispersion produced by Method 2 is shown by the quartiles of the two posterior parameter distributions in all scenarios and cases.

Table 2 gives an assessment of the sensitivity of posterior quantities to the assumed numerical prior correlation ρ in Method 1. In Table 2, the same posterior quantities considered in Table 1 are given for assumed ρ = –.50, 0, + .50, with physicians weighted equally, for the case where the true response probabilities are $({\overline{\theta }}_1,{\overline{\theta }}_2)$ = (0.4, 0.2). Compared to ρ = 0, assuming either ρ = –.50 or + .50 increases the posterior equivalence probabilities ${\pi }_{12}^E(.05)$ and ${\pi }_{12}^E(.10)$ by .04 and changes the lower bound of the 95% posterior CI by .01. It thus appears that posterior inferences are relatively insensitive to ρ within this range.

Table 2.

Sensitivity of Method 1 to the assumed numerical correlation ρ between the physician latent effects $({\epsilon }_{k,\mu },{\epsilon }_{k,\gamma })$.^a

			Posterior median (25th, 75th percentiles)
ρ	${\pi }_{12}^E(0.05)$	${\pi }_{12}^E(0.10)$	${\overline{\theta }}_1$	${\overline{\theta }}_2$
–.50	0.43 (0.21, 0.67)	0.64 (0.38, 0.84)	0.35 (0.30, 0.40)	0.27 (0.22, 0.31)
0	0.39 (0.18, 0.63)	0.60 (0.34, 0.81)	0.35 (0.31, 0.40)	0.27 (0.21, 0.31)
+ .50	0.43 (0.21, 0.67)	0.64 (0.38, 0.84)	0.35 (0.30, 0.40)	0.27 (0.22, 0.31)

^aSimulations are of a 70-subject trial with equally weighted physicians, for true $({\overline{\theta }}_1,{\overline{\theta }}_2)$ = (0.4, 0.2), evaluating the same posterior quantities as in Table 1.

To summarize the substantive conclusions of the simulations in Table 1, in the three cases where the true parameters are $({\overline{\theta }}_1,{\overline{\theta }}_2)$ = (.50, .50), (.20, .30), or (.20, .40), all combinations of Method and physician weights give very large posterior probabilities that ${\overline{\theta }}_2$ is either .05- or .10-equivalent to ${\overline{\theta }}_1$. In these three cases, Method 2, which incorporates physician covariates and reflects the prior more strongly by giving larger posterior medians for ${\overline{\theta }}_2$ than for ${\overline{\theta }}_1.$ When the true probabilities are (.40, .20), i.e. they are reversed so that treatment 1 is superior to treatment 2, the posterior equivalence probabilities are not large, ${\overline{\theta }}_1$ has larger posterior medians than ${\overline{\theta }}_2$, and most of the pairs of posterior 95% CIs either are disjoint or overlap slightly.

5 Sensitivity to prior bias and informativeness

The bins-and-chips elicitation method, and thus our proposed methodology, relies on first obtaining a sample of physician experts. In our application, choosing this sample was motivated by the desire to obtain priors from individuals who had experience treating idiopathic nephrotic syndrome with cyclophosphamide and MMF. This process was constrained by the fact that the pool of such physicians was limited. In general, practicing physicians typically have strong opinions, based on their experiences treating patients, and this was the case with our sample of experts. A key issue is that what is regarded as undesirable bias from one viewpoint may be regarded as valuable prior information from another. If such expert opinion is regarded as bias rather than useful prior information, then the negative connotation of the word “bias” reflects this viewpoint. This might motivate the desire for a sample of independent or impartial experts. However, in practice, such a sample might be difficult or impossible to obtain for physicians treating a particular rare disease. Such a viewpoint thus might motivate the use of a more conventional vague or noninformative prior, with no elicitation at all, or a frequentist analysis of the data. If, instead, elicited expert opinion is regarded as valuable information, then the resulting prior is a valid basis for performing a Bayesian analysis. This is the motivation for our proposed methodology. Introducing the subjectivity of expert opinion via the prior in the analysis does not mean that our method is not objective, however. While the use of subjective probabilities to quantify prior uncertainty is a major criticism of Bayesian inference, from the Bayesian point of view, “subjective” does not mean arbitrary; just as from the frequentist point of view, “objective” does not mean without assumptions.

We address this issue as follows. In the Bayesian setting, it is always worthwhile to assess the influence of one’s prior on posterior inferences. In the present setting, the following approach for constructing a set of alternative priors, and corresponding posterior inferences, provides a practical way to do this. These priors provide a set of intermediate approaches between the use of the informative prior that we have constructed and a noninformative prior.

To perform a sensitivity analysis of posterior inferences to the prior, for Method 1, we first define the expert-specific location parameters ${\xi }_{j,k}={\upsilon }_{j,k,\mu }$ and precision parameters ${\chi }_{j,k}={\upsilon }_{j,k,\gamma }.$ For Method 2, we define these to be ${\xi }_{j,k}={\upsilon }_{j,\mu }+{\beta }_{\mu }{X}_k$, and ${\chi }_{j,k}={\upsilon }_{j,\gamma }+{\beta }_{\gamma }{X}_k.$ Denoting ${\xi }_j$ = $({\xi }_{j,1},\dots ,{\xi }_{j,K})$ and ${\chi }_j$ = $({\chi }_{j,1},\dots ,{\chi }_{j,K})$ for j = 1, 2, we define the following two transformations of $\xi$ = $({\xi }_1,{\xi }_2)$ to adjust prior location (bias) and of $\chi$ = $({\chi }_1,{\chi }_2)$ to adjust prior informativeness. For location, one may specify several fixed values of $0\le \phi \le 1,$ which is a shift sensitivity parameter that replaces ${\xi }_2$ with $(1-\phi ){\xi }_1+\phi {\xi }_2.$ Since the prior bias is determined by ${\xi }_2-{\xi }_1$, specifying φ = 1 gives the bias of the unadjusted prior, but as $\phi \downarrow$ 0, the prior bias → 0. The maximum shift is obtained at φ = 0, where ${\xi }_2={\xi }_1,$ so the prior bias is 0. For precision, we specify several fixed values of $0<\lambda \le 1,$ a scale sensitivity parameter that replaces ${\chi }_j$ with $\lambda {\chi }_j$ for both j = 1 and $j=2.$ Thus, λ = 1 returns the original prior precision, while both priors become less informative as $\lambda \downarrow 0.$ Thus, for each specified pair of fixed values of $(\phi ,\lambda )$ used to transform the prior, computing the joint prior using either (5) or (6), one may compare particular posterior quantities obtained to those obtained for each $(\phi ,\lambda )$ pair with the corresponding posterior values for $(\phi ,\lambda )$ = (1,1), which gives the untransformed prior. In practice, to perform an analysis of sensitivity to both prior bias and prior informativeness when analyzing a given data set, one may choose a small number of values of $(\phi ,\lambda ),$ and assess each of several key posterior quantities. We will illustrate this below.

While any posterior quantities may be computed, the following are useful. In settings where the goal is to determine whether one treatment provides a given fixed improvement ${\delta }_{\theta }>0$ over the other in the key parameter, one may compute the posterior probability of at least δ superiority of θ₂ over ${\theta }_1,$ ${\pi }_{1,2,\phi ,\delta }^S(\delta )$ = $P_{\phi ,\lambda }({\theta }_1+{\delta }_{\theta }<{\theta }_2|\mathit{data}),$ or possibly the symmetric probability $P_{\phi ,\lambda }(|{\theta }_1-{\theta }_2|>{\delta }_{\theta }|\mathit{data}).$ To quantify equivalence in a trial where treatment 1 is the standard and treatment 2 is the experimental, a relevant posterior probability is the ε-equivalence probability ${\pi }_{1,2,\phi ,\delta }^E(\epsilon ),$ now also indexed by the prior transformation parameters $(\phi ,\lambda ).$ Another useful quantity may be a 95% posterior CI for ${\theta }_2-{\theta }_1,$ which we denote by ${\mathit{CI}}_{95,\phi ,\lambda }({\theta }_2-{\theta }_1).$

For illustration of how a prior-to-posterior sensitivity analysis may be done using a set of priors constructed from a matrix of $(\phi ,\lambda )$ pairs, we first simulated one data set very similar to the data obtained from the NEPHROMYCY trial by setting fixed values ${\theta }_{1,\mathit{true}}={\theta }_{2,\mathit{true}}=0.4$, and simulating binary responses for 35 patients in each arm. In the simulated arm 1, the treatment was efficacious for 14 (40%) of 35 children and for 16 (45.7%) of 35 children in arm 2. For each $(\phi ,\lambda )$, we constructed the prior using Method 1 with equal physician weights and computed three posterior values for this data set. Table 3 presents the posterior values for the 12 $(\lambda ,\phi )$ pairs obtained from φ = 1, 0.5, 0 and λ = 1, .75, .50, .25. In Table 3, the posterior probabilities of .05-equivalence ${\pi }_{1,2,\phi ,\delta }^E(.05)$ = Pr$({\theta }_1-.05<{\theta }_2|\mathit{data},\phi ,\delta )$ and .15-superiority ${\pi }_{1,2,\phi ,\delta }^S(.15)$ = Pr$({\theta }_1+.15<{\theta }_2|\mathit{data},\phi ,\delta )$, and the posterior 95% CI ${\mathit{CI}}_{95,\phi ,\lambda }({\theta }_2-{\theta }_1|\mathit{data}),$ are reported in each cell.

Table 3.

Prior-to-posterior sensitivity analyses performed on a 70-patient data set with 14/35 responses in arm 1 and 16/35 responses in arm 2.^a

		λ = 1	λ = 0.75	λ = 0.5	λ = 0.2
φ = 1	${\pi }_{1,2,\phi ,\delta }^E(.05)$	0.92	0.88	0.84	0.77
	${\pi }_{1,2,\phi ,\lambda }^S(.15)$	0.24	0.22	0.21	0.18
	${\mathit{CI}}_{95,\phi ,\lambda }({\theta }_2-{\theta }_1)$	(–0.09, 0.27)	(–0.13, 0.26)	(–0.17, 0.27)	(–0.20, 0.27)
φ = 0.5	${\pi }_{1,2,\phi ,\lambda }^E(.05)$	0.77	0.76	0.75	0.75
	${\pi }_{1,2,\phi ,\delta }^S(.15)$	0.17	0.17	0.15	0.16
	${\mathit{CI}}_{95,\phi ,\lambda }({\theta }_2-{\theta }_1)$	(–0.18, 0.26)	(–0.20, 0.26)	(–0.19, 0.26)	(–0.19, 0.25)
φ = 0	${\pi }_{1,2,\phi ,\lambda }^E(.05)$	0.77	0.75	0.76	0.74
	${\pi }_{1,2,\phi ,\lambda }^S(.15)$	0.16	0.15	0.15	0.15
	${\mathit{CI}}_{95,\phi ,\lambda }({\theta }_2-{\theta }_1)$	(–0.19, 0.26)	(–0.21, 0.26)	(–0.20, 0.26)	(–0.20, 0.25)

^aThe prior was constructed using Method 1 and equal physician weights and was transformed for each $(\phi ,\lambda )$ pair, and the posterior quantities ${\pi }_{1,2,\phi ,\lambda }^E(.05)$ = Pr$({\theta }_1-.05<{\theta }_2|\mathit{data},\phi ,\lambda ),{\pi }_{1,2,\phi ,\lambda }^S(.15)$ = Pr$({\theta }_1+.15<{\theta }_2|\mathit{data},\phi ,\lambda )$ and ${\mathit{CI}}_{95,\phi ,\lambda }({\theta }_2-{\theta }_1|\mathit{data})$ then were computed.

Table 3 shows that the posterior probability that the two treatments are 0.05-equivalent is 0.92 for the untransformed prior with $(\phi ,\lambda )$ = (1,1). For no shift in prior location (φ = 1), ${\pi }_{1,2,1,\delta }^E(.05)$ drops to 0.77 when the prior precision is reduced to 25% of its original value, i.e. λ = .25, which corresponds to a prior effective sample size of about.25 × 70 = 17.5. For prior shift parameter φ = 0.5 or 0, the value of ${\pi }_{1,2,\phi ,\delta }^E(.05)$ drops to values in the narrow range 0.74 to 0.77 for all λ. The posterior probability ${\pi }_{1,2,\phi ,\delta }^S(.15)$ of 0.15-superiority is 0.24 for the untransformed prior, and for φ = 1, this drops most, to 0.18, as the precision λ is reduced from 1 to 0.25. In contrast, for the shifted priors obtained by φ = 0.5 or 0, ${\pi }_{1,2,\phi ,\delta }^S(.15)$ is insensitive to $\lambda ,$ taking on values 0.15 to 0.17 in these six cases. The upper limit on the posterior 95% CI for θ₂–θ₁ is insensitive to all $(\phi ,\lambda )$ values, but for φ = 1, the lower limit decreases from –0.09 to –0.20 as λ drops from 1 to 0.25, and otherwise is insensitive to $(\phi ,\lambda )$ for φ = 0.5 or 0.

A natural question is whether a larger sample of experts might provide a more reliable mixture prior, and thus alter posterior inferences. To address this, we drew a bootstrap sample of size 17 from the set of $({\mu }_{1,k},{\gamma }_{1,k},{\mu }_{2,k},{\gamma }_{2,k})$ values obtained from the beta distributions fit to the elicited histograms. We then jittered each of these new values by adding independent N(0,.5²) noise to each $\text{logit}({\mu }_{j,k})$ and each $\text{log}({\gamma }_{j,k})$. We treated the resulting values as transformed prior beta parameters from an additional sample of 17 synthetic experts. We combined these new parameters with the original parameters from the actual sample of experts and computed a new mixture prior, again using Method 1 with equal weights. The results are summarized in Table (4) All posterior quantities, including 95% CIs, are very similar to the corresponding values in Table $(3).$ It thus appears, in this example, that doubling the number of experts does not alter one’s posterior inferences substantively in terms of either location or variability, at least if the new experts are similar to the original experts.

Table 4.

Prior-to-posterior sensitivity analyses repeated from Table 3, but using a new mixture prior computed from the 17 actual experts plus 17 synthetic experts obtained as a bootstrap sample from the set of $({\mu }_{1,k},{\gamma }_{1,k},{\mu }_{2,k},{\gamma }_{2,k})$ values.^a

		λ = 1	λ = 0.75	λ = 0.5	λ = 0.2
φ = 1	${\pi }_{1,2,\phi ,\delta }^E(.05)$	0.93	0.88	0.83	0.79
	${\pi }_{1,2,\phi ,\lambda }^S(.15)$	0.27	0.23	0.21	0.18
	${\mathit{CI}}_{95,\phi ,\lambda }({\theta }_2-{\theta }_1)$	(–0.1, 0.28)	(–0.13, 0.27)	(–0.16, 0.27)	(–0.18, 0.27)
φ = 0.5	${\pi }_{1,2,\phi ,\lambda }^E(.05)$	0.79	0.77	0.76	0.75
	${\pi }_{1,2,\phi ,\delta }^S(.15)$	0.16	0.16	0.15	0.15
	${\mathit{CI}}_{95,\phi ,\lambda }({\theta }_2-{\theta }_1)$	(–0.18, 0.25)	(–0.19, 0.27)	(–0.2,0.25)	(–0.19, 0.26)
φ = 0	${\pi }_{1,2,\phi ,\lambda }^E(.05)$	0.76	0.76	0.77	0.75
	${\pi }_{1,2,\phi ,\lambda }^S(.15)$	0.14	0.16	0.16	0.15
	${\mathit{CI}}_{95,\phi ,\lambda }({\theta }_2-{\theta }_1)$	(–0.20, 0.25)	(–0.20, 0.26)	(–0.19, 0.26)	(–0.19, 0.25)

^aThe 17 bootstrap sample values were jittered by adding independent N(0, .5²) noise to each $\text{logit}({\mu }_{j,k})$ and each $\text{log}({\gamma }_{j,k})$ before computing the new prior.

6 Discussion

We have provided a methodology for constructing informative parametric mixture priors, based on histograms of key treatment parameters elicited from expert physicians by applying the graphical method of Johnson et al.⁶ Our motivation was the desire to deal with settings where the sample size of a randomized trial is not large enough to obtain confirmatory results using conventional statistical methods, but physicians experienced with the disease and treatments are available to provide their opinions. Because we give methods that either do or not incorporate physician covariates in the marginal physician-specific priors, and also three different ways to weight physicians when computing the overall mixture prior, there are a total of six different versions of the methodology. Since posterior quantities appear to be insensitive to how physicians are weighted when computing the mixture, however, in practice, it seems best simply to weight the physicians equally. While we have focused on the case of a binary outcome, the approach may be adapted to real-valued or time-to-event outcome data in a straightforward manner. Because incorporating expert opinion into the prior used for a Bayesian analysis is inherently controversial, we also have provided an explicit method for constructing a set of alternative priors, each obtained by applying a location shift and a change in precision. This provides a framework for performing a sensitivity analysis in an explicit way to use as a basis for making informed conclusions about the comparative benefits of the two treatments.

The methodology proposed could be extended to accommodate multiarm trials, with K > 2 parameters. This would require one to elicit K histograms from each physician, however. Since it seems likely that some experts would be familiar with only a subset of the K treatments, and thus different experts might provide priors on different subvectors of $({\overline{\theta }}_1,\dots ,{\overline{\theta }}_K),$ the problem of weighting the experts when constructing a mixture prior might not be entirely straightforward.

Computer script, written in R, which was used to implement the methodology, is available as a Supplementary file.

Authors’ note

A list of the physician experts who participated in the elicitation is given in the supplementary materials.

Authors’ contributions

Peter Thall and Moreno Ursino made equal contributions.

Declaration of conflicting interests

The author(s) declared no potential conflicts of interest with respect to the research, authorship, and/or publication of this article.

Funding

The author(s) disclosed receipt of the following financial support for the research, authorship and/or publication of this article: Peter Thall’s research was supported by NCI grant 5-R01-CA083932 and grant IDEX from the Universite Sorbonne Paris Cite (2013, project 24). Moreno Ursino and Sarah Zohar were funded by the InSPiRe Project of the European Union Seventh Framework Programme for Research, Technological Development, and Demonstration under grant agreement FP HEALTH 2013-602144.

Supplemental material

Supplemental material for this article is available online.