Abstract
The relative chemistry from grain interiors to grain boundaries help explain why grain boundaries may be beneficial, detrimental or benign towards device performance. 3D Nanoscale chemical analysis extracted from atom probe tomography (APT) (10’s of parts-per-million chemical sensitivity and sub-nanometer spatial resolution) of twenty grain boundaries in a high-efficiency Cu(In, Ga)Se2 solar cell shows the matrix and alkali concentrations are wide-ranging. The concentration profiles are then related to band structure which provide a unique insight into grain boundary electrical performance. Fluctuating Cu, In and Ga concentrations result in a wide distribution of potential barriers at the valence band maximum (VBM) (−10 to −160 meV) and the conduction band minimum (CBM) (−20 to −70 meV). Furthermore, Na and K segregation is not correlated to hampering donors, (In, Ga)Cu and VSe, contrary to what has been previously reported. In addition, Na and K are predicted to be n-type dopants at grain boundaries. An overall band structure at grain boundaries is presented.
Introduction
A considerable surge in research has been directed toward introducing renewable energy technologies to today’s energy marketplace. Natural power sources such as wind, biomass, hydro, and solar constitute the most mature and viable renewable energy candidates1. The solar industry is currently made up of many different technologies that can be divided into two groups: Si-based wafers (polycrystalline, monocrystalline) and thin films, which currently occupy ~93% and ~7% of the market share, respectively1. Chalcopyrite and zinc-blende thin films (CdTe, CZTS, CIGS), along with perovskite technologies, have experienced large gains in record efficiency over the past four years2. Perovskite solar cells, although having increased the most in efficiency, have not yet entered the marketplace due to reliability issues3. Recent laboratory record-efficiency CdTe and CIGS cells have overcome those of poly-Si (poly-Si occupies 43.9% of global annual production), which may be indicative of a larger market share in the future1. Nevertheless, the efficiency gains have largely been empirically based, and a fundamental understanding of causes for the latest improvements is still lacking4. Further improvements in scalability, uniformity, and efficiency are likely still accessible. Recent CIGS increases in efficiency have stemmed from adding K into the solar cell absorber5–7. Many recent works have concluded that an alkali post-deposition treatment leads to surface modifications responsible for the improved efficiencies7–11. However, the role of alkalis at grain boundaries, as well as grain-boundary chemical character in general, still needs to be explored.
The unique self-compensating properties at CIGS surface and grain boundaries may be a significant reason why the material is efficient and cost effective. Interestingly, monocrystalline record efficiencies for CIGS are less than those of polycrystalline CIGS12. This goes against intuition, which assumes that a single crystal contains fewer defects than its polycrystalline counterpart, and therefore has longer charge-carrier lifetimes due to less recombination, leading to a higher cell efficiency. Perhaps the reason why poly-Cu(In, Ga)Se2 are capable of high-efficiencies is that their grain boundaries are either benign or beneficial. Or, do defects segregate to grain boundaries leaving intra-grain crystallinity purer than monocrystalline material? One theory held for over two decades is that the grain boundaries are naturally Cu-poor, which leads to a lower valence-band maximum (VBM)13–17. Because high-efficiency Cu(In, Ga)Se2 is a p-type semiconductor, a lowered VBM would be a hole barrier that would block holes from recombining with electrons at defect-rich grain boundaries. Various atom probe tomography (APT) and scanning transmission electron microscopy (STEM) energy dispersive X-ray spectroscopy (EDS)/electron energy loss spectroscopy (EELS) experiments have demonstrated that grain boundaries may be both Cu-poor and In-rich, as well as Cu-rich and In-poor18–20. This contribution will show that a wide variety of chemistries exist at grain boundaries and will help to elucidate the type of potential barriers.
Furthermore, Na segregation and more recently Na and K segregation for alkali-incorporated solar cells has been revealed by APT13,19–23. However, a minimal number of grain boundaries have been analyzed, and a statistical picture of the chemical variability is needed. The incorporation of Na, either by diffusion from the glass substrate or by post-deposition treatments, has been correlated with large grain sizes and increases in p-type conductivity, resulting in higher efficiency. Na has been theorized to assist in reducing n-type defects, InCu and/or VSe, thereby increasing the p-type conductivity and open-circuit voltage (Voc)24–27. Here we show no clear relationship of Na (K) to (In, Ga)Cu and VSe defect density at grain boundaries (GBs).
A wide variety of electrical properties at GBs have been reported via Kelvin probe force microscopy (KPFM), electron beam induced current (EBIC), cathodoluminescence (CL), photoluminescence, and EELS. For example, a change in work function from the grain interior to the grain boundary, ranging from +550 meV to −250 meV has been reported28–32. A “redshift” was observed at GBs via CL, indicating a donor-acceptor-like transition, presumably (In, Ga)Cu and VCu. Furthermore, a “blue shift” was also observed with excitation at low temperatures, indicating a reduction in potential fluctuations, which was theorized to be a result of high densities of donors and acceptors30,33,34. EBIC has shown both increases and decreases of current collection at GBs35,36. Here we also show a semi-statistical chemical study at the nanoscale for 20 GBs by means of APT. The chemistry at GBs will be compared to their adjacent grain interiors, which will explain some of the remarkably diverse reports from many studies of electrical properties at grain boundaries14,37.
Results and Discussion
Description of Analysis
All data discussed in the subsequent sections are taken from a 20.3%-efficient cell grown on a specialty glass that contains both K and Na38. Table 1 summarizes the chemistry and performance. Ga/Ga + In (GGI) for the cell is 0.26, and Cu/Ga + In (CGI) is 0.94.
Table 1.
Device characteristics of the solar cell used for APT analysis.
| Eff (%) | 20.3 |
| Jsc (mA/cm 2) | 35.2 |
| FF (%) | 80.2 |
| Voc (mV) | 718 |
The samples were prepared for APT and TEM analysis using an FEI Helios 600i DualBeam focused ion beam/scanning electron microscope (FIB/SEM) and FEI Nova NanoLab, similar to the technique described in Ref.39. APT data were collected using a LEAP 4000X Si instrument manufactured by Cameca Instruments, Inc., with laser energy of 5 pJ, a set point base temperature of 40 K, a detection rate of 1.5 ions per 100 pulses, and a laser pulse rate of 500 kHz. Laser energy and base temperature were optimized to get similar evaporation rates of the constituent elements for an accurate chemical profile of the device that correlates well with X-ray fluorescence (XRF) measurements of high-efficiency CIGS. A Philips CM200 TEM was used to capture the specimen dimensions before APT with the hardware described in Ref.40 that allowed for more accurate 3-D reconstructions.
Figure 1 demonstrates an example of chemical grain-boundary analysis discussed in subsequent sections. Figure 1(a) shows TEM images taken before and after atom probe analysis. Less than 1% of In (red), Se (blue) and Ga (yellow) ions are shown to give an illustration of the specimen tip shape. The dimensions of the physical volume measured by APT were confirmed by TEM, which was used to improve the accuracy of the reconstructed volume. For all APT specimens discussed in the subsequent sections, a TEM image was taken before, but not always after, atom probe analysis, depending upon whether the specimen survived the atom probe run. An APT reconstruction containing a GB is shown in Fig. 1(b). An isoconcentration surface of 0.35 at. % K (dark yellow) illustrates segregation to the GB in Fig. 1(b,c). Parameters such as compression factor, ion density, efficiency rate, and sphere-to-cone ratios were adjusted, so the GB in the reconstruction and TEM image were correlated. Mass spectra were background corrected and all peaks associated to known ions were ranged at full-width hundredth max. Chemical profiles perpendicular to the GBs were then calculated. Alkali segregation defined where the GB was located. In most cases this was verified by TEM diffraction contrast, and in other cases, the sample was either too thick, or there was a triple-point GB, making the paths difficult to decipher due to the 2-D projection information collected in a TEM image. Only planar Na and/or K segregation qualified as a grain boundary. Intra-grain “rod-like” defects where Na and K also segregated were observed within the analyzed specimens. These types of defects will not be discussed further in this contribution. A good overview of line defects present in Cu(In, Ga)Se2 may be found in Ref.41,42.
Figure 1.
Change in chemistry from the grain boundary to the grain interior . (a) Side-by-side of TEM images of the specimen before and after atom probe analysis used to identify volume of APT reconstruction. Top (bottom) is a TEM image taken after (before) atom probe analysis. (b) Reconstructed volume capturing a GB. Less than 1% of In (red), Se (blue) and Ga (yellow) ions are shown to give an illustration of the specimen tip shape. An isoconcentration surface of 0.35 at. % K (dark yellow) illustrates segregation to the GB. (c) A cylindrical region of interest, taken from dotted square box in (b), used to enclose the reconstructed ions for chemical analysis. The grain boundary is determined by K segregation, shown in dark yellow. (d) Average composition (at. %) of the first 6 nm (four slices) of both ends of the cylinder was calculated as a grain-interior chemical reference. That value was subtracted from the composition of each slice (1.5 nm thick along the axis of the cylinder), leading to the grain boundary, which resulted in a relative change of chemistry as a function of distance from the grain boundary. Errors: ± 0.2 at. % Cu, ± 0.1 at. % In, ± 0.3 at. % Se, ± 0.07 at % Ga, 0.04 at. ± % K, and ± 0.03 at. % Na.
The grain boundaries for which diffraction information using transmission electron microscopy was collected indicated they were random, high-angle grain boundaries. This information was not determined for all of the analyzed grain boundaries, due to the time-consuming nature of such analyses. They are most likely not twin boundaries, because those have been shown to be benign and contain no alkali segregation32. Figure 1(c) shows a cylindrical region of interest used to determine a chemical profile perpendicular to the GB. The cylinder is divided into 1.5-nm slices, which enclose many ions (~10 K) used for statistical chemical analysis. The GB bisects the cylinder, and the composition from the grain interior (either end of the cylinder) is compared to the composition at the GB. The average composition (at. %) of the first 6 nm (four slices) from both ends of the cylinder was calculated as a “grain-interior (GI)” chemical reference. That value was then subtracted from the composition of each slice (1.5 nm thick along the central axis of the cylinder) leading to the GB, which resulted in a relative change of chemistry as a function of distance from the GB to the GI. This relative change (at. %) will be defined as , where Χ is the chemical species (Cu, In, Ga, Se, Na, and K) and subscript BI denotes boundary-to-interior. Statistical errors were calculated to be: ± 0.2 at. % Cu, ± 0.1 at. % In, ± 0.3 at. % Se, ± 0.07 at. % Ga, 0.04 at. ± % K, and ± 0.03 at. % Na. Analysis was administered from both sides of the GB, which resulted in two separate values for each GB. Every GB analyzed was within 1 μm of the p-n junction, verified by a TEM measurement of the distance from the molybdenum-back contact to the reconstructed volume, which was in all cases greater than 1 μm.
Statistical
Figure 2 shows for all elements from the 20 grain boundaries and their adjacent grains. Each dash mark at the x-axis (20 for each element) corresponds to a light grey vertical line, which represents the value for each GB. There are two values for every vertical line, indicating two values for both grains that “sandwich” a GB. In many cases, the two values are nearly identical; but, in some cases they are notably different, which indicates the chemical variability from grain to adjacent grain. 95% (38/40) of were Cu-poor and 97.5% (39/40) were (In + Ga)-rich, which is most likely a result of many low-energy-of-formation charge-neutral ordered defect pairs. A negative value of supports the theory of a decrease in the VBM, resulting in a hole barrier43–47. However, there is a wide degree of , leading to a wide degree of potential barrier height. For example, ranges between 0.5 to −7.5 at. %, between −0.3 and +4.7, between −1.7 and 1 at. %, between −3.14 and +3.14 at. %, between 0.02 and 1.19 at. %, and between 0.49 and 1.86 at. %. From these data, a good overall picture is presented of the variability of the chemistry at the GBs, along with the extent of impurity atom segregation. As electrons and holes approach the GB, they may experience different outcomes due to the variable local defect density, which will be discussed in the following sections.
Figure 2.
Statistical . values of 20 grain boundaries were calculated as a relative change in chemistry from the grain boundary to grain interior, as described in Fig. 1. The errors for the different elements are ±0.2 at. % Cu, ±0.1 at. % In, ±0.3 at. % Se, ±0.07 at % Ga, 0.04 at. ±% K, and ±0.03 at. % Na.
Band Structure
Valence- and Conduction-Band Offsets
A well-understood relationship between the ratio of Ga content to the Group III elements and bandgap for Cu(In, Ga)Se2 is given by equation (1)48. The overall change in bandgap due to Ga incorporation is primarily due to the change in the conduction-band minimum (CBM), whereas Cu content is directly related to a shift in VBM, because of the Cu-d and Se-p anti-bonding hybridized states15. A drop in Cu results in a drop in VBM. We have previously shown a linear correlation to the Cu off-stoichiometry to bandgap by equation (2)49. The individual contributions of the VBM and the CBM to the total bandgap are given in equations (3) and (4) (see Ref.49 for detailed explanation).
| 1 |
| 2 |
| 3 |
| 4 |
Composition profiles of two grain boundaries, shown in Fig. 3(b,d), were used to calculate band gap, CBM, and VBM (Fig. 3(a and b)) using equations (2),(3) and (4). The band offsets are calculated with respect to stoichiometric CuInSe2 (which is shown in Fig. 3(a) and Fig. 3(c) as the horizontal axis). The total band gap is calculated by adding the VBM and CBM offsets to the known band gap of CuInSe2 (1.04 eV). Both GBs have a sharp increase in band gap (~45 and 110 meV over 4.5 nm) due to a reduction in Cu content leading to a sharp drop in the VBM. The CBM is also reduced due to a decrease in GGI for both GBs (−25 and −50 meV for GB 1 and 2, respectively). The potential barrier to charge carriers at a particular GB is related to the difference of chemistry from the GB to grain interior which varies due to chemical heterogeneity of the neighboring grains. The alkali concentration is different for both GBs (~1.4 and 0.5 at. % K, ~0 and 0.5 at % Na for GB1 and 2, respectively) demonstrating a representative range that is discussed below.
Figure 3.
Composition and band profiles from two representative grain boundaries. The errors for the different elements are ±0.2 at.% Cu, ±0.1 at.% In, ±0.3 at.% Se, ±0.07 at% Ga, ±0.04 at. %K, and ±0.03 at.% Na. The maximum errors for the band profiles are ±1.5 meV VBM, ±4.5 meV CBM, and ±5.5 meV band gap.
Composition profiles taken from all 20 GBs in Fig. 2 were used to calculate the CBM and VBM offsets from the GI to the GB. Figure 4 shows a variety of VBM and CBM offsets, due to Cu and Ga content, respectively. The average potential offset for the VBM and CBM is −79 ± 36 meV and −31 ± 11 meV, respectively. Couzine et al. reported a GGI reduction at the GB and attributed it to InCu defect energy being lower than that of GaCu 50. This contribution provides a quantitative statistical analysis and helps support their findings. Indium may be more likely to occupy the Cu site than Ga by realizing Pauling’s rules. The ionic radii and coordination number for In are more similar to Cu than Ga to Cu. In addition, APT results show that increases of Cu content lead to increases in Ga content, most likely due to a high energy of formation an antisite defect, GaCu (See Fig. 3 for a representative example).
Figure 4.

Valence band maximum (VBM) and conduction band minimum (CBM) potential offsets. Calculations were made by and values from twenty gain boundaries. Average values: −79 ± 36 meV and −31 ± 11 meV, for VBM and CBM respectively. The right sides indicate averages at the center line of box, while the edges of box are 1 sigma standard deviations and the capped lines indicate 2 sigma.
The geometry of the VBM potential barrier resembles a triangle; its width is related to its magnitude, where higher barriers are wider. GB width varied from 3 to 7 ± 1.5 nm, depending on the degree of . Volumes of alkali content greater than 0.2 at. % were picked to determine what constitutes a grain boundary. However, caution must be taken in these measurements, because local distortions most likely exist due to the difference in evaporation from the GI to the GB. A higher atomic density was measured at GBs, indicating a lower evaporation field that results in a reduction of spatial resolution51. Both the height and the width of the potential barrier are key parameters for recombination reduction, due to thermo-ionic emission across the barrier and tunneling through the barrier. Taretto et al. calculated the transmission probability as a function of height and width of a square barrier52. They showed that the barrier must have a minimum height of 300 meV and minimum width of 3 nm to impede recombination for a high-efficiency device. Therefore, a 80-meV VBM barrier at a charge-neutral GB may not be enough for optimal passivation.
Alkalis and Band Structure
A well-defined relationship between K and Na and band structure at grain boundaries and grain interiors still needs to be expanded upon. The lowest energy of formation for a K or Na substitutional defect is (K, Na)Cu for CIGS and for the ordered vacancy compound of CIGS, which is predicted by hybrid-functional theory45,53,54. The possible existence of (KxCu(1−x))(InyGa(1−y))Se2 and (NaxCu(1−x))(InyGa(1−y))Se2 alloys at the GBs further convolutes the band structure. Because Na and K are both isovalent with Cu and possess no p-orbital, they may mimic that of a VCu with regards to the VBM. However, this assumption still needs to be explored. Because alkali segregation at the GBs is at most ~2 at. %, its contribution to the band structure may be minimal.
If alkalis reside on Cu sites, then their contribution to charge carriers should be benign; yet, their incorporation has long been shown to increase p-type conductivity55,56. Long-standing theories that describe the phenomenon relate the presence of alkalis to the reduction of n-type defects: (In, Ga)Cu or VSe 26,57–59. However, there has been little experimental verification. Figures 5(a) and 4(b) plot the alkali content versus and at grain boundaries, respectively. The black lines in the Figure represent linear fits. An increase in and a decrease in are presumed to lead to n-type defects: (In, Ga)Cu and VSe,. Therefore, a negative slope of and/or versus would result in a correlation of alkali concentration to a decrease of n-type defects. Similarly, a positive slope of and/or versus would also result in a correlation of alkali concentration to an increase of n-type defects. Based on the linear fits, the slopes are opposite in sign and no such correlations are apparent. Furthermore, the inclusion of Na and K may result in the opposite—an overall n-type doping if they occupy what was a VCu defect from a charge-neutral ordered defect pair.
Figure 5.
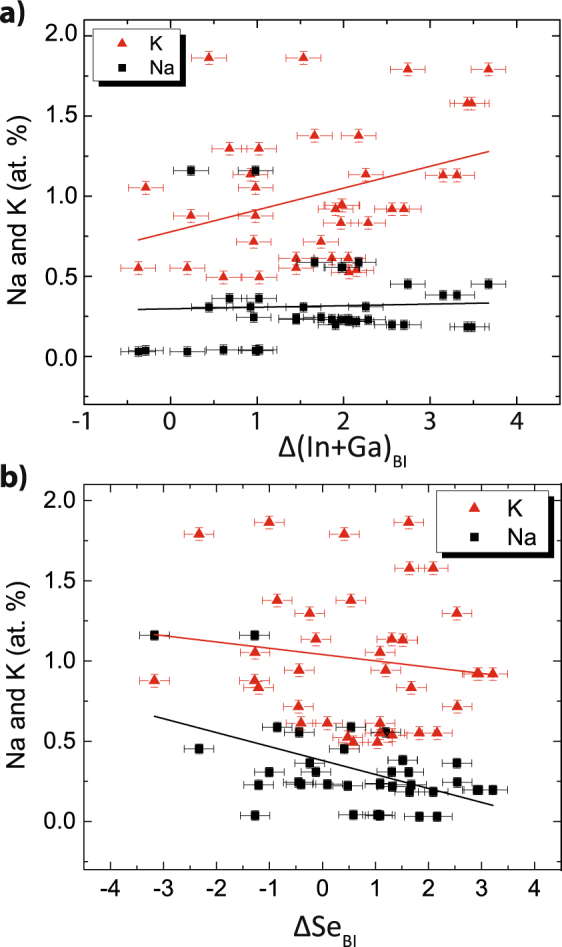
Alkali relationship to n-type defects. (a) Alkali segregation is compared to . A positive slope may indicate a correlation of alkali incorporation to a reduction of the n-type defect (In, Ga)Cu. However, no clear relationship is measured. (b) Alkali incorporation is compared to . A negative slope may indicate a correlation of alkali segregation to a reduction of the n-type defect VSe. Again, no clear relationship is measured.
The work of Yan et al. reported KPFM measurements on polycrystalline CIGS grown with and without alkalis. An increase in the work function (indicative of n-type doping) at GBs was reported for the absorber grown with Na, yet there was no measurable change work function at GBs for the absorber grown without alkalis60. With Yan et al.’s work and no correlation made of alkali incorporation to a reduction of n-type defects (Fig. 5), we propose that alkalis may act as an n-type dopant at GBs. Yuan et al. recently predicted that the diffusion of alkalis at the GIs is the reason why alkalis increase p-type conductivity55. They show that the solubility limit of Na and K at GIs is increased with temperature, resulting in larger quantities of NaCu (KCu) during growth. When the absorber cools, Na and K out-diffuse, leaving a high density of Vcu’s. The alkalis are then rinsed away before the CdS chemical bath. We now add to this theory and provide a missing link between the seemingly contradictory roles of alkalis at GBs and enhanced p-type doping. With the addition of the GB data presented in this report and in conjunction with the theory presented by Yuan et al., we presume alkalis increase the p-type doping at GIs and become n-type dopants at GBs. Equation (5) is a point defect bottom which combines Yuan et al.’s theory for bulk material with the present contribution’s predicted grain boundary point defects (Na and K may be used interchangeably in equation). In other words, out-diffuse from the GI, leaving a VCu behind which may either be rinsed away at the surface or occupy a VCu at the GB, leading to a p-type doping at the GI and an n-type doping at the GB. If the grains are columnar, the band bending at the GB induced by the n-type doping would reduce recombination and increase charge collection. Furthermore, the variable chemistry at the GB leads to variable magnitudes of band bending and potential barriers and may help explain the diverse electrical properties exhibited by techniques such as EBIC, KPFM, and CL (see section 4). The benefit of alkali incorporation may be two fold: increase p-type conductivity, and increase band bending at the GB.
| 5 |
Fluctuating potentials and high degree of compensation
Cu(In, Ga)Se2, a highly compensated semiconductor, has many more donors and acceptors (~1019) than free charge carriers (holes ~1017)45. At high enough temperatures where the donors and acceptors are ionized, the net free carrier concentration is the difference between the number of donors and acceptors shown in equation (6), where ND is donor concentration, NA is acceptor concentration and Nt is total free carrier concentration.
| 6 |
This leaves many ionized defects, whose electric fields cause fluctuating potentials on charge carriers. Shklovskii and Efros61 and Dirnstorfer et al.62 defined the relationship between the average potential fluctuations and ionized defects for highly doped semiconductors and Cu(In, Ga)Se2, respectively. From Fig. 1, we predict that the bands will fluctuate appreciably as a function of proximity to the GB, due to the increasingly large amount of compensation, i.e., many n-type point defects (InCu) and many p-type defects (VCu). The average magnitude of potential fluctuations is given by equation (7), where the defect density is assumed to be evenly distributed61,62:
| 7 |
where R is the radius of the enclosed volume and Nt is the total density of charged ions. Charge carriers will screen the ions and only be affected by ions within a radius, rs related to charge-carrier density, Nt defined by equation (8), where p is the hole density:
| 8 |
Combining equations (7) and (8) gives the potential fluctuation in terms of Nt and charge carrier density (ρ):
| 9 |
Activation energies of defects will also be affected by the potential fluctuations. Podor et al. showed that the energy to ionize a defect decreases as a function of the magnitude of potential fluctuations as defined by equation (10)63:
| 10 |
where E A is the activation energy, E o is the thermal ionization energy, α is a constant approximately 4 × 10−5 meV, and Nt is the defect density. Based on Fig. 1, the degree of compensation at the GB may be extreme, where a high density of VCu and (In, Ga)Cu defects (Nt ≈ 1021) are present. In this case, donors and acceptors would be at the band edges. Further fundamental analysis is needed to relate the increase in potential fluctuations at the GBs to overall cell performance.
Figure 6 provides a summary of our findings, demonstrating the band structure for two types of grain boundaries with small and large . Most grain boundaries measured are Cu- and Ga-poor and In-rich, resulting in negative potential shifts of the VBM and CBM, though not necessarily to the same extent. All random, high-angle grain boundaries analyzed had alkali segregation, which is presumed to lead to n-type doping and result in a positive potential.
Figure 6.
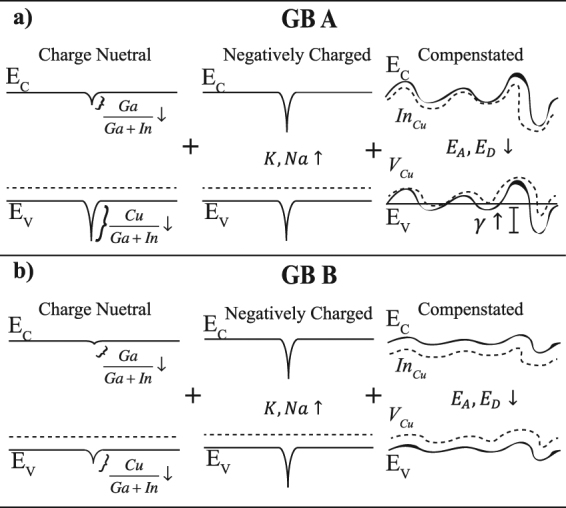
Grain-boundary band profiles. Grain-boundary A (B) refers to a large (small) . Grain-boundary A has a larger potential barrier to holes at the valence-band minimum. All grain boundaries are presumed to be doped n-type from alkali incorporation, where both have a positive potential. Grain-boundary A also exhibits larger potential fluctuations due to increased compensation. Dashed lines in the “Charge Neutral” and “Negatively Charged” diagrams represent the Fermi energy, and the position of the defect states, VCu and InCu, in the “Compensated” diagram. EA and ED are activation energy of acceptors (VCu) and donors (InCu) respectively.
Understanding EBIC, CL, and KPFM trends
We have shown a complex band structure resulting from the variable chemistry discussed in the preceding sections. We now discuss possible reasons why electrical properties measured by EBIC are also variable. EBIC is taken at short-circuit conditions and contrast is determined by current collection. Light (dark) regions, which correlate to high (low) current collections, could result from increased (decreased) charge separation and lead to a high (low) probability of carriers reaching the contacts. A GB with large n-type doping (due to significant K and Na content) would lead to a large potential and efficient charge collection. A GB with small potential could lead to inefficient charge separation and a large density of recombination centers. Also, a charge-neutral GB that contains many compensating defects, resulting in an offset at the VBM in conjunction with a potential due to n-type doping, would lead to even greater efficiency in charge separation. However, the electron beam would generate fewer electron-hole pairs, due to a larger bandgap. Clearly, there is a wide variety of band profiles that lead to variable current collection at GBs. Many works report a red shift at GBs measured by CL. The degree of red shift will be highly variable because the donor-acceptor pair transitions depend on VCu and (In, Ga)Cu defect densities. As shown in Fig. 2, the defect densities vary by more than an order of magnitude. The potential fluctuations also vary according to defect densities; therefore, they would lead to variable degrees in red shifts, because the donor and acceptor activation energies will also vary (equations (6),(7), and (10)). A wide variety of GB potentials are shown in many KPFM studies. A possible explanation is the variable alkali concentration, with the alkali presumed to be an n-type dopant. Because the alkali concentration also varies (Fig. 2), the potential should also vary.
Conclusion
The relationship between relative chemical changes from the grain interiors to grain boundaries relate and the band structure of CIGS solar cells was explored for a large number of grain boundaries. Highly accurate chemical profiles show large chemical variability, which lead to a spectra of band profiles. We provide the following five main conclusions: 1) Grain-boundary chemistry is highly variable, resulting in a wide distribution of potential barriers at the VBM (−10 to −160 meV) and CBM (−20 to −70 meV); 2) Na and K segregation is not correlated to hampering donors: (In, Ga)Cu and VSe; 3) Na and K are predicted to be n-type dopants at grain boundaries; 4) Potential fluctuations increase as a function of proximity to the grain boundary, due to increases in compensation, which leads to reductions in donor and acceptor activation energies; and 5) The previous four conclusions provide an explanation for electrical property variations seen in EBIC, CL, and KPFM.
Methods
Growth Process
CIGS solar cells were prepared on high-temperature specialty glass coated with sputtered molybdenum to serve as a back contact to the device. The CIGS absorber layer was deposited via a three-stage co-evaporation process described elsewhere, with modifications to controllably change the bandgap (Ga) profile64–66. The substrate temperature during the second stage, ~615 °C, was measured with a thermocouple placed on the backside of the glass. The devices were then allowed to cool and removed from the vacuum chamber. All absorbers were then finished into devices using the standard CdS and ZnO bilayer described by Contreras et al.64.
Sample Preparation
The samples were prepared for atom probe tomography (APT) and transmission electron microscopy (TEM) analysis using an FEI Helios 600i DualBeam focused ion beam/scanning electron microscope (FIB/SEM). A final 2-kV cleaning step was used to reduce the damage to about the outer 2 nm of the sample. This was verified by isolating the Ga regions that have mono-isotopic 69 Ga used in the FIB source from the regions with the naturally occurring 69 Ga and 71 Ga isotopic ratios within APT reconstructions. The end radii of the specimens analyzed ranged from 50–100 nm. APT data were collected using a LEAP 4000X Si instrument manufactured by Cameca Instruments, Inc. We used a laser energy of 5 pJ at a set point temperature of 40 K with a detection rate of 1.5 ions per pulse and a laser pulse rate of 500 kHz. The laser energy and base temperature were optimized to obtain equal evaporation rates of the constituent elements for an accurate chemistry profile of the sample that well represents the stoichiometry of CIGS. A Philips CM200 TEM was used to capture the specimens’ dimensions before and after APT using the hardware described in Gorman et al.40,67. This procedure allowed for more accurate 3-D reconstructions.
The datasets generated during and/or analysed during the current study are available from the corresponding author on reasonable request67.
Acknowledgements
We would like to thank Dr. Lorelle Mansfield for fruitful discussions and Dr. Miguel Contreras for providing the sample. This work was supported by the U.S. Department of Energy under Contract No. DE-AC36-08-GO28308 with the National Renewable Energy Laboratory. The atom probe used in this research is supported by NSF Award Number 1040456.
Author Contributions
A.S., B.G. and M.A. designed the experiments. A.S. carried out the experiments. A.S., M.A., B.G., D.D. and A.C. contributed to data analysis. A.S. wrote the manuscript. All authors provided feedback and edits.
Competing Interests
The authors declare that they have no competing interests.
Footnotes
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
- 1.Burger, B. et al. Fraunhofer ISE. Photovoltaics Reporthttps://eva.fing.edu.uy/pluginfile.php/120723/mod_resource/content/1/2016-03-11_Photovoltaics_Report.pdf (2016).
- 2.Green MA, Emery K, Hishikawa Y, Warta W, Dunlop ED. Solar cell efficiency tables (Version 45) Progress in Photovoltaics: Research and Applications. 2015;23:1–9. doi: 10.1002/pip.2573. [DOI] [Google Scholar]
- 3.Grätzel M. The light and shade of perovskite solar cells. Nature Publishing Group. 2014;13:838–842. doi: 10.1038/nmat4065. [DOI] [PubMed] [Google Scholar]
- 4.Shafarman, W. N. & Stolt, L. Cu (In, Ga) Se 2 Solar Cells. Handbook of Photovoltaic Science and Engineering2, (John Wiley and Sons, 2003).
- 5.Laemmle A, Wuerz R, Powalla M, Baden-württemberg ZS-W. Efficiency enhancement of Cu(In, Ga)Se2 thin-film solar cells by a post-deposition treatment with potassium fluoride. Physica Status Solidi (RRL) - Rapid Research Letters. 2013;634:631–634. doi: 10.1002/pssr.201307238. [DOI] [Google Scholar]
- 6.Reinhard P, et al. Cu(In, Ga)Se2 Thin-Film Solar Cells and Modules — A Boost in Efficiency Due to Potassium. IEEE Journal of Photovoltaics. 2015;5:656–663. doi: 10.1109/JPHOTOV.2014.2377516. [DOI] [Google Scholar]
- 7.Chirilă A, et al. Potassium-induced surface modification of Cu(In, Ga)Se2 thin films for high-efficiency solar cells. Nature materials. 2013;12:1107–11. doi: 10.1038/nmat3789. [DOI] [PubMed] [Google Scholar]
- 8.Pistor P, et al. Experimental indication for band gap widening of chalcopyrite solar cell absorbers after potassium fluoride treatment. Applied Physics Letters. 2014;105:63901. doi: 10.1063/1.4892882. [DOI] [Google Scholar]
- 9.Laemmle A, Wuerz R, Powalla M. Investigation of the effect of potassium on Cu(In, Ga)Se2 layers and solar cells KF-precursor KF-PDT. Thin Solid Films. 2015;582:27–30. doi: 10.1016/j.tsf.2014.10.088. [DOI] [Google Scholar]
- 10.Handick E, et al. Potassium Postdeposition Treatment-Induced Band Gap Widening at Cu(In, Ga)Se2 Surfaces - Reason for Performance Leap? ACS Applied Materials and Interfaces. 2015;7:27414–27420. doi: 10.1021/acsami.5b09231. [DOI] [PubMed] [Google Scholar]
- 11.Aguiar JA, et al. Revealing Surface Modifi cations of Potassium-Fluoride- Treated Cu(In, Ga)Se2: A Study of Material Structure, Chemistry, and Photovoltaic Performance. Advanced Materials Interfaces. 2016;3:1–7. doi: 10.1002/admi.201600013. [DOI] [Google Scholar]
- 12.Du H, Champness CH, Shih I. Results on monocrystalline CuInSe 2 solar cells. 2005;481:37–41. [Google Scholar]
- 13.Abou-Ras D, et al. Direct insight into grain boundary reconstruction in polycrystalline Cu(In, Ga)Se 2 with atomic resolution. Physical Review Letters. 2012;108:1–5. doi: 10.1103/PhysRevLett.108.075502. [DOI] [PubMed] [Google Scholar]
- 14.Siebentritt S, Igalson M, Persson C, Lany S. The electronic structure of chalcopyrites-bands, point defects and grain boundaries. Progress in Photovoltaics: Research and Applications. 2010;18:390–410. doi: 10.1002/pip.936. [DOI] [Google Scholar]
- 15.Persson, C. & Zunger, A. Compositionally induced valence-band offset at the grain boundary of polycrystalline chalcopyrites creates a hole barrier. Applied Physics Letters87, (2005).
- 16.Nichterwitz M, et al. Influence of grain boundaries on current collection in Cu(In, Ga)Se2 thin-film solar cells. Thin Solid Films. 2009;517:2554–2557. doi: 10.1016/j.tsf.2008.11.064. [DOI] [Google Scholar]
- 17.Persson C, Zunger A. Anomalous Grain Boundary Physics in Polycrystalline CuInSe 2: The Existence of a Hole Barrier. Physical Review Letters. 2003;91:1–4. doi: 10.1103/PhysRevLett.91.266401. [DOI] [PubMed] [Google Scholar]
- 18.Choi P-P, Cojocaru-Mirédin O, Wuerz R. Compositional gradients and impurity distributions in CuInSe 2 thin-film solar cells studied by atom probe tomography. Surface and Interface Analysis. 2012;44:1386–1388. doi: 10.1002/sia.4948. [DOI] [Google Scholar]
- 19.Cojocaru-mir O, et al. Characterization of Grain Boundaries in Cu(In, Ga)Se2 Films Using Atom-Probe Tomography. IEEE Journal of Photovoltaics. 2011;1:207–212. doi: 10.1109/JPHOTOV.2011.2170447. [DOI] [Google Scholar]
- 20.Stokes A, Al-Jassim M, Diercks D, Egaas B, Gorman B. Targeting Grain Boundaries for Structural and Chemical Analysis Using Correlative EBSD, TEM and APT. Microscopy and Microanalysis. 2015;21:43–44. doi: 10.1017/S1431927615001014. [DOI] [Google Scholar]
- 21.Cojocaru-mir O, et al. Characterization of Grain Boundaries in Cu(InGa)Se2 Films Using Atom-Probe Tomography. IEEE Journal of Photovoltaics. 2011;1:207–212. doi: 10.1109/JPHOTOV.2011.2170447. [DOI] [Google Scholar]
- 22.Stokes A, Gorman BP, Al-Jassim M. Semi-statistical Atom Probe Tomography Analysis of Thin Film Grain Boundaries. Microscopy and Microanalysis. 2016;22:644–645. doi: 10.1017/S1431927616004074. [DOI] [Google Scholar]
- 23.Keller J, et al. Grain boundary investigations on sulfurized Cu(In, Ga)(S,Se)2 solar cells using atom probe tomography. Solar Energy Materials and Solar Cells. 2013;117:592–598. doi: 10.1016/j.solmat.2013.07.034. [DOI] [Google Scholar]
- 24.Choi P-P, Cojocaru-Mirédin O, Wuerz R, Raabe D. Comparative atom probe study of Cu(In, Ga)Se2 thin-film solar cells deposited on soda-lime glass and mild steel substrates. Journal of Applied Physics. 2011;110:124513. doi: 10.1063/1.3665723. [DOI] [Google Scholar]
- 25.Rudmann D, et al. Efficiency enhancement of Cu(In, Ga)Se2 solar cells due to post-deposition Na incorporation. Applied Physics Letters. 2004;84:1–4. doi: 10.1063/1.1646758. [DOI] [Google Scholar]
- 26.Forest RV, et al. Reversibility of (Ag,Cu)(In, Ga)Se2 electrical properties with the addition and removal of Na: Role of grain boundaries. Journal of Applied Physics. 2015;117:1–6. doi: 10.1063/1.4915334. [DOI] [Google Scholar]
- 27.Wei S, Zhang SB, Zunger A. Effects of Na on the electrical and structural properties of CuInSe 2. Journal of Applied Physics. 1999;85:7214–7218. doi: 10.1063/1.370534. [DOI] [Google Scholar]
- 28.Hanna G, et al. Texture and electronic activity of grain boundaries in Cu(In, Ga)Se2 thin films. Applied Physics A: Materials Science and Processing. 2006;82:1–7. doi: 10.1007/s00339-005-3411-1. [DOI] [Google Scholar]
- 29.Jiang C, et al. Local built-in potential on grain boundary of Cu(In, Ga)Se2 thin films. Applied Physics Letters. 2004;84:3477–3479. doi: 10.1063/1.1737796. [DOI] [Google Scholar]
- 30.Hetzer MJ, et al. Direct observation of copper depletion and potential changes at copper indium gallium diselenide grain boundaries. Applied Physics Letters. 2005;86:1–3. doi: 10.1063/1.1906331. [DOI] [Google Scholar]
- 31.Baier R, et al. Electronic properties of grain boundaries in Cu(In, Ga)Se2 thin films with various Ga-contents. Solar Energy Materials and Solar Cells. 2012;103:86–92. doi: 10.1016/j.solmat.2012.04.002. [DOI] [Google Scholar]
- 32.Baier R, Abou-Ras D, Rissom T, Lux-Steiner MC, Sadewasser S. Symmetry-dependence of electronic grain boundary properties in polycrystalline CuInSe2 thin films. Applied Physics Letters. 2011;99:2011–2014. doi: 10.1063/1.3652915. [DOI] [Google Scholar]
- 33.Romero MJ, et al. Cathodoluminescence of Cu(In, Ga)Se2 thin films used in high-efficiency solar cells. Applied Physics Letters. 2003;83:4770–4772. doi: 10.1063/1.1631083. [DOI] [Google Scholar]
- 34.Romero, M. J., Repins, I., Teeter, G., Contreras, M. a & Al-jassim, M. A Comparative Study of the Defect Point Physics and Luminescence of the Kesterites Chalcopyrite Cu(In, Ga)Se2. 3349–3353 (2012).
- 35.Nichterwitz, M. Charge carrier transport in Cu(In, Ga)Se2 thin-film solar-cells studied by electron beam induced current and temperature and illumination dependent current voltage analyses (2012).
- 36.Abou-Ras D, et al. Analysis of Cu(In, Ga)(S,Se)2 thin-film solar cells by means of electron microscopy. Solar Energy Materials and Solar Cells. 2011;95:1452–1462. doi: 10.1016/j.solmat.2010.11.008. [DOI] [Google Scholar]
- 37.Rau U, Taretto K, Siebentritt S. Grain boundaries in Cu(In, Ga)(Se,S)2 thin-film solar cells. Applied Physics A: Materials Science & Processing. 2009;96:221–234. doi: 10.1007/s00339-008-4978-0. [DOI] [Google Scholar]
- 38.Contreras MA, et al. Wide bandgap Cu(In, Ga)Se2 solar cells with improved energy conversion efficiency. Progress in Photovoltaics: Research and Applications. 2012;20:843–850. doi: 10.1002/pip.2244. [DOI] [Google Scholar]
- 39.Thompson K, et al. In situ site-specific specimen preparation for atom probe tomography. Ultramicroscopy. 2007;107:131–139. doi: 10.1016/j.ultramic.2006.06.008. [DOI] [PubMed] [Google Scholar]
- 40.Gorman BP, Puthucode A, Diercks DR, Kaufman MJ. Cross-correlative TEM and atom probe analysis of partial crystallisation in NiNbSn metallic glasses. Materials Science and Technology. 2008;24:682–688. doi: 10.1179/174328408X293595. [DOI] [Google Scholar]
- 41.Couzinie-Devy F, Cadel E, Barreau N, Arzel L, Pareige P. Na distribution in Cu(In, Ga)Se2 thin films: Investigation by atom probe tomography. Scripta Materialia. 2015;104:83–86. doi: 10.1016/j.scriptamat.2015.03.028. [DOI] [Google Scholar]
- 42.Abou-Ras, D. et al. Compositional and electrical properties of line and planar defects in Cu(In, Ga)Se 2 thin films for solar cells - a review. physica status solidi (RRL) - Rapid Research Letters13. (2016).
- 43.Zhang SB, Wei S, Zunger A. Defect physics of the CuInSe 2 chalcopyrite semiconductor. Physical Review B. 1998;57:9642–9656. doi: 10.1103/PhysRevB.57.9642. [DOI] [Google Scholar]
- 44.Stokes A, Al-Jassim M, Diercks DR, Egaas B, Gorman B. 3-D point defect density distributions in thin film Cu (In, Ga) Se 2 measured by atom probe tomography. Acta Materialia. 2016;102:32–37. doi: 10.1016/j.actamat.2015.09.035. [DOI] [Google Scholar]
- 45.Schuler S, et al. Self-compensation of intrinsic defects in the ternary semiconductor CuGaSe 2. Physical Review B. 2004;69:1–9. doi: 10.1103/PhysRevB.69.045210. [DOI] [Google Scholar]
- 46.Lux-steiner MC, Sadewasser S, Hafemeister M, Siebentritt S. Large Neutral Barrier at Grain Boundaries in Chalcopyrite Thin Films. Physical Review Letters. 2010;104:1–4. doi: 10.1103/PhysRevLett.104.196602. [DOI] [PubMed] [Google Scholar]
- 47.Siebentritt, S. in Wide Gap Chalcopyrites (ed. Rau, U.) 260 (Springer, 2006).
- 48.Wei, S. & Zunger, A. Band offsets and optical bowings of chalcopyrites and Znbased IIVI alloys. Journal of Applied Physics3846, (1995).
- 49.Stokes, A., Al-jassim, M., Norman, A., Diercks, D. & Gorman, B. Nanoscale insight into the p-n junction of alkali- incorporated Cu(In, Ga)Se2 solar cells. Progress in Photovoltaics: Research and Applications (2017).
- 50.Couzinié-Devy, F., Cadel, E., Barreau, N., Pareige, P. & Kessler, J. Atom probe contribution to the caracterisation of CIGSe grain boundaries. Photovoltaic Specialists Conference (PVSC), 2011 37th IEEE 1966–1971 (2011). doi:10.1109/PVSC.2011.6186339
- 51.Haydock R, Kingham DR. Post-ionization of field-evaporated ions. Physical Review Letters. 1980;44:1520–1523. doi: 10.1103/PhysRevLett.44.1520. [DOI] [Google Scholar]
- 52.Taretto K, Rau U. Numerical simulation of carrier collection and recombination at grain boundaries in Cu (In, Ga) Se 2 solar cells Numerical simulation of carrier collection and recombination at grain boundaries in Cu(In, Ga)Se2 solar cells. Journal of Applied Physics. 2008;103:1–11. doi: 10.1063/1.2917293. [DOI] [Google Scholar]
- 53.Ghorbani E, et al. Hybrid-Functional Calculations on the Incorporation of Na and K Impurities into the CuInSe 2 and CuIn 5 Se 8 Solar-Cell Materials. The Journal of Physical Chemistry C. 2015;119:25197–25203. doi: 10.1021/acs.jpcc.5b07639. [DOI] [Google Scholar]
- 54.Cao Q, et al. Defects in Cu(In, Ga)Se2 chalcopyrite semiconductors: A comparative study of material properties, defect states, and photovoltaic performance. Advanced Energy Materials. 2011;1:845–853. doi: 10.1002/aenm.201100344. [DOI] [Google Scholar]
- 55.Yuan, Z. et al. Na-Diffusion Enhanced p-type Conductivity in Cu(In, Ga)Se2: A New Mechanism for Efficient Doping in Semiconductors. Advanced Energy Materials 1–7 (2016). doi:10.1002/aenm.201601191
- 56.Contreras MA, et al. High efficiency Cu(In, Ga)Se2-based solar cells: processing of novel absorber structures. Photovoltaic Energy Conversion, 1994. Conference Record of the Twenty Fourth. IEEE Photovoltaic Specialists Conference - 1994, 1994 IEEE First World Conference on. 1994;1:68–75 vol.1. [Google Scholar]
- 57.Niles DW, et al. Na impurity chemistry in photovoltaic CIGS thin films: Investigation with x-ray photoelectron spectroscopy. Journal of vacuum science and technology A. 1997;14:1–7. [Google Scholar]
- 58.Timmo K, et al. The effect of sodium doping to CuInSe2 monograin powder properties. Thin Solid Films. 2007;515:5887–5890. doi: 10.1016/j.tsf.2006.12.087. [DOI] [Google Scholar]
- 59.Laemmle a, Wuerz R, Powalla M. Investigation of the effect of potassium on Cu(In, Ga)Se2 layers and solar cells. Thin Solid Films. 2014;582:27–30. doi: 10.1016/j.tsf.2014.10.088. [DOI] [Google Scholar]
- 60.Yan Y, Jiang C, Noufi R, Wei S, Moutinho HR. Electrically Benign Behavior of Grain Boundaries in Polycrystalline CuInSe2 Films. Physical Review Letters. 2007;99:2–5. doi: 10.1103/PhysRevLett.99.235504. [DOI] [PubMed] [Google Scholar]
- 61.Shklovkii, B. I. & Efros, A. L. Electronic Properties of Doped Semiconductors (Springer, 2013).
- 62.Dirnstorfer I, et al. Characterization of Cu(In, Ga)Se2 Thin Films. Physica status solidi a. 1998;168:163–176. doi: 10.1002/(SICI)1521-396X(199807)168:1<163::AID-PSSA163>3.0.CO;2-T. [DOI] [Google Scholar]
- 63.Podor B. On the concentration dependence of the thermal ionisation energy of impurities in InP. Semiconductor Science and Technology. 1987;2:177–178. doi: 10.1088/0268-1242/2/3/008. [DOI] [Google Scholar]
- 64.Contreras MA, et al. Progress toward 20% efficiency in Cu(In, Ga)Se2 polycrystalline thin-film solar cells. Progress in Photovoltaics: Research and Applications. 1999;7:311–316. doi: 10.1002/(SICI)1099-159X(199907/08)7:4<311::AID-PIP274>3.0.CO;2-G. [DOI] [Google Scholar]
- 65.Gabor AM, et al. High-efficiency Cu(InxGa(1−x))Se2 solar cells made from (Inx,Ga1−x)2Se3 precursor films. Applied Physics Letters. 1994;65:198. doi: 10.1063/1.112670. [DOI] [Google Scholar]
- 66.Repins I, et al. 19.9%-efficient ZnO/CdS/ CuInGaSe2 Solar Cell with 81.2% Fill Factor. Prog. Photovolt: Res. Appl. 2008;16:235–239. doi: 10.1002/pip.822. [DOI] [Google Scholar]
- 67.Gorman BP, et al. Hardware and Techniques for Cross- Correlative TEM and Atom Probe. Microscopy Today. 2008;16:42–48. [Google Scholar]





