Spatially Organized β-Cell Subpopulations Control Electrical Dynamics across Islets of Langerhans

Abstract

Understanding how heterogeneous cells within a multicellular system interact and affect overall function is difficult without a means of perturbing individual cells or subpopulations. Here we apply optogenetics to understand how subpopulations of β-cells control the overall [Ca²⁺]_i response and insulin secretion dynamics of the islets of Langerhans. We spatiotemporally perturbed electrical activity in β-cells of channelrhodopsin2-expressing islets, mapped the [Ca²⁺]_i response, and correlated this with the cellular metabolic activity and an in silico electrophysiology model. We discovered organized regions of metabolic activity across the islet, and these affect the way in which β-cells electrically interact. Specific regions acted as pacemakers by initiating calcium wave propagation. Our findings reveal the functional architecture of the islet, and show how distinct subpopulations of cells can disproportionality affect function. These results also suggest ways in which other neuroendocrine systems can be regulated, and demonstrate how optogenetic tools can discern their functional architecture.

Introduction

The emergent properties of multicellular systems have led to increased study of the architecture and biological heterogeneity in governing spatiotemporal dynamics (1, 2). However, the inherent complexity in multicellular systems can render them difficult to study in their intact state. As a result, systems are often broken apart into more manageable pieces and their coupled functions and dynamics inferred from individual component properties (3, 4). Whereas subpopulations of systems are identifiable using these methods, their exact role in controlling dynamics and system regulation in the intact state is lost. New techniques that can study structures in their intact state, to preserve spatial information of signaling dynamics, will therefore help elucidate the role of cellular subpopulations in complex systems. One such system that shows complex multicellular regulation, yet has a tractable scale for studying with cellular imaging and computer modeling approaches, is the Islet of Langerhans, where dysfunction to the islet generally causes diabetes.

Islets of Langerhans are located throughout the pancreas, and secrete hormones including insulin and glucagon to maintain glucose homeostasis. β-cells within the islet secrete insulin in response to elevated glucose levels through regulated electrochemical processes (5). This includes metabolism of glucose to elevate ATP levels, inhibition of ATP-sensitive K⁺ (K_ATP) channels to depolarize the β-cell-generating bursts of action potentials, and elevated free-calcium activity ([Ca²⁺]_i) that triggers insulin granule exocytosis (6, 7). Upon elevated glucose, [Ca²⁺]_i is oscillatory, underlying pulsatile insulin secretion that enhances hepatic insulin action and is disrupted during the development of diabetes (8). Importantly, β-cells are electrically coupled via connexin-36 (Cx36) gap junctions, which synchronize electrical activity and strengthen the collective regulation and dynamics of insulin secretion (9, 10, 11). For example, a Cx36 knockout abolishes electrical synchronization in islets, shows altered plasma insulin oscillations, and leads to glucose intolerance (12, 13), and such behavior is observed in models of type 2 diabetes (14, 15). Therefore, the coupled electrical regulation within the islet is critically important for its function to secrete insulin and regulate glucose homeostasis.

Individual β-cells, when electrically isolated, show large variance in glucose sensitivity, metabolic activity, electrical dynamics, and insulin secretion (16, 17). This is distinct from the uniform coordinated electrical and secretory response in the intact islet. Understanding how cell variability contributes to the overall function of the islet, and how the presence of subpopulations of cells affects islet function in pathogenic conditions is poorly understood. For example, small populations of inexcitable cells that show altered K_ATP activity can suppress activity across the islet in the presence of coupling (11, 18, 19). The coordinated dynamics of electrical activity show spatial heterogeneity or “small world” properties in common with other biological systems, where like-dynamics are restricted to subregions of the islet (20, 21). Propagating calcium waves that mediate synchronization of [Ca²⁺]_i oscillations also initiate from subregions of the islet; this has been suggested as a pacemaker region defined by local excitability (22, 23). Despite observations suggesting that subpopulations of cells within the islet may affect several aspects of coordinated function, discovering their presence, characterizing their intrinsic behavior, and understanding how they contribute to coordinated islet function remains poorly characterized.

To study how functional subpopulations of cells may be distributed throughout multicellular structures such as the islet, and the role they may play in affecting global function, we are limited in ways to acutely perturb function and measure resultant responses. Here we apply optogenetics by using β-cell-specific Channelrhodopsin-2 (ChR2) expression (24) and time-dependent laser-scanning confocal activation to define the electrical regulation of subpopulations of cells within the islet. We combine this with quantitative fluorescence microscopy measurements of β-cell function and a multicellular computational model of coupled β-cell electrophysiology. With this, we test if islets of Langerhans contain discrete functional subpopulations and determine what effect these subpopulations have on controlling the coordinated electrical regulation and electrical dynamics.

Materials and Methods

Mice/animal care

Male and female mice were used under protocols approved by the University of Colorado Institutional Animal Care and Use Committee. Beta-cell-specific ChR2-YFP expression was achieved through crossing a Pdx-Cre^6Tuv/J (Pdx-Cre, Jax 014647; The Jackson Laboratory, Bar Harbor, ME) and a ROSA26Sor^{tm32(CAG-COP4∗H134R/EYFP)Hze/J} line (ChR2-YFP, Jax 024109; The Jackson Laboratory). Genotype was verified through qPCR (Transetyx, Memphis, TN). Mice were held in a temperature-controlled environment with a 12 h light/dark cycle and given continuous access to food and water. ChR2-YFP(−)/Pdx-Cre(+) littermates were used as controls.

Islet isolation

Islets were isolated from mice under ketamine/xylazine anesthesia (80 and 16 mg/kg) by collagenase delivery into the pancreas via injection into the bile duct; then the pancreas was harvested and digested, and islets were handpicked (25). Islets were cultured in RPMI medium (Corning, Tewksbury, MA) containing 10% fetal bovine serum, 100 U/mL penicillin, and 100 μg/mL streptomycin. Islets were incubated at 37°C, 5% CO₂ for 6–24 h before imaging.

Imaging

Isolated islets were mounted on 35-mm glass-bottom dishes in imaging solution (125 mM NaCl, 5.7 mM KCl, 2.5 mM CaCl₂, 1.2 mM MgCl₂, 10 mM HEPES, and 0.1% BSA, pH 7.4) and imaged using an LSM780 system (Carl Zeiss, Oberkochen, Germany) with a 20× 0.8 NA PlanApochromat objective at 37°C in the presence of 2, 5, and 11 mM glucose.

For [Ca²⁺] measurements, islets were loaded with 3 μm Rhod-2 AM (AAT Bioquest, Sunnyvale, CA) for 30 min at 37°C in imaging solution. Rhod-2 was excited using a 561-nm solid-state laser, which minimizes ChR2^H134R activation (26), and fluorescence emission was detected at 580–650 nm using a multianode PMT spectral detector. Images were acquired at ∼1 frame/s (scan time ∼650 ms) at ∼20 μm depth from the bottom of the islet.

ChR2 activation was achieved using a 458-nm Ar⁺ laser line. Activation regions in the islet were defined using the Zen software bleaching module (Carl Zeiss) and each activation region was set to scan 25 times over ∼1 s. Unless indicated, time-series were recorded alternating between 10 Rhod-2 images followed by a ChR2 activation sequence, and repeated for 40 s.

NADH(P)H autofluorescence was imaged under two-photon excitation using a tunable mode-locked Ti:sapphire laser (Chameleon; Coherent, Santa Clara, CA) set to 710 nm. Fluorescence emission was detected at 400–450 nm using the internal detector. Z-stacks of 6–7 images were acquired spanning a depth of 5 μm.

Cx36 function was measured using fluorescence recovery after photobleaching, as previously described (25). Islets were loaded with 12 μM Rhodamine-123 for 30 min at 37°C in imaging solution. Rhodamine-123 was excited using a 488-nm Ar⁺ laser line, and fluorescence emission was detected at 500–580 nm. Two baseline images were initially recorded. A region of interest was then photobleached for ∼30 s achieving, on average, a 44% decrease in fluorescence, and images were then acquired every 15 s for 6 min.

At 2 or 5 mM glucose, ChR2 activation was performed 10 min after glucose application, followed by measurements of NAD(P)H or Cx36 function. At 11 mM glucose, [Ca²⁺] measurements were performed 10 min after glucose application, followed by measurements of NAD(P)H.

Immunohistochemistry

Isolated islets were dissociated using Accutase (Sigma-Aldrich, St. Louis, MO) and plated into eight-chamber Nunc Lab-Tek dishes (Thermo Fisher Scientific, Waltham, MA) treated with 804G cell matrix. Twenty-four hours after plating, cells were fixed using 8% paraformaldehyde in PBS for 10 min. Antigen retrieval was first applied to the cells using 0.05% Trypsin with 10% CaCl2 in dH₂0 for 30 min at 37°C. Cells were then permeabilized using 0.1% Triton X-100 and 5% donkey serum in PBS for 2 h. Mouse anti-glucagon (Cat. No. ab10988; Abcam, Cambridge, UK) and guinea pig anti-insulin (Cat. No. ab7842; Abcam) primary antibodies were incubated with cells at a 1:500 dilution at 4°C for 24 h. Cy3 anti-guinea pig (Cat. No. 706-165-15; Jackson ImmunoResearch, West Grove, PA) and AlexaFluor 647 anti-mouse (Cat. No. 715-605-150; Jackson ImmunoResearch) secondary antibodies were applied to cells at a 1:500 dilution at room temperature for 2 h. After washing, cells were treated with DAPI fluoromount (Sigma-Aldrich) and imaged on a model No. LSM800 confocal microscope (Carl Zeiss). DAPI, YFP, Cy3, and Alexa647, respectively, were excited with laser lines at 440, 488, 561, and 640, and then respectively detected over 410–470, 500–545, 565–615, and 640–700-nm wavelength bands. In intact islets, FM 4–64FX was excited at 561 nm and detected over 600–620 nm.

Computational islet model

The multicellular islet model is based on the Cha-Noma single β-cell model, and has been previously described (18, 27). The membrane potential for each cell i is described through individual transmembrane current components:

$$-\mathit{C}\frac{\mathit{d}{\mathit{V}}_{\mathit{i}}}{\mathit{dt}}={\mathit{I}}_{\text{CaV}}+{\mathit{I}}_{\text{TRPM}}+{\mathit{I}}_{\text{SOC}}+{\mathit{I}}_{\text{bNSC}}+{\mathit{I}}_{\text{KDr}}+{\mathit{I}}_{\text{KCa}}+{\mathit{I}}_{\text{KATP}}+{\mathit{I}}_{\text{NaK}}+{\mathit{I}}_{\text{NaCA}}+{\mathit{I}}_{\text{PMCA}}+{\mathit{I}}_{\text{coup}}+{\mathit{I}}_{\text{ChR}2},$$ (1)

where the kinetics of each current are described in (27). The K_ATP channel current (I_KATP) is expressed as

$${\mathit{I}}_{\text{KATP}}={\mathit{g}}_{\text{KATP}}\cdot \mathit{p}{\mathit{o}}_{\text{KATP}}\cdot \left(\mathit{V}-{\mathit{V}}_{\mathit{K}}\right),$$ (2)

where the ATP and ADP dependence of open channel probability (po_KATP) is

$$\mathit{p}{\mathit{o}}_{\text{KATP}}=\frac{0.08\left(1+\frac{2\left[\text{ADP}\right]}{0.01}\right)+0.89{\left(\frac{\left[\text{ADP}\right]}{0.01}\right)}^2}{{\left(1+\frac{\left[\text{ADP}\right]}{0.01}\right)}^2\left(1+\frac{0.45\left[\text{ADP}\right]}{0.026}+\left(\frac{\left[\text{ATP}\right]}{0.05}\right)\right)}.$$ (3)

Heterogeneity in K_ATP density was modeled by varying g_KATP. Diazoxide application was modeled by modifying po_KATP to add an ATP-independent current:

$$\mathit{p}{\mathit{o}}_{\text{KATP}\left(\text{Diaz}\right)}=\mathit{\alpha }+\left(1-\mathit{\alpha }\right)\cdot \mathit{p}{\mathit{o}}_{\mathit{K}\left(\text{ATP}\right)},$$ (4)

where α is set to 0.1, as used previously (18).

The metabolic activity of the β-cell is determined by the flux of glucokinase (GK) activity and thus glycolysis and tCA cycle, described by

$${\mathit{J}}_{\text{glyc}}={\mathit{k}}_{\text{glyc}}.\frac{1}{1+{\left(\frac{{\mathit{K}}_{\mathit{G}}}{\left[\text{G}\right]}\right)}^{2.5}}.\frac{1}{1+\left(\frac{{\mathit{K}}_{\text{mATP}}}{\left[\text{ATP}\right]}\right)}.\left(\left[{\text{NAD}}_{\text{to}}\right]-\left[\text{NADH}\right]\right),$$ (5)

where [G] is the glucose concentration. Heterogeneity in GK activity was modeled by varying k_glyc, which is equivalent to the Glucokinase rate. The total nucleotide pyrimidine nucleotide concentration is [NAD_tot], and reduced form [NADH] is calculated by

$$\frac{\mathit{d}\left[\text{NADH}\right]}{\mathit{dt}}={\mathit{J}}_{\text{glyc}}+{\mathit{J}}_{\beta ,\text{ox}}-\frac{{\mathit{R}}_{\text{vol}}}{\mathit{N}}{\mathit{J}}_{\text{op}},$$ (6)

where J_β,ox represents the rate of β-oxidation, R_vol is the ratio between cytosolic and mitochondria volume, N is the stoichiometric conversion between NADH and ATP, and J_op is the ATP production through oxidative phosphorylation.

Spherical islet structures of 1000 cells were created with a sphere-packing algorithm (28). To functionally connect cells via Cx36: if nearest neighbors to each cell were within 20% of the cell radius, they were connected. This gave a mean ± SD number of connections per cell within the simulated islet of 5.3 ± 1.7. I_coup is the current through Cx36 gap junction channels and was modeled according to the potential between two cells i,j:

$${\mathit{I}}_{\text{coup}}=\sum _{\mathit{j}}{\mathit{g}}_{\text{coup}}^{\mathit{i},\mathit{j}}\left({\mathit{V}}_{\mathit{i}}-{\mathit{V}}_{\mathit{j}}\right).$$ (7)

Heterogeneity in Cx36 was modeled according to previous results as a γ-distribution with parameters k = θ = 4 (25). Each cell was assigned a conductance value according to the γ-distribution, and the g_coup between two connected cells was determined as the average assigned conductance of each cell. The distribution was scaled to give a mean g_coup between cells of 120 pS (22), as

$$\mathit{f}\left(\mathit{x},\mathit{k},\mathit{\theta }\right)=\frac{{\mathit{x}}^{\mathit{k}-1}{\mathit{e}}^{-\frac{\mathit{x}}{\mathit{\theta }}}}{{\mathit{\theta }}^{\mathit{k}}\left(\mathit{k}-1\right)!}.$$ (8)

I_ChR2 is the ChR2 photo-induced current and was described using a four-state ChR2 model (29). The current response is modeled through

$${\mathit{I}}_{\text{ChR}2}={\mathit{V}}_{\mathit{i}}{\mathit{g}}_{\text{CHR}2}\left({\mathit{O}}_1+\mathit{\gamma }{\mathit{O}}_2\right),$$ (9)

where O₁ and O₂ are open state probabilities, γ is the ratio of open state conductances, g_ChR2 is the conductance, and V_i as the membrane potential. Open and closed state equations are described in (29).

Random heterogeneity in parameters (see the Supporting Material) was created for each cell using a Gaussian distribution with mean μ and SD σ, as before (18). For assignment of spatial heterogeneity, islets were divided into five spatial partitions using a K-means clustering algorithm (30, 31). The parameter of interest was sorted by value and sequentially assigned to each spatial location, giving discrete locations of cells with similar parameter value. Heterogeneity of other parameters was decreased simultaneously to σ = 0.05^∗μ and randomly distributed across the islet. The combined model, consisting of 22 ODEs per cell with 1000 cells per islet, was implemented in C++, and solved using a forward Euler solver with time step of 150 μs. Simulations were run on single nodes with two hex-core 2.8 GHz Intel Westmere processors (Mountain View, CA).

For each simulation, the ChR2 activation protocol was first performed with [G] at 2 or 5 mM over ∼1 min, and then [G] was set to 11 mM glucose for 5 min.

Data analysis

All analysis was performed using custom scripts in MATLAB (The MathWorks, Natick, MA). [Ca²⁺]_i measurements were quantified by a peak detection algorithm testing for ChR2-stimulated action potentials on a pixel-by-pixel basis. A pixel was defined as active if [Ca²⁺]_i peaks were identified at the time of ChR2 stimulation and no more than 30% of the peaks identified could result from non-ChR2 stimulated events: in this way, we could quantify areas that may have been poorly stained with [Ca²⁺] indicator. Areas that could not be stimulated while activating the whole islet were not included in the analysis of subregion stimulation. Simulated [Ca²⁺] time-courses were analyzed using threshold-based peak detection, where a cell was defined if [Ca²⁺] was elevated above 175 nM at the time of ChR2 stimulation. NAD(P)H response for each quadrant was calculated by averaging the intensity across the z-stack fluorescence in that quadrant and calculating the percentage change between 11 and 5 mM glucose.

To quantify [Ca²⁺] oscillatory frequency in Cx36^−/− islets, the peak detection algorithm from above was used to record the spatial locations and times of all oscillations across an islet. Individual cells were located by segmented regions based on coincident time-points of detected oscillations. NAD(P)H responses were calculated by mapping each cellular region onto the NAD(P)H images and the response for each cellular location was calculated.

For immunofluorescence images, analysis for hormone staining and ChR2-YFP expression was restricted to single dissociated cells identified as single nuclei locations. Doublet, triplet, or aggregates of cells were excluded from analysis.

ANOVA was used to compare differences between multiple groups, followed by Tukey multiple comparison test for post hoc comparison. A Benjamini-Hochberg procedure (false-discovery rate of 0.1) was used where noted to test if each ANOVA within a set of experiments could be significant, in addition to a Bonferroni multiple-comparisons correction. Student t-test was used where noted. Here, ^∗ indicates p < 0.05, ^∗∗ indicates p < 0.01, ^∗∗∗ indicates p < 0.001, and ^∗∗∗∗ indicates p < 0.0001 comparing the experimental groups indicated.

Data availability

Data is available from the corresponding author upon request. Model code and MATLAB analysis tools are made available in the Supporting Material.

Results

Local ChR2 activation reveals regions of varying excitability

We first examined the spatial dependence of ChR2 activation and local membrane depolarization on [Ca²⁺]_i regulation across the islet. ChR2-YFP was expressed in β-cells under Cre-recombinase control (Fig. 1 A), through a Pdx-Cre line that shows early expression and lacks mosaicism (32). ChR2-YFP expressing cells were distributed throughout the islet (Fig. S1). Greater than 80% of insulin-positive cells expressed ChR2-YFP, whereas <10% of glucagon-positive cells and <10% of nonglucagon/insulin-positive cells expressed ChR2-YFP (Fig. S1, B and C). At basal (5 mM) glucose levels, activating ChR2 periodically across the whole islet led to coincident elevations of [Ca²⁺]_i across 84 ± 5% of the islet, rising immediately after excitation and subsequently decayed exponentially with a rate constant of ∼0.5 s⁻¹ (Fig. 1 B), consistent with previous findings (33).

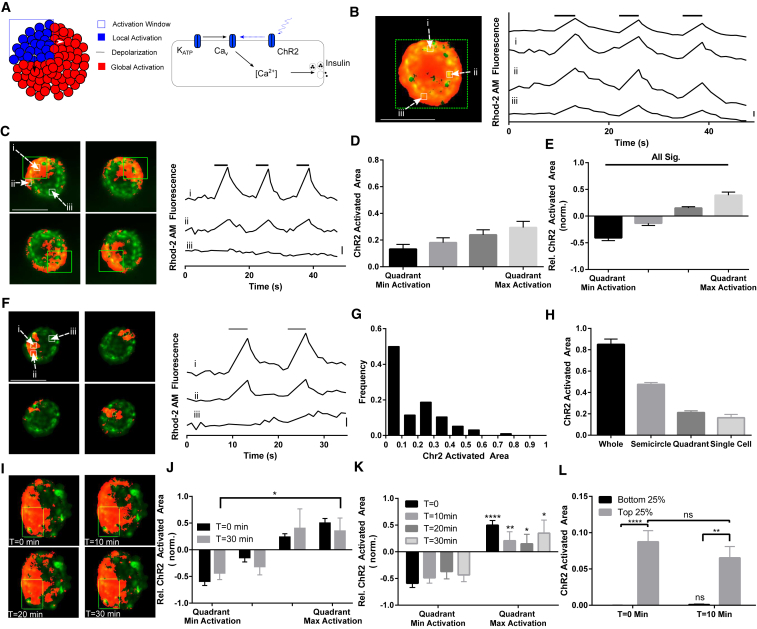
Figure 1.

ChR2 activation creates local [Ca²⁺]_i elevation in pancreatic islets. (A) A model of spatial activation of ChR2 in pancreatic islets. Activation regions within the islet are defined, where ChR2 is activated by 458 nm illumination leading to depolarization and opening of V-gated Ca²⁺ channels. (B) An activation region defined over the whole islet (left, green dashes) generates islet-wide [Ca²⁺]_i influx (left, orange). [Ca²⁺]_i increases rapidly after ChR2 activation, as measured by Rhod-2 fluorescence (right). (C) An activation region defined over a quadrant of the islet (left, green dashes) generates local [Ca²⁺]_i elevation, which extends outside of the activation region (left, orange). More distant areas of the islet show no [Ca²⁺]_i influx (right). (D) Mean ± SE ChR2-activated [Ca²⁺] resulting from quadrant activation regions, presented in rank order, normalized to islet size. (E) Mean ± SE intraislet variation in ChR2-activated [Ca²⁺] relative to the islet average. The relative area of ChR2-activated [Ca²⁺]_i over each quadrant (as in D) was expressed relative to the mean ChR2-activated [Ca²⁺]_i of each islet, and sorted from least to most. (F) Activation of smaller single-cell regions within islets similar to (C). [Ca²⁺] is elevated within and outside the activation region (right). (G) Distribution of the ChR2-activated area upon single-cell activation regions (n = 96 regions). (H) Mean ± SE ChR2-activated area of [Ca²⁺]_i elevation upon varying sizes of activation region. (I) Repeated activation of one quadrant is shown at 0, 10, 20, and 30 min. (J) Mean ± SE intraislet variation in ChR2-activated [Ca²⁺] as in (E), at time 0 and after 30 min of repeated ChR2 stimulation, sorted from least to most based on time-0 measurements. (K) As in (I), for minimum and maximum quadrants at 0, 10, 20, and 30 min during ChR2 stimulation. (L) Mean ± SE ChR2-activated area upon single-cell activation at time 0 and after 10 min of repeated ChR2 stimulation, averaged over the bottom and top 25% areas, and under a second stimulation sorted based on time-0 measurements. Scale bar in (B), (C), and (F) indicates 2% change in fluorescence. Data in (D) and (E) were averaged over n = 25 islets from six mice; data in (G) was averaged over n = 96 regions, 26 islets from five mice. Data in (I–L) were averaged over n = 10 islets from two mice. ^∗∗∗∗ indicates p < 0.0001, ^∗∗ indicates p < 0.01, ^∗ indicates p < 0.05 comparing experimental groups indicated. In (K), maximal values are compared to the minimal values at each time point. Image scale bars, 100 μm. To see this figure in color, go online.

Activating ChR2 across subregions of ∼25% of the islet (quadrants) elevated [Ca²⁺]_i across the window of ChR2 activation and extended it outside of the activation window, but not across the whole islet (Fig. 1 C). This activation caused variations in the level of elevated [Ca²⁺]_i that extended outside of the activation window (Fig. 1 D), suggesting some islet regions were more readily activated by ChR2. On average, the region that provided the least [Ca²⁺]_i stimulation activated ∼15% of the islet, which we refer to as the “ChR2-activated area”, whereas the region that provided the most [Ca²⁺]_i stimulation activated ∼30% of the islet. Relative to the mean ChR2-activated area for an islet, the minimum ChR2-activated area was ∼40% lower and the maximum ChR2-activated area ∼40% higher (Fig. 1 E). These regions of varying ChR2-activated [Ca²⁺]_i were independent of experimental parameters that included stimulation order, position within the microscope field of view, and ChR2-YFP expression (Fig. S2, A, C, and E).

Activation of single-cell-sized regions also elevated [Ca²⁺]_i outside of the activation window (Fig. 1 F), although with high variability (Fig. 1 G). Approximately 50% of cell-sized regions showed negligible activation of [Ca²⁺]_i outside the window and ∼50% of cell-sized regions showed significant activation with a small population showing substantial activation >50% of the islet. Overall, the amount of ChR2-activated area increased with the size of the illumination window (Fig. 1 H). Illuminating 100% of the islet led to a ChR2-activated area of 84 ± 5%, illuminating 50% of the islet led to a ChR2-activated area of 41 ± 5%, illuminating 25% of the islet led to a ChR2-activated area of 21 ± 4%, and illuminating single-cell regions (∼5% of the islet) led to a ChR2-activated area of 16 ± 3%.

Under repeated activation of ChR2 in quadrant subregions, those regions initially with the least ChR2-activated area continued to show, on average, the least ChR2-activated area over 30 min; this was significantly lower than those regions initially with the highest ChR2-activated area (Fig. 1, I–K). Similarly, upon sequential ChR2 activation of single-cell-sized regions, those cells that initially showed negligible activation of [Ca²⁺] continued to show significantly lower ChR2-activated area compared to those cells that initially showed high activation of [Ca²⁺], with no significant difference over time (Fig. 1 L). In addition, the level of heterogeneity (SD/mean of ChR2-activated area) did not significantly change with time, whether for quadrant regions (0.49 ± 0.08 at 0 min, 0.69 ± 0.20 at 30 min) or single-cell-sized regions (1.32 ± 0.21 at 0 min, 1.18 ± 0.17 at 10 min).

The duration of light exposure influences the amount of ChR2-activated area when illuminating 25% of the islet. Activating ChR2 using shorter 100-ms stimulation resulted in [Ca²⁺]_i elevating in less of the islet compared to the standard pulse durations of 1 s used above; but longer pulse durations of 10 s showed no difference compared to the pulse durations of 1 s (Fig. S2, F and G). Regions of the islet that showed a greater ChR2-activated area under standard 1-s pulse durations also showed greater ChR2-activated area under shorter 100-ms pulse durations (Fig. S2 H), indicating the intraislet variability in ChR2-activated area is independent of the activation protocol.

Therefore, within islets, at basal glucose, subregions of the islet exist that upon depolarization can more effectively recruit neighboring regions of the islet to show elevated [Ca²⁺]_i, independent of experimental protocols; and this occurs over several spatial scales from islet subregions to single-cell-sized regions.

β-cell metabolic activity controls variations in ChR2-stimulated [Ca²⁺]_i

Single β-cells dissociated from the islet are heterogeneous in the activity and dynamics of many factors underlying insulin secretion (34, 35). Islet regions containing β-cells with increased excitability could result in less ChR2-mediated depolarization required to depolarize neighboring regions and elevating [Ca²⁺]_i. To test whether regions of altered β-cell function affect the ChR2-activated area, we assessed glucose-metabolism via two-photon imaging of NAD(P)H (Fig. 2 A), alongside ChR2 activation and [Ca²⁺]_i imaging: where heterogeneity in β-cell glucose metabolism has been reported (16). To examine variations in intraislet metabolic activity, we first sorted regions by ascending levels of NAD(P)H, such that each islet had a region of minimum and maximum metabolic activity. NAD(P)H levels over 2, 5, and 11 mM glucose were relatively consistent between islets and quadrant regions of each islet (Fig. S3 A). The NAD(P)H signal includes NADH, which reflects changes glucose metabolism, but also NADPH and other autofluorescence signatures that do not reflect glucose metabolism. To exclude spatial variations in non-NADH signals, we examined the NAD(P)H response between 5 and 11 mM glucose, which has previously been shown to robustly reflect glucose metabolism (36). There were significant variations in the NAD(P)H response from 5 to 11 mM glucose within each (Fig. S3 B), where the difference between the quadrant-region of highest and lowest NAD(P)H response with an islet was 35 ± 5% (Fig. S3 C).

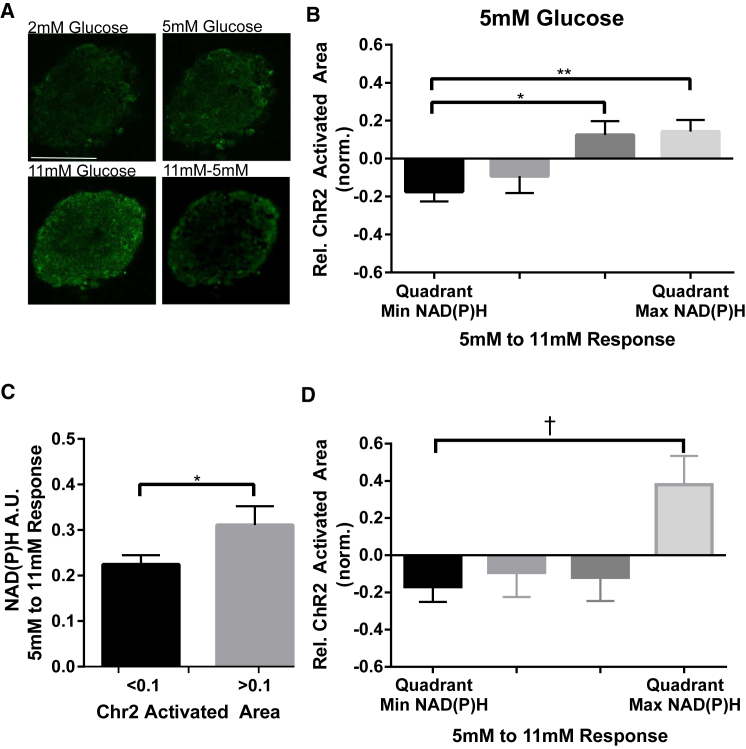
Figure 2.

Spatial variations in metabolic activity control electrical activity. (A) Representative images of NAD(P)H autofluorescence at glucose levels indicated, or change in NAD(P)H autofluorescence between indicated glucose levels. (B) Mean ± SE ChR2-activated area at 5 mM glucose for corresponding rank order quadrants of NAD(P)H response between 5 and 11 mM glucose. (C) Mean ± SE NAD(P)H response between 5 and 11 mM glucose for single-cell activation regions in which ChR2-activated area was low (<0.1) or high (>0.1). (D) As in (B) for ChR2-activated area at 5 mM glucose plus 150 μM diazoxide, for corresponding NAD(P)H response between 5 and 11 mM glucose plus 150 μM diazoxide. Data in (B) were averaged over n = 25 islets from six mice; data in (C) were averaged over n = 96 regions, 26 islets from five mice; data in (D) were averaged over n = 10 islets from three mice. ^∗ indicates p < 0.05, ^∗∗ indicates p < 0.01, comparing experimental groups indicated. For (B), this includes a Benjamini-Hochberg procedure and a Bonferroni correction (together with data in Fig. S3, D–H). † indicates p < 0.05 comparing experimental groups indicated, including a Benjamini-Hochberg procedure (together with unpublished data for four further conditions). Student t-test was used in (C) to calculate statistical significance. Scale bar in (A) indicates 100 μm. To see this figure in color, go online.

We compared quadrant-regions of NAD(P)H levels and response with the ChR2-activated area. The ChR2-activated area at 5 mM glucose varied significantly and substantially with the NAD(P)H response from 5 to 11 mM glucose (Fig. 2 B). Regions with the lowest NAD(P)H response between 5 and 11 mM glucose had a ChR2-activated area 17% less than the islet average, whereas the region of highest NAD(P)H response showed a ChR2-activated area that was 14% greater than the islet average. This indicates that at basal glucose, spatial heterogeneity in glucose metabolism within islets leads to spatial variations in the control of electrical activity. In contrast, the ChR2-activated area at 2 mM glucose did not vary significantly with NAD(P)H levels at 2 mM glucose nor did it vary with the NAD(P)H response from 2 to 5 mM glucose or from 2 to 11 mM glucose (Fig. S3, D–F), consistent with there being little metabolic heterogeneity at low (2 mM) glucose levels. We also examined the link between ChR2-activated area and NAD(P)H within single-cell regions. Cellular regions in which the ChR2-activated area was above the median area (10%) showed significantly greater NAD(P)H response from 5 to 11 mM glucose than cellular regions in which the ChR2-activated area was below the median area (Fig. 2 C). Thus, single-cell locations showing high ChR2-activated area also had correspondingly higher levels of glucose metabolism. In each case, the ChR2-activated area at 5 mM glucose showed only small or no variation with NAD(P)H level at 5 mM or the NAD(P)H response from 2 to 5 mM glucose (Fig. S3, G–J), consistent with those NAD(P)H measurements being less accurate assessments of metabolic activity (36).

To determine the influence of varying K_ATP density, we performed similar measurements with the addition of diazoxide, a K_ATP activator. In the presence of diazoxide, greater laser power was needed to elevate [Ca²⁺]_i and achieve a similar ChR2-activated area. Despite this, at 5 mM glucose the ChR2-activated area still varied significantly with the NAD(P)H response from 5 to 11 mM glucose (Fig. 2 D), as in the absence of diazoxide. Cx36 gap junction function is also heterogeneous within islets (25) and we measured gap junction permeability via fluorescence recovery after photobleaching, alongside ChR2-activaiton and [Ca²⁺]_i imaging (Fig. S4, A and B). The ChR2-activated area was not significantly different between regions of highest and lowest Cx36 gap junction permeability (Fig. S4 C).

Multicellular islet model demonstrates link between metabolic activity and ChR2-stimulated [Ca²⁺]_i

Variations in ChR2-activated [Ca²⁺]_i correlated with variations in metabolic activity over a range of spatial scales. β-cells are intrinsically heterogeneous in excitability, but the organization of this heterogeneity within the islet and how it may impact function is unknown. We asked whether specific spatial distributions of β-cell excitability were required, or whether random distributions were sufficient to describe our experimental observations. We implemented a multicellular islet model incorporating β-cell heterogeneity, which has previously described how the balance of gap junction coupling and K_ATP-regulated β-cell excitability controls islet function (18). We also included a four-state ChR2 current module (29). Although we did not measure glucokinase activity experimentally (instead we measured NAD(P)H responses), we introduced metabolic heterogeneity by varying GK activity with a distribution that matched that observed experimentally for NAD(P)H levels (37).

We first divided the simulated islet into spatial partitions, each containing ∼200 cells with a randomly defined subset of the variation in metabolic activity (glucokinase activity) (Fig. 3 A). At suboscillatory glucose conditions, quadrant-regions were activated by ChR2, followed by an increase to 11 mM glucose to induce [Ca²⁺]_i oscillations (Fig. 3 B; Movie S1). Activating quadrant-regions within the simulated islet led to [Ca²⁺]_i rises within the activation window and with significant intraislet variation in the ChR2 activation area (Fig. 3 C), consistent with experimental measurements (Fig. 3 D). Simulated measurements of glucokinase activity over quadrant regions showed intraislet variation that was comparable to the variation in experimentally measured NAD(P)H, where the difference between the quadrant-region of highest and lowest glucokinase activity was 36 ± 2% (Fig. 3 E). At 2 mM glucose, the ChR2-activated area did not vary significantly with metabolic activity (Fig. 3 F), consistent with experimental measurements (Fig. S3, D–F). However, at 5 mM glucose, the ChR2-activated area did vary significantly with metabolic activity (Fig. 3 G), consistent with experimental measurements (Fig. 2 B): here, quadrant-regions with minimum glucokinase activity showed the lowest ChR2-activated area, and regions with maximum glucokinase activity showed the highest ChR2-activated area. At 5 mM glucose, with the addition of an ATP-independent K_ATP channel current (+10% open channel conductance) to model diazoxide application (18), the ChR2-activated area still varied significantly with metabolic activity (Fig. 3 H), again consistent with experimental measurements (Fig. 2 D).

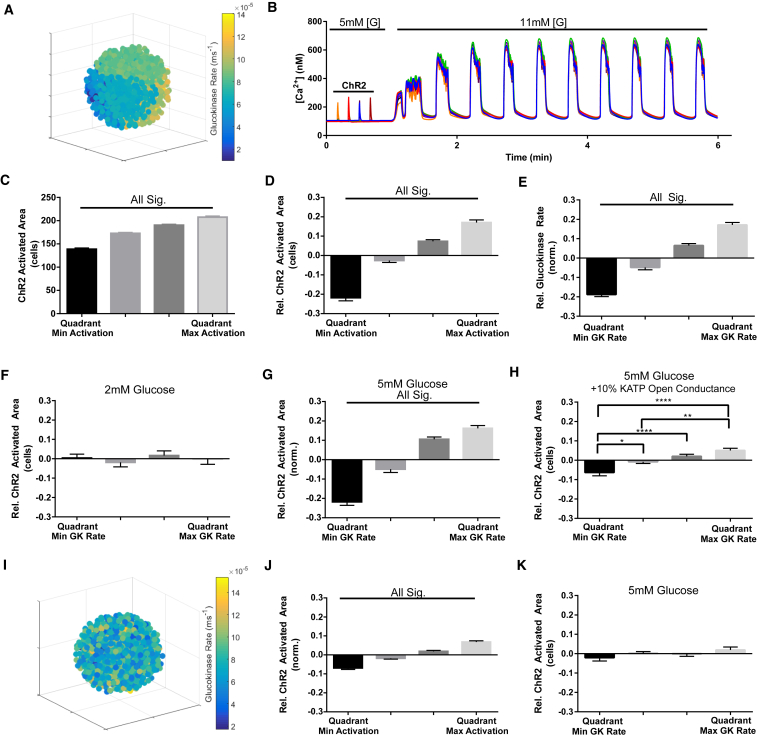
Figure 3.

Spatial domains in an islet model recapitulates ex vivo excitability. (A) Representative false-color map shows cellular GK rate over a simulated islet, where subregions of similar heterogeneity in GK rate are applied (other variables randomly distributed). Each sphere represents a simulated β-cell. (B) Representative time-course of [Ca²⁺] in five cells of a simulated islet is given following ChR2 protocol: glucose is held at a concentration of 5 mM for quadrant ChR2 activation, and then increased to 11 mM to stimulate [Ca²⁺] oscillations. (C) Mean ± SE of ChR2-activated area, given in terms of number of cells activated, by quadrant in rank order. (D) Mean ± SE intraislet variation in ChR2-activated area given relative to the simulated islet average. The relative area of ChR2-activated [Ca²⁺] over each quadrant was expressed relative to the mean ChR2-activated [Ca²⁺] of each simulated islet, and sorted from least to most. (E) Mean ± SE intraislet variation in GK rate given relative to the islet average, calculated in the same way as in (D). (F) Mean ± SE ChR2-activated area given relative to the islet average at 2 mM glucose, for each corresponding quadrant GK rate (as in D). (G) Mean ± SE ChR2-activated area given relative to the islet average at 5 mM glucose, for each corresponding quadrant GK rate at 5 mM glucose (as in F). (H) Mean ± SE ChR2-activated area given relative to the islet average at 5 mM glucose, for each corresponding ascending rank-ordered quadrant GK rate (as in D) under the addition of 10% K_ATP open channel conductance in all cells. (I) Representative false-color map shows cellular GK rate over a simulated islet, where random spatial distribution of heterogeneity is applied. (J) As in (D), for simulated islets with randomly distributed heterogeneity. (K) As in (G), for simulated islets with randomly distributed heterogeneity. Data in (C–H), (J–K) were averaged over n = 30 simulated islets. ^∗ indicates p < 0.05, ^∗∗ indicates p < 0.01, ^∗∗∗ indicates p < 0.001 comparing experimental groups indicated. To see this figure in color, go online.

To test the requirement for heterogeneity to be distributed into spatial domains of excitability, we distributed variations in glucokinase activity throughout the islet without any spatial organization (Fig. 3 I). However, there was no consistent relationship between variations in ChR2-activated [Ca²⁺]_i and variations in glucokinase activity (Fig. 3, J and K). This supports that cellular heterogeneity has some spatial organization, rather than being a purely random distribution.

Membrane depolarization controls [Ca²⁺]_i elevation. We examined whether metabolic heterogeneity had a similar impact in exerting varying depolarization in neighboring cells as with exerting varying [Ca²⁺]_i elevations (Fig. S5 A). Heterogeneity in membrane depolarization was observed under a similar ChR2 protocol, and this showed similar correspondence with metabolic activity. Notably regions with greater ChR2-activated area also showed a higher resting membrane potential, consistent with greater metabolic activity, ATP production, and K_ATP channel closure (Fig. S5, B–D).

The retained link between variations in ChR2-activated area and metabolic activity upon diazoxide application suggests that heterogeneity in metabolic activity and K_ATP regulation has a greater impact than heterogeneity on other factors that control excitability. To test this, we introduced heterogeneity in K_ATP channel density in spatial partitions as with simulations varying glucokinase activity (Fig. S6 A). Although similar variations in ChR2-activated area were observed, and intraislet variability in K_ATP channel density was also similar to that of glucokinase activity, there was no significant link between the intraislet variation in K_ATP channel density and the ChR2-activated area (Fig. S6, B–D).

Spatial organization to NAD(P)H and ChR2 responses

To test whether metabolic activity is spatially organized within the islet as predicted by the islet model, we first calculated the differences in the NAD(P)H response as a function of separation distance. For several baseline reference points within an islet, the change in NAD(P)H between 5 and 11 mM glucose was averaged over expanding areas of radius Δr (Fig. 4 A). The resultant “Δ NAD(P)H” response curve increased slowly as a function of radial distance (Fig. 4 B), indicating that areas of the islet distant from a reference point showed, on average, a more different NAD(P)H response than areas close to the reference point. This was independent of whether the reference point was at the center or more peripheral in the islet (data not shown). Replicate analysis of simulated islets with the two spatial distributions (Fig. 3, A and I) showed a similar slow increasing response curve for the spatially organized distribution, whereas a random organization showed no significant change with distance (Fig. 4 C). These findings were replicated by using pairwise differences in either small areas of NAD(P)H response for experimental measurements (Fig. 3, D and E) or cellular glucokinase activity for simulations (Fig. 3 F). The spatial scale of the experimentally measured NAD(P)H response matched the spatially ordered heterogeneity in glucose metabolism in simulated islets (Fig. 4, B–F), supporting the prediction that subregions of metabolic activity exist that can impact the spatial variations in excitability.

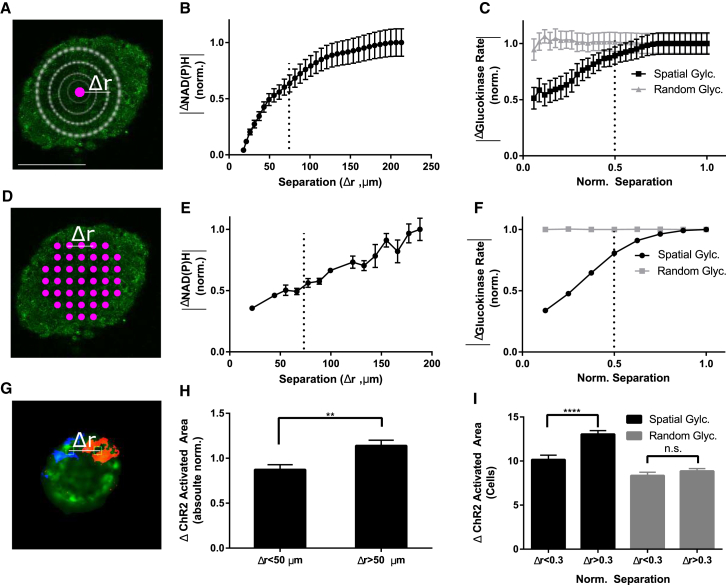
Figure 4.

Spatial analysis of NAD(P)H and ChR2-activated [Ca²⁺] responses. (A) Representative NAD(P)H intensity image, displaying how spatial correlations in the NAD(P)H response (between 5 and 11 mM glucose) were quantified. The ΔNAD(P)H response was calculated by the absolute difference taken between an initial NAD(P)H response measurement (purple), and the NAD(P)H response averaged over an outwardly expanding region (white circles) with radius Δr. (B) ΔNAD(P)H response shown as a function of radial distance Δr, as described in (A), normalized to the ΔNAD(P)H at the largest Δr. (C) Equivalent analysis to that in (B), calculated from GK rates in simulated islets with random spatial distribution of GK rate (gray) or subregions of similar GK rates (black). (D) Representative image showing how spatial differences in NAD(P)H response were quantified. The absolute differences in NAD(P)H response were calculated for several small regions (purple circles) separated by distance Δr, in a pairwise manner. (E) Shown here are mean absolute differences in NAD(P)H response between regions as a function of spatial separation Δr, as described in (D), normalized to the difference in response at maximal separation. (F) Equivalent analysis to that in (E), calculated from GK rates in simulated islets with random spatial distribution of GK rate (gray) or subregions of similar GK rates (black). Dashed lines in (B), (C), (E), and (F) indicate a distance of ∼6 cells. (G) Representative map of ChR2-activated [Ca²⁺]_i in an islet at 5 mM glucose (orange, blue), where activation regions are applied individually over a single cell. (H) Mean ± SE pairwise absolute differences in ChR2-activated [Ca²⁺] area were averaged by close (Δr < 50 μm) and far (Δr > 50 μm) differences (12–16 locations per islet), then normalized to the average ChR2-activated area for each islet. (I) Equivalent analysis to that in (H) calculated from single-cell ChR2-activated [Ca²⁺] in simulated islets with subregions of similar or random GK rates. Student t-test was used in (H) and (I). ^∗∗ indicates p < 0.01, comparing experimental groups indicated. Scale bar in (A) indicates 100 μm. To see this figure in color, go online.

To test whether there exists regions of similar excitability, we computed pairwise differences in the ChR2-activated area between each single-cell region within an islet (Fig. 4 G). These pairwise differences were sorted by the distance between the regions (Δr). There was a significant positive relationship between the difference in ChR2-activated area and the spatial separation distance (Fig. S7 A), where pairwise differences in closer (Δr < 50 μm) regions were significantly less different than more distant (Δr > 50 μm) regions (Fig. 4 H). Similar results were observed upon computing pairwise differences in the ChR2-activated area between each single-cell region within the simulated islet (Fig. 4 I; Fig. S7 B). Therefore, cells in closer proximity show more similar ChR2-activation of [Ca²⁺]_i, consistent with the islet model, and indicate excitability is also spatially ordered.

Wave origin correlates with lower metabolic activity and excitability

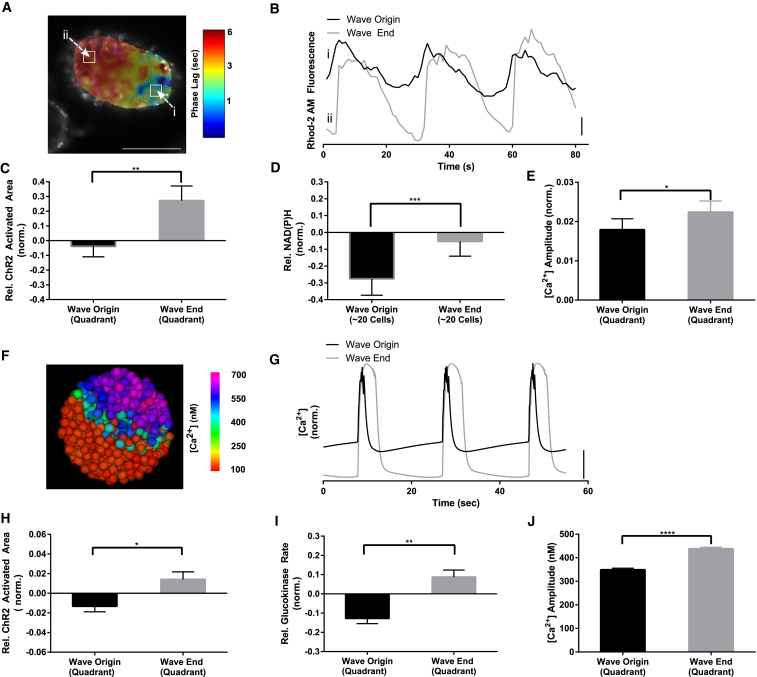
Coordinated [Ca²⁺]_i oscillations within islets at elevated glucose are synchronized by propagating waves that consistently originate in defined regions of the islet (23). We hypothesized that the observed metabolic heterogeneity may control these [Ca²⁺]_i wave dynamics at elevated glucose. To investigate how heterogeneity in β-cell function correlates with propagating calcium waves, we measured wave propagation associated with fast (<1 min.) [Ca²⁺]_i oscillations alongside ChR2-activation and NAD(P)H measurements or Cx36 permeability measurements. Using phase analysis (see Materials and Methods), propagating waves of [Ca²⁺]_i elevation were observed that had a consistent spatial origin and propagated across the islet in ∼2 s (Fig. 5, A and B), consistent with prior measurements (22, 23). The ChR2-activated area at 5 mM glucose in the quadrant of the wave origin was significantly less than the ChR2-activated area in the quadrant of the wave end, with a difference of 31 ± 12% (Fig. 5 C). Consistent with this, the NAD(P)H response from 5 to 11 mM glucose in the region of the wave origin was significantly less than both the NAD(P)H response at the wave end and the NAD(P)H response averaged over the whole islet (Fig. 5 D). Furthermore, the [Ca²⁺]_i oscillation amplitude at the wave origin was less than at the wave end (Fig. 5 E). The Cx36 gap junction permeability did not differ significantly between regions of the wave origin and end (Fig. S4 D). Therefore, surprisingly, spatial heterogeneity in glucose metabolism within the islet leads to subregions of lower metabolic activity and excitability that appear to control the origin of propagating calcium waves.

Figure 5.

Calcium wave origin corresponds to less excitable and metabolically active regions. (A) A representative phase map of [Ca²⁺] oscillations within an islet at 11 mM glucose, as calculated through Fourier analysis, which indicates a wave emerging in region of minimum phase (dark blue) and terminating in a region of maximum phase (dark red). (B) Representative time-courses from (A), showing phase lag of [Ca²⁺] waves. (C) Mean ± SE ChR2-activated area of [Ca²⁺] relative to the islet average, in quadrant of wave origin and wave end. (D) Mean ± SE NAD(P)H response (between 5 and 11 mM glucose) relative to the islet average, in selected regions of minimum and maximum phase, as indicated in (A). (E) Mean ± SE [Ca²⁺] oscillation amplitude (normalized to average Rhod-2AM fluorescence) in quadrants of wave origin and wave end. (F) A representative false-color map of [Ca²⁺] wave in a simulated islet, as in (A). (G) Representative time-courses from (F), showing phase lag of [Ca²⁺] waves. (H) Mean ± SE ChR2-activated area in quadrants of wave origin and wave-end in simulated islet, as in (C). (I) Mean ± SE GK rate in quadrants of wave origin and wave-end in simulated islet, as in (D). (J) Mean ± SE [Ca²⁺] oscillation amplitude in quadrants of wave origin and wave-end in simulated islet, as in (E). Data in (C–E) were averaged over n = 16 islets from four mice. Data in (H–J) were averaged over n = 30 simulated islets. ^∗ indicates p < 0.05, ^∗∗ indicates p < 0.01, ^∗∗∗ indicates p < 0.001, ^∗∗∗∗ indicates p < 0.0001 comparing experimental groups indicated. Student t-test was used in (C–E), (H–J) to calculate statistical significance. Vertical scale bars indicate 2% change in fluorescence in experiment or 100 nM change in [Ca²⁺]_i in simulated islets. Scale bar in (A) indicates 100 μm. To see this figure in color, go online.

We tested if this relationship is maintained in the islet model, where similar propagating [Ca²⁺]_i waves are observed (Fig. 5, F and G; Movie S2). The quadrant of wave origin had significantly lower ChR2-activated area than the quadrant of wave end (Fig. 5 H), whether considering propagation of membrane depolarization or the [Ca²⁺]_i elevation (Fig. S5 E). Further, the glucokinase activity at the wave origin was also significantly less than the glucokinase activity at the wave end (Fig. 5 I), and the [Ca²⁺]_i amplitude at the wave origin was less than at the wave end (Fig. 5 J). When introducing heterogeneity in K_ATP density, the conductance at the wave origin was significantly greater than at the wave end (Fig. S6 F). Therefore, spatially organized heterogeneity in metabolic activity is sufficient to control the origin and propagation of calcium waves across the islet.

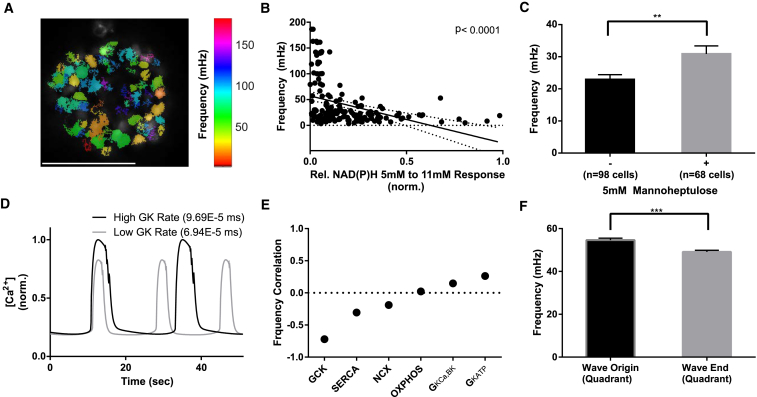
Intrinsic oscillatory frequency controls calcium wave propagation

The experimental observation and model agreement that calcium waves originate in regions of lower metabolic activity is not immediately intuitive. However, simulation results have suggested waves to originate in regions of higher oscillation frequency (23), and the [Ca²⁺]_i oscillation pattern is dependent on metabolic activity (38). To examine the link between metabolic activity and [Ca²⁺]_i oscillation frequency on a cellular scale, we analyzed cells in islets from Cx36^−/− mice, which lack gap junction conductance and [Ca²⁺]_i oscillation synchronization (13, 22) (Fig. 6 A; Movie S3). There was a significant negative correlation between cellular [Ca²⁺]_i oscillatory frequency and NAD(P)H response (Fig. 6 B), where cells with higher metabolic activity had slower [Ca²⁺] oscillations. Similarly, upon treating Cx36^−/− islets with the glucokinase inhibitor mannoheptulose, we observed a significant increase in the mean oscillatory frequency of those cells that remained active from 22 mHz ± 2 mHz to 30 mHz ± 4 mHz (Fig. 6 C), Therefore decreased metabolic activity increases [Ca²⁺]_i oscillation frequency.

Figure 6.

Metabolic activity connects intrinsic oscillatory frequency with wave origin. (A) A representative false-color map of β-cell [Ca²⁺]_i oscillatory frequency in a Cx36^−/− islet. (B) The relationship of NAD(P)H response between 5 and 11 mM glucose and the [Ca²⁺] oscillation frequency of individual β-cells within Cx36^−/− islets, together with linear regression (±95% confidence intervals). (C) Mean ± SE [Ca²⁺] oscillation frequency before (−) and after (+) addition of the GK inhibitor 5 mM D-mannoheptulose in individual β-cells within Cx36^−/− islets. (D) Representative time-courses of two uncoupled β-cells in the islet model with high or low GK rate. (E) Pearson correlation coefficient for the effect of heterogeneity in the indicated parameters on [Ca²⁺] oscillation frequency within the islet model. (F) Natural oscillation frequency of β-cells was averaged over regions corresponding to wave origin and wave-end, in electrically uncoupled islets that are simulated to have subregions of similar GK rates (see Fig. 3). Data in (B) represent n = 8 islets from three mice. Data in (C) represent n = 5 islets from two mice. ^∗∗ indicates p < 0.01, ^∗∗∗ indicates p < 0.001 comparing experimental groups indicated. Scale bar (A) indicates 100 μm. To see this figure in color, go online.

To examine the link among metabolic activity, oscillation frequency, and wave origin in the islet model we examined how the parameters used to represent cellular heterogeneity impacted the natural oscillation frequency in electrically uncoupled cells. The rate constant of glucokinase representing glucose metabolism showed the highest absolute (negative) correlation with oscillation frequency (Fig. 6, D and E). This is consistent with less metabolically active areas having a higher intrinsic oscillation frequency, in accordance with experimental measurements. K_ATP conductance also showed a (positive) correlation with oscillation frequency, although less than that of glucokinase, consistent with the reduced link we observed among K_ATP channel density, ChR2-activated [Ca²⁺]_i, and wave propagation (Fig. S6). In the absence of coupling, cells corresponding to the wave origin showed significantly faster oscillation frequencies than cells corresponding to the region of the wave end (Fig. 6 F).

Discussion

Islets of Langerhans show complex multicellular regulation through the electrical coupling between functionally heterogeneous cells. How different subpopulations of cells affect overall function is poorly understood. To dissect the functional architecture of the islet, we applied optogenetics, quantitative fluorescence microscopy, and computer modeling to detect functional subpopulations of cells cross the islet and characterize how they control overall cellular excitability and dynamics. We discovered that 1) metabolically active subpopulations of cells exert greater control over the electrical response of neighboring cells, 2) cellular heterogeneity with respect to glucose metabolism and excitability is spatially organized, and 3) metabolically less-active cells that show greater intrinsic oscillation frequency act as pacemakers to direct calcium wave propagation and synchronize oscillations.

Metabolically active subpopulations of cells control excitability

Heterogeneous β-cell function has been observed in β-cells dissociated from the islet (35, 39); and prior studies have suggested β-cell heterogeneity impacts islet function (23, 40, 41). Examining the role of heterogeneity in the intact islet is challenging due to the high coordination of the electrical response. However, by using ChR2 and sequential stimulation of individual cells or subregions, we could identify heterogeneous electrical responses in the intact islet. There exist subregions or subpopulations of cells that are more able to recruit surrounding cells to become active (Fig. 1). This control is consistent over time (Fig. 1) and independent of experimental parameters (Fig. S2), indicating an intrinsic property of the cell that can control excitability. Notably, in the intact islet ∼50% of cells are unable to recruit other cells to be active at 5 mM glucose, indicating ∼50% of cells show a low electrical response. This is similar to observations of [Ca²⁺]_i responses in islets lacking Cx36 and electrical coupling, where ∼50% of cells at 5 mM glucose show no [Ca²⁺]_i response (9). Although we observed the heterogeneity to be static over ∼30 min, determining whether it is static over longer timescales will be important in future work.

A major question is what factors underlie this heterogeneity in the intact islet. We observed that regions of high or low electrical control are correlated, respectively, with regions of high or low metabolic activity, as measured by higher or lower NAD(P)H responses, respectively. Results from the islet model predict regions with higher metabolic activity arise from higher levels of glucokinase, which would generate the greater NAD(P)H response that we measure (Fig. 3). Cells with higher levels of metabolic activity would therefore be more depolarized and closer to firing, as the model predicts (Fig. S5), and thus exert a greater gap junction-mediated depolarizing effect on neighboring β-cells. This effect also persisted under diazoxide application (Fig. 2). An important future goal will be to further characterize the heterogeneity in metabolic activity, including measuring factors such as glucokinase levels, mitochondrial membrane polarization, and ATP concentration. A recent study using eNpHr3, an alternative optogenetic tool to silence populations of cells, also demonstrated that subpopulations of cells exist within the intact islet that are important for maintaining electrical control (21). Notably these hub-cells had elevated glucokinase levels, which is consistent with our results and predictions. However, an important difference is that our study indicates metabolically active subpopulations of cells that exert electrical control do not correspond to pacemakers that initiate wave propagation (see below). Further, we can account for these cells being present under normal heterogeneity resulting from Gaussian distributions. Through using an NCAM marker, subsets of β-cells (β^high and β^low) have also been identified that show differential [Ca²⁺]_i and ATP elevation responses to glucose (42). β^low cells expressed GLUT2 and GCK significantly lower than β^high cells, which is also similar to the less metabolically active subpopulations we observe that are unable to recruit neighboring cells to elevate [Ca²⁺]_i.

Spatial organization of cell heterogeneity

Analysis of NAD(P)H responses and results from the islet model support the existence of spatial organization, and we observed consistent results between the organization of metabolic activity and ChR2-stimulated [Ca²⁺] (Fig. 4). We also observed regions of variability that exist over a range of spatial scales from quadrants of the islet to single-cell regions (Figs. 2 and 4). This is consistent with detailed examination of [Ca²⁺]_i dynamics revealing the islet to obey “small world network” principles (20, 43), where dynamics are more similar in localized regions of the islet. These spatial variations in metabolic activity are not visually identifiable from the NAD(P)H image, possibly as a result of spatially organized NADH levels/changes being masked by heterogeneity in NADPH or other fluorescence signals.

How does this spatial organization arise? One possibility is that cells within a domain originate from the same progenitor. Indeed, clusters of β-cells in the islet originate from a common progenitor, suggesting that properties of the progenitor may affect properties of offspring β-cells (44). Another possibility is one of self-organization, where the excitability of one cell may impact that of other cells. Therefore, more excitable cells that originate randomly may lead to neighboring cells becoming more excitable. For instance, we cannot completely exclude that there exists cross talk between electrical control and glucose metabolism, although this is excluded from our model, which is sufficient to explain experimental results. The ability of β-cell function and coupling to impact the organization of other β-cells in the islet has also been predicted, and differs in type 2 diabetes (45). A further distinction is the recent discovery of a neogenic niche where immature β-cells reside that may have altered function and which are spatially organized (46). A final possibility is that extrinsic factors such as blood flow architecture or innervation may pattern or functionally segment the islet into functional regions (47, 48).

Several studies have identified subpopulations of β-cells and their molecular basis (3, 42, 49, 50), which includes heterogeneity in genes underlying glucose metabolism, electrical regulation, and gap junction coupling. Our findings suggest these β-cell subpopulations will have spatial organization and be preferentially ordered together. As discussed above, low NCAM surface expression marks a subset of β-cells (β^low) that show reduced [Ca²⁺]_i and ATP elevation to glucose (42), and in a rat model of type 2 diabetes the proportion of β^low cells increased. Similarly, the Wnt effector fltp marks proliferative subpopulations of cells that preferentially expand in obesity or pregnancy, and which have reduced metabolic activity and Cx36 expression (50). The plasticity of the islet to vary between these subpopulations under pathological conditions would impact how depolarizations propagate throughout the islet to regulate [Ca²⁺]_i and insulin secretion. Islets are electrically quiescent below 6 mM glucose and transition to being electrically active above this level. We predict that if less metabolically active, inexcitable cells are spatially grouped and this population grows, the presence of isletwide depolarization will be compromised to impact insulin secretion and glucose homeostasis. Nevertheless, the precise spatial organization and the role of subpopulations in islet function and hormone release during conditions of diabetes, as well as in development and pregnancy, still remain to be fully determined.

Lower metabolic, high-frequency cells initiate propagating calcium waves

Synchronized [Ca²⁺]_i oscillations within islets enhance first-phase and second-phase pulsatile insulin release and insulin action (8, 12, 51). Propagating calcium waves mediate this synchronization and consistently emerge from specific subregions of the islet (22). We experimentally observed that regions of wave initiation linked to fast (<1 min) oscillations are regions of lower metabolic activity (Fig. 5). These results were replicated by the islet model, which also predicted that regions of wave initiation have a faster natural oscillation frequency (Fig. 6).

In models of pulsed coupled oscillators, the fastest oscillator sets the pace (52). Prior modeling studies predicted that wave initiation occurs in regions with higher metabolic activity and faster natural oscillation frequency (23). These studies used a model where oscillation frequency increases with increased glucose metabolism (53). However, we demonstrated experimentally in electrically uncoupled cells that a higher oscillation frequency is observed in subpopulations of cells that show a lower NAD(P)H response, or after partial metabolic inhibition (Fig. 6). Importantly the level of metabolic activity is still sufficient to elevate [Ca²⁺]. This inverse relationship between metabolic activity (GK activity) and oscillation frequency is also observed in our islet model (Fig. 6); (27), where wave initiation is driven by spatial locations of high natural oscillatory frequency due to lower-than-average metabolic activity (Fig. 6). Together, these results suggest that at elevated glucose, all cells are intrinsically capable of firing action potentials, but cells with lower levels of glucose metabolism have a higher intrinsic oscillation frequency. These cells are more likely to fire first, and therefore are more likely to first spread depolarization to neighboring cells and initiate the wave propagation. The subsequent path taken until the wave termination is influenced less by metabolic activity, and thus determined by factors still to be understood.

In the islet model, the link between metabolic activity and intrinsic oscillation frequency was the strongest, further suggesting glucose metabolism may be the dominating factor in affecting [Ca²⁺]_i oscillation frequency. Analysis of the β-cell model has shown that K_ATP closure and slow Ca_V inactivation determines the termination of an oscillation and thus oscillation frequency, with ER Ca²⁺ buffering also playing a role (27, 54). K_ATP, Ca_V, and SERCA conductance/activity are all ATP dependent. Thus, high glucose metabolism will reduce the termination of oscillations by Ca_V and K_ATP, and increase the oscillation period and lower the frequency. The presence of intrinsic metabolic oscillations has also been suggested (55), which may further enhance pacemaking action.

Further work is needed to determine other dynamical effects of spatial organization. For example, in a system where oscillators of similar frequency are spatially grouped, the network synchronization is optimal under weaker coupling regimes compared to systems with random spatial assignment of frequency (56). A recent modeling study using a coupled β-cell model showed that greater heterogeneity among β-cells increased synchronization (57). Thus, islet dysfunction after disruptions to Cx36 gap junction coupling, which can occur in several conditions linked to the development of diabetes (13, 14, 58), may be protected by spatially grouping cells of similar excitability and oscillation frequency.

Overall, these findings describe how spatially varying cellular heterogeneity can affect how the islet functions as a multicellular unit, with distinct subpopulations affecting different emergent multicellular properties. Many neuroendocrine systems show coordinated electrical and secretory responses that can remodel under physiological conditions, including pituitary GH-secreting cell networks (59, pituitary lactotrophs (60), or the adrenal medulla (61, 62). Given the electrical coupling within these systems, functional subpopulations may exert disproportionate control over the coordinated response. The use of optogenetic tools, computer modeling, and quantitative imaging provides the means to functionally dissect and test whether excitable subpopulations are present in these or other multicellular systems, and how they may control systemwide electrical responses and dynamics.

Author Contributions

M.J.W. designed and performed research, developed analysis and computational tools, analyzed data, and wrote the manuscript. N.W.F.L. performed research. R.K.P.B. designed research, verified results, and wrote the manuscript.

Editor: Stanislav Shvartsman.

Supporting Material

Movie S1. ChR2 Activation in the Islet Model

Representative simulation of [Ca²⁺]_i activity while activating each quadrant with ChR2 current source. Glucose is held at 5 mM in parallel with ex vivo experiments.

Movie S2. Wave Dynamics in Islet Model

Glucose is stepped up between 5 and 11 mM inducing initial [Ca²⁺]_i influx before settling into persistent [Ca²⁺]_i oscillations.

Movie S3. [Ca²⁺] Oscillations in Cx36^−/− Islet

Representative [Ca²⁺] oscillations in Cx36^−/− islet at 11 mM glucose.