Conformational Heterogeneity and FRET Data Interpretation for Dimensions of Unfolded Proteins

Abstract

A mathematico-physically valid formulation is required to infer properties of disordered protein conformations from single-molecule Förster resonance energy transfer (smFRET). Conformational dimensions inferred by conventional approaches that presume a homogeneous conformational ensemble can be unphysical. When all possible—heterogeneous as well as homogeneous—conformational distributions are taken into account without prejudgment, a single value of average transfer efficiency 〈E〉 between dyes at two chain ends is generally consistent with highly diverse, multiple values of the average radius of gyration 〈R_g〉. Here we utilize unbiased conformational statistics from a coarse-grained explicit-chain model to establish a general logical framework to quantify this fundamental ambiguity in smFRET inference. As an application, we address the long-standing controversy regarding the denaturant dependence of 〈R_g〉 of unfolded proteins, focusing on Protein L as an example. Conventional smFRET inference concluded that 〈R_g〉 of unfolded Protein L is highly sensitive to [GuHCl], but data from SAXS suggested a near-constant 〈R_g〉 irrespective of [GuHCl]. Strikingly, our analysis indicates that although the reported 〈E〉 values for Protein L at [GuHCl] = 1 and 7 M are very different at 0.75 and 0.45, respectively, the Bayesian R_g² distributions consistent with these two 〈E〉 values overlap by as much as 75%. Our findings suggest, in general, that the smFRET-SAXS discrepancy regarding unfolded protein dimensions likely arise from highly heterogeneous conformational ensembles at low or zero denaturant, and that additional experimental probes are needed to ascertain the nature of this heterogeneity.

Introduction

Single-molecule Förster resonance energy transfer (smFRET) is an important, increasingly utilized experimental technique (1, 2, 3, 4, 5, 6, 7, 8, 9) for studying protein disordered states, especially those of intrinsically disordered proteins (IDPs) (10, 11, 12, 13, 14, 15). Applications of smFRET to infer conformational dimensions of unfolded states of globular proteins (16, 17, 18) and IDPs (19, 20, 21, 22) have provided insights into fundamental protein biophysics including, for example, folding stability and cooperativity (23, 24, 25, 26, 27), transition paths (28, 29), and compactness of IDP conformations (20, 21) involved in fuzzy complexes (30, 31, 32, 33). Single-molecule conformational dimensions likely bear as well on biologically functional liquid-liquid IDP phase separation (34) because the amino acid sequence-dependent single-chain compactness of charged IDPs (35, 36, 37) are predicted by theory (38) to be closely correlated with these polyampholytic proteins’ tendency to undergo multiple-chain phase separation (39).

Basically, inference from smFRET data on measures of conformational dimensions such as radius of gyration R_g entails matching experimental average energy transfer efficiency 〈E〉_exp with simulated (or analytically calculated) transfer efficiency 〈E〉_sim predicted by a chosen polymer model. Using a Gaussian chain model or an augmented Sanchez mean-field theory, conventional smFRET inference procedures presume a homogeneous conformational ensemble that expands or contracts uniformly (17, 40, 41) in response to changes in solvent conditions such as denaturant concentration (42). Such an interpretation of smFRET data stipulated a significant collapse of unfolded-state conformations, as quantified by a substantial decrease in R_g, upon changing solvent conditions from strongly unfolding to folding by lowering denaturant concentration (16, 17). This smFRET prediction has led to a long-standing puzzle for Protein L (1, 43, 44, 45) because for this two-state folder (46), an apparently more direct measurement of R_g by small-angle x-ray scattering (SAXS) indicated that the average compactness of its unfolded-state conformational ensemble does not vary much with denaturant (1, 43). Similar behaviors have also been observed in SAXS experiments on other proteins (47).

Although the smFRET-SAXS puzzle remains to be fully resolved, several advances since the discrepancy was first noted (16) have contributed to clarifying the pertinent issues. A study using explicit-chain models questioned the general validity of conventional standard smFRET interpretation by showcasing that it incurs substantial errors in inferred R_g (48). A systematic analysis of subensembles of self-avoiding chains pinpointed the conventional procedure’s basic shortcoming in always presuming a homogeneous ensemble, an assumption positing particular forms of one-to-one mapping between average 〈R_g〉 and end-to-end distance 〈R_EE〉 that lead to grossly overestimated R_g values for small 〈E〉_exp values (21). In reality, however, as should be obvious from polymer theory and explicit-chain simulations of polymers, there is no general one-to-one mapping between 〈R_g〉 and 〈R_EE〉 if a homogeneous ensemble is not assumed, because there are significant scatters in the R_g-R_EE relationship (see, e.g., Fig. 2 of (21)). Therefore, 〈R_EE〉 cannot be a proxy for 〈R_g〉 in general. When conformational heterogeneity is recognized, as it is clearly observed in a number of smFRET experiments (18, 20, 49), our subensemble analysis prescribes a most probable radius of gyration, R_g⁰, for any given 〈E〉_exp (21). The same analysis shows that R_g⁰ can also correspond to the 〈R_g〉 of a distribution of R_g consistent with the given 〈E〉_exp (Fig. 5 F of (21)). When applied to an N-terminal IDP fragment of the Cdk inhibitor Sic1 (30, 31, 33), the subensemble-inferred, denaturant-dependent R_g⁰ is in good agreement with SAXS-determined R_g and NMR measurement of hydrodynamic radius, in contrast to conventional procedures that produced unphysical results (21).

In line with this conceptual framework that emphasizes conformational heterogeneity and polymer-excluded volume, two other recent explicit-chain simulation studies also concluded that conventional smFRET inference of R_g is inadequate (50, 51). Notably, the coarse-grained model simulation in (50) predicted an ≈3.0 Å contraction of average R_g for Protein L upon diluting GuHCl from 7.5 to 1.0 M. The authors surmised that 3.0 Å is “close to the statistical uncertainties” of SAXS-measured R_g values, and therefore a resolution of the smFRET-SAXS discrepancy for Protein L might be within reach (50). More recently, an extensive experimental-computational study of a destabilized mutant of spectrin domain R17 and the IDP ACTR also underscored the importance of explicit-chain simulations in the interpretation of smFRET data. Denaturant-dependent expansion of conformational dimensions was consistently observed for these proteins from multiple experimental methods as well as in all-atom explicit-water MD simulations (52, 53). Protein L, however, was not the subject of this investigation.

In view of recent results that apparently affirm an appreciable denaturant-dependent R_g for unfolded proteins—albeit not as sharp as posited by conventional smFRET interpretation—is an essentially denaturant-independent unfolded-state 〈R_g〉 as envisioned in the usual picture of cooperative protein folding tenable? To address this question, we determined computationally the distribution of R_g consistent with any given 〈E〉_exp and the derived probabilities that different 〈E〉_exp values are consistent with the same R_g values. Taking an agnostic view as to the merits of various experimental techniques, we invoked minimal theoretical assumption so as to let experimental data speak for themselves. For simplicity, we do not consider kinetic effects in smFRET measurements (54, 55, 56). Accordingly, our coarse-grained model incorporates only the most rudimentary geometry of polypeptide chains, without any detailed force field such as those applied in recent smFRET-related simulations (48, 50, 52). By this very construction, our analysis is unaffected by any known or potential limitations of current coarse-grained and atomic force fields (14, 57, 58, 59, 60, 61, 62). As detailed below, we found that simple conformational statistics dictates a broad distribution of R_g for most 〈E〉_exp values. Among such conditional (Bayesian (63)) P(R_g|〈E〉_exp) distributions for different 〈E〉_exp values, large overlaps exist even for significantly different 〈E〉_exp values. These results suggest that, even if published experimental data are taken at face value, conceivably the smFRET-SAXS discrepancy can be resolved provided sufficient denaturant-dependent conformational heterogeneity in the unfolded state is encoded by the amino acid sequence of the protein. Our analysis thus establishes a physical perimeter within which future experimental and theoretical smFRET analyses may proceed.

Methods

The C_α protein model and the sampling algorithm used here are the same as that in our previous study (21). The protein is represented by a sequence of n beads connected by C_α–C_α virtual bonds of length 3.8 Å. The potential energy is $E={\sum }_{i=2}^{n-1}{\mathit{ϵ}}_{\theta }{\left({\theta }_i-{\theta }_0\right)}^2+\left(1/2\right){\sum }_{i=1}^n{\sum }_{j=1}^n{\mathit{ϵ}}_{\text{ex}}{\left(R_{\text{hc}}/R_{ij}\right)}^{12}$, where ϵ_θ = 10.0 k_BT, θ_i is the virtual bond angle at bead i, θ₀ = 106.3° is the reference that corresponds to the most populated virtual bond angle in the PDB (64), k_B is the Boltzmann constant, T is the absolute temperature, ϵ_ex = 1.0 k_BT is the model protein’s self-avoiding excluded-volume repulsion strength, and R_ij = |R_j – R_i| is the distance between beads i,j, wherein R_i is the position vector for bead i. The excluded-volume (R_hc/R_ij)¹² term is set to zero for R_ij ≥ 10.0 Å. As in many protein folding simulations (25), we use a hard-core repulsion distance R_hc = 4.0 Å for most of the analysis presented below, although some results for R_hc = 3.14 or 5.0 Å (21) are also utilized to assess the robustness of our conclusions.

We conducted Monte Carlo sampling by applying the Metropolis criterion (65) at T = 300 K using an algorithm described previously (66) that assigns equal a priori probability for pivot and kink jumps (67, 68). The acceptance rate for the attempted chain moves was ≈30%. The first 10⁷ equilibrating attempted moves of each simulation were excluded from the tabulation of statistics. Subsequently, 10⁹ moves were attempted for each chain length n we studied to sample 10⁷ conformations for further analysis. Values of radius of gyration $R_g=\sqrt{n^{-1}{\sum }_{i=1}^n{\left|{\mathbf{R}}_i-{\mathbf{R}}_{\text{cm}}\right|}^2}$ (where ${\mathbf{R}}_{\text{cm}}=n^{-1}{\sum }_{i=1}^n{\mathbf{R}}_i$) and end-to-end distance R_EE = |R_n – R₁| were computed for the sampled conformations to determine the distribution P(R_g, R_EE) of populations centered at various (R_g, R_EE) with only narrow ranges of variations (bins) around the given R_g and R_EE values.

We focus here only on cases in which the dyes are attached to the two ends of the protein chain. FRET efficiency for a given conformation in the model with end-to-end distance R_EE is then calculated by the formula,

$$E\left(R_{\text{EE}}\right)=\frac{R_0^6}{R_0^6+R_{\text{EE}}^6},$$ (1)

where R₀ is the Förster radius of the dye. Based on the values of R₀ = 54 ± 3 Å given by Sherman and Haran (16) and R₀ = 54 Å provided by Merchant et al. (17) for the Alexa 488 and Alexa 594 dyes employed in their Protein L experiments, we set R₀ = 55 Å in most of the computation for Protein L below. For any given distribution P(R_EE), the average FRET efficiency is given by $\langle E\rangle =\int d{R}_{\text{EE}}E\left(R_{\text{EE}}\right)P\left(R_{\text{EE}}\right)$. The subscripts in the above expressions 〈E〉_exp and 〈E〉_sim are omitted hereafter for notational simplicity when the meaning of the average 〈E〉 is clear from the textual context. Protein L is a 64-residue α/β protein. To account for the added effective chain length due to the two dye linkers, we used n = 75 chains to model the unfolded-state conformations of Protein L. This prescription for the linkers is similar to the ten (69) or eight (17) extra residues used before. In addition to the exemplary computation for Protein L, simulations were also conducted for several other representative chain lengths (n = 50, 100, 125, and 150) and Förster radii (R₀ = 50, 60, and 70 Å) for future applications to other disordered protein conformational ensembles.

Results

Physicality of a subensemble approach to smFRET inference

To ensure that smFRET inference takes into account only physically realizable conformations, we recently introduced a systematic methodology to infer a most probable radius of gyration R_g⁰ from an experimental 〈E〉_exp by considering subensembles of self-avoiding walk (SAW) conformations with narrow ranges of R_g simulated using an explicit-chain model. For any such range (bin) centered around an R_g, the method provides a conditional distribution P(R_EE|R_g) for the end-to-end distance R_EE. An average FRET efficiency $\langle E\rangle \left(R_g\right)=\int d{R}_{\text{EE}}E\left(R_{\text{EE}}\right)P\left(R_{\text{EE}}|R_g\right)$ is then calculated. The most probable R_g⁰ is determined by matching 〈E〉_exp with 〈E〉(R_g), that is, by solving

$$\langle E\rangle \left(R_{\text{g}}^0\right)={\langle E\rangle }_{\text{exp}}$$ (2)

for R_g⁰ to arrive at R_g⁰(〈E〉) (wherein the “exp” is dropped from the average), which is the inverse function of 〈E〉(R_g). As documented before (18, 21) and outlined above, by explicitly allowing for unfolded-state conformational heterogeneity—which is expected physically (14, 15)—the subensemble SAW method circumvents the limitations of conventional smFRET inferences that presuppose a homogeneous conformational ensemble (16, 17, 41).

Based on the same conceptual framework, here we approach the question of smFRET inference from a complementary angle. Instead of starting from subensembles with a narrow range of R_g to derive P(R_EE|R_g), then 〈E〉(R_g⁰) and R_g⁰(〈E〉), here we start from subensembles with a narrow range of R_EE (smallest bin size $=0.5$ Å, see below), and hence a narrow variation of E (i.e., via Eq. 1; the E values in a narrow range may be taken as a single E value), to derive distribution P(R_g|R_EE) conditioned upon R_EE. Whereas P(R_g|R_EE) is related to P(R_EE|R_g) by Bayes’ theorem, P(R_g|R_EE) is of interest because it quantifies directly the possible variation in conformational dimensions when only a single 〈E〉_exp value is known. This is because for every single FRET efficiency E, the quantity P(R_g|R_EE) is sufficient to provide the conditional distribution P(R_g|E). Then, based on these derived P(R_g|E) distributions for all individual E values, the P(R_g|〈E〉_exp) distribution conditioned upon any value of 〈E〉_exp averaged from any underlying distribution P(E) of E can be readily obtained.

Estimation of conformational dimensions from FRET efficiency is highly model dependent because of insufficient structural constraint

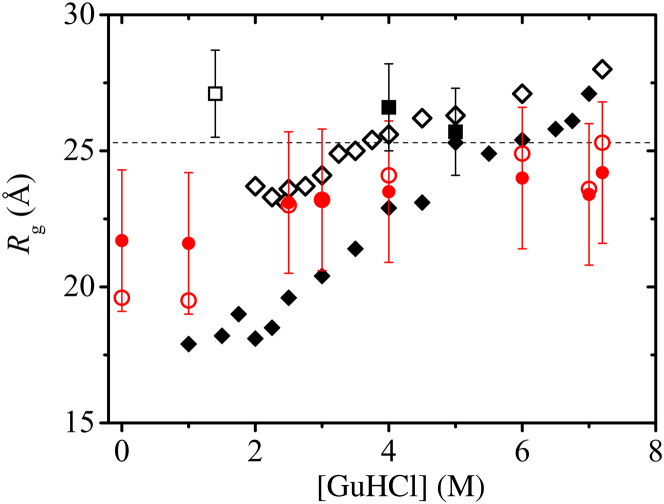
As an exemplary case, we applied this formulation to Protein L. Fig. 1 shows considerable discrepancies between SAXS- (squares) and smFRET-deduced (diamonds) 〈R_g〉 values, and that different smFRET inference approaches lead to very different pictures of how 〈R_g〉 of this protein varies with denaturant concentration. For a change in [GuHCl] from ≈7 to ≈2 M, conventional inference (diamonds) yielded large 〈R_g〉 decreases of ≈9 Å (solid diamonds, (16)) or ≈5 Å (open diamonds, (17)). In contrast, subensemble SAW methods (circles) stipulate a much milder variation with respect to [GuHCl]. For the same [GuHCl] change, the most probable R_g⁰ value decreases by ≈2 Å (open circles) whereas the change in root-mean-square $\sqrt{\langle R_g^2\rangle }\equiv {\left\{\int d{R}_g{R}_g^{2}P\left(R_g|{\langle E\rangle }_{\text{exp}}\right)\right\}}^{1/2}$ conditioned upon the published experimental 〈E〉_exp data is even smaller: it decreases by ≈1 Å (solid circles). When [GuHCl] is reduced further from 2 to 0 M, the total decrease over the entire [GuHCl] range is ≈5.5 Å for R_g⁰ but merely ≈2 Å for $\sqrt{\langle R_g^2\rangle }$. We computed distributions of R_g² and $\sqrt{\langle R_g^2\rangle }$ here because these quantities are determined by SAXS (47, 70). Our results are essentially unchanged if 〈R_g〉 is considered instead (see below).

Figure 1.

Unfolded-state dimensions of Protein L obtained from SAXS and various interpretations of smFRET experiments. Open and solid squares are results from previous time-resolved and equilibrium SAXS experiments by Plaxco et al. (46) at 2.7 ± 0.5° and 5 ± 1°C, respectively. The associated error bars represent 1 SD fitting uncertainties (kinetic data) or confidence intervals from two to three independent measurements (thermodynamic data). Subsequent equilibrium SAXS measurement at 22°C by Yoo et al. (43) produced essentially identical results. Open and solid diamonds are results from smFRET experiments, respectively, by Merchant et al. (17) (Eaton group, temperature not provided) and by Sherman and Haran conducted at “room temperature” (16). These prior experimental data were compared in a similar manner in (43). Here, the open and solid circles are from our analysis corresponding, respectively, to the most-probable R_g⁰ (21) and the root-mean-square $\sqrt{\langle R_g^2\rangle }$ value based on the experimental transfer efficiency 〈E〉 = 0.74 for [GuHCl] = 0 given by Merchant et al. (17), the 〈E〉 values for Protein L (corrected from the measured FRET efficiency 〈E_m〉) in SI Table 2 for the same reference, and the 〈E〉 values for [GuHCl] = 1 and 7 M in Sherman and Haran (16). A Förster radius of R₀ = 55 Å was used in our calculations. The error bars for the solid circles span ranges delimited by $\sqrt{\langle R_g^2\rangle \pm \sigma \left(R_g^2\right)}$, where σ(R_g²) is the SD of the distribution of R_g² at the given E value. The horizontal dashed line marks the R_g = 25.3 Å value we obtained from applying the scaling relation of Kohn et al. (71) to N = 74, where n = N + 1 = 75 is taken to be the equivalent number of amino acid residues for Protein L plus dye linkers. To see this figure in color, go online.

For every 〈E〉_exp data point we considered for Protein L using subensemble analysis, significant diversity in R_g² values that are nonetheless consistent with the given 〈E〉_exp is observed (Fig. 1, error bars for solid circles). In other words, this method can infer the full Bayesian distribution of R_g² for a given 〈E〉_exp and hence a rigorous error bar can be provided (whereas error bars are not provided for R_g⁰ because it represents a narrow range of R_g values that lead to a distribution of E values, which in turn average to an 〈E〉 (21)). Fig. 1 shows clearly that the large variations in inferred R_g² values and the large overlaps of the ranges of these variations at different [GuHCl] values imply that significant fractions of the unfolded conformational ensembles of Protein L at different [GuHCl] values can encompass conformations with very similar R_g values. Notably, the average R_g expected of a fully unfolded protein in good solvent of the same length as Protein L with dye linkers (horizontal dashed line, (71)) is within the $\sqrt{\langle R_g^2\rangle }$ error bars for [GuHCl] as low as 3 M. Even at zero denaturant, the R_g ≈ 24.5 Å value (upper error bar), at 1 SD from the mean, $\sqrt{\langle R_g^2\rangle }$, is only ≈1 Å from the average R_g expected of a fully unfolded conformational ensemble.

Conformations consistent with a given FRET efficiency generally have highly diverse radii of gyration

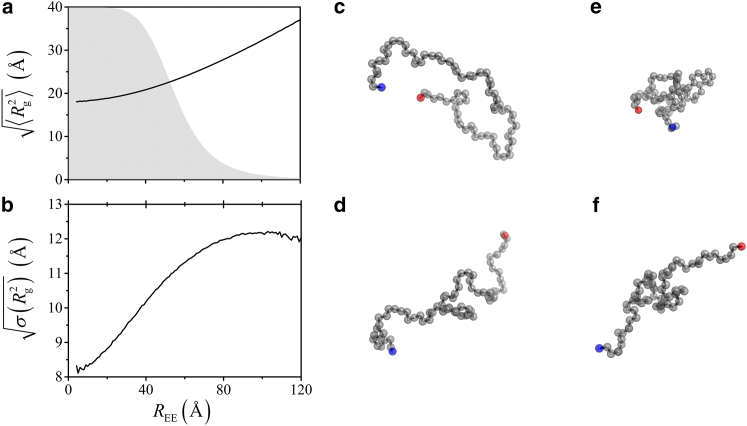
The diversity in R_g values that are consistent with a given R_EE (and therefore a given 〈E〉) is further illustrated in Fig. 2. For our Protein L model, the square root of the SD in R_g², $\sqrt{\sigma \left(R_g^2\right)}$, is substantial for the entire range of R_EE: it increases steadily from ≈8 Å for R_EE ≈ 0 to ≈12 Å for R_EE ≈ 120 Å (Fig. 2 b). Therefore, although $\sqrt{\langle R_g^2\rangle }$ of the conformations consistent with a given R_EE increases monotonically from ≈18 to ≈37 Å over the R_EE range in Fig. 2 a, knowledge of R_EE alone can barely narrow down the wide range of possible R_g values and vice versa (Fig. 2, c–f).

Figure 2.

Large variations in dimensions among conformations with a given end-to-end distance R_EE. (a) Root-mean-square $\sqrt{\langle R_g^2\rangle }$ and (b) the square root of the SD of R_g² as functions of R_EE. The gray profile in (a) shows the theoretical transfer efficiency Eq. 1 for n = 75 and R₀ = 55 Å in a vertical scale ranging from zero to unity. (c–f) Example conformations with the darker shaded (red and blue online) beads marking the termini of n = 75 chains. They serve to illustrate the possible concomitant occurrences of (c) small R_EE = 19.7 Å and large R_g = 26.3 Å; (d) large R_EE = 80.1 Å and large R_g = 26.2 Å; (e) small R_EE = 19.7 Å and small R_g = 14.2 Å; and (f) large R_EE = 80.4 Å and small R_g =19.8 Å. These examples underscore that there is no general one-to-one mapping from 〈R_EE〉 to 〈R_g〉. To see this figure in color, go online.

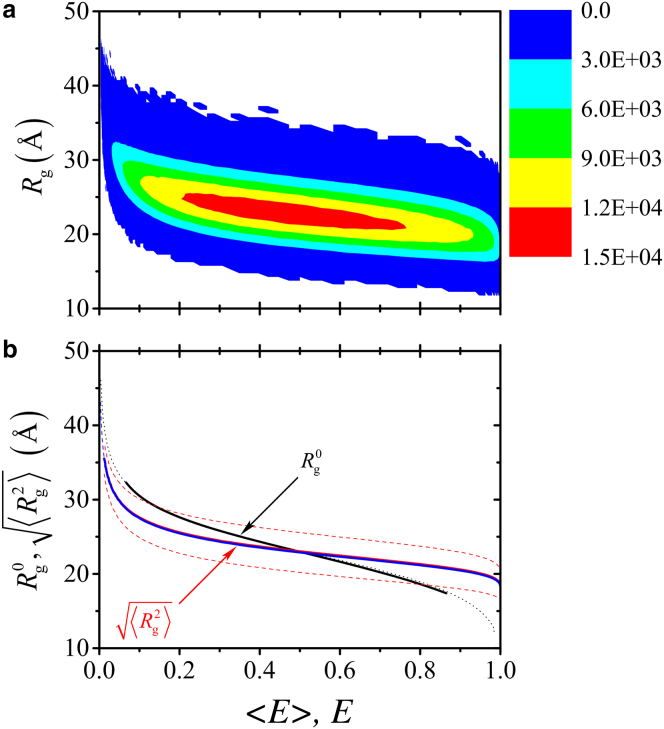
A panoramic view of the logic of smFRET inference on conformational dimensions is provided by Fig. 3, wherein P(R_g, R_EE) is converted to P(R_g, E) by Eq. 1. Using our model for unfolded Protein L as an example, the landscape in Fig. 3 a shows clearly that the R_g–E scatter is wide, with the most populated (red) region elongated mainly along the E axis with a small negative incline. Consistent with Fig. 1, this population distribution implies that even large variations in E do not necessitate much change in the R_g distribution. This feature of the R_g–E space is demonstrated more specifically by the $\sqrt{\langle R_g^2\rangle \left(E\right)}$ curve in Fig. 3 b (red solid curve; the dependence of 〈R_g〉 on E is essentially identical, blue solid curve), wherein an overwhelming majority of the E values are seen to be consistent with R_g values between 20 and 27 Å that are within 1 SD of $\sqrt{\langle R_g^2\rangle \left(E\right)}$ (red dashed curves). In contrast, conventional smFRET inference procedures—which are demonstrably unphysical in some situations (21)—posit a much more sensitive dependence of inferred 〈R_g〉 on 〈E〉 (Fig. S1). It is noteworthy that, for most E values, the variation of $\sqrt{\langle R_g^2\rangle \left(E\right)}$ is milder than that of R_g⁰(〈E〉); i.e., $\left|d\sqrt{\langle R_g^2\rangle }/dE\right|<\left|d{R}_g^0/d\langle E\rangle \right|$. In fact, this trend is already evident in Fig. 1 from the milder [GuHCl] dependence of $\sqrt{\langle R_g^2\rangle }$ (solid circles) than that of R_g⁰ (open circles).

Figure 3.

Perimeters of inference on conformational dimensions from Förster transfer efficiency. (a) Distribution P(R_g, E) of conformational population as a function of R_g and E for n = 75 and R₀ = 55 Å. The distribution was computed using R_EE × R_g bins of 1.0 Å × 0.5 Å. White area indicate bins with no sampled population. (b) Shown here is the most-probable radius of gyration R_g⁰(〈E〉) from our previous subensemble SAW analysis (21) (black solid curve) compared against root-mean-square radius of gyration $\sqrt{\langle R_g^2\rangle \left(E\right)}$ (red solid curve) computed by considering 30 subensembles with narrow ranges of R_EE. The latter overlaps almost completely with 〈R_g〉(E) computed using the same set of subensembles (blue solid curve). Another set of R_g⁰ (〈E〉) values (black dotted curve) and another set of 〈R_g〉(E) values (blue dashed curve) were obtained from the distribution in (a), respectively, by averaging over E at given R_g values and by averaging over R_g at given E values. Variation of radius of gyration is illustrated by the red dashed curves for $\sqrt{\langle R_g^2\rangle \pm \sigma \left(R_g^2\right)}$ as functions of E. The essential coincidence between the black solid and dotted curves and between the blue solid and dashed curves indicate that these results are robust with respect to the choices of bin size we have made. Note that the black solid curve for R_g⁰(〈E〉) does not cover 〈E〉 values close to zero or close to unity because larger R_g bin sizes (∼1.1–3.6 Å) than the current R_g bin size of 0.5 Å were used (Table S5 of (21)), thus precluding extreme values of 〈E〉 to be considered in that previous n = 75 subensemble SAW analysis (21). This limitation is now rectified for n = 75 (black dotted curve).

Conformations sharing similar radii of gyration can have very different FRET efficiencies

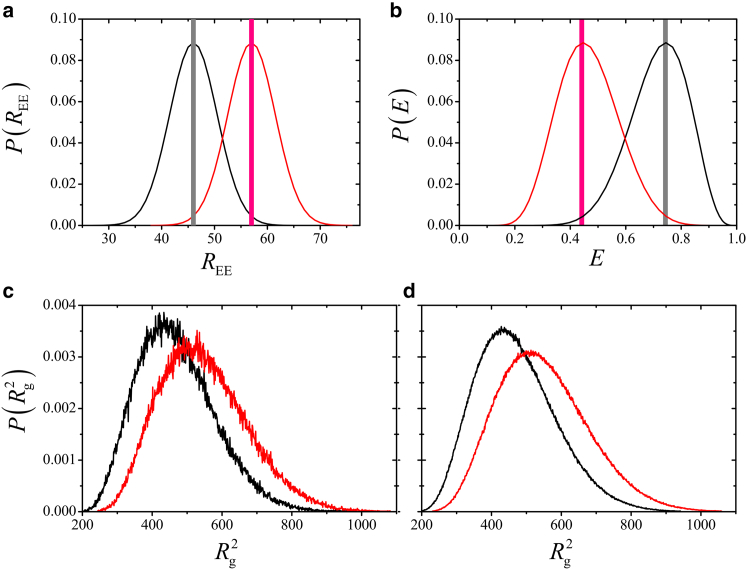
In light of the large diversity in R_g values conditioned upon a given E and the very mild variation of $\sqrt{\langle R_g^2\rangle }$ and σ(R_g²) with E (Fig. 3), one expects that conformations consistent with even very different E values share highly overlapping R_g values. We now characterize this overlap quantitatively by first considering two sharply defined representative R_EE values in Fig. 4 a (vertical bars depicting δ-function-like distributions) that correspond, by virtue of Eq. 1, to two sharply defined E values ≈0.45 and 0.75 (Fig. 4 b). These E values are representative because they coincide with the experimental 〈E〉_exp for Protein L at [GuHCl] = 7 and 1 M, respectively (16). The conditional distributions P(R_g²|E) for E = 0.45 and 0.75 overlap significantly, with the overlapping area ≈0.75 (Fig. 4 c). By definition, this area is the overlapping coefficient (OVL), used in statistical analysis for measuring similarity between distributions (72). OVL between two distributions is generally given by

$${\text{OVL}}_{\mathrm{1,2}}=\int dx\text{min}\left[P_1\left(x\right),P_2\left(x\right)\right],$$ (3)

where P₁(x) and P₂(x) are two normalized distributions of variable x. The P₁, P₂ distributions are P(R_g²|E = 0.45) and P(R_g²|E = 0.75) in Fig. 4 c.

Figure 4.

Substantially overlapping distributions of conformational dimensions can be consistent with very different Förster transfer efficiencies. (a) Given here are hypothetical distributions P(R_EE) of end-to-end distance R_EE. Two hypothetical sharp distributions at two R_EE values (vertical bars) and two hypothetical broad Gaussian distributions (bell curves) are centered at these two R_EE values, with SD of the Gaussian distributions chosen to be 20.3 Å. (b) Given here is the corresponding distribution P(E) of Förster transfer efficiency E. The left and right sharp distributions of P(R_EE) in (a) lead, respectively, to E ≈ 0.745 (right) and E ≈ 0.447 (left) in (b). The corresponding P(E) for the hypothetical Gaussian distributions in (a) entail broad distributions in E in (b) with mean values at 〈E〉 = 0.735 (right) and 〈E〉 = 0.453 (left), respectively. (c) The left and right curves are the conditional distributions P(R_g²|E), respectively, for the sharply defined E ≈ 0.745 and E ≈ 0.447 in (b). (d) Similar to (c) except the distributions of R_g² are now for the two broad P(E) distributions in (b). We denote these distributions as P(R_g²|〈E〉). The R_g² bin size in (c and d) is 1.0 Å². The OVL of the two normalized distribution curves in (c and d) are, respectively, 0.747 and 0.754. The percentages of population with R_g² ≥ 625 Å in the distributions in (c and d) are, respectively, 9.2 and 10.1% for E ≈ 0.745 and 〈E〉 = 0.735, and 25.2 and 26.3% for E ≈ 0.447 and 〈E〉 = 0.453. To see this figure in color, go online.

Because experimentally determined E values are often averages, not sharply defined (16, 17), it is necessary to address more realistic distributions of E on smFRET inference. We do so here by considering hypothetical broad Gaussian distributions for R_EE centered around the two sharply defined R_EE values (Fig. 4 a, curves, SD σ (R_EE) = 20.3 Å), resulting in broad distributions in E averaging to E = 0.45 and 0.74 Fig. 4 b, curves), which are essentially equal to the sharply defined E values of 0.45 and 0.75. Modifying the two sharply defined E values to two broad distributions of E has very little impact on either the individual R_g² distributions [P(R_g²|〈E〉)] or the overlap of the two P(R_g²|〈E〉) distributions (Fig. 4 d). The overlapping coefficient remains ≈0.75.

Although the distributions in Fig. 4, c and d, are very similar, there is a basic difference between two sharply defined E values and two broad distributions of E in regard to the conformations in the R_g² distributions. When the E values are sharply defined, there is no overlap in the actual conformations in the two P(R_g²|E) distributions because the conformational ensembles consistent with two sharply defined R_EE values are disjoint. However, when the two sets of E values are broadly distributed with overlapping R_EE and E values (Fig. 4, a and b, curves), some of the conformations from the two different R_g² distributions that contribute to the overlapping region in Fig. 4 d can be identical.

The distribution of radius of gyration consistent with a given single FRET efficiency is very similar to that consistent with a symmetric distribution of FRET efficiencies centered around it

This insensitivity of the distribution of R_g² (and therefore also of R_g) conditioned upon given E values to variations in the width of Gaussian-like distribution of E is not difficult to fathom. Given the mild variation of $\sqrt{\langle R_g^2\rangle }$ and σ (R_g²) with respect to E (Fig. 3 b) and the tendency for effects from E values on opposite sides of the average of a symmetric distribution to cancel each other, averaging over a range of E values centered around a given E (= 〈E〉) is not expected to result in an overall average R_g² and an overall distribution width that are substantially different from those for a sharply defined E = 〈E〉. For the sake of testing the robustness of this insensitivity, here we have used a large SD, σ(R_EE), for the hypothetical Gaussian distributions in Fig. 4 a. This σ(R_EE) is equal to the SD of the R_EE distribution for the full conformational ensemble (with the mean, 〈R_EE〉 = 59.1 Å). Beside the R_EE and E distributions in Fig. 4, we performed additional calculations using Gaussian distributions of R_EE centered at different averages, with different SDs that equal 0.1×, 0.25×, 0.5×, and 0.75× σ(R_EE). These constructs beget distributions of E with different $\langle E\rangle$ values. In all cases we considered, the resulting R_g² distribution for the given 〈E〉 is essentially the same across the different SDs as well as for the case with a sharply defined E = 〈E〉. This finding suggests that the $\sqrt{\langle R_g^2\rangle \left(E\right)}$ – E dependence in Fig. 3 b is not strictly limited to sharply defined E values. An essentially identical relationship should also be is applicable to the $\sqrt{\langle R_g^2\rangle \left(\langle E\rangle \right)}$ and associated σ (R_g²) values conditioned upon reasonably symmetric distributions of E with mean value 〈E〉. In other words, $\sqrt{\langle R_g^2\rangle \left(E\right)}$ in Fig. 3, which was originally constructed for sharply defined E values, is also expected to be a good approximation of $\sqrt{\langle R_g^2\rangle \left(\langle E\rangle \right)}$ for essentially symmetric distributions of E. More generally, the $\sqrt{\langle R_g^2\rangle \left(\langle E\rangle \right)}$ for any distribution P(E) of E, symmetric or otherwise, can be calculated readily as ${\left[\int dEP\left(E\right)\langle R_g^2\rangle \left(E\right)\right]}^{1/2}$ by using the 〈R_g²〉(E) values from Fig. 3.

Inference of conformational dimensions solely from FRET efficiency can entail significant ambiguity

To ascertain more generally the degree to which the R_g values consistent with different FRET efficiencies overlap, we extended the comparison in Fig. 4 c for two E values by computing the corresponding overlapping coefficients (Eq. 3) for all possible pairs of FRET efficiencies, E₁ and E₂:

$$\text{OVL}{\left(R_{\text{g}}^2\right)}_{E_1,E_2}=\int d{R}_{\text{g}}^2\text{min}\left[P\left(R_{\text{g}}^2|E_1\right),P\left(R_{\text{g}}^2|E_2\right)\right].$$ (4)

The heat map in Fig. 5 indicates substantial overlaps for a majority of (E₁, E₂). Among all possible (E₁, E₂) combinations, >30% have OVL ≥ 0.8, and close to 60% have OVL ≥ 0.6 (Fig. S2 a), meaning that their P(R_g²|E) distributions are quite similar. Notably, OVL increases significantly as E₁, E₂ increase above ≈0.4. We also computed averages of R_g² over the overlapping regime of the pairs of distributions. These averages represent conformational dimensions that are consistent with both E₁ and E₂. In a majority of the situations, the root-mean-square R_g² for the overlapping regime stays within a relative narrow range of ≈22–25 Å for our model of unfolded Protein L, even for E₁ and E₂ that are quite far apart (Fig. S2 b). Therefore, taken together with Figs. 1, 2, 3 and 4, the overview in Fig. 5 indicates that when an explicit-chain physical model is used to interpret/rationalize smFRET data (18, 21), as is the case here, the a priori expectation is that even substantial changes in 〈E〉_exp do not necessarily imply large changes in average R_g. In this light, previous smFRET-based stipulations of large denaturant-dependent changes in the 〈R_g²〉 of Protein L (16, 17) are demonstrably inconclusive in the absence of additional relevant experimental information, because they were based on conventional inference approaches that are not entirely physical (21). Moreover, as is evident from the examples in Fig. 6, the trend of a mild R_g–E variation that we saw previously (21) and in Figs. 1, 2, 3, 4 and 5 here, which is derived directly from explicit-chain polymer models, is expected to hold generally for other FRET systems of disordered proteins with different chain lengths and Förster radii as well.

Figure 5.

Ambiguities in FRET inference of conformational dimensions. The heat map provides for n = 75 and R₀ = 55 Å the overlapping coefficient $\text{OVL}{\left(R_g^2\right)}_{E_1,E_2}$ of pairs of R_g² distributions conditioned upon FRET efficiencies E₁ and E₂. Contours on the heat map are for $\text{OVL}{\left(R_g^2\right)}_{E_1,E_2}$ = 0.8, 0.6, 0.4, and 0.2, as indicated by the scale on the right. To see this figure in color, go online.

Figure 6.

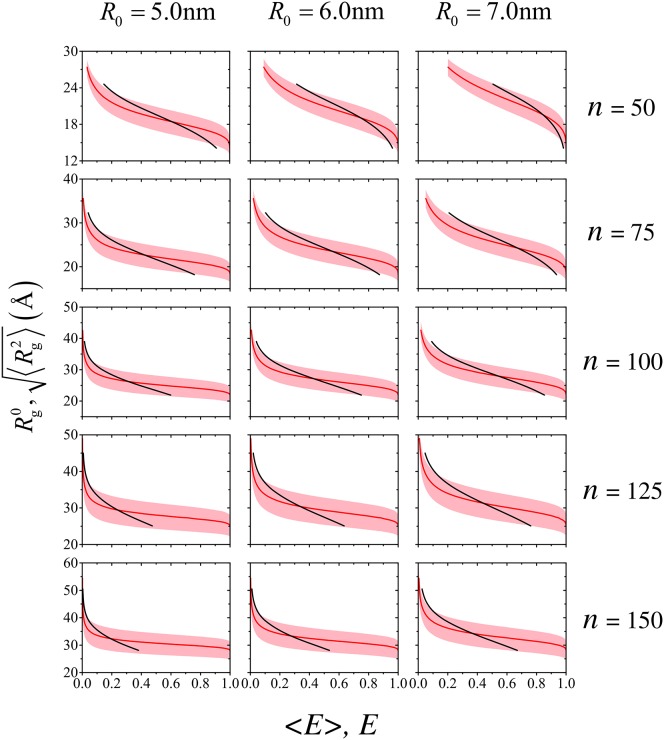
Most probable and root-mean-square radius of gyration. Shown here is generalization of the R_g⁰(〈E〉) (solid black curve traversing across the shaded region in each panel at a steeper incline), and $\sqrt{\langle R_g^2\rangle \left(E\right)}$ (curve at a milder incline in the middle of the shaded region in each panel) for R₀ = 55 Å and n = 75 in Fig. 3 to other Förster radii R₀ and chain lengths n. The shaded areas are bound by $\sqrt{\langle R_g^2\rangle \left(E\right)\pm \sigma \left(R_g^2\right)\left(E\right)}$, which were represented by red dashed curves in Fig. 3. As discussed in the text, the $\sqrt{\langle R_g^2\rangle \left(E\right)}$ curves computed here for sharply defined E values are expected to apply also to $\sqrt{\langle R_g^2\rangle \left(\langle E\rangle \right)}$ for essentially symmetric distributions of E where 〈E〉 denotes the mean value of E in such distributions. As pointed out above for Fig. 3, the black R_g⁰(〈E〉) curves shown here do not cover 〈E〉 values close to zero or unity because of the relatively large R_g bin sizes used previously (21). To see this figure in color, go online.

Discussion

Subensemble-derived conditional distributions of R_g are basic to smFRET inference

To recapitulate, here we have further developed the subensemble SAW approach to smFRET inference of conformational dimensions (21), which is based on the obvious principle that only physically realizable conformational ensembles should be invoked to interpret smFRET data. We focused previously on the most probable radius of gyration R_g⁰(〈E〉), which is derived from distributions of E conditioned upon a narrow range of R_g. Here we have considered the complementary quantity, $\sqrt{\langle R_g^2\rangle \left(E\right)}$, which is the root-mean-square value of R_g conditioned upon a given E. These quantities are not identical, but their variations with 〈E〉 or E are similar (Figs. 3 and 6). Relative to conventional approaches to smFRET inference, both R_g⁰(〈E〉) and $\sqrt{\langle R_g^2\rangle \left(E\right)}$ exhibit a milder dependence on smFRET efficiency, covering a range of R_g values consistent with polymer physics (21). By construction, R_g⁰(〈E〉) is appropriate if it is known or presumed that the disordered conformations populate a narrow range of R_g values or distribute symmetrically around an average R_g (21), whereas $\sqrt{\langle R_g^2\rangle \left(E\right)}$ is suitable when such knowledge or assumption is absent. Therefore, it is our contention that, given a single 〈E〉_exp in the absence of additional experimental data, the quantity $\sqrt{\langle R_g^2\rangle \left(E\right)}$ should serve well as the physically valid Bayesian inference. However, if the R_g values are known experimentally to be confined to a narrow range, which may be the case for certain IDPs, R_g⁰(〈E〉) would be the valid inference when no further information besides 〈E〉_exp and the confinement is available. The data provided in Fig. 6 and the Supporting Information of (21) as well as those in the present Figs. 3 and 6 are useful for this purpose.

Physically valid interpretation of smFRET data requires explicit-chain modeling

Conventional approaches to smFRET inference neglects possible sequence-dependent conformational heterogeneity of unfolded ensembles. They always enforce a full conformational ensemble that expands or contracts homogeneously (16, 17). Lacking an explicit-chain representation, this elementary unphysicality of conventional smFRET inference was often overlooked. Consequently, when 〈E〉_exp is small, these procedures force the entire ensemble to expand, leading to unrealistically high inferred 〈R_g〉 values (21). Although conformations with large R_EE (and hence small E or 〈E〉) and large R_g are part of our subensemble analysis (e.g., Fig. 2 f), these rare conformations in our simulations did not arise from physically unrealistic long Kuhn lengths or unrealistic intrachain repulsion as in conventional approaches (21). This is the fundamental reason why conventionally inferred 〈R_g〉 values differ from those simulated using physical, explicit-chain models (18, 21, 48, 50, 51), and that such simulations, for Sic1 (21) and Protein L (50), for example, produced smaller variations in 〈R_g〉 consistent with the limits prescribed by our subensemble SAW analysis (21) (Fig. S1).

In this perspective, recent computational investigations using explicit-chain simulations to rationalize smFRET data represent significant advances. These efforts include a study on Protein L using a denaturant-dependent construct based on a native-centric Gō-like side-chain potential (50) and an all-atom, explicit-water MD study on ACTR and an R17 variant (52, 53). In these studies, the conformational heterogeneity of unfolded/disordered ensembles encoded by amino acid sequences is taken into account either by a structure-specific Gō-like potential (50) or a transferrable atomic force field (52, 53). However, it should be emphasized that commonly used force fields may not capture the high degrees of folding cooperativity observed for real proteins (25). In particular, in comparison with experiment, the disordered conformational ensembles predicted by several atomic force fields are too compact (26, 57, 59, 73). Efforts to address this shortcoming are underway (60, 61, 62). For the case of Protein L, an earlier study (58) using a denaturant-dependent coarse-grained side-chain model similar to the one used in the recent study by Maity and Reddy (50) suggests that, even with an essentially native-centric potential, the model is insufficiently cooperative in comparison with experiment. Specifically, the predicted chevron plot for Protein L has a folding-arm rollover (58), which is absent in experiment (46). This behavior is related to denaturant-dependent shifts in the positions of transition and unfolded states in the model (58), which would likely lead to a reduction in 〈R_g〉 with decreasing [GuHCl]. We view these known limitations of current potentials for protein folding simulation as part of the very puzzle underscored by the smFRET-SAXS discrepancy. The crux of the matter is, if the degrees of folding cooperativity for some—albeit not all—proteins, such as Protein L, are indeed as high as envisioned by SAXS measurements (46), why are common force fields unable to capture the phenomenon (58)?

In lieu of attempting to provide an accurate model of sequence-specific interactions, our subensemble SAW approach to smFRET inference does not presume any particular model of sequence-dependent conformational heterogeneity. By itself, our approach merely establishes a perimeter for physically realizable conformational variation (21). The rationale is to let experiment take precedence in uncovering the actual conformational heterogeneity. In other words, P(R_g²|E) is a baseline distribution upon which any reweighting of conformational population by sequence-specific effects is to be considered without prejudgment. Under this conceptual framework, we make no generalization as to whether conformational dimensions of disordered proteins would or would not increase with increasing denaturant concentration. Such a verdict has to be made on a case-by-case basis depending on the nature of available experimental information in addition to the limited structural constraint provided by smFRET. For example, our previous study indicates that the dimensions of IDP Sic1 increase when [GuHCl] is increased from 1 to 5 M (21). A more recent in-depth study using smFRET, SAXS as well as other experimental probes and computation has demonstrated convincingly that conformational dimensions of the IDP ACTR and a destabilized mutant of globular protein R17 increase upon increasing [GuHCl] or [urea] (52, 53). It is of relevance, however, that unlike Protein L (46), R17 is not a two-state folder as its chevron plot has a nonlinear unfolding arm (74).

A hypothetical scenario for the case of Protein L

To make conceptual progress toward understanding the Protein L unfolded state, we first put aside potential experimental artifacts that might be caused, for example, by the sensitivity of R_g to the fitting range of the Guinier analysis and the difficulty in obtaining low-denaturant SAXS data (53). For the following consideration, we assume that the SAXS finding of an essentially denaturant-independent 〈R_g〉 ≈ 25 Å (46) and the smFRET data of a decreasing 〈E〉_exp with increasing denaturant (16, 17) are both valid. We then seek to rationalize the experimental data by constructing denaturant-dependent heterogeneous conformational ensembles consistent with both sets of data. In so doing, we are merely following an investigative logic commonly practiced in the construction of putative unfolded and IDP ensembles (53, 75, 76, 77). As explained below, a solution to the smFRET-SAXS puzzle is possible if, with decreasing denaturant, sequence-specific effects become increasingly biased to redistribute conformational population to high R_g² values such that a nearly constant $\sqrt{\langle R_g^2\rangle }\approx 25\mathrm{\AA }$ is maintained despite the shift of the baseline Bayesian distribution P(R_g²|〈E〉) to lower R_g² values due to increasing 〈E〉_exp with decreasing denaturant (Fig. 4).

How biased does such a denaturant-dependent conformational heterogeneity need to be? Using the example in Fig. 4 for unfolded Protein L at [GuHCl] = 1 and 7 M, an estimate of the necessary denaturant-dependent bias needed to resolve the smFRET-SAXS puzzle can be made. Consider the Bayesian distributions P(R_g²|E) (Fig. 4 c) and P(R_g²|〈E〉) (Fig. 4 d). These are baseline distributions that do not account for any sequence-specific effect. They show that ≈10% and ≈25%, respectively, of the E,〈E〉_exp ≈ 0.74 and E,〈E〉_exp ≈ 0.45 populations have R_g ≥ 25 Å (R_g² ≥ 625 Å²). This means that different subsets of these two conformational distributions can have the SAXS-observed $\sqrt{\langle R_g^2\rangle }\approx 25\mathrm{\AA }$. Indeed, possible sequence-specific reweighted distributions for Protein L that are consistent with both smFRET and SAXS may take the forms of the shaded symmetric regions in Fig. 7 (gray, and pink plus gray areas). These distributions are consistent with smFRET and SAXS because they both have $\sqrt{\langle R_g^2\rangle }\approx 25\mathrm{\AA }$ (thus consistent with SAXS), yet 〈E〉 ≈ 0.74 (〈E〉_exp at [GuHCl] = 1 M) for the gray distribution and 〈E〉 ≈ 0.45 (〈E〉_exp at [GuHCl] = 7 M) for the pink-plus-gray distribution.

Figure 7.

A hypothetical resolution of the Protein L smFRET-SAXS puzzle. The two distributions depicted by the black and red curves are from Fig. 4d, for 〈E〉 = 0.74 and 〈E〉 = 0.45, respectively. For R_g² ≥ 625 Å, the area shaded in pink is under the 〈E〉 = 0.45 (red) distribution but above the $\langle E\rangle =0.74$ (black) distribution, whereas the area shaded in gray is under the 〈E〉 = 0.74 (black) distribution. The R_g² < 625 Å areas that are in lighter shades are mirror reflections of the corresponding R_g² ≥ 625 Å areas with respect to R_g² = 625 Å. The sum total of the pink-plus-gray area (∼50% of P(R_g²|〈E〉 = 0.45)) represents a hypothetical ensemble with 〈E〉 ≈ 0.45 and $\sqrt{R_g^2}\approx 25$ Å, whereas the gray area (∼20% of P(R_g²|〈E〉 = 0.74)) represents a hypothetical ensemble with 〈E〉 ≈ 0.74 but nonetheless the same $\sqrt{R_g^2}\approx 25$ Å. Shown on the right are example conformations in these restricted ensembles, as marked by the arrows. Both conformations have R_g² = 700 Å² (R_g = 26.5 Å), but their different R_EE values entail different E values of $\approx 0.45$ (top) and $\approx 0.74$ (bottom). See text and Fig. 4 for further details.

That this holds true is easy to see if the distributions in question are for two sharply defined E values. In that case, we use the two P(R_g²|E) values in Fig. 4 c to define two restricted (unnormalized) distributions P_r(R_g²|E) such that P_r(R_g²|E) = P(R_g²|E) for R_g² < 625 Å² and P_r(R_g²|E) = min $\left[P\left(R_g^2|E\right),P\left(\left\{2\times 625{\text{Å}}^2-R_g^2\right\}|E\right)\right]$ for R_g² < 625 Å². Because of the mirror symmetry of these distributions with respect to R_g² = 625 Å, the values of their $\sqrt{\langle R_g^2\rangle }={\left[\int d{R}_g^2{R}_{\text{g}}^2{P}_r\left(R_g^2|E\right)\right]}^{1/2}$ are both ≈25 Å, even though E = 0.447 for all conformations in the P_r(R_g²|E = 0.45) distribution and E = 0.745 for all conformations in the P_r(R_g²|E = 0.75) distribution. This result is generalizable to the two broad P(E) distributions in Fig. 4 b. Consider $\int dEP\left(E\right)P_r\left(R_g^2|E\right)$. By definition, this integral gives exactly the R_g² ≥ 625 Å² parts (in darker shades) of the gray, and pink-plus-gray areas in Fig. 7 because P_r(R_g²|E) = P(R_g²|E) for R_g² ≥ 625 Å² and $P\left(R_g^2|\langle E\rangle \right)=\int dEP\left(E\right)P\left(R_g^2|E\right)$. The integral yields close approximations to the R_g² < 625 Å² lighter-shaded areas in Fig. 7 because $\sqrt{\langle R_g^2\rangle \left(E\right)}$ varies mildly in the range 0.2 ≤ E ≤ 0.95 (Fig. 3 b) that covers most of the P(E) distributions (Fig. 4 b). This procedure ensures that the conformational populations represented by the gray-plus-pink and gray areas in Fig. 7 preserve their respective $\langle E\rangle =\int dEEP\left(E\right)$ values because $\int dEP\left(E\right)P_r\left(R_g^2|E\right)$ preserves the average E at every R_g². Therefore, the shaded distributions in Fig. 7 represent conformations with different 〈E〉 ≈ 0.45 and 〈E〉 ≈ 0.74 but possess the same $\sqrt{\langle R_g^2\rangle }\approx 25\mathrm{\AA }$. This hypothetical scenario indicates that consistency between SAXS and smFRET is possible if sequence-induced heterogeneity entails a mild restriction to ∼2 × 25% = 50% of the conformational possibilities allowed by the 〈E〉_exp at [GuHCl] = 7 M, but imposes a more severe restriction to ∼2 × 10% = 20% of the conformational possibilities allowed by the 〈E〉_exp at [GuHCl] = 1 M (Fig. 7). It should be emphasized, however, that this is only one among many possible scenarios of denaturant-dependent conformational reweighting that can satisfy both smFRET and SAXS data. Further information about the reweighting may be offered by additional experimental data such as pair distributions from SAXS, but that is beyond the scope of this work.

The denaturant-dependent biases represented by the above estimates are intuitively plausible because the required biases of 50% → 20% for [GuHCl] = 7 M → 1 M are not excessive. These fractional restrictions are only rough estimates, but they serve to illustrate a key concept. It is conceivable that the required restrictions can be less. For instance, when the atomic size and shapes of amino acid side chains are taken into account, the actual intraprotein excluded volume effect can be stronger than that embodied by the R_hc = 4 Å repulsion distance in the C_α model. If $R_{\text{hc}}=5$ Å is used instead (21), the R_g distribution would shift upward by ≈1–3 Å (Fig. S3). In that case, the fractions of P(R_g²|〈E〉) with R_g ≥ 25 Å would increase, enabling significantly less denaturant-dependent biases of 81% → 43% (for [GuHCl] = 7 M → 1 M) to resolve the smFRET-SAXS discrepancy (Fig. S4).

Conclusions

We deem this scenario for Protein L viable pending further experiment because natural proteins are heteropolymers, not homopolymers. Their amino acid sequences encode for heterogeneous intrachain interactions, especially under strongly folding (low or zero denaturant) conditions, which logically can only lead to heterogeneous conformational ensembles even when the chains are disordered. Unfolded conformations are not Gaussian chains (78). The question is not whether heterogeneity exists but the degree of heterogeneity and its impact. Such heterogeneity is observable by NMR (79), in some cases even in high urea concentrations (80, 81), not only for proteins such as BBL that do not fold cooperatively (82), but also for two-state folders (as defined by an approximate equality of van’ t Hoff and calorimetric enthalpies of unfolding, and chevron plots with linear folding and unfolding arms (25, 83)) such as cytochrome c (84). The biophysics of protein folding processes that are macroscopically cooperative yet microscopically heterogeneous is readily understood theoretically (85, 86, 87). From a mathematical standpoint, it is definitely possible, as we envisioned above, for heterogeneous conformational ensembles that are distinct from random coils or SAWs to have overall random-coil or SAW dimensions nonetheless (21), as has been demonstrated by a recent study of the IDP Ash1 (88) and by hypothetical explicit-chain ensembles constructed to embody such properties (89, 90). The scenario we suggested for resolving the smFRET-SAXS discrepancy for Protein L posits an increased population of transient looplike disordered conformations with the two chain termini close to each other under native conditions. Is this feasible? Of relevance to this question is the experimental finding that conformations with enhanced populations of nonlocal contacts are involved in the folding kinetics of adenylate kinase (91, 92, 93). Conformations with similar properties have also been suggested by theory to be favored along folding transition paths (29). Recently, a disordered conformational state with such properties was identified for the protein drkN SH3 as well, though in this case it is induced by high rather than by low denaturant (18). All in all, it is clear from the above considerations that denaturant-dependent heterogeneity in disordered protein conformational ensembles is expected in general. To what degree and in what manner it may account for the smFRET-SAXS discrepancy will have to be ascertained by further experiment.

Recently, Fuertes et al. (94) make an observation similar to ours—among other results of theirs—that the smFRET-SAXS puzzle may be resolved by recognizing that a given R_EE can be consistent with a variety of R_g values. For the record, it is noted that one of the authors of this work (94) kindly sent their manuscript (submitted but unpublished at the time) to us after we shared with him our article on May 15, 2017 before submitting the original version of this article to this journal and making it publicly available on arXiv.org (arXiv:1705.06010).

Author Contributions

J.S. and H.S.C. designed the research. J.S., G.-N.G., and H.S.C. performed the research. J.S., G.-N.G., C.C.G., and H.S.C. analyzed the data. T.S. contributed computational tools. J.S. and H.S.C. wrote the paper.

Editor: Rohit Pappu.