Investigating the dosimetric effects of grid size on dose calculation accuracy using volumetric modulated arc therapy in spine stereotactic radiosurgery

Abstract

Purpose

Sharp dose gradients between the target and the spinal cord are critical to achieve dose constraints in spine stereotactic radiosurgery (SRS), however the accuracy of the doses to the spinal cord at these high dose gradients is sensitive to the how the dose is sampled across the structure using a discretized isotropic calculation grid. In this study, the effect of the grid size (GS) on the dosimetric accuracy of volumetric modulated arc therapy (VMAT) spine SRS plans was investigated.

Methods

The Eclipse v11.0 Anisotropic Analytical Algorithm (AAA) algorithm was used for dose calculation. Plan qualities of fifty treatment plans were evaluated with a GS of 2.5 (AAA’s default value), 1.5 and 1mm. All plans were prescribed to the 90% isodose line in 1 fraction. Parameters used for plan comparison included the distance-to-fall-off (DTF) between the 90% and 50% isodose levels in the axial plane, planning tumor volume (PTV) coverage to 99%, 95%, 5% and 0.03cc, dose to 10% (Cord_D10%) and 0.03cc (Cord_D0.03cc) of the spinal cord sub volume. The dosimetric accuracy was evaluated based on film dosimetry percent gamma pass rate, line profile through the cord. Calculation times between different grid sizes as well as DVH algorithm differences between two treatment planning systems (Eclipse vs Velocity) were compared. Paired t-test was used to investigate the statistical significance.

Results

The DTF decreased for all plans with 1mm compared to 1.5mm and 2.5mm GS (2.52±0.54mm, 2.83±0.58mm, 3.30±0.64, p<0.001). Relative to the 1mm GS, Cord_D0.03cc and Cord_D10% increased by 6.24% and 7.81% with the 1.5mm GS, and 9.80% and 13% with the 2.5mm GS. Film analysis demonstrated higher gamma pass rates for 1.5mm GS compared to 1 and 2.5mm GS (95.9%±5.4%, 94.3%±6.0%, 93.6%±5.4%, p<0.001), however 1mm GS showed better agreement in the high dose gradient near the cord. Calculation times for 1mm GS plans increased for 1.5 and 2.5mm GS (61% and 84%, p<0.001). The average difference between the two treatment planning systems was approximately 0-1.2%. A maximum difference of 5.9% occurred for Cord_D0.03cc for the 1mm GS.

Conclusion

Plans calculated with a 1mm grid size resulted in the most accurate representation of the dose delivered to the cord, however resulted in less uniform dose distributions in the high dose region of the PTV. The use of a 1.5mm grid size may balance accurate cord dose and PTV coverage, while also being more practical with respect to computation time.

Introduction

Spine stereotactic radiosurgery (SRS) has been shown to be an effective treatment option for spine metastases, relieving pain and neurological symptoms in order to improve to the quality of life of patients with metastatic disease. The feasibility and accuracy of an image guided stereotactic based approach has been demonstrated by multiple institutions as well as in a multi-institutional setting. (1-4) In spine SRS, the dose limiting factor is the spinal cord, which is in close proximity to the target volume and sometimes enveloped by epidural tumor. Sharp dose gradients between the target and the spinal cord are critical in order to achieve spinal cord dose constraints and tumor coverage to obtain tumor control in spine SRS.

Volumetric modulated arc therapy (VMAT) is a common treatment method for spine SRS.[5,6] VMAT is a form of intensity modulated radiotherapy (IMRT) in which the gantry rotates while simultaneously modulating the beam to deliver the desired dose distribution. In spine radiosurgery, VMAT is similar to IMRT in the ability to achieve tumor coverage while simultaneously sparing the spinal cord. (5) However, with the extra degree of freedom of rotation during beam delivery, sharper dose drop offs at the spinal cord and tumor interface have been observed.(6) With the combination of high definition multi leaf collimators (HD-MLC) and flattening filter free (FFF) beams, the achievable penumbra of the beam is on the order of 2-2.5mm (7-9) compared to 4-6mm achieved with flattened beams and typical, non-high definition, multi leaf collimators.(10, 11)

Uncertainties in the dose calculation on a discretized isotropic grid are a result of dose and position errors when dose is linearly interpolated between dose points on the calculation grid. Niemierko and Goitien showed that the magnitude of dose and positional errors depend on the width of the beam penumbra. It was recommended that a grid size 2.5 times the largest acceptable positional error should be used, assuming the acceptable positional error is in the range of 1 to a few millimeters.(12) In radiosurgery, high doses of radiation are delivered safely due to more rigid immobilization and localization techniques. In the early 2000’s, the localization and positional accuracy of linear accelerator based image guided radiosurgery was 1.36±0.11mm using DRRs and port films. (1) Current localization and positional techniques such as CBCT and 6 degree of freedom couches have improved the localization accuracy to 0.2-0.6mm(13), (14). Thus with the ability to achieve tighter positional accuracy as well as sharper dose gradients, the smallest grid size should then be used in for accurate dose calculation. However, dose calculations using a fine grid size increases computation time significantly and may not be practical.

Several studies have been performed looking at the grid size for different treatment sites and techniques. Through Fourier analysis, Dempsey et al found that 2.5mm grid size spacing is sufficient to reduce dose calculation error to less than 1% in IMRT.(15) Dose differences for varying grid sizes from 2-4mm resulted in dose discrepancies of 2-4% for head and neck IMRT. (16) For lung stereotactic treatments using dynamic arc therapy, an optimal grid size was found to be 3mm. (17) Uncertainties in the DVH calculation occur when interpolation and re-sampling are used to take account the differences in resolution between the volume image and the dose matrix. As well as how the DVH calculation algorithm segments and bins the voxels of the structure. These factors may have a greater impact for small structures, such as the spinal cord, especially at high dose gradient. For small structures, a small change in the volume estimation is a large fraction of the structure volume, resulting in a volume averaging effect. The accuracy of the dose calculation is critical in spine SRS where high gradients are used to satisfy dose constraints of the spinal cord while simultaneously achieving dose coverage to the target volume. The accuracy of the dose calculation in the high dose gradients are particularly sensitive to the position of the calculation points on the dose grid as well as the position of the grid overlaid on the structure. In this study we evaluate the dosimetric differences and calculation accuracy using a VMAT technique in spine SRS.

Methods and Materials

Patient Plan characteristics

Fifty patients previously treated at our institution with spine radiosurgery were included in the study. The 50 plans consisted of 36 thoracic (T) spine, 1 cervical (C) spine and 13 lumbar (L) spine cases. All patients were treated with a single fraction. The prescription dose was 12, 16 or 18Gy, prescribed to the 90% isodose line (IDL). The treatment planning CT for all plans were scanned using a 2mm slice thickness and a field of view of 600mm, resulting in 1.12x1.12mm pixel resolution. The treatment planning CT was rigidly fused to a contrast enhanced axial T1 and T2 weighted MR using a mutual information based algorithm in the registration workspace of Eclipse. The target volume and spinal cord were drawn on the MR and verified on the CT. The target volume and spinal cord were drawn as high-resolution segments, to allow for more precise delineation and evaluation. The average target volume size was 45.19cc and ranged from 8.62cc to 164.95cc. The average minimum distance between the target volume and the spinal cord was 0.77mm, ranging from 0mm to 3.4mm. Table 1 summarizes the characteristics of the target volumes in the study including the location, volume, epidural evolvement and classification of the target volume. The target volumes are classified as A: vertebral body only (Figure 1a), B: vertebral body and pedicles (Figure 1b, dotted line), C: vertebral body including anterior and posterior elements.

Table 1.

Summary of the fifty target volumes in the study including the location, target volume (cc), distance to fall off (DTF) (mm) between the 90% and 50% isodose line, target classification, and epidural evolvement.

Location	Volume (cc)	DTF (mm)	Classification	Epidural Evolvement
C5C6	50.98	3.4	A	No
T1	11.8	2.4	A	Yes
	12.21	2	B	No
T2T3	34.16	2.9	C	Yes
	47.26	2	C	Yes
	50.65	4.1	C	No
T3	8.62	2.1	C	No
	12.21	2.6	B	Yes
T3T4	18.75	2.2	B	No
T4	11.02	2	A	No
T5	15.57	1.6	C	Yes
	17.56	2	A	No
	18.66	2.4	B	Yes
T6	14.31	1.5	A	Yes
	34.5	3	B	Yes
	52.16	2	B	Yes
T6T7	33.04	1.5	B	Yes
	50.65	2.3	B	Yes
T7	30.75	1.8	C	Yes
T8	43.25	2.2	C	Yes
T9	19.84	2	C	Yes
	25.23	2.3	C	No
T9T10	62.02	2.4	B	No
	60.65	3.1	B	Yes
T10	31.3	3.1	A	No
	24.06	2.3	C	No
	26.06	2.6	B	Yes
T10T11	103.51	2.2	C	No
T11	40.26	2.5	C	Yes
	40.22	2.3	B	Yes
T12	36.82	2.7	B	Yes
	28.02	2.5	B	No
	33.55	2	B	Yes
	57.49	2.9	C	No
	46.04	2.4	A	No
	35.86	2.6	B	Yes
T12L1	164.95	2.5	C	No
L1L2	55.13	3.6	A	No
L2	43.86	2.5	B	Yes
	51.46	2.5	B	No
	53	3.1	B	No
	55.26	2.2	B	Yes
	64.18	2.8	C	No
	95.29	2.7	C	Yes
L3	61.61	3.3	B	No
L3L4	107.77	3.1	A	Yes
L4	53.11	2.6	A	No
	54.03	3.1	C	No
	42.14	3	A	No
L4L5	118.8	3.1	A	Yes

Figure 1.

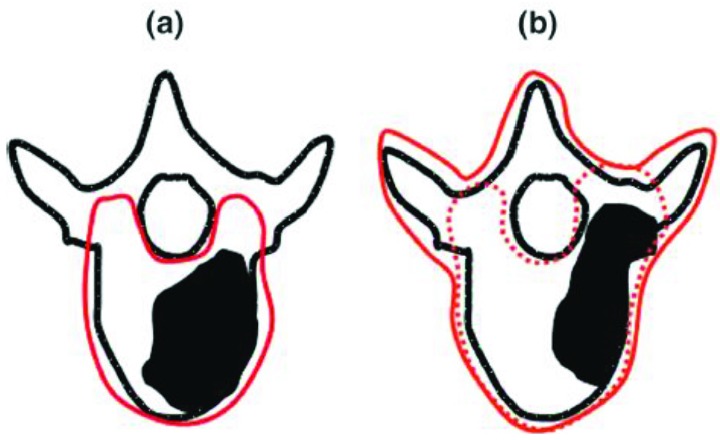
Classification of radiosurgery target volumes used in study, summarized in Table 1. A: vertebral body only (a), solid line. B: vertebral body and pedicles (b), dotted line. C: vertebral body including anterior and posterior elements (b), solid line. (Figure from RTOG 0631)

The plans were optimized in the Eclipse treatment planning system (v 11, Varian Medical Systems, Palo Alto, CA) and the final dose distribution was calculated using the Anisotropic Analytical Algorithm (AAA) version 11. All patients were planned with a volumetric modulated arc therapy (VMAT) technique. The plans consist of two partial arcs starting and stopping at posterior oblique angles (215°-145°) to avoid the rails on the couch top. Patient plans were planned and treated on an EDGE linear accelerator (Varian Medical Systems, Palo Alto, CA) equipped with a HD-MLC, with either 6 MV or 10 MV FFF beams. Plans were optimized so that the prescription dose covered greater or equal to 95% of the target volume. The spinal cord constraint that was required for patient treatment was no more than 10% of the partial spinal cord to receive 10Gy and a maximum dose of 14Gy to 0.03cc of partial spinal cord.

Plan Evaluation

Each of the fifty clinical plans was re-calculated with fixed monitor units (MU) for a 1, 1.5, and 2.5mm grid size (GS). A total of 150 plans, 50 for each grid size, were used to evaluate the effects of grid size. It should be noted, that because this was a retrospective study, the GS used to calculate and evaluate the original plan may not have been the same for all 50 plans, and was based on the planner’s choice and whether the case had epidural involvement. Of the original plans, 17 were calculated using a 2.5mm grid size, 14 with a 1.5mm, and 19 with a 1mm grid size. This discrepancy can be seen in the results section, where the dosimetric constraints of the partial spinal cord exceed tolerances when calculated with a different grid size.

Plans were compared by evaluating the PTV coverage, dose to 99% of the PTV (PTV_D99%) and 95% of the PTV (PTV_D95%) as well the hot spot, dose to 5% of the PTV (PTV_D5%) and dose to 0.03cc of the PTV (PTV_D0.03cc). The spinal cord was compared by evaluating the dose to 10% (Cord_D10%) and 0.03cc of the spinal cord sub volume (Cord_D0.03cc), where the spinal cord sub volume was contoured as the spinal cord visualized on the MR 6mm below and above the superior and inferior extent of the PTV. (4) The dose fall off was evaluated by measuring the smallest distance to fall off (DTF) between the 90% and 50% isodose line at isocenter in the axial plane. The DTF for each patient is presented in Table 1. The paired student’s t-test was utilized, where p<0.05 was considered to be statistically significant.

Film Verification

The original plan for each of the fifty target volumes was delivered and analyzed using Gafchromic EBT3 film (Ashland Inc, Bridgewater, NJ). Since each plan was recalculated using fixed MUs, the plans for the 1, 1.5, and 2.5mm GS were identical in regards to plan delivery (MU, dose rate, MLC motion). The film plane was oriented in the axial plane sandwiched in the center of the Brainlab acrylic slab phantom (Brainlab, Feldkirchen, Germany), dimensions of 30x30x10cm consisting of two 30x30x5cm slabs. The isocenter was placed at the center of the phantom. A calibration curve, delivered on the same day of the plan, was used to convert optical density to dose using 9 equivalent spaced dose steps ranging from 2.5 to 23.3Gy, depending on the prescription dose of the delivered plan.

The films were scanned using an Epson Expression 10000XL flatbed scanner (EPSON, Suwa, Japan). The films were scanned with a resolution of 150dpi in order to provide an accurate gamma calculation in areas of steep dose gradients. It was recommended by Low and Dempsey that the pixel spacing of the evaluated dose distribution should be sufficiently small relative to distance to agreement gamma criteria, as a rule of thumb less than 1/3 (18). Films were scanned approximately 16 hours after delivery, allowing for the time response dependency to plateau. In-house software was used to perform dose conversion and gamma analysis(19). The film was compared to the dose plane recalculated using a 1, 1.5 and 2.5mm grid size on the Brainlab slab phantom, exported at a 0.5mm resolution. Gamma analysis was performed using absolute dose analysis using a 3% dose and 1mm distance to agreement criteria (3%/1mm) to evaluate the differences in the dose distribution. (20) The film dosimetry uncertainty was evaluated, and was found to be approximately 1.7% for the green channel over the range used in our study. [19] The dose at isocenter from the film was also recorded to evaluate the absolute dose difference between the film and the plans. The isocenter dose was used in the study, not as an absolute dose measurement, but as a metric to evaluate the difference between the film and dose planes.

Calculation Time

The plans were calculated on a distributed calculation framework (DCF), where the control points of the VMAT plan are distributed over a framework agent server (FAS) environment. The calculation framework at our institution consists of thirteen FAS servers. Ten of the servers have a 64GB RAM, Intel® Xeon® CPU E5-2690 with 16 cores and three with 64GB RAM, Intel® Xeon® CPU E5-2680 with 24 cores. The time to calculate each plan on the original treatment planning CT with each grid size was documented and compared.

DVH Algorithm

The values obtained in this study used to evaluate the grid size difference were obtained from the Eclipse treatment planning system. The DVH algorithm can affect the displayed dose, depending on its method of dose binning, the shape interpolation algorithm and determination of whether a voxel resides inside a structure. As a comparison of the uncertainties that may arise from different DVH calculations, a subset of cases were exported to a separate treatment planning system, Velocity v 3.2.0 (Varian Medical Systems, Palo Alto, CA), to evaluate the differences in the DVH. The subset of cases included the ten cases with the shortest DTFs, ranging from 1.5 to 2mm. The dose planes and structure sets were exported to Velocity and the same dosimetric parameters were evaluated with the DVH calculated using Velocity’s DVH algorithm.

Results

Dosimetric Indices

The comparison of the PTV and spinal cord dosimetric indices for all fifty target volumes as well as the average percent difference for all fifty cases between the different grid sizes is summarized in Table 2. The differences between each grid size for all dosimetric indices were found to be statistically significant, p<0.001. On average over the 50 plans, the PTV coverage and hot spot increased by about 2% for the 1.5mm GS compared to both the 1mm and 2.5mm GS. Differences less than 1% in PTV coverage (p<0.001) occurred between the 1 and 2.5mm GS. With the 1.5 and 2.5mm GS, Cord_D10% increased by 7.8% and 13%, and the Cord_D0.03cc increased by 6.2% and 9.8%, compared to the 1mm GS, respectively. The largest differences occurred for the Cord_D10% and Cord_D0.03cc between the 2.5 and 1mm GS. The maximum difference was 23.2% and 22.7% for Cord_D10% and Cord_D0.03cc, respectively, which correlated to an absolute dose difference of 1.8 and 2Gy, respectively. The DTF decreased from the 1.5 to 1 mm GS by 0.31±0.2 mm and from the 2.5 to 1mm by 0.78±0.3 mm.

Table 2.

Comparison of dosimetric indices for PTV and spinal cord as a result of different grid sizes. Mean ± standard deviation with ranges given in parentheses (minimum, maximum). Percent difference for all fifty cases calculated between the 1, 1.5, and 2.5mm dose distributions. Average difference over 50 cases with ranges in parenthesis (minimum, maximum).

Grid Size	PTV_D99% (Gy)	PTV_D95% (Gy)	PTV_D5% (Gy)	PTV_D0.03cc (Gy)	Cord_D10% (Gy)	Cord_D0.03cc (Gy)	DTF Between 90% and 50% IDL (mm)
1mm	17.03±1.24 (11.66, 18.18)	17.72±1.20 (12.03, 18.73)	20.09±1.54 (13.55, 21.91)	20.96±1.58 (14.12, 23.08)	8.19±1.24 (4.77, 9.66)	10.50±1.66 (6.3, 13.37)	2.52±0.54 (1.5, 4.1)
1.5mm	17.31±1.25 (11.86, 18.43)	18.11±1.20 (12.32, 19.32)	20.34±1.54 (13.76, 22.08)	21.07±1.57 (14.32, 23.19)	8.83±1.36 (5.04, 10.67)	11.15±1.68 (6.66, 13.97)	2.83±0.58 (1.8, 4.5)
2.5mm	16.93±1.22 (11.57, 18.08)	17.84±1.17 (12.16, 19.03)	20.05±1.52 (13.61, 21.85)	20.65±1.56 (14.15, 22.72)	9.25±1.43 (5.17, 11.39)	11.52±1.61 (6.87, 14.05)	3.30±0.64 (1.7, 5.1)
1.5vs1mm	1.7% (0.3%, 3.2%)	2.2% (0.6%, 3.7%)	1.3% (0.4%, 1.9%)	0.5% (-0.8%, 1.6%)	7.8% (1.8%, 14.6%)	6.4% (1.1%, 12.7%)	0.31±0.2mm
2.5vs1.5mm	-2.20% (-3.8%, 0.9%)	-1.5% (-2.9%, 0.7%)	-1.4% (-2.9%,-0.8%)	-2.0% (-3.5%, 0.5%)	4.8% (1.6%, 9.2%)	3.5% (-0.7%, 10.2%)	0.47±0.2mm
2.5vs1mm	-0.54% (-3.0%, 1.2%)	0.7% (-2.5%,-1.7%)	-0.2% (-1.9%, 0.6%)	-1.5% (-3.7, 0.2%)	13.0% (5.4%, 23.2%)	10.1% (0.4%, 22.7%)	0.78±0.3mm

Figure 2 demonstrates the difference in cord dose between 2.5mm and 1mm GS and between 1.5mm and 1mm GS for both Cord_D10% and Cord_0.03cc relative to the DTF measured on the 1mm GS plan. The largest differences occur with the shortest DTF, of 1.5-2mm, when the plan is calculated and evaluated with a 2.5mm GS.

The DVH comparison of the dosimetric indices between Eclipse and Velocity are summarized in Table 3. On average, the overall difference between the two treatment planning systems was within 1.2%. The largest deviation between Eclipse and Velocity’s DVH calculation occurred for the Cord_D0.03cc for a 1mm grid size. The deviation between the two treatment planning systems for Cord_D0.03cc was 5.9% corresponding to a decrease of the PTV_99% of 0.9% as well.

Table 3.

Comparison of dosimetric indices for PTV and spinal cord as a result of different grid sizes for Eclipse and Velocity. Mean ± standard deviation with ranges given in parentheses (minimum, maximum). Average percent difference for all fifty cases between Velocity and Eclipse dosimetric parameters.

Grid Size		PTV_D99% (Gy)	PTV_D95% (Gy)	PTV_D5% (Gy)	PTV_D0.03cc (Gy)	Cord_D10% (Gy)	Cord_D0.03cc (Gy)
	1mm	16.59±1.89 (11.57, 17.82)	17.49±1.98 (12.16, 18.73)	19.82±2.34 (13.61, 21.63)	20.45±2.37 (14.15, 22.32)	9.24±1.26 (6.25, 10.64)	11.27±1.50 (7.59, 12.78)
Eclipse	1.5mm	17.07±1.98 (11.86, 18.43)	17.82±2.06 (12.32, 19.01)	20.19±2.44 (12.32, 19.32)	20.93±2.49 (14.32, 23.14)	8.76±1.22 (5.94, 10.11)	10.81±1.54 (7.37, 12.5)
	2.5mm	16.73±1.95 (11.66, 18.18)	17.34±1.200 (12.03, 18.61)	19.93±2.42 (12.16, 19.03)	20.83±2.54 (14.12, 23.08)	7.93±1.11 (5.39, 9.25)	9.9±1.46 (6.78, 11.79)
	1mm	16.39±1.90 (11.44, 17.56)	17.41±1.97 (12.11, 18.61)	19.86±2.35 (13.64, 21.76)	20.49±2.37 (14.22, 22.44)	9.23±1.29 (6.12, 10.50)	11.24±1.62 (7.43, 12.87)
Velocity	1.5mm	16.91±2.05 (11.73, 18.39)	17.76±2.06 (12.27, 19.02)	20.25±2.44 (13.81, 22.11)	21.02±2.49 (14.38, 23.11)	8.67±1.22 (5.78, 9.99)	10.73±1.54 (7.22, 12.64)
	2.5mm	16.54±2.00 (11.5, 18.11)	17.29±2.00 (11.98, 18.58)	19.88±2.40 (13.55, 21.71)	20.74±2.49 (14.13, 22.91)	7.95±1.11 (5.37, 9.22)	9.93±1.46 (6.72, 11.88)
	1mm	-1.2% (-3.3%, 0.1%)	-0.4% (-0.8%, 0%)	0.2% (0, 0.6%)	0.2% (-0.2%, 0.5%)	-0.2% (-2.1%, 2.1%)	-0.5% (-5.9%, 2.5%)
% Difference (Velocity – Eclipse)	1.5mm	-1.0% (-5.1%, 0.6%)	-0.3% (-0.6%, 0.1%)	0.31% (0.1%-0.5%)	0.4% (-0.1%, 1.0%)	-1.1% (-3.5%, 1.3%)	-0.8% (-3.4%, 2.5%)
	2.5mm	-1.2% (-5.2%, 0.2%)	-0.30% (-0.6%, 0%)	-0.3% (-0.6%, 0)	-0.4% (-1.6%, 0.2%)	0.3% (-2.0%, 2.2%)	0.3% (-2.7%, 4.1%)
1mm	94.3±6.0	1.22±1.8	11’36’’±2’48’’
1.5mm	95.9±5.4	-0.06±2.03	4’30’’± 47’’
2.5mm	93.6±5.4	0.40±2.09	1’53’’ ± 32’’
1vs1.5 mm	-1.6%	1.28%	61%
1.5vs2.5 mm	2.3%	-0.46%	58%
2.5vs1 mm	-0.7%	-0.82%	84%

Figure 2.

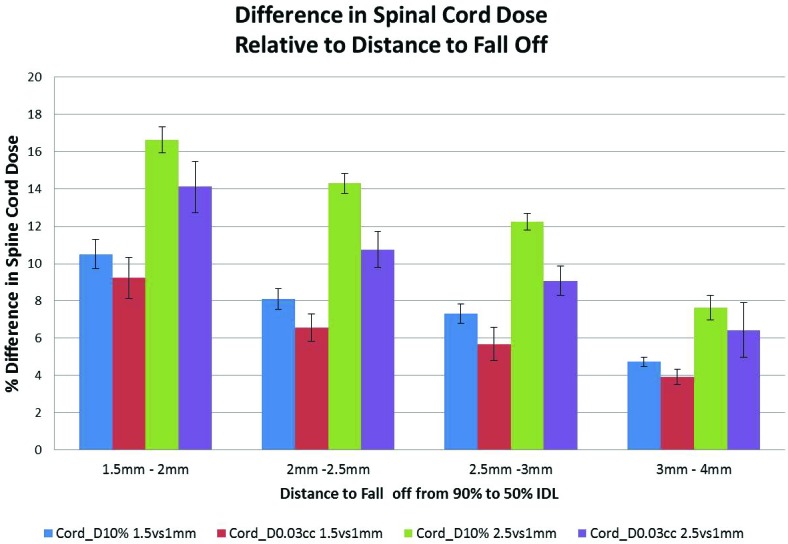
Percent difference in Cord_D10% and Cord_D0.03cc between 2.5 and 1.5mm GS compared to the 1mm GS, relative to the distance to fall off between the 90% and 50% isodose line measured on the 1mm GS plan. Average values are plotted with the standard error.

Film Results and Calculation Time

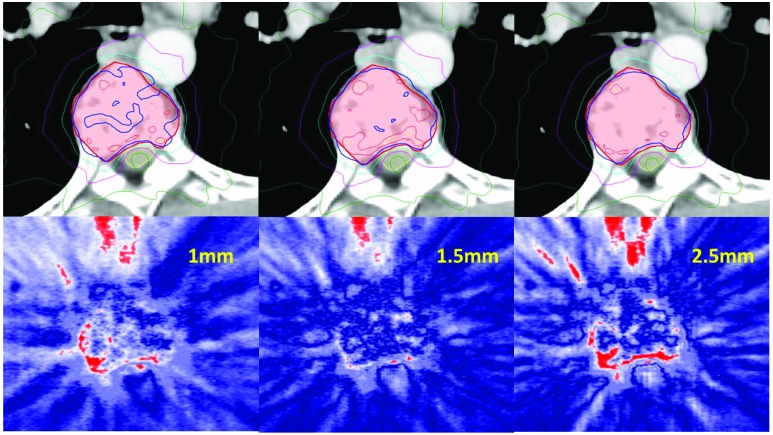
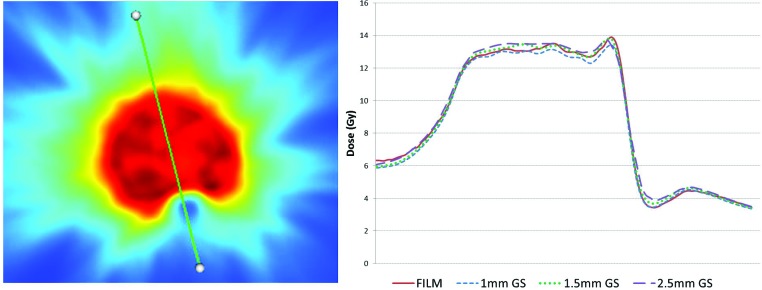
Table 4 summarizes the results of the film analysis. On average for all 50 cases, gamma pass rates were higher for the 1.5mm GS compared to both 1mm and 2.5mm GS. Although the 1mm GS had a better pass rate (94.3±6.0%) compared to the 2.5mm GS (93.6±5.4), the difference in the measured and calculated isocenter dose from the film was larger for the 1mm GS (1.22±1.8%) compared to both the 2.5mm GS (0.40±2.09%). Figure 3 shows an example of a T spine case of the dose distributions and gamma results of a plan calculated with a 1, 1.5 and 2.5mm GS. The 1mm GS shows better agreement with the film in the high gradient region between the PTV and the cord, Figure 4. However, the 1mm dose distribution is more non-uniform in the high dose region, reflective of the larger point dose difference and the decrease in the gamma pass rate. The dose distribution that best agreed with the film delivery, with an average 95.9% pass rate, was the 1.5mm GS using the 3%/1mm gamma pass rate criteria.

Figure 3.

Example of a T-spine case. Dose distribution on treatment planning CT (top row) using 1mm GS (left), 1.5mm GS (center) and 2.5mm GS (right). PTV outlined in red and spinal cord in yellow. The blue IDL is 18Gy, cyan is 14Gy, magenta IDL is 10Gy, dark green is 6Gy. Corresponding gamma map using 3%/1mm pass criteria; where blue is pass, white approaches 1, red is greater than 1 and fails.

Figure 4.

Dose distribution (left) with line profile through the cord. Corresponding line profile of the film (red), 1mm GS (blue), 1.5mm GS (green dash), and 2.5mm GS (purple) demonstrating the agreement between the film and the dose distribution in the high dose gradient between the cord and the PTV and the PTV high dose region.

The calculation time between the 1.5 and 1mm GS, and 2.5 and 1.5mm GS increased about 61% and 58%, respectively, whereas the time to calculate a 1mm GS plan compared to a 2.5mm GS plan increased by 84%.

Discussion

The choice of grid size can affect the displayed dose and dose values used to evaluate the PTV and organs at risk. Particularly in areas of high dose gradients and small structures, the placement of the grid relative to the structure is an important part of how the dose displayed and what percentage of the dose lies in the high dose gradient. For a smaller grid size, with less volume averaging, it would be expected that the PTV coverage increase and the spinal cord dose decrease in a high dose gradient. As expected, PTV coverage (PTV_D99% and PTV_D95%) increased when the GS was decreased from 2.5 to 1mm GS. However when the GS was decreased from 1.5 to 1mm, the spinal cord dose decreased and the PTV coverage decreased as well. This is most likely due to the less uniform dose distribution of the 1mm GS, which was confirmed with the lower gamma pass rate through the film analysis and a larger difference in isocenter dose. AAA is a deterministic calculation method, so no calculation noise exists as one would expect in a stochastic method such as Monte Carlo. The less uniform dose distribution may be due to the limitations of the treatment planning system’s ability to model the HDMLC, which is 2.5mm in width. When calculated on a 1mm GS, the dose distribution may need to be interpolated in the direction of the leaf width. Inaccuracies in the modeling of the tongue and groove effect may also lead to the dose differences in the direction of the leaf width as well as the dynamic leaf gap (DLG) in the direction parallel to the leaf movement.(21) In the Eclipse treatment planning system, the tongue and groove effect is modeled in the VMAT optimization algorithm by extending the leaf projection in the direction of the leaf width by a set amount, which is slightly smaller than the actual physical width of the tongue. This parameter is dependent on the MLC model which is preconfigured in the treatment planning system and little can be done to manually modify this parameter. Yang et al found that dose calculation accuracy could be furthered improved for the tongue and groove effect by developing a sampling method for the beam fluence matrix in their in-house dose calculation planning system.(22) The DLG is a parameter that takes into account the rounded leaf ends of the MLC. This parameter should be verified and can be optimized during commissioning to ensure that the treatment planning system can accurately model the delivered dose. (23)

The 1mm GS gives the best representation of the cord dose delivered to the patient. However if a plan is initially calculated using a 2.5mm GS, when recalculated using a 1mm GS to evaluate the dose distribution, the dose distribution is often much nosier and the coverage of the target volume near the cord may not be optimal. In order to achieve the best PTV coverage and cord sparing, optimization after a 1mm GS dose calculation, such as an intermediate dose calculation, may be needed to accurately locate the high dose gradient and to smooth out the mottled dose distribution in the high dose region of the PTV. An intermediate dose calculation takes into account the calculated dose distribution and fine tunes the dose distribution after the first optimization (24). However, this may not be practical in some clinical settings that may not have the computational resources that were used in this study since it doubles the calculation time. A 1.5mm GS may be more clinically feasible, providing good PTV coverage that agrees with film measurements. However, based on the study the calculated cord dose will be overestimated by 6-8%, or an absolute dose of 0.65Gy.

With the ability to create and evaluate plans with a sharper drop off, the risks of myelopathy and the under dosage of the tumor can be greater as the spinal cord dose nears the acceptable tolerance. When the average DTF was 5mm using a posterior IMRT technique (1), in cases with epidural involvement, the dose to the epidural tumor would have to be sacrificed in order to meet the cord tolerance. Because the DTF was not as rapid, part of the tumor still received 16Gy, which has been shown to be a therapeutic dose. (4) A common failure mode is caused by underdosage to the epidural space resulting in failure to control pain or decompress the spinal cord. (25) With a sharper DTF, the epidural disease can be better covered while simultaneously meeting cord tolerance. However, as the balance between the spinal cord dose limit and target coverage becomes precarious, the precision of treatment delivery and immobilization are imperative. Previous studies show that small inter-fractional motion can increase the spinal cord dose up to 13%. [26] With a sharper drop off and as the cord dose is pushed closer to tolerance, the dose to the spinal cord may be further increased resulting in greater risks of myelopathy.

Conclusion

1mm grid size plans resulted in the most accurate representation of the dose delivered to the cord, however resulted in nosier dose distributions in the high dose region of the PTV. The use of a 1.5mm grid size may balance the dose to the cord and the PTV coverage, while also being more practical with respect to computation time.