Application of the concept of biologically effective dose (BED) to patients with Vestibular Schwannomas treated by radiosurgery

Abstract

In the application of stereotactic radiosurgery, using the Gamma Knife, there are large variations in the overall treatment time for the same prescription dose, given in a single treatment session, for different patients. This is due to not only changes in the activity of the Cobolt-60 sources, but also to variations in the number of iso-centers used, the collimator size for a particular iso-center, and the time gap between the different iso-centers. Although frequently viewed as a single dose treatment the concept of biologically effective dose (BED), incorporating concurrent fast and a slow components of repair of sublethal damage, would imply potential variations in BED because of the influence of these different variables associated with treatment. This was investigated in 26 patients, treated for Vestibular Schwannomas, using the Series B Gamma-Knife, between 1999 and 2005. The iso-center number varied between 2 and 13, and the overall treatment time from 25.4–129.58 min. The prescription doses varied from 10–14 Gy. To obtain physical dose and dose-rates from each iso-center, in a number of locations in the region of interest, a prototype version of the Leksell GammaPlan^® was used. For an individual patient, BED values varied by up to 15% for a given physical iso-dose. This was due to variation in the dose prescription at different locations on that iso-dose. Between patients there was a decline in the range of BED values as the overall treatment time increased. This increased treatment time was partly a function of the slow decline in the activity of the sources with time but predominantly due to changes in the number of iso-centers used. Thus, variations in BED values did not correlate with prescription dose but was modified by the overall treatment time.

1. INTRODUCTION

Gamma Knife radiosurgery is used to treat a wide range of both malignant and benign conditions. It is frequently preferred to invasive surgical procedures because of the reduced risk of complications. The radiosurgical dose is most frequently given in a single treatment session, which is frequently referred to as a single dose exposure, although the treatment protocol for individual patients varies widely for the same disease. These variations in treatment protocols, that are largely ignored, result in marked changes in overall treatment times between patients, even for a defined prescription dose. This was recently illustrated in a series of 26 patients treated for Vestibular Schwannomas selected to illustrate the full range of this variation [¹]; the prescription dose varied between 10 and 14 Gy, the number of iso-centers used ranged from 2-13 and the overall treatment time, including the gaps between iso-centers, from ~ 25 to 130 min.

Since the radiation source is Cobalt-60, the exposure time will increase as the activity of the sources decays over time for totally standard protocols. It has been reported that morbidity related to, e.g. cranial nerves, was higher in a group of patients treated when the Cobalt-60 exposure was delivered at a high dose-rate, in comparison to the morbidity in a similar group of patients treated when the sources had decayed, thus significantly reducing the dose-rate [²]. In contrast a multivariate analysis of complications associated with the treatment of arterio-venous malformations at the same institution [³] provided no such evidence of a dependence of treatment response on overall treatment time within the range of treatment times examined. When the source activity declines the time taken to give a treatment will increase, which is automatically calculated by the treatment planning system. However, the changes in the calibration dose-rate of the machine, measured at the center of a spherical phantom of radius 80 mm made of ABS plastic, should not be equated with changes in dose-rate within the target volume in individual patients because of the individual patients’ geometry. The actual dose-rate in the target volume in different patients is highly variable, as discussed previously [¹].

Another key variable is the wide variation in the number of iso-centers used to treat an individual patient, which is influenced by the complexity of the plan required to adequately cover the target volume. Here again there are suggestions in the literature that a relatively small number of iso-centers may increase the efficacy of a given prescription dose [³].

The treatment time in Gamma Knife radio-surgery is presently identified as the radiation ‘beam on’ time, since none of the machines currently used in clinical practice record the time interval between the end of one and the start of treatment with another iso-center. These gaps in the irradiation time will be variable in the older Leksell Gamma Knife units, averaging 6 min for the model B. With the new generation of the machine, Perfexion^®, the beam off time is short – of the order of 6 seconds but short gaps still exist. Thus the overall treatment time is always the beam on time plus the total time of any gaps, including any unscheduled gaps, so the use of a larger number of iso-center will also significantly increase the overall treatment time as will the use of smaller as opposed to larger collimator sizes. Given the large number of variables involved in any treatment it is perhaps not a surprise that it is difficult to determine the importance or not of any one of these, individually.

These variations in the way the dose to the target volume is administered in a single session would in radiobiological terms represent the application of a variable number of different sized dose fractions (one for each iso-center) given at different dose-rates in the target tissue (a feature of collimator size and patient geometry) with multiple incomplete repair intervals (the gap between the different doses administered) and not as a single dose exposure. In this complex treatment situation the biological effect of a given exposure is best evaluated using a modification of the Biologically Effective Dose Model (BED) formulation which incorporates parameters that take account of the repair of sublethal radiation damage occurring when radiation treatment times are extended. Up until now, in publications related to the radiobiology of radiosurgery [^4-6], nearly always only the ‘basic’ BED model has been used. This ‘basic’ model always assumes acute dose exposures, and thus does not take into account the effects of changing dose-rate and the intervals between iso-centers, when sublethal irradiation damage is still being repaired. The use of such a ‘basic’model, to calculate equivalent fractionated stereotactic radiotherapy doses is equally flawed, since even with a few fractions, as used for example with the introduction of the eXtend system in Gamma Knife radiosurgery [⁷], the time taken to give the total dose on each treatment day is of the order of 20 – 45 min (beam on time) and thus the role of the repair of sublethal damage over each treatment session still needs to be considered as well as that between treatment sessions.

In conventional radiotherapy, the effects of changes in dose-rate and of the kinetics of repair of sublethal radiation damage, with the introduction of inter-fraction intervals of less than 24 h, is now increasingly well understood. This is particularly so for central nervous system tissue. Based on animals studies it is now well recognized that the kinetics of repair of sublethal damage in tissues can best be described by a bi-exponential model. There is a short half-time for repair of less than 15 min and a longer one of 2-3 h. This is based on both single dose (no gaps) studies with a changing range of dose-rates [⁸], from the study of fractionated doses with variable incomplete repair intervals [^9-10] or from data involving the combination of these two approaches [¹¹]. The clinical consequences of developing new fractionated protocols (e.g. CHART) based on a monophasic repair model have resulted in an excess number of myelopathy cases after the treatment of patients with head and neck cancer with multiple dose fractions/day [^9,12].

In radiosurgery the failure to take into account a fast component of repair will underestimate the amount of repair occurring, particularly when treatment sessions vary between approximately 10-60 min. There is likely to be a decline in biological effect as overall treatment times increase over this period. The effect of extended delivery times has already been raised as an issue in other radiotherapy treatment modalities that result in an extension of the irradiation time, including intensity modulated radiation therapy (IMRT). In cell studies designed to mimic this approach [¹³], doses of 2 Gy (conventional fraction size) were delivered over time periods up to 60 min. The surviving fraction of tumor cells in vitro increased as a result of the reduced biological effectiveness with increasing exposure time. This would be expected in a cell population with a short repair half-time.

In an earlier publication [¹] theoretical calculations were carried out to illustrate the effects of dose-rate, due to ⁶⁰Co source decay and also the effects of changing the overall treatment time on the biological effective dose. The latter was achieved by changing the time interval between iso-centers or reducing the number of iso-centers. In the present investigation the treatment plans of a group of 26 patients were selected to represent the range of potential treatments for large Vestibular Schwannomas. The tumors selected resulted in some compression of the brain stem, which was the normal tissue most at risk from such treatments. Prescription doses of 10, 12, 13 and 14 Gy were used; all treatments were carried out with the Leksell Series-B Gamma Knife. The number of iso-centers varied between 2 and 13 and the overall treatment times, assuming a gap between iso-centers of 6 min, ranged from 25.4 – 129.58 min. Analysis was carried out using a modification of the Leksell Gamma Knife planning system so the dose prescription to individual voxels within a region of interest, that contained the target volume, could be determined. In this way the variation in biologically effective dose (BED) for the brain stem for a given physical irradiation dose within individual patients and between patients could be investigated. This would determine the effect of the different variables associated with treatments in these patients on this tissue. The authors accept that these concepts might be considered to be complex, when applied to radiosurgery, but these radiobiological considerations should at least be considered by those that actually prescribe doses to patients using this treatment modality. This particularly applies to neurosurgeons since radiosurgery is now very frequently included within their training program.

2. MATERIALS AND METHODS

2.1 Patient population

A group of 26 patients with Vestibular Schwannomas, aged 30-72 (median 53, average 52) years, treated at the Gamma Knife Centre, Cromwell Hospital, London, UK, between 11 May 1999 and 14 March 2005, were selected for the present analysis. All Patients were treated with the Leksell Series B Gamma Knife, and selection was designed to encompass the full range of treatments applied over this period, i.e. the range of different number of iso-centers used (2-13), and a variation in the overall treatment times (25.4 – 129.58 min). The treatment time is a function of the number of iso-centers, their collimator sizes, and the change in the activity of the ⁶⁰Co sources over the selected period. Overall treatment time represents the beam on time plus the sum of the interval between the different iso-centers. Since the set up time between iso-centers is not recorded in the patients treatment records in Leksell GammaPlan^® a nominal interval of 6 min was adopted for each collimator change/repositioning based on discussions with Series B Gamma Knife users. The total physical prescription dose to the tumor margin varied between 10 Gy and 14 Gy, and this was delivered to between the 40% and 60% iso-dose. Details of the iso-center number and overall treatment time of the 26 individual patients used in this study are given in Table 1. The ranges of maximum tumor doses, relative to the prescription dose, are given in Table 2. The initial tumor volumes, as a function of the prescription dose, are given in Table 3.

Table 1.

Variation in the number of iso-centers and overall treatment times used on a series of patients with large Vestibular Schwannomas. The prescription dose varied between 14 and 10 Gy, delivered to the 40 – 60 % iso-dose using a Series-B Gamma Knife.

Prescription dose (Gy)/	Overall treatment time (min)
Iso-center number	20-30	30-40	40-50	50-60	60-70	70-80	80-90	> 90
14 Gy
3 iso-centers (2 gaps*	25.40	-
4 iso-centers (3 gaps)		-	41.28	-
5 iso-centers (4 gaps)		-	40.28	-
6 iso-centers (5 gaps)				-	67.78	-
13 iso-centers (12 gaps)							-	129.58
13 Gy
3 iso-centers (2 gaps)			-	54.55	-
6 iso-centers (5 gaps)				-	61.58	74.91	-
7 iso-centers (6 gaps)					-	74.89	84.61	91.96
						75.36	-	92.30
8 iso-centers (7 gaps)							-	124.25
12 Gy
2 iso-centers (1 gap)	29.62	-
4 iso-centers (3 gaps)	-	32.65	-
		39.97
5 iso-centers (4 gaps)			-	50.47	-
6 iso-centers (5 gaps)				-	63.07	73.97	-
7 iso-centers (6 gaps)						-	80.38
8 iso-centers (7 gaps)				-	63.43	-
10 Gy
5 iso-centers (4 gaps)	-	38.16		-
6 iso-centers (5 gaps)		-	49.79
7 iso-centers (6 gaps)			-	57.21	-
8 iso-centers (7 gaps)					-	73.93	-

^*Nominal gap period 6 min.

Table 2.

Variation in the maximum tumor doses (100% iso-dose), relative to the different prescription doses that were prescribed to a range of iso-doses (40-60%).

Prescription dose (Gy)	Range of maximum tumor doses (Gy)
14	23.3 – 29.8
13	23.6 – 30.2
12	21.4 – 23.3
10	21.8 – 22.2

Table 3.

Variation in the initial mean tumor volume (±SD), plus the range of initial volumes, for Vestibular Schwannomas treated with a prescription dose of either10, 12, 13 or 14 Gy.

Dose (Gy)	Mean Volume ± SD (cc)	Volume Range (cc)	Sample size
10	9.5± 4.5	4.4  16.8	4
12	3.4± 1.76	1.4  6.5	8
13	3.6± 1.36	1.8  6.7	9
14	3.4± 1.5	2.3  6.0	5

2.2 Calculation of biological effective dose

The biological effectiveness of a given total physical radiation dose to the brain stem and to the tumor will depend on the specific radiation protocol. For any given location on a physical iso-dose, in a Gamma Knife plan, the total physical dose is made up of the summation of the individual physical doses at that location from the different iso-centers. Thus the dose-rate and dose contributions, at a given location, will vary depending on its relative position to the iso-center being delivered, and the exposure times for those specific iso-centers. To obtain the physical dose-rates for a number of locations in the region of interest a prototype research version of the Leksell GammaPlan^® has been written that computes the dose-rate from each of the individual iso-centers in the plan in a cube with a matrix of 31 x 31 x31 voxels. Note that the physical dose in an arbitrary voxel, from any iso-center is its dose-rate multiplied with its exposure time. The total dose in any voxel is then the summation of the different contributions from every iso-center used.

For acute radiation exposure to a single dose ‘D’, the biologically effective dose (BED) is given by the equation:

Equation 1.

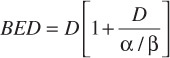
where α/β represents a tissue specific constant [¹⁴]. For this ‘basic’ equation to be valid all of the exposure must be given in a very short time (relative to any repair half-time for sublethal damage) and as a consequence there is no need to take into account the effects of any significant repair of sublethal radiation damage over the period of any exposure. Gamma Knife treatments do not represent acute, single dose, exposures nor a single continuous exposure; they involve multiple exposures, as defined by the number of iso-centers, with short gaps between each of the different exposures. Thus the calculation of the BED for a Gamma-Knife treatment needs to take into account these variables, as defined by the following extended model:

Equation 2.

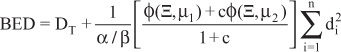
where is a complicated function of the protocol and the repair rates; the effects of dose-rate, the inter-iso-center time and the exposure time are mediated via this function. ‘µ₁’ and ‘µ₂’ represent two sublethal repair rates and ‘c’ the partition coefficient of the slower component (‘µ₁’ > ‘µ₂’). It should be noted that the absolute partitioning between the two repair processes ‘µ₁’ and ‘µ₂’ is 1.0/[1+c] and c/[1+c], respectively. The total dose, ‘D_T’, is the summation of the different doses delivered to a given voxel in by the treatment, delivered by the ‘n’ iso-centers, where ‘d_i’ is the dose delivered by the ‘i^th’ iso-center. Full detail, of the derivation of this model can be found elsewhere [^{11, 15-16}]. Experiments in the rat spinal cord were used to derive the values of the repair kinetic parameters for normal CNS tissue [⁸]. Half-times for the repair of sublethal irradiation damage of 0.19 h (ln2/µ₂) and 2.16 h (ln2/µ₁); partition coefficient ‘c’ (0.98), were obtained from these studies with an associated α/β ratio of 2.47 Gy. These values have been adopted for use in the present study to calculate BED for doses to the normal brain stem; the tumors treated causing some compression of this normal tissue structure. Comparable parameters for Vestibular Schwannomas are not yet available, but may be similar to those for normal CNS tissue.

BED values were calculated for all voxels in the 31 x 31 x 31 matrix covering the original region of interest. From these data it was possible to evaluate, for each patient, the variation in BED values for a fixed physical iso-dose due to variations in the physical dose protocol for the different voxels on that iso-surface. In order to obtain sufficient BED values for comparative purposes, voxels with a specified iso-dose (± 0.01 Gy) were routinely used. In addition to within patient variations in BED values for the prescription dose given, between patients variation were also examined to determine the effect of variations in overall treatment time for a fixed number of iso-centers and also the effect of changing the number of iso-centers to treat to a given prescription dose. The matrix of total physical doses and the associated BED values for each voxel, also enabled treatment plans to be compared on the conventional basis of the physical dose or in terms of iso-BED.

2.3 BED treatment plan

In order to be able to display the BED iso-effect levels for CNS tissue and to compare these with conventional physical iso-dose lines over MR images, the prototype research version of the Leksell GammaPlan^® was modified to allow the import of a matrix of 31 x 31 x31 individual BED values calculated using the equation described above. The voxels in the BED matrix had an identical configuration to those in the physical dose matrix. Based on this BED matrix, iso-effect lines for different selected BED values could be drawn using the same standard approach used to construct and display physical iso-dose lines with Leksell GammaPlan^®.

3. RESULTS

3.1 Variations in BED within and between individual patients

In any Gamma Knife treatment plan the dose to a given voxel for a specific iso-dose is made up of the contributions at that point from each of the individual physical doses of the iso-centers used to create an appropriate treatment plan. This is illustrated in Figure 1 for a simple three iso-center treatment plan, for a tumor with an initial volume of 2.3 cc. The figure shows the 50 % iso-doses for the three individual iso-centers. This involved the use of two equally weighted treatments, using 14 mm diameter collimators (iso-center 1 and 3), and a smaller dose contribution from a 4 mm collimator (iso-center 2). Although it is not possible to show the largest likely variation in the protocol to the prescription iso-dose in a single image, it is obvious that the largest contribution from iso-center 2 will be in voxels close to point 3. Iso-center 2 will only make a relatively small contribution to the total dose at point 1, where there are approximately equally dose contributions from iso-center1 and 3. For this patient, where the prescription dose to the combined 50% iso-dose was 14 Gy, the voxel with the maximum dose contribution from iso-center 1 (shot 1) was 12.36 Gy, with dose contributions of 0.17 and 1.47 Gy from shots 2 and 3 respectively (Table 4). The highest dose contribution in a voxel from shot 2 was 1.97 Gy with the contribution from iso-centers 1 and 3 being 6.98 and 5.05 Gy, respectively. The corresponding percentage total dose contributions and the dose-rates, which clearly varied over the period of irradiation, are also given in Table 4. Using these three dose prescriptions the BED values for CNS tissue in these voxels were calculated. This varied from a lowest value of 77.6 up to a 10% higher value of 85.3. Protocols for voxels with the largest individual dose contribution from a single iso-center will have the greatest biological effect, since BED values are a complex function of the dose and dose squared (see Equation 2). The units associated with the biologically effective dose values (BED values) are also Gray (Gy), but this should not be confused with the unit of physical dose, which is a measure of absorbed energy in tissue. To avoid confusion in this manuscript biological effective doses are simply referred to as BED values.

Figure 1.

MR image showing the location of the 50% iso-dose lines for the three iso-centers used in the of the contrast enhanced tumor (red lines). The resultant 50% prescription iso-dose (yellow line) is also indicated; prescription dose 14 Gy. This also represented the maximum dose to the brain stem. The relative dose contributions of the prescription iso-dose will vary with location. The labels and arrows for ‘Point 1’, ‘Point 2’ and ‘Point 3’ are explained in the text.

Table 4.

Maximum variation in the biological effective dose (BED) in the same patient, for individual voxels on the same iso-surface dose (14 Gy prescription dose) treated with 3 iso-centers (see Figure 1)

	Iso-center contribution (Gy)	Relative dose contribution (%)	Dose rate (Gy/min)	BED
Point 1 (max BED)	12.36 (shot 1) 1.47 (shot 3) 0.17 (shot 2)	88.3 10.5 1.20	2.36 0.28 0.06	85.3 (+10.0%)
Point 2 (median BED)	9.55 (shot 1) 4.09 (shot 3) 0.36 (shot 2)	68.2 29.2 2.60	1.82 0.78 0.13	80.8 (+4.2%)
Point 3 (min BED)	6.98 (shot 1) 5.05 (shot 3) 1.97 (shot 2)	49.9 36.0 14.1	1.33 0.96 0.97	77.6 (Reference)

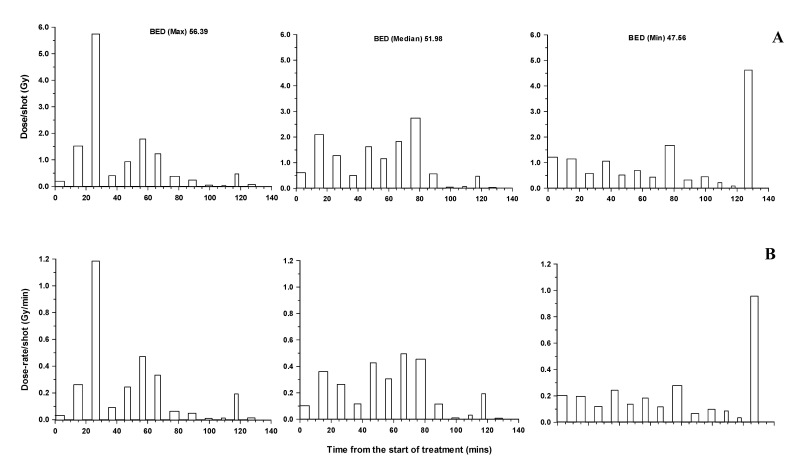
In a more complex treatment plan involving 13 iso-centers, for a tumor with an initial volume of 6.0 cc, the variation in the dose and dose-rate for three voxels are shown in Figures 2 (a and b). The voxels associated with protocols that were associated with the maximum (56.4), a median (52.0) and minimum (47.6 Gy) BED value are illustrated. All of these voxels receives the same total physical dose of 13 Gy. For these more complex treatments, quick judgement as to the voxels likely to be associated with the highest biologically effective doses are difficult. The maximum individual dose contribution to the total physical dose varies from ~ 6 Gy to very small values and the dose-rate from as high as ~1.2 Gy/min down to very small values. Clearly for an individual voxel the dose-rate varies considerably over the period of treatment. In this patient, voxels on the prescription iso-dose of 14 Gy that represented the maximum, median and minimum BED values were 57.7, 55.5 and 53.4 respectively. The BED values for the lower, 12 Gy physical iso-dose, were 49.2, 45.3 and 41.4. Clearly for fixed physical iso-doses of 14, 13 and 12 Gy there was some overlap in their biological effectiveness.

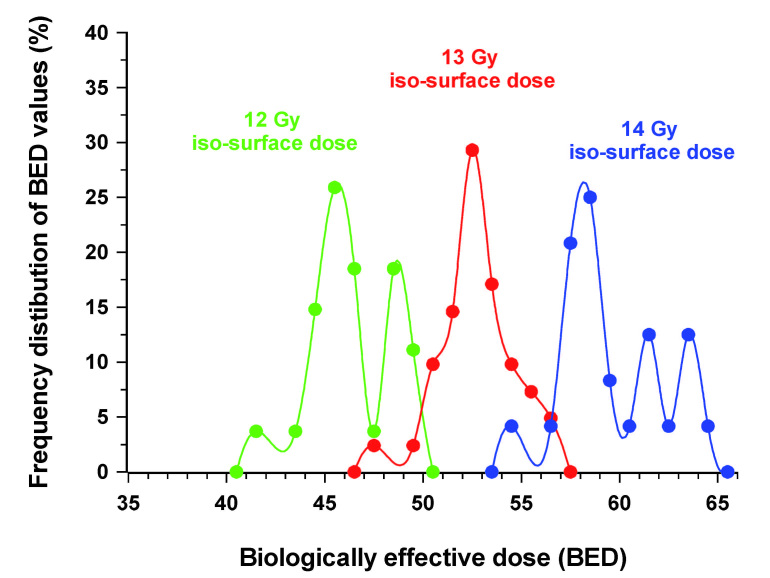
The frequency distribution of BED values, for the above patient, for voxels irradiated with a total physical dose of either 14, 13 or 12 Gy, are presented in Figure 3. To obtain this BED value distribution the physical dose range evaluated was widened slightly (± 0.02 Gy) to increase the number of sampled voxels. BED values for each physical dose were then placed in bins, e.g. 50.00 – 50.99 Gy; 51.00 – 51.99 Gy etc. The widening of the physical dose range did not change the range of BED values. The peak frequency in the incidence of BED values was 45.5, 52.5 and 58.0 Gy for physical iso-doses of 12, 13 and 14 Gy, respectively. There was clearly a significant overlap in biological effectiveness between voxels treated with 13 and 14 Gy and to a lesser extend between 12 and 13 Gy. In this example there was no overlap in BED values between 12 and 14 Gy.

Figure 3.

Frequency distribution of BED values for voxels in a patient treated using 13 iso-centers, with a prescription dose of 14 Gy (± 0.02 Gy). The BED values for voxels on that iso-dose are compared with those for the 13 and 12 Gy (± 0.02 Gy) physical iso-doses.

Figure 2.

Time related changes in dose contribution (A) from individual iso-centers (shots) and the associated dose-rate (B) for individual voxels on the 13 Gy iso-dose of a patient treated with a total of 13 iso-centers. The protocols for the voxels illustrated are those associated with the maximum, median and minimum BED values in the brain stem.

For this patient treated with a prescription dose of 14 Gy, using 13 iso-centers, the BED values for CNS tissue, of 54.2 – 64.1, were well below those for the previous patient treated with only 3 iso-centers that received the same prescription dose (range of BED values 77.6 – 85.3), indeed they were more comparable with the BED values derived for points on the 11 Gy iso-dose on the treatment plan of the patient treated with 3 iso-centers. In this comparison both the iso-center number and the overall treatment time have changed, the latter from 25.4 to 129.58 min.

3.2 Effects of changes in overall treatment time

The effects of a modest increase in overall treatment time for two patients treated with the same number of iso-centers with a prescription dose of 13 Gy are illustrated in Table 5. The overall treatment times were 61.6 and 74.9 min. BED values in these two patients were in the range 70.7 to 54.6, i.e. + 15% to 10% around an arbitrary BED reference value of ~ 61. In both patients, the voxel with a protocol showing that treatment comprised, in effect, a large dose > 10 Gy plus 5 additional doses < 1 Gy to obtain the cumulative dose of 13 Gy,was associated with the largest BED value.

Table 5.

Variation in BED values for two patients both treated using with 6 iso-centers to a fixed prescription dose of 13 Gy. The overall treatment time was longer in the second patient. The BED values relate to voxels with the maximum, a median and the minimum value. Dose contributions and dose-rates are given for doses from an iso-center that delivered >1.0 Gy, the range of the other values are given in parentheses. A BED value of ~ 61 was used as the reference again to which all other values were compared.

Patient 1 (treatment time 61.6 min)				Patient 2 (treatment time 74.9 min)
Iso-center protocol	Iso-center dose (Gy)	Dose-rate (Gy/min)	BED	Iso-center dose (Gy)	Dose-rate Gy/min)	BED
1 (Max)	11.56 (0.46  0.09)	1.42 - (0.22  0.02)	70.7 (+15.2%)	10.50 - (0.68  0.22)	0.87 - (0.09  0.03)	64.6 (+6.4%)
2 (Median)	8.40 2.60 (0.84 – 0.33)	1.51 0.31 (0.18 – 0.06)	66.0 (+7.5%)	8.24 2.25 (0.85 – 0.14)	0.68 0.34 (0.12 – 0.02)	60.8 (Reference)
3 (Min)	7.50 3.40 (0.94 – 0.1)	0.92 1.63 (0.17 – 0.02)	61.3 (Reference)	5.60 3.54 2.50 (1.00 – 0.1)	0.46 0.48 0.40 (0.4 – 0.16)	54.6 (-10.1%)

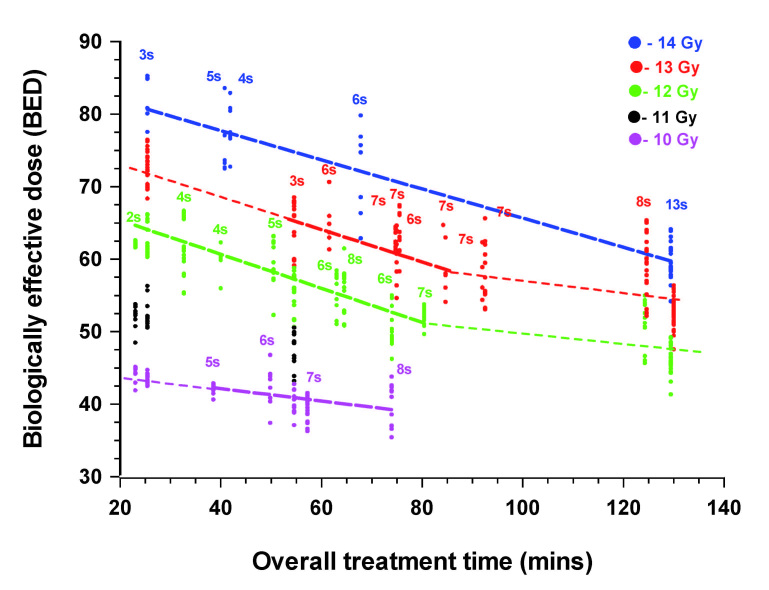
Variations in the BED values for all 26 patients treated with either a prescription dose of 14, 13, 12 or 10 Gy are shown in Figure 4. The BED values of all voxels receiving the prescription dose are plotted as individual data points for each patient. In addition, for selected cases, the BED values obtained for iso-doses below the prescription dose are also plotted. This gives some indication of the changes in equivalent biological effect of a given prescription dose as the overall treatment time is increased. This is either as a direct consequence of the decline in the activity of the ⁶⁰Co sources or because of the increasing number of iso-centers used. A larger number of iso-centers will increase the overall treatment time, in part, because of the nominal 6 min time gaps between them. The results show that the BED values varied for a given fixed physical iso-dose within a patient and that the degree of variation between patients was considerable. For patients treated with a small number of iso-centers in < 30 min, the BED values varied considerably for a given prescription dose, although they were clearly still related to the prescription dose of 12 and 14 Gy. However, with longer overall treatment times the BED values decline markedly. For prescription dose treatments given in 60 – 80 min, with an intermediate 6 7 iso-centers, the biological effective dose was still clearly related to the physical dose prescription. However, this approximate tripling of the overall treatment time resulted in a decline in biological effective dose, compared with the shortest (< 30 min) treatment times, with fewer iso-centers, equivalent to a relative decline in physical dose terms of ~1 Gy.

Figure 4.

Overall treatment time related changes in the BED values for the 5 cases with Vestibular Schwannomas treated with a prescription dose of 14 Gy , the 9 treated with 13 Gy, the 8 treated with 12 Gy and 4 treated with 10 Gy. For each patient the BED value for all voxels on the prescription iso-dose sampled (± 0.01 Gy) are plotted. In addition, the BED values are also plotted for the 13, 12, 11 and 10 Gy physical iso-doses for the patient treated with 3 iso-centers, to a prescription dose of 14 Gy (25.4 min) and the 11 and 10 Gy iso-doses in the patient treated with only 2 iso-centers to a prescription dose of 12 Gy (23.6 min). Similarly the BED values for the 12, 11 and 10 Gy iso-doses were plotted for the 3 iso-center patient treated with a prescription dose of 13 Gy in the shortest time (54.6 min) and for the two cases where the overall treatment time was > 120 min. The variation in BED, with overall treatment time was well correlated (r > 0.95) for treatment times between 2 and 80 min and in the case of the limited number of cases treated to a prescription dose of 14 Gy over the whole time range.

Using treatments given in overall treatment times of 20 – 80 min there was a clear linear dose relationship between the time and the BED values (r > 0.95), irrespective of the prescription dose. The regression lines for prescription doses of 14, 13 and 12 Gy were parallel to each other, and even the 13 Gy regression line could clearly be extrapolated back to the 13 Gy points for the patient treated with 3 iso-centers (25.4 min). The regression line fit to the 4 patients treated using a 10 Gy prescription dose was shallower.

Relatively few patients in this series were treated for longer than 90 min and these largely received a prescription dose of 13 Gy, with only a single patient receiving the highest prescription dose of 14 Gy. There is an indication that of the two patients treated in > 120 min, the patient treated with 14 Gy received a biological effective dose equivalent to between 13 and 12 Gy compared with the patient treated over a similar time period where the prescription dose was 13 Gy. The major difference between these two patients was in the number of iso-centers used and hence the number of gaps where no further damage is being induced, but where repair of sublethal damage will occur. There is also the suggestion based on this limited data the change in BED values, with increasing time, is much less marked between 90 and 125 min than between 20 and 80 min.

3.3 Conventional physical Gamma-plans vs. BED dose plans

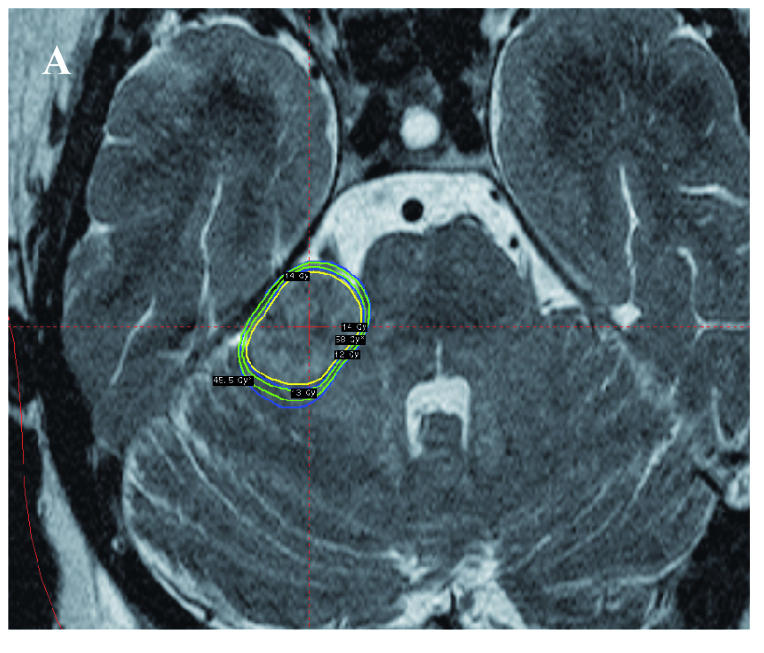
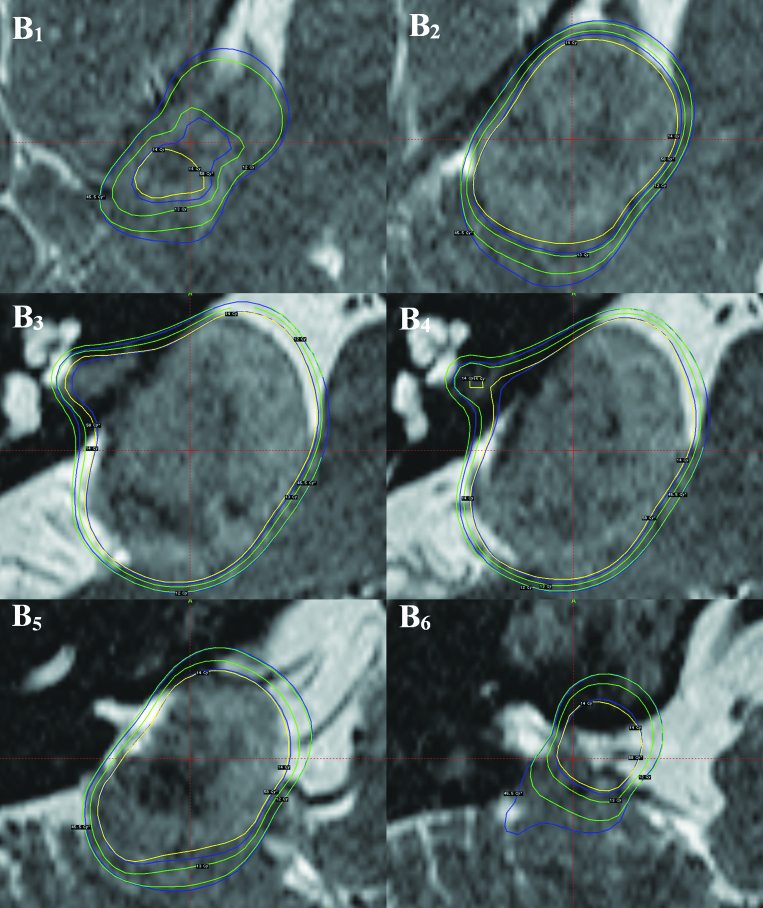
Clearly, from the analysis presented above, there is variation in the biologically effective dose (BED) for a given physical iso-dose. This indicates that any BED value based Leksell Gamma Knife plan, would deviate from the present treatment plans, which are based on physical dose. To illustrate this, the modified version of Leksell GammaPlan^® was used to plot and compare the conventional physical dose plan with a BED based plan in the same patient. The patient treated with 13 iso-centers was used for this purpose. The physical iso-dose lines of 14, 13 and 12 Gy were compared with BED values for the brain stem of 45.5 and 58.0. These BED values represent those that most frequently define the physical iso-dose of 12 Gy and the prescription dose of 14 Gy (see Figure 3). Representative images from these comparative dose plans are shown in Figure 5. The gross tumor volume (GTV) in this patient was 5.97 cc, of which 93% was covered by the BED iso-effect value of 58. This compared with only 91% covered by the physical prescription iso-dose of 14 Gy (Fig 5A). Indicated in Figures 5B_1-6 are representative T₂ weighted images showing both physical iso-dose and BED iso-effect values superimposed. These are represented for the 14 Gy physical prescription iso-dose in this patient and the two lower physical iso-dose values of 13 and 12 Gy as yellow and green lines, respectively. The 58 BED iso-effect value, representing approximately 45% of all voxels with a total physical dose of 14 Gy (Fig 3) and the 45.5 BED iso-effect value, representing approximately 25% of all voxels with a total physical iso-dose of 12 Gy are given for comparison. A majority of images (Fig 5B_3-6) illustrate that the 58 BED iso-effect lines are frequently approximately co-incident with the 14 Gy physical iso-dose lines. However, there are significant deviations when the 58 BED iso-effect lines approach the 13 Gy physical iso-dose lines. These represent relative ‘hot spots’ in the brain stem (Fig 5B_{1, 2, 5}). The volume of brain stem associated with such relative ‘hot spots’ was 0.63 cc. This represents 59.4% of the 13-14 Gy physical iso-dose tissue volume of 1.06 cc. Only in a single region was there evidence that the 58 BED iso-effect value was lower than the 14 Gy physical iso-dose, indicating a relative ‘cold spot’ in tumor assuming comparable repair kinetic parameters (Fig 5B_3-4). This also applied to the 45.5 BED iso-effect value, relative to the 12 Gy physical iso-dose line.

Figure 5.

Overview image, indicating the general location of a large Vestibular Schwannoma impinging on the brain stem (A) and representative detailed slices in the region of the target volume (B_1-6), all images show the 14 Gy prescription physical iso-dose line (yellow) and the associated physical iso-dose lines of 13 and 12 Gy (inner and outer green lines, respectively). The two BED iso-dose lines with values of 58 and 45.5 are indicated for comparison (inner and outer blue lines, respectively). For further explanation see the text.

4. DISCUSSION

The prescription dose for the treatment of Vestibular Schwannomas varied between 10 and 14 Gy for the patients in this study. Although there was a slight overlap with other groups, the group of 4 patients treated for the largest tumors (up to a volume of 16.8 cc) received the lowest prescription dose of 10 Gy. All other dose groups had a similar range of volumes, with the change in prescription dose simply reflecting the changing clinical views as to the most effective prescriptions dose for the treatment of this type of lesion. This question has still not been adequately resolved; however, in the light of the present findings this remaining uncertainty can now be more adequately understood.

Clearly the biological effectiveness of a given physical dose will decline as the number of iso-centers is increased and/or the overall treatment time increases for a fixed number of iso-centers. Treatments with a small number of iso-centers, given in a short overall treatment time, have the largest biological effective dose. This supports the results of a multi-variate analysis of clinical observations which suggested this trend [³]. Claims that relate efficacy or complications to a given physical dose, as in the same publications for the 12 Gy volume, have to be viewed with caution, since the biological effectiveness of 12 Gy can clearly change both within the same patient but, more markedly, between patients because of differences in the treatment protocol for a given physical dose. The simplest details of the variation in protocols are rarely discussed in radiosurgical publications and single dose exposure is frequently assumed. However, differences in protocols are of obvious importance in treatments where exposure times are long and where repair of sublethal radiation damage is likely to be a variable time dependent factor.

The concept that, what was termed an ‘extended linear-quadratic model’ might be pertinent to the large fractional doses used in stereotactic radiosurgery was perhaps initially raised by Guerrero and Li [¹⁷]. The extension was the introduction of a single short repair half-time (~ 0.2 h) into the ‘basic’ BED equation. It was argued that, as compared with conventional fractionated irradiation with small fractional doses, the exposure times associated with large, equivalent, single doses are long and influenced by the repair of sublethal irradiation damage. They supported this claim by demonstrating that the extended equation provided a better fit to iso-effects for total doses given at different dose/fraction than the ‘basic’ equation (without repair) for published experimental data. This included radiation-induced brain damage in rats (LD₅₀) and spinal cord injury. In such studies treatments given in one session were indeed single doses with no gaps. This approach is akin to the incomplete repair model of Thames [¹⁸], which was used to compare different dose fraction schedules, in particular those with incomplete repair intervals involving multiple dose fractions/day.

An alternative approach [¹⁹] was used in a study associated with patients treated with Trigeminal Neuralgia, where a single long (6.5 h) repair half-time was used in the calculation of BED values. Although these authors acknowledged that repair was thought to be associated with a fast and a slow component of repair they chose, in isolation, a long repair half-times of 6.5 h and an associated α/β ratio of 1.5 Gy. The source of these values was not identified in the original manuscript. The use of such a long half-time for repair would seriously underestimate the amount of repair, relative to other approaches, and suggested that even with single iso-center treatments that the BED values did not change with the calibration output of the Gamma Knife over a ⁶⁰Co source cycle. The use of such a long half-time for repair would imply that in conventional radiotherapy, repair of sublethal damage which would be nearly complete within the standard 24 hour interval between fractions [²⁰]. A repair process acknowledged to be associated with two components does not allow one of those components to be meaningfully used in isolation. The use of the calibration dose-rate of the Gamma Knife to compare with the biological outcome is inappropriate since repair of sublethal radiation-induced damage has to be related to the actual voxel dose-rate and consequently the overall treatment time in an individual patient. This is variable even for a fixed calibration output being dependent on the individual patient geometry. Claims about any effect based on machine calibration factors have to be viewed with caution as is discussed in detail elsewhere [¹].

The current results, using repair parameters derived from an experimental study, clearly show that the biological effective dose is strongly influenced by the overall treatment time, which in itself is influenced by both source activity and the number of iso-centers used with the Gamma Knife, plus the associated gaps between the radiation exposures. This was particularly marked for overall treatment times up to between 60 and 80 min, and was equally applicable to physical prescription doses of 12-14 Gy. This is the result of the importance of the fast component of repair, the introduction of which provided a better fit to experimental data [⁸] for CNS tissue and accounted for the decline in the efficacy of radiation exposure in studies designed to simulate the effects of prolonged dose fractions delivered using IMRT [^{13, 21-22}]. With even longer overall treatment times, there is an indication at least for patients treated to a prescription dose of 13 Gy and by extrapolation 12 Gy that between 60 and 130 min the influence of overall treatment time is less important, a reflection of the increase in the importance of the slower component of repair in the model. This would not appear to apply to the cases treated to a prescription dose of 14 Gy, where the decline in BED values continued at the same rate as in the 20 to 80 min treatment period interval. The single patient treated with a prescription dose of 14 Gy in ~130 min involved 13 iso-centers, and hence 12 gaps, when repair will occur even when no additional damage was being induced. This resulted in an effective dose being similar to 13 Gy given with only 8 iso-centers in approximately the same time period.

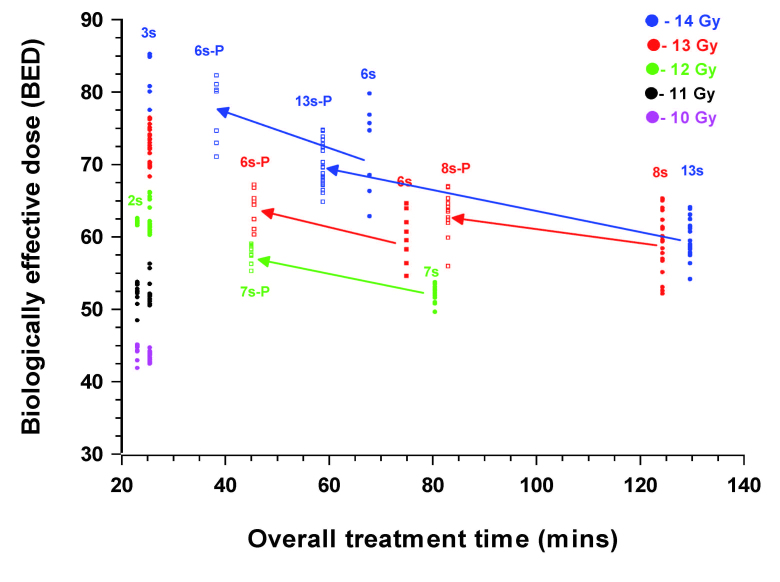
With a newer Gamma Knife system, Perfexion®, the manual changing and repositioning of collimators has been replaced by an automated system, thereby reducing the nominal 6 min interval between iso-centers to approximately 6 sec (0.1 min). For any of the treatment schedules used on cases treated in the present series this would have had a marked effect on the overall treatment time resulting in all cases in an increase in the biological effective dose. The implications of these changes in treatment times for a selected group of 5 cases are shown in Figure 6. In cases, initially treated in 60 80 min, the increase in the BED value was the most marked. For the case where the overall treatment time was only reduced from ~ 125 to 80 min only a small change was noted. All BED values, relative to the original physical prescription dose of the cases, were still in the range 85 down to 50 Gy. The BED values also still vary with the original prescription dose. Patients treated with many iso-centers over longer periods received lower biologically effective doses. Moreover, in individual cases, where the plan is tailored to conform to the target volume the variation in the BED values remains. The associated variations in the equivalent dose were in the order of ~1 Gy. These observations suggest that the BED will be a useful additional and effective tool with which to evaluate Gamma Knife treatment plans.

Figure 6.

Overall treatment time related changes in the BED values for the 2 cases with Vestibular Schwannomas treated with a prescription dose of 14 Gy , 2 treated with 13 Gy, the 1 treated with 12 Gy, either as planned using the Series B Gamma-Knife (solid symbols) or as simulated using Perfexion® (open symbols). The BED values for the 10-14 Gy physical iso-doses for two case, treated using the Series B Gamma-Knife with either a prescription dose of 14 Gy (3 iso-centers) or 12 Gy (2 iso-centers) is given for comparison. BED values for all voxels sampled on the prescription iso-dose (± 0.01 Gy) for each patient are plotted.

It was indicated in the introduction to this manuscript that the normal tissue considered to be at risk in these cases was the brain stem. The size and location of the Vestibular Schwannomas treated were such that some compression of this structure occurred. It is thus appropriate to compare the BED values obtained from the present analysis with those obtained from conventional radiotherapy, where ‘tolerance doses’ for CNS tissue are based on larger volume of normal tissue exposures. The spinal cord is frequently taken to have a similar radio-sensitivity to the brain stem and tolerance dose to this tissue are well established. A total dose of 50 Gy, delivered as 25 daily fractions of 2 Gy (acute exposure) over 5 weeks (5 times/week) is universally accepted as the tolerance dose. Based on the same α/β ratio of 2.47 Gy, as used in the present analysis, the associated BED value would be 90.5. This is above the present range for what would, in comparison, be small volumes of tissue irradiated. In some centers, particularly in the United Kingdom, a more conservative approach is adopted in relation to spinal cord tolerance. A total dose of 44 Gy, in daily fractions of 2 Gy, is given before exposure to the spinal cord is shielded. In this case the associated BED value is 79.5. In comparison the currently accepted whole brain tolerance dose of 30 Gy given in 10 daily fractions of 3 Gy, to which Gamma Knife radiosurgery is offered as a boost, is associated with a BED value of 52.5. In the present study, only 3 cases treated using a prescription dose of 14 Gy, received BED values in excess of the equivalent of the conservative dose adopted for the spinal cord (44 Gy in 2 Gy fractions) and then only to a part of the small volume exposed to that dose. While this implies that all patients in this small cohort study were not at any significant risk of developing severe brain stem complications, it also indicates that the range of biological effective dose delivered was considerable, reinforcing the need for biological effective dose planning so that some patients are not significantly undertreated, relative to others, using this treatment modality. The proposed model takes account of the different variables associated with Gamma Knife treatments and would allow more uniform biological effective doses to be delivered to individual patients.

5. CONCLUSION

This study has demonstrated, using a BED model that included a fast and a slow component of repair, that there was considerable variation in the biological effective dose both within individual patients and between patients for a fixed physical prescription dose. For example, if a patient treated with a prescription dose of 14 Gy in 3 iso-centers (over ~25 min) is taken as a reference, then all other patients treated with a prescription dose of 14 Gy would, on the basis of the application of the BED concept with two components of repair, have received a dose equivalent to between 14 and 11 Gy. Thus it is proposed that in treatment planning the effects of changes in overall treatment time should be considered in order that patients are treated with more biologically equivalent doses, as a first step, in improving the outcome of radiosurgical treatment.

ACKNOWLEDGEMENTS

This study was supported, in part, by Elekta Instrument, Stockholm, Sweden. However, the views expressed represent those of the authors. The authors would like to thank to Dr Ian Paddick for valuable discussions and for supplying the information given in Figure 1.

DISCLOSURE

The authors report no conflict of interest concerning the material and methods used in this study or the findings specified in this paper.