Abstract
Volumetric modulated arc therapy (VMAT) is a new technique for efficient delivery of intensity modulated dose distributions. This study investigates a single isocenter VMAT technique to treat multiple brain metastases to 15 - 24 Gy. The Pinnacle3 SmartArc VMAT optimization plugin was used for all VMAT plans. A non-coplanar arc technique using five 100° arcs and one isocenter was compared with a conformal arc technique which used anywhere from 5 to 9 arcs with at least one isocenter per target. Comparison was done using the Conformality Number (CN), Prescription Isodose to Target Volume (PITV), Homogeneity Index (HI), Conformity-Gradient Index (CGI) as well as the 12 Gy isodose volume in the normal brain from which the risk of symptomatic necrosis (S-NEC) was calculated. The VMAT technique resulted in plans with a maximum delivery of 15 minutes, regardless of the number of targets. The VMAT technique provided superior conformity for large targets but for small targets the conformal arc technique resulted in superior conformity. For all targets, the conformal arc technique resulted in superior dose fall off outside of the target. The VMAT technique resulted in an increase in the 12 Gy volume over the conformal arc technique, with an accompanying increase in risk of S-NEC. While the 12 Gy volume was still within an acceptable clinical range, 4 out 20 patients showed a significant increase (15-20%) in absolute risk of S-NEC. Thus the VMAT technique resulted in clinically acceptable plans with vast reductions in treatment time.
Keywords: VMAT, intracranial, multiple metastases, smartArc, single isocenter
1. INTRODUCTION
Stereotactic radiosurgery delivers high doses in single fractions to small targets. Intracranial SRS to treat multiple brain metastases is commonly performed using multiple conformal arcs delivered using cone collimators of varying diameters mounted to a linear accelerator. Using this technique for multiple or large volume targets requires multiple treatment isocenters, often with cone changes during the treatment. For large numbers of targets, this can be a time consuming process. Recent advances in radiotherapy technology and optimization have resulted in the introduction of Volumetric Modulated Arc Therapy (VMAT), which uses continuously rotating gantry motion to deliver conformal dose distributions using a continuously moving Multileaf collimator (MLC). The use of VMAT for SRS is attractive as it potentially allows treatment of multiple targets with a fewer number of arcs and only one isocenter, vastly increasing the treatment efficiency.
VMAT has been investigated for SRS of single, small intracranial targets.[1-3] Kang et. al. [4] devised a novel optimization method to optimize collimator and table angles to minimize the sharing of leaf pairs between multiple targets. Two studies have also investigated one implementation of VMAT, RapidArc, for multiple targets [5, 6]. These studies looked at multiple, both coplanar and non-coplanar arcs for a limited number of patient geometries and target numbers and showed that a single isocenter technique could provide similar conformity of that from multiple isocenter VMAT techniques. Audet et. al.5 showed that multiple non-coplanar arcs resulted in superior plans to single and coplanar arcs for lesions greater than 7 mm in diameter. The current study investigates a different implementation of VMAT, SmartArc, in the Pinnacle3™ Treatment Planning System (v9.100, Philips Radiation Oncology Systems, Fitchburg, WI), for the treatment of 1-6 brain metastases of varying sizes and inter-target distances in twenty patients.
2. METHODS AND MATERIALS
2.1 Patients
Twenty consecutive patients were selected for analysis. These were the same patients used by Soisson et. al. [7]. The target descriptions are shown in Table 1. Median target volume was 0.38 mL and the average volume was 1.06 mL.
Table 1.
Patient and target parameters
| Patient | # Targets | Location | Dose (Gy) | Volume (mL) | Total Volume (mL) |
| 1 | 1 | R. Occipital | 21 | 0.52 | 0.52 |
| 1 | L. Parietal | 18 | 0.32 | 6.64 | |
| 2 | 2 | L. Periventricular | 15 | 5.81 | |
| 3 | R. Frontal | 18 | 0.16 | ||
| 4 | R. Temporal | 18 | 0.35 | ||
| 1 | R. Post. Frontal | 21 | 0.61 | 3.77 | |
| 3 | 2 | L. Medial | 21 | 1.24 | |
| 3 | R. Ant. Frontal | 21 | 1.92 | ||
| 1 | Cerebellar | 21 | 0.45 | 1.86 | |
| 4 | 2 | L. Post. Frontal | 21 | 0.34 | |
| 3 | L. Ant. Frontal | 21 | 1.07 | ||
| 1 | L. Frontal | 18 | 0.82 | 2.77 | |
| 5 | 2 | R. Parietal | 14 | 0.65 | |
| 3 | R. Cerebellar | 18 | 1.30 | ||
| 1 | L. Cerebellar | 20 | 0.93 | 3.22 | |
| 2 | R. Occipital | 20 | 0.60 | ||
| 6 | 3 | R. Frontal | 20 | 1.45 | |
| 4 | L. Frontal | 20 | 0.08 | ||
| 5 | L. Frontal Parietal | 20 | 0.12 | ||
| 6 | R. Temporal | 20 | 0.04 | ||
| 1 | L. Parietal | 15 | 2.48 | 5.78 | |
| 7 | 2 | R. Cerebellar | 18 | 0.04 | |
| 3 | R. Occipital | 15 | 3.26 | ||
| 1 | L. Cerebellar Post. | 15 | 0.07 | 0.58 | |
| 8 | 2 | L. Cerebellar Inf. | 15 | 0.40 | |
| 3 | L. Cerebellar Ant. | 17 | 0.04 | ||
| 4 | R. Frontal | 21 | 0.07 | ||
| 9 | 1 | R. Occipital | 20 | 0.84 | 7.17 |
| 2 | L. Frontal | 20 | 6.33 | ||
| 1 | R. Frontal | 21 | 1.79 | 2.94 | |
| 2 | L. Frontal | 21 | 0.43 | ||
| 10 | 3 | R. Frontal Low | 21 | 0.16 | |
| 4 | R. Frontal Medial | 21 | 0.03 | ||
| 5 | R. Thalamus | 21 | 0.07 | ||
| 6 | L. Temporal | 17 | 0.46 | ||
| 1 | R. Frontal | 21 | 0.15 | 0.33 | |
| 11 | 2 | L. Midbrain | 15 | 0.10 | |
| 3 | R. Temporal | 21 | 0.08 | ||
| 1 | Paracentral | 15 | 10.79 | 11.26 | |
| 12 | 2 | R. Occipital Lat. | 21 | 0.12 | |
| 3 | R. Occipital Med. | 21 | 0.21 | ||
| 4 | L. Parietal | 21 | 0.14 | ||
| 1 | L. Frontal | 18 | 1.92 | 2.17 | |
| 13 | 2 | R. Cerebellar | 23 | 0.10 | |
| 3 | R. Parasellar | 23 | 0.15 | ||
| 1 | L. Parietal | 21 | 0.06 | 0.22 | |
| 14 | 2 | L. Post. Frontal | 21 | 0.04 | |
| 3 | R. Low Frontal | 18 | 0.10 | ||
| 4 | L. Ant. Frontal | 21 | 0.02 | ||
| 1 | R. Occipital | 21 | 0.14 | 0.24 | |
| 15 | 2 | L. Occipital | 24 | 0.05 | |
| 3 | L. Parietal | 24 | 0.05 | ||
| 16 | 1 | R. Frontal | 18 | 2.61 | 3.02 |
| 2 | L. Temporal | 21 | 0.41 | ||
| 17 | 1 | R. Temporal | 21 | 1.62 | 3.54 |
| 2 | L. Frontal | 21 | 1.92 | ||
| 18 | 1 | L. Cerebellar | 15 | 5.13 | 5.13 |
| 19 | 1 | L. Frontal | 24 | 1.03 | 1.23 |
| 2 | R. Temporal | 24 | 0.20 | ||
| 20 | 1 | Medial | 21 | 1.19 | 1.19 |
2.2 VMAT Treatment Planning
The same VMAT planning technique was used for all twenty patients. All treatment planning was performed in the Pinnacle3™ radiotherapy treatment planning system (v9.100, Philips Radiation Oncology Systems, Fitchburg, WI). The treatment machine was a Varian 21EX with the HD MLC, for which the center 40 leaves have a leaf width, when projected to isocenter, of 0.25 cm. Treatment isocenter was a point at the geometric center of the brain region of interest (ROI). Five non-coplanar 100° arcs were created at couch angles 90°,125°,160°,235° and 200°. Arcs at couch angles 235° and 200° rotated from 150° to 50°, with the remainder rotating from 310° to 210° (IEC Convention). The collimator angle was varied between 180°, 135° and 90° for a subset of plans covering a range of target numbers and orientations, with an optimal value of 180° obtained which was subsequently used for all presented VMAT plans. The dose rate was allowed to vary continuously up to 600 MU/minute.
All arcs were optimized simultaneously using the SmartArc optimization plugin in Pinnacle3™. Optimization used a minimum dose objective on each target equal to the prescription dose, a maximum dose objective on each target equal to the 125% of the prescription dose, corresponding to a prescription to the 80% isodose line, and a maximum dose and maximum dose-volume objective on the normal brain structure. The normal brain structure was the targets plus 3 mm subtracted from the total brain. The 3mm margin between the lesions and the normal brain was chosen to allow for a significantly steep dose fall of between the edge of a target and the normal brain volume. The dose grid during optimization was 2 x 2 x 2 mm3. Optimization consisted of 40 iterations followed by a warm-start with another 40 iterations and finally a third warm-start segment weight optimization for 10-15 iterations. Each arc’s delivery time was limited to 180 seconds so that the total beam-on time would not exceed 15 minutes. A final dose calculation was then performed at a dose grid resolution of 1 x 1 x 1.25 mm3. Plans were then normalized such that 98% of all targets received their respective prescription doses.
2.3 Linear Accelerator Cone-Based Treatment Planning
All twenty patients were treated using a linear accelerator cone-based treatment technique, referred to from here on as ‘conformal arc’ plans. These treatment plans were selected for comparison with the VMAT planning technique. The plans were performed in the Pinnacle RTPS (v8.2) and delivered with a Varian 600 C/D using circular collimators ranging from 4 – 30 mm in diameter, in 2 mm increments. Each target was treated with at least 5 arcs, generally to a single isocenter at the center of the target. For 7/60 targets, multiple isocenters were used due to irregular target shape. Plans were created with the aim of complete target coverage while keeping the prescription isodose to target volume (PITV) to less than 2.0. The dose was calculated with a dose grid resolution of 1 x 1 x 1.25 mm3.
2.4 Plan Quality
The plan quality for each patient for both the VMAT and conformal arc plans was assessed using the PITV, Conformality Number (CN), Homogeneity Index (HI) and the estimated risk of symptomatic radiation necrosis (S-NEC). The PITV[8] was calculated as a measure of how well the prescription isodose line conformed to the target and was calculated by:
(1.1).
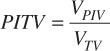
whereVPIV is the prescription isodose volume and VTV is the target volume. As the PITV approaches 1, the prescription isodose line conformity to the target improves. The CN[9, 10] was calculated as a second measure of the conformity of the prescription dose to the target that also includes the location of the prescription isodose volume relative to the target volume and was calculated by:
(1.2).
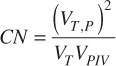
Where VT,P is the volume of the target covered by the prescription dose, VT is the target volume and VPIV is the prescription isodose volume. The HI was calculated to compare the dose gradient within the targets and was calculated by:
(1.3).
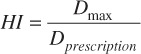
Where Dmax is the maximum target dose and Dprescription is the target prescription dose.[11] A further set of scores known as the conformity-gradient index (CGI) was also calculated for each target[12]. This score consists of two components – CGIG and CGIC representing gradient and conformity respectively. CGIG is a measure of the gradient outside of the target, more specifically the distance required to decrease from the prescription dose to 50% of the prescription dose. The score is calculated by assuming that the prescription isodose line and the 50% isodose line are spherical in shape with radii R100% and R50%. A distance of 3 mm has been derived from linac based SRS as the ideal difference between R100% and R50%. A CGIG score of 100 equates to a distance of 3 mm between R100% and R50%, a score less than 100 equates to a distance greater than 3 mm and a score greater than 100 equates to a distance less than 3 mm.
(1.4).
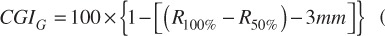
(1.5).
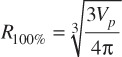
(1.6).
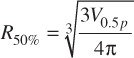
Where Vp is the prescription isodose volume, V0.5p is the volume contained by 50% of the prescription dose. The CGIC is calculated as the inverse of the PITV. A final combined plan quality score, CGI, is then calculated as follows:
(1.7).
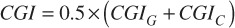
The metrics described above were calculated on a per-target basis for each patient. The metrics were also calculated for the targets split into groups based on their volume: small (< 0.1 mL), medium (0.1 to 1 mL) and large (> 1 mL). For four of the VMAT patients and one conformal arc patient, the isodose line covering 50% of the prescription dose was confluent for multiple targets. For these targets, the radius of the 50% isodose line for the sides of the target away from the neighboring targets, that is, away from the confluent isodose lines, was estimated. The radius was estimated by overlaying a spherical point of interest and identifying the radius at which the sphere approximated the dimensions of the isodose line.
With the aim of calculating the risk of brain necrosis, in addition to the above metrics, the volume of the brain receiving at least 12 Gy was calculated. Korytko et. al. derived a relationship between the volume of the brain receiving 12 Gy and S-NEC [13].The absolute S-NEC was calculated as follows:
(1.8).

Where V12 is the 12 Gy isodose volume of the brain and α = 1.74476 and β = 0.0696394[7].
3. RESULTS
The estimated delivery time was nearly 15 minutes for all treatment plans, regardless of the number of targets. This is significantly less than the typical conformal arc treatment time of approximately 15 minutes per isocenter treated. The calculated PITV, CN and HI metrics are presented in Figure 1. For small targets, the PITV for the conformal arc plans are on average superior to VMAT plans (p = 0.02, t = 2.69). For medium targets, there is no statistical difference between the two techniques and for large targets (> 1 mL); the VMAT technique was superior to the conformal arc technique (p = 0.0002, t = 4.738). Similar results were obtained for the CN: the conformal arc technique was superior for small targets (p = 0.012, t = 2.924), no difference was observed for the medium targets and the VMAT technique was superior to the conformal arc technique for large targets (p = 0.0002, t = 4.757)
Figure 1.
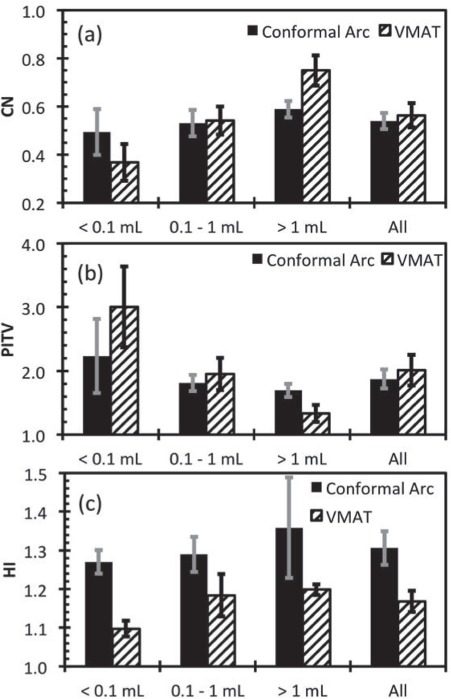
Calculated PITV, CN and HI for all targets split into different groups based on target volume. The error bars represent ± 1 standard error of the mean.
The HI was largest for the conformal arc technique. This reflects the different optimization techniques used in planning, where the conformal arc plans were optimized to increase the peak dose within the target to increase the dose gradient outside of the target, whereas the VMAT technique was simply optimized to achieve minimum dose coverage of the target and reduction of dose outside of the target. That is to say, the conformal arc technique resulted in peaked dose distributions within the target whereas the VMAT plans result in more homogenous target doses.
The CGI metrics are shown in Figure 2. For all target sizes, the average CGIG score for the conformal arc technique was superior to the VMAT technique, with p = 0.001 and t> 4.7 for all target sizes. This suggests that the conformal arc technique is able to achieve a sharper dose gradient outside of the target. The VMAT technique resulted in no statistically significant difference in CGIC for small and medium targets compared with the conformal arc technique (p = 0.113 and t = 1.697 and p = 0.636 and t = 0.478 for small and medium targets respectively). For large targets, the VMAT technique resulted in higher CGIC scores on average (p<0.001, t = 4.983).
Figure 2.
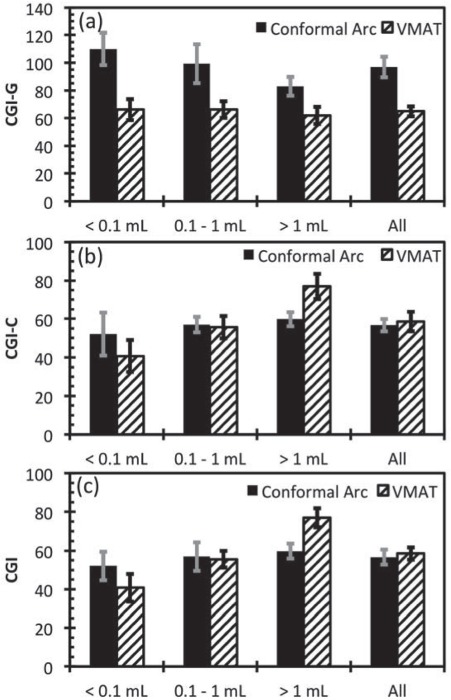
CGIG, CGIC and CGI for targets grouped into sizes and for all targets. The error bars represent ± 1 standard error of the mean.
Figure 3(a) and 3(b) show 12 Gy volume for the two techniques and the calculated absolute risk of S-NEC for conformal arc and VMAT respectively for all patients. It can be seen that the VMAT technique yields for most patients a modest increase in the 12 Gy volume, and hence risk of S-NEC with the exception of patients 10 and 12 for which a substantial increase in the 12 Gy volume and the risk of S-NEC was observed and for patient 18 for which a modest decease in the 12 Gy volume and the risk of S-NEC was observed. However, as observed by Korytko and colleagues[13], the predicted risks for S-NEC for patient 10 and 12 are still within the clinical range for Gamma Knife SRS for patients with metastatic lesions having a 12 Gy volume larger than 15 mL (cf. Figure 4 in Ref. [13]). The change in absolute risk of S-NEC ranged from 2% – 31.31% for the entire patient cohort considered.
Figure 3.
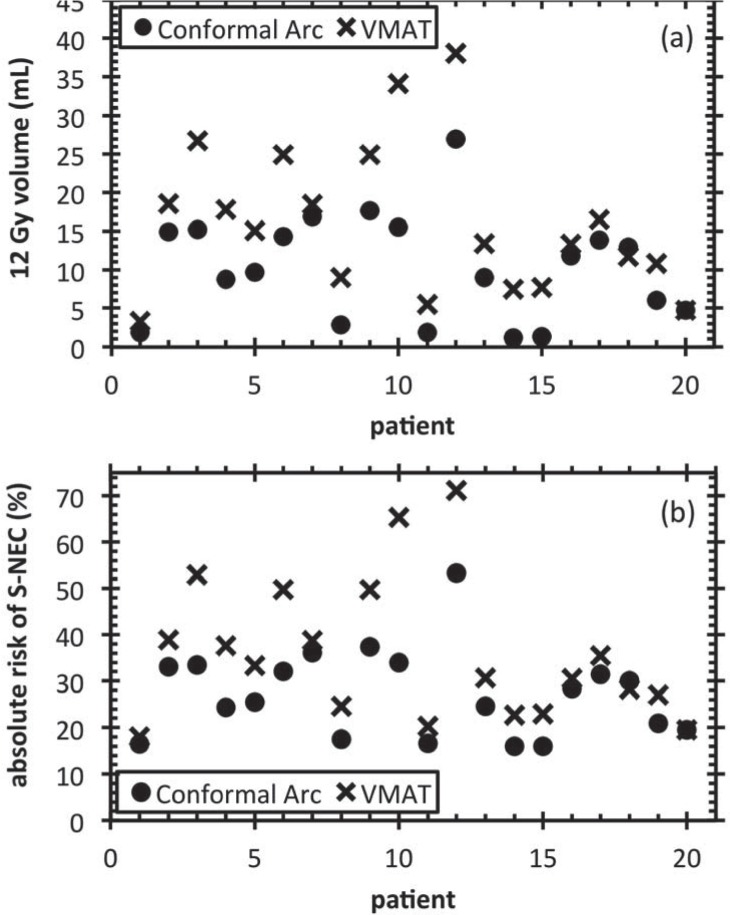
(a) 12 Gyisodose volume for all targets and (b) Calculated S-NEC for all patients
Figure 4.

12 Gy volume plotted against the number of targets for all patients for (a) conformal arc and (b) VMAT techniques. The difference in the 12 Gy volume and absolute risk of S-NEC between the two techniques is plotted in (c) and (d) respectively. Difference in the absolute risk of S-NEC between VMAT and conformal arc technique. A positive difference means that the VMAT absolute risk of S-NEC is higher.
Figure 4(a) and 4(b) show the 12 Gy volume as a function of the number of targets for the conformal arc and VMAT plans respectively. Figure 4(c) and 4(d) show the change in 12 Gy volume and absolute risk of S-NEC respectively as a function of the number of targets. The Spearman rank correlation test was performed to determine whether there was any correlation between the 12 Gy volume or absolute risk of S-NEC with the number of targets. It can be seen that there is no statistical correlation between the 12 Gy volumes and the number of targets for the conformal arc technique but there was a statistically significant moderate correlation for the VMAT technique. This translates to a statistically significant strong correlation between the increase in the 12 Gy volumes and increase in absolute risk of S-NEC and the number of targets with the VMAT technique.
4. DISCUSSION
This comparison of VMAT with conformal arc techniques for intracranial SRS shows that VMAT provides superior dose conformity for large targets. This finding should however be taken with a grain of salt, since it only applies to the multi-isocenter cone based conformal arc technique employed here. For instance, using a conformal arc technique in which a Micro-leaf MLC is used for beam shaping could result in more conformal plans than are possible with the multi-isocenter conebased conformal arc technique employed here for large, irregularly shaped targets. However, the dose fall off outside of the target is superior with the conformal arc technique for all target sizes, and the dose conformity is superior with the conformal arc technique for small targets. The reduction in dose gradient with VMAT manifests in the increase in the absolute risk of S-NEC due to the larger volumes of normal brain receiving doses greater than 12 Gy. As expected, the magnitude of the increase in the absolute risk of S-NEC for 19/20 patients is related to the number of targets: Figure 4 shows the difference between the absolute risk of S-NEC with VMAT and conformal arc showing an increase in the difference with increasing number of targets.
The Paddick conformity index (equivalent to the CN used in the current study) for the multiple arc, single isocenter technique presented by Clark et. al.[6] for medium and large targets are within the CN ranges presented in the current study. The 12 Gy isodose volumes delivered to the brain also compare well with those presented by Clark et. al.[6]: For patients with three targets, Clarke et. al. presented 12 Gy volumes of 22.3 – 25.8 mL (mean 23.94 mL) which are on average greater than the results in the current study for patients with three targets, of 5.5 – 26.75 mL (mean 14.94 mL) (cf. Figure 4(b)).
The VMAT technique is worth investigating in comparison with helical tomotherapy, another intensity modulated arc delivery technique that also offers improvements in delivery efficiency for multiple metastases. Soisson et. al.[7] compared helical tomotherapy with the same conformal arc plans for the same data set used in the current study. Tomotherapy was shown to result in similar plan quality to VMAT when compared with the conformal arc technique: Improved conformity for large targets but reduced conformity for small targets and inferior dose fall off outside of the target. Using a one-way ANOVA test with a threshold for statistical significance of 0.05, there is no statistical difference between the increase in absolute risk of S-NEC from VMAT and tomotherapy over conformal arc (p = 0.689).
The patients that had the largest increase in absolute risk of S-NEC typically had three or more targets grouped together within close proximity. This meant that the optimizer would often create apertures that covered all of the targets at once. This is a drawback of the optimization technique in that all arcs attempt to deliver dose to all targets. A more advanced technique might be to specify which targets each arc can deliver dose to, however this option is not available in the current software.
These results must be taken in the context of the vast improvements in delivery efficiency. All plans require approximately 15 minutes or less, regardless of the number of targets. Typically the conformal arc technique for multiple targets (requiring multiple isocenters) can take up to 15 minutes per isocenter.
In conclusion, this study presents a single isocenter, multiple non-coplanar arc VMAT technique for delivery of SRS to multiple brain metastases. The presented technique results in superior conformity for large targets when compared with a cone based conformal arc technique and presents a vast improvement in delivery efficiency yielding clinically acceptable estimates for the risk of symptomatic necrosis following VMAT SRS.
REFERENCES
- 1. Fogliata A., Clivio A., Nicolini G., Vanetti E., Cozzi L., Intensity modulation with photons for benign intracranial tumours: a planning comparison of volumetric single arc, helical arc and fixed gantry techniques. Radiotherapy & Oncology, 2009; 89: p. 254-262. [DOI] [PubMed] [Google Scholar]
- 2. Lagerwaard F.J., Meijer W.M., van der Hoorn E.A.P., Verbakel W.F.A.R., Slotman B.J., Senan S., Volumetric modulated arc radiotherapy for vestibular schwannomas. Int J Radiat Oncol Biol Phys, 2009; 74(2): p. 610-615. [DOI] [PubMed] [Google Scholar]
- 3. Wolff H.A., Wagner D.M., Christiansen H., Hess C.F., Vorwerk H., Single fraction radiosurgery using RapidArc for treatment of intracranial targets. Radiat. Oncol., 2010; 5: p. 77-86. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4. Kang J., Ford E.C., Smith K.S., Wong J., McNutt T.R., A method for optimizing LINAC treatment geometry for volumetric modulated arc therapy of multiple brain metasteses. Medical Physics, 2010; 37(8): p. 4146-4154. [DOI] [PubMed] [Google Scholar]
- 5. Audet C., Poffenbarger B.A., Chang P., Jackson P.S., Laundahl R.E., Ryu S.I., Ray G.R., Evaluation of volumetric modulated arc therapy for cranial radiosurgery using multiple noncoplanar arcs. Medical Physics, 2011; 38(11): p. 5863-5872. [DOI] [PubMed] [Google Scholar]
- 6. Clark G.M., Popple R.A., Young P.E., Fiveash J.B., Feasibitlity of single-isocenter volumetric modulated arc radiosurgery for treatment of multiple brain metastases. Int J Radiat Oncol Biol Phys, 2010; 76(1): p. 296-302. [DOI] [PubMed] [Google Scholar]
- 7. Soisson E.T., Mehta M.P., Tome W.A., A comparison of helical tomotherapy to circular collimator-based linear-accelerator radiosurgery for the treatment of brain metastases. J Am Clin Oncol, 2011; 34(4): p. 388-94. [DOI] [PubMed] [Google Scholar]
- 8. Shaw E., Kline R., Gillin M., Souhami L., Hirschfeld A., Dinapoli R., Martin L., Radiation-Therapy Oncology Group - Radiosurgery Quality Assurance Guidelines. International Journal of Radiation Oncology Biology Physics, 1993. 27(5): p. 1231-1239. [DOI] [PubMed] [Google Scholar]
- 9. Paddick I. A simple scoring ratio to index the conformity of radiosurgical treatment plans. J Neurosurg., 2000; 93 (Suppl 3): p. 219-22. [DOI] [PubMed] [Google Scholar]
- 10. van’t Riet A., Mak A.C.A., Moerland M.A., Elders L.H., vanderZee W., A conformation number to quantify the degree of conformality in brachytherapy and external beam irradiation: Application to the prostate. International Journal of Radiation Oncology Biology Physics, 1997; 37(3): p. 731-736. [DOI] [PubMed] [Google Scholar]
- 11. Wagner T.H., Bova F.J., Friedman W.A., Buatti J.M., Bouchet L.G., Meeks S.L., A simple and reliable index for scoring rival stereotactic radiosurgery plans. International Journal of Radiation Oncology Biology Physics, 2003; 57(4): p. 1141-1149. [DOI] [PubMed] [Google Scholar]
- 12. Schell M.C., Bova F.J., Larson D.A., Leavitt D.D., Lutz W.R., Podgorsak E.B., Wu A., AAPM Report No. 54: Stereotactic Radiosurgery, Report of AAPM task group 42. 1995; College Park, MD: American Association of Physicists in Medicine;. [Google Scholar]
- 13. Korytko T., Radivoyevitch T., Colussi V., Wessels B.W., Pillai K., Maciunas R.J., Einstein D.B., 12 Gy gamma knife radiosurgical volume is a predictor for radiation necrosis in non-AVM intracranial tumors. Int J Radiat Oncol Biol Phys, 2006; 64(2): p. 419-24. [DOI] [PubMed] [Google Scholar]


