Automatic Detection of Seismocardiogram Sensor Misplacement for Robust Pre-Ejection Period Estimation in Unsupervised Settings

Abstract

Seismocardiography (SCG), the measurement of the local chest vibrations due to the movements of blood and the heart, is a non-invasive technique for assessing myocardial contractility via the pre-ejection period (PEP). Recently, SCG-based extraction of PEP has been shown to be an effective means of classifying decompensated from compensated heart failure patients, and thus can be potentially used for monitoring such patients at home. Accurate extraction of PEP from SCG signals hinges on lab-based population data (i.e., regression curves) linking particular time-domain features of the SCG signal to corresponding features from reference standard bulky instruments such as impedance cardiography (ICG). Such regression curves, in the case of SCG, have always been estimated based on the “ideal” positioning of the SCG sensor on the chest. However, in settings such as the home where users may position the SCG measurement hardware on the chest without supervision, it is likely that the sensor will not always be placed exactly on this “ideal” location on the sternum, but rather on other positions on the chest as well. In this study, we show for the first time that the regression curve for estimating PEP from SCG signals differs significantly as the position of the sensor changes. We further devise a method to automatically detect when the sensor is placed in any position other than the desired one in order to avoid inaccurate systolic time interval estimation. Our classification algorithm for this purpose resulted in 0.83 precision and 0.82 recall when classifying whether the sensor is placed in the desired position or not. The classifier was tested with heartbeats taken both at rest, and also during exercise recovery to ensure that waveform changes due to positioning could be accurately discriminated from those due to physiological effects.

I. Introduction

Wearable sensing of the mechanical aspects of cardiovascular health has become an important field of research recently, with one area of emphasis in particular focusing on the estimation of systolic time intervals (e.g., the pre-ejection period [PEP]) outside of clinical settings. PEP is the time elapsed between the electrical depolarization of the ventricular muscle and the ensuing opening of the aortic valve [2], and is a surrogate measure of myocardial contractility Specifically, increased PEP signifies decreased contractility [3], and vice versa, since a weakened myocardium will have lowered maximal rate of left ventricular pressure increase (dP/dt_max) during isovolumetric systole.

One prevalent disorder associated with a weakened myocardium—and thus impaired contractility—is heart failure (HF) [4], where the heart is unable to supply sufficient blood to meet the demands of the tissues and organs. HF afflicts nearly 6 million Americans, and is associated with one in nine deaths each year [5], [6]. With the increasing cost of healthcare and the increase of the elderly population, it is important to realize out-of-clinic disease management [7]. A major challenge in managing HF patients is the lack of technologies available for monitoring a patient’s health status at home. Wearable sensing systems for measuring PEP outside of clinical settings can potentially provide insight regarding an HF patient’s health status, and thus allow titration of care.

Unfortunately, existing technologies for noninvasive PEP measurement are obtrusive, and impractical for large scale use in HF monitoring. For example, the reference standard for noninvasive PEP measurement is echocardiography which requires a large and expensive apparatus to be operated by trained medical staff [8]. Impedance cardiography (ICG), was validated against echo as a reliable way of measuring PEP [9], however, it is also difficult to use in out-of-clinic settings. ICG is obtrusive to measure as it requires a trained medical professional to apply eight electrodes to the subject and operate the measuring device [10], [11]. In [8], the authors developed an unobtrusive way to obtain ICG through textile integration. There is also an increased interest in optical fiber sensors and their integration into smart textiles for non-invasive monitoring of cardiac parameters [12], [13]. However, a more convenient way that would allow users to wear their standard clothing and still be able to obtain continuous PEP measurements is still needed. Moreover, although some studies have shown that serial ICG measurements can predict the risk of acute decompensation [14], the requirement of frequent office visits and sensitivity to electrode positioning make this technology inapplicable on a larger scale [15].

Recent studies have shown that ballistocardiogram signals (BCG), a measurement of the recoil forces of the body in response to the ejection of blood from the heart through the vasculature [16], and seismocardiogram (SCG) signals, representing the local chest vibrations associated with heart and blood movement, can be used to estimate systolic time intervals including PEP [17], [18]. In contrast to the ICG, SCG and BCG measurements do not require any medical professional to administer the test, and in terms of hardware can be rather compact and unobtrusive as BCG can be measured using a modified weighing scale and SCG can be measured using low-noise accelerometers [19]–[22]. Additionally, our group recently demonstrated that the PEP measured using electrocardiogram (ECG) and SCG waveforms taken by a small wearable patch before and after walking can be used to distinguish between compensated and decompensated HF patients, indicating that the measured SCG signal quality is sufficiently high for this clinical population for cardiovascular health assessment purposes [23].

One challenge with using SCG signals for PEP estimation is that the position of the accelerometer on the chest may affect the relationship between the “AO” point detected on the SCG signal and the ground truth aortic valve opening timing detected by a reference standard measurement (e.g., an ICG). The placement of the SCG sensor varies in the literature with some of the earlier works placing it on the xiphoid process [18]. In our work, we consider the mid-sternal position as the reference position. For the mid-sternal SCG measurements, the AO point corresponds to the B point of the ICG closely in time across different subjects and thus can directly be used as the endpoint for PEP time interval estimation (with the ECG Q-wave being the starting point). However, since SCG is a measure of local accelerations of the chest wall, changing the positioning of the sensor can change the shape of the SCG signal [24], and thus the relationship between the AO point detected by the SCG and the actual timing of aortic valve opening. Specifically, the regression curve linking Q-AO to Q-B intervals across subjects would have different slope and y-intercept for each position on the chest for SCG measurements. Thus, if the position of the accelerometer on the chest is not known a-priori, the timing intervals extracted from the SCG signals may not accurately reflect the underlying physiology of the heart.

This positioning problem is not an issue when using BCG since it is a measure of entire body vibrations rather than local chest vibrations. However, the main advantage of using SCG over BCG is the possibility of continuous monitoring, which can allow for monitoring in the context of normal stressors encountered by the person during their everyday activities (e.g., analyzing the changes in the SCG in response to exercise or other stressors as opposed to simply a once-per-day measurement by the scale).

It is essential to study how research efforts cross domains from clinical to non-clinical settings, and vice versa, to verify that both are congruent [25]. Hence, in this paper, we quantitatively study how the positioning of the accelerometer affects the slope and y-intercept of the regression function (linking Q-AO to Q-B across subjects) and devise a method that enables the person using the wearable device to know whether or not the accelerometer is placed in the ideal (mid-sternal) position. The user will accordingly be able to adjust the positioning of the device and avoid computation of inaccurate estimates for the days on which the device is misplaced. This will be an important step in allowing ECG and SCG measurements to be used, for example, by HF patients at home for monitoring changes in underlying condition and adjusting therapies accordingly.

II. Methods

A. Protocol

This study was conducted under a protocol reviewed and approved by the Georgia Institute of Technology Institutional Review Board (IRB). All subjects provided written informed consent before experimentation. Data were collected from ten healthy subjects: five females and five males (demographics: 24.7±2.3 years, 170±11.6 cm, 70±10.5 kg).

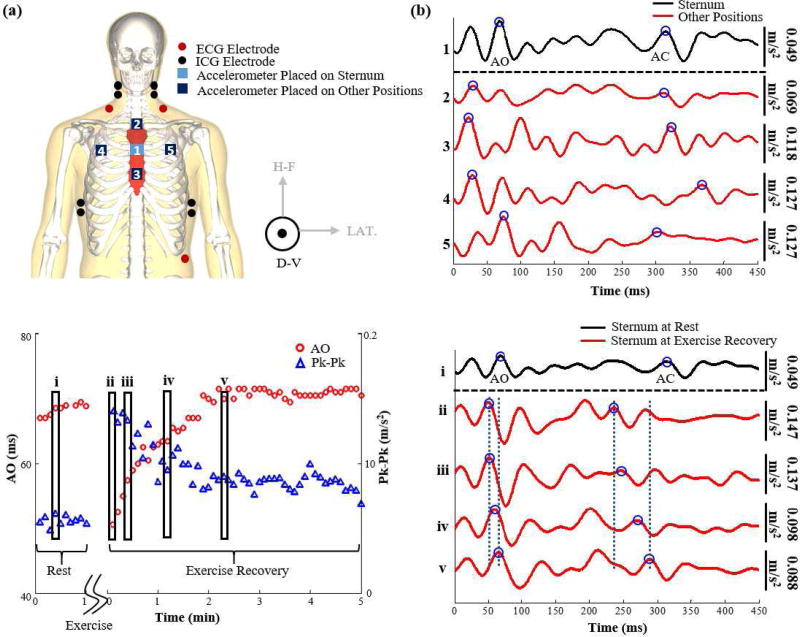
The experiment was performed on two consecutive days. On the first day, each subject was asked to stand still for 60 seconds with accelerometers placed on the mid-sternum, approximately 7.5 cm to the right, and 7.5 cm to the left to obtain baseline measurements. The subject then performed a stepping exercise for one minute after which he was asked to stand still for 5 minutes to monitor the recovery. On the second day, the same protocol was repeated except the accelerometers were placed on the mid-sternum, 5 cm above (upper-sternum), and 5 cm below (lower-sternum). This placement was selected to be slightly less distance than the horizontal “misplacement” to closer simulate expected conditions in practice. On both days, ECG and ICG signals were collected as well. ECG was used as timing reference for beat detection and segmentation, and the B-point of the ICG was used as a reference method for detection of the aortic valve opening [26], [27]. Figure 1(a) shows the sensor placement on both days combined and Figure 1(b) shows the SCG signals obtained from the different placements of accelerometers.

Fig. 1.

(a) Modified from [1]. An illustration of the experimental setup. ECG, ICG and SCG signals were collected. SCG was collected on two separate days; the first day included SCG signals from an accelerometer on the sternum, and accelerometers to the left and right of it and the second day included SCG signals from an accelerometer on the mid-sternum and accelerometers on the upper and lower sternum. Each of these accelerometers measure three dimensional SCG but only the dorsoventral component was used in this analysis. (b) A 450 ms portion of one ensemble averaged beat of an SCG signal collected from the accelerometer placed on the sternum vs SCG signals collected from the other accelerometers at rest. . All these ensemble averages begin at the time of occurrence of the ECG R-peak The mid-sternal signal was doubled in scaling to make the comparison easier. It can be observed that the waveforms are very different in their shapes and result in different estimations of the aortic valve opening (AO) and aortic valve closure (AC) points. (c) The variation in AO and peak-to-peak amplitude of the dorsoventral SCG signal collected from mid-sternum as the physiological state of the subject changes between rest and exercise recovery. It can be noted that right after exercise the AO time decreases while the peak-to-peak amplitude increases only to stabilize back to baseline value as time passes. The five rectangles represent the AO and peak-to-peak values of the five waveforms shown in part (d) for the different physiological states. (d) A 450 ms portion of an ensemble average of dorsoventral SCG beats collected from the sternum during rest and different states during exercise recovery. We can observe that the waveforms look similar for a time shift and an increase in amplitude after exercise.

B. Hardware

The ECG and the ICG signals were measured using the BN-EL50 and BN-NICO wireless measurement modules (BIOPAC Systems, Inc., Goleta, CA), then transmitted wirelessly to the data acquisition system (MP150, BIOPAC Systems, Inc., Goleta, CA) for subsequent digitization at 2 kHz. To detect the small body vibrations in response to cardiac ejection (i.e., SCG signals), we used ultra-low noise and small-footprint 356A32 instrumentation accelerometers (PCB Piezotronics, Inc., Depew, NY). The accelerometers are powered by the Model 482C15 sensor signal conditioner (PCB, Piezotronics, Inc., Depew, NY). Only the signals along the dorsoventral direction from the accelerometers were analyzed in this project.

C. Data Processing

The SCG, ICG and ECG signals were filtered with finite impulse response (FIR) Kaiser window band-pass filters (cutoff frequencies: 0.8–30 Hz for SCG, 0.8–35 Hz for the ICG and 0.8–40 Hz for the ECG). These cutoff frequencies were selected because they are sufficient to preserve the waveform and detect the needed features. The R-peaks in the ECG signal were detected and the minimum R–R interval was calculated for each subject separately. The timings of the R-peaks were used as reference points to segment the rest of the measured signals for each subject into individual heartbeats with a window length equal to the minimum R-R interval. The extracted heartbeats from each of the measured signals were averaged together to obtain ensemble averaged traces with reduced noise [28].

D. Feature Extraction

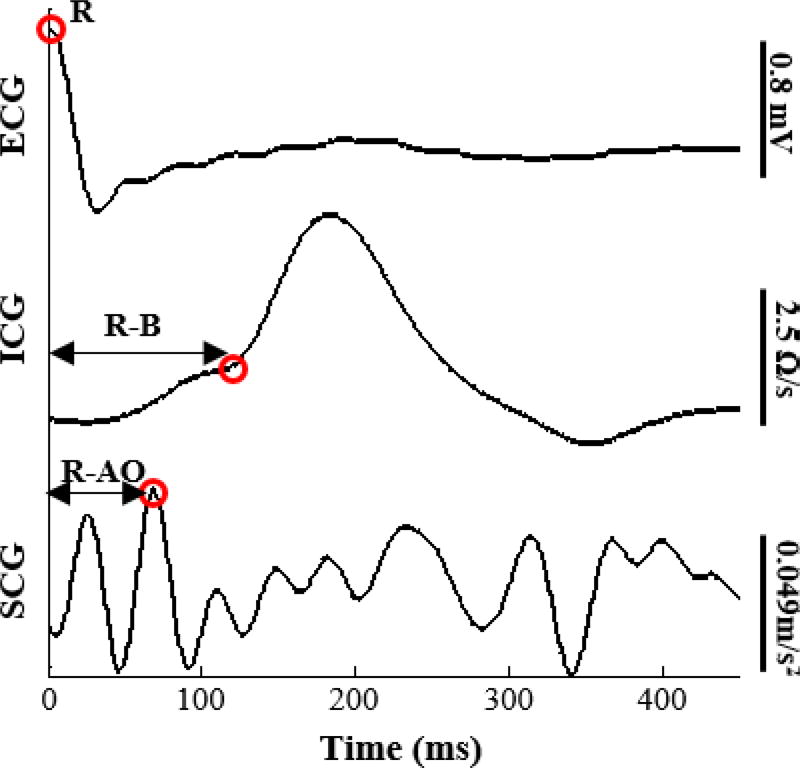
There is a lack of well-defined standards for the fiducial points of cardiomechanical signals, including SCG, due to how the morphology of the signal is affected by age, sex, and heart conditions. In a recent study, a delineation algorithm was designed to detect the fiducial points of the SCG signal, including the AO-point, by training an algorithm on 48,318 manually annotated cardiac cycles and resulted in good accuracy when tested on healthy individuals [29]. Additionally, many of the papers in literature detected the AO-point as the second positive peak of the SCG signal [17], However, we have found with our measurements, with standing rather than supine subjects, that this peak is not necessarily reproducible from person to person, and the noise in the measurements can easily corrupt this peak’s detection as compared to the detection of the largest peak (positive or negative). Hence, to detect AO from the dorsoventral SCG signals, the timing of the minimum or maximum absolute magnitude in the first 200ms is detected [30]. The B-point (inflection point) of the first derivative of ICG was obtained by detecting the maximum peak of the first derivative of ICG [11].

Figure 2 shows ensemble averages of ECG, ICG, and mid-sternal SCG with the relevant features annotated. Figure 1(c) shows how the AO and Peak-to-Peak values vary between the rest and exercise recovery physiological states and Figure 1(d) shows example SCG waveforms from one accelerometer location at different physiological states. The first waveform in Figure 1(d) is an SCG waveform taken when the subject is at rest while the rest of the waveforms are taken at different times during the post exercise recovery. The waveforms are identical in shape and the only change is a time shift to the left (i.e, AO and AC points occur at earlier times in the heart beat cycle) and an increase in the peak-to-peak amplitude of the waveform. By the end of exercise recovery, the SCG signal becomes identical to the original baseline rest SCG signal. Thus, since the shape of the signal for one sensor position does not change radically during the different physiological states while different waveforms from different sensor placements do change significantly even at the same physiological state (as shown in Figure 1(b)), we should be able to distinguish between the desired sensor placement at any physiological state versus other sensor placements.

Fig. 2.

Ensemble averaged beats of ECG, ICG, and mid-sternal SCG signals with the R-peak, B-point, and AO-point annotated.

E. Correlation During Rest and Exercise Recovery

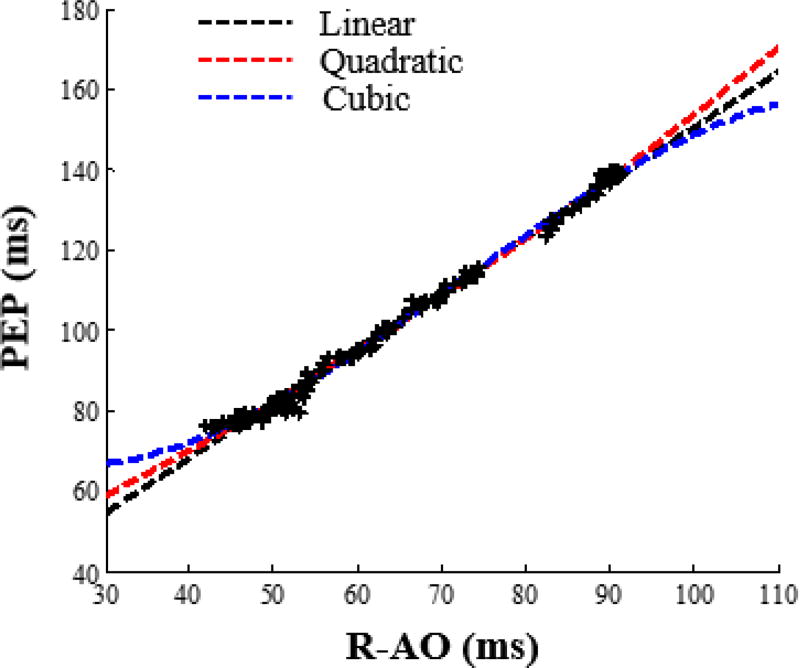
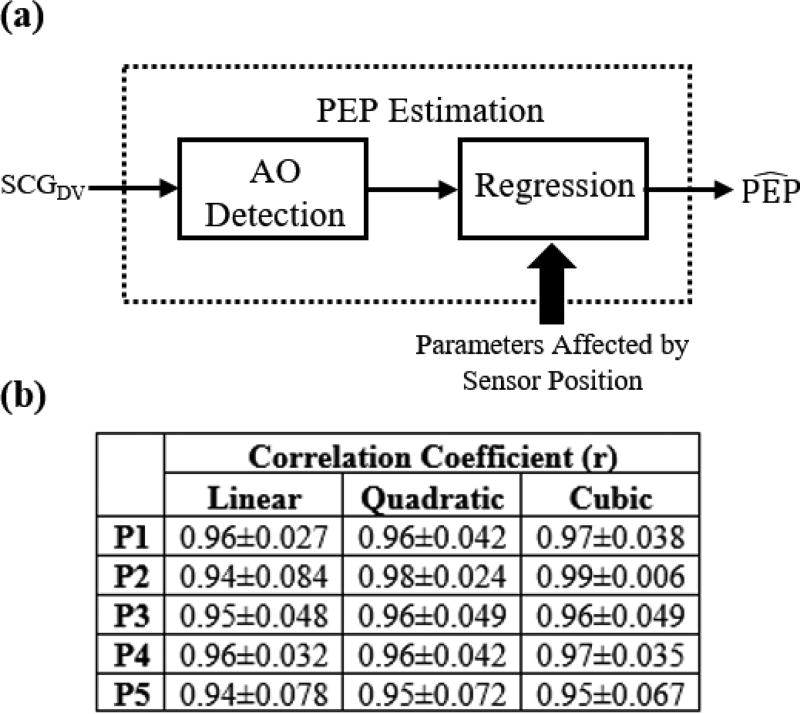
To quantitatively investigate how the change in the AO point of SCG for different accelerometer positions affects PEP estimation, a correlation analysis was performed between R-AO intervals and R-B intervals for the different sensor positions. Every six beats of the signals at rest were averaged together to obtain ensemble averages with 50% overlap and every 10 beats of the signals during exercise recovery were also averaged together to obtain ensemble averages with 50% overlap. Six beats were sufficient for noise reduction when the subject was at rest, and was long enough to capture a typical respiratory cycle, while a higher number of beats was used for ensemble averaging during exercise recovery because of the increased postural sway as compared to rest. PEP (the timing at which the B-point – the opening of the aortic valve – occurs) was calculated. Although PEP is defined as the time elapsed between the Q-point in the ECG and the B-point in the ICG [27], detecting the Q-point in the ECG is not always as robust as detecting the R-point. Hence, in our analysis we used the R-peak in ECG as a reference and estimated PEP as the R-B interval since we are most interested in relative changes in PEP rather than absolute measures, and the QR interval is typically consistent from beat-to-beat. Additionally, the RAO intervals of all SCG ensemble averages were calculated. Linear, quadratic and cubic regression were then performed with the y-value being the R-B interval (PEP) and the x-value being the R-AO interval and the correlation coefficient r, were found for each type of regression. Figure 3 shows these regression curves for one of the subjects when the accelerometer is placed on the mid-sternal position, and Figure 4(a) describes the PEP estimation process.

Fig. 3.

Linear, quadratic and cubic regression curves for one subject with the accelerometer placed on the mid-sternal position.

Fig. 4.

(a) A block diagram showing the process of estimating PEP from the AO points detected from SCG signals using regression. (b) The average correlation coefficient r obtained from linear, quadratic, and cubic regression for the five different positions across all subjects.

F. Classification of Different Positions of Accelerometers

To automatically determine when an accelerometer is placed in the desired position (mid-sternal position) or a different position, we implemented binary classification. This is done by extracting features from the SCG waveforms of all positions, giving different labels to instances obtained from the mid-sternal SCG versus instances obtained from SCG from different positions, dividing the instances we have into training and testing sets, and training a classifier on the training sets in order to predict the class of the instances in the test sets. While, in future work, it may be more desirable to allow measurements from all sites on the chest and to be able to correct for different positions to still obtain high quality RAO estimates, providing an indication of a “usable” versus “unusable” recording was determined to be an important initial step and thus represents the focus of this paper.

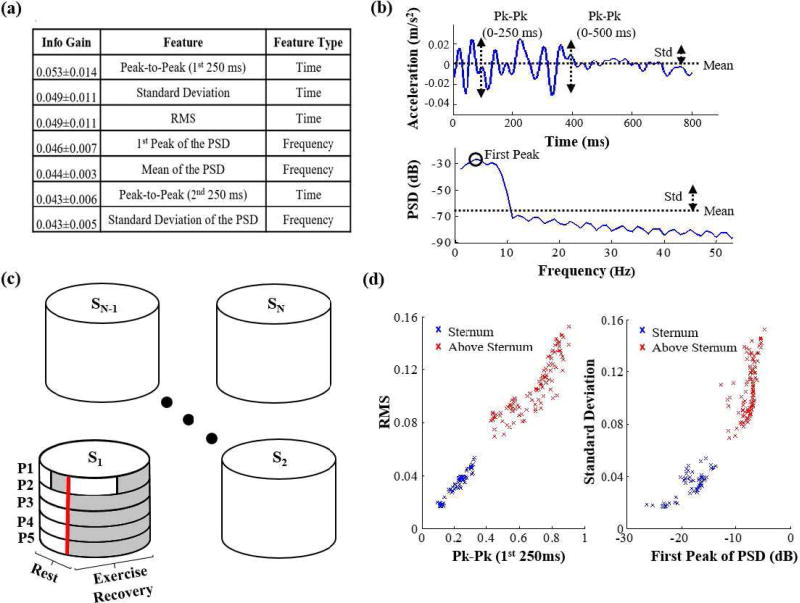
The same ensemble averages of the SCG signals used for the AO point detection were used for extracting features from these signals; specifically, a set of 26 temporal and spectral features were extracted. Those features consisted of: mean, kurtosis, skewness, median, standard deviation, peak-to-peak (0–250 ms and 250–500ms), RMS and peak to RMS ratio (0–250 ms and 250–500 ms) as temporal features and band power in the following bands (0–3Hz, 3–6Hz, 6–9Hz, 9–12Hz, 1215Hz, 15–18Hz), 1st, 2nd and 3rd peak of the PSD, frequency of the 1st, 2nd and 3rd peak of PSD, mean of the PSD, kurtosis of the PSD, skewness of the PSD, and standard deviation of the PSD as frequency domain features. Figure 5(a) shows the top features in terms of the average information gain provided by each feature, with information gain being a measure of the reduction in entropy (a measure of impurity) of the class variable after the value for the feature is observed, i.e.:

$$\mathit{\text{IG}}(T,a)=H(T)-H(T|a)$$ (1)

where H is the entropy function, T are the training instances and α is the attribute (features) in question [31]. The entropy function H(X), which is the expected number of bits needed to encode a randomly drawn value of X, is a measure of impurity of the set of training examples and is given by:

$$H(X)=-\sum _{i=1}^{n}p(x_i){\text{log}}_{2}p(x_i)$$ (2)

Figure 5(b) shows an illustration of some of those features in the time and frequency domain.

Fig. 5.

(a) The top attributes (features) organized in the order of descending average of information gain among the 10 training sets. (b) an illustration of some of the top features in the time and frequency domain. (c) The training and testing sets for training and testing the classifier on subject 1. The shaded areas are features that are excluded from the training set and included in the testing sets when trying to detect the sensor position for subject 1. (d) the best feature in terms of info gain (Peak-to-Peak in the 1^st 250 ms) plotted against the 3^rd feature (RMS) and the 2^nd feature (Standard deviation) plotted against the 4^th feature (1^st peak of the PSD) for one position (upper-sternum) compared to the mid-sternal position in one of the test sets. It is clear that those features result in two distinct clusters for these two positions which indicates that the position of the sensor (accelerometer) can be accurately detected.

The above mentioned features were extracted from SCG ensemble averages for all accelerometers’ positions for each subject. Instances from SCG acquired with an accelerometer in the mid-sternal position were associated with the label −1 while instances from all other positions were associated with the label +1. Multiple training and testing sets were created. For every subject to be tested, the training set included rest and exercise recovery instances from all other subjects, half the rest and exercise recovery instances from the SCG acquired with the accelerometer placed on the mid-sternum for that subject, and only rest instances from SCG acquired by accelerometers from all other positions. Four separate test sets were created with each of them consisting of the other half of the rest and exercise recovery instances of the mid-sternal SCG and the exercise recovery instances from SCG acquired by one of the differently placed accelerometers. This division resulted in a total of 10 training sets (one per subject) and 40 test sets (4 per subject for each of the 10 subjects).

We exclude the exercise recovery instances from all positions different than the mid-sternal position from the training sets for the subject being tested, because we assume that we will not have that information when the device is initially calibrated for a particular subject. More specifically, when the subject wears the device for the first time under the supervision of a medical professional, it will be placed in the ideal position and several other positions for a duration of 60 seconds each. The subject (who may, for example, be a patient with HF at the index visit) will then be asked to perform the six-minute walk test with the device placed in the mid-sternal position (which justifies using some of the exercise recovery data from the mid-sternal position). These initial measurements that are collected only when the patient uses the device for the first time, are used for calibration purposes, and hence, can be included in the training set. An illustration of the division of features into training and testing sets for one subject is shown in Figure 5(c).

A boosted J-48 decision tree classifier with Adaptive Boosting algorithm was trained on each of the training sets and tested on the corresponding test sets for each subject to predict whether the SCG features are acquired from an accelerometer placed in the mid-sternal position or other positions [32], [33].

There are many advantages for using the J-48 Decision tree classifier as compared to other possible classifiers: 1) Decision trees are not sensitive to outliers since pruning is applied [31]; 2) Decision trees are non-parametric thus alleviating concerns about the data being linearly separable; 3) There is no need to tune different parameters as is the case with support vector machines, for example, which enables implementation of the same classifier for every subject; 4) Decision trees implicitly implement a form of feature selection by using the features with higher info gain as the top nodes in the tree [31]. Moreover, adaptive boosting improves the performance of the decision tree by running the classifier for a number of iterations (10 in our case) and improving it by accounting for incorrectly classified instances from the training set at each iteration.

III. Results and Discussion

A. PEP and R-AO Correlation Results for SCG from Different Sensor Positions

For each subject, the correlation coefficient resulting from the linear, quadratic and cubic regression between R-AO and PEP was calculated for every position. Results show high correlation for all positions which indicates that all positions are usable. However, each position, for the same subject, has its own unique regression curve relating to the B-point of the ICG, and we need to have the initial regression parameters for each position and be able to detect exactly where the sensor is placed each day, which is not the case, in order to be able to use all the positions. Thus, if a person wears the device on successive days, and positions the device in different places on different days, even with the same underlying R-wave to aortic valve opening timing, the measurements from the SCG itself may be completely different and one would not know if the person’s underlying cardiovascular function changed, or if the device position changed, in comparing data from one day against the other.

This demonstrates that a position detection algorithm is needed to distinguish whether the wearable device is placed on the mid-sternum or not. Specifically, using the initially calibrated parameters, obtained from the linear, quadratic and cubic regression functions used with the mid-sternal SCG, to estimate PEP when the sensor is placed somewhere else, would result in inaccurate estimations.

A summary of the obtained correlation coefficients, r, averaged across all subjects is shown in Figure 4(b). Additionally, Table I shows the average of absolute PEP estimation errors(ms) resulting from using the initially calibrated parameters obtained from the mid-sternal position when the accelerometer is placed in each of the 5 positions.

TABLE I.

Average Absolute PEP Estimation Errors (ms) For Each Position

	Error in PEP Estimation (ms)
	Linear					Quadratic					Cubic
	PI	P2	P3	P4	P5	PI	P2	P3	P4	P5	PI	P2	P3	P4	P5
Subject 1	2.5	4.8	22.6	24.2	8.7	1.5	5	21.3	27.4	9.6	1.4	5.1	38	24.7	8.1
Subject 2	3.4	4.7	6.5	10.4	12.1	1.7	5.8	5.6	11.9	12.5	1.6	5.9	6.1	11.7	12.8
Subject 3	5.8	16.7	8.7	60.4	252.6	5.5	19	19.2	31.6	807.8	5.2	16.2	18.9	472.6	22358
Subject 4	1.2	5.3	11.8	18.1	6.7	1.1	2.9	5.7	16.2	6.4	0.9	3	5.6	15.2	4.5
Subject 5	5.0	52.9	79.8	46.3	41.18	5	52.5	79	125.8	109.1	4.2	345.8	830.3	78.1	137.4
Subject 6	2.7	10.9	10.7	15.2	12.9	2.6	10.6	10.4	14.4	11.6	2.4	11.3	10.6	14	11.6
Subject 7	2.9	27.9	105.4	28.5	54.8	2.7	30.6	130.5	28.4	54.6	2.5	20	222.8	17.9	33.8
Subject 8	2.0	10.1	35.9	54.9	84.4	1.8	9.7	29.6	33.9	35.7	1.7	6.5	46.2	101.1	260
Subject 9	5.9	167.1	107.1	5.2	10.8	3.4	106.4	115.2	8.3	12.8	1.8	150.1	143.7	7.5	12.6
Subject 10	4.2	6.3	5.8	21.3	6.1	3.3	9.5	11.1	30.4	6	3.3	8.4	10.5	16.8	5.6
Average	3.6	30.7	39.4	28.4	49.0	2.9	25.2	42.8	32.8	106.6	2.5	57.2	133.3	76	2284.4

B. Classification Results

To quantify the performance of the classifier, we used precision and recall as our metrics. Precision (or positive predictive value) is defined as the fraction of retrieved instances that are relevant while recall (or sensitivity) is defined as the fraction of relevant instances that are retrieved [34]. In other words, a recall of 1, would indicate that we are detecting every time the sensor is placed in any position other than the mid-sternal position, and a precision of 1 would indicate that all those detected instances are actually in a position different than the mid-sternal one. Equations (3) and (4) are the mathematical formulas for precision and recall respectively:

$$P=\frac{\mathit{\text{tp}}}{\mathit{\text{tp}}+\mathit{\text{fp}}}$$ (3)

$$R=\frac{\mathit{\text{tp}}}{\mathit{\text{tp}}+\mathit{\text{fn}}}$$ (4)

where tp is the number of true positives (instances correctly classified as belonging to the undesired class), fp is the number of false positives (instances incorrectly classified as belonging to the undesired class), and fn is the number of false negatives (instances incorrectly classified as belonging to the desired class).

With our classifier, we obtained a precision of 0.83 and a recall of 0.82. Considering that the classifier should return a +1 when a misplacement is detected and a −1 when no misplacement is detected, then, if the user is wearing the device every day of the year, i.e. 365 days, and is placing it in a position other than the desired one 100 days, we will be able to detect the incorrect placement and notify the user on 82 of these days. On 17 of the remaining 265 days, the user will be incorrectly notified to check the position of the device. This inconvenience of having the patient double check the position of the device on 17 days is insignificant when compared to the additional 82 days of correct PEP estimations that would have otherwise been inaccurate and could have potentially resulted in incorrect medical decisions. It is worth mentioning that gender based anatomical differences may impact the results for female subjects compared to male subjects. Hence, the training and testing of the classifier was performed again after excluding all instances related to positions 4 and 5 in figure 1(a), since they are the positions that are most likely to cause differences in signals based on gender and are also less likely to occur than positions 2 and 3. The results obtained were a precision of 0.83 and a recall of 0.81, which indicates that the inclusion or exclusion of those positions does not affect the results by much.

From Table I, we can notice that for subject 4, for example, calculations of PEP detection error resulted in an absolute average error of 1.2 ms when the device is correctly placed, 18.1 ms when it is placed to the right of the sternum, 6.7 ms when it is placed to the left of the sternum, 5.3 ms when it is placed in an upper-sternum position, and 11.8 ms when it is placed in a lower-sternum position. Each of these errors can be reduced to an average error of 1.2 ms in PEP estimation every time a wrong placement of the wearable device is detected. One should consider the possibility that day-by-day measurements would be compared against one another, but that the subject would position the device differently from one day to the next. In this case, having a different placement would lead to the R-AO interval meaning something very different on day 2 compared to day 1, etc.

It is also worth noting that the peaks that characterize the SCG waveform shape obtained from the mid-sternal position change at other positions, rendering it difficult to even identify the main peaks of the waveform in certain positions. Therefore, detection of SCG sensor misplacement could also be useful for improving the robustness of SCG measurements in unsuper-vised settings overall, for parameters beyond PEP.

Figure 5(d) shows a clear separation between one test set’s features from an SCG signal obtained from an accelerometer placed on the mid-sternal position compared to an SCG signal obtained from an accelerometer placed above the mid-sternal position in the form of two distinct clusters.

C. Limitations

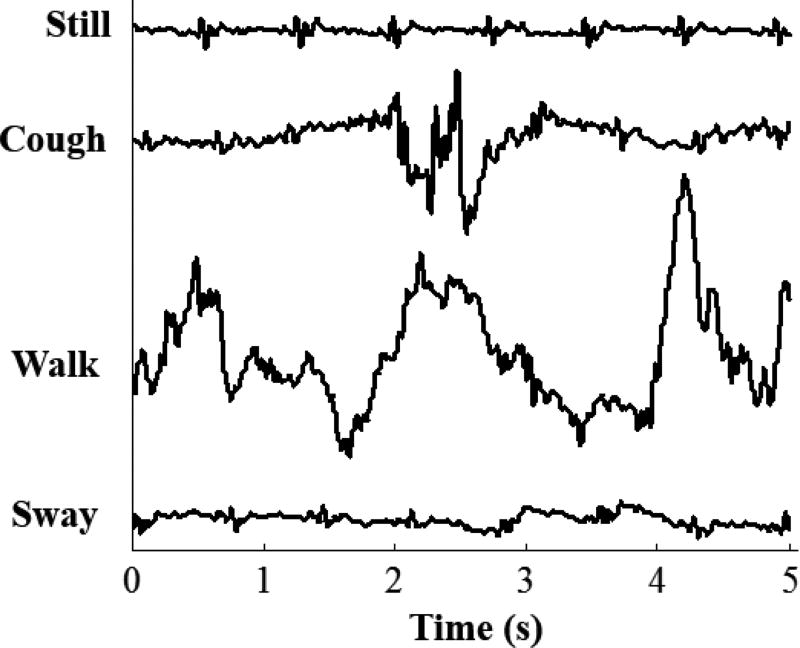
This work was limited by the number of subjects, and the instances from all those subjects were used in the training sets of each subject, except the one on which the algorithm is being tested. Thus, a larger set of subjects would result in a higher number of instances which would most likely improve the precision and recall obtained when classifying the mid-sternal versus other positions of sensor placement. Moreover, this study took into consideration the different physiological states the subject may pass through during the day but it did not consider the pathophysiological difference such as the changes that may occur in a patient’s condition. Hence, since the end goal of using a wearable SCG device is monitoring patients with HF to avoid exacerbations, the classification method presented in this work should be tested on those patients to make sure that it provides an analogous level of performance. Additionally, since assigning the B-point of the ICG is not always trivial, using echocardiography instead of ICG for future studies would provide a better gold standard to compare against. Moreover, this study is based on empirical data and does not include a mechanical model that justifies the differences observed from placing the sensors in different positions. Finally, the data were collected in a controlled setting with the subjects standing in an ideal posture as still as possible, hence, noise resulting from chest movement such as coughing was not quantified. Figure 6 shows a five second data segment of the mid-sternum SCG signal in an ideal posture, and standing still, compared to that when a subject is coughing, walking, and swaying.

Fig. 6.

Sternum SCG signal when the subject is standing still, and the noise resulting from the subject coughing, walking, and swaying.

IV. Conclusions and Future Work

We have shown that when SCG is used for PEP estimation, placing the accelerometer on different positions on the chest area results in different regression parameters. Hence, using the already calculated regression parameters from an SCG measured from the ideal position (mid-sternal position), for a certain subject, would result in inaccurate PEP estimation if the sensor is placed in a slightly different position. Therefore, we devised a method to detect when the sensor is placed in a position different than mid-sternum, in order to be able to provide feedback to the user to re-position the wearable device and avoid inaccurate measurements (or use the information regarding incorrect placement in post-processing to analyze the data accordingly). Future work will address the issue of noise resulting from chest movement either through filtering it out from the signal or gating the signal when noise occurs.

In a practical scenario, when the wearable device is used by a patient with HF, an initial calibration will be conducted first under the supervision of a medical professional, to calculate the regression parameters and obtain the training instances. After that, the patient will be wearing this device every day, which would enable the physicians to continuously monitor the patient’s PEP, and as a result, the contractility of his heart. Additionally, the patient will be warned when the algorithm detects a sub-optimal placement of the device and will be asked to reposition it to guarantee accurate estimation of PEP. Such estimations of PEP at home, in particular in response to activity, can potentially allow early detection of decompensation, and the changing of therapies to avoid hospitalization.