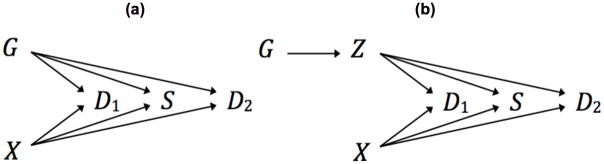The Impact of Selection Bias on Estimation of Subsequent Event Risk

Abstract

Background

Studies of recurrent or subsequent disease events may be susceptible to bias due to selection of subjects who both experience and survive the primary indexing event. Currently, the magnitude of any selection bias, particularly for subsequent time-to-event analysis in genetic association studies, is unknown.

Methods and Results

We used empirically inspired simulation studies to explore the impact of selection bias on the marginal hazard ratio (HR) for risk of subsequent events among those with established coronary heart disease (CHD). The extent of selection bias was determined by the magnitudes of genetic and non-genetic effects on the indexing (first) CHD event. Unless the genetic HR was unrealistically large (> 1.6 per allele) and assuming the sum of all non-genetic HRs was less then 10, bias was usually less than 10% (downward towards the null). Despite the low bias, the probability that a confidence interval included the true effect decreased (undercoverage) with increasing sample size due to increasing precision. Importantly, false positive rates were not affected by selection bias.

Conclusions

In most empirical settings, selection bias is expected to have a limited impact on genetic effect estimates of subsequent event risk. Nevertheless, due to undercoverage increasing with sample size, most confidence intervals will be over precise (not wide enough). When there is no effect modification by history of CHD, the false positive rates of association tests will be close to nominal.

Introduction

Advances in acute treatments and public health policies have shifted the balance of coronary heart disease (CHD) such that an increasing number of individuals are surviving a first clinical CHD event (e.g. myocardial infarction [MI]) and living with established coronary heart disease¹. In the UK and USA, these numbers are estimated to be 3 and 16 million, respectively². These individuals are at very high risk of subsequent or recurrent coronary and cardiovascular events, which can be fatal, disabling, and/or require ongoing costly interventions².

Despite the extent of the problem, little is known about risk factors for subsequent CHD events in comparison to first CHD events. As a result, risk stratification in survivors is limited while secondary prevention advice beyond lipid management has remained largely unaltered over 3 decades³. More importantly novel therapies beyond lipid lowering, anti-platelets and anti-hypertensives have been slow to emerge. The high residual risk in those with CHD suggests the existence of other risk factors such as those predisposing to rupture of atherosclerotic plaques rather than to the development and progression of atherosclerosis⁴. In this regard, identification of genetic variants associating with subsequent CHD events may offer the most promising approach to identifying relevant and novel molecular pathways, which may in turn be amenable to therapeutic modification.

A key reason for our knowledge deficit here is the lack of suitable resources to facilitate prospective study of genetic and non-genetic risk factors among individuals with established CHD. Few cohorts of CHD individuals exist relative to general population cohorts that are more common. In response, the GENIUS-CHD consortium⁵ has been developed, bringing together more than 60 prospective studies of over 250,000 individuals with established CHD including data on genes, biomarkers, and incidence of subsequent fatal and non-fatal events.

Despite such efforts, a methodological barrier to studying subsequent CHD events (e.g., a second MI after a first non-fatal MI) is the problem of selection bias. Here we consider two sources of selection bias: index event bias and survival bias. Index event bias occurs when selecting a subset of subjects based on the occurrence of an index event (e.g., the first clinical event). This selection can induce correlations between previously independent risk factors among those selected^6,7, which can lead to biased associations. To be more specific, those suffering a first event on the basis of exposure to a particularly strong risk factor may have lower levels of exposure to other individually weaker, independent risk factors. This then mitigates the risk of a subsequent event, despite ongoing exposure to the strong risk factor. A frequently cited example of index event bias is the association of patent foramen ovale with the first occurrence of cryptogenic stroke but not with stroke recurrence⁷. Index event bias may also contribute to the apparent protective effect of adiposity on risk of subsequent CHD events, the so-called “obesity paradox”⁸. Moreover, because subjects can only be included in a study after surviving up to the time of inclusion, survival bias may also inflate the bias further still. Thus, in the context of subsequent event studies for CHD, the impact of selection bias may be important because any bias due to selecting individuals on an indexing event (i.e., index event bias) is compounded by selecting surviving subjects (i.e., survival bias).

The influence of these biases on estimates of genetic effects on subsequent CHD events is currently unknown. This is important because, contrary to most observational studies⁹, genetic studies are less prone to confounding bias¹⁰, thus leaving selection bias as the potentially major source of bias¹¹. In this simulation study, we sought to quantify the magnitude of index-event bias and survival bias on the associations of genetic and non-genetic exposures with time to event data as well as binary data in relation to subsequent CHD risk.

Methods

To quantify the impact of index-event bias and survival bias, we simulated data of the type anticipated to be encountered in the GENIUS-CHD consortium⁵. We focus on the marginal (i.e., unconditional) association of a genetic or non-genetic exposure of interest while averaging over all other covariates because 1) the primary analysis in the GENIUS-CHD consortium similarly focuses on marginal associations, and 2) a comprehensive set of other risk factors may not be collected in all cohorts/sites to allow estimation of a uniform conditional association. More specifically, we focus on the estimators of marginal associations from logistic or Cox regression that do not correct for index event bias and survival bias. Please see Jiang et al. 2016¹² and Jiang et al. 2015¹³, for a detailed discussion on marginal and conditional associations.

Specifically, we simulate data with the aim of estimating the effect of a gene variant or a biomarker on subsequent CHD events when the first event can be either fatal or non-fatal. The term “subsequent CHD events” is used in preference to “recurrent” given that fatal events are not recurrent and also to capture the wide range of CHD events that may be of interest to investigators both individually (e.g. subsequent MI, subsequent revascularization, subsequent heart failure admissions) and as composite endpoints. For the purposes of these simulations described below, we use MI as our exemplar indexing event and subsequent CHD event.

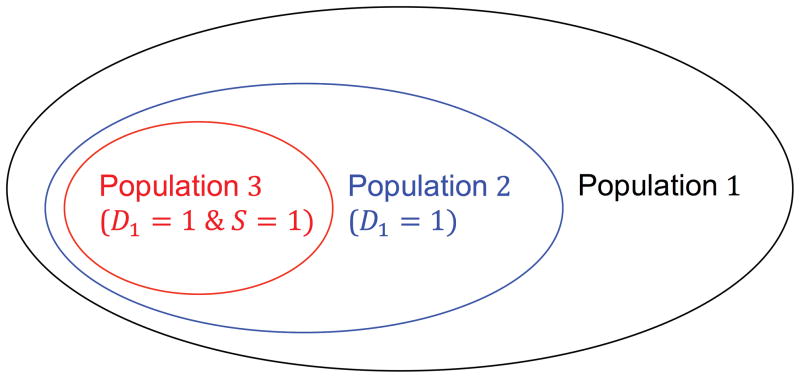
Thus, let D₁ denote the first event and S be the indicator of surviving the first event. Using the notation, we define three populations (Figure 1): population 1 the “general population” that was at risk of a first event, population 2 the subpopulation who had a first event, and population 3 the subpopulation who had a first event and survived. We study the index event bias alone using population 2, as well as the combined effect of index event bias and survival bias using population 3. In the remaining Methods section, we briefly outline the methods and defer technical details to the Supplementary Materials.

Figure 1. Three populations.

D₁ denotes the first/index event. S is the indicator of surviving the first event. Population 1 = general population; population 2 = those with a first event (fatal and non-fatal cases); population 3 = those with a non-fatal first event.

Scenario 1

We first consider the scenario depicted in the directed acyclic graph in Figure 2(a). Here G denotes the genotype (coded as the number of minor alleles) at a single nucleotide polymorphism (SNP) of interest, X denotes the combined effect of all the remaining (known and unknown) genetic and non-genetic exposures (e.g., diet and exercise) that are assumed to be independent of G, and D₂ denotes the subsequent event. Note that we assume D₁ affects survival not directly but through G and X. We initially set the minor allele frequency (MAF) of G, π, to 0.3, which is the median MAF of discovered genetic variants for MI based on empirical GWAS data (CARDIoGRAMplusC4D Consortium¹⁴). We simulated X to be normally distributed with mean zero and standard deviation one. The first event D₁ is binary throughout and is generated from a logistic regression model

Figure 2. Directed acyclic graphs.

(a) Scenario 1: the genetic variant (G) associates with risk of first event (D₁), survival (S), and risk of subsequent event (D₂). (b) Scenario 2: the genetic variant encodes a biomarker (Z) that associates with risk of first event, survival, and risk of subsequent event.

$$log\{P(D_1=1)/P(D_1=0)\}={\alpha }_0+{\alpha }_{G}G+{\alpha }_{X}X,$$ (1)

where α₀ is set to achieve an overall disease rate of c₁. We initially set c₁ to 0.2%, following the approximate incidence of MI in the general population²; in a later sensitivity analysis, we vary c₁ between 0.1% and 1% to capture the variable MI rates in different populations and conditions as well as different type of MI (e.g., ST elevation and non-ST elevation infarcts). We manipulate exp(α_G), the HR of G, from 1 to 1.3, 1.6, 2, and 3. We also manipulate exp(α_X), the HR of X, from 3 and 5 to 10, where an HR of 10 means that the total effects of all the possible protective and harmful genetic and non-genetic exposures (except G) sum up to 10, which is a plausible extreme of these influences. Similarly, the survival indicator S is binary and is generated from a logistic regression model

$$log\{P(S=0)/P(S=1)\}={\gamma }_0+{\gamma }_{G}G+{\gamma }_{X}X,$$ (2)

where γ₀ is set to achieve an overall index event death rate of c_S. In empirical CHD data, c_S can be as high as 30% if all deaths² from the index MI (including those who get treated in hospital and those who die suddenly at home and never get to hospital) are counted; among those who get treated in hospital, c_S can be as low as 10%. Thus, we initially set c_S to 20%, a value between the two extremes. When D₂ represents time to subsequent event, it is generated from a proportional hazards model (assuming the baseline time to event follows an exponential distribution with rate parameter 2)

$$\lambda (T\mid G,X)=2T\text{exp}({\beta }_{G}G+{\beta }_{X}X),$$ (3)

with the censoring rate of (1-c₂). We initially set c₂, the incidence of subsequent CHD events, to 5%, which approximates the observational occurrence of subsequent MI². When D₂ is binary, it is generated from a logistic regression model

$$log\{P(D_2=1)/P(D_2=0)\}={\beta }_0+{\beta }_{G}G+{\beta }_{X}X,$$ (4)

where β₀ is set to achieve the occurrence of the subsequent MI of 5%. In all simulation studies, we set α_G = γ_G = β_G and α_X = γ_X = β_X, that is, G has equal conditional effects on both initial fatal and non-fatal events as well as subsequent CHD events and X also has equal conditional effects on the three outcomes. We use a sample size of 25000, which represents the median sample size of more than 80 GWAS (see Supplemental Materials). In all simulations, we estimate the marginal effect of G on D₂, which is the hazard ratio (HR) or odds ratio (OR) of G in the standard Cox model or logistic regression model with G as the sole risk factor; we refer to it as the naïve estimate.

Scenario 2

We also consider a mediation setting (Figure 2(b)) in which G influences D₁, S, and D₂ through a known biomarker (and through no other path), denoted as Z. We assume that 5% or 10% variance of Z is explained by G. To reflect the direct effect of Z, we replace α_GG, γ_GG, and β_GG in equations (1), (2), (3) and (4) by α_ZZ, γ_ZZ, and β_ZZ, respectively. Here, we focus on the estimates for the marginal G and D₂ association and the marginal Z and D₂ association using the standard Cox model or logistic regression model with G or Z as the sole risk factor; we again refer to them as the naïve estimates.

Calculation of the true marginal association

To calibrate bias of the naïve estimates for the marginal association (i.e., HR or OR) of G on D₂ in scenario 1 and for the marginal associations of G on D₂and Z on D₂ in scenario 2, we calculate the corresponding true marginal associations. This is achieved by the counterfactual method, in which we simulate the outcome in both the presence and the absence of the exposure G conditional on the distribution of X observed in the population of interest (i.e., population 2 or 3; see Supplementary Materials) and then we estimate the marginal associations in the same manner as described above.

Evaluation metrics

The scenarios are evaluated using the following metrics. We assess the percentage bias for the naïve estimates of marginal association against the true marginal association. We also assess the coverage of the 95% confidence interval (CI), which has an expected value of 0.95 for a well-behaved CI. In addition, we evaluate the type 1 error (i.e., the proportion of falsely rejecting the null hypothesis of no association when there is no association) and power (i.e., the proportion of rejecting the null hypothesis when there is an association) at the nominal significance level of 0.05. All results are based on 5000 replications of the scenarios.

Results

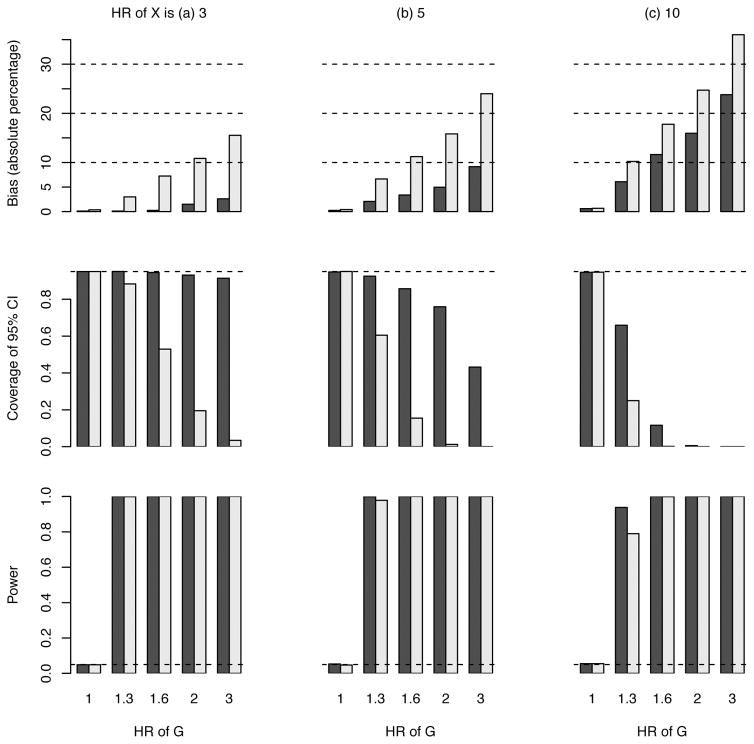
Figure 3 presents the results exploring selection bias in the time to event analysis of the G effect on subsequent CHD events (scenario 1). When the genetic exposure has no effect (i.e., the HR of G is 1), there is also no selection bias in either populations 2 (who had a first event) or 3 (who had a first event and survived) and the type 1 error is correctly controlled at 0.05. When the genetic exposure has an effect, the bias in population 2 (index event bias alone) is generally less than 10% unless the HRs of both G and X become large (e.g., 2 and 10, respectively). The bias in population 3 (cumulative effect of index event bias plus survival bias) is, as expected, larger than the bias in population 2, but still less than 10% unless the HR of G is greater than 1.3; all biases described here and below are downward towards the null. Figure S1 illustrates, for one set of effect sizes of G and X that are used to simulate the outcomes, the true and naïve estimates of the marginal effect size of G with populations 2 and 3. However, the CI may have poor coverage due to the large sample size and hence small variance associated with the (biased) estimate of the HR of G. Additional details are presented in Supplementary Table S1.

Figure 3. Results of the estimated hazard ratio (HR) for a genetic variant that associates with risk of first event, survival, and risk of a subsequent CHD event (scenario 1).

Power under the HR of 1 for G means type 1 error. The black bars pertain to population 2 (selection of subjects with fatal or non-fatal first events) and the grey bars to population 3 (selection of subjects with non-fatal first events). The dashed line in the middle panel indicates the expected coverage of 0.95. The dashed line in the lower panel indicates the nominal significance level of 0.05. Sample size is set at 25000.

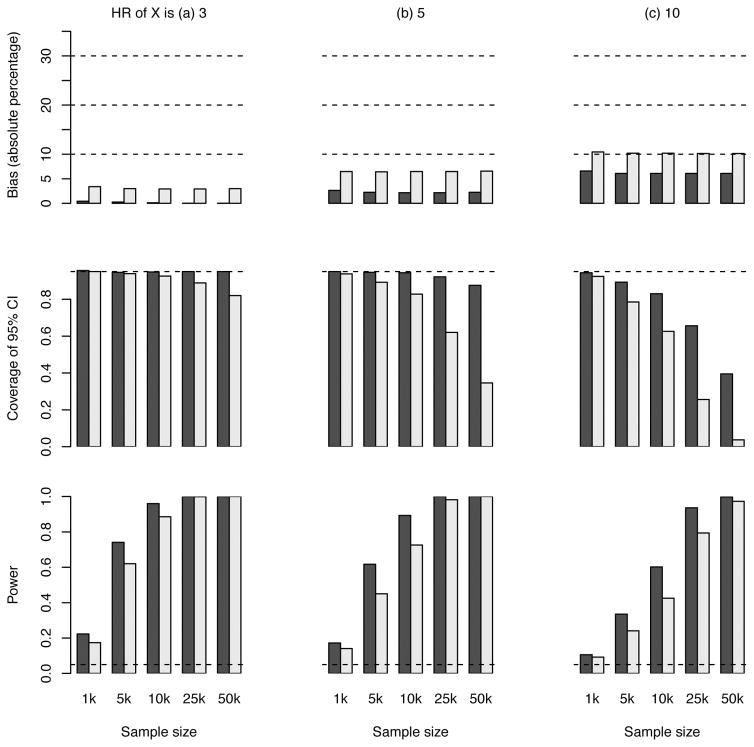
In sensitivity analyses, we evaluated the bias as the overall disease rate in the general population c₁, rate of non-censored subsequent CHD events c₂, index event death rate c_S, and SNP MAF π varied. We observe from Figure S2 that the bias is generally insensitive to any of these parameters. To explore power and bias in other sample sizes, the simulation scenario 1 was repeated using a sample size of 1000, 5000, 10000, and 50000. The results in Figure 4 show that, as the sample size increases, the bias stays similar. Meanwhile, power increases and coverage tends to fall below the nominal level, both owing to the shrunken variance for the (biased) estimate of HRs.

Figure 4. Results of the estimated hazard ratio (HR) for a genetic variant (scenario 1) with different sample sizes.

The HR of G is set to 1.3. The black bars pertain to population 2 (selection of subjects with fatal or non-fatal first events) and the grey bars to population 3 (selection of subjects with non-fatal first events). The dashed line in the middle panel indicates the expected coverage of 0.95. The dashed line in the lower panel indicates the nominal significance level of 0.05.

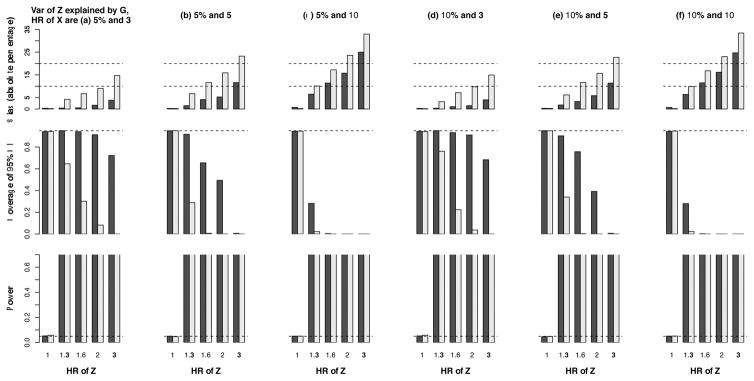
In Figures 5 and 6, we show the results of HR for a genetic exposure G and a phenotypic exposure Z, respectively, in scenario 2. The bias, due to index event bias alone or the cumulative effect of index event bias plus survival bias, is generally less than 10% when the HR of G is ≤1.3. The test of Z is more powerful than that of G. However, the bias in the latter test is smaller. More detailed results are provided in Supplementary Tables S2–S3, which also reveal agreement between the empirical standard error and the mean of standard error estimates.

Figure 5. Results of the estimated hazard ratio (HR) for a genetic variant that encodes a biomarker that associates with risk of first event, survival, and risk of a subsequent CHD event (scenario 2).

Power under the HR of 1 for Z means type 1 error. The black bars pertain to populations 2 (selection of subjects with fatal or non-fatal first events) and the grey bars to population 3 (selection of subjects with non-fatal first events). The dashed line in the middle panel indicates the expected coverage of 0.95. The dashed line in the lower panel indicates the nominal significance level of 0.05.

Figure 6.

Results of the estimated hazard ratio (HR) for a non-genetic biomarker that associates with risk of first event, survival, and risk of a subsequent CHD event (scenario 2) Power under the HR of 1 for Z means type 1 error. The black bars pertain to populations 2 (selection of subjects with fatal or non-fatal first events) and the grey bars to population 3 (selection of subjects with non-fatal first events). The dashed line in the middle panel indicates the expected coverage of 0.95. The dashed lines in the lower panel indicate 1.00 and 0.05 (the nominal significance level).

The results for OR estimates are presented in Supplementary Tables S4–S6 showing similar patterns as for the HR estimates. For the OR, we further compared power of rejecting the null-hypotheses between populations 1, 2, and 3. Under our simulation scheme that G and X have equal effects on both initial and subsequent CHD events, the power is higher in population 1 than in population 2 (e.g., 100% versus 89.3% when the ORs of G and X are 1.3 and 10, respectively, in scenario 1). This difference in power is not only attributable to the difference of the true marginal OR but also the selection bias. The power is higher in population 2 than in population 3 (e.g., 89.3% versus 76.7% when the ORs of G and X are 1.3 and 10, respectively, in scenario 1) due to the loss of high-risk subjects. The impact of selection bias on the observed MAF is increasing the MAF from 0.300 to 0.330 and 0.328 for populations 1, 2, and 3, respectively, in a realistically extreme case (the ORs for G and X are 1.3 and 10, respectively, in scenario 1).

To explore whether our findings apply to other designs, we repeated scenario 1 with a 1:1 case-control design. We showed in Table S7 and Figure S3 that case-control studies are similarly affected by selection bias as cohort studies. For example, in an extreme case (the ORs for G and X are 3 and 10, respectively), bias was 9.59% in cohort studies versus 9.64% in case-control studies.

Discussion

The current simulation study, designed to mimic the scenarios encountered in studies of subsequent CHD events such as those proposed by the GENIUS-CHD consortium, demonstrated that selection biases (i.e., index event bias or/and survival bias) have little impact on gene-disease association estimates when the genetic risk factors have the modest effects observed in most studies. Typically, bias was greater when genetic risk factors had very large effects (i.e., HR of G ≥ 2). We confirmed that the type 1 error rate was unaffected, given that selection bias cannot occur when a gene has no effect on disease and assuming an absence of effect modification by history of disease. However, coverage probabilities of confidence intervals could be considerably less than the nominal level, and they decreased to 0 with increasing sample sizes and selection bias pressure (i.e., larger HRs of G and X on the occurrence of an indexing event). Given the agreement between the empirical standard error and the mean of standard error estimates, the observed undercoverage seems to be predominantly caused by bias in the point estimate.

Previously, methodological reports addressing the problem of selection bias in association studies have done so in the context of non-genetic or phenotypic exposures^6,15–17. In this setting, Greenland suggested that in most instances the magnitude of selection bias compared to confounding bias is modest. This was partially reiterated by Smits et al.¹⁷, only finding an appreciable selection bias in scenarios where the effect on the first event was very large. However, with an increasing focus on the genetic context of subsequent CHD⁵, a more specific question has arisen about the impact of selection bias in studying those who have been selected on and have survived a potentially fatal index event. While some studies have examined the impact of selection bias on effect estimates in case-control studies^18,19, to our knowledge this question has not been addressed for time to event analysis of longitudinal cohort studies exploring associations with recurrent or subsequent CHD events.

Few studies have directly compared genetic risk of first versus subsequent CHD events to explore the comparability of these simulation studies to real examples. Our group, however, has previously compared the effects of the 9p21 risk variant on first incidence of CHD to subsequent CHD events, finding a more attenuated association for the latter: HR 1.19 per risk allele with 95%CI (1.17, 1.22) versus HR 1.01 per risk allele with 95%CI (0.97, 1.06)²⁰. Given that 9p21 has a small effect size (HR or OR ≤ 1.3) in the unselected population, the observed 9p21 results for subsequent CHD events are unlikely to be solely attributable to index event bias or survival bias but possibly to other factors such as risk-modifying therapies.

An important simplification of our simulation study was to focus on genetic and non-genetic exposures that are free of confounding bias. This may seem unrealistic, however, our focus was predominantly on selection bias in genetic exposures. Because the assortment of genetic variants at meiosis and conception occurs at random and is independent of other factors, one may expect the association of genes with an outcome to be affected less by confounding, especially when there is no population stratification. However, in real life settings, selection bias and confounding bias are likely to both affect effect estimates of the association between environmental exposures and subsequent CHD events, making causal inference of such associations challenging.

Another simplification we made is the assumption that D₁ affects survival not directly but through G and X. This assumption does not necessarily agree with all biological mechanisms. However, and importantly so, this simplification does not change the simulation results. Given that D₁ is caused by both X and G (through Z), selection bias is induced by conditioning on a certain level of D₁, which results in a correlation between X and G. Allowing D₁ to be related to S will change the absolute number of survival but will not change the correlation between X and G, because D₁ itself is caused by these variables.

Our simulations involved a prospective cohort design, raising the question of whether they apply to other designs most notably case-control studies. To provide some insight, we repeated scenario 1 with a 1:1 case-control design and we showed that case-control studies are similarly affected by selection bias as cohort studies. While cohort and case-controls studies are equally susceptible to selection bias of the type considered here (i.e., selection bias due to selecting upon subjects surviving a first (CHD) event), it is well known that case-control studies may also be affected by other selection biases in the general population (i.e., those who did not experience a CHD event). For example, in a retrospective case-control study, inclusion in the study may depend on the exposure status (e.g., a drug), which results in selection bias. However, this is a different type of selection bias as discussed here, see for example van Rein et.al.,²¹ for a discussion of this more generic form of selection bias.

In genetic association studies, another common source of bias is “winner’s curse”, in which the disease risk of a newly identified genetic association is overestimated due to low statistical power for identifying the genetic association at a stringent genome-wide significance level. The bias from winner’s curse differs from the index-even/survival bias considered here in several ways. First, the former bias results from selecting estimates whose p-values pass the stringent genome-wide significance level while the latter results from selecting a population stratum. Second, the former is related to statistical power and hence sample size while the latter is not. Lastly, the former is biased upward whereas the latter is downward.

There are some limitations to our study. First, we recognize that part of these assessments could have been performed using analytical derivations instead of simulation studies. For example, Sperrin et al.²² presented an interesting analytical assessment of the obesity paradox, although our focus on time to event analyses, would have made a similar analytic solution as Sperrin et al. difficult. Second, we focused primarily on the marginal effect estimate without adjusting for any covariates as explained earlier, although we accept that in some cases the conditional effect estimate may be of more interest²³. Nonetheless, in the case of conditional effects, we would expect performance to improve if the covariates included are related to the outcome, in which case our simulations can be seen as a worst-case scenario of performance when none of the covariates related to the outcome are included. In particular, if the principal components for ancestry are included to account for population stratification, their correlations with the SNP of interest would diminish the selection bias because only the variability in the SNP that is unexplained by the principal components is subject to the selection bias. Finally, we have focused on the 5% nominal significance level and the 95% CI. Alternatively, a GWAS typically adopts a genome-wide significance level that is much smaller than 5% (e.g., 5×10⁻⁸). We have focused on 5% in our simulation studies because (1) the genome-wide significance level would require a substantial number of replicates and cause the simulation studies to become impractical, (2) since the type 1 error is unaffected by selection bias, the use of any significance level would not change our conclusions, and (3) while the GENIUS-CHD and similar consortiums are interested in “high-throughput” work, considerable effort is invested in performing Mendelian randomization (that is, instrumental variable) analyses which typically uses the 5% nominal significance level.

In conclusion, bias due to selecting subjects with a history of disease is relatively small in genetic association studies for subsequent events, such as those for recurrent or subsequent CHD. Importantly, unless the associations are modified by the presence or absence of the first event, the type 1 error rate remains unaffected. Alternatively, the problem of selection bias may be absent entirely if the causes of the first disease event do not influence disease progression. These findings support the methodological validity of seeking common genetic variants for risk of subsequent events for CHD and potentially other diseases where recurrence and progression is clinically relevant. However, while tests are valid, researchers should be aware that despite the likely low degree of bias, the probability that the confidence intervals include the true effect decreases with increasing sample size, resulting in coverage often (much) lower than the nominal level (e.g., 95%).

Clinical Perspective.

As a community, we have made great advances in reducing mortality from acute coronary heart disease (CHD). Consequently, however, more people are surviving and living with established CHD and remaining at significant risk of future cardiac events and death. Attention is now turning to discover genetic variants and biomarkers that confer risk of CHD progression in the hope that novel findings might uncover novel mechanistic insights into recurrent or progressive heart disease, such as processes promoting plaque vulnerability or rupture. Such insights could potentially lead to development of new drugs, influencing mechanisms beyond lipid and thrombosis pathways. The GENIUS-CHD Consortium has been developed to specifically address the task of identifying risk variants and markers of subsequent events among those with established CHD. However, studying those with established disease brings its own challenges. Selection of individuals who both experience and survive a primary index CHD event leads to bias which may impact all findings. In this paper, using empirically inspired simulation studies, we demonstrate that unless the observed genetic effects are very large, association findings will be minimally impacted by selection bias (attenuated to the null), although with increasing sample size confidence intervals are less likely to include the true effect. As common genetic variants have small effect sizes, we thus expect genetic association studies of disease progression or recurrence to yield relatively unbiased estimates. This study and findings therefore have implications for CHD as well as any other condition where disease progression is important.

Appendix: GENIUS-CHD Consortium

Axel Åkerblom, Ale Algra, Hooman Allayee, Peter Almgren, Jeffrey L. Anderson, Maria G. Andreassi, Chiara V. Anselmi, Diego Ardissino, Benoit J. Arsenault, Christie M. Ballantyne, Ekaterina V. Baranova, Hassan Behloui, Thomas O. Bergmeijer, Connie R. Bezzina, Eythor Bjornsson, Simon C. Body, Bram Boeckx, Eric (H.) Boersma, Eric Boerwinkle, Peter Bogaty, Peter S. Braund, Lutz P. Breitling, Hermann Brenner, Carlo Briguori, Jasper J. Brugts, Ralph Burkhardt, Vicky A. Cameron, John F. Carlquist, Clara Carpeggiani, Kathryn F. Carruthers, Gavino Casu, Gianluigi Condorelli, Sharon Cresci, Nicolas Danchin, Ulf de Faire, John Deanfield, Graciela Delgado, Panos Deloukas, Kenan Direk, Robert N. Doughty, Heinz Drexel, Nubia E. Duarte, Marie-Pierre Dubé, Line Dufresne, James C. Engert, Niclas Eriksson, Natalie Fitzpatrick, Luisa Foco, Ian Ford, Keith A.A. Fox, Bruna Gigante, Crystel M. Gijsberts, Domenico Girelli, Yan Gong, Daniel F. Gudbjartsson, Emil Hagström, Jaana Hartiala, Stanley L. Hazen, Claes Held, Anna Helgadottir, Harry Hemingway, Mahyar Heydarpour, Imo E. Hoefer, Kees Hovingh, Jaroslav A. Hubacek, Stefan James, Julie A. Johnson, J. Wouter Jukema, Marcin P. Kaczor, Karol A. Kaminski, Jiri Kettner, Marek Kiliszek, Marcus Kleber, Olaf H. Klungel, Daniel Kofink, Mika Kohonen, Salma Kotti, Pekka Kuukasjärvi, Bo Lagerqvist, Diether Lambrechts, Chim C. Lang, Jari O. Laurikka, Karin Leander, Vei-Vei Lee, Andreas Leiherer, Petra A. Lenzini, Daniel Levin, Daniel Lindholm, Marja-Liisa Lokki, Paulo A. Lotufo, B. Khan Mahmoodi, Anke H. Maitland-van der Zee, Nicola Martinelli, Winfried März, Nicola Marziliano, Ruth McPherson, Olle Melander, Ute Mons, Jochen D. Muehlschlegel, Joseph B. Muhlestein, Cristopher P. Nelson, Chris Newton Cheh, Oliviero Olivieri, Grzegorz Opolski, Colin N. Palmer, Guillaume Pare, Gerard Pasterkamp, Carl J. Pepine, Witold Pepinski, Alexandre C. Pereira, Anna P. Pilbrow, Louise Pilote, Jan Pitha, Rafal Ploski, A. Mark Richards, Christoph H. Saely, Nilesh J. Samani, Ayman Samman-Tahhan, Marek Sanak, Pratik B. Sandesara, Markus Scholz, Agneta Siegbahn, Tabassome Simon, Juha Sinisalo, J. Gustav Smith, John A. Spertus, Kari Stefansson, Alexandre F. R. Stewart, David J. Stott, Wojciech Szczeklik, Anna Szpakowicz, Michael W.T. Tanck, Wilson H. Tang, Jean-Claude Tardif, Jur M. ten Berg, Andrej Teren, George Thanassoulis, Joachim Thiery, Gudmundur Thorgeirsson, Gudmar Thorleifsson, Unnur Thorsteinsdottir, Stella Trompet, Frans van de Werf, Yolanda van der Graaf, Pim Van der Haarst, Sander W. van der Laan, Ragnar O. Vilmundarson, Salim S. Virani, Frank L.J. Visseren, Efthymia Vlachopoulou, Lars Wallentin, Johannes Waltenberger, Els Wauters, Arthur A.M. Wilde