Pyramidal cell-interneuron circuit architecture and dynamics in hippocampal networks

Summary

Excitatory control of inhibitory neurons is poorly understood due to the difficulty of studying synaptic connectivity in vivo. We inferred such connectivity through analysis of spike timing and validated this inference using juxtacellular and optogenetic control of presynaptic spikes in behaving mice. We observed that neighboring CA1 neurons had stronger connections, and that superficial pyramidal cells projected more to deep interneurons. Connection probability and strength were skewed, with a minority of highly connected hubs. Divergent presynaptic connections led to synchrony between interneurons. Synchrony of convergent presynaptic inputs boosted postsynaptic drive. Presynaptic firing frequency was read out by postsynaptic neurons through short-term depression and facilitation, with individual pyramidal cells and interneurons displaying a diversity of spike transmission filters. Additionally, spike transmission was strongly modulated by prior spike timing of the postsynaptic cell. These results bridge anatomical structure with physiological function.

Introduction

The common currency of neural computation is the transmission of action potentials from presynaptic to postsynaptic neurons. Neural circuit computation relies upon action potential transmission, and thus changes in transmission efficacy are vital for information storage. In particular, connectivity between excitatory neurons and local interneurons (feedback inhibition, including lateral inhibition), is believed to gate afferent drive (Fernandez-Ruiz et al., 2017, Milstein et al., 2015, Somogyi and Klausberger, 2005), control local synchrony (Stark et al., 2014), and dictate competitive interactions within the excitatory population (Buzsaki, 2010, Trouche et al., 2016). Therefore, a mechanistic understanding of neural circuit operations requires not only connectomic mapping of circuit elements, but also the elucidation of the parameters that affect the dynamic properties of individual synaptic connections that support circuit computation.

Synaptic connectivity and strength are usually assayed through paired intracellular recording of the pre- and postsynaptic cells, a method that is impractical in awake-behaving animals, particularly in deep brain structures. An alternative, albeit indirect, approach is to use in vivo multi-electrode extracellular recordings, which provide the timing of spikes recorded in parallel from hundreds of neurons. With such data, it has been suggested that synaptic properties can be deduced from the reliability and precision of spiking in one neuron in the milliseconds after a spike of another cell (Constantinidis and Goldman-Rakic, 2002, Henze et al., 2002, Marshall et al., 2002, Perkel et al., 1967, Toyama et al., 1981). However, to accurately detect monosynaptic connections requires that pairwise interactions be isolated from indirect polysynaptic drive, as well as from ubiquitous common ‘third party’ inputs, which have the potential to synchronize neurons that lack direct synaptic coupling (Ostojic et al., 2009). A reliable way to rule out the possibility of third party coordination is to demonstrate that postsynaptic spikes are causally related to the spiking of a single presynaptic neuron.

To determine an accurate method for detecting synaptic connections from spike timing data, we decoupled presynaptic neurons from the ongoing network activity through single cell juxtacellular current injection or optogenetic stimulation of small groups of cells. We focused on the strong excitatory-to-inhibitory synapses in the CA1 region (Gulyas et al., 1993), as weak connections are likely missed with this spike transmission-based approach. First, we generated a “ground-truth” dataset in which we identified monosynaptic pyramidal cell drive of local interneurons, and validated two models for detection of such connections. This enabled us to identify monosynaptic connections amongst nearly 30,000 pyramidal cell-interneuron pairs recorded in behaving mice and rats, and examine the functional architecture and dynamics of the excitatory to inhibitory circuit.

Using this approach, we uncovered the anatomical organization and several dynamic properties of pyramidal cell-interneuron connections. Key findings include elucidating the space constant for connection strength, time constants for presynaptic cooperativity and postsynaptic receptivity, and support for the role of common excitatory inputs in generating synchrony amongst interneurons. Additionally, we found that a diversity of short-term facilitation and short-term depression dynamics were simultaneously expressed by different connections of single presynaptic and postsynaptic neurons. Given that inhibition controls the dynamics of pyramidal cell activity, these findings have important implications for the organization and construction of cell assemblies (Buzsaki, 2010, Dupret et al., 2013, Trouche et al., 2016).

Results

We obtained recordings of CA1 neuronal ensembles from freely behaving and awake/sleeping mice (N = 9) and rats (N = 4) and awake head-fixed mice (N = 8). Neurons were separated by type (pyramidal cells versus interneurons; see Methods). Potential synaptic connections between neuron pairs were assessed by examining the short-latency interactions between cell pairs using spike train cross-correlograms (CCGs) (Figure 1D–F; see Methods). In a dataset of >400,000 neuron pairs, we examined a total of 29,964 excitatory to inhibitory pairwise interactions and 8,602 interactions amongst inhibitory cells.

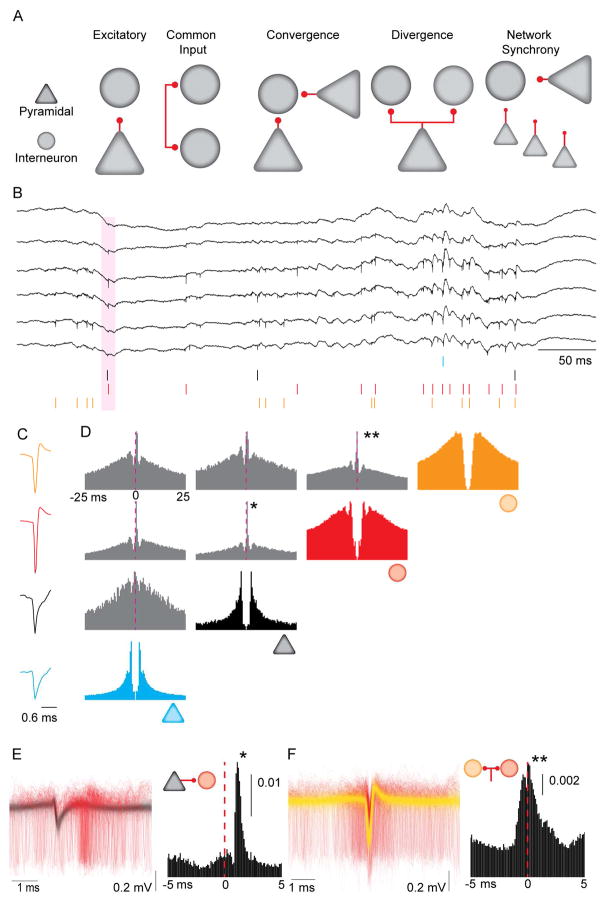
Figure 1. Synaptic interactions, common drive and circuit motifs inferred from spike train correlations.

A. Circuit motifs hypothesized to result in short-latency spike-spike correlations. B. Example wideband (0.1– 6,000 Hz) extracellular traces obtained from dorsal CA1 pyramidal layer. Colored ticks represent spikes from single units sorted offline. Pink shaded area is a putative instance of monosynaptic spike transmission from a pyramidal neuron (black tick) to an interneuron (red tick). C. Mean waveforms for the four units shown in B. D. Autocorrelations (in color) and CCGs (in grey) for the four units from B and C. Dashed line shows 0 ms lag from the reference spike. CCG binned at 1 ms. Note that both pyramidal neurons have positive (~ 1 ms) latency peaks in their pairwise CCGs with the interneurons (*), while the CCG between the two interneurons has a peak at 0 ms lag (**). E. Left: 4,000 randomly sampled traces (filtered at 0.3 – 6 kHz) aligned to the spike of the pyramidal neuron (in black), with the spikes from the postsynaptic interneuron (in red), from the pair highlighted with the asterisk in D. Right: High resolution CCG (0.1 ms bins) for the same pair. Vertical scale bar is non-corrected probability. F. Left: 4,000 randomly sampled traces (filtered at 0.3 – 6 kHz), aligned to the spike of the interneuron in yellow, with the spikes from the second interneuron in red, from the pair highlighted with the double asterisk in Panel D. Right: High resolution CCG (0.1 ms bins) for the same pair. Vertical scale bar is non-corrected probability.

Figure 1D illustrates short time-scale interactions for four selected neurons, in which two pyramidal neurons (PYR1, PYR2) potentially excited the same two interneurons (INT1, INT2). This is evidenced by the short-latency delays between peak firing from the reference spike of the pyramidal neuron (time 0) and the putative interneuron, visible in the CCG (~1–2ms delay; Figure 1D, E). In contrast, the CCG between the two interneurons showed a zero-centered peak (INT1–INT2 peak: ~0 ms, Figure 1D, F). This zero-centered synchrony, sometimes referred to as ‘zero time’ lag correlation (Diba et al., 2014, Engel et al., 1991, Roelfsema et al., 1997) may be due to the two interneurons sharing a common excitatory drive (e.g., PYR1 and PYR2), or to interactions amongst the interneurons. In a first set of experiments, we examined monosynaptic drive for evoked spikes of presynaptic neurons, and compared this drive to that observed during spontaneous activity. We then examined how such connections compared with, and contributed to, zero-centered synchrony amongst interneurons.

Identification of monosynaptic spike transmission from pyramidal neurons to interneurons

We used two methods to test the hypothesis that monosynaptic connections from PYR to INT can be reliably detected from spike timing. The goal of both approaches was to provide a comparison of spike transmission probabilities for evoked (experimentally driven) and spontaneous (network driven) spikes.

In the first approach, we evoked action potentials in single presynaptic PYRs using juxtacellular electrodes (Pinault, 1996), while recording extracellular spikes of local INTs (~50–100 μm estimated inter-somatic distance; Figure 2A). We used juxtacellular current pulses to induce spikes in PYRs (Figure 2B; median gain = 23.2 Hz, median percent increase: 470%, N = 18). The juxtacellular stimulation protocol approached the limits (Doose et al., 2016) of experimentally evoked spike-time precision in PYRs in vivo (mean/median standard deviation of first spike latency after pulse onset = 13.0 ms). To validate that evoked presynaptic spikes were indeed decoupled from network drive, we assessed the degree of synchrony between the evoked spikes and the activity of other pyramidal cells. As compared to spontaneous spikes, evoked spikes were significantly less likely to occur within ±2 ms of spikes of either other PYR presynaptic to the same INT (p=0.002, N =26) or all other PYR (p=0.03, N =18). As ±2 ms is the window of maximal presynaptic cooperativity (see later in Figure 5), this demonstrates significant decoupling from the network on timescales relevant to presynaptic cooperativity.

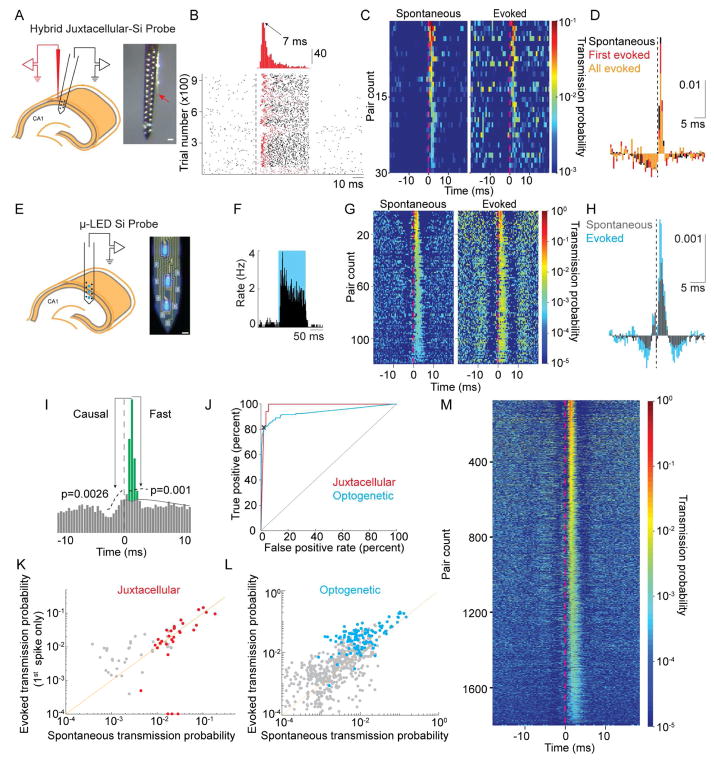
Figure 2. Single pyramidal neurons discharge postsynaptic interneurons.

A. Left: Schematic of the experiment for combined juxtacellular – extracellular recordings. Only six electrode sites are shown for clarity. Right: photomicrograph of hybrid probe. The tip of the juxtacellular electrode (red arrow) is ~50–100 μm from the closest electrode site on the silicon probe. Scale bar is 50 μm. B. Example juxtacellular stimulation of a pyramidal neuron. Top: histogram of delay times to first spike after stimulus onset. Bottom: raster of 963 trials. Dashed line is stimulus onset (50 ms duration). The first spike of each trial is colored red. C. CCGs of 30 pyramidal to interneuron pairs demonstrating similarity in spike transmission for both spontaneous and juxtacellularly evoked presynaptic spikes (all evoked spikes). D. Mean, baseline corrected CCG for spontaneous (black) or juxtacellularly evoked presynaptic spikes (first spike only in red, all evoked spikes in orange). Vertical scale bar is corrected probability. E. Left - Schematic of recording with μ-LED silicon probe. Right – photomicrograph of the silicon probe with three μLEDs illuminated. Scale bar is 15 μm. F. Example PSTH of spiking response to optogenetic stimulation of a ChR2-expressing pyramidal neuron. G. CCGs of 118 pairs demonstrating similarity in spike transmission for both spontaneous and optogenetically evoked presynaptic spikes. H. Mean, baseline corrected CCGs for spontaneous (black) or optogenetically evoked (blue) presynaptic spikes. Vertical scale bar is corrected probability. I. Illustration of parameters used to define connections from CCGs. Significant connections were those in which the peak was above the confidence bounds indicated by the dashed lines. Spike transmission probability defined by area in green (see Methods). J. Receiver–operator characteristic curve for synapse classification, with the threshold for P_causal shown by the black X for the optogenetic classifier. This P_causal was used to define the confidence bounds in Panel I (see Methods). K. Correlation of spike transmission probability for spontaneous spikes versus those evoked by juxtacellular current injection. Neuron pairs classified as connected are shown in red, non-significant peaks for all excitatory to inhibitory CCGs in black. L. Same as in J for optogenetic stimulation (connections in blue). For clarity, 32 non-significant points are not shown M. 1,754 monosynaptic connections identified in a dataset of 29,964 PYR/INT pairs.

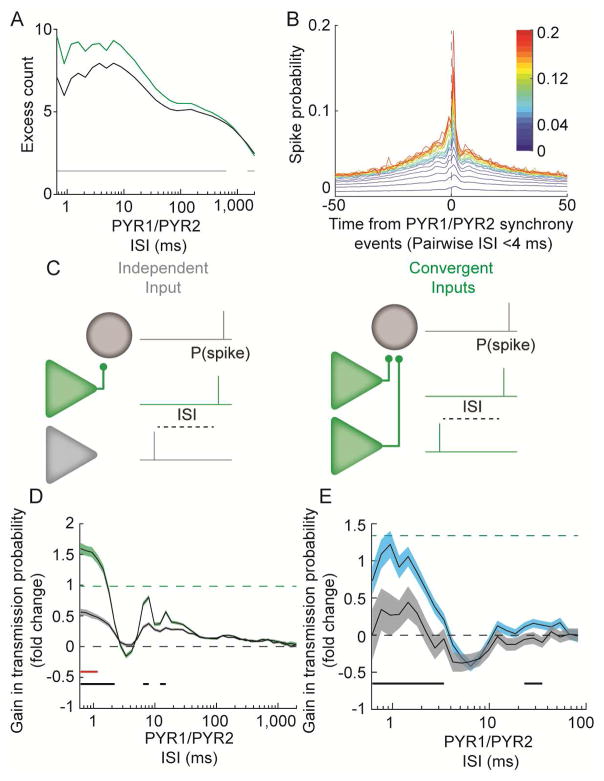
Figure 5. Presynaptic cooperativity increases spike transmission probability.

A. Pyramidal neuron pairs which share a postsynaptic target (green) synchronize more at short ISIs than pairs lacking a common postsynaptic target (gray). B. Mean CCGs between synchronous events for pairs of convergent PYR and INT. Color code is summed transmission probability for connections to common interneuron. C. Schematic illustrating how spike transmission probability was assessed after convergent spiking. D. During spontaneous activity, spike transmission is highest following temporally synchronous spiking of pairs of pyramidal neurons for which both are presynaptic (green), as compared to pairs of pyramidal cells in which one is connected and the other is not (grey) (shaded area is SEM). Dashed line is the mean expected linear summation of the transmission probabilities for the two PYR in the convergent case. Solid lines below traces indicate ISIs with significant differences between the convergent and independent case (black), or the convergent case and the arithmetic mean indicated by the dashed line (red). Wilcoxon rank sum test, p < 1.25⁻³. E. During optogenetically induced presynaptic activity a similar gain through cooperativity was observed, indicating that the synchrony of the two presynaptic cells, and not hidden third parties, explained the overall boost in spike transmission. Shaded area is SEM.

CCGs were computed independently for spontaneous and evoked spikes (Figure 2C, D), and spike transmission probability was calculated as excess synchrony in the 0.8–2.8 ms bins above baseline co-modulation (green area, Figure 2I; see Methods). To assess spike transmission probability following maximally decoupled spikes, we considered only the first evoked spike after the stimulation onset. Transmission probabilities for spontaneous and first evoked spikes were significantly correlated (r=0.79, p<1.11⁻⁶, N = 30, Figure 2K), and the mean transmission probability for spontaneous spikes did not differ from the first evoked spikes (sign test, p=0.86, N =18, Figure S2B). Importantly, deviance in transmission probability for spontaneous versus first evoked spikes did not correlate with the mean time to the first evoked spike (r=0.153, p=0.416, N =30) nor with the standard deviation of the time to the first evoked spike (r=0.151, p=0.423, N =30). This suggests that the degree of decoupling of the presynaptic cell from the network cannot explain the difference between transmission probabilities for spontaneous versus evoked spikes. Finally, to assess transmission probability during spontaneous decoupling of presynaptic activity from identified convergent inputs, we tested transmission efficacy for spikes in which the presynaptic cell fired and other convergent inputs were silent within a ±2 ms time window. Consistent with our evoked experiments, the spike transmission probability for all spontaneous spikes matched that for the spontaneously decoupled spikes (sign test, p=0.26, N =30) thus suggesting that the major part of the observed CCG peak is indeed a pairwise effect. Combined, these results support the conclusion that pyramidal cell-interneuron CCG peaks reflect monosynaptic connections.

In our second approach, we used focal optogenetic stimulation to increase the firing rate of small numbers of pyramidal cells (Figure S2C), effectively scaling up the experiment in order to gain a more quantitative estimate of the distribution of the pairwise interactions. To record and activate hippocampal CA1 pyramidal neurons, mice expressing channelrhodopsin-2 under control of a excitatory neuron specific promoter (CaMKII::ChR2 mice; see Methods) were implanted with four-shank silicon probes equipped with 12 μLEDs (Figure 2E) (Kim et al., 2016). Since the light sources in this device are intermingled with the recording sites, sub-μW light power is sufficient to activate small numbers of pyramidal cells confined to the vicinity of the light from a single recording shank (Wu et al., 2015) and, importantly, the activity of the light-modulated neurons can be simultaneously monitored during stimulation (Wu et al., 2015). We examined the CCGs of 224 optogenetically excited PYR cells and 88 simultaneously recorded INT (yielding 954 potential connections, N = 4 mice), and identified 118 PYR-INT pairs (N = 94 PYR, N = 26 INT) with significant peaks in the CCG (see Methods). As we found with the juxtacellular experiments, CCGs for these pairs were similar when constructed with optogenetically evoked spikes or spontaneous spikes (Figure 2G, H), and the spike transmission probabilities were highly correlated (Figure 2L; r = 0.85, p < 1.89⁻³⁴). The optogenetic stimulation was of insufficient magnitude to evoke ripple-frequency oscillations in the LFP, requiring more than ~15–20 neurons (Stark et al., 2014). Nevertheless, coordinated activity in this frequency range is observable as secondary peaks in the PYR-INT CCGs (Figure 2G, H), reflecting interactions between excitatory and inhibitory neurons within small local circuits. Spike transmission was significantly higher during optogenetic stimulation as compared to baseline (Wilcoxon rank sum, p < 9.0⁻³⁰). This suggests that more than one optogenetically activated presynaptic pyramidal cell was driving the same interneuron, possibly including optogenetically excited presynaptic terminals of other pyramidal cells. When the number of presynaptic neurons firing together in 2 ms was considered, transmission probability was not different for spontaneous versus optogenetically evoked spikes (Figure S2D), suggesting that presynaptic cooperativity could explain the gain in spike transmission probability during optogenetic stimulation. The data from both our juxtacellular and optogenetic experiments thus support the hypothesis that pyramidal cell-interneuron CCG peaks can be reliably used to identify monosynaptic connections.

We used the spike transmission during juxtacellular current or optogenetic stimulation as our ‘ground truth’ data in determining synaptic connectivity. With this labeled data, we tested the accuracy of two synapse detection algorithms applied to spontaneous spiking activity. In our first approach, we considered the cross correlation between the presynaptic and postsynaptic cells. Under this framework, synaptic interactions were assumed to produce excess synchrony above that expected from lower frequency co-modulation induced by common network drive. The low frequency network co-modulation was dissociated from the high frequency synaptic synchrony by convolving the observed CCG with a partially hollow Gaussian kernel (Stark and Abeles, 2009) and only pairs with significant high frequency synchrony (Figure 2I, ‘fast’) were retained for subsequent analysis. In addition to ‘fast’ pairwise synchrony in excess of slow co-modulation, we assumed that the synaptic interaction must produce significant excess synchrony in the causal direction, with the peak in the CCG at positive lags higher than that observed at negative lags (Figure 2I, ‘causal’). The performance of a classifier defined by the ‘fast’ and ‘causal’ elements of the pairwise interaction was determined by its receiver operating characteristic curve (Figure 2J), which showed a true positive rate of 81.3% and a false positive rate of 2.1% at our optimal performance threshold (Provost and Fawcett, 2001).

As an independent approach, we used a generalized linear model that derives the expected spike transmission kernel while explicitly modeling the origin of the network co-modulation (Pillow et al., 2008) by including regressors for multi-unit activity, and phasic modulation by ripple and theta oscillations. The algorithms had strikingly similar detection accuracy and quantitative agreement on the contribution of the single pre-synaptic input to the increase in the post-synaptic firing rate (Figure S3). Since both algorithms performed equally well, we used the simpler and computationally more efficient convolution method to classify (see Methods) a large set of potential connections in 29,964 PYR-INT pairs, yielding 1,754 monosynaptic connections (Figure 2M).

Divergent monosynaptic pyramidal cell-interneuron connections contribute to zero-lag interneuron-interneuron synchrony

We next addressed the hypothesis that ‘zero lag’ peaks in the CCGs between pairs of interneurons (< 1 ms; Figure 1F) reflect a common drive of neuronal pairs from divergent presynaptic neurons (Diba et al., 2014, Ostojic et al., 2009, Senzai and Buzsaki, 2017). Such synchrony was not always exactly zero-centered, possibly due to axonal conduction delays, and thus we first aimed to determine if such a situation could be mistaken for monosynaptic drive. We compared CCGs for PYR-INT and INT-INT pairs with different inter-somatic distances (by choosing cells recorded on different shanks of the silicon probe; Figure 3A, B, N = 4 rats). PYR-INT pairs with significant CCG peaks could be detected up to 600 μm apart (Figure 3A, C, green), while INT-INT pairs with significant CCG peaks could be detected across all shanks placed in the pyramidal layer (up to 1.4 mm distance; Figure 3C, black). For PYR-INT pairs, inter-somatic distance strongly correlated with the time of the peak in the cross correlation, even when regressing out the influence of connection strength on peak timing (partial r² of distance and lag = 0.49, p <10⁻⁵; Figure 3C). Similarly, the peak delay between INT-INT increased with inter-somatic distance (partial r² of distance and lag = 0.35, p = 10⁻⁵, N = 4 rats; Figure 3C). Importantly, the distribution of the delays to the CCG peak for connected PYR-INT pairs and synchronous INT-INT pairs, at ≥200 μm (Figure 3D), showed that the two peaks were distinct. These observations show that the timing of the CCG peak can effectively disambiguate ‘zero lag’ synchrony between INT-INT pairs and the monosynaptic drive seen between PYR-INT pairs.

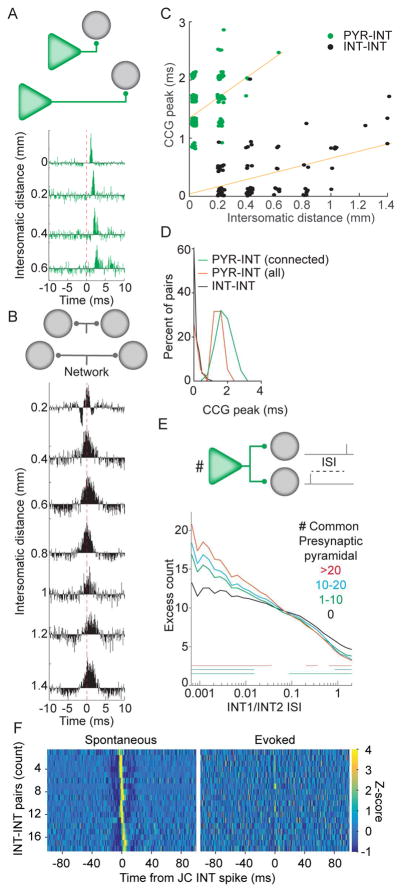
Figure 3. Monosynaptic connectivity can be dissociated from synchrony induced by convergent input.

A. CCGs of example PYR-INT pairs recorded at different inter-somatic distances. Distance is calculated based upon the presynaptic and postsynaptic neuron being recorded on specific shanks of the silicon probe, with 200 μm inter-shank spacing. Axonal conduction delay produces a rightward shift of the peak with increasing inter-somatic distance. B. CCGs of example interneuron-interneuron pairs recorded at different inter-somatic distances, calculated as in A. Note that the temporal shift with distance is less than that for the pairs in A. C. The timing of CCG peaks in monosynaptic PYR-INT pairs and synchronous INT-INT pairs have different slopes and y-intercepts. Note that weak PYR-INT pairs were excluded from the visualization but not the calculation of the slope. Horizontal jitter of points is for illustration only. D. Distribution of CCG peaks for all PYR-INT and INT-INT pairs for ≥200 μm distance. E. Interneurons that share presynaptic pyramidal neuron inputs (green, blue, red), spike more synchronously than those that do not (black). Note that the magnitude of synchrony scales with the number of shared presynaptic pyramidal cells. Bars mark significance, Bonferonni corrected, Wilcoxon rank sum, p < 0.0017. F. INT-INT CCGs for pairs in which one INT was recorded and stimulated with the juxtacellular electrode, constructed with either spontaneous or evoked spikes.

To evaluate the potential contribution of local excitatory inputs to the ‘zero lag’ synchrony seen amongst interneurons, we first assessed whether the observation of multiple convergent inputs influences interneuron coordination. Highly synchronous interneuron pairs are expected to have more spikes emitted at short interspike intervals (ISIs). Therefore, we calculated the distribution of interspike intervals between spikes from two interneurons and compared the observed distribution to a resampled data set in which the spike trains were shifted relative to one another (see Methods). In support of common excitatory inputs contributing to ‘zero-lag’ INT-INT synchrony, interneurons with more shared presynaptic partners exhibited significantly, and proportionally, more short pairwise ISIs (Figure 3E). To test for the ability of interneurons to generate synchrony amongst themselves (Hu et al., 2011), we stimulated single interneurons with a juxtacellular electrode (mean gain during stimulation: 59.1 Hz, SD 46.6 Hz, N = 9 stimulated interneurons in 3 mice), while monitoring the extracellular spiking of other local (~ 50–100 μm inter-somatic distance) interneurons with a silicon probe. CCGs constructed with spontaneously occurring juxtacellular spikes exhibited significant zero-centered peaks, while CCGs constructed with evoked spikes had no, or significantly, diminished, zero-centered peaks (Figure 3F, Figure S4), suggesting that interneuron-interneuron interactions alone may not be sufficient for generating zero-lag synchrony.

The spatial convergence and divergence of pyramidal cell-interneuron connections is highly skewed

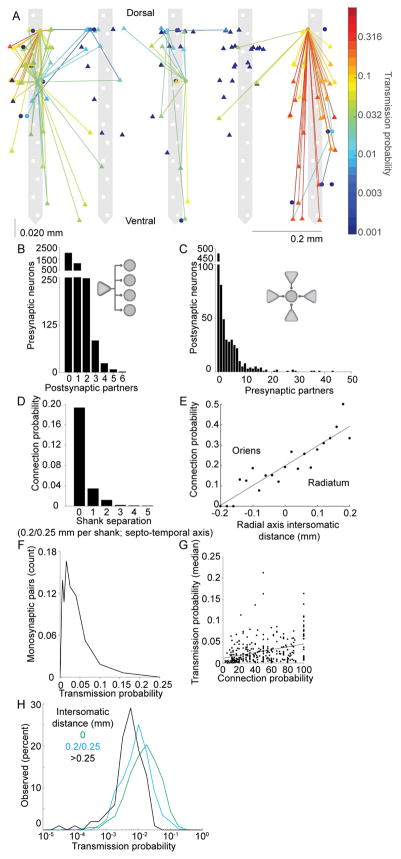
Figure 4A illustrates the connectivity map of pyramidal cells and interneurons recorded in a single session, showing that individual pyramidal neurons targeted multiple interneurons (Figure 4B) and that multiple pyramidal cells converged on the same interneuron (Figure 4C). The probability of finding a connection decreased with increased distance along the septo-temporal axis (Figure 4D), as expected, due to the increasing number of potential targets in larger volumes. We observed a higher probability of connections from superficial pyramidal neurons onto deep interneurons (Figure 4E). The magnitude of spike transmission probability between PYR-INT varied several orders of magnitude and its distribution was skewed (Anderson-Darling test for normality p < 0.05; Figure 4F). We found a significant positive correlation (r = 0.33; p = 7.66⁻⁹, N = 784) between the magnitude of spike transmission probability and the density of PYR-INT convergence for individual INT (Figure 4G). This potentially suggests that interneurons receiving more connections from local PYR also tend to have apparently stronger connections with local PYR cells. Stronger spike transmission may be explained by properties of the synapse (i.e., larger conductance), or postsynaptic features (i.e., more depolarized resting membrane potential and/or lower threshold voltage) or a combination of these factors. Finally, we demonstrated that spike transmission probability decreased with increased distance between PYR-INT pairs (ranksum, same shank vs one shank away p = 2.92⁻¹⁷, one shank away vs two shanks away, p = 6.0⁻⁶, correlation coefficient of distance with spike transmission probability, p = −0.19, p = 5.0^−17; Figure 4H), which is not due to differences in synchrony among local versus distant pyramidal neurons, as pyramidal cells on the same shank, as compared to those recorded on separate shanks, were equally likely to fire at short latency (2–5 ms) inter-spike intervals (rank sum test for excess synchrony p > 0.05, see Methods). Finally, we assessed the effect of brain state on PYR-INT connection strength at different intersomatic distances, and found that distal pairs, as compared to pairs recorded on the same shank, had more of a decrease in spike transmission probability during sleep as compared to wake (Figure S4B).

Figure 4. Anatomical features of pyramidal – interneuron connections.

A. Connectivity map of an example recording session. Pyramidal cells (triangles) and interneurons (disks) are superimposed on the recording sites of the 5-shank probe. Horizontal jitter of cell bodies within shanks is for illustration purposes only. Note convergence of several pyramidal neurons onto shared interneurons. B. Distribution of PYR-INT divergence. C. Distribution of PYR-INT convergence. D. Probability of PYR-INT connections as a function of intersomatic distance along the septo-temporal axis. E. Probability of PYR-INT connections as a function of inter-somatic distance along the radial (deep-superficial) axis. Positive distances correspond to the case where the pyramidal neuron was more superficial, while negative distances indicate that the pyramidal neuron was deeper. F. Distribution of spike transmission probability between PYR-INT pairs. G. Spike transmission probability as a function of PYR-INT convergence. Only within-shank connections are included (connection probability is the percent of connected versus all recorded pyramidal neurons). Stronger PYR-INT connections are associated with larger convergence. H. Distribution of connection strengths for increasing inter-somatic distances along the septo-temporal axis.

Temporal cooperativity of pyramidal neurons enhances spike transmission probability

Synchronous spiking of a presynaptic population (in this case two neurons) is expected to facilitate spike transmission due to synaptic integration. First, we identified such synchronous events and found that pyramidal neuron pairs that shared a postsynaptic target were more likely to co-fire at short intervals (< 10 ms), compared to those that did not have a shared postsynaptic partner (Figure 5A). Though our synchrony measure controls for firing rate (see Methods), we also saw an increase in short ISI synchrony when explicitly equalizing the rates between the two groups (data not shown).

We next examined the statistics of the postsynaptic spiking at times of high presynaptic synchrony (defined as two presynaptic neurons spiking with an ISI of < ±2 ms). For pairs with strong summed transmission probabilities surrounding the second spike in a synchronous event (time zero) the postsynaptic rate was increased (Figure 5B), suggesting that connected PYR– INT pairs also receive temporally organized excitation, possibly in combination with a synchronizing effect of feedback inhibition.

We next examined how the relative timing of presynaptic spikes of multiple pyramidal neurons affected spike transmission probability to a common postsynaptic target (Figure 5C). We found that temporal proximity of spiking of convergent inputs resulted in a robust gain in PYR-INT spike transmission probability (rank sum, p < 10⁻¹¹ up to 2.2 ms ISI common (N = 7404) vs independent (N = 15600) triplets; Figure 5D) even above what would be expected for the linear sum of the mean transmission probability of the two presynaptic neurons (sign test, observed > linear sum, p < 6.0⁻⁸ to 1 ms, Figure 5D; slope of linear sum vs observed at 0.4 ms ISI = 1.11; see Figure S6). Similarly, convergent inputs from two optogenetically activated presynaptic pyramidal neurons significantly boosted transmission probability (rank sum, p < 1.1⁻⁴, from 0.8–3.4 ms ISI, common (N = 919) vs independent (N = 873) triplets; Figure 5E).

Short-term facilitation and depression dynamics are diverse and specific to individual connections

The history of spiking activity in circuits is known to modulate the strength of synapses, and this process is usually referred to as short-term plasticity (i.e., facilitation or depression) (Abbott et al., 1997, Stevens and Wang, 1995, Zucker and Regehr, 2002). Although we did not record postsynaptic potentials, changes in which are typically utilized in measures of short-term plasticity (i.e., paired-pulse facilitation/depression), we nevertheless sought to determine whether similar processes are observed for spike transmission probability.

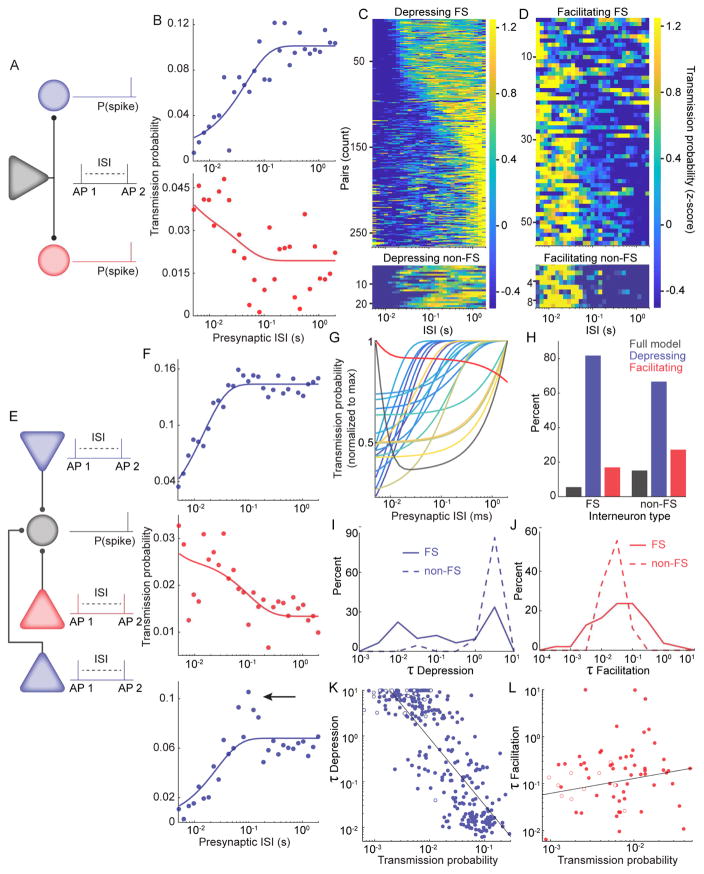
We analyzed the transmission probability for PYR-INT pairs as a function of the ISIs of the presynaptic pyramidal cell (Figure 6A, E). Data for each pair were fit with a classical model of dynamic synaptic filters (Tsodyks et al., 1998, Tsodyks and Markram, 1997). We found that 357/1768 neuron pairs were fit with either the full model (N =23), or reduced models consisting of either solely depression (N =287 pairs; Figure 6B, C, F) or facilitation (N =64 pairs; Figure 6B, D, F). Interestingly, some pairs had maximal transmission probability at specific ISIs, which was not always captured by the most parsimonious model (Figure 6F). Divergent pyramidal cells were observed to make both facilitating and depressing connections with different postsynaptic targets (N = 30 pyramidal cells that showed both facilitation and depression; Figure 6B). Furthermore, single postsynaptic interneurons were observed to have both facilitating and depressing connections with different convergent presynaptic pyramidal cells (N = 39 interneurons; Figure 6F). For example, Figure 6G shows a single postsynaptic interneuron with 21 presynaptic inputs: 19 depressing, one facilitating and one mixed. Both FS and non-FS types of postsynaptic interneurons exhibited facilitation and depression (Figure 6C, D, H), though significantly more depressing connections were made with FS postsynaptic interneurons than with non-FS neurons (χ² test, P(χ² > 8.47) = 0.0145, N = 336 pairs; Figure 6H). We observed a wide range of time constants for both depression (Figure 6I) and facilitation (Figure 6J). The depression time constant was significantly shorter for FS postsynaptic interneurons, even when accounting for differences in transmission probability between FS and non-FS types (ANCOVA, Lawley-Hotelling Trace = 18.58 p = 2.2⁻⁵, df = 284). Stronger connections had shorter depression time constants (r= − 0.82, p= 1.8⁻⁷⁰, N =287; Figure 6K), while no relationship was observed between facilitation time constant and connection strength (r=0.14, p=0.25, N = 64; Figure 6L). These data show that the expression of a specific short-term dynamic is not restricted by the identity of the postsynaptic cell nor the short-term dynamic expressed by other connections of the same presynaptic or postsynaptic neuron. Thus, short-term plasticity appears specific for individual synapses, not for neurons.

Figure 6. Short-term facilitation and depression are diverse and specific to connections, not single cells.

A. An example pyramidal cell connected to two postsynaptic interneurons (divergence). The spike transmission probability of a second presynaptic spike was assessed at variable interspike intervals (ISI) after a first spike emitted by the same pyramidal cell. B. Top: An example connection that exhibited depression, as evidenced by lower spike transmission probability at short presynaptic ISIs. Bottom: An example connection that exhibited facilitation, as evidenced by higher spike transmission probability at short presynaptic ISIs. Both postsynaptic interneurons were connected to the same presynaptic cell. C. The z-scored spike transmission (color axis) at each presynaptic ISI (columns) is plotted for all neuronal pairs for which the depression only model provided the most parsimonious fit (rows sorted by τ_depression). Data shown separately for FS and non-FS postsynaptic cells. D. Same as C for facilitating pairs. E. An example postsynaptic interneuron with three presynaptic pyramidal neurons (convergence). F. Top and middle, Example connections that exhibited depression and facilitation, respectively. Bottom: An example connection that exhibited depression. Arrow indicates a peak in the transmission probability at specific ISIs (~ 100 ms), which is not captured by the parsimonious synaptic model. G. Synaptic model fits for a single postsynaptic interneuron with 21 presynaptic pyramidal cell partners. H. Percent of FS and non-FS postsynaptic interneurons for which either the full model, depression only, or facilitation only, had the best fit. I. Distribution of depression time constants for FS (solid line) and non-FS (dashed line) postsynaptic interneurons, for pairs which the fit was best for depression. J. Distribution of facilitation time constants for FS (solid line) and non-FS (dashed line) postsynaptic interneurons, for pairs which the fit was best for facilitation. K. Correlation of depression time constant with transmission probability. Filled circles are FS, and open circles are non-FS postsynaptic interneurons. One data point (outlier) is not shown but is included in the statistical test). L. Correlation of facilitation time constant with transmission probability. Filled circles are FS, and open circles are non-FS postsynaptic interneurons. Three data points (outliers) are not shown but are included in the statistical test.

Prior postsynaptic spike timing modulates transmission probability more than variations in instantaneous rate

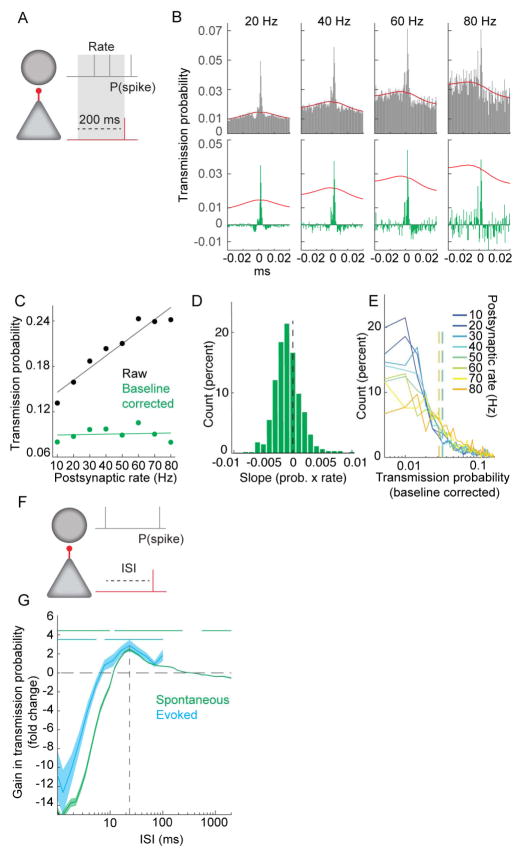
Given the profound influence of the spiking history of the presynaptic cells and other neurons in the network, we next turned to how the spiking history of the postsynaptic cell modulates spike transmission. To examine the effect of postsynaptic excitability, measured as firing rate, on transmission probability, we measured the transmission probability during selected times in which the postsynaptic neuron spiked at specific rates (10–80 Hz) prior to presynaptic spiking (Figure 7A–B). For baseline corrected CCGs, there was a small, but significant, negative effect of rate on transmission probability (median slope of transmission probability/rate = − 7.3^−5; sign test different from zero, p = 7.0⁻⁶; Figure 7C–E), suggesting weaker additional drive at higher rates.

Figure 7. Postsynaptic interneuron spike timing affects spike transmission more than rate.

A. Schematic of analysis for B–E, examining effect of postsynaptic rate on transmission probability. B. Top. CCGs from an example pair for which the firing rate of the postsynaptic neuron during the preceding 200 ms was 10 – 80 Hz. Bottom. Same as in B, but with baseline correction applied. Red lines are baseline (see Methods). C. Transmission probability versus postsynaptic rate for the example pair in B. D. Distribution of baseline corrected slopes (as shown in C) for the population (sign test, p = 7.0⁻⁸, N = 621). E. Distribution of baseline corrected transmission probabilities at each postsynaptic rate for all neurons (N = 621). Vertical dashed lines are mean transmission probability for that postsynaptic rate. F. Schematic of analysis for assessing the effect of the interval of the last postsynaptic spike prior to the presynaptic spike on the transmission probability. G. Gain in transmission probability at different ISIs for postsynaptic spikes preceding the presynaptic spike for spontaneous (green) and optogenetically induced postsynaptic spikes (blue; N = 2 PV::ChR2 mice). Horizontal lines denote significant difference from zero Wilcoxon paired sign test p< 0.00125. Dashed line at 24 ms denotes the ISI with the greatest boost in transmission efficacy. Shaded area is SEM.

We next examined whether the timing of the last postsynaptic spike relative to a given presynaptic spike affected the probability of spike transmission (Figure 7F). In contrast to the weak effect of rate, the timing of the last postsynaptic spike strongly affected the spike transmission probability of the next presynaptic spike, exhibiting clear refractoriness for ISIs less than 10ms and an enhancement of transmission that peaked at 24 ms (Figure 7G). The peak is likely due to the intrinsic properties of the postsynaptic interneurons, as this boost in transmission probability was also observed when only optogenetically-evoked postsynaptic spikes in PV::ChR2 mice were considered (Figure 7G, blue; N = 2 PV::ChR2 mice). The gain at 20–30 ms is consistent with the known role for pyramidal-interneurons interactions in driving gamma frequency oscillations (Buzsaki and Wang, 2012). These findings support the idea that spike-transmission probability measure is more related to the features of synaptic connections rather than network-controlled effects.

Discussion

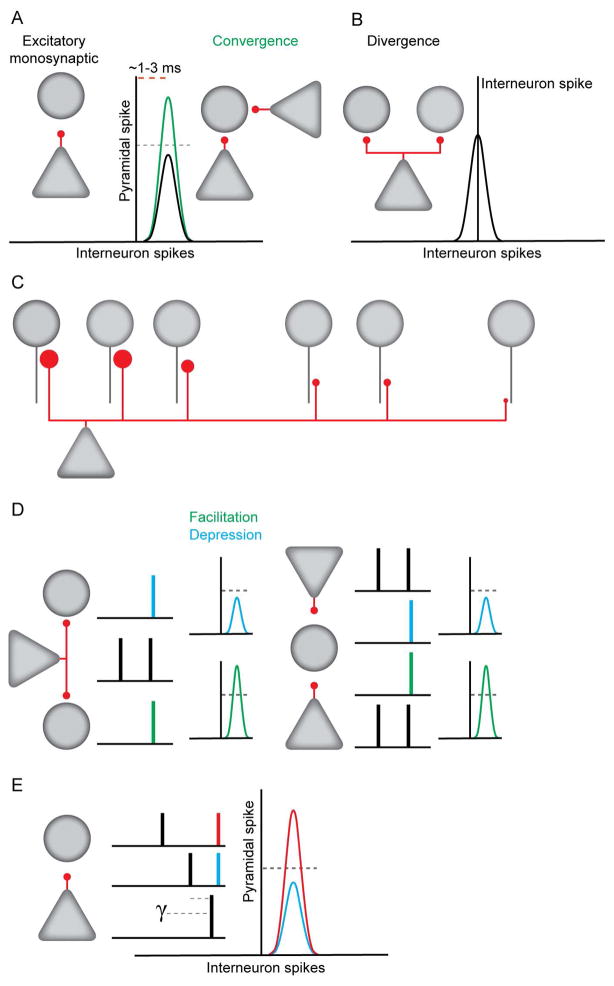
Inhibition plays an important role in coordinating the timing of principal cell output and modulating the integration of afferent inputs (Buzsaki, 1984, Isaacson and Scanziani, 2011). Excitatory inputs contribute to the rate and timing of such inhibition. We thus investigated how excitatory monosynaptic connectivity between pyramidal cells and interneurons could be inferred from reliable spike transmission from pre- to postsynaptic neurons in behaving animals. This approach permitted fine-grained analysis of the basic functional architecture and dynamics of hippocampal excitatory-to-inhibitory local circuits (Figure 8).

Figure 8. Organization and dynamics of pyramidal cell-interneuron monosynaptic connections.

A. Single pyramidal neurons evoke spikes in interneurons at short latencies. Convergent inputs boost transmission probability. B. CA1 pyramidal neurons synchronize local interneurons. C. Connection strengths decrease with inter-somatic distance. D. Monosynaptic transmission probability exhibits activity dependent short-term facilitation and depression. Left: Single pyramidal neurons make both depressing and facilitating connections. Right: Single interneurons receive both depressing and facilitating connections. E. Spike transmission probability is increased if the interval since the last postsynaptic spike is in the gamma frequency range.

Spike cross-correlations can reveal monosynaptic spike transmission between pyramidal cells and interneurons

Our findings provide support for the detection of monosynaptic connectivity from spike timing relationships. We employed juxtacellular stimulation and optogenetic methods to decouple the spikes of presynaptic pyramidal cells from background network activity that could potentially contaminate estimates of pairwise coupling. Using both stimulation techniques, we found that spike transmission probability for evoked spikes was strongly correlated with that observed for spontaneous activity. In the experiments in which spikes were evoked with single-cell juxtacellular stimulation, there was no difference in spike transmission when comparing evoked to spontaneous spiking. These results suggest that estimates of spike transmission probability can extract monosynaptic, pairwise drive. As a note of caution, for brain regions in which network-induced synchrony causes temporally offset, high-frequency pairwise coordination, independent verification of this detection method may be required.

As most experiments will not be able to causally confirm synaptic connectivity, we used our “ground truth” data to validate two synapse detection models. The first assumes that synaptic interactions should induce directed, short-latency synchrony that is additively in excess of the lower frequency network co-modulation of the presynaptic and postsynaptic neurons (Stark and Abeles, 2009). The second method explicitly models the network co-modulation by fitting the synaptic transfer kernel while accounting for how the postsynaptic firing rate is modulated by multi-unit activity, and ripple and theta oscillations. Both methods revealed ~80% true positive rates and <5% false positive rates. Existing statistical methods for synapse detection provide a probability of observing excess synchrony beyond some null distribution (Platkiewicz et al., 2017). With our labeled data, we can convert these likelihoods into the statistic of interest, the probability of synaptic connectivity. Importantly, future researchers may use this dataset as a testbed for comparing the effectiveness of various other statistical techniques that seek to draw causal conclusions from correlated spiking.

Pyramidal neuron common drive contributes to synchrony amongst interneurons

Pairs of interneurons often display so-called ‘zero-lag’ synchrony, detected as near zero-centered peaks (< 1 ms) in the cross-correlogram. Possible mechanisms generating such synchrony include shared excitatory inputs (Diba et al., 2014, Senzai and Buzsaki, 2017), and synaptic or gap junction coupling between interneurons (Mancilla et al., 2007, Traub et al., 2001). Here, we observe that interneurons that share many presynaptic partners spike together more often at short interspike intervals, as compared to pairs which share fewer or no presynaptic partners (Figure 3). This lends experimental support for the involvement of shared excitatory drive (Butler and Taube, 2017, Diba et al., 2014, Eggermont, 1992, Jackson et al., 2003, Kreiter and Singer, 1996, Nowak et al., 1995, Peyrache et al., 2015, Schwarz and Bolz, 1991, Senzai and Buzsaki, 2017, Swadlow et al., 1998). Additionally, we observed that juxtacellular stimulation of single interneurons strongly reduced their synchrony with other interneurons (Figure 3). These findings demonstrate that common excitatory drive is an important factor in initiating interneuron synchrony, although other mechanisms, such as synaptic and gap junction coupling between interneurons, should not be dismissed (Galarreta and Hestrin, 2001).

Importantly, we demonstrate that such common excitatory drive/gap junction coupling can be dissociated from monosynaptic connections. The peak delay between the spikes of the presynaptic pyramidal cell and interneuron pairs was 0.8–2.8 ms, while the peak synchrony amongst interneurons tended to occur with less than one millisecond delay, and there was little overlap in the delay distributions. For both PYR-INT and INT-INT pairs, temporal delays correlated with inter-somatic distance, but at a given distance the peak time of the INT-INT synchrony was usually one millisecond shorter than the peak time of the monosynaptic PYR-INT peak. This delay difference likely corresponds to the additional charge time of the interneuron membrane from the EPSP onset to spike (Fricker and Miles, 2000). Together, these results suggest that spike transmission from pyramidal cells to interneurons can be dissociated from other forms of temporal coordination, so long as the distance between neurons is known.

Architecture of the excitatory to inhibitory circuit

To elucidate quantitative features of the pyramidal cell-interneuron circuit, we grouped together the numerous interneuron types within CA1 (Klausberger and Somogyi, 2008), with the exception of optogenetically identified PV⁺ neurons.

In general, the excitatory drive was local with most connections confined to <200 μm inter-somatic distance (Figure 4) (Csicsvari et al., 1998). This may be explained in part by the fact that the CA1 pyramidal layer forms a 2-D sheet, resulting in the number of potential targets increasing with distance. For ‘fan-out’ pyramidal-cell interneuron connections, the distribution of connection probability was strongly skewed. While most pyramidal cells were observed to have had zero or one interneuron partner, a small minority had more than five. Spike transmission probability also decreased with distance (Figure 4). This finding suggests that the activity of single pyramidal cells can be isolated by lateral inhibition because local interneurons are more strongly recruited than distant ones. This arrangement could explain why pyramidal cells in close proximity do not represent overlapping spaces within an environment (Redish et al., 2001). In addition to the septo-temporal distance effects, we have shown that superficial CA1 pyramidal neurons are more effective at discharging interneurons than those in the deep sublayer, supporting previous observations in a small subset of PV⁺ interneurons (Lee et al., 2014). Such asymmetric organization of inhibition may assist in segregating different streams of information originating from the medial versus lateral entorhinal cortex and entering distinct CA1 sublayers (Masurkar et al., 2017).

We also found a skewed distribution in the number of presynaptic partners converging onto a postsynaptic interneuron (‘fan-in’ connections). While the majority of interneurons had only a few local pyramidal cell partners, a subset of interneurons had several dozen (Figure 4). As assessed by spike transmission probability, the distribution of connection strengths between pyramidal cell-interneuron pairs was also strongly skewed and depended on brain state (awake versus sleep states). The overall stronger spike transmission in the waking state, compared to sleep, can be due to altered firing patterns and/or the contribution of subcortical neurotransmitters (Hasselmo, 2006). The mechanisms that tonically affect spike transmission warrant further studies. Importantly, the distribution of spike transmission strength was not random in anatomical space because there was a reliable correlation between connection probability and spike transmission probability. These observations imply that interneurons that lie at the right end of a continuum of synaptic strength distribution also have more local presynaptic partners. Such an organization implies that a subset of interneurons is constantly excited by many pyramidal cells, thus providing continuous inhibition, whereas interneurons at the left end of the distribution can be controlled by unique patterns of pyramidal cell activity, possibly enabling tailored inhibitory control.

In principle, several different models can account for the above findings. Anatomical studies have shown that PV⁺ cells have larger dendritic trees and receive far more excitatory inputs than other interneuron types (Gulyas et al., 1999). Therefore, one option is that the observed heterogeneity in excitatory convergence was due to sampling multiple types of interneuron (Klausberger and Somogyi, 2008). However, this is unlikely given that the number of presynaptic partners forms a similarly skewed distribution for both fast-spiking interneurons (such as the majority of PV⁺ cells) and non-fast-spiking clusters in the larger dataset (Figure S5). One might also argue that the detection of interneurons with few presynaptic partners simply reflects a sampling problem, or could indicate that these interneurons receive disproportionally more inputs from more distant or extra-CA1 cells. While our experiments cannot exclude these possibilities, the correlation between cell body proximity and synaptic strength weighs against this argument, at least within the CA1 region. Alternatively, distinct motifs (Song et al., 2005), combined with lognormal rules of connection strength distribution (Mizuseki and Buzsaki, 2013), might form the backbone of local neuronal communication. In support of this view, previous findings have shown that both the firing rates and sequential activation patterns of CA1 pyramidal cells and interneurons are correlated during spontaneous states and optogenetic activation (Stark et al., 2015).

Presynaptic cooperativity enhances spike transmission probability

Pyramidal neurons in CA1 temporally organize into assemblies (Harris et al., 2003), whose expression is hypothesized to involve competition between orthogonally tuned assemblies via lateral inhibition (Buzsaki, 2010). The limited number of inhibitory neurons relative to pyramidal cells suggests that individual interneurons are shared by subsets of the pyramidal neuron population dependent upon their needs at a given time (Dupret et al., 2013). We found that temporally proximal spiking of pyramidal neurons, as occurs during assembly activation, enhances spike transmission probability. Such enhancement is also observed for juxtacellularly and optogenetically evoked presynaptic spikes, suggesting that network driven increased excitability of the postsynaptic interneuron is unlikely to make a major contribution to this effect. However, we did find that near-synchronous spiking of pyramidal neuron pairs (<2 ms interspike intervals) occurred when their postsynaptic targets had a higher firing rate, and that pyramidal neuron pairs which target common postsynaptic interneurons fire together more often than those with no shared targets. This increase in pyramidal cell synchrony may reflect a synchronizing effect of recurrent inhibition (Cobb et al., 1995), though excitatory inputs from CA3 pyramidal cells may also play a role. Such recurrent interactions may underlie the propensity of CA1 circuits to generate ripple oscillations in response to transient excitation (Stark et al., 2014). Overall, these observations suggest that a change in synaptic strength between pyramidal cells and interneurons, in particular via the relative timing of multiple pyramidal neurons, can effectively reconfigure CA1 circuits and potentially pyramidal neuron assemblies.

Activity dependence of spike transmission probability depends upon presynaptic spike history

A critical component of circuit dynamics and computation is the short-term plasticity of excitatory synaptic transmission (Abbott et al., 1997, Stevens and Wang, 1995, Zucker and Regehr, 2002), including from pyramidal cells to interneurons in CA1 (Ali et al., 1998, Losonczy et al., 2002). Due to the difficulty in obtaining recordings of monosynaptic EPSPs in vivo, the majority of the supporting data in this field has been obtained in vitro (but see Pala and Petersen, 2015). Such experiments are necessarily performed under artificial conditions, such as elevated extracellular Ca²⁺ concentration, which are known to critically affect synaptic transmission. Furthermore, most studies have utilized stimulus patterns which do not have the same statistics as in vivo spike trains. We thus investigated the short-term plasticity of pyramidal-interneuron connections in vivo, using spike transmission probability as a metric. The mechanisms underlying short-term plasticity of transmission probability likely include those typically associated with short-term plasticity of synaptic transmission (Zucker and Regehr, 2002). However, other factors may also be involved, such as conduction failures, level of presynaptic cooperativity, as well as refractoriness and resonance of the postsynaptic neuron (Figure 7).

We found that the relationship between presynaptic interspike interval and transmission probability was more complex than predicted by in vitro data. A fraction of single pyramidal neurons made a depressing connection with one interneuron and a facilitating connection with another, as described in the neocortex in vitro (Markram et al., 1998, Reyes et al., 1998). However, we additionally found that the expression of facilitation or depression is not dependent upon the identity of the postsynaptic neuron, as has been suggested previously (Ali et al., 1998), because the direction of short-term plasticity can vary even between different connections of the same postsynaptic interneuron. Additionally, many of the connections we observed had dynamics that were more complex than facilitation or depression. This included examples of connections which had ‘preferred’ interspike intervals, some correlating to the resonant properties of some interneurons as well as the timescales of hippocampal population rhythms. The role of postsynaptic resonance is supported by our finding that transmission probability is highest for specific postsynaptic ISI’s (Figure 7), which are in the temporal range of spiking resonance observed in interneurons recorded in vitro (Beatty et al., 2015, Pike et al., 2000). Overall, our findings indicate that short-term plasticity is synapse-specific rather than neuron-specific, and that frequency filtering of spike transmission can be exploited for tuning network dynamics.

Short-term plasticity may play an important role in hippocampal circuit operations including: routing excitatory inputs (Abbott et al., 1997), shifting somatic/proximal dendritic inhibition to distal dendritic inhibition within place fields (Fernandez-Ruiz et al., 2017, Pouille and Scanziani, 2004), and redistribution of interneuron membership in cell assemblies during learning (Dupret et al., 2013, Trouche et al., 2016). In this way, interneurons could provide enhanced inhibition required to facilitate the temporal synchronization of pyramidal cells and maintain the stability of currently active assemblies while suppressing competing ones. Transient interneuron recruitment may be critical to organizing the cell assembly sequences that underlie numerous cognitive functions. In general, plastic changes in the engagement of inhibitory feedback circuitry enable the dynamic regulation of excitability in cortical microcircuits. The present study provides a novel and comprehensive understanding of the short-term dynamics of monosynaptic connections between pyramidal neurons and interneurons in vivo.

STAR Methods

CONTACT FOR REAGENT AND RESOURCE SHARING

Further information and requests for resources and reagents should be directed to and will be fulfilled by the Lead Contact, Gyorgy Buzsaki (Gyorgy.Buzsaki@nyumc.org)

EXPERIMENTAL MODEL AND SUBJECT DETAILS

All protocols were approved by the Institutional Animal Care and Use Committee of New York University.

CaMKII::ChR2 mice are the F1 generation of homozygous CaMKII-Cre (005359; www.jax.org) crossed with homozygous Ai32 mice (012569; www.jax.org). Expression of channelrhodopsin-2 (h134r) is restricted to pyramidal neurons (Stark et al., 2012).

PV::ChR2 mice are the F1 generation of homozygous PV-Cre (008069; www.jax.org) crossed with homozygous Ai32 mice (012569; www.jax.org). Expression of channelrhodopsin-2 (h134r) is restricted to parvalbumin expressing neurons (Stark et al., 2012).

For both strains, male mice aged 6–12 months were used for all experiments.

METHOD DETAILS

Juxtacellular/extracellular recording in awake head-fixed mice

Mice (N = 8) were implanted with titanium head plates (Guo et al., 2014). A 50 μm stainless steel ground wire was implanted between the skull and dura over the cerebellum. A ~200 μm diameter craniotomy was made and the dura was removed over dorsal hippocampus (mm from bregma: −1.75, lateral 1.75). The craniotomy was covered with Kwik-Sil (World Precision Instruments) until the day of recording. Mice were habituated to head fixation over one week, and were allowed to run on top of a 15 cm diameter wheel during fixation. On the day of recording, the Kwik-Sil was removed, and the combined juxtacellular electrode – silicon probe (glass electrode pulled from 1 mm OD 0.7 mm ID borosilicate glass, TW100F-4, WPI; silicon probe was either a A1x32-Poly2 or A1x32-Poly3 (NeuroNexus) affixed with light cure epoxy (Norland Products Inc) or dental acrylic) was lowered 1 mm to the ventral cortex overlying CA1 using a 3-axis robotic manipulator (Sutter MP-285) and left in place for 20–30 minutes to allow the tissue to relax. Electrodes were then lowered in 20 μm steps until sharp-wave ripple oscillations could be observed, at which point the advancement was slowed to 5 μm steps until a cell was encountered. Pulses of 50–100 ms, ~1–10 nA were applied either at a regular 1 Hz, or at irregular intervals randomly jittered from trial to trial from 0.5–1.5 or 1.5–2.5s, until spikes were elicited in the juxtacellularly recorded neuron, at which point stimulation was continued until at least 1000 spikes were elicited. Spikes which occurred during the stimulus were considered as evoked, and those which occurred at all other times were considered as spontaneous.

Extracellular recordings and cell-type specific optogenetic manipulation in freely behaving mice

Thirty-two channel silicon probes (20 μm intersite spacing) with integrated μLEDs (Kim et al., 2016, Wu et al., 2015), or 64 channel silicon probes with diode-coupled optic fibers affixed to the shanks (Stark et al., 2012), were implanted in 6–12 month old male CaMKII::ChR2 (N = 4) or PV::ChR2 mice (N = 5). Stimulation protocols were programmed via a Power1401 microprocessor (Cambridge Electronic Design), controlling μLEDs directly, or laser diodes through a constant current source (Thorlabs Inc). Recordings lasted >3 hours, while mice freely behaved in their home cage. We stimulated with 100ms half sine waves, 50 and 100 ms square pulses, with random inter-stimulus interval (minimum time of 500 ms, maximum 6000 ms).

Data acquisition

Juxtacellular signals were acquired with an IR-183 amplifier (Cygnus; www.cygnustech.com), then filtered (0.01–6 kHz), digitized (20 or 30 kHz) and recorded using an Intan RHD2000 system (Intan Technologies LLC). Extracellular signals were recorded directly with the same RHD2000 system using the same parameters.

Spike sorting

Isolating spike waveforms from nearby neuronal sources is a known challenge for extracellular recordings. Waveform feature based clustering prohibits the detection of spikes emitted from two neurons within 1.2 ms. Template-based clustering algorithms partially solves this issue, and for this reason we used Kilosort (Pachitariu et al., 2016), to extract and classify waveforms from the broadband (20 or 30 kHz sampling) signal recorded from mouse CA1. We systematically defined many more clusters than the number of expected recordable neurons (4–16 times the number of recording channels) and merged units according to similar waveforms and common refractoriness. Free parameters used for automated sorting are listed below:

ops.Nfilt	(4 to 16) * numberChannels
ops.nt0	32
ops.whitening	‘full’
ops.nSkipCov	1
ops.whiteningRange	32
ops.criterionNoiseChannels	0 to 0.1
ops.Nrank	3
ops.nfullpasses	6
ops.maxFR	20000
ops.fshigh	300
ops.ntbuff	64
ops.scaleproc	200
ops.Th	[4 10 10]
ops.lam	[5 20 20]
ops.nannealpasses	4
ops.momentum	1./[20 800]
ops.shuffle_clusters	1
ops.mergeT	.1
ops.splitT	.1
ops.initialize	‘no’
ops.spkTh	.25
ops.loc_range	[3 1]
ops.long_range	[30 6]
ops.maskMaxChannels	5
ops.crit	.65
ops.nFiltMax	10000

Previously published units from the rat were extracted using KlustaKwik which is a non-template based method (Harris et al., 2000, Mizuseki et al., 2009). A subset of spiking data from the mouse was extracted with both spike sorting algorithms (Kilosort vs Klustakwik) and qualitatively comparable results were found for estimating the presence/absence of a synapse (data not shown) likely due to the fact that the peak of the synaptic synchrony (1.5 –2.5 ms) falls outside of the spike shadowing window (−0.6 – +0.6 ms).

Cell classification and radial distance estimation

Cell types were classified according to: mean firing rate, mode inter-spike interval, burstiness, and spike asymmetry (Sirota et al., 2008). Burstiness was the proportion of spikes with <6 ms ISI divided by baseline rate, calculated as the mean number of spikes with ISIs 50–100 ms apart. The data were z-scored and mapped to a 3 dimensional sub-space using t-SNE (perplexity = 30, number of iterations = 500). Following this dimensionality reduction, grouping was achieved via the density-based spatial clustering of applications with noise (DBSCAN) algorithm with radius ε = 5 and the minimum neighborhood size 5. Under a wide range of parameters, a fast-spiking cluster always emerged, however, the current values were chosen to disambiguate a second class of interneuron. The chosen protocol also split the pyramidal population, which is known to be heterogeneous. Because pyramidal cell diversity was not the focus of the present work, the pyramidal populations were re-merged. A subset of the recordings were done in PV::ChR2 mice in which parvalbumin positive interneurons could be driven with light. In these mice (N = 5), the fast-spiking interneuron group (N = 18) showed significantly more light modulation than the non-FS cluster (N = 38) (Figure S1C). The three neuronal groups were also physiologically confirmed by identifying mono-synaptic connections from the pyramidal cluster to the two interneuron clusters (Figure S1).

The position of the unit on the radial axis (dorsal to ventral) was taken as the recording site with the largest amplitude, non-filtered waveform. This was referred to the center of the pyramidal cell layer which was defined by the recording site with the largest ripple amplitude and nonnegative sharp-wave deflections (Mizuseki et al., 2011).

Optogenetic Modulation

To determine whether a unit was light modulated two criteria were required, 1) statistically significant increase in firing, and 2) an increase in firing rate >50% of the spontaneous rate. To test for significant rate changes, the number of spikes emitted during each pulse was tabulated and compared to the number emitted during the same interval within two seconds prior to light delivery. These counts were tested using a Wilcoxon ranksum non-parametric test of means and only units with highly significant (p < 10⁻¹⁰) firing rate increases were retained. These stringent methods were used to maximize decoupling of the presynaptic neuron from the background network activity.

Validation of synapse detection and connection strength estimation using baseline corrected cross-correlation

First, only light-modulated pyramidal cells that emitted >1000 spikes during stimulation were considered. For presynaptic spikes emitted during light stimulation, cross-correlations (0.4 ms binning) were generated with the spike trains from each interneuron. To generate true positive labels, two criteria were required, 1) the peak in the CCG needed to exceed that from the slowly co-modulated baseline, and 2) the peak in the causal direction (positive lags) needed to be significantly larger than the largest peak in the anti-causal direction (negative lags). To generate the lower frequency baseline, λ_slow, the observed CCG was convolved with a “partially hollow” Gaussian kernel (Stark and Abeles, 2009), with a standard deviation of 10 ms, with a hollow fraction of 60%. The probability of obtaining an observed (or higher) synchrony count in the m^th time lag of the observed CCG (0.8 to 2.8ms), given the expected, low frequency baseline rate λ_slow(m) in the same bin was estimated using the Poisson distribution (Abeles, 1982, Stark and Abeles, 2009) with a continuity correction,

$$P_{\mathit{fast}}\left(n\text{or}\mathit{more}\mid {\lambda }_{\mathit{slow}}(m)\right)=1-\sum _{x=0}^{n-1}\frac{e^{-{\lambda }_{\mathit{slow}}(m)}{\lambda }_{\mathit{slow}}{(m)}^x}{x!}-.5\ast \frac{e^{-{\lambda }_{\mathit{slow}}(m)}{\lambda }_{\mathit{slow}}{(m)}^n}{n!}$$

The probability of obtaining the observed (or higher) synchrony count in the positive m^th time lag of the observed CCG (0.8 – 2.8ms), higher than the maximum λ_anticausal (−m) at a negative time lag from −2.0 to 0 ms, was similarly estimated using the Poisson distribution with a continuity correction,

$$P_{\mathit{causal}}\left(n\text{or}\mathit{more}\mid {\lambda }_{\mathit{anticausal}}(-m)\right)=1-{\sum }_{x=0}^{n-1}\frac{e^{-\lambda }{\mathit{anticausal}}^{(-m)}{\lambda }_{\mathit{anticausal}}{(-m)}^x}{x!}-0.5\ast \frac{e^{-\lambda }{\mathit{anticausal}}^{(-m)}{\lambda }_{\mathit{anticausal}}{(-m)}^n}{n!}$$

During stimulations, connections were labeled as synapses if both P_fast and P_causal were < 0.01. To unambiguously label non-connected pairs, both P_fast and P_causal were required to be > 0.1.

For spontaneous spikes emitted outside of stimulation windows, P_causal and P_fast were calculated at the peak CCG count observed at lags between 0.8 – 2.8ms. Only pairs with P_fast <0.001 were considered. P_causal was then varied as a threshold for synapse classification in the receiver operator characteristic analysis using the experimentally labeled connections as the “ground truth” tags. The optimal operating point (P_causal = 0.0026) was calculated using the MATLAB R2016b function perfcurve.

The synaptic strength was estimated as the excess in causal spike transmission probability from that expected given λ_slow. Therefore, the spike transmission probability after n presynaptic spikes was defined as

$$\text{spike}\text{transmission}\text{probability}={\sum }_{m=0.8ms}^{2.8ms}\left(\mathit{CCG}{(m)}_{\mathit{observed}}-{\lambda }_{\mathit{slow}}(m)\right)/n$$

GLM methods

Since the convolution technique (Stark and Abeles, 2009) is agnostic to the source of slow-timescale synchrony, it was possible that the synchrony captured could be influenced by the spiking-history of the post-synaptic neuron. We were also interested in how much of the slow-timescale modulation could be explained by known sources of modulation. Thus, we developed a complementary pairwise GLM (Harris et al., 2003; Pillow et al., 2008) to capture fast timescale synchrony between putative PYR-INT pairs.

The GLM was used to predict the time-varying hazard λ of observing a spike in the post-synaptic neuron according to an inhomogeneous Poisson process, as a function of a number of known time-varying regressors R_r(Θ) (Figure S3)

$${\lambda }_t=\prod _{r=1}^{N_R}{R}_{r,t}(\mathit{\Theta })$$

Where Θ are the parameters corresponding to each regressor. Each regressor was of an exponential form. The prediction was evaluated according to the negative log-likelihood of observing the post-synaptic spike train given the time-varying hazard, assuming an inhomogeneous Poisson process:

$$l(S_2\mid \mathit{\Theta })=-\sum _{t=0}^T{\lambda }_t+\sum _{s\in S}{S}_{2_t}·\mathit{log}({\lambda }_t)$$

Parameters were fit by minimizing the negative log-likelihood using MATLAB R2016’s fmincon routine.

To remain agnostic to the exact form of the time-varying transmission probability from the pre-to the postsynaptic neuron, we fit a piece-wise function (Figure S3. 1J, E) with a weight corresponding to each bin (Δ_t=0.008ms; +/− 0.016ms; 40 weights). The center bin was not estimated due to concerns about spike shadowing. The contribution of the presynaptic spike train S₁ was defined by:

$$R_{\mathit{pre}}=\mathit{exp}\left(S_1\ast K_{\mathit{pre}}\right)$$

Where K_pre is the estimated transmission kernel. To decrease the computational run time we calculated efficient gradient calculation routines, taking advantage of the fact that the convolution by one-hot vectors (since $\frac{dK}{d{k}_i}-\delta (t-i{\mathrm{\Delta }}_t)$, the Dirac delta function) are equivalent to time-shifts corresponding to the position of the time bin i. This approach allowed us to directly compare the form of the convolution and GLM obtained kernels (Figure S3). We used the same approach to capture the influence of the post-synaptic cells own spiking history:

$$R_{\mathit{post}}=\mathit{exp}\left(S_2\ast K_{\mathit{post}}\right)$$

Where K_post is the fitted post-history kernel. Since the post-kernel must be symmetric, the first half (20) kernel weights were estimated and subsequently duplicated.

A sum-of-squares penalty term $L_2=\alpha \left(K_{\mathit{pre}}^T{K}_{\mathit{pre}}+K_{\mathit{post}}^T{K}_{\mathit{post}}\right)$ was applied to prevent overfitting of the fast-timescale parameters, where α = 20.

To capture the effect of network level theta modulation, we used a circular Von-Mises type regressor (Harris et al., 2003):

$$R_{\theta }(t)=\frac{exp(\kappa ·cos(\overline{{\varphi }_{\theta }}-{\varphi }_{\theta }(t))}{2\pi I_0(\kappa )}$$

Where κ is the depth modulation parameter which controls the sharpness of the neuron’s tuning to the preferred theta phase $\acute{{\varphi }_{\theta }}$ (analogous to the variance of a non-periodic distribution). I₀ is the 0^th order modified Bessel function and ϕ_θ(t)is the local network theta phase calculated from the LFP.

To capture ripple modulation, we used a modified version of the theta regressor to prevent overfitting during periods of no ripple modulation:

$$R_{\mathit{RIP}}(t)={\left[\frac{\mathit{exp}\left(\kappa ·\mathit{cos}\left(\acute{\theta }-\theta (t)\right)\right)}{2\pi I_0(\kappa )}\right]}^{P_{\mathit{RIP}}}$$

Where P_RIP is the binarized local ripple power recorded from the LFP and all other parameters are equivalent to those in the theta regressor.

The multi-unit-activity (MUA), defined as the total spike count from all neurons recorded in a given trial in bin t, was also used as a regressor:

$$R_{\mathit{MUA}}(t)=\mathit{exp}\left(M·\mathit{MUA}(t)\right)$$

Where M is a gain parameter. Finally, the baseline firing rate was fitted as:

$$R_0(t)=\mathit{exp}(F_0)$$

Where F₀ defined the natural logarithm of the baseline firing rate (Hz).

The transmission kernels obtained from the GLM were defined as multiplicative increases in rate above the baseline firing rate as captured by the other regressors. However, the fast-timescale component of the convolution method was defined in absolute units of spikes/bin. To compare the two (Figure S3), we converted the fast-timescale component to a multiplicative rate by dividing by the slow-timescale synchrony:

$$K_{\mathit{conv}}=\frac{\mathit{CCG}-{\lambda }_{\mathit{slow}}}{{\lambda }_{\mathit{slow}}}$$

When calculating the ROC curve, we performed the reverse operation, converting the GLM kernels into absolute units relative to the slow-timescale baseline λ_slow,GLM. To obtain λ_slow,GLM (Figure S3), we first generated the time-varying rate from the product of the regressors and their estimated parameters. We then averaged the rate in the m^th bin surrounding each spike from the presynaptic cell, for all bins in the CCG. We then used the same equations defined for the convolution technique to calculate P_fast and P_causal for the GLM fits.

The classification performance of the p-value feature (described above) was compared to two other features (Figure S3). Excess causal synchrony was defined as the sum of the 0.8–2.8ms bins, normalized by the sum of the kernel. Excess causal – anticausal synchrony was defined as:

$$\frac{{\sum }_{m=0.8ms}^{2.8ms}{\lambda }_{\mathit{fast}}(m)-{\sum }_{m=-0.8ms}^{-2ms}{\lambda }_{\mathit{fast}}(m)}{{\sum }_{-\infty }^{\infty }{\lambda }_{\mathit{fast}}(m)}$$

Separability (Fig. 1E) was defined as the binary loss classification accuracy of a linear SVM using a given feature.

Detection of fast INT-INT and PYR-INT synchrony

To detect fast synchrony, independent of synapse detection, two consecutive 0.4ms CCG bins must have shown greater (P_fast < 0.01) synchrony than expected from λ_slow.

Calculation of the inter-spike interval distribution

For each pair of neurons, we first counted the number of instances in which Neuron A fired followed by Neuron B at some ISI = Δt without either neuron firing during Δt. This count was compared against a null distribution in which a constant value from 0–30 seconds was added to each spike train, thus preserving first order spike train statistics but shuffling second order interactions. In this manner, spike trains were shuffled 1000 times and the excess ISI count was measured in the number of standard deviations the observed count was higher/lower than the mean of the shuffled distribution. Statistics comparing different groups were done through non-parametric Wilcoxon ranksum comparison of these means.

Spike transmission probability conditioned on prior neural activity

We considered how spike transmission depended upon the previous activity of the presynaptic neuron (Figure 6), the postsynaptic neuron (Figure 7G), and other simultaneously recorded convergent or divergent pyramidal cells (Figure 5). For comparing how the timing of prior activity from other neurons (including the postsynaptic cell) influences spike transmission, we retained only those spikes from presynaptic Neuron 1 that followed that of Neuron 2 at some ISI = Δt during which neither neuron spiked in the interim. From these sub-sampled spikes, the spike transmission probability was calculated as before. For cases in which the prior activity of the presynaptic cell was under study (e.g. short-term depression/facilitation), we retained only those spikes from Neuron 1 that followed prior spiking at some ISI = Δt. Again, the spike transmission probability was calculated as before. Δt was chosen from N = 40 logarithmically spaced ISIs from 0.5 ms to 2000ms).

We also considered how the rate of the postsynaptic cell at the time of presynaptic spiking influenced spike transmission probability. For this analysis, we calculated the instantaneous firing rate of the postsynaptic cell 0 to 200 ms before each presynaptic spike and sub-sampled the presynaptic spiking accordingly. From these sub-sampled spikes, the spike transmission probability was calculated as above.

Analysis of short-term facilitation and depression

Short-term facilitation and depression were measured by comparing how spike transmission probability of the second spike of a presynaptic “burst” changed as a function of interspike interval. Following Tsodyks and Markram’s analysis of short-term plasticity (Tsodyks et al., 1998, Tsodyks and Markram, 1997), we fit three models to describe how spike transmission probability is affected by presynaptic inter-spike interval. For the full model with both depression and facilitation, the synaptic filter, I, was defined as the transmission probability at each presynaptic ISI as:

$$I=A\ast (S+F\ast D),\text{where}S=U\ast e^{-\mathit{ISI}/{\tau }_{\mathit{synapse}}}D=1-U\ast e^{-\mathit{ISI}/{\tau }_{\mathit{depression}}}F=U\ast e^{-\mathit{ISI}/{\tau }_{\mathit{facilitation}}}+U\ast \left(1-U\ast e^{-\mathit{ISI}/{\tau }_{\mathit{facilitation}}}\right)$$

The constant, A, reflects the asymptotic connection strength as defined by the spike transmission probability. τ_synapse, τ_depression, τ_facilitation reflect the time constants describing synaptic integration, depression, and facilitation. The range of τ_synapse was 0–3 ms, while the range of τ_depression and τ_facilitation were between 0–10,000 ms. The constant U is an abstract free parameter that reflects the amount of synaptic “resources” available with every presynaptic spike.

The depression only model took the same form except,

$$I=A\ast (S+D)$$

Similarly, for the facilitation only model

$$I=A\ast (S+F)$$

To compare the model fits with different degrees of freedom (N = 4 for facilitation and depression, N = 5 for the full model), the goodness-of-fit was assessed with an adjusted R² and compared to that in which the models were fit 1000 times to data in which ISIs were randomly shuffled. Depressing synapses were those in which the observed adjusted R² was >95% larger than the shuffled data and the difference between the full model R² and the depression R² was <95% from the difference in the shuffled models. The same criteria was used for the facilitating connections using the adjusted R² from the facilitation only model. Connections requiring the full model were those with adjusted R² >95% higher than that observed in the shuffled data and could not be defined by the more parsimonious models.

Ripple detection

Ripple detection was performed on the recording site in the center of the pyramidal cell layer with the largest ripple amplitude. The 20 or 30 kHz sampled data was band-pass filtered from 100–200 Hz, squared and z-score normalized. Ripples were defined as events starting at 1SD, peaking at >2 SD, and remaining at >1SD for <200ms and >20ms around the peak. When possible, a control detection protocol was performed on a channel whose recording site was external to the hippocampus, and false positive “ripple” events (e.g. muscle artifacts) detected on both channels were removed. Ripples events were removed for synapse detection and the tabulation of interspike intervals. To increase the number of synchronous events under study, ripples were included for the analysis of how spike transmission changes as a function of prior network activity. Excluding ripples from this analysis decreases the resonant boost at ripple frequency in Figure 5B, but otherwise does not qualitatively change the outcome of the present analyses.

QUANTIFICATION AND STATISTICAL ANALYSIS

All statistical analyses were performed in MATLAB (MathWorks). All tests were two-tailed. Tests include: Non-parametric Mann-Whitney U test, Wilcoxon’s signed rank test, Kruskal-Wallis one-way analysis of variance, two-way analysis of variance. Correlations were computed using Pearson’s or Spearman’s correlation coefficient, noted in text. When comparing multiple time points (e.g. Figure 5F), the alpha level was Bonferroni-corrected according to the number of repeated tests (time points).

DATA AND SOFTWARE AVAILABILITY

LFP and spike data will be deposited in http://CRCNS.org and freely available upon publication.

• Pyramidal cell-interneuron monosynaptic connections identified using spike timing

• Skewed distribution of connection probability and strength

• Short-term plasticity of connection strength is synapse specific

• Presynaptic cooperativity and postsynaptic timing impact spike transmission probability