Off-resonance NOVEL

Abstract

Dynamic nuclear polarization (DNP) is theoretically able to enhance the signal in nuclear magnetic resonance (NMR) experiments by a factor γ_e/γ_n, where $\gamma$’s are the gyromagnetic ratios of an electron and a nuclear spin. However, DNP enhancements currently achieved in high-field, high-resolution biomolecular magic-angle spinning NMR are well below this limit because the continuous-wave DNP mechanisms employed in these experiments scale as ${\omega }_0^{-n}$ where n ∼ 1–2. In pulsed DNP methods, such as nuclear orientation via electron spin-locking (NOVEL), the DNP efficiency is independent of the strength of the main magnetic field. Hence, these methods represent a viable alternative approach for enhancing nuclear signals. At 0.35 T, the NOVEL scheme was demonstrated to be efficient in samples doped with stable radicals, generating ¹H NMR enhancements of ∼430. However, an impediment in the implementation of NOVEL at high fields is the requirement of sufficient microwave power to fulfill the on-resonance matching condition, ω_0I = ω_1S, where ω_0I and ω_1S are the nuclear Larmor and electron Rabi frequencies, respectively. Here, we exploit a generalized matching condition, which states that the effective Rabi frequency, ${\omega }_{1S}^{eff}$, matches ω_0I. By using this generalized off-resonance matching condition, we generate ¹H NMR signal enhancement factors of 266 (∼70% of the on-resonance NOVEL enhancement) with ω_1S/2π = 5 MHz. We investigate experimentally the conditions for optimal transfer of polarization from electrons to ¹H both for the NOVEL mechanism and the solid-effect mechanism and provide a unified theoretical description for these two historically distinct forms of DNP.

I. INTRODUCTION

Dynamic nuclear polarization (DNP) is now well established as a method to enhance the sensitivity of high-field nuclear magnetic resonance (NMR) experiments. Specifically, polarizing agents are introduced into the NMR sample, usually in the form of stable radicals, and microwave irradiation at or near the electron Larmor frequency, ω_0S, induces the transfer of the electron spin polarization to the nuclei enhancing the NMR signal intensity. If DNP and NMR experiments are performed at the same magnetic field and temperature, a maximum signal enhancement of ${\gamma }_e/{\gamma }_{1H}=658$ can be achieved for protons, where γ_e and γ_1H are the gyromagnetic ratios of electrons and protons.

In recent years, DNP in combination with magic-angle spinning (MAS) NMR has enabled a multitude of new structural studies of biomolecular systems^1–9 and a variety of materials^10–20 at magnetic fields up to 18.8 T (800 MHz for ¹H or 527 GHz for g ∼ 2 electrons). The current DNP mechanisms used in the 5-18.8 T regime rely on continuous-wave (CW) microwave radiation generated by dedicated gyrotons.^21–23 Unfortunately, these CW DNP mechanisms, i.e., the solid-effect (SE),^24–27 cross-effect (CE),^28–31 and thermal mixing (TM),³² decrease in efficiency as ω_0I, the nuclear Larmor frequency, increases. The Overhauser effect (OE)^33–35 recently observed in insulating solids appears to be an exception to this trend although a fundamental understanding for the field dependence of this mechanism is yet to be developed.³⁶ However, for all four CW DNP mechanisms, the signal enhancements at very high fields are still well below the theoretical maximum of 658.

In pulsed DNP methods, microwave pulses induce polarization transfer and these methods are, in principle, better suited for DNP at high magnetic fields for two reasons. First, by applying microwave pulses of specific length, phase, amplitude, and/or shape, possibly in combination with RF pulses, the electron-nucleus system is manipulated in a manner where the polarization transfer efficiency is independent of ω_0I. Analogous polarization transfer schemes such as cross polarization and INEPT are ubiquitous in NMR and are essential in the detection of low-gamma nuclei like ¹³C and ¹⁵N.^37,38 Second, microwave irradiation with a low duty cycle minimizes unwanted sample heating.³⁹

One recently successful approach to pulsed DNP is the NOVEL (nuclear orientation via electron spin locking) experiment,^40–42 where polarization is transferred from electrons to nuclei via electrons spin locked by an on-resonance microwave field. The matching condition for NOVEL requires that the electron Rabi frequency, ω_1S, equals the nuclear Larmor frequency, ω_0I, and is thus a microwave rotating-frame/nuclear laboratory-frame matching condition, ω_1S = ω_0I, closely analogous to Hartmann-Hahn cross polarization^37,43 (vide infra). We have recently shown that NOVEL is fast and efficient in producing bulk ¹H polarization, yielding enhancements up to 430 in a frozen glycerol/water matrix doped with the narrow-line radical trityl OX063, a system of general applicability in biomolecular DNP/MAS NMR.⁴⁴ We note that these experiments were performed at 0.35 T (15 MHz for ¹H or 9.8 GHz) because of the availability of pulsed microwave technology at this frequency.^44–48

The major obstacle to extending the NOVEL experiment to high-field MAS NMR is the substantial Rabi frequency required to fulfill the matching condition, ω_1S = ω_0I. Currently, there are kilowatt microwave amplifiers operating at frequencies up to 94 GHz [corresponding to (ω_01H/2π) = 143 MHz]⁴⁹ that can generate coherent microwave pulses. In addition, gyroamplifiers are under development that operate as high as 250 GHz or (ω_01H/2π) = 380 MHz.⁵⁰ However, these are modest ¹H Larmor frequencies, and it is desirable to perform pulsed DNP at 600-800 MHz where is it more difficult to fulfill the NOVEL matching condition.

As mentioned above, NOVEL is based on ideas similar to the cross-polarization (CP) experiment³⁷ used widely in MAS NMR⁵¹ and proposed initially by Hartmann and Hahn in 1962.⁴³ In particular, in a CP experiment, transfer of polarization occurs between two dipole-coupled nuclear species when both are irradiated at equal Rabi frequencies in their respective rotating frames. In general, the effective Rabi frequency is given by ${\omega }_{1I}^{eff}=\sqrt{{\mathrm{\Omega }}_I^2+{\omega }_{1I}^2}$, where ${\mathrm{\Omega }}_I={\omega }_{0I}-{\omega }_{RF}$ is the RF resonance offset and ω_1I is the nuclear Rabi frequency. The initial CP experiments employed RF irradiation applied on resonance for both nuclei (Ω_I = 0). However, off-resonance RF irradiation (Ω_I $\ne$ 0) can be used in order to satisfy the Hartmann-Hahn matching condition with reduced RF powers.⁵² This technique is also exploited in the SPECIFIC-CP scheme to perform frequency selective cross-polarization.⁵³

In this study, we show that the high-power requirement for microwave irradiation in the NOVEL scheme can be relaxed by irradiating the electron spins off-resonance. Instead of the commonly used NOVEL on-resonance condition, ω_1S = ω_0I, we exploit the general matching condition, $\sqrt{{\mathrm{\Omega }}_S^2+{\omega }_{1S}^2}={\omega }_{0I}$, with ${\mathrm{\Omega }}_S={\omega }_{0S}-{\omega }_{\mu \mathit{w}}$ the microwave resonance offset. Using this condition in an “off resonance NOVEL” experiment, we obtain an enhancement factor of 266 using a microwave amplitude of only 5 MHz, which is roughly 70% of the enhancement factor obtained with on-resonance NOVEL at a ¹H Larmor frequency of 15 MHz. Going further off resonance (Ω_S → ω_0I), the generalized matching condition evolves to the conventional CW SE matching condition, ω_μw = ω_0S ± ω_0I. We investigate both theoretically and experimentally the gradual transition between these two historically distinct DNP mechanisms. Our observations provide new perspectives for the implementation of pulsed DNP at high magnetic fields.

II. THEORETICAL ANALYSIS

In this section, we present an analytical description of microwave-induced magnetization transfer in an ensemble of coupled electron-nuclear spin systems, denoted by S and I, respectively. We divide the calculation into the following four steps. (1) We calculate an effective Hamiltonian for the coupled two-spin system under microwave irradiation using an appropriate interaction frame and average Hamiltonian theory (AHT)^54,55 with reasonable approximations. (2) We determine the time evolution of the initial density matrix under the influence of the effective Hamiltonian. (3) We calculate the scaling factors for the net enhancement factors from the alignment of the initial electron polarization and the spin-locking microwave irradiation. Finally, (4) we describe the experiments in frozen-solution or powder samples by incorporating orientational averaging.

A. The effective Hamiltonian

The Hamiltonian in the electron rotating frame and the nuclear lab frame is given in (1) and consists of the following terms from left to right: the microwave offset term, the nuclear Zeeman Hamiltonian, the secular and pseudo-secular hyperfine coupling terms, and the microwave excitation field. The microwave irradiation phase is set to −y to mimic the experimental settings,

$$\mathcal{H}={\mathrm{\Omega }}_S{S}_z-{\omega }_{0I}{I}_z+A{S}_z{I}_z+B{S}_z{I}_y-{\omega }_{1S}{S}_y.$$ (1)

Note that the pseudo-secular hyperfine couplings, B_xS_zI_x and B_yS_zI_y, are combined in BS_zI_y, with $B=\sqrt{B_x^2+B_y^2}$. The Hamiltonian can be transformed to a frame tilted by an angle θ around S_x such that the effective field of the electrons is along the z′ direction. The Hamiltonian in the tilted frame is calculated using the unitary operator $U_{tSL}=e^{-i\theta S_x}$, where the subscript “tSL” denotes a tilted, spin locked frame,

$$H_0^{\prime }=U_{tSL}^{†}{H}_0{U}_{tSL},$$

$$\begin{array}{ccc}\hfill H_0^{\prime }& =\hfill & {\omega }_S^{eff}{S}_{z^{\prime }}-{\omega }_{0I}{I}_z+A\left(S_{z^{\prime }}cos\theta +S_{y^{\prime }}sin\theta \right)I_z\hfill \\ & & +B\left(S_{z^{\prime }}cos\theta +S_{y^{\prime }}sin\theta \right)I_y,\hfill \end{array}$$ (2)

where tan(θ) = ω_1S/Ω_S and ${\omega }_S^{eff}=\sqrt{{\mathrm{\Omega }}_S^2+{\omega }_{1S}^2}$.

To investigate magnetization transfer mediated by the hyperfine interaction, we transform to an interaction/rotating frame of the nuclear Zeeman interaction and the effective microwave field [for compactness, we use the notation for c_θ = cos(θ) and s_θ = sin(θ)] which yields for the transformed Hamiltonian

$$\begin{array}{ccc}\hfill {\tilde{H}}_0^{\prime }& =\hfill & e^{i{\omega }_S^{eff}{S}_{z^{\prime }}t}{e}^{-i{\omega }_{0I}{I}_{z}t}\left(A{S}_{z^{\prime }}{I}_z{c}_{\theta }+A{S}_{y^{\prime }}{I}_z{s}_{\theta }+B{S}_{z^{\prime }}{I}_y{c}_{\theta }\right.\hfill \\ & & +\left.B{S}_{y^{\prime }}{I}_y{s}_{\theta }\right)e^{-i{\omega }_S^{eff}{S}_{z^{\prime }}t}{e}^{i{\omega }_{0I}{I}_{z}t}.\hfill \end{array}$$ (3)

Since the Hamiltonian in this frame is time dependent, we employ AHT to calculate the effective Hamiltonian and corresponding time evolution operator. In Eq. (3), the second and third terms are modulated by the single frequencies ${\omega }_S^{eff}$ and ω_0I, respectively, and are averaged in the effective Hamiltonian. The first term is not modulated by either of the two rotations and will survive in the average Hamiltonian. The fourth term in Eq. (3) is modulated at both frequencies and leads to the NOVEL/SE magnetization transfer upon matching the two frequencies. We consider the first and fourth terms for further analysis,

$$\begin{array}{ccc}\hfill {\tilde{H}}_0^{\prime }& =\hfill & A{c}_{\theta }{S}_{z^{\prime }}{I}_z+B{s}_{\theta }\left(S_{y^{\prime }}{I}_y{c}_{{\omega }_S^{eff}t}{c}_{{\omega }_{0I}t}-S_{x^{\prime }}{I}_x{s}_{{\omega }_S^{eff}t}{s}_{{\omega }_{0I}t}\right.\hfill \\ & & -\left.S_{y^{\prime }}{I}_x{c}_{{\omega }_S^{eff}t}{s}_{{\omega }_{0I}t}+S_{x^{\prime }}{I}_y{s}_{{\omega }_S^{eff}t}{c}_{{\omega }_{0I}t}\right).\hfill \end{array}$$ (4)

The $S_{z^{\prime }}{I}_z$ term commutes with the rest of the effective Hamiltonian. Moreover, in the system of interest, the narrow-line radical trityl, this term is small and does not lead to polarization transfer if we consider initial polarization in $S_{z^{\prime }}$. We therefore neglect it. The remaining terms in Eq. (4) can now conveniently be rewritten in terms of the double and zero quantum bases using the double quantum (DQ) $I_x^{14}=S_{x^{\prime }}{I}_x-S_{y^{\prime }}{I}_y$, $I_y^{14}=S_{x^{\prime }}{I}_y+S_{y^{\prime }}{I}_x$, and $I_z^{14}=\frac{S_{z^{\prime }}+I_z}{2}$ and zero quantum (ZQ) $I_x^{23}=S_{x^{\prime }}{I}_x+S_{y^{\prime }}{I}_y$, $I_y^{23}=S_{x^{\prime }}{I}_y-S_{y^{\prime }}{I}_x$, and $I_z^{23}=\frac{S_{z^{\prime }}-I_z}{2}$ operators,

$${\tilde{H}}_0^{\prime }=\frac{B{s}_{\theta }}{2}\left(\begin{array}{c}-cos\left(\left({\omega }_S^{eff}-{\omega }_{0I}\right)t\right)I_x^{14}+sin\left(\left({\omega }_S^{eff}-{\omega }_{0I}\right)t\right)I_y^{14}\\ +cos\left(\left({\omega }_S^{eff}+{\omega }_{0I}\right)t\right)I_x^{23}+sin\left(\left({\omega }_S^{eff}+{\omega }_{0I}\right)t\right)I_y^{23}\end{array}\right).$$ (5)

The matching conditions are ${\omega }_S^{eff}-{\omega }_{0I}=0$ for DQ and ${\omega }_S^{eff}+{\omega }_{0I}=0$ for ZQ magnetization transfer, respectively. If we choose the microwave resonance offset frequency and amplitude such that the parameters are close to the ZQ matching condition, i.e., $\mathrm{\Delta }\equiv {\omega }_S^{eff}+{\omega }_{0I}\approx 0$, then the DQ term oscillates rapidly and can be ignored in the average Hamiltonian. A similar analysis is possible for the DQ condition. Assuming $\left|{\omega }_S^{eff}\right|,\left|{\omega }_{0I}\right|\gg B$, the first (zeroth) order effective Hamiltonian can be calculated as the average Hamiltonian over a time period τ near the ZQ condition,

$$\begin{array}{ccc}\hfill {\overline{\tilde{H}}}_0^{\prime }& =\hfill & \frac{B{s}_{\theta }sin\left(\frac{\mathrm{\Delta }\tau }{2}\right)}{2\left(\mathrm{\Delta }\tau 2\right)}\left(cos\left(\frac{\mathrm{\Delta }\tau }{2}\right)I_x^{23}+sin\left(\frac{\mathrm{\Delta }\tau }{2}\right)I_y^{23}\right)\hfill \\ & =\hfill & \frac{B{s}_{\theta }sin\left(\frac{\mathrm{\Delta }\tau }{2}\right)}{2\left(\mathrm{\Delta }\tau 2\right)}\left(e^{-i\frac{\mathrm{\Delta }\tau }{2}{I}_z^{23}}{I}_x^{23}{e}^{i\frac{\mathrm{\Delta }\tau }{2}{I}_z^{23}}\right).\hfill \end{array}$$ (6)

B. Time evolution of the density matrix

Since the effective Hamiltonian from Eq. (6) is no longer time dependent, the corresponding evolution operator can be written as

$${\overline{\widetilde{U^{\prime }}}}_0=e^{-i\frac{\mathrm{\Delta }\tau }{2}{I}_z^{23}}{e}^{-i\frac{B{s}_{\theta }sin\left(\frac{\mathrm{\Delta }\tau }{2}\right)}{\mathrm{\Delta }\tau }t{I}_x^{23}}{e}^{i\frac{\mathrm{\Delta }\tau }{2}{I}_z^{23}}.$$ (7)

To calculate the density matrix at any given time, the initial density matrix, ${\rho }_0=S_{z^{\prime }}$, can be divided into the zero- and double-quantum bases,

$$S_{z^{\prime }}=I_z^{23}+I_z^{14}.$$ (8)

Only the zero-quantum part of the density matrix evolves and the double-quantum remains unaffected. The density matrix at time t is given by

$$\begin{array}{ccc}\hfill {\rho }_t& =\hfill & {Ũ}_0^{\prime }{S}_{z^{\prime }}{Ũ}_0^{\prime †}=I_z^{23}cos\left(\frac{B{s}_{\theta }sin\left(\mathrm{\Delta }\tau /2\right)}{\mathrm{\Delta }\tau }t\right)\hfill \\ & & -I_y^{23}sin\left(\frac{B{s}_{\theta }sin\left(\mathrm{\Delta }\tau /2\right)}{\mathrm{\Delta }\tau }t\right)cos\left(\frac{\mathrm{\Delta }\tau }{2}\right)\hfill \\ & & +I_x^{23}sin\left(\frac{B{s}_{\theta }sin\left(\mathrm{\Delta }\tau /2\right)}{\mathrm{\Delta }\tau }t\right)sin\left(\frac{\mathrm{\Delta }\tau }{2}\right)+I_z^{14}.\hfill \end{array}$$ (9)

The nuclear polarization transferred at time t is calculated by projecting the density matrix ρ_t on I_z,

$$⟨I_z^{†}\left|{\widetilde{U^{\prime }}}_0{S}_{z^{\prime }}{{\widetilde{U^{\prime }}}_0}^{†}\right.⟩=\frac{1}{2}\left(1-cos\left(B{s}_{\theta }\frac{sin\left(\mathrm{\Delta }\tau /2\right)}{\mathrm{\Delta }\tau }t\right)\right).$$ (10)

At the matching condition, Δ = 0, the polarization transfer is maximum at $t=\frac{\left(2k+1\right)2\pi }{B{s}_{\theta }},k\in I$. The first maximum in the electron-nuclear polarization transfer occurs at

$$t=\frac{2\pi }{B{s}_{\theta }}=\frac{2\pi }{B}\frac{\sqrt{{\mathrm{\Omega }}_S^2+{\omega }_{1S}^2}}{{\omega }_{1S}}.$$ (11)

Equation (11) shows that the polarization transfer time depends on the strength of the anisotropic hyperfine coupling (the electron-nuclear dipolar interaction), B, the microwave resonance offset, Ω_s, and the microwave amplitude, ω_1S.

C. Scaling factors

In the above analysis, we have considered the initial magnetization ${\rho }_0=S_{z^{\prime }}$ in the tilted frame. For effective spin-locking, $S_{z^{\prime }}$ must align with the microwave field during the mixing period. Therefore, in the on-resonance NOVEL experiment (and in standard CP in MAS NMR), a π/2 tilt pulse with a phase perpendicular to the mixing irradiation is applied before the mixing period. However, if Ω_S $\ne$ 0, only a fraction of the polarization aligns with the microwave field following the π/2 tilt pulse. This spin-locking efficiency is determined by the angle between the magnetization and the microwave irradiation and can be described by the scaling factors, which we derive below for NOVEL as well as for SE, see Table I.

TABLE I.

NOVEL and SE experimental schemes and matching conditions.

	NOVEL	SE
π/2 pulse	Yes	No
Scaling factor	${\kappa }_{NOVEL}={\left(\frac{{\mathrm{\Omega }}_S}{{\omega }_S^{eff}}\right)}^3\mp {\left(\frac{{\mathrm{\Omega }}_S}{{\omega }_S^{eff}}\right)}^2\pm 1$	${\kappa }_{SE}=c_{\theta }=\frac{{\mathrm{\Omega }}_S}{{\omega }_S^{eff}}$
On resonance, matched NOVEL or CW SE	ΩS = 0	ΩS = ±ω0I
On resonance μw amplitude	ω1S = ω0I	ω1S $\ll$ω0I
Off resonance, matched NOVEL	$\mathrm{\Delta }=\sqrt{{\mathrm{\Omega }}_S^2+{\omega }_{1S}^2}-{\omega }_{0I}\approx 0$	$\mathrm{\Delta }=\sqrt{{\mathrm{\Omega }}_S^2+{\omega }_{1S}^2}-{\omega }_{0I}\approx 0$
Slow (not matched)	Δ $\ne$ 0	Δ $\ne$ 0

In our NOVEL experiments, the tilt pulse and the mixing pulse have the same amplitude and frequency; only their phases differ by π/2. The effective microwave Hamiltonian for the tilt pulse is

$$\begin{array}{ccc}\hfill H_{eff}^{tilt}& =\hfill & {\mathrm{\Omega }}_S{S}_z+{\omega }_{1S}{S}_x={\omega }_S^{eff}\left(cos\left(\theta \right)S_z+sin\left(\theta \right)S_x\right)\hfill \\ & =\hfill & {\omega }_S^{eff}\left(e^{-i\theta S_y}{S}_z{e}^{i\theta S_y}\right).\hfill \end{array}$$ (12)

The initial polarization is ρ₀ = S_z, and following the pulse, the polarization is

$${\rho }_1=e^{\left(-i{H}_{eff}^{tilt}t\right)}{\rho }_0{e}^{\left(i{H}_{eff}^{tilt}t\right)}.$$ (13)

Using ${\omega }_S^{eff}t=\pi /2$ and transforming to the tilted frame, as we did to obtain Eq. (2), the polarization during the spin-lock irradiation can be expressed as follows:

$$\begin{array}{ccc}\hfill {\rho }_1^{\prime }& =\hfill & e^{\pm i\theta S_{x^{\prime }}}{e}^{-i\theta S_{y^{\prime }}}{e}^{-i\frac{\pi }{2}{S}_{z^{\prime }}}{e}^{i\theta S_{y^{\prime }}}{S}_{z^{\prime }}{e}^{-i\theta S_{y^{\prime }}}{e}^{i\frac{\pi }{2}{S}_{z^{\prime }}}{e}^{i\theta S_{y^{\prime }}}{e}^{\mp i\theta S_{x^{\prime }}}\hfill \\ & =\hfill & S_{z^{\prime }}\left(c_{\theta }^3\pm s_{\theta }^2\right)+S_{x^{\prime }}{s}_{\theta }{c}_{\theta }+S_{y^{\prime }}\left(c_{\theta }^2{s}_{\theta }\mp s_{\theta }{c}_{\theta }\right).\hfill \end{array}$$ (14)

The ± sign is to consider both the cases of spin-lock phase $\mp y$. The projection on $S_{z^{\prime }}$ gives the scaling factor for the spin-lock efficiency in NOVEL,

$$\begin{array}{ccc}\hfill {\kappa }_{NOVEL}& =\hfill & ⟨{\rho }_1^{\prime }\left|S_{z^{\prime }}\right.⟩=c_{\theta }^3\mp c_{\theta }^2\pm 1\hfill \\ & =\hfill & {\left(\frac{{\mathrm{\Omega }}_S}{{\omega }_S^{eff}}\right)}^3\mp {\left(\frac{{\mathrm{\Omega }}_S}{{\omega }_S^{eff}}\right)}^2\pm 1.\hfill \end{array}$$ (15)

In the SE experiment, the initial π/2 pulse is absent, see Table I. In this case, the scaling factor for the spin-lock efficiency is simply the projection of ${\omega }_S^{eff}$ on z,

$${\kappa }_{SE}=c_{\theta }=\frac{{\mathrm{\Omega }}_S}{{\omega }_S^{eff}}.$$ (16)

We are now able to describe the build-up of nuclear polarization during electron-spin locking in a NOVEL and a SE experiment in a single equation,

$$s=\kappa ⟨I_z^{†}\left|{\widetilde{U^{\prime }}}_0{S}_{z^{\prime }}{{\widetilde{U^{\prime }}}_0}^{†}\right.⟩=\frac{\kappa }{2}\left(1-cos\left(B{s}_{\theta }\frac{sin\left(\mathrm{\Delta }\tau /2\right)}{\mathrm{\Delta }\tau }t\right)\right),$$ (17)

where κ is the scaling factor defined in Eqs. (15) and (16) depending on whether the tilt pulse is on or off.

D. Polarization transfer in NOVEL and SE in a frozen solution

To produce an experimentally realistic transfer curve for the nuclear polarization in frozen solution samples, we need to powder average the transferred polarization [calculated in Eq. (17)] over all orientations. Using the Euler angle set (α,β,γ) to define an orientation with respect to the external static magnetic field and $b=\frac{{\mu }_0{\gamma }_S{\gamma }_I{\hslash }^2}{4\pi r^3}$, the expression for the anisotropic hyperfine coupling, B, is given by

$$B=-\frac{3}{2}bsin\left(2\beta \right).$$ (18)

The polarization after powder averaging over the Euler angles is

$$⟨S⟩\left(t\right)=\frac{1}{8{\pi }^2}{\int }_0^{2\pi }d\alpha {\int }_0^{\pi }d\beta sin\left(\beta \right){\int }_0^{2\pi }d\gamma s\left(\alpha ,\beta ,\gamma \right).$$ (19)

From Eqs. (17)–(19), the powder-averaged nuclear polarization is given as

$$⟨S⟩\left(t\right)=\frac{1}{2}{\int }_0^{\pi }d\beta sin\left(\beta \right)\frac{\kappa }{2}\left(1-cos\left(-\frac{3bsin\left(2\beta \right)}{2}{s}_{\theta }\frac{sin\left(\mathrm{\Delta }\tau /2\right)}{\mathrm{\Delta }\tau }t\right)\right).$$ (20)

Equation (20) can be used to simulate the ¹H polarization transfer curves and the field profiles for the SE and NOVEL DNP experiments, both of which rely on pseudo-secular hyperfine coupling terms for the transfer of magnetization. In this description, the microwave irradiation frequency and amplitude can be chosen arbitrarily. If ω_μw = ω_0S, i.e., on-resonance microwave irradiation Ω_S = 0, electron coherence is transferred efficiently when ω_1S = ω_0I, which is the case in on-resonance NOVEL. If ω_μw = ω_0S ± ω_0I and ω_1S $\ll$ ω_0I(Ω_S ≈ ω_0I), magnetization is transferred in the form of polarization as in CW SE and requires a long contact time, generally $\sim 5\times T_{1n}$.

Equation (20) shows that if the generalized matching condition, $\mathrm{\Delta }\equiv {\omega }_S^{eff}-{\omega }_{0I}=0$, is fulfilled, then electron-nuclear polarization transfer rate is optimal for any value of Ω_S between 0 and ±ω_0I. This observation can be exploited to relax the high microwave-power requirement for NOVEL, while keeping a substantial polarization transfer rate and enhancement factor. We will refer to the case Δ = 0 as the off-resonance NOVEL condition (see Table I). This approach not only identifies the matching conditions for optimal polarization transfer in the NOVEL scheme but also highlights the relevance of the generalized matching condition in the case of the SE mechanism. When SE experiments are performed with very high microwave power, the generalized matching condition will optimize the enhancements. Furthermore, Eq. (20) shows that for the off resonance, matched condition (Δ = 0), transfer is faster for higher microwave amplitude, ω_1S, and smaller offset Ω_S because $sin\theta ={\omega }_{1S}/{\omega }_S^{eff}$.

III. EXPERIMENTAL METHODS

A. At 9.8 GHz/0.35 T/15 MHz

NMR/EPR/DNP experiments at 15 MHz/9.8 GHz (X band) were performed on a Bruker ElexSys E580 X-band EPR spectrometer using an EN 4118X-MD4 (ENDOR) probe containing a dielectric microwave resonator. Microwave pulses were amplified using a 1 kW travelling-wave tube (TWT) amplifier 117X (Applied Systems Engineering, Fort Worth, TX). High-power CW microwaves up to 10 W were generated with a Bruker AmpX10 amplifier. The RF field in the resonator was focused with an external tuning/matching circuit built around the ENDOR probe. NMR signals were detected with an iSpin-NMR system (SpinCore Technologies, Inc., Gainesville, FL) with RF pulses amplified using a 1000 W LPI-10-21001 linear pulse amplifier (ENI, Rochester, NY).

¹H NMR signals were acquired using a solid-echo sequence (π/2)_X − τ − (π/2)_Y − τ − echo with 90° pulses of 2.0 μs and τ = 20 μs, with the phases of the pulses cycled through the conventional eight steps. ¹H–¹H dipolar couplings lead to a short nuclear T₂ in our sample, and therefore each solid echo consisted of 128 points and was acquired with a detection bandwidth of 1 MHz. The signal was zero filled up to 1024 points prior to Fourier transformation.

The NOVEL pulse sequence is shown in Fig. 1 and uses a presaturation sequence consisting of a train of 120° pulses to remove previously existing nuclear polarization. Subsequently, nuclear polarization is generated by repeating the NOVEL sequence for several seconds, with a typical repetition rate of 1 kHz. The microwave cavity was maximally overcoupled. The microwave power used to generate the Rabi field ω_1S = γ_eB₁ and the length of the lock pulse were varied for different experiments as indicated in the figure captions. Following generation of bulk ¹H polarization, an NMR acquisition was performed. NMR signal enhancements were determined by comparing the spectral intensities of the microwave on and off signals.

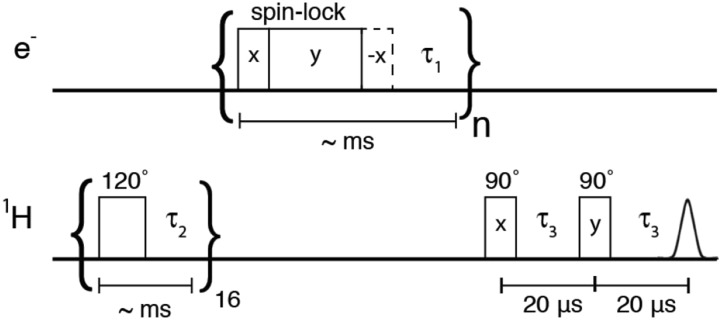
FIG. 1.

Pulse sequence for NOVEL experiments at 9.8 GHz/0.35 T/15 MHz. The ¹H polarization is saturated with a train of 120° pulses followed by the NOVEL sequence consisting of an on-resonance spin-lock on the electrons. An optional flip back pulse (dashed lines) is also included to enhance the repetition rate of the experiment. Signal enhancements by DNP are measured on ¹H directly. For pulsed SE experiments, the initial and final 90° pulses on the electrons are omitted.

The sample for X-band DNP experiments contained 6–10 mM trityl OX063 in d₈-glycerol:D₂O:H₂O 60:30:10 v:v:v with 1M urea. Thin-wall precision quartz EPR sample tubes with an outer diameter (OD) of 4 mm were used (Wilmad-LabGlass), which were filled to a sample volume of 50 μl. The sample temperature was maintained at 80 K using a CF 935 flow cryostat with liquid nitrogen as a cryogen and an ITC 503S temperature controller (Oxford Instruments).

Note that enhancement numbers may vary by ±50 between different measurements due to the low signal-to-noise ratio in the off-signal, variations in the trityl concentration, and exact placement and volume of the sample in the resonator. To enable a reasonable comparison of enhancement numbers between series of measurements, the enhancement observed in the on-resonance NOVEL experiment was used as a calibration.

B. At 140 GHz/5.0 T/212 MHz

NMR/EPR/DNP experiments at 212 MHz/140 GHz were performed on a spectrometer described by Smith et al. (fixed microwave frequency of 139.997 GHz).⁵⁶ Coherent pulses as well as continuous-wave (CW) microwaves are available at a power level of ∼100 mW generated by a Virginia Diodes (Charlottesville, VA) active multiple chain (AMC). A coiled silver TE₀₁₁ resonator, with an effective sample volume estimated to be 200 nl, serves both as a microwave resonator and an RF coil for detection of NMR signals.⁵⁷ The NMR RF circuit is balanced for both ¹H and ¹³C using a transmission-line circuit. The result is a voltage node in the center of the coil where the WR-8 waveguide is attached. A Resonance Research (Billerica, MA) field-mapping unit (FMU) measures the ¹H resonance frequency of a water sample placed just below the cryostat in the magnet bore.⁵⁸

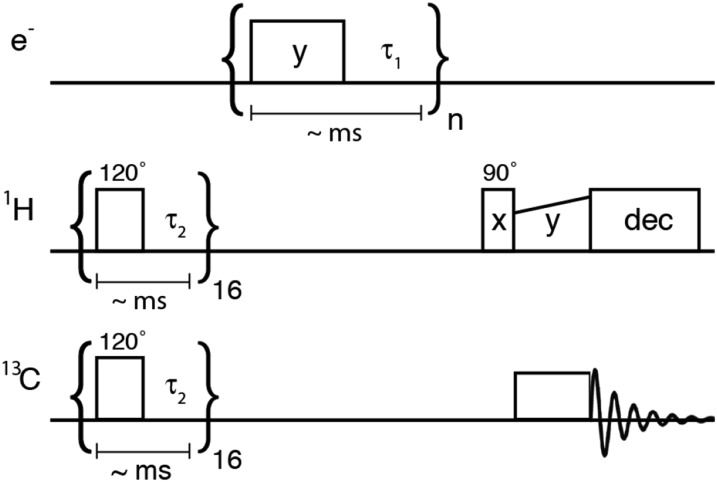
A significant ¹H NMR background signal (presumably from the plungers used to tune the microwave cavity) made it difficult to quantify DNP enhancements via direct detection of ¹H. Therefore, at 212 MHz/140 GHz we determined ¹H NMR enhancements via ¹H–¹³C cross-polarization with the sequence shown in Fig. 2. The sample consisted of ∼10 mM trityl OX063 in ¹³C-glycerol:D₂O 60:40 and was kept at a temperature of 80 K.

FIG. 2.

Pulse sequence for SE experiments at 140 GHz/5.0 T/212 MHz. The sequence begins with the saturation of the ¹H and ¹³C magnetization. Subsequently ¹³C–¹H cross-polarization is used to measure ¹H dynamic nuclear polarization. Microwave irradiation is applied in pulses or CW.

IV. SIMULATIONS

Microwave field profiles (Fig. 3), Zeeman field profiles (Figs. 4 and 5), and polarization-transfer curves (Fig. 6) were simulated using a MATLAB (Mathworks, Natick, MA) script based on Eq. (20). All of the simulations used a distribution in the values for the hyperfine interaction, b, as well as a distribution in the microwave resonance offset, Ω_S. A uniform distribution in b of 1.5–2.5 MHz reproduced the experimental polarization transfer curves discussed below. Values of b for a single electron-¹H coupling were determined experimentally for Finland trityl in frozen glycerol/water via ENDOR to be ≤|1 MHz|.^59,60 This discrepancy with the coupling strength determined from the simulations arises because the unpaired electron on Finland trityl, or in our experiments on trityl OX063, interacts with tens of ¹H’s located at roughly the same distance both on the trityl molecule and in the solvent. We model the polarization transfer from one electron to many ¹H using a single pseudosecular hyperfine interaction term in the spin Hamiltonian with an effective coupling, b_eff, which is stronger than b for the individual electron-¹H interactions.^60–62 The Ω_S distribution was determined from the experimental echo-detected EPR spectrum of trityl OX063 in frozen glycerol/water.

FIG. 3.

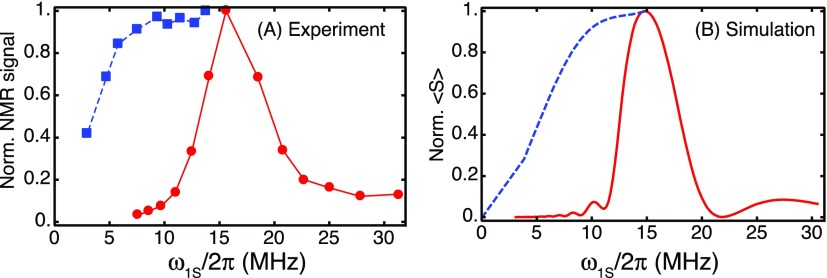
Microwave field profiles for on-resonance NOVEL (red, solid lines) and for off-resonance NOVEL (blue, dashed lines). The lines connecting the data points are a guide to the eye. (a) Experimental results; (b) simulations with Eq. (20). In the experimental on-resonance NOVEL experiments, the microwave amplitude is varied from 7.5 to 31.5 MHz (data reproduced with permission from Mathies et al., J. Phys. Chem. Lett. 7, 111 (2016). Copyright 2016 American Chemical Society). The mixing time was 8 μs. In the off-resonance NOVEL experiments, the microwave amplitude was varied from 3 to 14 MHz, while the microwave frequency was adjusted to satisfy the generalized matching condition, $\sqrt{{\mathrm{\Omega }}_S^2+{\omega }_{1S}^2}={\omega }_{0I}$. The mixing time was 500 ns.

FIG. 4.

Zeeman field profiles for on-resonance NOVEL [ω_1S/2π = ω_0I/2π = 15 MHz, (a) and (b), cyan data points and curves] and SE for various microwave amplitudes, ω_1S. (a) and (c) show the experimental data; (b) and (d) are simulated field profiles based on Eq. (20). All simulations and experiments employed an 8.5 μs mixing time. The maximum amplitudes in the numerical simulations follow Eq. (20) as plotted in Fig. 5(a). The experimental data are normalized to the amplitude of the on-resonance NOVEL signal.

FIG. 5.

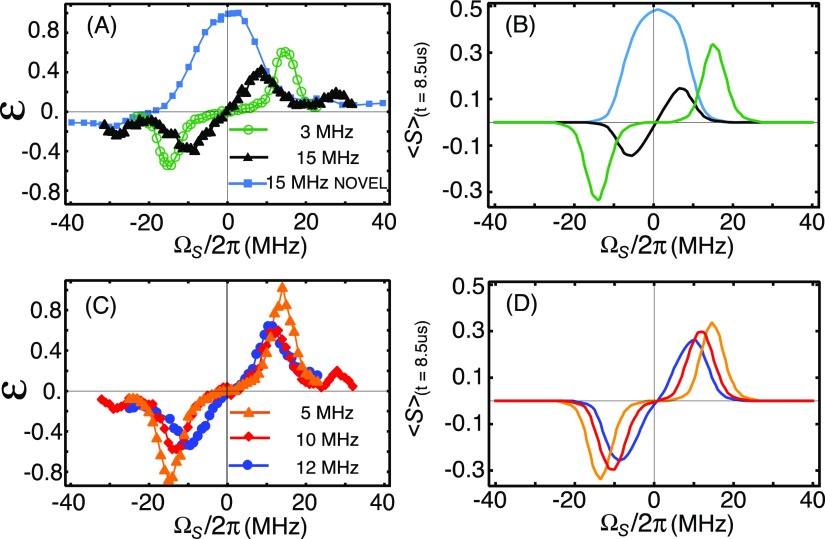
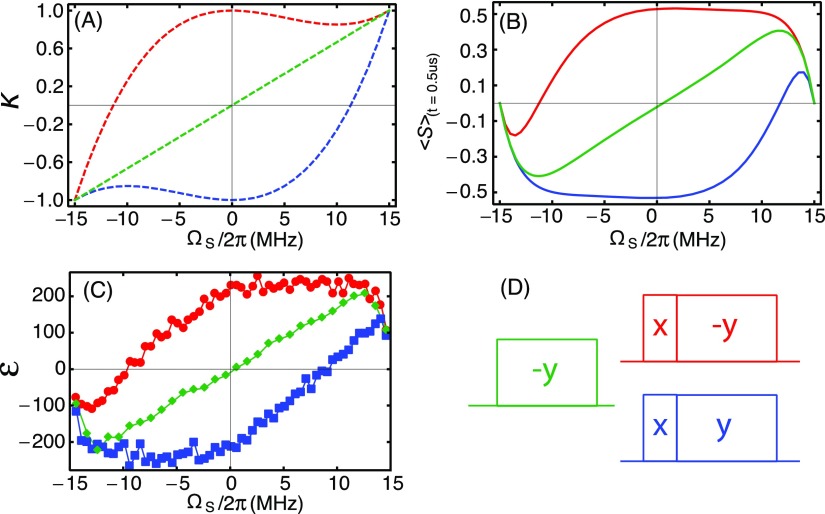
Zeeman field profiles for off-resonance NOVEL and SE. Red and blue: (90°)_X–(spin-lock)_−Y and (90°)_X–(spin-lock)_Y, respectively, green: (spin-lock)_−Y. (a) NOVEL (red and blue) and SE (green) scaling factors (κ_NOVEL and κ_SE) according to Eqs. (15) and (16). (b) NOVEL and SE enhancements according to Eq. (20) averaged over a distribution in b and Ω_S values as described in Sec. IV. (c) Experimental matched NOVEL and SE Zeeman field profiles. The mixing time was 500 ns for all simulations and experiments. (d) The pulse sequences with color coding.

FIG. 6.

Electron-nuclear polarization transfer curves for off-resonance NOVEL [(a): experiment and (b): simulation] and SE [(c): experiment and (d): simulation] with the following Rabi fields and resonance offset fields (in MHz): (ω_1S,Ω_S) = (10,12.5; blue), (5,13.98; red), (3,14.54; green), (5,−13.98; black), and (10,14.85; orange).

For all simulations, the ¹H Larmor frequency ω_0I/2π was set to 15 MHz corresponding to B₀ = 0.35 mT. For simulation of the Zeeman field profiles, the microwave resonance offset, Ω_S/2π, was varied from −40 MHz to +40 MHz. In the off-resonance Zeeman field profiles (Fig. 4), the amplitude of ω_1S was held constant as displayed with color-coding and a mixing time of 8.5 μs was used. In the matched Zeeman field profiles (Fig. 5), the values of ω_1S are adjusted at each Ω_S to maintain Δ = 0 and a mixing time of 500 ns was employed. For the polarization transfer curves in Fig. 6, the values of (Ω_S,ω_1S) are provided in the caption.

The Hamiltonian is averaged over the time period $\tau =2\pi /{\omega }_S^{eff}$ for all simulations. In principle, τ is the common period of the two frequencies ω_0I and ${\omega }_S^{eff}$ and should be calculated by taking the inverse of the greatest common divisor (GCD) of the two frequencies. For spins that are matched or for off-resonance spins with small Δ, these two frequencies are (approximately) the same and we can use $\tau =2\pi /{\omega }_S^{eff}$. To simulate the Zeeman field profiles and polarization-transfer curves, we ignore the spin packets with Δ > 2.5 MHz because the polarization transfer times become exceedingly long and spin-lock efficiency is poor. To simulate the microwave field profile for on-resonance NOVEL [Fig. 3(b), red, solid line] Δ was not restricted, but instead the mixing time was limited to 300 ns.

V. RESULTS

A. 9.8 GHz/0.35 T/15 MHz

1. High enhancements with off-resonance NOVEL

The theoretical analysis above suggests that the microwave power requirement of the on-resonance, matched NOVEL experiment, ω_1S = ω_0I, can be relaxed by irradiating the electrons off resonance using the generalized matching condition, $\sqrt{{\mathrm{\Omega }}_S^2+{\omega }_{1S}^2}={\omega }_{0I}$. Figure 3 shows (a) experimental and (b) simulated on-resonance and off-resonance microwave field profiles in solid red and dashed blue lines, respectively, at 9.8 GHz/15 MHz for trityl OX063 in a frozen glycerol/water matrix.

On resonance only ω_1S is varied and the enhancement drops rapidly when the applied microwave amplitude becomes lower than 15 MHz (solid lines). At a microwave amplitude of 10 MHz, the enhancement is less than 10% of the maximum enhancement. In contrast, in the off-resonance experiment, ω_μw and ω_1S are adjusted for each data point such that Δ = 0 and the enhancement is still 90% of the on-resonance enhancement at a microwave amplitude of 7 MHz. At 5 MHz this number drops to 70% and at 3 MHz to 40%. Thus, the experiments in Fig. 3(b) show that NOVEL can be efficient even if the on-resonance microwave power requirement is not satisfied.

2. Zeeman field profiles

In our previous publication,⁴⁴ we reported the experimental Zeeman field profile for the on-resonance NOVEL experiment (ω_1S = ω_0I). These data (cyan data points and curves) are reproduced here in Fig. 4(a) (experiment) and Fig. 4(b) (simulation). The field profile shows a single peak centered at the field position at which the highest electron-spin echo intensity was observed in the EPR spectrum of trityl OX063 (on resonance, Ω_S = 0). In this field profile, the microwave amplitude is maintained constant at 15 MHz, which implies that Δ becomes non-zero as soon as the microwave irradiation is off resonance. For Δ $\ne$ 0 (off resonance) the polarization transfer is very slow and enhancements decrease.

Figure 4 also shows the Zeeman field profiles for the SE for various microwave powers. The profiles have the shape typically observed in CW SE experiments with a maximum positive enhancement near ω_μw = ω_0S − ω_0I (double-quantum condition) and maximum negative enhancement near ω_μw = ω_0S + ω_0I (zero-quantum condition).^{32,56,63–66} However, as the microwave amplitude is increased, the observed enhancement maxima shift inward, away from the typical SE matching condition, toward Ω_S = 0. This shift is governed by the generalized matching condition $\sqrt{{\mathrm{\Omega }}_S^2+{\omega }_{1S}^2}={\omega }_{0I}$: polarization transfer is most efficient when Δ = 0. At high microwave amplitudes (ω_1S), the effective field on the electrons $\left({\omega }_S^{eff}\right)$ is barely affected by the change in the offset (Ω_S). Hence, the matching condition broadens with increasing microwave amplitude, leading to broad enhancement maxima. This effect is particularly noticeable in the field profiles with ω_1S/2π = 12 MHz and 15 MHz (blue and black data points and curves).

For SE, the highest enhancement is observed at a microwave amplitude of 5 MHz [the orange data points in Fig. 4(c)]. This maximum is determined by the increasing alignment of the spin-lock field with the electron polarization [expressed in the scaling factor κ_SE, Eq. (16), and plotted in Fig. 5(a), green curve] as Ω_S → ω_0I on the one hand and an increase of the polarization transfer time as Ω_S increases [Eq. (11)] on the other hand. Equation (20) comprises both functions and is plotted as a function of Ω_S in Fig. 5(b) (green solid curve with κ_SE). The enhancement maxima in the field profiles in Fig. 4 roughly fall on this “matched SE field profile.” It is well reproduced in an experiment where the microwave amplitude is adjusted for each value of Ω_S to remain on the generalized matching condition, see the green data points in Fig. 5(c).

The red and blue curves in Fig. 5(a) show the scaling factors for NOVEL (κ_NOVEL) as a function of Ω_S for the spin-lock phases −y and +y, respectively. In Figs. 5(b) and 5(c), the corresponding matched NOVEL Zeeman field profiles are plotted. For NOVEL as well as for SE, the shape of the field profile is dominated by the scaling factor once the matching condition is fulfilled. This leads to the remarkable asymmetry in the enhancement below and above resonance. The relative phase of the lock pulse determines whether off-resonance NOVEL is efficient at Ω_S> or <0 as described by Eq. (15). The dip at the edges is due to the mixing time (t = 500 ns) becoming too short for polarization transfer.

3. Polarization transfer during the lock pulse

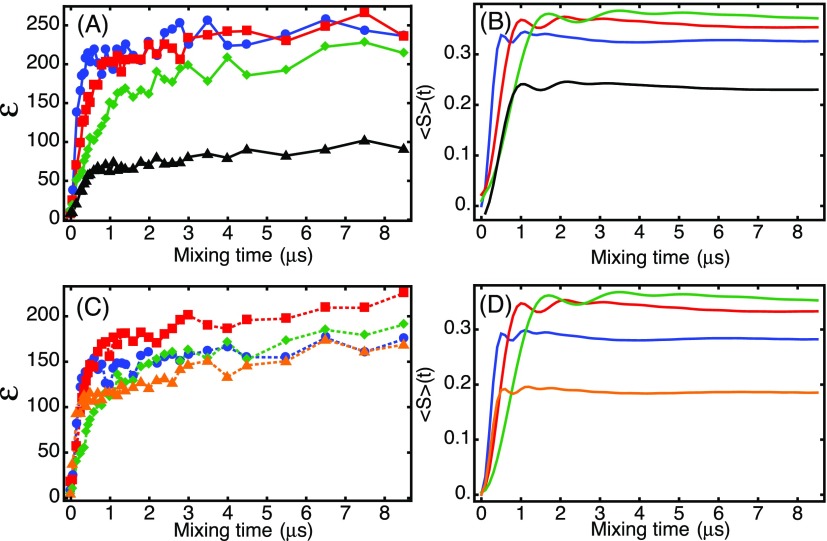
When Δ = 0, the electron-nuclear polarization transfer time is determined by the hyperfine coupling strength and $sin\theta ={\omega }_{1S}/{\omega }_S^{eff}$, see Eq. (11). Thus, higher microwave power is expected to result in faster transfer of polarization. To investigate this experimentally, we simulated and measured the ¹H NMR signal enhancement as a function of the length of the electron spin-lock pulse for both NOVEL and SE at several microwave power levels. Experimental data are shown in Fig. 6(a) (NOVEL) and Fig. 6(c) (SE). These polarization transfer curves show a rapid increase of the enhancement within the initial 1 μs. After that, the enhancement increases only slowly with the mixing time. Simulations of the polarization transfer are shown in Fig. 6(b) (NOVEL) and Fig. 6(d) (SE). The simulations account for powder averaging [Eq. (20)], a uniform distribution of the electron-nucleus dipolar interaction, b, centered around 2 MHz, and a distribution in Ω_S according to the EPR line width. The blue, red, and green curves are for off-resonance NOVEL [Fig. 6(a): experiment and Fig. 6(b): simulation] and for SE [Fig. 6(c): experiment and Fig. 6(d): simulation] with decreasing microwave amplitudes of 10, 5, and 3 MHz. As expected, and reproduced by the simulations, the polarization transfer within the initial 1 μs slows as we decrease the microwave amplitude and go further off-resonance to remain on the generalized matching condition.

The matched transfer times, shown in blue, red, and green, are within experimental error, the same for NOVEL and SE. The tilt pulse plays no role for the polarization transfer time but affects the spin-locking efficiency and thereby the enhancement. The matched SE polarization transfer curves [Figs. 6(c) and 6(d)] show that more polarization transfer can be achieved with a microwave amplitude of 5 MHz (red) than with 10 MHz (blue) because the spin-lock efficiency suffers for SE when |Ω_S| becomes small. The black curves in Figs. 6(a) and 6(b) illustrate the polarization transfer with NOVEL on the generalized matching condition but with a poor spin lock [see Fig. 5(a)]. The transfer is fast, but the enhancement suffers. These curves reinforce the importance of alignment between polarization and the spin-lock. With high microwave powers, the 90° pulse is crucial to align the polarization with the spin-lock irradiation. Far off resonance (Ω_S ≈ ω_0I), the spin-lock efficiencies become similar for NOVEL and SE [Fig. 5(a)]. In this regime, the tilt pulse loses its relevance and NOVEL and SE converge.

The orange curves in Figs. 6(c) and 6(d) are for off-resonance SE with ω_1S/2π = 10 MHz and Ω_S/2π = 14 MHz ≈ ω_0I/2π. In this experiment, a small number of the electron spins satisfy the matching condition due to the width of the EPR spectrum, and they lead to the initial rapid transfer. However, a larger number of the spins are off-resonance at ${\mathrm{\Omega }}_S/2\pi =14\text{MHz}$, yet in good alignment with the microwave irradiation. These spin packets lead to a slow build-up of nuclear polarization, on the μs time scale, leading to a final enhancement that is similar to the enhancement observed at the generalized matching condition. The slow build-up contribution to the enhancement is not reproduced in the simulations because we did not account for the off-resonance spin packets with Δ > 2.5 MHz.

4. Optimization of the electron spin lock sequence

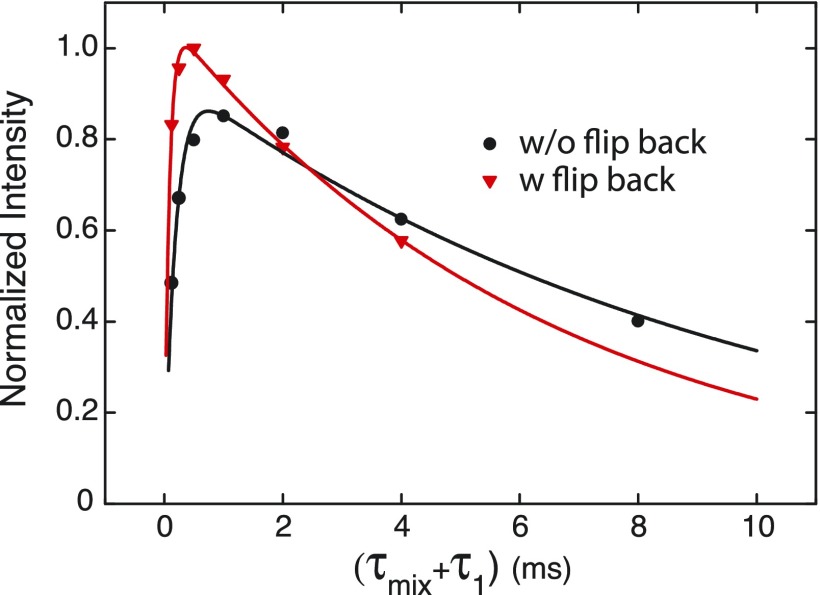
In the NOVEL experiment, the spin lock sequence transfers polarization to the nuclear spins followed by a period τ₁ to recover the electron Z-magnetization to thermal equilibrium prior to repeating the spin-lock sequence. Figure 7 shows the results of optimization of the recycle delay in an on-resonance NOVEL experiment. The black data points show ¹H NMR signal enhancements with the standard NOVEL sequence as shown in Fig. 1. For the red data points, the y locking pulse was followed by a −x 90° flip back pulse to restore the electron polarization to z. This reduces the optimal τ₁ from 1 ms to 0.5 ms and leads to an increase in the maximum enhancement of 15%.

FIG. 7.

Optimization of the experimental recycle delay for on-resonance NOVEL experiments at 9.8 GHz. Black: normal spin-lock as shown in Fig. 1 and red: the spin-lock pulse is followed by a −x flip back pulse.⁴⁴ The bulk polarization build-up time before each ¹H NMR acquisition was 2 s, and the number of NMR acquisitions was 128.

The dependence of the enhancement on τ₁ is well represented by the following equation:

$$\epsilon =A{e}^{-{\tau }_1/T_{1n}^{*}}\left(1-e^{-{\tau }_1/T_{1e}^{*}}\right).$$ (21)

The parameter A reflects the efficiency of the polarization transfer during the locking pulse and thereby limits the maximum enhancement. The decay of the enhancement with longer τ₁ is characterized by $T_{1n}^{*}$, which is a measure of how quickly the enhanced nuclear polarization returns to thermal equilibrium. The characteristic time $T_{1e}^{*}$ is determined by how fast electron z-magnetization is recovered and can again be transferred in between experiments and set a minimum τ₁. Fits to the data in Fig. 7 resulted in the following parameters: without a flip back pulse A = 0.95, $T_{1n}^{*}=$9.6 ms, and $T_{1e}^{*}=$ 0.2 ms and with a flip back pulse A = 1.07, $T_{1n}^{*}=$ 6.5 ms, and $T_{1e}^{*}=$ 0.1 ms. These numbers encompass multiple effects—the electronic longitudinal relaxation, T_1e, the rate of polarization transfer from ¹H that interact directly with the electrons to bulk ¹H, and electron spectral diffusion.

The pulsed SE experiments from Fig. 5(c) were performed with a 500 ns mixing time and a recycle delay of 1 ms, which makes the duty cycle 0.05%. The maximum enhancement observed (at Ω_S/2π = 12.6 MHz and ω_1S/2π = 8 MHz) is only slightly lower than with NOVEL. The absence of the initial π/2 pulse means that there is no need to wait for relaxation of the electron spins back to z. The last term in Eq. (21), $1-e^{-{\tau }_1/T_{1e}^{*}}$, can be removed, and this suggests that the optimal enhancement is obtained when irradiation is applied continuously (cf. Sec. VI). On our 9.8 GHz spectrometer, CW SE with a Rabi field of 2.3 MHz produced an enhancement of 379, which constituted a 35% increase compared to optimized pulsed SE in this same series of experiments.

B. 140 GHz/5.0 T/212 MHz

In a standard CW SE experiment at 140 GHz/212 MHz, we obtained a ¹H NMR signal enhancement of 23. On the same instrument, enhancements up to 144 were reported by Smith et al. on a sample containing 40 mM trityl OX063.^56,67 However, trityl has recently been shown to aggregate at concentrations above ∼10 mM. In order to avoid possible interference by the formation of aggregates, we decided to limit the trityl concentration to 10 mM, similar to the concentration in our experiments at 9.8 GHz/15 MHz.

The 100 mW maximum power on the 140 GHz instrument typically yields ω_1S/2π = 5 MHz, which is small compared to the ¹H Larmor frequency of 212 MHz. Following the generalized matching condition, $\sqrt{{\mathrm{\Omega }}_S^2+{\omega }_{1S}^2}={\omega }_{0I}$, Ω_S/2π = 0.1 MHz smaller than ω_0I, which is negligible compared to the FWHM of the trityl OX063 EPR spectrum at this field (about 40 MHz). Hence, there is no point in pursuing NOVEL at this field and pulsed SE experiments that we simply performed on the DQ solid-effect matching condition (ω_μw = ω_0S − ω_0I) at a magnetic field of 5.0012 T (or ¹H Larmor frequency of 212.94 MHz) at a microwave frequency of 139.997 GHz (g_x = g_y = 2.003 19 and g_z = 2.002 58 for trityl OX063).

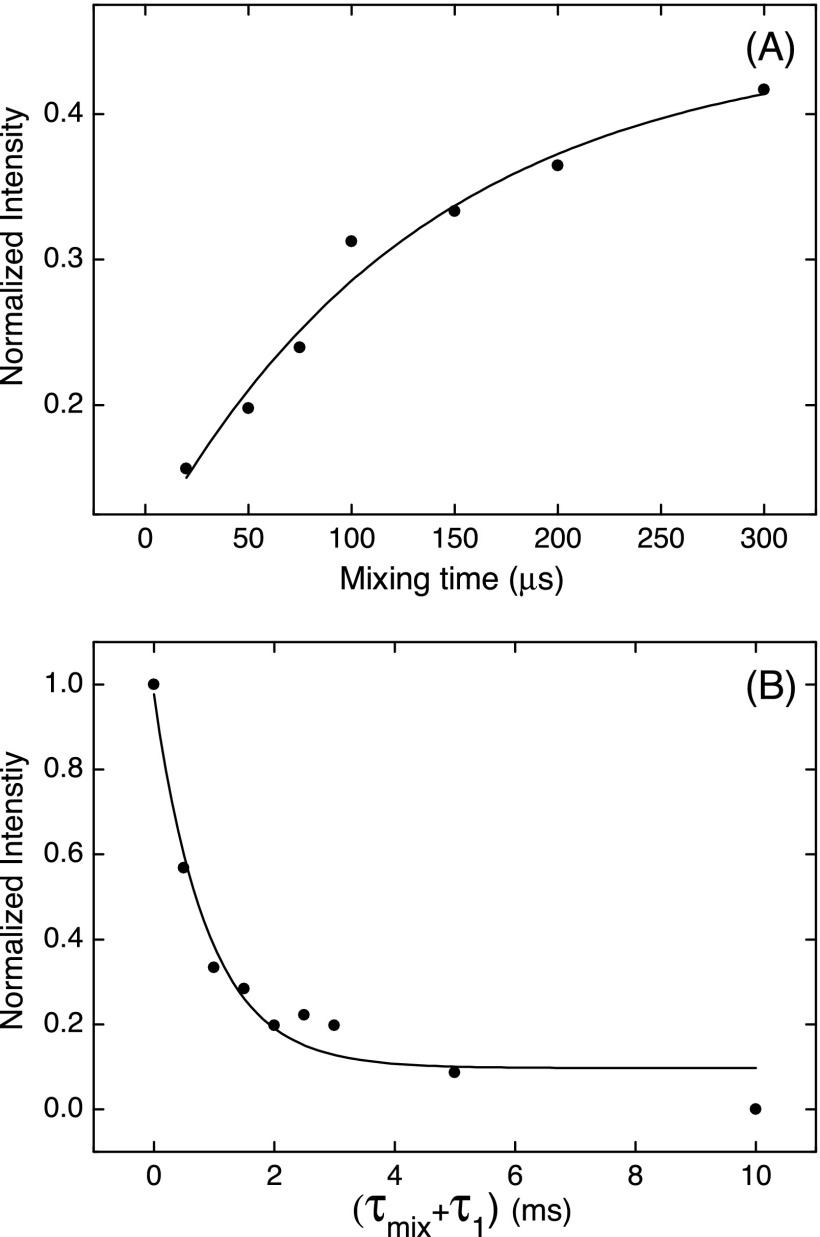
Figure 8(a) shows the dependence of the SE polarization transfer curve at 140 GHz. This curve looks very different from the curves recorded at X band shown in Fig. 6. There is no initial rapid increase of the enhancement followed by a plateau. Instead, the transfer curve can be fitted with a single exponential with a characteristic time constant of 134 μs. In contrast, with ω_1S/2π = 5 MHz, Ω_S/2π = 213 MHz, and b = 2 MHz (value based on the simulations of the build-up curves in Fig. 6), Eq. (11) puts the first maximum in the polarization transfer after a much shorter time of 14 μs.

FIG. 8.

(a) Mixing time optimization at a constant recycle delay of 1 ms and (b) τ₁ optimization with a constant mixing time of 150 μs. The total polarization build-up time before each NMR acquisition was 10 s. Each data point is an average of 1024 acquisitions.

Figure 8(b) shows the dependence of the ¹H NMR enhancement on the repetition time at a constant mixing time of 150 μs. The enhancement decays exponentially as the duty cycle of the microwave irradiation goes down from 100%. At a recycle delay of 1 ms (duty cycle 15%), the enhancement is 33% of the enhancement obtained with CW irradiation. A fit of a single exponential gives a characteristic decay time of 0.9 ms.

VI. DISCUSSION

The experiments at 9.8 GHz/15 MHz on a sample of trityl OX063 in a frozen glassy matrix show that the high microwave power requirement for the NOVEL pulsed-DNP scheme can in part be relaxed. By adjusting the microwave frequency offset in the range $0<\left|{\mathrm{\Omega }}_S\right|\le {\omega }_{0I}$ while satisfying the generalized matching condition, $\sqrt{{\mathrm{\Omega }}_S^2+{\omega }_{1S}^2}={\omega }_{0I}$, we obtain an enhancement of 266 (which amounts to 70% of the enhancement in on-resonance NOVEL, ω_1S/2π = 15 MHz) using only one third of the microwave amplitude (Ω_S/2π ≈ 14 MHz, ω_1S/2π = 5 MHz) or 1/9th of the microwave power. With off-resonance irradiation, the time required for transfer of polarization from the radical to a nearby ¹H increases in our experiments from about 300 ns on resonance (amplitude 15 MHz) to about 1 μs at a Rabi field of 5 MHz. These results suggest that a NOVEL experiment is feasible using current instrumentation at 94 GHz/143 MHz, where 5 ns π/2 pulses (Ω_S/2π = 50 MHz) are routinely accomplished.^68,69

This observation and the results of the other DNP experiments reported here are readily interpreted with the unified theoretical description presented above in which NOVEL transforms to SE and vice versa as the Rabi fields and resonance offsets are varied. In contrast, in the majority of the literature, NOVEL and SE DNP are treated separately. The term solid effect is generally reserved for DNP by irradiation with CW microwaves on the forbidden EPR lines of a narrow-line radical or transition-metal (Ω_S = ±ω_0I). The polarization transfer is effectively described by inserting the transition rates obtained from matrix diagonalization in Hilbert space into the appropriate rate equations.^{64,65,67,70–73} In recent years, this description has been improved and extended to an ensemble description to include coherence, to Liouville space to fully consider relaxation, and with multiple nuclei to include spin diffusion.^74–78 An exception is the work of Wenckebach and co-workers, who explicitly discussed the possibility Ω_S $\ne$ ±ω_0I to qualitatively explain Zeeman field profiles of SE.⁶³ Henstra and Wenckebach also presented a thorough description of on-resonance NOVEL (Ω_S = 0), which includes the possibility of transfer to multiple nuclei.⁷⁹ Both in NOVEL and SE, the transfer of polarization originates from the pseudo-secular hyperfine coupling terms, which arise from the electron-nuclear dipolar coupling and make the zero- and double-quantum transitions partially allowed. In the description presented here, we investigate the polarization transfer in an ensemble of dipolar-coupled electron-nucleus spin systems for an arbitrary Rabi field and frequency offset. Using AHT, we derive the matching condition for effective polarization transfer. On-resonance NOVEL and the CW SE DNP follow from satisfying this general matching condition at opposite extremes.

Note that the off-resonance NOVEL experiment discussed here differs from the dressed-state solid effect (DSSE) implemented by Weis et al.^80,81 The DSSE also employs Hartmann-Hahn cross polarization to transfer electron polarization to ¹H but utilizes RF irradiation applied simultaneously with the microwave spin lock. Polarization transfer in the DSSE is shown to occur for on-resonance microwave irradiation (Ω_S = 0) together with an RF resonance offset approximately equal to the microwave amplitude Ω_S ≈ ω_1S.

Electron-nuclear polarization transfer is optimal at the generalized matching condition, and therefore satisfying that condition is critical to optimizing DNP in both NOVEL and SE experiments. Application of off-resonance microwaves with an amplitude satisfying the matching condition enables the low-power NOVEL experiment shown in Fig. 1. In conventional CW SE experiments, the generalized matching condition is usually ignored. This is not a concern as long as these experiments are performed with Rabi fields much smaller than the ¹H Larmor frequency (ω_1S $\ll$ ω_0I) because in this situation the SE matching condition is close to Ω_S = ±ω_0I. However, at higher microwave amplitudes, following the matching condition will accelerate the polarization transfer and lead to larger enhancements. This is illustrated by the Zeeman field profiles in Fig. 4, where enhancement maxima are observed on the generalized matching condition. The width of the enhancement peaks is determined by the width of the EPR line, which is accounted for in the simulations by taking a distribution in Ω_S determined by the trityl EPR spectrum (∼7 MHz FWHM at ω_0S/2π = 9.8 GHz). At higher microwave amplitudes, the enhancement peaks in the SE profiles broaden beyond the EPR line width because ω_1S starts to dominate ${\omega }_S^{eff}$ and thereby mismatching Δ.

At the generalized matching condition, the electron-nuclear polarization transfer time depends on the pseudosecular hyperfine coupling and the Rabi field relative to the frequency offset as described by Eq. (11). A stronger dipolar coupling will lead to a faster transfer, but we note that Eq. (11) is only valid when $\left|{\omega }_S^{eff}\right|,\left|{\omega }_{0I}\right|\gg B$. Powder averaging and the presence of a distribution in the dipolar coupling parameters attenuate the expected transient oscillations in the experimental polarization transfer curves in Figs. 6(a) and 6(c). The best match between the simulations [Figs. 6(b) and 6(d)] and the experiments is obtained with a uniform distribution in b spanning 1.5-2.5 MHz. These values are more than a factor of two higher than the individual electron-¹H coupling strengths experimentally observed in Finland trityl.^59,60 This large effective b-value^61,62 arises from dipolar couplings of the unpaired electron on trityl with tens of neighboring ¹H, which are at similar distances and all available for DNP transfer, and is a perquisite of using trityl as a polarizing agent. The transfer curves in Fig. 6 also show that a smaller Rabi field and a larger microwave resonance offset indeed lead to a slower polarization transfer. This implies that the use of a longer spin-lock pulse could further optimize the enhancements by off-resonance NOVEL reported here, which were acquired with a lock-pulse length of only 500 ns.

Separate from the matching condition, the alignment of the electron polarization with the microwave irradiation during the lock pulse limits the electron polarization available for transfer. This alignment is expressed by the scaling factors κ_NOVEL and κ_SE [with a 90° tilt pulse, Eq. (15), and without a tilt pulse, Eq. (16)]. Figure 5(a) shows the scaling factors plotted vs. Ω_S. Figure 5(b) shows the products of the scaling factors with the matching condition and demonstrates how the scaling factors shape the Zeeman field profiles. In NOVEL, the sign of the scaling factor depends on the phase of the lock pulse relative to the tilt pulse, and this determines whether high enhancements are obtained above or below resonance. In SE, the scaling factor crosses zero for Ω_S = 0 and explains the decrease in the enhancements as the microwave amplitude is increased above 5 MHz, which was also observed in the field profiles in Fig. 4.

The misalignment of the electron polarization and ${\omega }_S^{eff}$ could be resolved by applying an on-resonance theta pulse before the (off-resonance) mixing period. In this approach, the tilt angle theta can be adjusted for complete alignment such that the scaling factor is one for all values of Ω_S. The experiments reported here were performed on a standard Bruker X-band pulsed EPR spectrometer, which is equipped with four channels plus a separate ELDOR source but does not allow rapid frequency switching. Hence, we could not implement on-resonance theta pulses. However, we do not expect this to have a strong impact on the enhancement. The Zeeman field profiles for off-resonance NOVEL in Fig. 5(c) (red and blue curves) show that as far off resonance as 12-13 MHz, the enhancement is, within experimental error, the same as in the on-resonance experiment. The eventual decrease in the enhancement when Ω_S → ω_0I is caused by slow polarization transfer and not by an unfavorable scaling factor (in fact, κ_NOVEL approaches ±1).

In an NMR sample prepared for DNP, the concentration of nuclei to be polarized is typically much smaller than the concentration of polarizing agents. Repetition of the electron-nuclear polarization transfer scheme in combination with ¹H–¹H spin diffusion is required to build up bulk ¹H polarization. In general, fast repetition and short transfer times lead to the highest nuclear polarization. In NOVEL, the repetition rate of the spin-lock sequence is limited by the time needed for recovery of electron z-magnetization to about 1 kHz, as shown by the experimental data in Fig. 7. Application of a flip-back pulse immediately after the lock pulse allows an increase of this rate to about 2 kHz and an increase in the enhancement of about 15% to a factor of 430. Thus, under our experimental conditions, in spite of the limitation on the repetition rate imposed by the NOVEL scheme, very high ¹H NMR signal enhancement factors are observed. In SE, no principal limitation on the repetition rate exists, which suggests that CW SE will always lead to higher enhancements than pulsed SE. Both in our experiments at 9.8 GHz and at 140 GHz, CW SE performs better than pulsed SE. Nevertheless, at high fields, pulsed SE might still be the method of choice. In static (non-MAS) cross-effect DNP, Hunter et al. observed an increase in the enhancement when microwaves are applied in 20 ns pulses at repetition rates varying from 2.5 to 80 kHz as opposed to in CW at the same average power.⁶⁹ They attribute this increase in enhancement to the larger excitation bandwidth of the 20 ns pulses. We do not expect such an advantageous effect to occur in SE experiments with trityl in frozen glycerol/water because the polarization transfer times are much longer (in the several-100 ns to microsecond range) and the benefits of a larger excitation bandwidth are negligible.

On the 140 GHz/212 MHz spectrometer, the microwave amplitude at full power (100 mW) is 5 MHz and negligible compared to the ¹H Larmor frequency. Putting Ω_S/2π = 212 MHz, we calculate a polarization transfer time of 14 μs from Eq. (11), which is much longer than the transfer times ≤1 μs at X band. At such long polarization transfer times, it becomes more difficult to accumulate bulk ¹H polarization while competing with nuclear relaxation and to hold the electron spin lock while competing with the electronic relaxation in the rotating frame ($T_{1\rho e}$). The experimentally observed transfer time is even slower. The polarization transfer curve in Fig. 8(a) does not show the rapid increase of the enhancement followed by a plateau where it increases slowly (characteristics of the transfer curves at X-band, see Fig. 6) but can be fitted with a single exponential with a characteristic time of 134 μs. This slow, mono-exponential polarization transfer curve is likely due to the large width of the EPR spectrum of trityl at 140 GHz. At this high frequency, the spectrum is dominated by g-anisotropy and the FWHM is about 40 MHz. This means that a large fraction of the electron spin packets will be off condition by more than Δ = 2.5 MHz and will have a correspondingly slow polarization transfer. In addition, the large width of the trityl EPR spectrum will also make the spin locking itself ineffective because most radicals are outside the excitation bandwidth. Thus, in our attempt at implementation of NOVEL/SE at high fields, we encounter two practical problems, which together lead to low DNP enhancements. (1) Rabi fields are much smaller than the ¹H Larmor frequency. (2) EPR spectra increasingly broaden. In the remaining paragraphs, we will further discuss these two problems and potential solutions.

In the description of conventional CW SE, it is assumed that ω_1S $\ll$ ω_0I and the microwave term in the Hamiltonian is treated as a perturbation. It follows that the electron-nuclear transition amplitude is $\propto B{\omega }_{1S}/{\omega }_{0I}$ and the transition probability and the DNP enhancement will scale $\propto {\left(B{\omega }_{1S}/{\omega }_{0I}\right)}^2$.^{63,64,70,75,82} In the description of NOVEL/SE presented here, the dependence on ω_0I is more subtle. Assuming that ω_1S is fixed, as ω_0I increases, ω_1S will make up a smaller part of ${\omega }_S^{eff}=\sqrt{{\mathrm{\Omega }}_S^2+{\omega }_{1S}^2}$ (on the matching condition $\mathrm{\Delta }={\omega }_S^{eff}\pm {\omega }_{0I}\approx 0$), leading to slower polarization transfer and thereby lower enhancements. For CW SE with ω_1S $\ll$ ω_0I, Ω_S → ω_0I to keep Δ = 0 and the polarization transfer time will be proportional to $\left(\sqrt{{\mathrm{\Omega }}_S^2+{\omega }_{1S}^2}/{\omega }_{1S}\right)\approx {\mathrm{\Omega }}_S/{\omega }_{1S}\approx {\omega }_{0I}/{\omega }_{1S}$, recovering the outcome of the perturbation treatment. Thus, as the static magnetic field increases, larger microwave amplitudes are desirable.

Although much progress has been made in recent years,^23,39,83,84 generating high-power microwaves at frequencies >100 GHz remains challenging. Additional complications arise from guiding to and focusing the microwaves at the NMR sample and from sample heating. The following strategy may alleviate these challenges partially. In the experiments at X-band, the enhancement increases by only 35% when applying CW microwaves as opposed to pulses at a duty cycle of 0.05%. On the Bruker X-band EPR spectrometer, microwaves can be generated with the TWT at ∼1 kW with a maximum duty cycle of about 1% or with the AmpX amplifier at 10 W in CW. This factor of 100 increase in peak power constitutes a factor of 10 increase in the microwave amplitude and shortens the polarization transfer time by the same factor [Eq. (11)]. At high ω_0I, shortening of the transfer time could be crucial to obtaining higher enhancement factors and is worthwhile investigating experimentally.

To achieve the optimal DNP enhancement, excitation of the full EPR pattern is crucial. However, the EPR spectra of all known radical polarizing agents broaden at high fields due to g-anisotropy. Perhaps high-spin transition-metal complexes, for which the second-order pattern narrows with an increased magnetic field, like Gd-DOTA, can play a role in solving this matter.^85,86 Alternative approaches are to sweep the field or the microwave frequency, or to use shaped pulses for broad-band excitation.^87,88 The former has been implemented in the Integrated Solid Effect (ISE).^89,90 This scheme has been successfully applied to transfer the high electron polarization from photo-excited triplet states to ¹H at X band^91–96 and recently with polarizing agents of general applicability.⁹⁷ In these experiments, the microwave amplitude is kept at the on-resonance NOVEL condition, while the frequency is swept adiabatically across the full width of the EPR spectrum.⁹⁸ Because the sweep is adiabatic, the electron polarization of all spin packets will, at some point during the sweep, align with the effective field, effectively keeping the scaling factor at one. Polarization transfer will take place from those spin packets for which the generalized matching condition is approximately met (Δ ≈ 0) and sufficient time is allowed for transfer, as determined by Eq. (11). This suggests that the efficiency of the ISE can be further optimized by amplitude modulation during the frequency sweep to keep Δ = 0 at all times and by adjusting the sweep rate to allow for the slower polarization transfer further off resonance. Both approaches to broad-band excitation do require dedicated microwave sources, which can generate high-power, high-frequency shaped pulses. However, the recent development of dedicated gyroamplifiers⁵⁰ and frequency tunable gyrotrons⁹⁹ and the use of an arbitrary waveform generator (AWG) to improve the efficiency of NOVEL¹⁰⁰ suggest that their availability may not be so far away.

VII. CONCLUSION

We have shown experimentally at 9.8 GHz/15 MHz that the microwave power requirement for the NOVEL pulsed-DNP scheme can be relaxed by irradiating the electrons with off-resonance microwaves on the generalized matching condition. Experimental results are in agreement with the unified theoretical description presented here for NOVEL and SE based on an ensemble of dipolar-coupled electron-nuclear spin-systems. Polarization transfer rates are optimal on the generalized matching condition both for NOVEL and SE and depend on the dipolar coupling strength and the microwave amplitude and resonance offset. The scaling factors quantify the fraction of electron polarization available for transfer to the nuclei and strongly affect the shape of the Zeeman field profiles for NOVEL and SE. The experimental results and theoretical framework presented here lay a foundation for the continued development of pulsed DNP methods and their implementation at high magnetic fields.