Abstract
Epileptic seizure is the common neurological disorder, which is generally identified by electroencephalogram (EEG) signals. In this paper, a new feature extraction methodology based on optimum allocation sampling (OAS) and Teager energy operator (TEO) is proposed for detection of seizure EEG signals. The OAS scheme selects the finite length homogeneous sequence from non-homogeneous recorded EEG signal. The trend of selected sequence by OAS is still non-linear, which is analyzed by non-linear operator TEO. The TEO convert non-linear but homogenous EEG sequence into amplitude–frequency modulated (AM–FM) components. The statistical measures of AM–FM components used as input features to least squares support vector machine classifier for classification of seizure and seizure-free EEG signals. The proposed methodology is evaluated on a benchmark epileptic seizure EEG database. The experimental results demonstrate that the proposed scheme has capability to effectively distinguish seizure and seizure-free EEG signals.
Keywords: Electroencephalogram, Optimum allocation sampling, Teager energy operator, Least square support vector machine
Introduction
Epilepsy is a chronic neurological disorder which affects more than 1% of the worlds population, included the all age’s people [1]. Epilepsy is characterized by repetitive seizures which occur numerous per day to less than per annum [2]. Seizures activity is induced by abrupt and inordinate electrical discharges by a group of brain neurons [3, 4]. Clinically, electroencephalogram (EEG) recording is the prominent tool for analysis and detection of epilepsy. In the manual efforts, trained neurologist try to find the spikes in EEG related to sudden discharges of neurons to detect seizure [5]. Although such visual efforts are costly, time consuming, and error prone [6]. Therefore, need to develop automatic analysis and identification method for measurement of accurate changes of EEG signals during epileptic seizure.
Recently, numerous features extraction methods have been proposed in literature for detection of epileptic seizure. The EEG signal consider as stationary, the time and frequency domain features are extracted [7, 8]. The non-stationary behavior of EEG signals is analyzed by time–frequency representation base features [9, 10]. The linear prediction filter modeled the time series signals and energy of prediction error signal of modeled signal is used to identify the seizure interval [11]. EEG signals are modeled by fraction linear prediction method [12]. The energy of EEG signal and modeling error used as features with support vector machine (SVM) classifier for EEG signals classification [12]. Clustering technique based features are used for detection of epileptic EEG signals [13]. Various time–frequency based methods are presented, which consider EEG signals as non-stationary like short time Fourier transform [6], wavelet transform [9], and multi-wavelet transform [10]. EEG signals decompose into approximation and detail by discrete wavelet transform (DWT) and approximate energy of wavelet coefficients consider as feature for detection epileptic EEG epochs by probabilistic neural network (PNN) classifier [14]. A non-stationary signal analysis method empirical mode decomposition (EMD) based features are proposed for identification of epilepsy [15–17]. Two and three dimensional phase space representation based features are extracted from EMD computed IMFs and least squares SVM (LS-SVM) classifier is reported for classification [18]. The spectral features are extracted from tunable-Q wavelet transform (TQWT) decomposed signals and used with bagging for detection of seizure activity [19]. The non-linear parameters are also find vital utility in feature extraction for epileptic EEG signals. The Kraskov entropy non-linear feature with TQWT is apply to identify epileptic seizure EEG signals [20]. A non-linear features based on fractal dimension, higher order spectra, entropies, and Hurst exponent are extracted, which classification performance is evaluated by fuzzy classifier [21]. The other nonlinear parameters which extract the epilepsy information from EEG signals are as follows: approximate entropy [22], correlation dimension [23], and Lyapunov exponent [24].
More recently, optimum allocation sampling (OAS) scheme is used for optimum selection of samples with minimum variability from long length EEG sequences [25, 26]. OAS finds application in EEG signals analysis by feature extraction and classification methods [26, 27]. Although, such methods directly apply feature extraction without considering the non-linear trend of EEG signals. The improved feature extraction can be provided by exploring the non-linearity of EEG components in terms of linear amplitude or frequency component. The Teager energy operator (TEO) is non-linear operator which is generally used for analysis of wide variety of non-linear signals [28, 29]. Some of the common application of TEO are: speech classification [29], damage identification [30], and amplitude–frequency modulated (AM–FM) component separation [31]. In other words, by virtue of OAS scheme and TEO non-linear operator, complexity of non-homogeneous and non-linear EEG signals can be better explored.
In this paper, we are presenting a new methodology based on OAS and TEO for detection of seizure EEG signals. It is very hard to evaluate randomly, homogeneous EEG time series samples from long length non-homogeneous EEG time series for meaning full feature extraction. In this work, the OAS scheme is applied on non-homogeneous EEG time series to evaluate stationary and homogeneous EEG time series. In OAS method the EEG sequence divided into stationary sub-sets or groups and from each sub-set, the optimum selection of samples is carried out on the basis of minimum variance concept. In spite, computing the stationary and homogeneous EEG time series but still nature of EEG time series is non-linear that also requires to analyze. A non-linear TEO is used to explore the non-linearity of optimally allocated homogeneous EEG time series. The TEO separates the non-linear EEG time series into well defined AM–FM components. The statistical measures of AM–FM components are used as input features to LS-SVM classifier for classification of seizure and seizure-free EEG signals.
Methodology
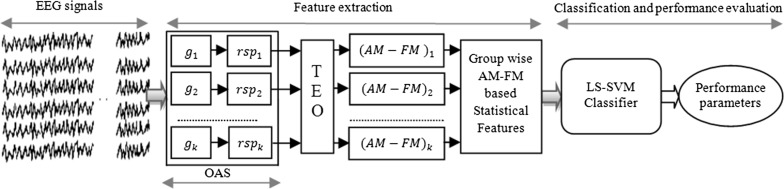
The proposed methodology for automatic detection of seizure EEG signals is depicted in Fig. 1 by four sub blocks: EEG signals (data-set), feature extraction, classification, and performance evaluation. The description of each sub blocks as follows.
Fig. 1.
An OAS and TEO based algorithm for classification of EEG signals. g group, rsp representation sample points
Data-set
The proposed method is tested on one freely available EEG data-set which can be assessed as describe in [32]. The data-set consist of five subsets Z, O, N, F, and S, formed by control and epileptic patients EEG signals. Each subset contain recording of 100 single channel EEG signals having 23.6 s duration and 173.61 sampling frequency. The subsets Z and O formed by acquiring the EEG signals, from the scalp of five healthy subjects in eyes open and closed condition, respectively. Subsets N, F, and S formed from epileptic patients recorded EEG signals, out of these subsets N and F formed in seizure-free intervals and subset S recorded at the time of seizure activity. The two classes are formed for detection of epileptic seizure EEG signals: one with subset S represents seizure class and other is formed with subsets N and F which is termed as seizure-free class.
Feature extraction
As recorded EEG time series shows the non-homogeneous and non-linear nature. It is very hard to extract the characteristics of such complex signal by direct feature extraction methods. In this paper, EEG signals is analyzed in two steps: optimally allocation sampling and TEO. These steps are followed by AM–FM based statistical feature extraction.
Optimum allocation sampling
Optimum allocation refers to a method of sample allocation, used with stratified sampling. OAS is drafted for handling large size of non-homogeneous sequence with the least computational cost. The OAS scheme divides long length non-homogeneous sequence into some homogenous groups and discovers the representative sample points from each group. As recorded EEG signals contain long length of non-homogenous sequence with respect to time period, this study intends to apply OAS for discovering representation sample points from each group minimizing the variance. In this study, at first, we settle on the total sample size (n) from the length of EEG signal with a desired confidence interval and confidence level using sample size calculator [33]. Then we determine the optimum sample size for each group using the OAS scheme by following equation that considers the variability among observations in each group,
| 1 |
where n(i) is the optimum sample size of the ith group, is the sequence size of the ith group, and is the variance of the jth channel of the ith group. If are the sample sizes obtained by Eq. (1) from the group sizes, respectively, the sum of all obtained sample sizes from all the groups in a class EEG signal will be equal to n, i.e., In this study, the number of homogeneous groups of EEG signals, obtain by OAS are four [27]. The total number of samples in EEG signal or population is then number of samples in each group or group size is Total sample size n is 3287 of the EEG signal is obtained by using sample size calculator [33]. This sample size is obtained by considering confidence level and confidence interval is For total sample size n, each group sample size can be obtained by Eq. (1), which is shown in Table 1. So, for each EEG signal optimum samples are selected by OAS for further processing. A detailed description of the OAS method is available in references [26, 27, 34].
Table 1.
Optimally allocated samples (AOSs) in each group of S and SF EEG signals
| Groups | Size | Group wise calculated sample size | |
|---|---|---|---|
| S | SF | ||
| 758 | 850 | ||
| 1024 | 1024 | ||
| 835 | 772 | ||
| 1024 | 1024 | ||
| 808 | 860 | ||
| 1024 | 1024 | ||
| 886 | 805 | ||
| 1024 | 1024 | ||
| AOS | Total n | 3287 | 3287 |
| Total N | 4096 | 4096 | |
Teager energy operator
The TEO is a non-linear differential operator, which assess the modulation energy of non-linear EEG signal. This modulation energy demodulated in to AM–FM components using energy separation algorithm [35]. AM–FM components of kth group OAS, can be defines as [35, 36]:
| 2 |
| 3 |
where is TEO for kth group that can be defined as:
| 4 |
and,
| 5 |
In discrete domain TEO can be defined as [36]:
| 6 |
The above equation clearly shows that the computation of TEO at any point relies on current, previous, and next samples, not on the entire time samples, which shows its instantaneous nature. So, TEO provides finest time resolution in discrete time counterpart.
AM–FM components based statistical features
In this work, OAS and TEO based features are proposed for classification of seizure and seizure free EEG signals. TEO extract the AM–FM components from stationary and homogeneous EEG time series obtained by OAS technique. The statistical measures of AM–FM components proposed as valuable features for extracting the attributes of EEG signals. AM based statistical features are: minimum, maximum, first quartile, and third quartile. FM based statistical features are: median, mean, and standard deviation (SD). The minimum, maximum, first quartile, median, and third quartile are compositely represents five point summary in a database. This five number summary provides a clear representation of EEG signals characteristics, preserve in AM–FM components [37]. The symmetric nature of EEG signals can be assessed by central tendency and variability measures. The mean and SD are used for measuring the central tendency and variability of EEG signals, respectively [37].
Let kth group EEG signal AM component is and FM component is Following equations are used for computation of AM–FM based features [37]:
| 7 |
| 8 |
| 9 |
| 10 |
| 11 |
| 12 |
| 13 |
where n is number of samples in AM–FM components.
Classification
The statistical performance of proposed method is computed by LS-SVM classifier. The resultant equation of LS-SVM classifier [38]:
| 14 |
where is number of feature vectors, ) are support values, (+ 1 or − 1) is class label of pth input feature vector is kernel function, and b is bias term. In this paper, the utility of radial basis function (RBF) kernel is tested [38],
| 15 |
where is width of RBF kernel.
Performance evaluation
The sensitivity (SEN), specificity (SPE), accuracy (ACC), error rate detection (ERD), and Matthews correlation coefficient (MCC) have been introduced to assess the performance of LS-SVM classifier [20, 39]. The robustness of proposed framework for EEG signals classification applications like seizure disorder detection in clinical settings by above parameters, the 10-fold cross validation method is applied to compute these parameters.
Results and discussion
EEG signals complexity is explored by OAS and TEO based features for classification. The OAS scheme selects the optimum number of homogeneous samples from each EEG signal. The optimally selected sample from OAS is used by non-linear TEO for extraction of AM–FM components. The different statistical measures of AM–FM components used as feature to extract the characteristics of EEG signal. This process is carried out for each EEG signal of each class to construct the feature set. The statistical analysis of proposed features set shown in Tables 2 and 3, by range and probabilistic (p) value of Kruskal–Wallis statistical test. In Tables 2 and 3, all groups statistical features based on AM component show higher range for seizure EEG signals. This could be happened because of higher amplitude variation for seizure class EEG signals with respect to opposite class EEG signals. The median and mean both are the measure of central tendency, so they both show similar nature or higher value for seizure free EEG signals, in Tables 2 and 3. The SD of FM component feature shows higher range for all groups seizure EEG signals, in Tables 2 and 3. This might be happened because of higher variability of seizure EEG signals with respect to its opposite class EEG signals. The lower p-value of all features in Tables 2 and 3, assessed their better discrimination ability of proposed features for both classes EEG signals. The statistical analysis of proposed features motivated us to use these features input to LS-SVM classifier for classification of seizure and seizure free EEG signals.
Table 2.
Range (mean ± SD) and p-value of AM–FM based features for different groups
| Features | EEG signal | Groups | |||
|---|---|---|---|---|---|
| Group 1 | Group 2 | ||||
| Mean ± SD | P-value | Mean ± SD | P-value | ||
| S | 0.21 ± 0.40 | 1.36 × 10−20 | 0.17 ± 0.43 | 3.99 × 10−15 | |
| SF | 0.001 ± 0.019 | 0.002 ± 0.020 | |||
| S | 15,164.42 ± 91,276.29 | 3.17 × 10−55 | 6986.66 ± 7440.20 | 1.15 × 10−57 | |
| SF | 1078.283 ± 1049.443 | 953.445 ± 794.704 | |||
| S | 104.48 ± 63.37 | 3.42 × 10−63 | 102.46 ± 62.36 | 3.93 × 10−64 | |
| SF | 13.257 ± 7.805 | 13.009 ± 7.440 | |||
| S | 411.06 ± 225.10 | 1.63 × 10−64 | 424.17 ± 228.68 | 3.61 × 10−65 | |
| SF | 65.231 ± 34.295 | 65.310 ± 35.734 | |||
| S | 0.721 ± 0.119 | 2.16 × 10−09 | 0.705 ± 0.117 | 2.43 × 10−12 | |
| SF | 0.790 ± 0.129 | 0.787 ± 0.126 | |||
| S | 0.9345 ± 0.1581 | 1.2 × 10−17 | 0.9103 ± 0.1596 | 1.74 × 10−23 | |
| SF | 1.0741 ± 0.1716 | 1.0744 ± 0.1645 | |||
| S | 1.18 ± 0.88 | 2.45 × 10−6 | 1.06 ± 0.46 | 6.96 × 10−08 | |
| SF | 1.157 ± 0.288 | 1.162 ± 0.311 | |||
Table 3.
Range (mean ± SD) and p-value of AM–FM based features for different groups
| Features | EEG signal | Groups | |||
|---|---|---|---|---|---|
| Group 3 | Group 4 | ||||
| Mean ± SD | P-value | Mean ± SD | P-value | ||
| S | 0.16 ± 0.40 | 7.84 × 10−16 | 0.18 ± 0.40 | 2.72 × 10−15 | |
| SF | 0.001 ± 0.009 | 0.005 ± 0.031 | |||
| S | 10,364.60 ± 20,727.67 | 1.34 × 10−56 | 8093.80 ± 11,366.96 | 2.58 × 10−55 | |
| SF | 2823.767 ± 26,581.638 | 1043.689 ± 1372.878 | |||
| S | 92.39 ± 55.96 | 3.2 × 10−64 | 88.69 ± 55.35 | 3.1 × 10−62 | |
| SF | 12.627 ± 7.247 | 13.268 ± 7.823 | |||
| S | 401.92 ± 222.95 | 2.85 × 10−65 | 385.93 ± 211.37 | 2.45 × 10−64 | |
| SF | 62.912 ± 34.125 | 66.001 ± 37.661 | |||
| S | 0.714 ± 0.116 | 7.87 × 10−12 | 0.713 ± 0.117 | 3.04 × 10−12 | |
| SF | 0.799 ± 0.129 | 0.800 ± 0.133 | |||
| S | 0.9311 ± 0.1465 | 2.63 × 10−21 | 0.9299 ± 0.1478 | 2.02 × 10−21 | |
| SF | 1.0879 ± 0.1710 | 1.0853 ± 0.1751 | |||
| S | 1.19 ± 0.71 | 3.23 × 10−04 | 1.190 ± 0.819 | 8.07 × 10−07 | |
| SF | 1.175 ± 0.309 | 1.151 ± 0.267 | |||
The statistical parameters SEN, SPE, ACC, ERD, and MCC are the performance measures of LS-SVM classifier. For validation of proposed method by above parameters using LS-SVM classifier, the 10-fold cross validation method is applied. The RBF kernel of LS-SVM classifier is tested, which parameters sigma and gamma are group wise empirically selected, in Table 4. Table 4 shows the group wise performance parameters of proposed method. It is observed from Table 4 that the group 1 provides best performance parameters with LS-SVM classifier compared to other groups. It could be happen because of group features shows better discrimination performance by lower p-values compared to other groups features. The group 1 performance parameters are as follows: ACC is 98%, SEN is 98.96%, SPE is 97.55%, ERD is 6.25%, and MCC is 95.5%. Table 5 presents, the comparison of proposed method with other state-of-the-art methods and proposed method provides better performance parameters, form most of the methods. The classification results of proposed method for detection of seizure EEG signals makes it a viable choice in automatic epileptic seizure disorder detection in clinical applications.
Table 4.
Group wise performance parameters of proposed method
| Groups/classifier parameters | ACC (%) | SEN (%) | SPE (%) | ERD (%) | MCC (%) |
|---|---|---|---|---|---|
| 98.00 | 98.96 | 97.55 | 6.25 | 95.50 | |
| 96.00 | 94.90 | 96.53 | 12.24 | 90.97 | |
| 97.33 | 94.23 | 98.98 | 7.69 | 94.10 | |
| 96.00 | 96.81 | 95.63 | 12.77 | 90.96 |
Table 5.
Comparison of proposed method with other state-of-art methods
| Authors | Features/method | Classifier | Performance (%) | |||
|---|---|---|---|---|---|---|
| ACC | SEN | SPE | MCC | |||
| Altunay et al. [11] | Linear prediction error energy | – | 93.6 | 92.00 | NA | NA |
| Joshi et al. [12] | FLP error energy and signal energy | SVM | 95.33 | 96 | 95 | NA |
| Siuly et al. [13] | Clustering | LS-SVM | 94.18 | 94.92 | 93.44 | NA |
| Gandhi et al. [14] | DWT and energy of wavelet coefficients | PNN | 99.33 | 99.6 | 99 | NA |
| Pachori and Patidar [15] | EMD, SODP based-confidence area measure | ANN | 97.75 | 97.68 | 98.07 | NA |
| Bajaj and Pachori [16] | Area measure of analytic IMFs of EEG signals | – | – | 90 | 89.31 | NA |
| Sharma and Pachori [18] | EMD and phase space representation | LS-SVM | 98.67 | 100.00 | 96.00 | NA |
| Hassan et al. [19] | TQWT and bagging | Bootstrap aggregating | 98.40 | 98.33 | 98.60 | NA |
| Patidar and Panigrahi [20] | TQWT and Kraskov entropy | LS-SVM | 97.75 | 97.00 | 99.00 | 96.00 |
| The proposed work | OAS and TEO | LS-SVM | 98 | 98.96 | 97.55 | 95.50 |
Conclusion
This paper explored the utility of OAS and TEO in feature extraction for complex EEG signal. The OAS scheme analyzed the non-homogenous nature of EEG signal by diving it into groups and representation sample points are selected from each group to form homogeneous EEG group. The non-linear nature of selected length homogeneous EEG signal is analyzed by TEO. TEO separate non-linear EEG signal into well defined AM–FM components. The statistical measures of AM–FM components are used to construct the group-wise feature set for classification of seizure and seizure free EEG signals. The groups performance is evaluated by statistical parameters computed through the LS-SVM classifier. The group 1 provides best performance parameter as: ACC is 98%, SEN is 98.96%, SPE is 97.55%, ERD is 6.25%, and MCC is 95.5%. These parameters are also better as compared to several existing methods for classification of seizure and seizure free EEG signals.
Future directions of this research work, in proposed OAS method the number of groups is selected empirically by stratification process. In near future, we would like improve empirically stratification process by adaptive stratification process based on statistical properties of test signal.
Acknowledgments
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Contributor Information
Sachin Taran, Email: taransachin2@gmail.com.
Varun Bajaj, Email: bajajvarun056@yahoo.co.in.
Siuly Siuly, Email: siuly.siuly@vu.edu.au.
References
- 1.Global campaign against epilepsy. Programme for Neurological Diseases, Neuroscience (World Health Organization), International Bureau of Epilepsy, and International League against Epilepsy. Atlas: epilepsy care in the world. World Health Organization; 2005.
- 2.Mormann F, Andrzejak RG, Elger CE, Lehnertz K. Seizure prediction: the long and winding road. Brain. 2006;130(2):314–333. doi: 10.1093/brain/awl241. [DOI] [PubMed] [Google Scholar]
- 3.Ray GC. An algorithm to separate nonstationary part of a signal using mid-prediction filter. IEEE Trans Signal Process. 1994;42(9):2276–2279. doi: 10.1109/78.317850. [DOI] [Google Scholar]
- 4.Mukhopadhyay S, Ray GC. A new interpretation of nonlinear energy operator and its efficacy in spike detection. IEEE Trans Biomed Eng. 1998;45(2):180–187. doi: 10.1109/10.661266. [DOI] [PubMed] [Google Scholar]
- 5.Mosh SL, Perucca E, Ryvlin P, Tomson T. Epilepsy: new advances. Lancet. 2015;385(9971):884–898. doi: 10.1016/S0140-6736(14)60456-6. [DOI] [PubMed] [Google Scholar]
- 6.Duque-Muz L, Espinosa-Oviedo JJ, Castellanos-Dominguez CG. Identification and monitoring of brain activity based on stochastic relevance analysis of shorttime EEG rhythms. Biomed Eng Online. 2014;13(1):123. doi: 10.1186/1475-925X-13-123. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Srinivasan V, Eswaran C, Sriraam AN. Artificial neural network based epileptic detection using time-domain and frequency-domain features. J Med Syst. 2005;29(6):647–660. doi: 10.1007/s10916-005-6133-1. [DOI] [PubMed] [Google Scholar]
- 8.Polat K, Gne S. Classification of epileptiform EEG using a hybrid system based on decision tree classifier and fast Fourier transform. Appl Math Comput. 2007;187(2):1017–1026. [Google Scholar]
- 9.Uthayakumar R, Easwaramoorthy D. Epileptic seizure detection in EEG signals using multifractal analysis and wavelet transform. Fractals. 2013;21(02):1350011. doi: 10.1142/S0218348X13500114. [DOI] [Google Scholar]
- 10.Guo L, Rivero D, Pazos A. Epileptic seizure detection using multiwavelet transform based approximate entropy and artificial neural networks. J Neurosci Methods. 2010;193(1):156–163. doi: 10.1016/j.jneumeth.2010.08.030. [DOI] [PubMed] [Google Scholar]
- 11.Altunay S, Telatar Z, Erogul O. Epileptic EEG detection using the linear prediction error energy. Expert Syst Appl. 2010;37(8):5661–5665. doi: 10.1016/j.eswa.2010.02.045. [DOI] [Google Scholar]
- 12.Joshi V, Pachori RB, Vijesh A. Classification of ictal and seizure-free EEG signals using fractional linear prediction. Biomed Signal Process Control. 2014;9:1–5. doi: 10.1016/j.bspc.2013.08.006. [DOI] [Google Scholar]
- 13.Siuly S, Li Y, Wen PP. Clustering technique-based least square support vector machine for EEG signal classification. Comput Methods Programs Biomed. 2011;104(3):358–372. doi: 10.1016/j.cmpb.2010.11.014. [DOI] [PubMed] [Google Scholar]
- 14.Gandhi T, Panigrahi BK, Bhatia M, Anand S. Expert model for detection of epileptic activity in EEG signature. Expert Syst Appl. 2010;37(4):3513–3520. doi: 10.1016/j.eswa.2009.10.036. [DOI] [Google Scholar]
- 15.Pachori RB, Patidar S. Epileptic seizure classification in EEG signals using second-order difference plot of intrinsic mode functions. Comput Methods Programs Biomed. 2014;113(2):494–502. doi: 10.1016/j.cmpb.2013.11.014. [DOI] [PubMed] [Google Scholar]
- 16.Bajaj V, Pachori RB. Epileptic seizure detection based on the instantaneous area of analytic intrinsic mode functions of EEG signals. Biomed Eng Lett. 2013;3(1):17–21. doi: 10.1007/s13534-013-0084-0. [DOI] [Google Scholar]
- 17.Bajaj V, Pachori RB. Classification of seizure and nonseizure EEG signals using empirical mode decomposition. IEEE Trans Inf Technol Biomed. 2012;16(6):1135–1142. doi: 10.1109/TITB.2011.2181403. [DOI] [PubMed] [Google Scholar]
- 18.Sharma R, Pachori RB. Classification of epileptic seizures in EEG signals based on phase space representation of intrinsic mode functions. Expert Syst Appl. 2015;42(3):1106–1117. doi: 10.1016/j.eswa.2014.08.030. [DOI] [Google Scholar]
- 19.Hassan AR, Siuly S, Zhang Y. Epileptic seizure detection in EEG signals using tunable-Q factor wavelet transform and bootstrap aggregating. Comput Methods Programs Biomed. 2016;137:247–259. doi: 10.1016/j.cmpb.2016.09.008. [DOI] [PubMed] [Google Scholar]
- 20.Patidar S, Panigrahi T. Detection of epileptic seizure using Kraskov entropy applied on tunable-Q wavelet transform of EEG signals. Biomed Signal Process Control. 2017;34:74–80. doi: 10.1016/j.bspc.2017.01.001. [DOI] [Google Scholar]
- 21.Acharya UR, Sree SV, Ang PCA, Yanti R, Suri JS. Application of non-linear and wavelet based features for the automated identification of epileptic EEG signals. Int J Neural Syst. 2012;22(02):1250002. doi: 10.1142/S0129065712500025. [DOI] [PubMed] [Google Scholar]
- 22.Srinivasan V, Eswaran C, Sriraam N. Approximate entropy-based epileptic EEG detection using artificial neural networks. IEEE Trans Inf Technol Biomed. 2007;11(3):288–295. doi: 10.1109/TITB.2006.884369. [DOI] [PubMed] [Google Scholar]
- 23.Lehnertz K, Elger CE. Spatio-temporal dynamics of the primary epileptogenic area in temporal lobe epilepsy characterized by neuronal complexity loss. Electroencephalogr Clin Neurophysiol. 1995;95(2):108–117. doi: 10.1016/0013-4694(95)00071-6. [DOI] [PubMed] [Google Scholar]
- 24.Beyli ED. Lyapunov exponents/probabilistic neural networks for analysis of EEG signals. Expert Syst Appl. 2010;37(2):985–992. doi: 10.1016/j.eswa.2009.05.078. [DOI] [Google Scholar]
- 25.Li Y. A novel statistical algorithm for multiclass EEG signal classification. Eng Appl Artif Intell. 2014;34:154–167. doi: 10.1016/j.engappai.2014.05.011. [DOI] [Google Scholar]
- 26.Siuly S, Li Y. Discriminating the brain activities for brain–computer interface applications through the optimal allocation-based approach. Neural Comput Appl. 2015;26(4):799–811. doi: 10.1007/s00521-014-1753-3. [DOI] [Google Scholar]
- 27.Siuly S, Wang H, Zhang Y. Detection of motor imagery EEG signals employing Naive Bayes based learning process. Measurement. 2016;86:148–158. doi: 10.1016/j.measurement.2016.02.059. [DOI] [Google Scholar]
- 28.Kvedalen E. Signal processing using the Teager Energy Operator and other nonlinear operators. Master, University of Oslo Department of Informatics, p. 21 (2003).
- 29.Zhou G, Hansen JH, Kaiser JF. Classification of speech under stress based on features derived from the nonlinear Teager energy operator. In: Proceedings of the 1998 IEEE international conference on acoustics, speech and signal processing, May 1998, vol. 1, p. 549–552 (1998).
- 30.Cao M, Xu W, Ostachowicz W, Su Z. Damage identification for beams in noisy conditions based on Teager energy operator-wavelet transform modal curvature. J Sound Vib. 2014;333(6):1543–1553. doi: 10.1016/j.jsv.2013.11.003. [DOI] [Google Scholar]
- 31.Santhanam B, Maragos P. Energy demodulation of two-component AM–FM signal mixtures. IEEE Signal Process Lett. 1996;3(11):294–298. doi: 10.1109/97.542159. [DOI] [Google Scholar]
- 32.Andrzejak RG, Lehnertz K, Mormann F, Rieke C, David P, Elger CE. Indications of nonlinear deterministic and finite-dimensional structures in time series of brain electrical activity: dependence on recording region and brain state. Phys Rev E. 2001;64(6):061907. doi: 10.1103/PhysRevE.64.061907. [DOI] [PubMed] [Google Scholar]
- 33.Sample Size Calculator. https://www.surveysystem.com/sscalc.htm.
- 34.Cochran WG. Sampling techniques. 3. New York: Wiley; 1977. [Google Scholar]
- 35.Maragos P, Kaiser JF, Quatieri TF. Energy separation in signal modulations with application to speech analysis. IEEE Trans Signal Process. 1993;41(10):3024–3051. doi: 10.1109/78.277799. [DOI] [Google Scholar]
- 36.Boudraa AO, Cexus JC, Salzenstein F, Guillon L. IF estimation using empirical mode decomposition and nonlinear Teager energy operator. In: First international symposium on control, communications and signal processing, p. 45–48 (2004).
- 37.De Veaux RD, Velleman PF, Bock DE. Intro stats. 3. Boston: Pearson Addison Wesley; 2008. [Google Scholar]
- 38.Suykens JA, Vandewalle J. Least squares support vector machine classifiers. Neural Process Lett. 1999;9(3):293–300. doi: 10.1023/A:1018628609742. [DOI] [Google Scholar]
- 39.Li Y, Wen P. Analysis and classification of EEG signals using a hybrid clustering technique. In: 2010 IEEE/ICME international conference on complex medical engineering (CME), July 2010, p. 34–39 (2010).