Maximizing the Signal Gain of Electrochemical-DNA Sensors

Abstract

Electrochemical DNA (E-DNA) sensors have emerged as a promising class of biosensors capable of detecting a wide range of molecular analytes (nucleic acids, proteins, small molecules, inorganic ions) without the need for exogenous reagents or wash steps. In these sensors, a binding-induced conformational change in an electrode-bound “probe” (a target-binding nucleic acid or nucleic-acid-peptide chimera) alters the location of an attached redox reporter, leading to a change in electron transfer that is typically monitored using square-wave voltammetry. Because signaling in this class of sensors relies on binding-induced changes in electron transfer rate, the signal gain of such sensors (change in signal upon the addition of saturating target) is dependent on the frequency of the square-wave potential pulse used to interrogate them, with the optimal square-wave frequency depending on the structure of the probe, the nature of the redox reporter, and other features of the sensor. Here, we show that, because it alters the driving force of the redox reaction and thus electron transfer kinetics, signal gain in this class of sensors is also strongly dependent on the amplitude of the square-wave potential pulse. Specifically, we show here that the simultaneous optimization of square-wave frequency and amplitude produces large (often more than 2-fold) increases in the signal gain of a wide range of E-DNA-type sensors.

Graphical abstract

First reported in 2003, electrochemical DNA (E-DNA) biosensors are reagentless, single-step sensors comprised of a redox-reporter-modified nucleic acid “probe” attached to an interrogating electrode.¹ Originally used for the detection of DNA^2–9 and RNA¹⁰ targets, the platform has since been expanded to the detection of a wide range of small molecules,^11,12 inorganic ions,^13,14 and proteins,^12,15–17 including antibodies,^18,19 via the introduction of aptamers and nucleic-acid-small molecule and nucleic-acid-peptide conjugates as recognition elements (reviewed in refs 20 and 21). Irrespective of their specific target, all of these sensors are predicated on a common mechanism: binding alters the efficiency with which the attached redox reporter approaches the electrode due to either the steric bulk of the target or the changes in the conformation of the probe.^1,12,18 Given this mechanism, these sensors are quantitative, single-step (wash-free), and selective enough to perform well even in complex clinical samples.^12,15 They are likewise supported on micrometer-scale electrodes²² and require only inexpensive, handheld driving electronics (analogous to the home glucose meter²³), suggesting they are well suited to applications at the point-of-care.

Motivated by the potential advantages of the E-DNA sensing platform, numerous research groups have explored their fabrication and optimization over the past decade. Specifically, efforts have been made to improve the platform’s signal gain (change in signal upon the addition of saturating target) by optimizing the frequency of the square-wave potential ramp employed,¹¹ the density with which the target-recognizing probes packed onto the electrode,^11,24 probe structure,²⁵ the redox reporter employed,²⁶ and the nature of the monolayer coating the electrode.²⁵ Contributing to these studies, we describe here a more comprehensive study of the extent to which the square-wave voltammetric approach itself can be optimized to achieve maximum signal gain. Specifically, we have investigated the effect of varying the square-wave frequency, amplitude, and “potential step-size” on the gain of E-DNA sensors, evaluating each parameter as a function of the others as well as of the structure of the E-DNA probe, its packing density, the nature of its redox-reporter, and the monolayer chemistry used to coat the sensing electrode.

RESULTS AND DISCUSSION

Signaling in E-DNA sensors is driven by binding-induced changes in the rate of electron transfer from the attached redox reporter (Figure 1).¹ Given this, the signal gain (signal change upon the addition of saturating target) of E-DNA sensors can be enhanced by optimizing the parameters of the square-wave potential sweep used to interrogate the sensor (Figure 1). We have previously shown, for example, that E-DNA signal gain is a strong function of square-wave frequency. This occurs because the sensitivity of square-wave voltammetry to a given rate of electron transfer is a function of the square-wave frequency, enough so that many E-DNA architectures switch from “signal-on” (the binding of target increases peak current) to “signal-off” (binding suppresses peak current) behavior as the square-wave frequency is varied.²⁷ The rate of electron transfer, however, depends not only on the accessibility of the redox reporter to the electrode, but also on the potential driving the redox reaction. E-DNA gain should thus also depend on the amplitude of the square-wave potential step, albeit in a manner that is itself dependent on the square-wave frequency. Here, we explore this interplay in an effort to further improve E-DNA signaling.

Figure 1.

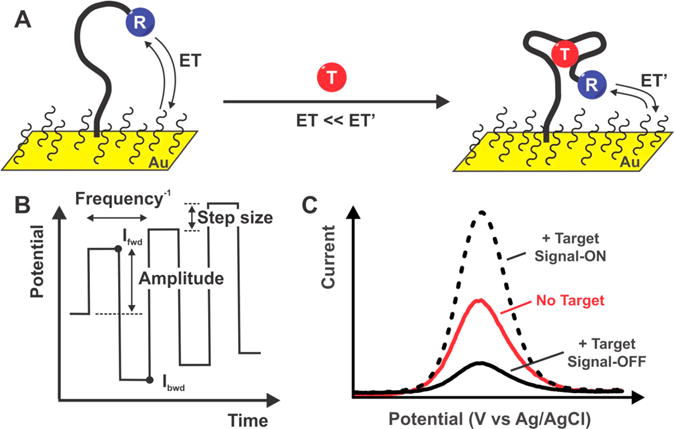
(A) E-DNA sensors detect their target analytes (“T”) via a binding-induced conformational change in their DNA probes. This alters the rate of electron transfer (ET vs ET′) from an attached redox reporter (“R”). (B) Square-wave voltammetry is typically employed to convert this change in electron transfer rates into a change in observed current. In this technique, we apply a rising, “staircase” potential waveform and measure the Faradaic current at the end of each square pulse. A voltammogram (current versus potential) is generated from this by taking the difference between each subsequently measured current (I_fwd − I_bck). Because of this sampling protocol, square-wave voltammetry can be “tuned” to be more or less sensitive to specific electron transfer rates. For example, it is relatively insensitive to transfer reactions that are much more rapid than the square-wave frequency because the Faradaic current from such a reaction will have decade to near zero before the current is measured as the end of the pulse. (C) This signal gain of E-DNA sensors (the relative signal change seen upon the addition of saturating target) is a strong function of square-wave frequency. Indeed, many E-DNA sensors can be switched from “signal-on” behavior (positive gain, in which binding causes an increase in current) to “signal-off” behavior (negative gain) simply by altering the square-wave frequency. Here, we explore the extent to which the square-wave frequency dependence of E-DNA signal gain is also a function of the amplitude (and other parameters) of the square-wave pulse.

As predicted by the above arguments, E-DNA signal gain is a strong, simultaneous function of both the frequency and the amplitude of the square-wave pulse. To see this, we first recorded square-wave voltammograms from an aminoglycoside-detecting sensor (using methylene blue as the redox reporter) using 154 different combinations of amplitude (over the range 1–100 mV) and frequency (5–5000 Hz) in both the presence and the absence of the sensor’s target. Using these, we then assembled 2D numerical maps of peak current in the presence and absence of target as a function of these square-wave parameters (see Figure S1). The ratio of these maps then, in turn, produces a numerical map of signal gain as a function of these square-wave parameters (Figure 2A). From these three maps (peak current in the presence and absence of target, and signal gain), we see that, although the largest peak currents are associated with the highest amplitudes and frequencies, the greatest signal gain is seen at an intermediate amplitude and frequency pairings. The highest positive (“signal-on”) gain, +315%, is achieved, for example, at an amplitude of 25 mV and a frequency of 750 Hz. The most negative (“signal-off”) gain, −82%, in contrast, is seen at 25 mV and 20 Hz. These values reflect 2-fold increases in magnitude relative to the previously reported signal-on and signal-off gains of this sensor.^27,28

Figure 2.

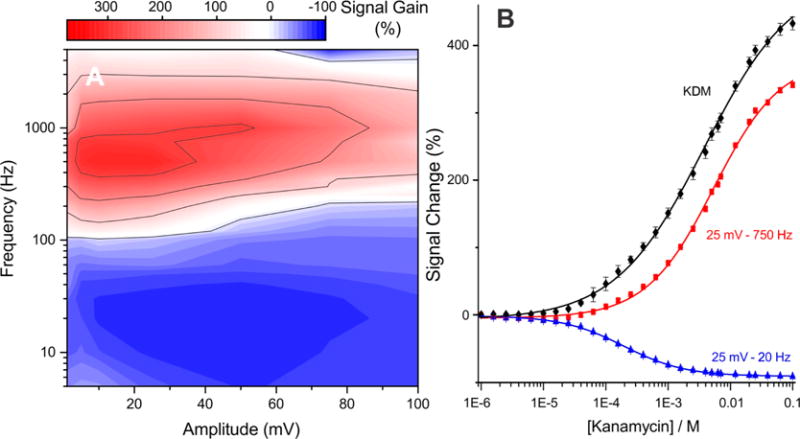
Signal gain of E-DNA sensors is a strong function of both the frequency and the amplitude of the square-wave pulse. (A) Shown, for example, is a map of signal gain (relative change in current upon addition of “saturating” target) of an aminoglycoside-detecting sensor;²⁹ depending on the amplitude/frequency pair the gain ranges from +315% (signal-on behavior) to −82% (signal-off behavior). (B) To more clearly illustrate these two behaviors, we show here the sensor’s response to its target when interrogated at an amplitude of 25 mV and frequencies of either 750 Hz (signal-on behavior; red curve) or 20 Hz (signal-off behavior; blue curve). Because the gains observed at these two frequencies differ in sign, taking their difference (kinetic differential measurements; KDM; black curve) leads to still greater gain.²⁸ As expected, the signal change at 50 mM target using this amplitude frequency pair is in excellent agreement with the signal gain predicted by the map on the left.

Simultaneous optimization of amplitude and frequency likewise improves kinetic differential measurements (KDM), a means of both correcting baseline drift and improving signal gain.²⁸ Specifically, KDM subtracts the signals recorded at signal-on and signal-off square-wave frequencies to improve signal gain and thus signal-to-noise ratios. Conveniently, because these two signals also often drift in concert (when, for example, sensors are deployed in complex sampling environments²⁸), KDM also provides a means of removing baseline drift. Using KDM, we have previously reported signal gain of 190% for the aminoglycoside sensor at a fixed amplitude of 25 mV.²⁸ By instead picking optimized signal-on and signal-off amplitude/frequency pairings, this increases to 430%, a more than 2-fold enhancement (Figure 2B).

In contrast to amplitude and frequency, we find that the “potential step-size” employed in the square-wave scan, which defines the resolution of the voltammogram, plays only a minor role in defining E-DNA signal gain. For example, whereas the gain of our aminoglycoside sensor is +315% at a potential step-size of 1 mV, this only rises to +335% when the potential step-size is increased to 5 mV (see Figure S2). We attributed this trivially small increase in signal gain to the fact that increasing the step-size increases variability in the peak currents due the concomitant reduction in voltammogram resolution.

The intrinsic electron transfer rates of different reporters, such as methylene blue or ferrocene, vary, as does thus, in turn, the amplitude/frequency pairing at which signal gain is maximized. To illustrate this, we recorded signal gain/amplitude/frequency maps for aminoglycoside sensors employing as redox reporter either anthraquinone, which transfers electrons more slowly than methylene blue,^30,31 or ferrocene,³² which transfers electrons much more rapidly. Consistent with the rather sluggish electron transfer of anthraquinone, its optimal amplitude and frequency are 10 mV and 100 Hz, values that are 2.5- and 7.5-fold lower, respectively, than the optima of the equivalent sensor employing methylene blue (compare Figure 3A and Figure 2A). Moreover, even at its optimal parameters, the signal gain of the anthraquinone-based sensor is only +173%, which is one-half that seen for methylene blue, and the sensor does not exhibit signal-off behavior at any combination of amplitude and frequency we have investigated. Consistent with the much more rapid electron transfer of ferrocene, in contrast, the ferrocene-based sensor does not produce signal-on behavior at any frequency we have investigated (Figure 3B). Given the extremely rapid intrinsic electron transfer rate of ferrocene, we expect that signal-on behavior would only be observed at frequencies above 25 kHz. At such high frequencies, the background current increases so significantly that we can no longer extract the peak current. The square-wave frequency that produces the largest magnitude signal-off signal gain, −43%, is 7.5 kHz (at an amplitude of 25 mV). This frequency is 10 times greater than the optimal signal-off frequency seen for our methylene blue-based sensor.

Figure 3.

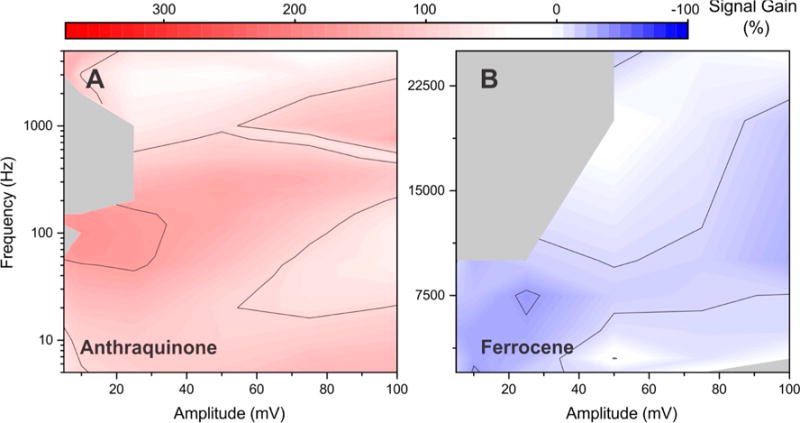
Optimal square-wave amplitude and frequency pairing (and the signal gain observed at this pairing) is a strong function of the redox reporter the sensor employs. We illustrate this here using aminoglycoside-detecting sensors modified with either (A) anthraquinone, which exhibits rather sluggish electron transfer, or (B) ferrocene, which transfers electrons much more rapidly than methylene blue. The largest magnitude gains produced by the two are +173% and −43%, respectively, values that are far poorer than the +315% gain observed for an optimized sensor employing methylene blue (Figure 2). Both sensors were fabricated at the same packing density employed in Figure 2.

Presumably due to interactions (steric or otherwise) between neighboring probes,^11,24,33,34 E-DNA signal gain is dependent on the density with which the probes are packed on the electrode surface. Motivated by this, we have also investigated the extent with which the optimal amplitude/frequency pairing of the aminoglycoside sensor (with a MB reporter) depends on this parameter. To do so, we varied the packing density by changing the probe concentration employed during sensor fabrication,²⁴ finding that, as had previously been shown,^11,24 signal gain is a strong function of packing density. The signal-on gain of the sensors, for example, varies between +220% and +315% as we vary the concentration of probe used during fabrication from 20 to 500 nM (see Figure 2A versus Figure 4A and B). The highest gain for all of the sensors with the three different packing densities, however, is seen at the same amplitude/frequency pair (Figure 4).

Figure 4.

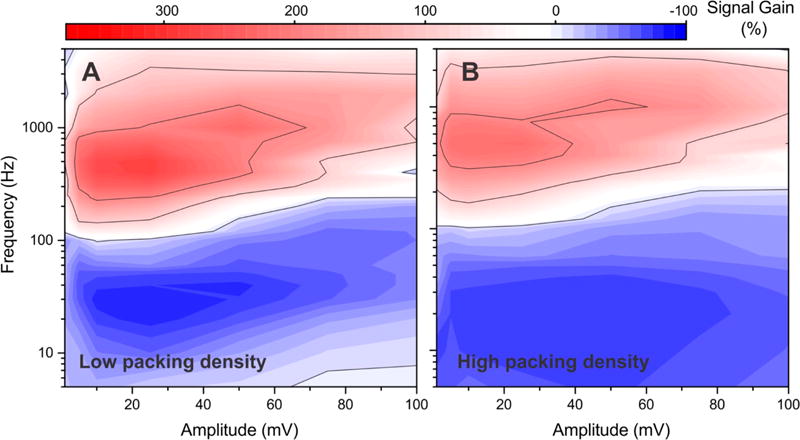
Although E-DNA signal gain is a strong function of the density with which the DNA probes are packed on the surface,^11,24 the amplitude/frequency pairing at which this is observed is itself independent of probe density. To see this, we recorded signal gain maps for the aminoglycoside sensor (with a methylene blue reporter) fabricated by depositing the probe at concentrations of either (A) 20 nM or (B) 500 nM. These resulted in 1.1-fold and 1.4-fold decreases in signal gain, respectively, in comparison to sensors fabricated using a more optimal probe concentration of 200 nM (Figure 2A). The optimal amplitude/frequency pairing, however, is effectively indistinguishable across all three packing densities.

The rate of electron transfer from an E-DNA probe is influenced by the length of the monolayer through which the electrons must tunnel,²⁵ and thus the amplitude/frequency optimum might also depend on this parameter. To explore this, we have characterized methylene-blue-employing aminoglycoside sensors fabricated using either 3-mercapto-1-propanol (C-3) or 11-mercapto-1-undecanol (C-11) as the monolayer in place of the 6-mercapto-1-hexanol (C-6) monolayer used in the above studies. We find that sensors fabricated using the C-3 monolayer produce a signal-on gain of +372% at an amplitude of 10 mV and a frequency of 1000 Hz (Figure 5A), values that are 2.5-fold lower and 1.3-fold higher than the optimal parameters for the C-6 monolayer (Figure 5A versus Figure 2A). We likewise observe the greatest magnitude signal-off gain (−88%) for this monolayer at an amplitude of 25 mV and a frequency of 30 Hz, and a kinetic differential measurement gain of 460% (Figure 5A). The latter value is, by a modest margin, the highest gain we have obtained for this sensor under any set of fabrication and operational conditions. Unfortunately, however, such short monolayers are quite unstable,³⁵ leading to poor sensor stability. Sensors fabricated using C-11 monolayer, in contrast, are exceptionally stable,^35,36 but they produce lower signal gains than those seen for the C-6 monolayer. Under optimal signal-on conditions, for example, the gain of the C-11 aminoglycoside sensor only reaches +195% (at an amplitude and frequency of 10 mV and 40 Hz; Figure 5B). The maximum signal-off gain of this sensor is, at −11% (at an amplitude 5 mV and a frequency of 250 Hz), likewise quite small, and thus KDM produces a gain of only 206%.

Figure 5.

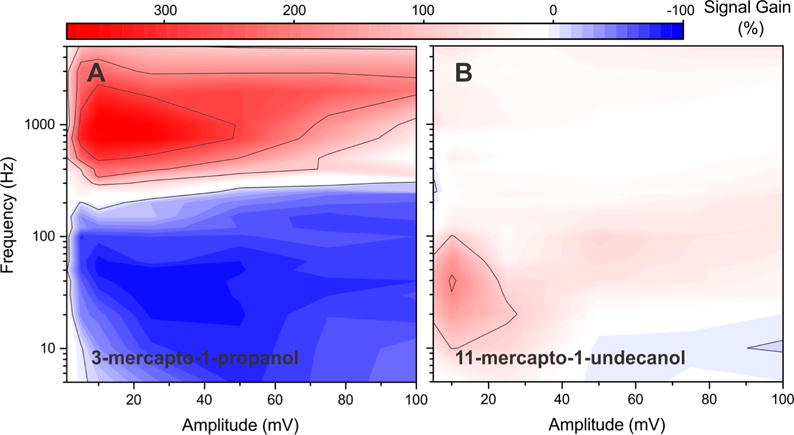
Thickness of the monolayer coating of the electrode affects electron transfer kinetics from E-DNA sensors and thus also affects signal gain and the optimized square-wave electrochemical parameters. (A) A signal gain map recorded for an aminoglycoside sensor employing a three-carbon monolayer (C-3; 3-mercapto-1-propanol), for example, exhibits a 1.2-fold increase in maximum signal gain relative to the thicker, more commonly employed six-carbon monolayer (C-6; 6-mercapto-1-hexanol). (B) The gain of a sensor fabricated using a 11-carbon monolayer (C-11; 11-mercapto-1-undecanol) is, in contrast, 1.6-fold poorer than that of the six-carbon monolayer (Figure 2A). Of note, however, three-carbon monolayers are rather unstable, likely reducing the value of this means of improving signal gain.

The improved signal gain we observe upon optimizing the square-wave frequency and amplitude of the aminoglycoside-detecting sensor also holds for other sensors as well. The signal gain map of a sensor employing the cocaine-binding aptamer of Stojanovic,^37,38 for example, achieves maximal signal-on gain of +200%, when interrogated at a square-wave amplitude of 50 mV and frequency of 1000 Hz (Figure 6A), a near 2-fold increase over previously reported values.²⁷ Combined with signal-off gain of −39% (at 5 mV and 5 Hz), this leads to a kinetic differential measurement gain of 239%.

Figure 6.

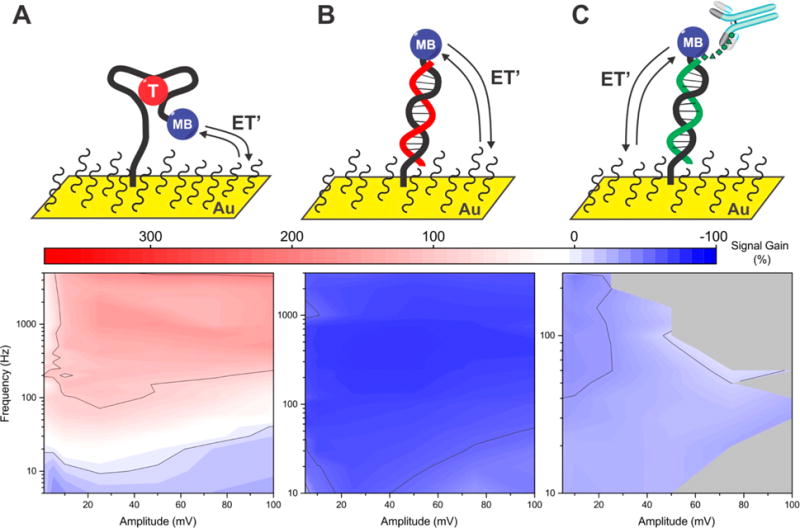
Optimal square-wave electrochemical parameters differ depending on the structure of the E-DNA probe employed. (A) Optimal performance for a sensor employing a cocaine binding aptamer, for example, occurs at 50 mV and 1000 Hz, where its gain reaches +200%. This contrasts with the maximum gain observed for the aminoglycoside sensor (Figure 2), which is one-half again greater and occurs at 25 mV and 750 Hz. (B) In contrast, a linear-strand E-DNA sensor (for the detection of oligonucleotides³⁹) remains signal-off at all amplitude/frequency pairings we have investigated, achieving maximum magnitude gain of −77% at 25 mV and 400 Hz. (C) Finally, a peptide-presenting “scaffold” E-DNA sensor that detects anti-FLAG antibodies¹² is likewise only signal-off, achieving maximum magnitude gain of −52% at 10 mV and 240 Hz.

Other classes of E-DNA sensors also show an enhancement of signal gain via the optimization of square-wave amplitude and frequency. To demonstrate this, we first fabricated a methylene-blue-modified “linear probe” E-DNA sensor³⁹ for the detection of hybridization (Figure 6B). For this sensor, which transitions between an unstructured, single-stranded probe and double-stranded probe-target duplex, we observed only signal-off behavior, with the highest magnitude gain, −77%, found at an amplitude and frequency of 25 mV and 400 Hz (Figure 6B). The voltammograms that we recorded at frequencies below 10 Hz, where we expect signal-on behavior, are too noisy to allow for the robust extraction of peak currents. We then fabricated a DNA-peptide “scaffold” sensor for the detection of antibodies (Figure 6C).¹² In this sensor architecture, a rigid, 26-base double-stranded DNA/PNA scaffold is immobilized to the electrode surface via a flexible linker. The distal terminus of this is modified with both methylene blue and a 10-residue FLAG peptide that specifically binds anti-FLAG antibodies.¹⁸ Antibody binding reduces the efficiency with which the methylene blue approaches the electrode surface, again leading to an easily measured change in peak current. We find that this scaffold sensor exhibits a maximum signal-off gain of −52% at optimized amplitude and frequency of 10 mV and 240 Hz (Figure 6C). Similar to the DNA hybridization sensor, however, this sensor did not produce signal-on behavior over any of the amplitude/frequency pairs we have investigated, presumably due to the sluggish electron transfer rates associated with its rather rigid target-bound probe. These results illustrate the observation that frequencies at which the E-DNA-type sensors flip from signal-on to signal-off behavior depend on the structural details of (and thus electron transfer rates of) the bound and unbound probes, both of which differ from one sensor architecture to the next.

The amplitude-dependence of E-DNA signal gain occurs because changes in the amplitude of the square-wave pulse (E_SW) differentially alter the rates of electron transfer from bound and unbound probes. To illustrate this, we recorded voltammograms from an aminoglycoside-detecting sensor at a constant frequency of 100 Hz while varying the amplitude (Figure 7A and B) and then extracted the underlying “forward” and “backward” components from them (see Figure S3). Using the peak potential from these components, we calculated electron transfer rates (k_f and k_b in s⁻¹) using Butler–Volmer formalism (eqs 1 and 2).⁴⁰ We used this approach, as opposed to the more commonly used approaches of Komorsky-Lovric and M. Lovric, because, at >1 × 10⁻² cm s⁻¹, the electron transfer rates of the surface attached redox couple are too rapid to be accurately extracted using the latter theory.^34,41,42

$$k_{\mathrm{f}}=k_0{\mathrm{e}}^{-\alpha (nF/RT)(E-E^0)}$$ (1)

$$k_{\mathrm{r}}=k_0{\mathrm{e}}^{(1-\alpha )(nF/RT)(E-E^0)}$$ (2)

Here, α is the electron transfer coefficient (assumed to be 0.5; see ref 43), E is the peak potential (at a given amplitude), n is the number of electrons (two for methylene blue), and F, R, and E⁰ are Faraday’s constant, the gas constant, and the standard potential, respectively. Finally, k₀ (in s⁻¹) is the heterogeneous electron transfer rate, which is an intrinsic property of the redox reporter and is the same for both the forward and the reverse reactions (although it may differ in the presence or absence of target). From these fits, we find that reverse rate constants change more dramatically with amplitude $(k_{\mathrm{r}}^{\text{bound}}/k_{\mathrm{r}}^{\text{unbound}}=0.7-{\mathrm{e}}^{-(84\text{mV}/E_{\text{sw}})})$ than do the forward rate constants $(k_{\mathrm{f}}^{\text{bound}}/k_{\mathrm{f}}^{\text{unbound}}=0.6-0.5{\mathrm{e}}^{-(29\text{mV}/E_{\text{sw}})})$, thus accounting for the strong inter-relationships between square-wave frequency, square-wave amplitude, and the signal gain of E-DNA-type sensors.

Figure 7.

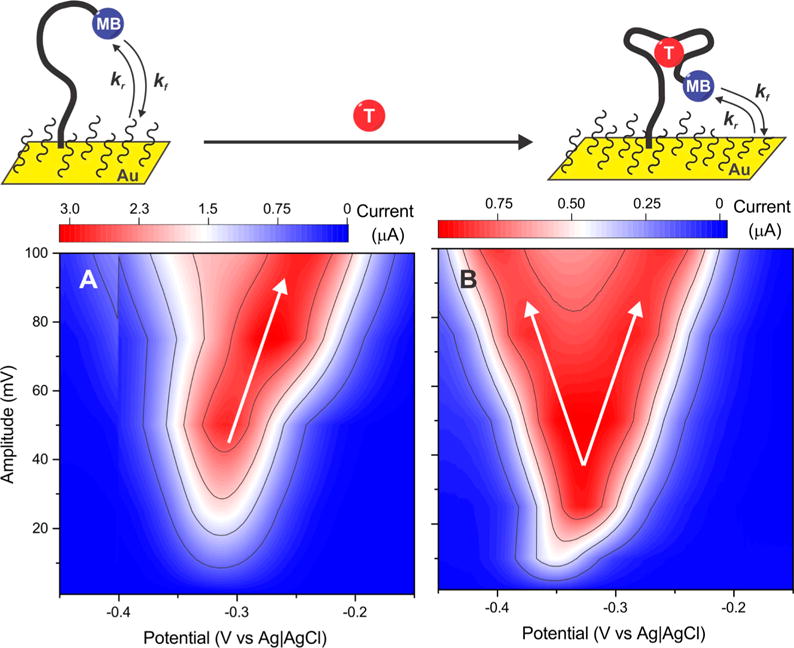
Because the rates of the forward (k_f) and backward (k_r) electrochemical reactions of its redox reporter are not the same in the absence and presence of target, the signal gain of E-DNA sensors is influenced by both the amplitude and the frequency of the square-wave potential pulse. To see this, we recorded voltammograms of the aminoglycoside sensor varying in amplitude at a constant frequency (100 Hz). (A) In the absence and (B) in the presence of saturating concentration of kanamycin, we observe a peak splitting in the voltammograms, which is more prominent in the bound state at amplitudes higher than 50 mV. We rationalized this effect to the respective rates of reduction (k_f) and oxidation (k_r) of the redox reporter, which changes between the bound and unbound states, further requiring a fine-tuning of the square-wave amplitude and frequency to maximize the sensor signal gains.

CONCLUSION

Optimization of the square-wave amplitude/frequency pairing used to interrogate E-DNA sensors can lead to large improvements in their signal gain, with the optimal parameters depending on the structure of its probe, the nature of its redox reporter, and the chemistry of its self-assembled monolayer (although, surprisingly to us, not on the probe’s packing density). Using optimized parameters for an aminoglycoside E-AB sensor, for example, pushes its gain up by a factor of ~2.5 relative to the best previously reported value. Similar results obtained for a variety of other E-DNA-type sensors suggest that this optimization could prove important for effectively all sensors in this broad class. Moreover, as a number of other electrochemical biosensor architectures rely on binding-induced changes in electron transfer kinetics (including, for example, sensors reliant on electrochemical impedance spectroscopy or alternating current voltammetry¹⁷), the observations reported here may be of still broader impact.

MATERIALS AND METHODS

Materials and Instruments

NaCl, KCl, KH₂PO₄, NaH₂PO₄, and NaOH were acquired from Fischer Scientific (NJ). H₂SO₄ was purchased from EMD (USA), and 2 mm gold electrodes, fritted Ag|AgCl electrodes, and platinum wire were from CHInstruments (TX). 6-Mercapto-1-hexanol, 11-mercapto-1-undecanol, 3-mercapto-1-propanol, tris(2-carboethyl)-phosphine hydrochloride (TCEP), cocaine, and murine monoclonal anti-FLAG M2 antibody were obtained from Sigma-Aldrich (MO). Kanamycin monosulfate was purchased from GoldBio.com (MO), and ethanol was obtained from Gold Shield Distributors (CA). 2 and 7/8″ microcloth, 1 μm monocrystalline diamond suspension, and 0.05 μm micropolish alumina powder were obtained from Buehler (IL). All were used as received.

Gold Electrodes’ Polishing and Electrochemical Cleaning

E-DNA biosensors were fabricated as previously described.⁴⁴ Briefly, we initially polished 2 mm diameter gold disk electrodes on a microcloth soaked with an oil-based slurry of 1 μm diamond particles followed by their sonication in ethanol for 5 min. Mirror finished surfaces were obtained through a finer polishing again using a microcloth soaked in an aqueous suspension of 0.05 μm alumina. We removed the excess of alumina particles by sonicating the freshly polished electrodes in ethanol for 5 min and dried them under N₂.

We cleaned the electrodes electrochemically by cycling the potential 500 times between −0.4 and −1.35 V versus Ag|AgCl at 2 V s⁻¹ in an aqueous solution of 0.5 M NaOH using a three-electrode setup (as for all electrochemical measurements, reference Ag|AgCl, counter electrode platinum, and a CHInstrument 660D potentiostat). The electrodes were then transferred into a 0.5 M H₂SO₄ solution where the potentiostat applied an oxidizing potential of 2 V versus Ag|AgCl for 5 s followed by a reducing potential of −0.35 V versus Ag|AgCl for 10 s. We cycled the electrodes rapidly between −0.35 and 1.5 V versus Ag|AgCl at 4 V s⁻¹ to clean the gold surface for 10 cycles. The electrodes were slowly cycled at 0.1 V s⁻¹ over the same window for 2 cycles. Finally, we performed an etching step in a solution of 0.1 M H₂SO₄ and 0.01 M KCl by slowly cycling them at 0.1 V s⁻¹ for 5 cycles starting with an initial potential window of 0.2–0.75 V that is increased to 1.5 V in 0.25 V increments. We determined the electroactive area of each gold electrode by integrating the area under the curve of the gold oxide reduction peak that we observed in a solution of 0.05 M H₂SO₄ at 0.1 V s⁻¹ between −0.35 and 1.5 V vs Ag|AgCl and dividing it by 422 μC cm⁻². With this cleaning procedure, we were able to generate a surface area of ~0.03 cm².

Functionalization of Gold Electrodes

The electrochemically cleaned gold electrodes were then incubated for 1 h in 100 μL of a 200 nM (aptamer-based sensors or if stated differently), 25 nM of anchor DNA (DNA-peptide scaffold sensors), or 500 nM (linear DNA sensor) solution of custom oligonucleotides commercially acquired from BioSearch Technologies Inc. (Novato, CA; see sequences below in Table 1) or PNA Bio (CA) previously reduced in a 10 mM solution of TCEP for 30 min. The electrodes were then thoroughly rinsed in deionized water before immersing them in a 2 mM 6-mercapto-1-hexanol (or otherwise stated) overnight at 4 °C. The sensors were rinsed again with deionized water to remove any excess of nonspecifically adsorbed 6-mercapto-1-hexanol.

Table 1.

Nucleotide Sequences Used in This Work^a

sequence name	sequence (5′ to 3′)
C6-aminoglycoside aptamer-MB	SH-(CH2)6-GGGACTTGGTTTAGGTAATGAGTCCC-T-MB
C11-aminoglycoside aptamer-MB	SH-(CH2)11-GGGACTTGGTTTAGGTAATGAGTCCC-T-MB
C6-aminoglycoside aptamer-Aq	SH-(CH2)6-GGGACTTGGTTTAGGTAATGAGTCCC-T-Aq
C6-aminoglycoside aptamer-Fc	SH-(CH2)6-GGGACTTGGTTTAGGTAATGAGTCCC-T-Fc
C6-cocaine aptamer-MB	SH-(CH2)6-AGACAAGGAAAATCCTTCAATGAAGTGGGTCG-T-MB
C6-27-mer DNA scaffold-MB	SH-(CH2)6-GCAGTAACAAGAATAAAACGCCACTGC-MB
complementary PNA scaffold	DYKDDDDKGG-CAGTGGCGTTTTATTCTTGTTACTG
C6-linear E-DNA-MB	SH-(CH2)6-ATTATTTTTTATTTATTTTTATTTTATTTTATTTTTTATT-MB
target for linear E-DNA sensor	AATAAAAAATAAAATAAAATAAAAATAAATAAAAAATAAT

^aSH-(CH₂)₆- (C6) and SH-(CH₂)₁₁- (C11) represent a hexanethiol and undecanethiol chain that are used to anchor on the 6-mercapto-1-hexanol or 11-mercapto-1-undecanol monolayers, respectively; MB, Aq, and Fc represent the redox reporters methylene blue, anthraquinone, and ferrocene, respectively. All of the redox reporters are covalently attached to a T nucleotide, which was incorporated in the sequence using phosphoramidite chemistry by BioSearch Technologies Inc.

Acquisition of Signal Gain Maps and Dose–Response Curves

Square-wave voltammograms of the modified electrodes were recorded at various combinations of pulse amplitudes, frequencies, and “potential step-size” by scanning the potential between −0.05 and −0.45 V versus Ag|AgCl in a phosphate buffer saline solution (PBS: 137 mM NaCl, 2.7 mM KCl, 10 mM Na₂HPO₄, and 2 mM KH₂PO₄) at pH 7.2. The peak current was further extracted for each of the previous electrochemical parameter combinations by subtracting the baseline current from the peak maxima. Peak currents maps of pulse amplitude versus frequency were then built. The same approach was used upon immersion of the sensors in a saturating solution of target (50 mM kanamycin, 1 mM cocaine, 1 μM 40 bases linear oligonucleotide complement, 100 nM complementary PNA, and then 30 μg mL⁻¹ of FLAG antibody). The peak current map obtained in the presence of saturating amounts of target was then normalized against the map acquired in buffer to obtain the maximal signal change at each respective pulse amplitude/frequency combinations. Having determined the optimal electrochemical signals, dose–response curves were acquired to corroborate the results presented in the maps.