Using the population-shift mechanism to rationally introduce “Hill-type” cooperativity into a normally non-cooperative receptor

Abstract

Allosteric cooperativity, which nature uses to improve the sensitivity with which biomolecular receptors respond to small changes in ligand concentration, could likewise be of use in improving the responsiveness of artificial biosystems. Thus motivated, we demonstrate here the rational design of cooperative molecular beacons, a widely employed DNA sensor, using a generalizable population-shift approach in which we engineer receptors that equilibrate between a low-affinity state and a high-affinity state exposing two binding sites. Doing so we achieve cooperativity within error of ideal behavior, greatly steepening the beacon’s binding curve relative to that of the parent receptor. The ability to rationally engineer cooperativity should prove useful in applications such as biosensors, synthetic biology and “smart” biomaterials, in which improved responsiveness is of value.

Graphical abstract

Using the Population-Shift Mechanism to Rationally Introduce Hill-Type Cooperativity into a Biomolecular Receptor

Nature uses cooperativity to improve the sensitivity of bioreceptors to subtle changes in ligand concentration. Here we rationally engineer this useful property into a normally non-cooperative biosensor, significantly enhancing its responsiveness. The ability to rationally engineer cooperativity should prove useful in many biotechnologies such as such as biosensors, molecular logic gates, and responsive materials.

The ability to respond sensitively to small changes in a molecular input is critical to many biological processes. Such ability allows cells and organisms to react to subtle molecular cues and to convert complex input signals into decisive, effectively binary outputs.^[1] An enhanced ability to detect small changes in molecular concentration would likely also prove of value in many biotechnologies. The ratio between an effective dose and a toxic dose of some drugs, for example, can be as little as 4-fold,^[2] and thus to measure these with clinically-relevant precision requires sensors that respond robustly to small changes in drug concentration.

Driven by the advantages associated with enhanced molecular responsiveness evolution has invented a number of mechanisms, including sequestration, amplification cascades, and receptor co-localization, by which the relative insensitivity of single-site receptors (e.g., they require an 81-fold concentration change to transition from 10% to 90% occupancy) can be overcome.^[1] To date many of these mechanisms have been exploited to improve the responsiveness of biotechnologies ranging from molecular^[3] and genetic^[4] logic gates to ultra-responsive biosensors^[5,6] and digital, “all-or-none” drug-delivery systems.^[7,8] Allosteric cooperativity, however, which is arguably the simplest solution to this problem,^[9,10] has seen adaptation to only a handful of small-molecule^[11,12] and biopolymer-based receptors.^[13–16] Here we explore and articulate design principles underlying this mechanism by engineering it into a normally non-cooperative receptor, thus improving its ability to respond to subtle concentration changes.

The occupancy of an allosterically cooperative receptor goes as

$$\frac{\left[\mathit{\text{complex}}\right]}{\left[\mathit{\text{complex}}\right]+\left[\mathit{\text{free}}\mathit{\text{receptor}}\right]}=\frac{{\left[\mathit{\text{target}}\right]}^{n_H}}{{\left[\mathit{\text{target}}\right]}^{n_H}+{K_{\mathit{\text{Half}}}}^{n_H}}$$ Eq. 1

where K_Half is the concentration at which half of all binding sites are occupied and n_H, the “Hill coefficient,” provides a convenient metric of cooperativity: a system is non-cooperative at n_H = 1, and approaches maximum cooperativity as n_H approaches the number of binding sites on the receptor.^[17] (Note: here we discuss positive cooperativity, which steepens the binding curve. Negative cooperativity, in contrast, broadens the curve; e.g., ref^[13]). The resultant higher order dependence on concentration narrows the range over which a receptor transitions from largely unbound to largely bound, increasing the robustness of its response to small changes in input (Figure 1a). Specifically, the width of a receptor’s dynamic range (defined conventionally as the ratio of the target concentrations at which occupancy is 90% and 10%, C₉₀ and C₁₀, respectively) is related to the Hill coefficient by^[18–20]

$$\mathit{\text{Dynamic}}\mathit{\text{Range}}=\frac{C_{90}}{C_{10}}={81}^{\frac{1}{n_H}}$$ Eq. 2

The dynamic range thus collapses from 81-fold for a non-cooperative receptor to just 9-fold for a maximally cooperative, two-site analogue, significantly enhancing the extent to which receptor occupancy changes with small changes in target concentration.

Figure 1.

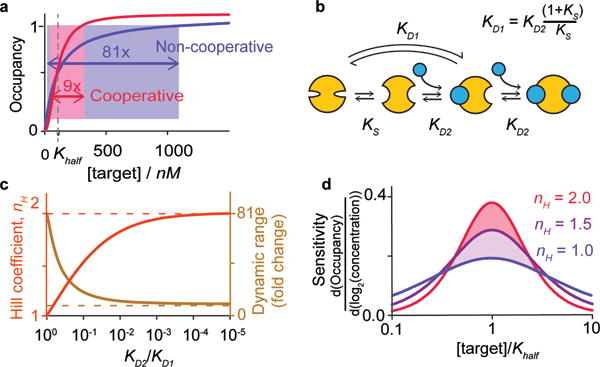
(a) Allosteric (“Hill-type”) cooperativity provides a means of overcoming the 81-fold dynamic range of single site receptors (red) to produce steeper, more responsive behavior (blue). Cooperativity arises when multiple binding sites interact such that the first binding event improves the affinity of subsequent binding events. (b) To design this we employ the population-shift mechanism, in which the first binding event is coupled to an unfavorable conformational change, reducing its affinity (K_D1) relative to that of the second binding event (K_D2). (c) While maximal cooperativity (dashed lines) is only achieved if the second binding event is infinitely more favorable than the first, near-ideal behavior is rapidly approached as the relative affinity of the subsequent binding event rises. (d) Even modest cooperativity significantly improves sensitivity to small changes in concentration (shown here as the relative change in occupancy per two-fold change in target concentration).

Allosteric cooperativity is achieved when the binding of one copy of a target molecule improves the affinity with which subsequent copies of the same molecule bind to other, distal, sites on the same receptor (Figure 1b), changing in turn the shape of the binding curve (Figure 1a).^[21–23] Cooperativity, also called homotropic allostery (all sites bind identical molecules), thus differs from heterotropic allostery (sites bind different molecules), which instead alters the placement (i.e., midpoint) of the binding curve without changing its underlying shape. While extensive literature exists regarding the design of heterotropically allosteric receptors,^[24–26] the rational design of cooperativity has seen relatively little success,^[11–16] perhaps because details of the mechanism render its design rather non-intuitive. First, the all-or-nothing effect of cooperativity requires the creation of systems in which a higher affinity site is occupied only after a lower affinity site that binds the same ligand is already filled. Second, in contrast to heterotropic allostery, homotropic allostery occurs at binding sites that are identical or near identical, and thus it requires perhaps more finesse to alter the affinity of one independently of the others.

Given the above arguments our goal is to design multi-site receptors for which the affinity of the first binding event is poorer than that of subsequent binding events. To achieve this we have employed the population-shift mechanism (see, by analogy, refs^{[15, 27]}). That is, we have designed receptors that interconvert between two conformations, the more stable of which is “closed,” exhibiting low affinity for the target, and the less stable of which is “open,” exposing multiple high affinity binding sites (Figure 1b). The first binding event shifts the conformational equilibrium “up-hill” toward the latter, higher affinity state. As subsequent binding events need not “pay the cost” associated with this unfavorable conformational change, their affinity is enhanced relative to that of the first, producing a cooperative response. For the simplest case of a receptor opening to expose two identical binding sites, the dissociation constant of the first binding event, K_D1, will be higher (i.e., poorer affinity) than that of the second, K_D2, by the relationship

$$K_{D1}=K_{D2}\frac{1+K_S}{K_S}$$ Eq. 3

where K_S is the equilibrium constant for the shift between the closed and open conformations. The extent of cooperativity, in turn, depends on the ratio of the affinities of the binding events by^[28]

$$n_H=\frac{2}{1+\sqrt{\frac{K_{D2}}{K_{D1}}}}$$ Eq. 4

From this relationship it is apparent that maximum cooperativity (n_H equals the total number of binding sites) is only achieved when subsequent binding events are infinitely more favorable than the first (i.e., K_D2 << K_D1). Fortunately for our design efforts, however, the asymptotic approach towards maximal cooperativity (Figure 1c) and, thus, maximum responsiveness (Figure 1d) is rapid. Specifically, a two-site receptor achieves a Hill coefficient of 1.5 when the ratio K_D2/K_D1 reaches just 0.1 (i.e., when, at 37°C, the gap between the binding events is only 6 kJ/mol). This reduces the receptor’s dynamic range from 81-fold to just 19-fold, significantly increasing sensitivity to small changes in target concentration.

As our design test bed we have employed molecular beacons,^[29] a widely used optical^[30,31] and electrochemical^[32] sensor for the detection of DNA and RNA. Molecular beacons are DNA molecules containing self-complementary ends and modified on their termini with an optically reporting fluorophore-quencher pair (Figure 2, top). In the absence of target the beacon’s ends hybridize to form a stem-loop that brings its reporters into proximity, reducing fluorescence. Hybridization of the loop to a complementary target sequence breaks the stem, separating the reporters and increasing their output. As expected, the binding of a “traditional,” molecular beacon is non-cooperative, exhibiting a Hill coefficient of 1.02±0.09 and a dynamic range of 74(±22)-fold, values within error of those predicted for single-site binding (Figure 2, bottom).

Figure 2.

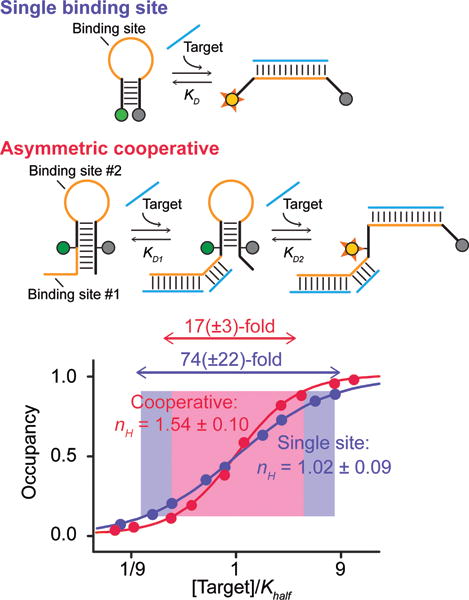
(Top) As a test bed for our design efforts we use molecular beacons, a commonly employed sensor for the detection of specific nucleic acids.^29–32 (Middle) To introduce cooperativity we added a second binding site contained partially within the 5′ strand of the stem and partially within an appended single-stranded tail. Binding to either site disrupts the stem, pushing the conformational equilibrium towards the higher affinity state. (Bottom) The binding of an unmodified molecular beacon is not cooperative, producing a Hill coefficient (n_H) and dynamic range within error of the 1 and 81-fold values expected. The tailed beacon, in contrast, achieves a Hill coefficient of 1.54±0.10, shrinking the dynamic range to 17(±3)-fold. Error estimates here and elsewhere reflect estimated 95% confidence intervals.

Our first design efforts were inspired by a previous, heterotropically allosteric beacon in which the binding of one molecule controls the affinity of a second, different target molecule, shifting the midpoint of the binding curve without changing its shape.^[24] This consists of a stem-loop containing one binding site in its loop and a second partially within a single-stranded tail and partially within the beacon’s double-stranded stem. The binding of a target molecule to either the tail or the loop weakens the stem, shifting the beacon’s population toward the open, binding-competent conformation and improving the affinity with which the second ligand binds. Here we have made the two binding sites identical (Figure 2, middle), rendering the beacon cooperative and producing a steeper, more responsive curve than seen for either the parent or the heterotropically allosteric beacon. Against a 14-base target, for example, that overlaps with five (of nine) bases in the stem the tailed beacon achieves a Hill coefficient of 1.54±0.10 and, correspondingly, a dynamic range of 17(±3)-fold (Figure 2, bottom). In contrast a 13-base target overlapping with just 4 bases in the stem (thus producing a smaller energy gap), produces a Hill coefficient of only 1.40±0.10 and a dynamic range of 23(±6)-fold (Figure SI 1).

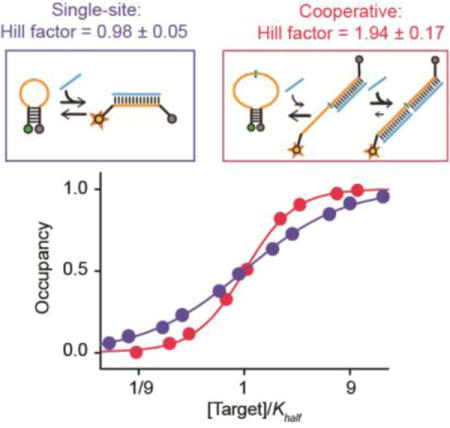
To achieve performance closer to the theoretical maximum it is necessary to increase the energy gap between the first and second binding events (i.e., to decrease K_S), which can be done by altering the stability (sequence), of the stem.^[27] The stem of the tailed beacon, however, also serves as part of a target-binding site and thus altering it would also change the beacon’s specificity. To circumvent this we designed a second, “symmetric” cooperative beacon that places two identical binding sites within the single-stranded loop with only minor stem overlap with the stem (Figure 3, top). Because the persistence length of double-stranded DNA is long^[33] the strain associated with the binding of even a single target molecule to this loop destabilizes the stem and shifts the population towards the high-affinity conformation, improving the affinity of the second binding event. Furthermore, we can “tune” the energy gap between the two dissociation constants by altering the sequence or length (and thus stability) of the stem without altering the specificity of the two target binding sites. Using a stable six base-pair, GC-rich stem for which K_S = 0.0025 at 39°C) this construct achieves a Hill coefficient of 1.94±0.17 and a dynamic range of 9.6(±1.6)-fold (for a 14-base target), values within error of those expected for a perfectly cooperative two-site receptor (Figure 3, bottom). Weakening the stem by converting a single base pair from GC to AT raises K_S to ~0.14, reducing the Hill coefficient to 1.43±0.13, and broadening the dynamic range to 22(±6)-fold (Figure SI1).

Figure 3.

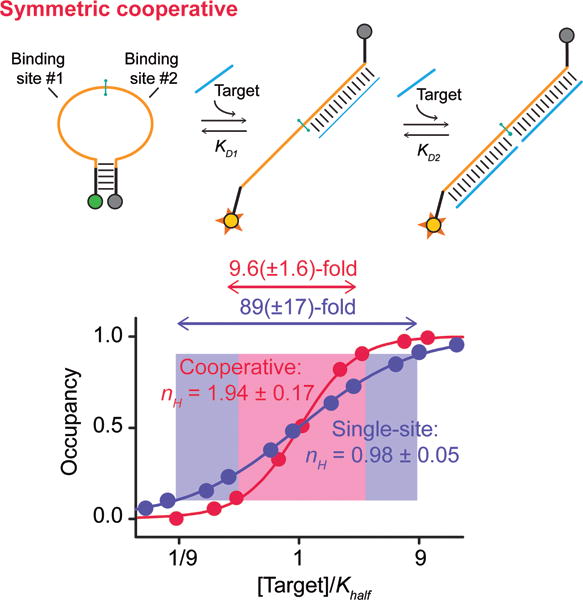
(Top) Our second design places two target-binding sites within the beacon’s single-stranded loop, rendering it possible to stabilize the stem (i.e., increase the energy gap between the two binding events) without altering specificity. (Bottom) Using a rather stable stem and a 14-base target this achieves a Hill coefficient of 1.94±0.17 and a dynamic range of 9.6(±1.6)-fold, within error of ideal behavior. Shorter targets and/or less stable stems reduce cooperativity by reducing the energy gap between the first and second binding events (Figures SI1, SI2).

The symmetry of the latter beacon renders it a convenient platform with which to dissect the thermodynamics underlying our design. To do so we have explicitly measured K_D1 and K_D2, the affinities of the first and second binding events using a control construct identical to the symmetric beacon save that the binding sites differ in sequence (Figure 4a). This provides a means of verifying equation 4, the theoretical relationship between the Hill coefficient and the ratio of binding affinities. For example, plugging the K_D1 and K_D2 observed for this control construct (at 39°C; Figure 4b) into equation 3 predicts n_H = 1.88, which is within the error of the 1.94±0.17 observed for the equivalent symmetric beacon under the same conditions (Figure 3, bottom). Conducting this experiment over a range of temperatures, which alters the conformational equilibrium constant and in turn, K_D1, we find that, as expected, this relationship holds even as the ratio of affinities varies over orders of magnitude. Specifically, as K_S decreases monotonically from 0.78 (at 58°C) to 0.0025 (at 39°C) the receptors shift monotonically from effectively single-site behavior to near-perfect two-site cooperativity (Figures 4c, SI3).

Figure 4.

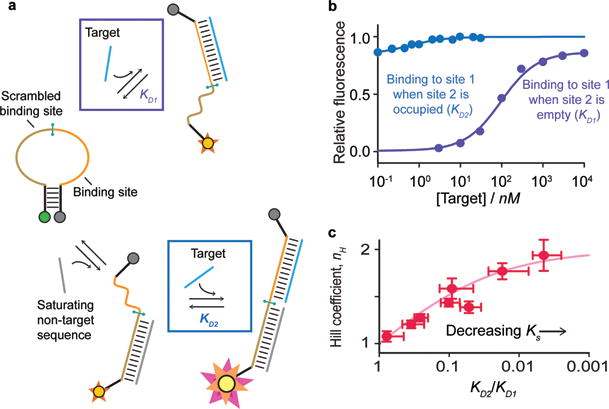
(a) The modular structure of our symmetric cooperative beacon allows exploration of the thermodynamics underlying its design. To do so we employed a construct in which the two ligand binding sites are distinct, allowing independent measurement of K_D1 and K_D2. (b) Shown are the affinities (at 39°C) measured when the other binding site is empty (purple), and when it is occupied (blue); note that, the latter occurs on a beacon that is already largely open, and thus produces only a fifth of the total signal change. The affinities obtained from this control predict n_H = 1.88 for our sensor (eq. 3), within experimental error of the observed value (Figure 3). (c) Measuring K_D2, K_D1 (using the control construct), and n_H (using the cooperative beacon) over a range of temperatures we find that the expected relationship between these values (eq. 3) holds even as the ratio of the binding affinities varies over orders of magnitude.

A number of bioinspired mechanisms have been used to enhance the precision of biosensors^[5,6] and to improve the responsiveness of drug delivery systems,^[7,8] synthetic biology “circuits,”^[4] and molecular logic gates.^[3] To date, however, Hill-type cooperativity, a simple mechanism by which biology enhances the cell’s ability to sense small changes in the concentration of molecular cues,^[1] has seen little use in artificial biosystems. In response we have demonstrated here the utility of employing the population-shift mechanism to rationally introduce cooperativity into molecular beacons, greatly increasing the sensitivity with which they respond to subtle changes in molecular concentration.

We note in closing that the modular structure of molecular beacons may render their re-engineering particularly straightforward. We nevertheless believe the design strategies described here will prove general. That is, the principles that the population shift mechanism provides a ready route to cooperativity, and that the switching equilibrium constant need only be of order 0.1 to generate significantly improved responsiveness, will be generalizable to other receptors. For example, a large body of literature already demonstrates the rational introduction of binding-induced conformational changes into normally static biomolecules,^[24–26] suggesting that, although design details may differ, cooperativity could similarly be introduced into a range of receptors via mechanisms such as, for example, binding-induced folding.