Abstract
The efficiency with which square-wave voltammetry differentiates faradic and charging currents makes it a particularly sensitive electroanalytical approach, as evidenced by its ability to measure nanomolar or even picomolar concentrations of electroactive analytes. Because of the relative complexity of the potential sweep it uses, however, the extraction of detailed kinetic and mechanistic information from square-wave data remains challenging. In response, we demonstrate here a numerical approach by which square-wave data can be used to determine electron transfer rates. Specifically, we have developed a numerical approach in which we model the height and the shape of voltammograms collected over a range of square-wave frequencies and amplitudes to simulated voltammograms as functions of the heterogeneous rate constant and the electron transfer coefficient. As validation of the approach, we have used it to determine electron transfer kinetics in both freely diffusing and diffusionless surface-tethered species, obtaining electron transfer kinetics in all cases in good agreement with values derived using non-square-wave methods.
Graphical abstract
INTRODUCTION
Square-wave voltammetry (SWV), an electroanalytical technique that involves the application of repeating square-shaped potential pulses superimposed on a staircase potential sweep, enables the effective discrimination of faradic processes from charging currents.1 It achieves this by imposing two opposite square-wave pulses of the same height at each staircase potential step and measuring the resultant current at the end of each pulse, ifwd and ibwd. Taking the difference between these currents returns a net voltammogram with improved signal-to-noise ratios relative to those of, for example, cyclic voltammetry.1,2 This, in turn, makes SWV one of the most sensitive electroanalytical techniques, enabling the detection of metal ions and organic molecules at nanomolar and picomolar concentrations, respectively.1
In this work, we build on prior approaches aimed at determining the electron transfer kinetics using SWV by modulating the height (amplitude) or the width (frequency) of the square-wave pulses.1,3 This earlier work includes that of Lovrić4,5 who, for example, developed a mathematical method termed “quasi-reversible maximum” that extracts electron transfer kinetics from the maximum in a plot of SWV peak current versus square-wave frequency. Mirčeski and co-workers,6–9 in contrast, have developed a mathematical method that extracts electron transfer kinetics from the relationship between SWV peak current and square-wave amplitude, with the maximum on this plot again correlating with the electron transfer rate. These methods have allowed the determination of the electron transfer rates of a range of freely diffusing8 and surface-anchored6 redox couples, including linear and duplex DNA strands modified with a redox reporter.10,11 Historically, however, these approaches have been limited to the measurement of relatively slow transfer rates of redox couples undergoing quasi-reversible or irreversible electron transfer reactions.3,8,12 This leaves uncharacterized many important and fully reversible redox couples, which transfer electrons more rapidly. Here, we have expanded upon this prior literature and developed a method of extracting electron transfer rates from SWV data which overcomes this limitation, enabling access to much more rapid electron transfer kinetics than is possible with the prior approaches.
The methods of Lovrić and Mirčeski rely on the fact that SWV peak height is defined by the interplay between the forward and backward electron transfer rates and the frequency and amplitude of the square-wave pulse.1 Specifically, Lovrić’s approach5 extracts rates using the relationship between the square-wave frequency and the height of the resultant voltammetric peaks. This works because changing the square-wave frequency optimizes the time scale of the measurement to the time scale of electron transfer and, in turn, influences the peak height. Mirčeski’s approach,8 in contrast, extracts kinetic information from the relationship between square-wave amplitude and the height of the resultant voltammetric peaks. This works because changing the square-wave amplitude alters the driving force underlying electron transfer, changing the rates of the forward and backward electron transfer reactions and thus altering peak splitting and, in turn, peak height.
The success of the methods of Lovrić and Mirčeski demonstrates that information regarding electron transfer kinetics can be extracted by observing peak height as a function of either square-wave frequency or square-wave amplitude. Building on this, we describe here an approach that captures both effects simultaneously, potentially providing more information regarding rates than methods that extract rates by varying only one or the other. Specifically, we present a numerical approach that, by simultaneously modeling both the heights and shapes of voltammetric peaks, is able to measure electron transfer kinetics for reactions that had proven too rapid to measure using prior SWV methods.
Our approach to extracting electron transfer kinetics uses numerical simulations to model the height and the shape of experimental SWV scans collected over a range of frequencies and amplitudes. To do so, we first numerically model the experimental setup as a simple, one-dimensional electrochemical cell. As examples, we explore here two such cases: (1) a freely diffusing redox couple and (2) a redox couple that is confined to the electrode surface via a short, flexible linker. We define two boundaries in each model, one representing the surface of the working electrode and the other representing either the bulk of the solution (Figure 1A) or the cell wall (Figure 1B). The reaction considered in all cases is reversible and is defined as
| (1) |
where n represents the number of electrons transferred. The electrode boundary condition for both oxidized, O, and reduced, R, species is set in all cases to “flux” as defined by Fick’s second law of diffusion
| (2) |
| (3) |
where DO and DR are experimentally determined diffusion coefficients (for ferrocenemethanol, e.g., which we use below, both DO and DR are 7.8 × 10−6 cm s−1)13 and CO and CR represent the concentrations of the oxidized and reduced species, respectively, and are both functions of time, t, and distance from the electrode surface, x. Per eq 1, the initial conditions are and CR = 0 and the right boundary conditions are set as follows:
- Case 1: diffusive redox couple
(4) - Case 2: surface-confined redox couple
(5)
Figure 1.
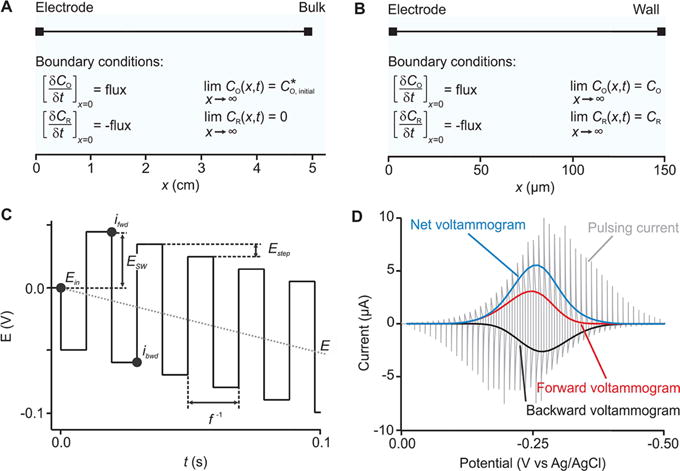
Description of the numerical model. Our approach starts with one-dimensional numerical models; shown are models for (A), a freely diffusing redox couple, and (B), a diffusionless, surface-bound redox couple. (C) We then simulated the response of these to SWV using a square waveform of frequency f and amplitude ESW. This is superimposed on a staircase that ramps the mean potential (the mean potential per pulse pair, E) by a potential step size per cycle, Estep. In response to this varying potential, the system produces an oscillating faradic current (gray trace in D). We deconvolute this into “forward” and “backward” voltammograms (red and black curves in D) by extracting the current at specific times (ifwd and ibwd). The difference between these two voltammograms then returns a “net” voltammogram (blue curve in D).
Equation 4 describes the case of the bulk boundary that is positioned far from the electrode surface so that (bulk concentration of oxidized species) and where CR = 0 remains constant at all t and is unaffected by the electrode reaction. Equation 5, in contrast, describes the case of a thin-layer cell with an inert wall, which mimics the physics of an electroactive monolayer on an electrode surface. It does so by limiting the length of the electrochemical cell to x ≪ (2Dt)1/2, which is smaller than the length of the diffusion layer for a given experimental time t. On the basis of the diffusion coefficient of ferrocenemethanol (which, again, we use below), we set x = 150 μm. As the concentration of the oxidized species, CO, decreases, the concentration of the reduced species, CR, necessarily increases according to the flux (Figure 1A,B). We adjusted the initial surface concentration (CO or CR depending whether the redox couple undergoes reduction or oxidation), using the peak current of the experimental voltammograms, which is directly proportional to the concentration of the redox couple.
We set the fluxes (eqs 2 and 3) in the solution domain of the numerical environment to obey the Butler–Volmer formalism of electron transfer kinetics
| (6) |
| (7) |
| (8) |
| (9) |
where k0 is the heterogeneous rate constant (in cm s−1), α is the electron transfer coefficient, E is the ramping potential (Figure 1C), E0 is the standard potential (V), iO is the oxidation current, iR is the reduction current, and F, R, n, and T are Faraday constant, the gas constant, the number of electrons, and the temperature (here 298 K), respectively.
Having defined the physics of the electrochemical system, we next modeled the potential waveform that SWV uses (Figure 1C). To do so, we use the following
| (10) |
| (11) |
| (12) |
where Ein is the initial potential of the square waveform (Figure 1C), Estep is the potential step size, ESW is the square-wave amplitude, and f is the square-wave frequency. To create the square waveform, we used a Heaviside function (flsmsign) that generates values between +1 and −1 and multiplied it by the amplitude of the square-wave pulse (eqs 10 and 12). To render the pulses a close approximation to square, we used an input argument of 0.001 for this function (eq 12). We generated the ramping square-wave potential program applied at the electrode by adding this to a staircase waveform obtained using a modulo operator (mod) of the given Estep (eq 11) (Figure 1C). Multiplying the fluxes (eqs 8 and 9) calculated at each time point in the voltammetric sweep by n and F, we generate a current decay trace (gray curve in Figure 1D). We then plot the calculated currents at the end of each positive and negative square-wave pulse (referred to as forward, ifwd, extracted at t = 0.5pf−1 and backward, ibwd, extracted at t = pf−1, where p is the pulse number) as functions of the ramping potential (Figure 1D; red and black curves, respectively). Finally, we subtract the forward voltammogram from the backward voltammogram to produce the net voltammogram (Figure 1D—blue curve).
The improved ability of our numerical approach to extract heterogeneous rate constants, k0, and electron transfer coefficients, α, from SWV data stems from the ability to reproduce not only the height of the three SWV peaks (forward, backward, and net) but also their shape. The latter is particularly important for the measurement of rapid electron transfer kinetics, conditions under which square-wave peak shape is more strongly influenced than peak height by changes in amplitude and frequency.1 For example, when the unitless ratio of the electron transfer rate to the square-wave frequency, k0/f, increases above ~3 × 105 (for square-wave amplitudes of order 25–50 mV, with the exact cutoff depending on the amplitude), the peak will begin to split (Figure S1). Under these circumstances, the rate of electron transfer becomes more strongly related to the peak shape than to the peak height (Figure S2).1,12 Models that use only peak heights, obviously, cannot capture such effects, leaving them poorly suited for accessing rapid electron transfer kinetics. Indeed, in practice, the methods of Lovrić5 and Mirčeski8 are limited to the determination of rates falling below ~10−2 cm s−1 (106 s−1). Our approach, in contrast, can accurately recover rates to at least 10 cm s−1 (equivalent to 109 s−1; see, e.g., the transfer kinetics of ferrocenemethanol below).
As a first test of our approach, we determined the electron transfer kinetics of the well-characterized ferrocenemethanol redox couple FcMeOH/FcMeOH+ in solution. This couple undergoes an electrochemically reversible one-electron transfer reaction at rates as rapid as ~8–9 cm s−1 (as determined using scanning electrochemical microscopy14), with both forms of the couple being chemically stable in aqueous solution. We characterized this system using SWV data collected at square-wave amplitudes of 25, 50, and 75 mV and frequencies ranging from 20 to 1000 Hz. Although SWV minimizes the contribution of the formation of the electric double layer to the observed current, we have not been able to remove this contribution completely. For this reason, we compare our numerical simulations (Figure 2, dotted lines) with background-subtracted experimental voltammograms (Figure 2, solid line). When doing this, we find that setting k0 to 10 ± 1 cm s−1 and α to 0.50 ± 0.03 reproduces the shapes and heights of the resultant voltammograms (forward, backward, and net) collected at all frequencies and amplitudes (Figure S3). Supporting the validity of our approach, these values are effectively indistinguishable from the 8 ± 1 cm s−1 and 0.44 ± 0.03 reported previously.14
Figure 2.
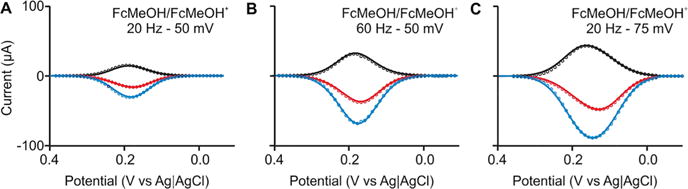
Freely diffusing redox couple. As the first test of our approach, we determined the electron transfer rate of the redox couple FcMeOH/FcMeOH+ when free in solution by recording square-wave voltammograms at various frequency/amplitude combinations (see the full panel in Figure S3). Shown are experimental voltammograms (solid lines) and calculated voltammograms derived from our numerical model (circles) using the values of k0 = 10 ± 1 cm s−1 and α = 0.50 ± 0.03. These values are in good agreement with previously reported values of 8 ± 1 cm s−1 and 0.44 ± 0.03,14 respectively. Here and elsewhere in this work, the confidence intervals represent standard errors derived from least squares fits of the model for the forward, backward, and net voltammograms collected at all of the square-wave frequency/amplitude pairs used.
Our approach is also able to determine the kinetics of surface-confined electrochemical systems. To explore this, we first characterized the electrochemistry of ferrocene covalently attached to a gold electrode via a hexanethiol chain incorporated into a 6-mercapto-1-hexanol self-assembled monolayer (Figure 3A). Recording voltammograms at frequencies ranging from 200 to 1000 Hz and amplitudes of 25, 50, and 75 mV, we observed an oxidation process at a peak potential of E ≈ 0.21 V (Figure 3B). The frequencies at which the peak becomes apparent, however, are 10 times higher than those at which the same peak becomes significant for the redox couple in solution (Figures 3B–D vs 2A–C). We also observed that the width of the net voltammograms increases slightly as we increased the amplitude from 25 to 75 mV. Both of these observations are in line with the rapid electron transfer kinetics of this couple.1
Figure 3.
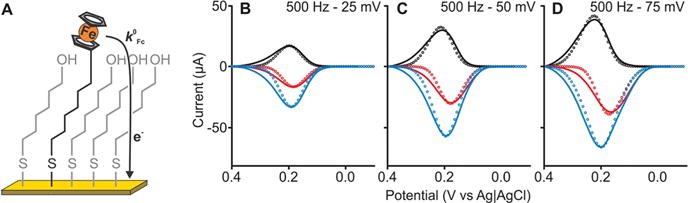
Surface-tethered ferrocene. We immobilized the ferrocene/ferrocenium couple using a hexanethiol chain diluted in a 6-mercapto-1-hexanol monolayer (A) and measured square-wave voltammograms (full line traces in B–D and other frequencies in Figure S4). We matched the experimental results to our numerical model to extract k0 = 8 ± 2 cm s−1 (or ) and α = 0.50 ± 0.03. These are in good agreement with the values previously reported for similar systems.15,16
To determine the electron transfer kinetics of the surface-bound couple, we matched the experimental data from immobilized ferrocene to simulations generated using our diffusionless, surface-bound model. For the values k0 = 8 ± 2 cm s−1 and α = 0.50 ± 0.03, our simulated voltammograms were in good agreement with the experimental data at all frequencies and amplitudes (Figures 3B–D and S4). The electron transfer kinetics values we extracted are effectively indistinguishable from the 6 cm s−1 previously estimated using a laser-induced temperature-jump method.15 Of note, this close correspondence occurs despite slight differences in the widths of our calculated and observed voltammogram peaks at more positive potentials, an effect that we attribute to the heterogeneity of the polycrystalline gold17,18 or interactions between the redox couple and the self-assembled monolayer23 and that we see for several of the other systems described below. That is, the formation of a self-assembled monolayer on polycrystalline gold is known to initiate noticeable variations in peak shape, which is thought to arise because of interactions between neighboring redox couple caused by heterogeneity in the self-assembled monolayers.18,19
The units of centimeters per second for are a reminder that our model uses a thin-layer cell to mimic the physics of an electroactive monolayer adsorbed on an electrode surface. Following the discussion by Smalley et al.,15 we can convert these units of centimeters per second to per second using the tunneling equation20
| (13) |
| (14) |
where k0(x) is the rate of electron transfer for a surface-confined redox couple located at a distance x (in Å) from the electrode surface, k0 (x = 0) is the rate of electron transfer for a surface-confined redox couple located at x = 0, and β is the exponential decay coefficient, which depends on the activation energy of the reaction and nature of the medium through which the electron transfers, on the order of 1.0 Å−1 for systems involving tunneling across self-assembled alkane monolayers similar to that used here.16 The thickness of the monolayer we use is 8.0 Å.21 Using this value in eqs 13 and 14, we obtain for the ferrocene/ferrocenium couple, once again in good agreement with previously reported values, which range from 2.4 × 105 to 26 × 105 s−1 for similar systems.15,16 We can likewise set x = 0 to estimate the electron transfer rate we would observe whether the monolayer was absent. Doing so, we obtain , which is effectively indistinguishable from the value we obtained for the FcMeOH/FcMeOH+ couple free in solution, , determined by substituting the value of k0 (in cm s−1) measured in solution (Figure 2) into eqs 13 and 14.
Our approach to extracting electron transfer rates overcomes the limitation of previously described square-wave methods regarding the estimation of rapid electron transfer kinetics. For example, as noted above, our approach produces a of 2.7 (±0.7) × 105 s−1 for ferrocene adsorbed on a gold surface that is within error of prior measurements taken via the indirect laser-induced temperature-jump method.18 Using the method of Lovrić,4,5 in contrast, which relies only on the peak current of net voltammograms (Figure S5), we find that the quasi-reversible maximum is located at ~1000 Hz, corresponding to (for α = 0.5). The 2 order of magnitude deviation of the Lovrić approach likely originates from experimental limitations in SWV, where an increasing contribution from double-layer charging to the background current of square-wave voltammograms overwhelms the signal arising from the faradic process at high frequencies (>1000 Hz), lowering the precision with which the quasi-reversible maximum can be defined.
Having validated our model for the determination of the single-electron transfer reaction of ferrocene in both diffusive and surface-confined states, we next verified the applicability of the approach for the study of the more complex, two-electron organic redox couple methylene blue/leucomethylene blue, which is widely used as a redox reporter in electrochemical biosensors.4,22 Specifically, we conjugated maleimide-modified methylene blue to a dithiol-terminated hexane chain, which we then incorporated into a 6-mercapto-1-hexanol monolayer on a gold electrode (Figure 4A) and recorded voltammograms at frequencies ranging from 20 to 1000 Hz and amplitudes of 25, 50, and 75 mV (Figures 4B–D and S6). Doing so, we found that the width of the voltammogram peak changed when comparing with the ferrocene surface-anchored redox couple not only because of the change in the electron transfer kinetics but also because of a change in the square-wave frequencies used to measure the process. We then carried out numerical simulations to determine the electron transfer kinetics of methylene blue using these experimental data. Here, it is important to note that our model did not include the intermediate mechanistic steps involved in the two-electron reduction of methylene blue but rather carried out simulations assuming an electrochemically reversible, simultaneous two-electron reaction. Despite this simplification, we nevertheless observed reasonable agreement between our numerical simulations and the experimental voltammograms when k0 = 1.5 ± 0.5 cm s−1 and α = 0.37 ± 0.02. Specifically, using eqs 13 and 14 and a monolayer thickness of 8.0 Å, we find that . This is some 8 times faster than the value Lovrić has previously4 determined for this couple on a mercury electrode to be 0.6 × 104 s−1, presumably because of differences in how the couple interacts with the surface, that is, nonspecific adsorption to mercury versus coupling via an alkanethiol linker strongly chemically adsorbed on gold along with limitations in the quasi-reversible maximum analysis described above.
Figure 4.
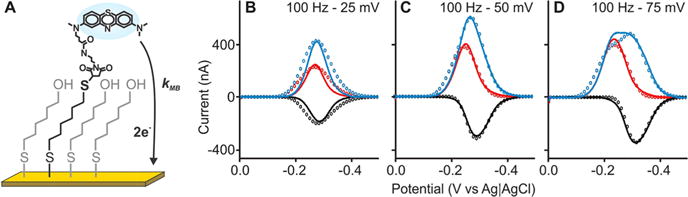
Surface-tethered methylene blue. (A) We used maleimide chemistry to immobilize methylene blue to a gold surface via a six-carbon-linker dithiol chain with a 6-mercapto-1-hexanol monolayer covering the rest of the surface. We then measured square-wave voltammograms (full line traces) at a frequency of 100 Hz (see the other frequencies in Figure S6) and amplitudes of (B) 25, (C) 50, and (D) 75 mV. When we impose k0 = 1.5 ± 0.5 cm s−1 and α = 0.37 ± 0.02 in our numerical model, we find that the resultant simulated voltammograms closely match the experimental voltammograms.
Given the importance of methylene blue in biosensor applications,24–26 we next measured its electron transfer kinetics when it is attached to a linear DNA strand. Specifically, we fabricated gold electrodes coated with a mixed thiol monolayer of hydroxyl-terminated six-carbon alkane chains, some of which were modified with a 20-nucleotide linear DNA sequence attached via its 5′ end. The linear DNA strand was, in turn, modified with a methylene blue on its 3′ terminus (distal from the electrode). Square-wave voltammograms recorded at frequencies ranging between 20 and 1000 Hz and amplitudes of 25, 50, and 75 mV (Figures 5B–D and S7) match our numerical simulations well when k0 = 0.4 ± 0.1 cm s−1 and α = 0.37 ± 0.02. The best-fit value of α for the methylene blue on a surface-attached DNA strand is quite close to the value obtained for methylene blue attached directly to the surface (Figure 4). This suggests that the symmetry of the reaction (the extent to which the oxidation and reduction reactions progress through the same transition state) remains unchanged between the two systems, as seen by others for other redox couples.27,28
Figure 5.
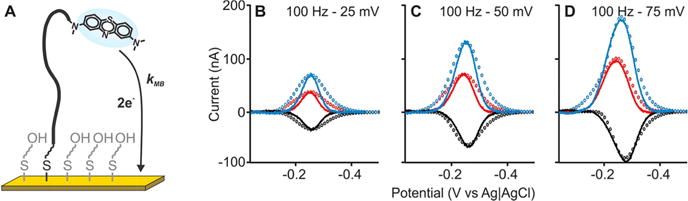
Determination of electron transfer kinetics from a methylene blue-modified, 20-base linear DNA. (A) For this, we immobilized a 20-base linear DNA modified with methylene blue on its distal terminus onto a gold electrode coated with a 6-mercapto-1-hexanol monolayer. We then measured square-wave voltammograms (full line traces) at a frequency of 100 Hz (see the other frequencies in Figure S7) and amplitudes of (B) 25, (C) 50, and (D) 75 mV. When we use k0 = 0.4 ± 0.1 cm s−1 and α = 0.37 ± 0.02 in our numerical model, we find that the resultant simulated voltammograms closely match these experimental voltammograms.
Here, we describe a numerical approach to extracting electron transfer kinetics from experimental square-wave voltammograms and its validation using well-known, well-characterized diffusive and electrode-bound redox couples. Our approach numerically models both the electrochemical cell (as a one-dimensional environment) and the potential program used in SWV. By matching the resultant simulated square-wave voltammograms with voltammograms obtained experimentally over a range of various frequencies and amplitudes, we were able to determine the kinetic parameters k0 and α for three well-characterized electrochemical systems. The rates we determined in all three cases, which are at least an order of magnitude more rapid than those accessible using previously reported SWV methods, are in good agreement with the values previously determined using other, more cumbersome electro-analytical techniques (e.g., scanning electrochemical microscopy). We thus believe that our numerical approach is a potentially generalizable means of extracting kinetic parameters from SWV data, one that couples the impressive sensitivity of SWV with an ability to measure even relatively rapid transfer kinetics.
MATERIALS AND METHODS
Materials and Instruments
NaCl, KCl, KH2PO4, NaH2PO4, and NaOH were acquired from Fischer Scientific (NJ, USA). 6-Ferrocenyl-1-hexanethiol, ferrocenemethanol (FcMeOH), 6-mercapto-1-hexanol, 1,6-hexanedithiol, dimethylsulfoxide (DMSO), phosphate-buffered saline, trifluoroacetic acid (TFA), and tris(2-carboxyethyl)phosphine hydrochloride (TCEP) were obtained from Sigma-Aldrich (MO, USA). Maleimide-modified methylene blue was obtained from ATTO-TEC GmbH (Siegen, Germany), ethanol was obtained from Gold Shield Distributors (CA, USA), H2SO4 was obtained from EMD (USA), and 2 mm gold electrodes, fritted Ag|AgCl electrodes, and platinum wire were obtained from CH Instruments (TX, USA). Microcloth (2–7/8″), 1 μm monocrystalline diamond suspension, and 0.05 μm micropolish alumina powder were obtained from Buehler (IL, USA). All were used as received. We used for all electrochemical measurements an Ag/AgCl reference, a platinum counter electrode, and a CH Instrument 660D potentiostat.
Preparation of SH-C6-maleimide-methylene-blue
We carried out the reaction of maleimide-modified methylene blue (1.7 μmol in 50 μL of DMSO) with excess 1,6-hexanedithiol (170 μmol) overnight. We purified the product from the crude reaction mixture by reverse-phase high-performance liquid chromatography (HPLC) (C18 column) using an acetonitrile gradient in water with 0.1% TFA. The desired compound (20% yield) was collected and characterized using UV/vis and electrospray ionization mass spectrometry (MB-Maleimide-SC6SH+ = 629 g mol−1).
Nucleotide Sequence Used
The linear DNA used in our studies was of sequence
where SH-(CH2)6-represents a hexanethiol chain that was used to anchor the chain in a 6-mercapto-1-hexanol monolayer and MB represents a covalently attached methylene blue. Methylene blue is covalently attached to a thymine nucleotide, which was incorporated in the sequence using standard phosphoramidite solid-phase chemistry by Biosearch Technologies Inc.
Gold-Electrode Polishing and Electrochemical Cleaning
We polished and cleaned the gold electrodes following an established protocol.29 Briefly, the electrodes were first polished on a microcloth pad soaked with a diamond suspension slurry and then moved to another pad soaked with a finer 0.05 μm alumina powder aqueous suspension. Electrodes were sonicated after completing each polishing step in ethanol for ~5 min. The electrodes were then electrochemically cleaned first in a 0.5 M NaOH solution by cycling the potential between −0.4 and −1.35 V versus Ag/AgCl at a scan rate of 2 V s−1 for 500 cycles. The gold electrodes, as for all other measurements, were used as working electrodes in a three-electrode setup with a platinum counter electrode and an Ag/AgCl reference electrode. The electrodes were then moved to a 0.5 M H2SO4 solution where an oxidizing potential of 2 V was applied for 5 s. A reducing potential of −0.35 V was then applied for 10 s. We then cycled the electrodes rapidly (4 V s−1) in the same solution between −0.35 and 1.5 V for 10 cycles followed by 2 cycles recorded at 0.1 V s−1 using the same potential window. Finally, we determined the electroactive area of the electrodes by cycling the potential twice between −0.35 and 1.5 V at a scan rate of 0.1 V s−1 in 0.05 M H2SO4 and then integrating the area under the curve of the gold oxide reduction peak. From this, we obtain an averaged 0.03 cm−2 electroactive area.
Functionalization of Gold Electrodes
The freshly cleaned gold electrodes were then immersed in a solution of 200 nM of the desired compound for 1 h at room temperature. For this, a 100 μM acetonitrile solution of 6-ferrocenyl-1-hexanethiol, a 1 μM aqueous solutions of SH-C6-maleimide-methylene blue or a 200 nM linear DNA modified with methylene blue were reduced using a 10 mM TCEP aqueous solution for 1 h at room temperature. The modified electrodes were thoroughly rinsed with water and then transferred into a 2 mM 6-mercapto-1-hexanethiol solution for overnight incubation.
Measure of Square-Wave Voltammograms
We measured square-wave voltammograms between −0.1 and 0.4 V to record the oxidation of ferrocene and between 0 and −0.45 V to record the reduction of methylene blue. For the study of the FcMeOH/FcMeOH+ couple in solution, we recorded square-wave voltammograms in a 1 mM solution of FcMeOH with 0.1 M KCl for the supporting electrolyte. The amplitude of the square-wave pulse was varied among 25, 50, and 75 mV while its frequency was varied from 20 to 1000 Hz to cover the wide range of electron transfer kinetics exhibited by either ferrocene or methylene blue. The potential step size used was kept constant at 1 mV throughout all measurements.
Numerical Model
The model for determining the heterogeneous electron transfer kinetics using SWV was developed in COMSOL Multiphysics v5.2. Access to this software was kindly granted to us by the Pennathur Group under license no. 1008778. Reported k0 and α values were obtained by performing a least squares fit of the modeled forward, backward, and net voltammograms to the experimental voltammograms at a given frequency/amplitude pair. This is repeated for each experimental square-wave frequency/amplitude pair, with the reported k0 and α values and their confidence intervals being the average and standard error of the parameters extracted from the complete set of frequency/amplitude pairs. The standard error on the extracted value thus informs on the accuracy of our approach to capture both the shape and the height of the voltammogram. Although the standard error represents less than 10% of the extracted k0, we believe that this can be refined because we are currently dependent on user input for the different combinations of square-wave amplitude, square-wave frequency, k0, and α because no analytical solution is available for this problem and the numerical simulations are computationally very demanding.
Supplementary Material
Acknowledgments
This work was supported partially by a grant from the National Institutes of Health (grant R01AI107936) and by a grant from the W. M. Keck Foundation. P.D.-D. was supported in part by Fonds de recherche du Québec—Nature et Technologies and the Natural Sciences and Engineering Research Council of Canada with postdoctoral fellowships. N.A.-C. was supported by the Otis Williams Postdoctoral Fellowship of the Santa Barbara Foundation. H. Li was partially supported by Swiss National Science Foundation with an “Early Postdoc Mobility fellowship”.
ABBREVIATIONS
- Fc
ferrocene
- MB
methylene blue
- TCEP
tris(2-carboxyethyl)phosphine hydrochloride
Footnotes
Supporting Information
The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.langmuir.7b00359.
The effect of the electron transfer kinetics and square-wave amplitude on the shape of the voltammogram peak along with other voltammograms obtained at different square-wave frequency and amplitude combinations for the different electrochemical systems (PDF)
ORCID
Philippe Dauphin-Ducharme: 0000-0002-0490-7115
Netzahualcóyotl Arroyo-Currás: 0000-0002-2740-6276
Kevin W. Plaxco: 0000-0003-4772-8771
Notes
The authors declare no competing financial interest.
References
- 1.Mirčeski V, Komorsky-Lovrić S, Lovrić M. Square-Wave Voltammetry: Theory and Application. Springer; Berlin: 2007. [Google Scholar]
- 2.Laborda E, González J, Molina Á. Recent advances on the theory of pulse techniques: A mini review. Electrochem Commun. 2014;43:25–30. [Google Scholar]
- 3.Mann MA, Bottomley LA. Cyclic Square Wave Voltammetry of Surface-Confined Quasireversible Electron Transfer Reactions. Langmuir. 2015;31:9511–9520. doi: 10.1021/acs.langmuir.5b01684. [DOI] [PubMed] [Google Scholar]
- 4.Lovrić M, Komorsky-Lovrić Š. Square-wave voltammetry of an adsorbed reactant. J Electroanal Chem. 1988;248:239–253. [Google Scholar]
- 5.Komorsky-Lovrić Š, Lovrić M. Measurements of redox kinetics of adsorbed azobenzene by “a quasireversible maximum” in square-wave voltammetry. Electrochim Acta. 1995;40:1781–1784. [Google Scholar]
- 6.Mirčeski V, Lovrić M. Split square-wave voltammograms of surface redox reactions. Electroanalysis. 1997;9:1283–1287. [Google Scholar]
- 7.Mirčeski V, Guziejewski D, Lisichkov K. Electrode kinetic measurements with square-wave voltammetry at a constant scan rate. Electrochim Acta. 2013;114:667–673. [Google Scholar]
- 8.Mirčeski V, Laborda E, Guziejewski D, Compton RG. New Approach to Electrode Kinetic Measurements in Square-Wave Voltammetry: Amplitude-Based Quasireversible Maximum. Anal Chem. 2013;85:5586–5594. doi: 10.1021/ac4008573. [DOI] [PubMed] [Google Scholar]
- 9.Gulaboski R, Mirčeski V. New aspects of the electrochemical-catalytic (EC′) mechanism in square-wave voltammetry. Electrochim Acta. 2015;167:219–225. [Google Scholar]
- 10.Abi A, Ferapontova EE. Unmediated by DNA Electron Transfer in Redox-Labeled DNA Duplexes End-Tethered to Gold Electrodes. J Am Chem Soc. 2012;134:14499–14507. doi: 10.1021/ja304864w. [DOI] [PubMed] [Google Scholar]
- 11.Phares N, White RJ, Plaxco KW. Improving the Stability and Sensing of Electrochemical Biosensors by Employing Trithiol-Anchoring Groups in a Six-Carbon Self-Assembled Monolayer. Anal Chem. 2009;81:1095–1100. doi: 10.1021/ac8021983. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.O’Dea JJ, Osteryoung JG. Characterization of quasi-reversible surface processes by square-wave voltammetry. Anal Chem. 1993;65:3090–3097. [Google Scholar]
- 13.Sun P, Mirkin MV. Kinetics of Electron-Transfer Reactions at Nanoelectrodes. Anal Chem. 2006;78:6526–6534. doi: 10.1021/ac060924q. [DOI] [PubMed] [Google Scholar]
- 14.Velmurugan J, Sun P, Mirkin MV. Scanning Electrochemical Microscopy with Gold Nanotips: The Effect of Electrode Material on Electron Transfer Rates. J Phys Chem C. 2009;113:459–464. [Google Scholar]
- 15.Smalley JF, Feldberg SW, Chidsey CED, Linford MR, Newton MD, Liu Y-P. The Kinetics of Electron Transfer Through Ferrocene-Terminated Alkanethiol Monolayers on Gold. J Phys Chem. 1995;99:13141–13149. [Google Scholar]
- 16.Smalley JF, Finklea HO, Chidsey CED, Linford MR, Creager SE, Ferraris JP, Chalfant K, Zawodzinsk T, Feldberg SW, Newton MD. Heterogeneous Electron-Transfer Kinetics for Ruthenium and Ferrocene Redox Moieties through Alkanethiol Monolayers on Gold. J Am Chem Soc. 2003;125:2004–2013. doi: 10.1021/ja028458j. [DOI] [PubMed] [Google Scholar]
- 17.Chidsey CED, Loiacono DN. Chemical functionality in self-assembled monolayers: structural and electrochemical properties. Langmuir. 1990;6:682–691. [Google Scholar]
- 18.Chidsey CED, Bertozzi CR, Putvinski TM, Mujsce AM. Coadsorption of ferrocene-terminated and unsubstituted alka-nethiols on gold: Electroactive self-assembled monolayers. J Am Chem Soc. 1990;112:4301–4306. [Google Scholar]
- 19.Lee LYS, Sutherland TC, Rucareanu S, Lennox RB. Ferrocenylalkylthiolates as a Probe of Heterogeneity in Binary Self-Assembled Monolayers on Gold. Langmuir. 2006;22:4438–4444. doi: 10.1021/la053317r. [DOI] [PubMed] [Google Scholar]
- 20.Bard AJ, Faulkner LR. Electrochemical Methods: Fundamentals and Applications. Wiley; 2000. [Google Scholar]
- 21.Lyshevski SE. Dekker Encyclopedia of Nanoscience and Nanotechnology. 3rd. Taylor & Francis; 2014. Seven Volume Set. [Google Scholar]
- 22.Schoukroun-Barnes LR, Macazo FC, Gutierrez B, Lottermoser J, Liu J, White RJ. Reagentless, Structure-Switching, Electrochemical Aptamer-Based Sensors. Annu Rev Anal Chem. 2016;9:163–181. doi: 10.1146/annurev-anchem-071015-041446. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Sagara T, Kawamura H, Nakashima N. Electrode Reaction of Methylene Blue at an Alkanethiol-Modified Gold Electrode As Characterized by Electroreflectance Spectroscopy. Langmuir. 1996;12:4253–4259. [Google Scholar]
- 24.White RJ, Plaxco KW. Exploiting Binding-Induced Changes in Probe Flexibility for the Optimization of Electrochemical Biosensors. Anal Chem. 2010;82:73–76. doi: 10.1021/ac902595f. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Dauphin-Ducharme P, Plaxco KW. Maximizing the Signal Gain of Electrochemical-DNA Sensors. Anal Chem. 2016;88:11654–11662. doi: 10.1021/acs.analchem.6b03227. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Arroyo-Currás N, Somerson J, Vieira PA, Ploense KL, Kippin TE, Plaxco KW. Real-time measurement of small molecules directly in awake, ambulatory animals. Proc Natl Acad Sci USA. 2017;114:645–650. doi: 10.1073/pnas.1613458114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Murray RW. Chemically modified electrodes. Acc Chem Res. 1980;13:135–141. [Google Scholar]
- 28.Uzawa T, Cheng RR, White RJ, Makarov DE, Plaxco KW. A Mechanistic Study of Electron Transfer from the Distal Termini of Electrode-Bound, Single-Stranded DNAs. J Am Chem Soc. 2010;132:16120–16126. doi: 10.1021/ja106345d. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Xiao Y, Lai RY, Plaxco KW. Preparation of electrode-immobilized, redox-modified oligonucleotides for electrochemical DNA and aptamer-based sensing. Nat Protoc. 2007;2:2875–2880. doi: 10.1038/nprot.2007.413. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


