Adder and a coarse-grained approach to cell size homeostasis in bacteria

Abstract

Cell size control and homeostasis is a long-standing subject in biology. Recent experimental work provides extensive evidence for a simple, quantitative size homeostasis principle coined adder (as opposed to sizer or timer). The adder principle provides unexpected insights into how bacteria maintain their size without employing a feedback mechanism. We review the genesis of adder and recent cell size homeostasis study on evolutionarily divergent bacterial organisms and beyond. We propose new coarse-grained approaches to understand the underlying mechanisms of cell size control at the whole cell level.

Introduction

Size homeostasis is a basic feature of life. A group of newly born or dividing cells will exhibit a distinct distribution of sizes (Figure 1a). Without underlying coordination of growth and the cell cycle, this distribution would diverge over generations, leading to cell sizes that span many orders of magnitude. However, most microorganisms change their size by only twofold between birth and division, with the width of the size distributions being much smaller than their mean. This fidelity in the cell size maintenance points to the existence of size control mechanisms.

Figure 1.

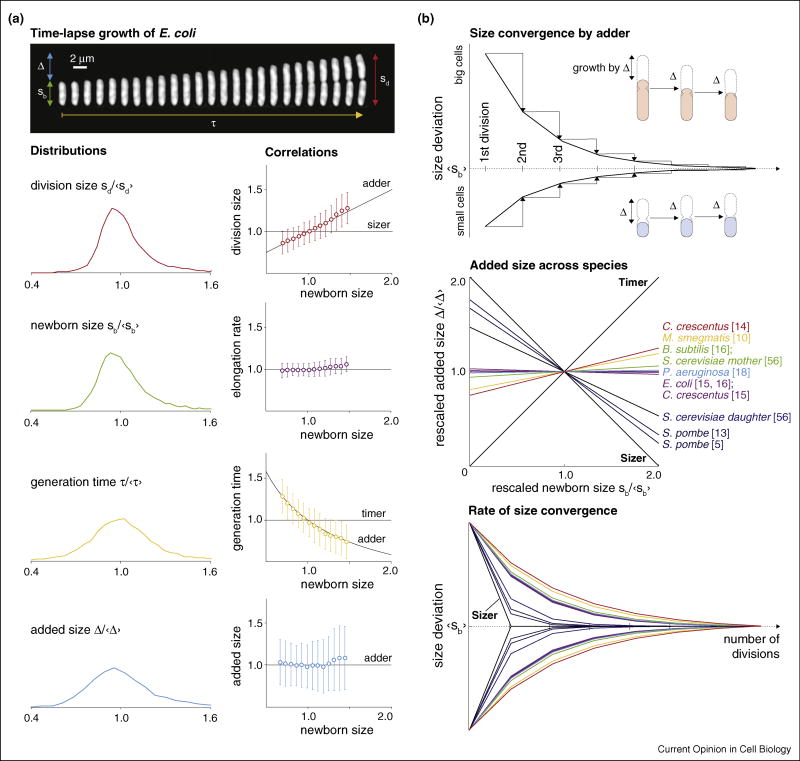
Single cell growth parameters and size convergence by adder. (a) Top panel: timelapse images of an E. coli cell from birth to division in rich soytone medium at 37°C. Interval between images is 45 s. Bottom panel: distributions of four growth parameters in increasing order of coefficient of variance (CV). The x-axes of the distributions are normalized by their respective means. The single cell correlations between the growth parameters and newborn size can be used to test sizer, timer, and adder. (b) Top panel: adder corrects size deviations passively by adding constant Δ between birth and division and dividing in the middle, irrespective of the birth size. Every generation cuts the size difference between the mother’s newborn size and the average newborn size by half, following a geometric series. Newborn size converges to the average, which is equivalent to Δ. Middle panel: most published single-cell data show bacteria in general behave as perfect adder or near-perfect adder, whereas yeast behave closer to sizer. Bottom panel: using the Δ vs. s_b correlations, we can predict size convergence (colors correspond to those in the middle panel). Perfect sizer would reach the target size just after one generation, whereas timers would never converge their size.

Cell size control research requires quantitative information from single-cell data. Indeed, the field has benefited from single-cell measurement of cellular growth from time-lapse images since it began a century ago [1–3]. However, only recently has experimental technology become sophisticated enough to generate data with the throughput and spatiotemporal resolution required to rigorously test previously proposed hypotheses [4–8,9•]. With the new single-cell data, notions that microbes measure a critical size (‘sizer’) or a specific time elapsed during the cell cycle (‘timer’) to trigger division are no longer supported [10•,11–14,15••,16••,17,18].

Two recent papers independently provided extensive experimental evidence for the ‘adder’ principle of size homeostasis [15••,16••].² This principle states that all cells under a steady-state growth condition add a nearly constant size between birth and division, regardless of their birth size (Figure 1b). The model has been used to explain size convergence in evolutionarily divergent bacterial organisms [17,19]. Size homeostasis by adder represents a fundamental departure from a feedback-based view.

This article is organized as follows. In the first half, we describe the origin of several cornerstone models in cell size control and homeostasis in bacteria. This is continued with a more in-depth discussion of the adder principle and its implications. In the second half, we discuss the challenges involved in studying the underlying molecular mechanism. We explain the power of a coarse-grained approach using recent examples in bacterial physiology and cell cycle research.

From sizer and timer to adder in cell size homeostasis

Consider the life cycle of Escherichia coli from birth to division (Figure 1a). All growth parameters show distributions with a well-defined peak. One naturally associates the width of the distributions with the ‘tightness’ of regulation of these parameters. Early on, researchers measured the coefficient of variation (CV) of the distributions of the division size and the generation time [21,22]. This led to the first quantitative models on size control. For example, Koch and Schaechter concluded that “a cell grows until it has reached a critical size” [4], because the division size distribution was narrower than that of the generation time, thus sizer. Had the CV of the generation time been smaller than that of the division size, they may instead have concluded timer.

While both sizer and timer are obvious models for size control, they fail to explain single-cell growth data [10•,11–14,15••,16••,17,18]. The failure of these models is not apparent from the distributions, but requires correlations between the growth parameters. That is, if a cell divided at a critical size (sizer), then its size at division would be constant despite its birth size (Figure 1a). If the cell instead divided after a constant time has elapsed since birth (timer), then generation time would be independent of the birth size. Neither the division size nor the generation time is constant relative to the birth size, inconsistent with the data.

In contrast to sizer or timer, cells following adder simply add on average a constant size, Δ, between birth and division regardless of their birth size (Figure 1a, bottom right panel). This alone ensures size homeostasis (Figure 1b, top panel). To see this, consider a cell born exactly at Δ. This cell grows by Δ, doubling its size. When it divides in the middle its two daughters are born at the same size as the previous generation. However, a cell born smaller than Δ will more than double its size, and its daughters are born slightly bigger than it was. Over successive generations, the difference between the initial newborn cell size and Δ progressively diminishes. Analogously, cells born larger than Δ also dilute out their size deviations with every division. The size of all newborn cells will converge to Δ after several consecutive divisions irrespective of their initial size. Consequently, the average newborn size of a steady-state population is identical to Δ, which is determined by the growth condition.

So far, this has been shown for several evolutionarily divergent bacterial species such as Caulobacter crescentus, E. coli, Bacillus subtilis, and Pseudomonas aeruginosa [12,15••,16••,17,18]. For the summary and comparison of these studies, see Table 1.

Table 1.

Summary of select single-cell experiments for microbial cell size study.

Organism	Methods	Experimental conditions	Cell number	Definition of cell size	Slope of Δ vs. sb
S. pombe [5]	Agarose pad	1	<100	Length	−0.76
S. pombe [13]	Microfluidics	5	347 926	Length	−0.67 ± 0.053
S. cerevisiae [56]	Agarose pad	6	50–200	Volumea	0.06 ± 0.08 (mother)
					−0.47 ± 0.08 (daughter)
M. smegmatis [10•]	Microfluidics	1	520	Length	0.19 ± 0.065
C. crescentus [14]	Microfluidics	5	~104–105	Area	0.25 ± 0.06
C. crescentus [15••]	Agarose pad	1	565 (stalked)	Length	0.0023 (stalked)
			141 (swarmer)		−0.006 (swarmer)
E. coli [15••]	Microfluidics	2 (wildtype)	~103	Length	0.0147; 0.0189
		1 (mutants)			(LB media; M9 media)
E. coli [16••]	Microfluidics	7 (wildtype)	84 699	Length, volume	−0.01 ± 0.012
		2 (mutants)	8105		0.01 ± 0.055
B. subtilis [16••]	Microfluidics	4	24 758	Length, volume	0.06 ± 0.021
P. aeruginosa [18]	Agarose pad	2	117	Length	0.03 ± 0.023 (wildtype)

^aVolume was measured by the total fluorescence level per cell.

The adder principle has several profound implications. First, adder describes cell size homeostasis without feedback. Cells employing adder passively converge their size within a few generations without the need of active measurement of their absolute size (Figure 1b). This is in stark contrast with the checkpoint-based models in eukaryotes for coordinating growth and the cell cycle, where each cell is described to actively control its own size.

Second, adder provides a general quantitative framework to help us understand size homeostasis for a wide range of organisms, including eukaryotes. Reanalysis of published data predicts that cell size converges like adder even when the added size is linearly correlated with birth size (Figure 1b).³ Surprisingly, the flatworm Dugesia tigrina behaves according to adder by growing a constant bodily area from the head piece after transverse splitting [19]!

Third, adder reveals a hierarchy of physiological control of an exponentially elongating cell. The added size and the elongation rate are the primary spatial and temporal controls of cellular reproduction, respectively. Other growth parameters such as birth size, division size, or generation time are completely characterized by and slaved to these two basic control parameters [16••]. Septum position exhibits a tight distribution independent of the other growth parameters.

The discovery of adder was made possible by modern single-cell data with throughput and precision that was not previously available. We anticipate more basic principles will be discovered by exploring other phenomenological parameters such as cell shape [23•], which will be aided by new and precise measurements [24,25]. Inevitably, we will also need to address the mechanisms underlying these phenomenological principles. This requires a new approach discussed below.

Mechanism of size control

Adder presents a unifying phenomenological principle for size homeostasis, but its mechanism is challenging to study for two reasons. First, it is the generality of the adder principle, which describes size homeostasis independent of the major molecular differences among organisms. As illustrated below, two evolutionarily distant organisms use different sets of genes for their cell cycle regulation, yet they can follow the same phenomenological principles at the cellular level. Second, it is the holistic nature of cell size control, which makes it difficult to rely on genetic approaches aimed at identifying genes involved in cell size control [26,27]. Mutations in any genes that affect cellular physiology will cause changes in the cell size.

For molecular mechanisms of size control, consider E. coli and B. subtilis. They are a textbook example of how Gram-negative and Gram-positive organisms are fundamentally different in their cell cycle at the molecular level. In E. coli, premature replication initiation is prevented by SeqA, which sequesters hemi-methylated DNA after initiation, but no seqA homologs exist in B. subtilis [28,29]. In E. coli, Min proteins oscillate from pole to pole to prevent formation of DNA-less minicells, whereas Min proteins show no oscillations in B. subtilis [30]. Despite these molecular differences, both E. coli and B. subtilis share common phenomenological characteristics at the cellular level such as multifork replication for cell cycle progression and the adder principle for cell size homeostasis.

Genetic screening in cell size study can be further limited because mutations in many genes can have secondary effects on cell size. Imagine, for instance, E. coli strains with mutations in topo IV (a type II topo), which would resolve topological catenations of replicating circular chromosome less efficiently than the wildtype. As a consequence, chromosome segregation and cell division would be delayed, thus causing an increase in cell size. However, it would be absurd to consider topo IV as a cell size control gene.

In our view, cell size control research will greatly benefit from a coarse-grained approach from physics or engineering as proposed before [31,32]. Without referring to any molecular details, cellular reproduction can be understood in terms of discrete ‘modules’ that carry out distinct functions [31]. These modules can be grouped into ‘kernels’, namely, major processes for cellular reproduction such as the cell cycle, cell wall synthesis, protein production, and metabolism. Each of these kernels is governed by an organism-specific set of genes, but their overall function is conserved from organism to organism. The cell must coordinate different kernels in space and time to maintain physiological homeostasis during cellular growth. The coordination in steady-state growth requires balance of flux, or flow of information, metabolites, or substrates, from one kernel to another.

Below are two examples of how coarse-grained models allow for a quantitative understanding of cellular systems. Both use distinct methods which are devoid of molecular details, yet give insight into how the cell coordinates major processes. A third example illustrates how molecular mechanisms can be understood in the context of a coarse-grained view of cellular processes in the first two examples.

Coarse-grained approach to protein composition

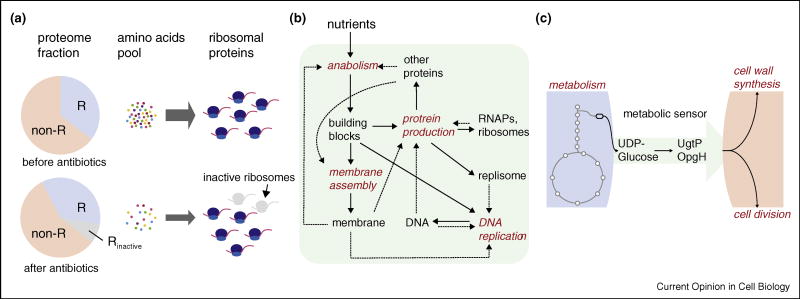
The power of the coarse-grained approach is that it allows for experimentally testable, quantitative predictions without the knowledge of individual molecules. A recent body of work successfully describes the proteome composition by partitioning it into ‘sectors’ which comprise functional sets of proteins [33,34]. The fraction of the ribosomal sector with respect to the rest can be understood as a result of balancing the amino acid flux between the protein production kernel and the metabolism kernel. If translation is partially inhibited by antibiotics which target ribosomes, the demand for amino acids reduces. As a result, the fraction of metabolic enzymes in the total proteome reduces, and cells re-establish the relative fraction of the ribosomal and non-ribosomal proteome sectors as they reach new steady-state growth (Figure 2a, from top to bottom panels). The total fraction of ribosomal proteins (both active and inactive) was shown to increase linearly with the growth rate [33]. The measured changes in proteome composition and the growth rate are in quantitative agreement with predictions based on coarse-grained flux balance analysis.⁴ A next step would be to apply a similar approach to cell size control [16••,35], by addressing the total number of proteins per cell, which is a good proxy of cell size.

Figure 2.

Examples of coarse-grained approach to physiology and cell cycle study. (a) Proteome partitioning: in this study of coordination between cell growth and protein composition, the proteome is divided into two ‘sectors’ depending on whether the protein is ribosomal (R) or non-ribosomal (non-R). In steady-state growth, the ratio between R and non-R sectors is determined by balance between the supply and demand of amino acids. If some ribosomes become inactive by sub-lethal concentration of antibiotics that inhibits translation, demand for amino acid reduces. This eventually also reduces supply of amino acids because less ribosomes are available to make the proteins for catabolism, causing reduced amino acid flux. (b) Coarse-grained view of intracellular processes underlying cellular reproduction presented in recent study [38•]. (c) A ‘metabolic sensor’ that coordinates metabolism and cell division. The common substrate UDP-glucose is converted from Glucose-6-P (shown as a hexagon) in the glycolysis pathway after two consecutive steps. These enzymes together with UDP-glucose serve as the metabolic sensor that passes the information about nutrient quality from the metabolism kernel to the cell division kernel.

The cell as a self-replicating factory

Another example of the coarse-grained approach is to view the cell as a ‘self-replicating factory’, in the vein of von Neumann’s self-reproducing automaton [37,38•]. Recent work presents cellular growth as six ‘processing units’ of cellular production machinery working in concert to produce more machinery in the presence of unlimited supply of raw materials [38•]. In this case, the growth rate during balanced growth is the production rate of a self-replicating factory consisting of optimally scheduled processing units. The predicted distribution of doubling time is a universal Log-Frechet form, in remarkable quantitative agreement with the recent single-cell data [38•,39,40]. We believe that, in future study, the language of proteome ‘sectors’ and ‘processing units’ can be brought together to formulate a quantitative framework to address the relationship between cell size and growth kinetics.

The role of molecules in the coarse-grained approach

Coarse-grained approaches can be powerful in that they can make predictions without the knowledge of molecular details. However, they are often based on correlations and can be limited in providing mechanistic insights. For coarse-grained models to be biologically meaningful, they should be able to provide context for molecules, for example, in coordinating growth, the cell cycle, and cell size control [41]. One such example is a ‘metabolic sensor’, which has been described to transmit information about nutrient conditions to cell division machinery [42•,43]. Experimental data suggest that glucosyltransferases (UgtP in B. subtilis and OpgH in E. coli) and their substrates UDP-glucose can cause delay in cell division by preventing FtsZ ring formation in a nutrient-dependent manner. In nutrient rich conditions, UgtP/OpgH is abundant and accumulates in the midcell to prevent premature cell division, whereas in nutrient poor conditions the enzyme is too sparse to inhibit FtsZ ring formation. Thus, a metabolic sensor is a mediator of flux between the metabolism kernel and the cell cycle (division) kernel, which manifests in cell size. Many additional papers have been aimed at discovering these coordinating components [44–51]. Such molecular and biochemical information is useful, since it can help quantify the flux and the dynamic properties of the metabolic sensor, revealing how information flows in the system.

Concluding remarks

Cell size and growth rate are the ultimate outcomes of all intracellular processes. This holistic nature of cell size control is the source of both fascination and frustration in studying its underlying mechanism [52–55]. The adder principle of size homeostasis in bacteria is a telling example of how we can find new ways to think about this long-standing problem with the help of quantitative and phenomenological approaches. Future challenges will involve bridging the gaps between phenomenological principles and molecular mechanisms. To this end, and inspired by the generality of the adder principle discussed in this article, we propose a coarse-grained view of cellular growth consisting of kernels, namely, intracellular processes grouped by their functions. Predictability of the cell’s response to perturbations to the coordinations between kernels will be an important step forward in understanding the mechanism of cell size control and homeostasis.