Abstract
We examined the effects of the framing of time on delay discounting. Delay discounting is the process by which delayed outcomes are devalued as a function of time. Time in atitrating delay discounting task is often framed in calendar units (e.g., as 1 week, 1 month, etc.). When time is framed as a specific date, delayed outcomes are discounted less compared to the calendar format. Other forms of framing time; however, have not been explored. All participants completed atitrating calendar unit delay-discounting task for money. Participants were also assigned to one of two delay discounting tasks: time as dates (e.g., June 1st, 2015) or time in units of days (e.g., 5000 days), using the same delay distribution as the calendar delay discounting task. Time framed as dates resulted in less discounting compared to the calendar method, whereas time framed as days resulted in greater discounting compared to the calendar method. The hyperboloid model fit best compared to the hyperbola and exponential models. How time is framed may alter how participants attend to the delays as well as how the delayed outcome is valued. Altering how time is framed may serve to improve adherence to goals with delayed outcomes.
Keywords: delay discounting, temporal discounting, framing, context, human
Impulsivity is a multifaceted construct denoting several forms of potentially maladaptive behavior (Green & Myerson, 2013; Stahl et al., 2013). Commonly studied forms include the inability to refrain from a prepotent response (behavioral inhibition), lapses of attention, and insensitivity to delayed consequences (de Wit, 2008). Insensitivity to delayed consequences is encompassed by delay discounting, which is the decrease in the present value of temporally remote outcomes (Mazur, 1987). If someone chooses a smaller sooner reward over a larger but more delayed reward, this behavior is termed impulsive, whereas if someone forgoes a smaller sooner reward to receive a larger later reward, this behavior is termed self-controlled (Logue, 1988). For example, someone may forgo a dessert with tonight’s dinner to achieve better health in the long term.
Delay discounting is associated with the acquisition and maintenance of maladaptive behaviors. For example, substance abuse is consistently linked to greater discounting of reward value by delay (de Wit, 2008). Better understanding the mechanisms of substance abuse is important because of its high economic and societal costs. In the United States, the total annual economic cost of tobacco use alone is over $190 billion (CDC, 2005). Problematic users of alcohol (e.g., Petry, 2001), cigarettes (e.g., Bickel, Odum, & Madden, 1999; Mitchell, 1999), cocaine (e.g., Heil, Jonhson, Higgins, & Bickel, 2006), heroin (e.g., Madden, Petry, Badger, & Bickel, 1997), and methamphetamine (e.g., Hoffman, Moore, Templin, McFarland, Hitzemann, & Mitchell, 2006) discount delayed outcomes more than control participants who do not use these substances. In addition to substance abuse, delay discounting is also related to problematic gambling behaviors (e.g., Petry, 2001; Reynolds, 2006), obesity (e.g, Fields, Sabet, & Reynolds, 2013; Hendrickson & Rasmussen, 2013), and a variety of unhealthy behaviors, such as sedentary activity patterns and lack of safety belt use in automobiles (e.g., Daugherty & Brase, 2010).
Because steep delay discounting is related to socially significant behaviors, the development of techniques to reduce the degree of discounting could be helpful. For example, Bickel and colleagues (Bickel, Yi, Landes, Hill, & Baxter, 2011) provided working memory training to people with stimulant abuse because working memory capacity is related to the degree of delay discounting (see Wesley & Bickel, 2014). Although the intervention did not increase working memory capacity, the participants discounted money less by delay at the end of training compared to a group that received sham training. After brief training in Acceptance and Commitment Therapy (ACT) to increase tolerance for distressing and uncomfortable events and experiences, college undergraduates discounted delayed monetary outcomes less steeply (Morrison, Madden, Odum, Friedel, & Twohig, 2014). These and other recent examples (e.g., Black & Rosen, 2011; Hendrickson & Rasmussen, 2013) provide promising evidence that delay discounting, despite being generally consistent within an individual (see e.g., Odum, 2011a), can be decreased by therapeutic means. These methods, however, are time and resource intensive, making their implementation limited.
Another possible influence on delay discounting, which we investigate here, is the manner in which delay discounting decisions are framed. Framing refers to the context in which a decision is presented ( Tversky & Kahneman, 1981). This technique is of particular interest because it can be readily and immediately implemented. In a large meta-analysis, Kühberger (1998) demonstrated that framing has strong influences on decision making. Specifically, Kühberger identified several aspects such as reference points, outcome salience, and response mode that affect which option is preferred. For example, in studies that change the reference point of a decision, participants are often confronted with identical outcomes that are framed as either gains or losses. When the outcome is framed as a gain, participants are more likely to choose that outcome than when the outcome is framed as a loss, despite both outcomes being otherwise identical.
Tversky and Kahneman’s (1981) disease outbreak scenario provides a well-known example of the effects of changing the reference point of a decision. Participants are assigned to either a gain or a loss scenario in which they must choose between two outcomes: one certain and one probabilistic. In the gain scenario, participants choose between a certain gain (200 out of 600 lives saved) or a probabilistic outcome. In the loss condition, participants choose between a certain loss (400 out of 600 lives lost) or the same probabilistic outcome as in the gain scenario. The certain outcomes are functionally equivalent, in that 200 people will live and 400 people will die in each case. Despite the identical outcomes, however, participants in the gain scenario more frequently pick the certain outcome than participants in the loss scenario pick the certain outcome.
In delay discounting, framing outcomes as gains or losses affects decision making as well. For example, in a phenomenon know as gain-loss asymmetry or the sign effect, delayed gains are generally discounted more steeply than delayed losses. In separate conditions, Murphy, Vuchinich, and Simpson (2001) asked undergraduate college participants about either gaining or losing a hypothetical $500 outcome at various delays. The delayed $500 was discounted more steeply by delay (was worth less in the present) when it was framed as a gain than when it was framed as a loss. This general finding has been replicated in other studies and with other populations (e.g., Baker, Johnson, & Bickel, 2003; Ohmura, Takahashi, & Kitamura, 2005; Tanaka, Yamada, Yoneda, & Ohtake, 2014).
Another framing manipulation, how the delays are described, is a relatively unexplored yet potentially powerful influence on delay discounting. For example, across several experimental conditions, Read, Frederick, Orsel, and Rahman (2005) found that framing time as a specific date resulted in less discounting of rewards than framing time in calendar unit form (e.g., days, weeks, months, and years). In one condition, participants were asked to report the amount of money they would be willing to wait to receive at a certain delay instead of taking the immediate, smaller amount. The delayed amounts were smaller on average, indicating less discounting, when time was framed as a specific date than when time was framed in calendar units. This finding held true for a variety of delay durations, outcome amounts, and with hypothetical and real rewards. Similar results have been found in other studies (Klapproth, 2012; LeBoeuf, 2006).
One surprising finding from Read and colleagues (2005) was that when delayed rewards were framed as specific dates, point estimates of the rate of discounting appeared linear, indicative of exponential discounting. In exponential discounting (Samuelson, 1937), the present value of an outcome decreases by the same proportion per unit time. This finding was unexpected, because many studies examining delay discounting have found instead that discounting is hyperbolic: the present value of an outcome decreases proportional to the delay (Ainslie, 1992). Specifically, reward value decreases by an increasingly smaller proportion as delay increases (e.g., Bickel et al., 1999; Myerson & Green, 1995; Rachlin, Raineri, & Cross, 1991). Due to the nature of the procedure they used and the range of the indifference points obtained, Read et al. (2005) were not able to fit a theoretical model to their data to ascertain whether the present value of the delayed rewards was best described by an exponential or hyperbolic function.
Therefore, one of the main goals of the present study was to determine the best-fitting model for discounting when delays are described as specific dates. The theoretical model that best describes the discounting process is important, because different models can make different predictions about behavior (see Mazur, 2006; Odum, 2011a). For example, due to the deeply bowed shape of the hyperbolic curve relating present value to delay, hyperbolic discounting readily predicts the phenomenon of preference reversal. In this difficult behavior pattern, people may initially prefer a larger later reward, but as the time to obtaining the rewards draws nearer, switch their preference (‘defect’) to the smaller sooner outcome. This phenomenon is familiar to people with addiction problems, for example, in which someone may quit taking a drug in hopes of achieving better health, only to relapse to drug use to gain a short-term high.
In this paper, we will evaluate three models to determine which provides the best description of the discounting process when delays are framed as specific dates. Equation 1 is an exponential model (Samuelson, 1937):
In this model, V is the present (discounted) value of a delayed outcome, A is the amount of that future outcome, D is the delay to the outcome, and k quantifies the degree to which the delayed outcome loses value as a function of delay. The mathematical constant e is approximately equal to 2.718 and is the base of the natural logarithm. Equation 2 is a hyperbolic model (Mazur, 1987):
The notion for Equation 2 is the same as Equation 1. Equation 2 has been found to provide a better fit to data from non-human as well as human participants in delay discounting experiments (e.g., Bickel et al., 1999; Madden, Begotka, Raiff, & Kastern, 2003; Mazur, 1987; see Odum, 2011a). We evaluated the fit of a third model as well, which for data from human participants often provides a better account than Equation 2 (e.g., McKerchar et al., 2009; Myerson & Green, 1995). Equation 3 is a hyperboloid model represented as
The notion is as in Equations 1 and 2, with the addition of s as a scalar of delay and/or amount. If s is 1.0, Equation 3 reduces to Equation 2.
In addition to determining which theoretical model provided the best fit for discounting data when delays were framed as specific dates, we also sought to explore the generality of the framing effect. Framing time as a specific date, as opposed to calendar units, has been shown to reduce delay discounting. Could framing time differently than calendar units also increase the degree of delay discounting? To investigate the flexibility of the delay framing effect, we also compared the degree of discounting when delays were framed in solely days to the degree of discounting obtained when delays were framed in calendar units (days, weeks, months, and years). Thus, this study had two novel goals: 1) determine the effect of a new method of framing delays and 2) determine the best fit theoretical model when delays to rewards are framed in three different ways: in calendar units, as specific dates, and in days. Based on prior results obtained with a different procedure (Read et al., 2005), we predicted that when time was framed as a specific date, participants would discount less than when time was framed in calendar units (days, weeks, months, and years). Because of the novelty of the manipulation, we did not have a specific prediction for the degree of discounting obtained when time was framed in units of days as opposed to calendar units (days, weeks, months, and years). Finally, based on prior results (e.g., Myerson & Green, 1995; Rachlin et al., 1991), we predicted that the hyperbolic-type models (Equations 2 & 3) would provide a superior fit to the indifference points than the exponential model (Equation 1).
Method
Participants
Seventy-six undergraduate students (31 male, 45 female; mean age 21 years) took part in this experiment. Participants were recruited from a variety of introductory courses at Utah State University through classroom announcements and an online registration system. All students received course/laboratory credit or extra credit for participation. Of the 76 participants, 41 students (17 male, 24 female) were randomly assigned to the specific date condition and 35 students (14 male, 21 female) were randomly assigned to the days condition.
Procedure
Participants completed the experiment at a desk with a touch-screen computer in a private office. Each task in the experiment was programed using E-Prime computing software. All participants completed an informed consent document that was approved by the Utah State University Institutional Review Board. Each session lasted approximately 1 hour. During the experimental session, participants also completed two unrelated delay-discounting tasks for food (data not presented here).
Delay Discounting
In each condition, participants completed two titrating delay discounting tasks for hypothetical money: calendar units delay framing (days, weeks, months, and years) and framing of delays as specific dates or days. The order of the two tasks (calendar and dates/days) was random. Participants were not assigned to both the specific dates and days tasks to avoid the possibility of carryover effects. Each task began with instructions similar to those found in Odum, Baumann, and Rimington (2006), which read:
“The following choices are hypothetical, and you will not receive the actual outcomes. There are no ‘right’ or ‘wrong’ answers. Please just pick the choice that you prefer. Please note that the choices will switch sides randomly across questions. Please give special attention to the units of time as well as the amount that you are being asked a bout.”
The delay discounting tasks determined the present value of the delayed outcome ($100) at a variety of delays. The procedure for all three delays was the same; only the manner in which time was framed differed. Each delay began with the following question: “Would you prefer $50 now or $100 in (delay)?” The position (left and right sides of the screen) of the immediate and delayed options was assigned randomly for each trial. The participant chose between the immediate and the delayed amounts using the touchscreen monitor. After each choice, the immediate amount was adjusted per Du, Green and Myerson (2002). On the first question, the immediate amount was increased (if the delayed amount was chosen) or decreased (if the immediate amount was chosen) by $25. On the subsequent questions, the immediate amount was adjusted by 50% of the proceeding adjustment. The tenth question completed each delay presentation and the amount of the small immediate option on that trial was used as the indifference point for analysis. The indifference point represents the present value of the delayed amount at that delay.
In each condition, the two tasks differed in how time was framed. The specific date condition had two tasks: time framed as specific dates (cf. Read et al., 2005) and the calendar unit titrating task (e.g., Du et al., 2002). In the calendar unit delay discounting task, each participant experienced six delays in the following order: 1 week, 2 weeks, 1 month, 6 months, 5 years, and 25 years (cf. Rachlin et al., 1991). In the specific date delay discounting task, participants experienced the same delays framed as specific dates. The dates were derived using the date that the participant completed the task. For example, if the participant completed the task on January 1st, 2014, they would see the following six delays: January 8th, 2014; January 15th, 2014; January 31st, 2014; June 30th, 2014; December 31st, 2018; December 26th, 2038, in that order.
The days condition had two tasks: time framed as days and the calendar unit task (e.g., Du et al., 2002). In the calendar unit titrating delay discounting task, each participant experienced seven delays in the following order: 1 day, 1 week, 2 weeks, 1 month, 6 months, 5 years, and 25 years (cf. Rachlin et al., 1991). For the days delay discounting task, each participant experienced the same delays, but described in terms of days: 1 day, 7 days, 14 days, 30 days, 180 days, 1825 days and 9125 days, in that order. The delay distribution in the days condition differed from the delay distribution in the specific date condition described in the paragraph above because we found in a preliminary study that discounting between the calendar unit and days unit tasks was already substantially different at the shortest delay (1 week). Therefore, to allow us to more fully characterize the discounting curves, we added the 1-day delay for the calendar unit and days unit tasks in this condition.
Data Analysis
The three models of delay discounting (Equation 1, Equation 2, & Equation 3) were fit to the median indifference points for each task through nonlinear regression (Graphpad Prism®). Equation 3 (the hyperboloid; Myerson & Green, 1995) was selected over Equation 2 (the hyperbola; Mazur, 1987) and over Equation 1 (the exponential; Samuelson, 1937) using the Akaike Information Criterion (AIC; reported in the “Results” section), which compares goodness of model fits while selecting for the most parsimonious model. Inferential statistical analyses were not conducted with the k parameter from Equation 3 because in the Myerson and Green (1995) model, the value of the k parameter interacts with the s parameter. Therefore, an independent interpretation of k is not appropriate.
Prior to fitting the models to the median indifference points, we applied the Johnson and Bickel (2008) suggested criteria for identifying non-systematic discounting. The first criterion is if an indifference point increases by more than 20% of the previous indifference point. The second criterion is if the final indifference point is not less than 90% of the first indifference point. Data sets meeting either criterion or both criteria were excluded. We only applied the criteria to data from the calendar unit task. If a participant’s data met the exclusion criteria for the calendar unit task, all data from that participant were excluded from analysis. We did not exclude data from the dates and days tasks for non-systematic discounting because we did not want to limit our ability to detect different patterns of discounting for these experimental tasks. In practice, however, removing all data from participants with nonsystematic data for the calendar unit task removed nonsystematic data for the experimental tasks as well, because participants with nonsystematic data for one task had nonsystematic data for the other task.
Data from 4 and 9 participants were removed from the final analysis for date and days conditions, respectively, for not meeting the Johnson and Bickel (2008) criteria for non-systematic discounting in the calendar unit task. Comparisons of age and gender variables did not identify differences between participants whose data were removed for non-systematic discounting and those whose data remained.
To quantify the degree of discounting by delay, we calculated Area Under the Curve (AUC; Myerson, Green, & Warusawitharana, 2001). AUC is the sum of the area between each indifference point: x2 – x1[(y1+y2)/2]. The values x1 and x2 are the delays and y1 and y2 are the indifference points for those delays. AUC can range between 0 and 1, with lower AUC indicating greater discounting by delay and higher AUC indicating less discounting by delay. AUC was compared for the task with calendar unit delays versus the task with delays framed as specific dates, and for the task with calendar unit delays versus the task with delays framed as days. Differences in AUC between tasks in each condition were analyzed using the Wilcoxon Matched-Pairs Signed Rank Test, which is a non-parametric statistic to analyze within-subject differences with two data points (essentially a non-parametric paired t-test). For across condition comparisons (e.g., comparison of the AUC from the date and days condition), the Mann Whitney U (essentially a non-parametric independent samples t-test) was used. These tests were chosen because AUC was not normally distributed for time framed as days (W = 0.87, p < .01) and time framed in the calendar unit form in the days condition (W = 0.92, p < 0.05) or time framed in the calendar unit form in the date condition ( W = 0.92, p < .05). AUC was normally distributed for time framed as dates (W = 0.99, p = 0.).
Results
Model Fits
The three models of delay discounting were fit to the median indifference points for each task using nonlinear regression. We used a two-stage analysis to determine the best fitting model overall. First, the fit of the exponential model (Equation 1) was compared to the fit of the hyperbolic model (Equation 2). The Akaike Information Criteria (AIC) and R2 both favored the hyperbolic model (Table 1). Across the tasks, the median R2 for the exponential model was 0.86, whereas for the hyperbolic model the median R2 across the tasks was higher at 0.94. Next, the hyperbolic (Equation 2) and hyperboloid (Equation 3) model fits were compared using AIC and R2 values. Both measures favored the hyperboloid model (Table 1). The hyperboloid model provided an excellent fit to the median indifference points (median R2 across tasks = 0.99) and the improvement in fit exceeded the loss of parsimony of the extra free parameter in the hyperboloid model as compared to the hyperbolic model as assessed by the AIC.
Table 1.
Equation 1 (Exponential) vs. Equation 2 (Hyperbolic) Model vs. Equation 3 (Hyperboloid) Fits of Group Median Indifference Points
| Median R2 | ||||
|---|---|---|---|---|
| AIC | Exponential | Mazur (1987) | ||
| Date | ||||
| Date | 5.99 | 0.81 | 0.93 | |
| Calendar | 6.57 | 0.91 | 0.97 | |
| Days | ||||
| Days | 4.14 | 0.85 | 0.92 | |
| Calendar | 7.03 | 0.86 | 0.95 | |
|
| ||||
| Mazur (1987) | Myerson and Green (1995) | |||
| Date | ||||
| Date | 7.74 | 0.93 | 0.99 | |
| Calendar | 9.43 | 0.97 | 0.99 | |
| Days | ||||
| Days | 2.03 | 0.92 | 0.98 | |
| Calendar | 17.66 | 0.95 | 0.99 | |
Note. Comparison of Equation 1 (exponential), Equation 2 (hyperbolic) and Equation 3 (hyperboloid) model fits of group median indifference points. AIC favors Equation 3, as do the median R2 values.
To further evaluate the appropriateness of the hyperboloid model, Equation 3 was fit to the indifference points for individual participants for each task. Table 2 displays the median values of the individual fits for the k and s parameters as well as the median R2 values for each task. Equation 3 provided a good description of the individual participant data. The median R2 ranged from 0.95 to 0.97. We also determined whether the value of the exponent, s, was different from 1.0 using Wilcoxon Signed Ranks tests. For each task, the s parameter was significantly different from 1.0, indicating that this parameter is important in accounting for the variance in indifference points from individual participants (Table 2).
Table 2.
Equation 3 (Hyperboloid) Median Model F its to Individual Indifference Points
| k | s | R2 | Wilcoxon Signed Rank Test | ||
|---|---|---|---|---|---|
| Date Condition | |||||
| Date | 0.01 | 0.73 | 0.95 | − 424.0* | |
| Calendar | 0.03 | 0.76 | 0.96 | − 432.0** | |
| Days Condition | |||||
| Days | 0.13 | 0.66 | 0.97 | − 224.0* | |
| Calendar | 0.007 | 0.59 | 0.97 | − 256.0* |
p < .05,
p < .01
Table 1. Equation 3 (hyperboloid) was fit to the median indifference points for each participant. Median values of the individual fits are reported. The Wilcoxon Signed Rank Test values report the comparison of the s parameter to the specific value of 1.
Therefore, multiple forms of evidence indicate that the hyperboloid model (Equation 3) provided the best fit to the data for each task. The next analyses compare how steeply money was discounted when the delays were framed in units in the calendar unit task versus as specific dates (first condition) and days (second condition).
Date Condition
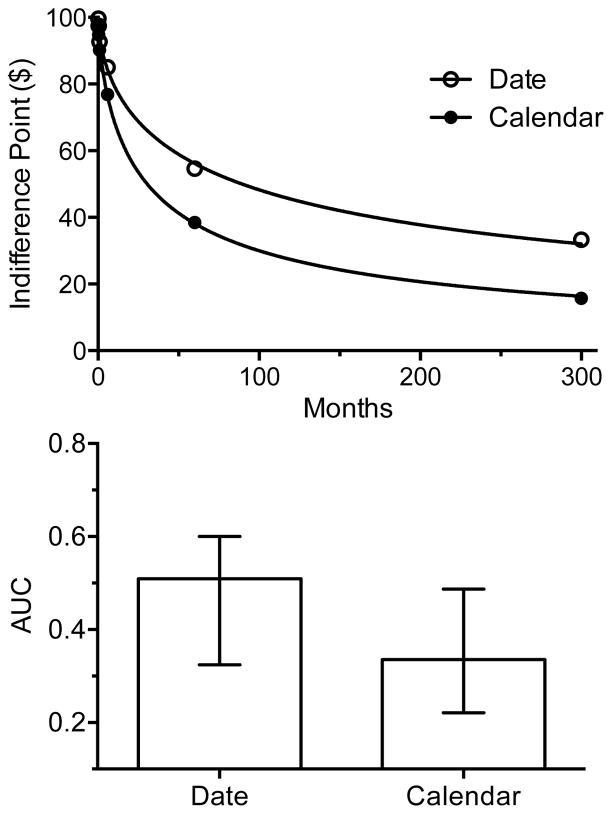
For both the date and calendar unit discounting tasks, the present value of money decreased as the delay increased (Figure 1, top panel). The median indifference points decreased less when the delays were framed as specific dates than when the delays were framed in calendar unit units of time. The hyperboloid model (Equation 3) provided a good fit to the group median indifference points. For the specific date condition, k, s, and R2 were 0.003, 0.62 and 0.99, and for the calendar unit condition, k, s, and R2 were 0.008, 0.71, and 0.99, respectively.
Figure 1.
Date vs. Calendar Discounting Hyperboloid Model Fits and AUC Comparisons
Hyperboloid model fits of group median indifference points for calendar units and specific date delay discounting for $100. Wilcoxon Matched-Pairs Signed Rank Test results for within subject AUC scores for standard vs. date delay discounting. Medians with interquartile range reported.
To provide a summary measure of the steepness of discounting, Figure 1 (bottom panel) also presents the AUC obtained in the specific date task and the AUC obtained in the calendar unit task. The AUC was significantly greater in the specific date condition (median = 0.51) as compared to the AUC in the calendar unit condition (median = 0.34; W = − 351.00, p < .05). This finding shows that framing time as a specific date, rather than in calendar units of time (days, weeks, etc.), resulted in less discounting by delay.
We also examined the relation between the degree of discounting across the two different ways of framing the delay. The AUC for the specific date task and calendar unit task were significantly and moderately positively correlated (Spearman Rho r = 0.54, p < .001). Participants who showed steep discounting, and had a low AUC in one version of the task, tended to show steep discounting, and had a low AUC, in the other version of the task. Conversely, participants who showed more moderate discounting, and had a high AUC in one version of the task, tended to show more moderate discounting, and had a high AUC, in the other version of the task.
Days Condition
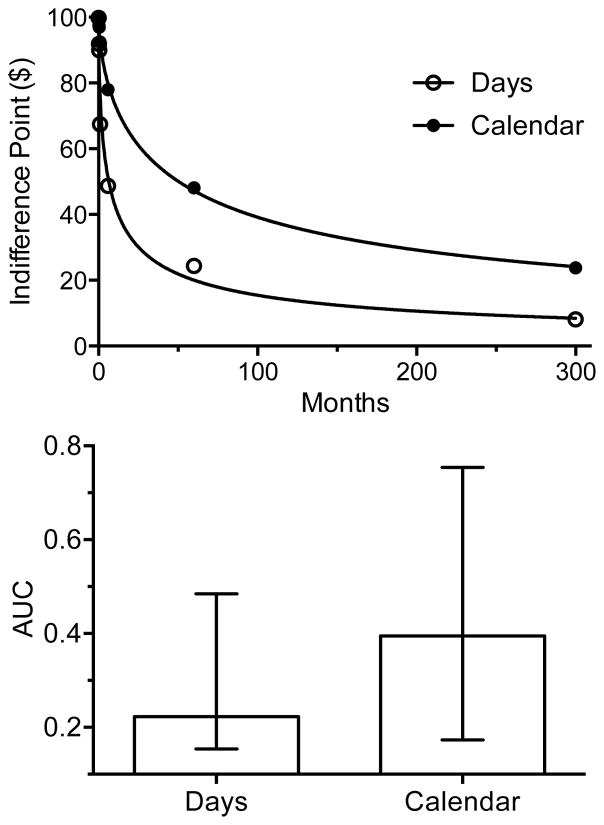
Figure 2 (top panel) shows that for both the calendar units and days units discounting tasks, the present value of the money decreased as the delay increased. The median indifference points decreased more when the delays were framed as days than when the delays were framed in calendar units (days, weeks, etc.). The hyperboloid model (Equation 3) provided a good fit to the indifference points. For the days conditions k, s, and R2 were 0.037, 0.61, and 0.98, whereas for the calendar units condition, k, s, and R2 were 0.005, 0.64 and 0.99, respectively.
Figure 2.
Days vs. Calendar Units Delay Discounting Hyperboloid Model Fits and AUC Comparisons
Hyperboloid model fits of group median indifference points for calendar and days units delay discounting for $100. The bottom panel Wilcoxon Matched-Pairs Signed Rank Test results for within subject AUC scores for standard vs. days delay discounting. Medians with interquartile range reported.
Figure 2 (bottom panel) compares the AUC obtained in the days task (in which the delays were expressed in terms of the number of days) and the AUC obtained in the calendar units task (in which delays were expressed in different units of time). The AUC was significantly less in the days task (median = 0.22) as compared to the AUC in the calendar units task (median = 0.40; W = 171.00, p < .001, Figure 2, bottom panel). Thus, delays degraded present value more when delays were framed as days than when delays were framed in calendar units.
The AUC for the days and calendar units titrating delay discounting tasks were significantly and strongly positively correlated within individuals (Spearman Rho r = 0.75, p < .001). Participants who showed steep discounting, and had a low AUC in one version of the task, tended to show steep discounting, and had a low AUC, in the other version of the task. Conversely, participants who showed more moderate discounting, and had a high AUC in one version of the task, tended to show more moderate discounting, and had a high AUC, in the other version of the task.
Comparisons Across Conditions
We also compared AUC across conditions, despite procedural differences. We compared the AUC from the calendar units titrating delay discounting tasks from the specific date and days conditions to each other to investigate whether they produced similar levels of discounting. These results should be interpreted with caution because the number of indifference points differed across the calendar unit tasks (six for the date condition and seven for the days condition). Despite these procedural differences, AUC did not significantly differ between groups (U = 412.00, p = 0.66). Also, we compared AUC for the specific date and days conditions. AUC was significantly different between groups (U = 237.00, p < .01) with participants discounting less when time was framed as specific dates than when time was framed as days. In conclusion, participants in the date and days conditions discounting similarly when time was framed in the calendar units method, but discounted differently when time was framed in specific dates or days. Discounting when delays were framed as days was steeper than when discounting was framed in specific dates.
Discussion
There were three main findings in the present experiment. First, how time is framed had clear effects on the degree of delay discounting. When time was framed as a specific date, participants discounted less steeply than they did when time was framed in calendar units (weeks, months, years). Conversely, when time was framed in days, participants discounted more steeply than they did when time was framed in calendar units. Second, the pattern of discounting when delays were framed as specific dates was not exponential, as had been suggested from prior work. Instead, the hyperboloid model (Equation 3; Myerson & Green, 1995) provided a superior fit to the indifference points than the hyperbolic (Equation 2; Mazur, 1987) and the exponential (Equation 1; Samuelson, 1937) models. Finally, the degree of discounting in the calendar task was significantly positively correlated with the degree of discounting for both the date and days tasks. Below we discuss each of these findings in turn.
Results of the time framed as specific dates condition replicates previous findings that framing delays as specific dates results in less discounting than when time is framed in the calendar units of weeks, months, and years (LeBoeuf, 2006; Read et al., 2005). This finding was demonstrated using both hyperboloid model fits and AUC. Additionally, this finding held when we examined discounting using an adjusting procedure that obtained indifference points at a wide range of delays (Du et al., 2002), expanding the generality of this effect to a different delay discounting procedure than has been used previously.
The hyperboloid model (Equation 3) provided a better fit to the indifference point data from all of the tasks than either the exponential (Samuelson, 1937; Equation 1) or hyperbolic (Equation 2) models. This finding is in contrast to that of Read et al. (2005), who found that point estimates of the rate of discounting showed a linear, rather than hyperbolic, decrease with increases in delay when delays were framed as specific dates. They suggested it was possible that the manner in which specific dates were framed could change not only the degree of discounting but also the form of the discount function (hyperbolic vs. exponential). Read and colleagues did not use the same procedure for generating indifference points, nor did they use as wide of a range of delays, as we did in the present study. Specifically, we used shorter delays, which comprise a range over which the functions may differ substantially. These procedural differences may have allowed us to more fully characterize the discount function. Thus, changing the delay frame, while changing how steeply delayed outcomes are discounted, does not appear to change the discounting process per se. Changes in discounting produced by delay framing would seem to be changes in the degree of discounting, not the kind of discounting.
We also found that not only did the hyperbolic (Equation 2) provide a better fit to the indifference points than the exponential model (Equation 1), a newer hyperboloid model (Equation 3) provided a superior fit than the hyperbolic model did. The data from discounting with different delay frames support those from a variety of studies (see McKerchar et al., 2009) showing that at least for human data, the hyperboloid provides a better description of the indifference points from delay discounting procedures. The superiority of the fit of the hyperboloid model exceeded that obtained by just adding an additional free parameter, because the AIC penalizes models for the added complexity inherent with more parameters. Instead, the hyperboloid model appears to capture meaningful variability in the form of the discount function generated by nonlinear effects of amount and/or time. At shorter delays, the indifference points decrease more steeply than predicted by the simple hyperbola, and at longer delays, the indifference points decrease less steeply than the simple hyperbola (see Odum, Baumann, & Rimington, 2006). In conclusion, while the framing of time did alter the degree to which delayed outcomes were discounted, the manner in which delays were framed did not change which model provided the best description of the form of the discount function.
Importantly, we have generalized the effect of altering how delays are framed to include framing delays in solely units of days (e.g., 1,825). Framing time in units of days was found to have the opposite effect of framing time as specific dates. The time framed as days task resulted in greater discounting compared to the calendar method of framing time in units of days, weeks, months and years.
A number of explanations exist for why framing time differently affects delay discounting. First, participants may have discounted delays framed in units of days more steeply because the high number of days may have been so large that the participants simply stopped attending to the delayed option. The opposite may be true for the date condition: framing time as a specific date may have increased how intently the participant attended to the delayed outcome.
There is evidence that changing attending to delayed outcomes changes the degree of discounting. For example, in the ‘explicit zero’ effect (Radu, Yi, Bickel, Gross, & McClure, 2011) the default or null outcomes are stated directly. Rather than ‘a little now vs. a lot later’, for example, choices are described as ‘a little now and nothing later vs. nothing now and a lot later’. This form of framing reduces the degree of delay discounting. Due to evidence from a series of experiments that drew attention to distant past or future events, Radu et al. (2011) concluded that the ‘explicit zero’ reduction in the steepness of delay discounting is due to enhanced attending to the future outcomes.
An alternative, and not necessarily mutually exclusive possibility, is that when a delay is presented as a larger number (e.g., 1,825 days), the delay is perceived to be longer than when it is framed as a smaller number (e.g., 5 years). That is to say, despite the two methods describing the same objective time, they may not represent the same subjective time. People who perceive time as passing more quickly (i.e., overestimate the passage of time) show steeper discounting of money than people who perceive time as passing more slowly (Baumann & Odum, 2012). Therefore, in the present experiment, if framing delays in terms of days makes the delays appear longer, that could result in steeper discounting.
An additional explanation is that how time is framed may affect the valuation of delayed rewards. Specific neural structures such as the orbitofrontal cortex that allow an organism to experience the value of delayed rewards (Bar, 2009) have been shown to be involved in delay discounting processes (Torregrossa, Quinn, & Taylor, 2008). The orbitofrontal cortex is thought to be involved in the encoding of the quality, quantity, probability, and timing of a delayed reward (Windmann et al., 2006). Windmann and colleagues found that how outcomes are framed affects the extent to which this neural mechanism is engaged in the decision making task. Using the Iowa gambling task, they found that different areas of the orbitofrontal cortex were activated depending on the perceived risk of the task. When greater risk was involved, the medial orbitofrontal cortex showed greater activation. When less risk was involved, the lateral orbitofrontal cortex showed greater activation. Patak and Reynolds (2007) found that delay discounting might also involve an assessment of risk. They asked participants about the likelihood that they would actually receive the delayed outcome. The longer the delay, the less was the perceived chance of actually receiving the delayed outcome. When delays are framed as specific dates, the outcome may be perceived as more certain and when time is framed in days, the outcome may be perceived as less certain. Therefore, how time is framed may differentially activate the neuroanatomical areas involved in valuation, resulting in different perceived levels of outcome risk.
Future research should focus on expanding the generality of the effects of framing time on delay discounting. For example, how does delay framing affect discounting of larger amounts (e.g., $10,000)? Would delay-framing effects generalize to non-monetary. outcomes (e.g., food), or to smaller units of time (e.g., 1 week vs. 0.019 years)? Delay framing may prove useful in applied and clinical settings. For example, when setting goals for abstinence, giving a specific date as a goal instead of a period of time may be a more effective strategy. Therefore, a goal for abstinence framed as “through January 31st, 2014” may be more effective than a goal of “at least 30 days”. Framing the outcome more effectively may increase the present value of the delayed reward, therefore increasing the likelihood of obtaining that goal. Finally, future research should investigate the mechanism of the delay framing effect.
There are at least two potential limitations of the present study. First, we used hypothetical outcomes instead of real rewards. Perhaps the results would differ if people actually received the consequences of their choices. Studies that have explicitly compared the degree of discounting and the shape of discounting curves obtained using hypothetical and real outcomes generally find good concordance between the two methods though (see Odum, 2011a, for a complete discussion).
Second, the sample size used in the present study was not as large as in Read et al. (2005), who found that when delays were framed as specific dates, the pattern of discounting across delays appeared to suggest an exponential decay process rather than a hyperbolic one. In the present study, we replicated the main effect from Read and colleagues, that the degree of discounting was reduced when delays were framed as specific dates. Our adjusting procedure that obtained indifference points at a variety of delays allowed us to fit a theoretical model to the data, which Read and colleagues were not able to do. Thus, while the limited data of Read et al. suggested discounting might be exponential with delays framed as specific dates, our more extensive investigation of that element of their findings does not support that suggestion. Our sample size was sufficient to allow detection of the main result, that discounting is shallower with delays framed as specific dates, and therefore we do not believe that sample size was a factor in our finding that the shape of the discounting curve was hyperboloid in nature.
Regardless of the mechanism of the effect of framing of time on delay discounting and possible limitations of our procedure, the present study replicated the relation between the degree of discounting as measured in one task and the degree of discounting as measured in another task (see Odum, 2011b; Johnson & Bickel, 2002; Rodzon, Berry, & Odum, 2011). Participants who tended to show steep discounting as measured in the calendar untis task showed steep discounting as measured in the other task (either date- or days-framed discounting). Similarly, people who show steep discounting of one type of outcome tend to show steep discounting for another type of outcome (Charton & Fatino, 2008; Odum, 2011b), and people who show steep discounting at one time point tend to show steep discounting when assessed at other time points (up to a year later; Kirby, 2009; Simpson & Vuchinich, 2000). These types of findings and others have led us to suggest in that delay discounting may have enduring trait-like aspects (Odum, 2011a, 2011b).
Fortunately, in addition to trait influences, delay discounting also shows strong state influences and is also potentially modifiable. Some promising interventions to reduce the degree to which people discount delayed outcomes include neurocognitive rehabilitation through working memory enhancement (Bickel et al., 2011), financial education and training (Black & Rosen, 2011), and acceptance and mindfulness interventions (Hendrickson & Rasmussen, 2013; Morrison et al., 2014). These interventions, though providing encouraging results, are in some cases time- and resource-intensive. Framing manipulations, however, are potentially immediate and relatively easily accomplished (Radu et al., 2011), and thus provide a promising additional avenue for research into effective ways to modify maladaptive steep delay discounting.
Acknowledgments
The authors would like to thank Hamilton Mendenhall and Justin Stonecipher for help with data collection and Greg Madden for helpful discussion.
References
- Ainslie G. Picoeconomics: The strategic interaction of successive motivational states within the person. Cambridge: UK: Cambridge University Press; 1992. [Google Scholar]
- Baker F, Johnson MW, Bickel WK. Delay discounting in current and never-before cigarette smokers: Similarities and differences across commodity, sign, and magnitude. Journal of Abnormal Psychology. 2003;112(3):382–392. doi: 10.1037/0021-843X.112.3.382. [DOI] [PubMed] [Google Scholar]
- Bar M. The proactive brain: Memory for predictions. Philosophical Transactions of the Royal Society B: Biological Sciences. 2009;364(1521):1235–1243. doi: 10.1098/rstb.2008.0310. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baumann AA, Odum AL. Impulsivity, risk taking, and timing. Behavioral Processes. 2012;90(3):408–414. doi: 10.1016/j.beproc.2012.04.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bickel WK, Odum AL, Madden GJ. Impulsivity and cigarette smoking: delay discounting in current, never, and ex-smokers. Psychopharmacology. 1999;146:447–545. doi: 10.1007/PL00005490. [DOI] [PubMed] [Google Scholar]
- Bickel WK, Yi R, Landes RD, Hill PF, Baxter C. Remember the future: working memory training decreases delay discounting among stimulant addicts. Journal of Biological Psychiatry. 2011;69(3):260–265. doi: 10.1016/j.biopsych.2010.08.017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Black AC, Rosen MI. A money management-based substance use treatment increases valuation of future rewards. Addictive Behaviors. 2011;36:125–128. doi: 10.1016/j.addbeh.2010.08.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Centers for Disease Control and Prevention. Smoking-attributable mortality, years of potential life lost, and productivity losses—United States, 2000–2004. Journal of the American Medical Association. 2005;301(6) doi: 10.1001/jama.301.6.593. [DOI] [Google Scholar]
- Charlton SR, Fantino E. Commodity specific rates of temporal discounting: Does metabolic function underlie differences in rates of discounting. Behavioural Processes. 2008;77(3):334–342. doi: 10.1016/j.beproc.2007.08.002. [DOI] [PubMed] [Google Scholar]
- Daugherty JR, Brase GL. Taking time to be healthy: Predicting health behaviors with delay discounting and time perspective. Personality and Individual Differences. 2010;48:202–207. doi: 10.1016/j.paid.2009.10.007. [DOI] [Google Scholar]
- de Wit H. Impulsivity as a determinant and consequence of drug use: a review of underlying processes. Addiction Biology. 2008;14:22–31. doi: 10.1111/j.1369-1600.2008.00129.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Du W, Green L, Myerson J. Cross-cultural comparisons of discounting delayed and probabilistic rewards. The Psychological Record. 2002;52:479–492. doi: 10.1037/e527342012-639. [DOI] [Google Scholar]
- Fields SA, Sabet M, Reynolds B. Dimensions of impulsive behavior in obese, overweight, and healthy-weight adolescents. Appetite. 2013;70:60–66. doi: 10.1016/j.appet.2013.06.089. [DOI] [PubMed] [Google Scholar]
- Green L, Myerson J. How many impulsivities? A discounting perspective. Journal of the Experimental Analysis of Behavior. 2013;99(1):3–13. doi: 10.1002/jeab.1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Heil SH, Johnson MW, Higgins ST, Bickel WK. Delay discounting in currently using and currently abstinent cocaine-dependent outpatients and non-drug-using matched controls. Addictive Behaviors. 2006;31:1290–1294. doi: 10.1016/j.addbeh.2005.09.005. [DOI] [PubMed] [Google Scholar]
- Hendrickson KL, Rasmussen EB. Effects of mindful eating training on delay and probability discounting for food and money in obese and healthy-weight individuals. Behaviour Research and Therapy. 2013;51:399–409. doi: 10.1016/j.brat.2013.04.002. [DOI] [PubMed] [Google Scholar]
- Hoffman WF, Moore M, Templin R, McFarland B, Hitzemann RJ, Mitchell SH. Psychopharmacology. 2006;188(2):162–170. doi: 10.1007/s00213-006-0494-0. v. [DOI] [PubMed] [Google Scholar]
- Johnson MW, Bickel WK. Within-subject comparison of real and hypothetical money rewards in delay discounting. Journal of the Experimental Analysis of Behavior. 2002;77(2):129–146. doi: 10.1901/jeab.2002.77-129. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Johnson MW, Bickel WK. An algorithm for identifying nonsystematic delay-discounting data. Experimental and Clinical Psychopharmacology. 2008;16(3):264–274. doi: 10.1037/1064-1297.16.4.321. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kirby KN. One-year temporal stability of delay-discounting. rates. Psychonomic Bulletin & Review. 2009;16(3):457–462. doi: 10.3758/PBR.16.457. [DOI] [PubMed] [Google Scholar]
- Klapproth F. The date-delay framing effect in temporal discounting depends on substance abuse. Behavioural Processes. 2012;90:420–423. doi: 10.1016/j.beproc.2012.03.013. [DOI] [PubMed] [Google Scholar]
- Kühberger A. The influence of framing on risky decisions: A meta-analysis. Organizational behavior and Human Decision Processes. 1998;75(1):23–55. doi: 10.1006/obhd.1998.2781. [DOI] [PubMed] [Google Scholar]
- LeBoeuf RA. Discount rates for time versus dates: The sensitivity of discounting to time-interval description. Journal of Marketing Research. 2006;43:59–72. doi: 10.1509/jmkr.43.1.59. [DOI] [Google Scholar]
- Logue AW. Research on self-control: An integrating framework. Behavioral and Brain Sciences. 1988;11(4):665–679. doi: 10.1017/S0140525X00053978. [DOI] [Google Scholar]
- Madden GJ, Andrea MB, Bethany RR, Kastern LL. Delay discounting of real and hypothetical rewards. Experimental and Clinical Psychopharmacology. 2003;11(2):139–145. doi: 10.1037/1064-1297.11.2.139. [DOI] [PubMed] [Google Scholar]
- Madden GJ, Petry NM, Badger GJ, Bickel WK. Impulsive and self-control choices in opioid-dependent patients and non-drug-using control participants: drug and monetary rewards. Experimental and Clinical Psychopharmacology. 1997;5(3):256–262. doi: 10.1037/1064-1297.5.3.256. [DOI] [PubMed] [Google Scholar]
- Mazur JE. An adjusting procedure for studying delayed reinforcement. In: Commons ML, Mazur JE, Nevin JA, Rachlin H, editors. Quantitative analysis of behavior: Vol. 5. The effect of delay and intervening events on reinforcement value. Erlbaum; Hillsdale, NJ: 1987. pp. 55–73. [Google Scholar]
- Mazur JE. Mathematical models and the experimental analysis of behavior. Journal of the Experimental Analysis of Behavior. 2006;85:275–291. doi: 10.1901/jeab.2006.65-05. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McKerchar TL, Green L, Myerson J, Pickford TS, Hill JC, Stout SC. A comparison of four models of delay discounting in humans. Behavioural Processes. 2009;81:256–259. doi: 10.1016/j.beproc.2008.12.017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mitchell SH. Measures of impulsivity in cigarette smokers and non-smokers. Psychopharmacology. 1999;146(4):455–464. doi: 10.1007/pl00005491. [DOI] [PubMed] [Google Scholar]
- Morrison KL, Madden GJ, Odum AL, Friedel JE, Twohig MP. Altering impulsive decision making with an acceptance-based procedure. Behavior Therapy. 2014;45(5):630–639. doi: 10.1016/j.beth.2014.01.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Murphy JG, Vuchinich RE, Simpson CA. Delayed reward and cost discounting. The Psychological Record. 2001;51:571–588. doi: 10.3386/w6410. [DOI] [Google Scholar]
- Myerson J, Green L. Discounting of delayed rewards: models of individual choice. Journal of the Experimental Analysis of Behavior. 1995;64:263–276. doi: 10.1901/jeab.1995.64-263. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Myerson J, Green L, Warusawitharana M. Area under the curve as a measure of discounting. Journal of the Experimental Analysis of Behavior. 2001;76:235–243. doi: 10.1901/jeab.2001.76-235. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Odum AL, Baumann AAL, Rimington DD. Discounting of delayed hypothetical money and food: effects of amount. Behavioral Processes. 2006;73:278–284. doi: 10.1016/j.beproc.2006.06.008. [DOI] [PubMed] [Google Scholar]
- Odum AL. Delay discounting: I’m a k, you’re a k. Journal of the Experimental Analysis of Behavior. 2011a;96:427–439. doi: 10.1901/jeab.2011.96-423. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Odum AL. Delay discounting: Trait variable? Behavioural Processes. 2011b;87:1–9. doi: 10.1016/j.beproc.2011.02.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ohmura Y, Takahashi T, Kitamura N. Discounting delayed and probabilistic monetary gains and losses by smokers of cigarettes. Psychopharmacology. 2005;182:508–515. doi: 10.1007/s00213-005-0110-8. [DOI] [PubMed] [Google Scholar]
- Patak M, Reynolds B. Question-based assessments of delay discounting: Do respondents spontaneously incorporate uncertainty into their valuations for delayed rewards? Addictive Behaviors. 2007;32:351–357. doi: 10.1016/j.addbeh.2006.03.034. [DOI] [PubMed] [Google Scholar]
- Petry NM. Delay discounting of money and alcohol in actively using alcoholics, currently abstinent alcoholics, and controls. Psychopharmacology. 2001;154:243–250. doi: 10.1007/s002130000638. [DOI] [PubMed] [Google Scholar]
- Rachlin H, Raineri A, Cross D. Subjective probability and delay. Jounral of the Experimental Analysis of Behavior. 1991;55(2):233–244. doi: 10.1901/jeab.1991.55-233. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rachlin H. Notes on discounting. Journal of the Experimental Analysis of Behavior. 2006;85:425–435. doi: 10.1901/jeab.2006.85-05. doi:1901/jeab.2006.85-05. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Radu PT, Yi R, Bickel WK, Gross JJ, McClure SM. A mechanism for reducing delay discounting by altering temporal attention. Journal of the Experimental Analysis of Behavior. 2011;96(3):363–385. doi: 10.1901/jeab.2011.96.363. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Read D, Frederick S, Orsel B, Rahman J. Four score and seven years from now: The date/delay effect in temporal discounting. Management Science. 2005;51(9):1326–1335. doi: 10.1287/mnsc.1050.0412. [DOI] [Google Scholar]
- Reynolds B. A review of delay-discounting research with humans: relations to drug use and gambling. Behavioural Pharmacology. 2006;17(6):651–667. doi: 10.1097/fbp.0b013e3280115f99. [DOI] [PubMed] [Google Scholar]
- Rodzon K, Berry MS, Odum AL. Witin-subject comparison of degree of delay discounting using titrating and fixed sequence procedures. Behavioural Processes. 2011;86(1):164–167. doi: 10.1016/j.beproc.2010.09.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Samuelson PA. A note on the measurement of utility. Review of Economic Studies. 1937;4:155–161. doi: 10.2307/2967612. [DOI] [Google Scholar]
- Simpson CA, Vuchinich RE. Reliability of a measure of temporal discounting. The Psychological Record. 2000;50:3–16. [Google Scholar]
- Stahl C, Voss A, Schmitz F, Nuszbaum M, Tüscher O, Lieb K, Klauer KC. Behavioral components of impulsivity. Journal of Experimental Psychology: General. 2013;143(2):850–886. doi: 10.1037/a0033981. [DOI] [PubMed] [Google Scholar]
- Tanaka SC, Yamada K, Yoneda H, Ohtake F. Neural mechanisms of gain-loss asymmetry in temporal discounting. Journal of Neuroscience. 2014;34(16):5595–5602. doi: 10.1523/JNEUROSCI.5169-12.2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Torregrossa MM, Quinn JJ, Taylor JR. Impulsivity, compulsivity, and habit: The role of the orbitofrontal cortex revisited. Biological Psychiatry. 2008;63(3):253–255. doi: 10.1016/j.biopsych.2007.11.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tversky A, Kahneman D. The framing of decisions and the psychology of choice. Science. 1981;211(4481):453–458. doi: 10.1126/science.7455683. [DOI] [PubMed] [Google Scholar]
- Wesley MJ, Bickel WK. Remember the future II: meta-analysis and functional overlap of working memory and delay discounting. Biological Psychiatry. 2014;75(6):435–448. doi: 10.1016/j.biopsych.2013.08.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Windmann S, Kirsch P, Mier D, Stark R, Walter B, Güntürkün O, … Vaitl D. On framing effects in decision making: Linking lateral versus medial orbitofrontal cortex activation to choice outcome processing. Journal of Cognitive Neuroscience. 2006;18(7):1198–1211. doi: 10.1162/jocn.2006.18.7.1198. [DOI] [PubMed] [Google Scholar]