DYNAMIC HETEROGENEITY IN LIFE HISTORIES

Abstract

Longitudinal data on natural populations have been analyzed using multi-stage models in which survival depends on reproductive stage, and individuals change stages according to a Markov chain. These models are special cases of stage-structured population models. We show that stage-structured models generate dynamic heterogeneity: life history differences produced by stochastic stratum dynamics. We characterize dynamic heterogeneity in a range of species across taxa by properties of the Markov chain: the entropy, which describes the extent of heterogeneity, and the subdominant eigenvalue, which describes the persistence of reproductive success during the life of an individual. Trajectories of reproductive stage determine survivorship, and we analyze the variance in lifespan within and between trajectories of reproductive stage. We show how stage-structured models can be used to predict realized distributions of lifetime reproductive success. Dynamic heterogeneity contrasts with fixed heterogeneity: unobserved differences that generate variation between life histories. We show by example that observed distributions of lifetime reproductive success are often consistent with the claim that little or no fixed heterogeneity influences this trait. We propose that dynamic heterogeneity provides a “neutral” model for assessing the possible role of unobserved “quality” differences between individuals. We discuss fitness for dynamic life histories, and the implications of dynamic heterogeneity for the evolution of life histories and senescence.

Introduction

In recent decades, longitudinal capture-mark-recapture (CMR) data on individuals have become available for many natural populations (Sandercock 2006), along with statistical tools for their analysis (Lebreton et al. 1992). Individual-based CMR analyses have yielded descriptions of average patterns and variation among individuals in the timing, level, and distribution of reproduction and mortality (Loison et al. 1999, Cam et al. 2002, Moyes et al. 2006). These analyses were stimulated by and have raised important questions about the evolutionary forces (such as trade-offs or constraints) that shape life histories (Viallefont et al. 1995, Ricklefs & Cadena 2007), and about the meaning and significance of phenotypic variation within populations (McGraw & Caswell 1996, Link et al. 2002, Pelletier et al. 2007).

Many CMR studies are based on multi-stage models, in which individuals are tracked by their reproductive stage (e.g., immature, mature non-breeder, mature breeder) and by, say, age (or time) (Nichols & Kendall 1995). In multi-stage models, survival depends on reproductive stage and possibly age, and individuals progress through reproductive and mortality states according to a stochastic process, typically a Markov chain. These multi-stage models can generate what we call dynamic heterogeneity, which we define as life history differences among individuals that are generated by the stochastic process that describes changes in stage. We distinguish between dynamic heterogeneity and fixed heterogeneity, which is defined as differences between individuals that are fixed at birth.

In longitudinal studies, fixed heterogeneity is usually assumed to be due to variation in individual latent traits that affect survival, fertility or transition rates between stages. The extent of unobserved fixed heterogeneity is estimated using random-effects models, an approach stimulated in part by Vaupel & Yashin’s (1985) discussion of frailty, whereas stage transitions are directly observed. As in Vaupel & Yashin, the latent traits that generate fixed heterogeneity are often assumed to be individual characteristics such as genotype or maternal environment that are measurable in principle but have not been observed. In contrast, the stage transitions that lead to dynamic heterogeneity are observed, although any particular model for them must be estimated. Although multi-stage models have now been estimated for many natural populations (Appendix Table), the dynamics of stage transitions and the ecological and evolutionary implications of dynamic heterogeneity have been little explored.

It is (or should be) well known that CMR models are particular cases of stage-structured population models (Nichols et al. 1992, Fujiwara & Caswell 2002). Stages can be defined not just in terms of reproductive success but also in terms of other traits such as developmental stage, size or weight. Dynamic heterogeneity arises when stage transitions are probabilistic, and different individuals may follow different sequences of stages as they age. Many examples of such heterogeneity are provided by plants (Horvitz & Tuljapurkar 2008). Thus our approach, although focused on species that have been studied using CMR methods, applies more broadly to many stage-structured populations.

Here we synthesize analyses of stage-structured models in order to describe life histories as dynamic processes, obtaining new insights and predictions about the evolution of life histories and the maintenance of phenotypic variation. In these models, some life history parameters may also depend explicitly on age. After defining multi-stage models, we show that dynamic heterogeneity can be characterized by two properties of the estimated multi-stage Markov chain: the entropy, which describes the extent and pattern of heterogeneity, and the subdominant eigenvalue, which describes the correlation of reproductive stages during the life of an individual. We compare dynamic heterogeneity across a number of species (Appendix Table). We then show how trajectories of reproductive stage (i.e., age-specific sequences of reproductive outcomes) map into survivorship curves, and analyze the variance in lifespan within and between trajectories of reproductive stage. Next, we assess whether realized distributions of lifetime reproductive success can be generated solely by dynamical heterogeneity or whether the realized distributions appear to be influenced by fixed heterogeneity We then discuss patterns of senescence predicted by multi-stage models. Using these results, we propose that dynamic heterogeneity provides a “neutral” model for assessing the possible role of unobserved “quality” differences between individuals. Then we describe the theoretical relationship between dynamic heterogeneity and fitness, generalize the Lotka equation to describe trajectories of reproduction, and review the connection between multi-stage CMR models and the stage-structured models widely used to study plants and some animals (e.g., as in Tuljapurkar and Horvitz 2006). Finally, we discuss the implications of dynamic heterogeneity for the evolution of life histories and senescence, and point to necessary extensions of multi-stage CMR models.

Throughout this paper we use the term stage to mean a categorical classification of individuals. In much of our discussion, stage is the same as reproductive stratum, i.e., a category defined by maturity and reproductive success. But the features of stage-structured models that we discuss are more general, and apply to situations in which individuals are classified not just by levels of reproduction but also by size, physiological condition, or other traits.

Multi-stage CMR models

Data and Illustrative Examples

Multi-stratum CMR data consist of records of the detection/nondetection of individuals and of their status with respect to some measurable trait (e.g., whether they are immature or breeding and if reproduction occurs, how many offspring an individual produces). These records are usually based on annual observations during or after the reproductive season. In most cases individuals are marked at birth, but in some cases we only know ages relative to the first marking event. Measures of reproductive success vary with the species. For birds, they include the number of eggs laid, number of hatchlings, number of fledglings, and the number of recruits (e.g., Cam & Monnat 2000, McCleery et al. 2002). For many mammals, they include whether a offspring is produced, and whether the offspring dies early or late in the breeding year or survives to the following year (e.g., Tavecchia et al. 2005, Moyes et al. 2006).

The multi-stage models we focus on sort living individuals into stages based on measures of annual reproductive success. Here we use the following generic model defined with respect to reproductive stages: immatures are stage 1, mature individuals who attempt to breed occupy stages of increasing reproductive success labeled as 2, 3, to K − 1, and there is a single mature but non-breeding stage K. The amount of reproduction (number of immatures produced) by an individual of age a in stage i is F_i(a). An individual of age a in stage i in the current year has a probability P_i(a) of surviving to the following year, and a probability R_i(a) of being observed (recaptured) in the current year. There is a probability ψ_ij that an individual in reproductive stage i this year and who survives will be in reproductive stage j in the following year and this probability is the i, j element of a matrix Ψ. We use the CMR convention that transitions run from i to j, which differs from the convention in population projection matrices. This framework is based upon Nichols et al. (1992) and Nichols & Kendall (1995) and can be extended, e.g., if the survival or transition probabilities depend on the number of years spent in each reproductive stage (Hestbeck et al. 2002, Brownie et al. 1993), or if the parameters depend on other measured covariates. There may be cases in which the survival rate is a function not just of the current stage but also of the destination stage (Brownie et al. 1993). We exclude such possibilities for the present but return to them in the last section. Our discussion of dynamic heterogeneity extends to these more general models.

We use two illustrative examples throughout. The first is based upon data from the population of the Mute Swan, Cygnus olor, at Abbotsbury, U.K. (for details see e.g., McCleery et al. 2002, Charmantier et al. 2006) that we have analyzed using a multi-stage CMR model (Orzack et al. 2008a, submitted). In our model, in each year every female was categorized as being in one of 5 reproductive stages: immature (stage 1), having a “low” clutch size of 1–4 (stage 2), having a “medium” clutch size of 5–6 (stage 3), having a “high” clutch size of 7–12 (stage 4), or being non-reproductive in that year after having reproduced at least once previously (stage 5). Table 1 shows the estimated transition matrix Ψ; full details of this model are available on request. The swans exhibit a positive relationship between annual survival and annual reproduction, so that P_i and F_i increase with stage i for all breeding stages 2–4. Such a positive relationship, observed in several species (e.g., Cam et al. 2002), conflicts with the common assumption that there is a negative trade-off between reproduction and survival, and is often interpreted as a correlation driven by differences in fixed traits that determine individual “quality” (van Noordwijk and de Jong 1986). The data and our CMR model exclude pre-breeding mortality, and all breeders are assumed to be detected. Our second example is theoretical, and is defined by the transition matrix,

$$\mathrm{\Psi }=\left(\begin{array}{ccc}\hfill {\psi }_{11}\hfill & \hfill {\psi }_{12}\hfill & \hfill {\psi }_{13}\hfill \\ \hfill 0\hfill & \hfill {\psi }_{22}\hfill & \hfill {\psi }_{23}\hfill \\ \hfill 0\hfill & \hfill {\psi }_{32}\hfill & \hfill {\psi }_{33}\hfill \end{array}\right).$$ (1)

Table 1.

Transition Ψ matrix for swans

	I	L	M	H	N
I	0.585	0.198	0.191	0.026	0
L	0	0.212	0.419	0.100	0.269
M	0	0.113	0.4444	0.250	0.193
H	0	0.074	0.342	0.447	0.137
N	0	0.111	0.220	0.056	0.613

Immatures (stage 1) can stay in that stage or transition to reproductive stage 2 or 3, while mature individuals move between reproductive stages 2 and 3. Stage-specific survival rates are P₁, P₂, P₃, and fertilities are F₂, F₃. We simulate reproductive trajectories generated by Markov chains such as (1) using standard methods (Ripley 1987).

Many Real-world Examples

Multi-state CMR methods have been used to describe life histories in many natural populations. We found 41 published studies involving 36 species: 10 mammal, 20 bird, 4 amphibian/reptilian, 1 insect, and 1 plant (see Appendix). Most studies differentiate between pre-breeding immature individuals, non-breeding adult individuals and one or multiple stages of breeding outcomes. Our focus in these real-world examples is on estimates of transition rates Ψ and age-specific survival rates P_i. To simplify comparisons, we do not consider here other parameters that may have been studied in particular cases, such as the effects of particular years, physiological condition, or weather. Not all of the studies report all parameter estimates; some studies only describe part of the life cycle for reasons of data limitation, or focus on only one life stage in the original publication. We use 22 studies, most of which have a detailed resolution of reproductive strata and include immatures (see Appendix).

Dynamic Heterogeneity in Reproduction

What and How Much

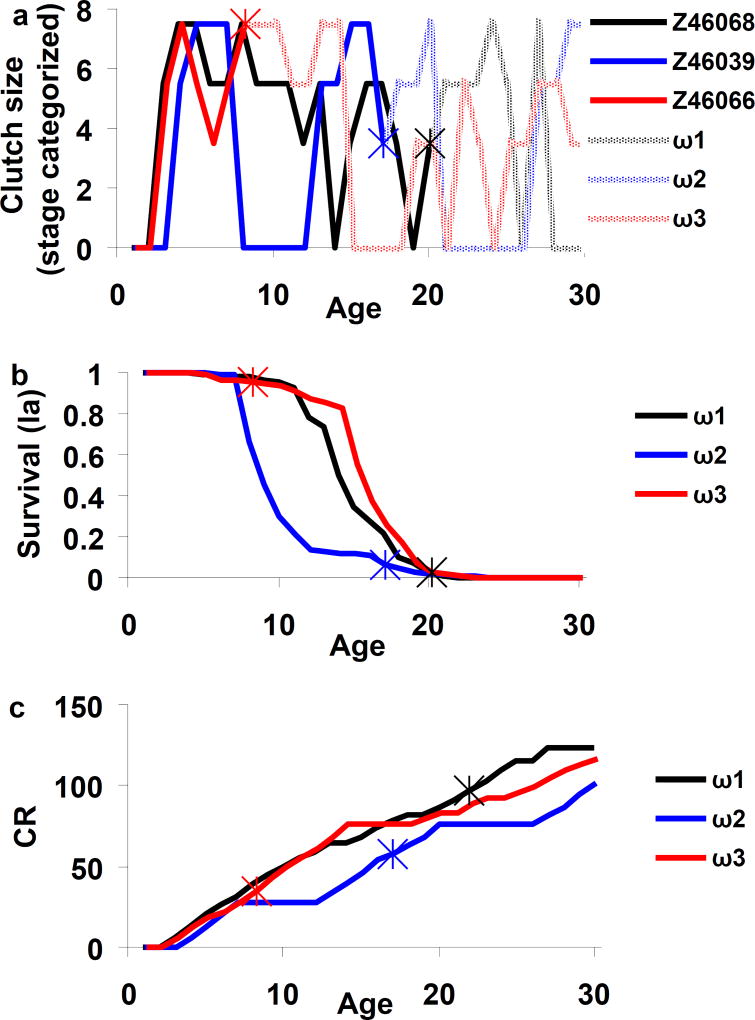
The Abbotsbury swan data illustrate what we mean by dynamic heterogeneity in reproductive success. The three trajectories in Fig. 1a indicate observed clutch size by age for 3 females, with stars marking the age when a female was last seen (ignore for the moment the lines past the starred ages). These females produced very different clutches at the same ages and have different amounts of cumulative reproduction; the full data set reveals large differences among females in any given year. Reflecting this variability, the estimated matrix Ψ (Table 1) has nonzero probabilities of transition between all reproductive stages. For each female in Fig. 1a, starting at the last observed (starred) age, we used Ψ to simulate a sequence of stages (lines labeled ω₁,ω₂,ω₃ in Fig 1a) out to age 30 years. Each simulated sequence ω is a possible trajectory of reproductive stages and cumulative reproduction (CR) varies between trajectories (Fig. 1b). Since annual survival rate depends on reproductive stage in that year, every trajectory ω has a distinct associated survivorship that applies to any bird following that trajectory (Fig. 1c). Thus dynamic heterogeneity in reproduction drives heterogeneity in both components of fitness. We next explore and quantify variation in the sequencing of reproductive stages, without considering mortality, and then examine the resulting variation in fitness. Although the stochastic transitions described by the matrix Ψ do not consider mortality, they are a generating process for the life history. As we show below, the trajectories defined by this process can then be used to study the mean and variance of age at death, lifetime reproduction, fitness, and so on.

Fig. 1.

a) Observed reproductive stage dynamics for number of eggs per clutch for three Mute Swans (Z46068, Z46039, Z46066) (solid lines) up to the age of their last resighting. The last resighting is marked by a star. Light-colored lines show a possible simulated sequence of reproductive stages after last sighting. The sequences ω₁,ω₂,ω₃ are three out of a multitude of possible trajectories that follow transition matrix Ψ (Table 2).

b) Survivorship l(a) at age a for the three trajectories ω₁,ω₂,ω₃, c) Cumulative reproduction (CR) (number of eggs laid by age a). The last resighting is marked by a star in panels b, c.

How much dynamic heterogeneity is implied by a matrix Ψ ? Consider the set of matrices shown in Table 2. With matrix Ψ₁, immatures transition to stage 2, then stage 3, then alternate between these on the reproductive trajectory ω in Table 2. With Ψ₂, immatures transition to stage 2 or to stage 3 and stay, ending up on trajectory ω₁ or ω₂ in the table. In contrast, Ψ₃ generates trajectories after maturity along which individuals repeatedly change stage; three possible trajectories are shown in the table. Clearly Ψ₃ generates the highest diversity of reproductive trajectories.

Table 2.

Alternative Ψ matrices

Ψ1	0.5	0.5	0
	0	0	1	ω = (2, 3, 2, 3, …)
	0	1	0
Ψ2	0.5	0.25	0.25	ω1 = (2, 2, 2, 2, …)
	0	1	0	ω2 = (3, 3, 3, 3, …)
	0	0	1
Ψ3	0.5	0.5	0	ω1 = (2, 2, 3, 2, …)
	0	0.6	0.4	ω2 = (2, 3, 3, 3, …)
	0	0.5	0.5	ω3 = (2, 3, 2, 2, …)

Over T years with K stages there are K^T possible trajectories; from these trajectories the matrix Ψ generates the actual trajectories relevant to a particular life history (by assigning probability weights to the different trajectories). We define the amount of dynamic heterogeneity for a transition matrix Ψ as its entropy H, which is the rate at which the diversity of trajectories increases with their length (Shannon 1948, Pielou 1977).

To understand entropy, consider Ψ in equation (1), where an individual in stage 2 stays in stage 2 with probability ψ₂₂ or moves to stage 3 with probability ψ₂₃. If we observe the transitions made by many individuals in stage 2, the diversity of their choices is described by an entropy H(2) = −[ψ₂₂ logψ₂₂ + ψ₂₃ logψ₂₃]. If a stage 2 individual always moves to stage 3 (as in example Ψ₁, Table 2), or always remains in stage 2 (as in example Ψ₂), entropy H(2) = 0. But if a stage 2 individual can stay in stage 2 or move to stage 3, H(2) > 0. As the probability of moving becomes more even between destination stages, H(2) increases and has a maximum value of log 2 when ψ₂₂ = ψ₂₃ = 1/2. A similar entropy measure H(3) describes transitions out of stage 3. The dynamic heterogeneity H of matrix (1) is an average (see Table 4) of H(2) and H(3) weighted by the stationary proportions π₂, π₃ of these stages along trajectories. Hence H is an average measure of “randomness” in stage transitions. The precise mathematical proof that H measures randomness is the celebrated Shannon-McMillan theorem (e.g., see Khinchin 1957).

Table 4.

Measures for Ψ in equation (1)

Quantity	Value for equation (1)
Stationary distribution	π = (0, (1 − ψ22), (1 + ψ33))/(1 − λ1)
Entropy	π2[ψ22 log ψ22 + (1 − ψ22)log(1 − ψ22)] + π3[ψ33 log ψ33 + (1 − ψ33)log(1 − ψ33)]
Subdominant Eigenvalue	λ1 = (ψ22 + ψ33 − 1)
Autocorrelation coefficient	ρ = λ1 = (ψ22 + ψ33 − 1)
Correlation Time	τ = −1/[log(ψ22 + ψ33 − 1)]
Expected time to leave stages 1, 2, 3	1/(1 − ψ11), 1/(1 − ψ22), 1/(1 − ψ33)

Examples 1, 2, 3 in Table 2 have entropies H₁ = H₂ = 0 and H₃ = 0.682. When H = 0 there is just one reproductive trajectory (example 1, Table 2) or a small fixed number of trajectories (example 2, Table 2). At the other extreme, if an individual has an equal probability of moving to any of the K stages, H has its maximum possible value H_max = log K. We remove any effect of the number of stages by using the ratio H/(log K) which we call the scaled entropy. This ratio positions the life history on a scale of dynamic heterogeneity from 0 to 1.

For the swan example, the estimate of the scaled entropy is 0.85 = (entropy/maximum entropy) = 1.18/log(4) for the four mature stages (Table 2); as might be expected for most real-world systems, the entropy is not at the limits of complete determinism or complete randomness. If the transient immature stage is included, the scaled entropy is lowered to 0.73, because the number of stages is increased but the entropy itself is not altered. The high entropy reflects both variability in reproductive stage along any single reproductive trajectory and between reproductive trajectories.

Does Reproductive Success Persist?

Do individuals tend to be persistently successful or unsuccessful? Do “fixed” quality differences influence the variability in reproduction over time? One way to quantify persistence is to measure the correlation between a individual’s reproductive stage at age a₁ and its reproductive stage at a later age a₁ + t. For the Markov transition matrix, the correlation between its current reproductive stage and its stage t years later can be computed exactly in terms of the eigenvalues and eigenvectors of the transition probability matrix. The magnitude of this correlation falls off as

$$e^{(\text{log}|{\lambda }_1|)t}=e^{-t/\tau },\text{where }\tau =-1/(\text{log}|{\lambda }_1|)>0,$$

where λ₁ is the leading subdominant eigenvalue of the matrix. The quantity τ is a characteristic time. For ages separated by τ years, the correlation between reproductive stages is e⁻¹ ≈ 0.37, and for ages separated by an interval 2τ years the correlation is e⁻² ≈ 0.14. So the value of an individual’s current reproductive stage as a predictor of its future reproductive stage declines as we look further into the future, and τ is a time scale that measures the persistence of reproductive success or failure. The ratio of τ to the length of the breeding span (defined as the average time between first breeding and last detection or death) is a relative measure of persistence. If immature stages are transient, we use the subdominant eigenvalue of that part of Ψ that includes only mature stages.

In example (1), τ = 1/log(|ψ₂₂ + ψ₃₃ − 1|) (Table 4). This expression is intuitively sensible: as ψ_ii increases, so does an individual’s tendency to stay in stage i, and so does the influence of current stage on the future. For swans the subdominant eigenvalue over the mature stages is 0.468, the characteristic time τ = −(1/log 0.468) = 1.32 years. Thus, we can expect a female that lays a large clutch this year to continue laying large clutches only for the next 2–3 years; subsequent clutch sizes may well be small. This shows that reproductive success is only weakly persistent along a female’s life.

Another descriptor of persistence is the average length of time $\overline{t_i}$ spent in stage i by an individual who has just reached that stage. For equation (1), $\overline{t_i}=1/(1-{\psi }_{\mathit{\text{ii}}})$, a value that increases with ψ_ii. In contrast to these t̄_i, the characteristic time τ captures transitions back and forth between stages. The value of t̄_i for our generic model is the mean time spent as an immature individual (conditional on survival) and can often be usefully compared with an empirical estimate. For the swans, t̄_i in the five stages are 2.41, 1.27, 1.79, 1.81, and 2.58 years, respectively. To determine the time spent as an immature we add 2 years to $\overline{t_1}$, because all females spend their first two years as immatures (this interval is not reflected in matrix Ψ); the resulting estimate of 4.41 years for the average time spent as an immature is close to the empirical estimate of 4.32 years. For other stages, the estimates show some persistence, but all t̄_i, i > 1 are small relative to the expected lifetime for swans of 8.7 years. Thus females usually make multiple transitions between stages throughout their breeding lives. Expected lifetime here and below reflects both variation in stage and the effect of stage on survival; in a later section we describe how expected lifetime is computed.

Of course these estimates of persistence times and residence times are conditional on survival, and mortality would simply reduce them. So the key biological question of whether success persists can be answered using τ. We return to the effect of mortality in the final section.

Entropy versus Persistence

By definition, the correlation time τ increases with the probabilities ψ_ii that individuals stay in the same reproductive stage i. However, there is no necessary association between entropy and persistence: in equation (1), entropy is low when persistence is low (i.e., when ψ₁₁ and ψ₂₂ are both small) but entropy is also low when persistence is high (i.e., when ψ₁₁ and ψ₂₂ are both large). Thus we can have low entropy (low diversity of reproductive trajectories) associated with high correlation (individuals are likely to remain in reproductive stages). This combination matches a common view of life histories in which one or a few fixed reproductive trajectories exist in any given species. This limit contrasts with more dynamical life histories, which may, for example, have low entropy along with low correlation, such that individuals are likely to change reproductive stages frequently. The latter is an unconventional picture of reproductive strategies, but is common in our sample of species. In life histories with many stages, the only sure way of characterizing entropy and correlation is to compute these metrics. Although an examination of the transition rates, say of the probability of staying in a stage versus leaving it, is qualitatively useful, the properties of a dynamic life history depend on all the transition rates.

Entropy and Persistence Across Species

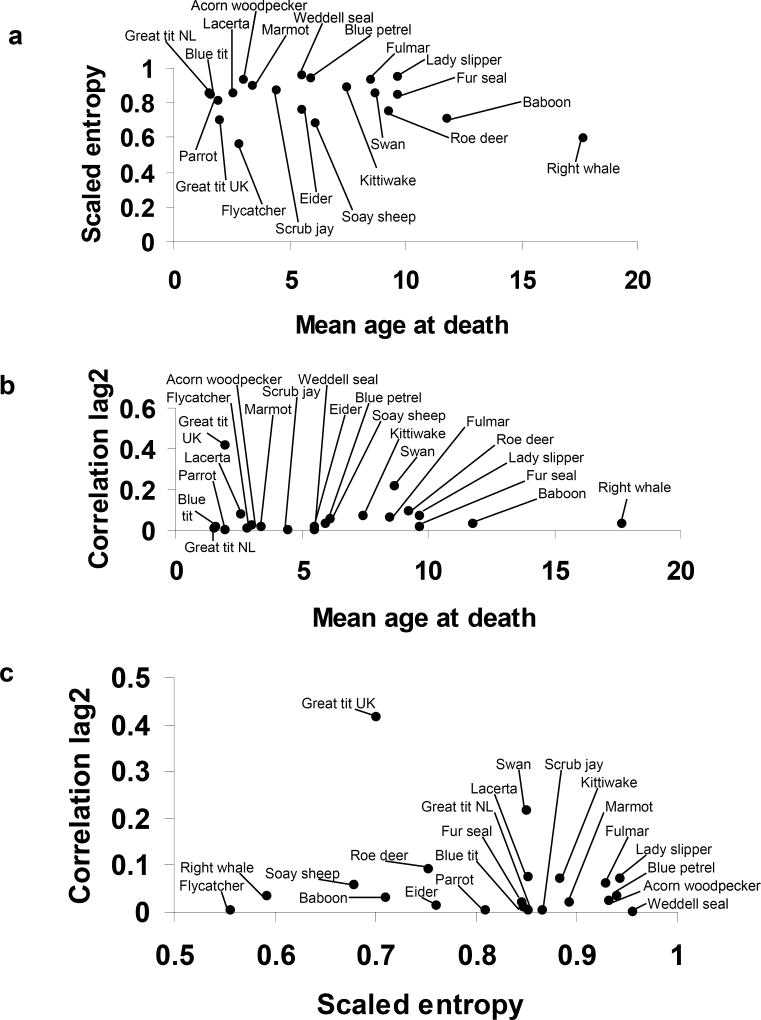
The Swan example is not exceptional in terms of its entropy. Estimates of scaled entropy ranged from 0.55 and 0.95 for the 21 studies shown in Figure 2a, indicating that individuals of most species frequently switch reproductive stages throughout their lives. The species with the lowest entropy is the Pied Flycatcher; individuals of this species fail to recruit offspring in most years (average residence time in the failed state is 4.35 years) and if they are successful in one year they almost always fail in the following year. We also found a low entropy for Right Whales, who have long birth intervals (5.2 years) and therefore spend many years without a calf; when individuals calve they return to a stage without a calf in the following year. In both cases there are relatively few trajectories that individuals can follow.

Fig. 2.

a) Scaled entropy (entropy/maximum entropy) versus mean age of death for 21 species, b) correlation between the current reproductive stage and the reproductive stage two years versus mean age at death, c) correlation as in (b) plotted against scaled entropy.

To describe the temporal correlation between reproductive stage we computed the characteristic time τ as discussed above and report the correlation exp(−2/τ) between current reproduction and reproduction 2 years later. Most species show very low autocorrelation in their reproductive success over time (see Fig. 2b). For the swans τ = 1.32 years and the 2-year correlation is 0.23; all but one species have 2-year correlations much less than < 0.12. Only the English Great Tit population has a much higher correlation of 0.42. Females of this species frequently lay medium sized clutches and rarely switch to lower or high clutch sizes, but if they manage to lay a large clutch they are then likely to lay another large clutch the next year. Comparison with the Great Tit population in the Netherlands is difficult for reasons that we discuss in the next section.

The diversity of trajectories, expressed by the entropy, is not correlated with the serial autocorrelation of reproductive stages between years, as can be seen from Fig. 2c. Thus these two metrics likely describe distinct features of the biology of individual life histories. Even the two species with low entropy (Flycatchers and Whales) have low serial autocorrelation despite the long times they remain in one state on average (for Flycatchers, 4.3 years in the failed breeding state, for Whales, 5.2 years without a calf).

We conclude that neither entropy or the autocorrelation of reproductive stage changes between species in any systematic way. In our sample, long-lived species do not show fundamentally different transition dynamics in reproduction compared to short-lived species, and mean lifespan does not affect either entropy or correlation. We note that in most CMR studies on open populations the event of death is confounded with permanent emigration.

Fitness Components

Our dynamical approach allows us to examine variance in fitness components in terms of variation among trajectories of reproductive stage. This variation is generated by differences in the realized trajectories that individuals follow through stages and is not due to any differences between individuals in their transition probabilities or stage-specific survival or reproduction. Recall Figs 1b and 1c, which show accumulated reproduction and survivorship for the three trajectories of reproductive stages for Mute Swans shown in Fig 1a. Clearly, heterogeneity over time in individual reproductive success generates variance between individuals in the fitness components of reproduction and survival.

Mortality, Survivorship and Cumulative Reproduction

Every individual follows a reproductive trajectory ω that determines survivorship l_a(ω) to age a. To describe average survival or reproduction over a large cohort of individuals, we must average over trajectories. The probability ν(ω) of observing a trajectory ω can be written down using the transition matrix and the fact that, in our examples, all individuals are born into stage 1. The population average survivorship is

$${\overline{l}}_a=\sum _{\omega }\nu (\omega )l_a(\omega ).$$ (2)

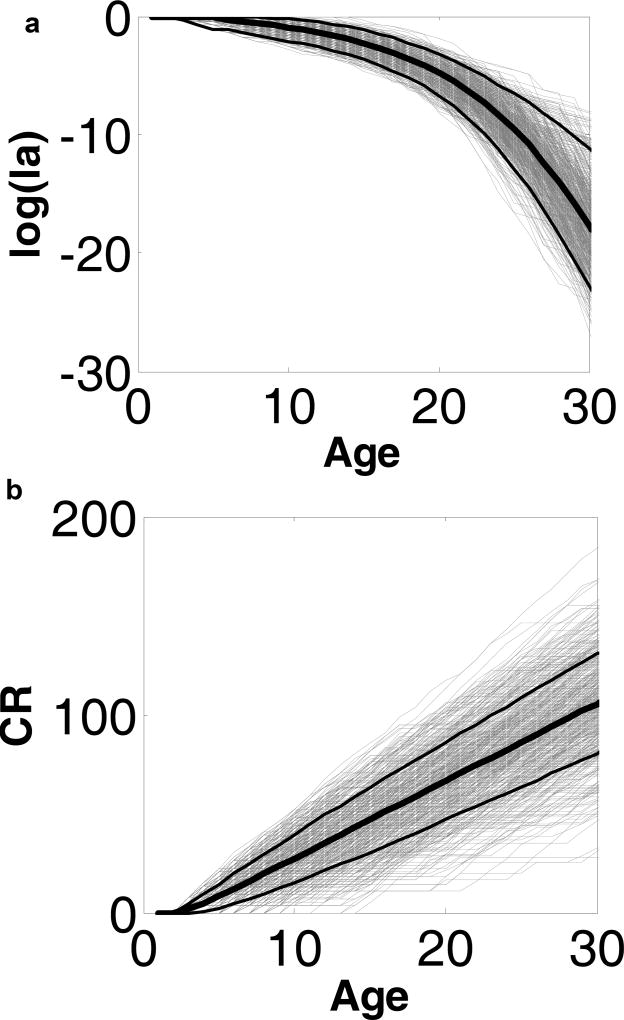
Fig 3a shows the substantial variation in survivorship around the population mean for the Mute Swans. The corresponding variation in cumulative reproduction along trajectories is shown in Fig 3b; this cumulative reproduction is conditional on survival but, of course, lifetime reproductive success includes the effect of survival as discussed further below.

Fig. 3.

a) Survival rates for a large number of trajectories (thin grey lines) for Mute Swans. b) cumulative reproduction (CR) as number of eggs by age. Black thick lines show means and dotted lines show 95% confidence intervals based on 1000 simulated trajectories.

To quantify dynamic heterogeneity of mortality we consider the distribution of the individual age of death T. For a reproductive trajectory ω = (i₁,i₂,i₃,…), the probability of dying at age a is

$${\varphi }_a(\omega )=l_{a-1}(\omega )(1-P_{i_a}(a)),$$ (3)

the average age at death is

$$\overline{(T|\omega )}=\sum _{a}a{\varphi }_a(\omega ),$$ (4)

and the variance in age at death along this trajectory is, say, σ² (T | ω). Averaging over trajectories yields a population average age at death T̅, which is the expected lifetime of an individual, and a variance in age at death σ² (T). Without dynamic heterogeneity, every individual would follow one reproductive sequence so the population and the trajectory means and variances would be equal. But with dynamic heterogeneity there is variance within trajectories as well as variance between trajectories, so that

$${\sigma }^2(T)=\sum _{\omega }\nu (\omega ){\sigma }^2(T|\omega )+\sum _{\omega }\nu (\omega ){(\overline{(T|\omega )}-\overline{T})}^2,=\text{Var}.\text{within traj}.+\text{Var}.\text{between traj}.$$ (5)

Variance in age at death between trajectories is caused by differences in sequences of reproductive stages, whereas the variance within a trajectory reflects the stage-specific association between mortality and reproduction as an individual ages. For the Swans we estimate an expected age at death at the population level T̅ of 8.7 years, but expected age at death varies between trajectories from a low of 4 years to a high of 18 years. The variance in age at death between trajectories is 5.1, much lower than the variance of 16.7 in age at death within trajectories.

Variance in Lifetime Reproductive Success

Along a stage trajectory ω = (i₁,i₂,i₃,…) an individual who dies at age T has Lifetime Reproductive Success (LRS)

$$C(T,\omega )=\sum _{a=1}^T{R}_{i_a}(a).$$

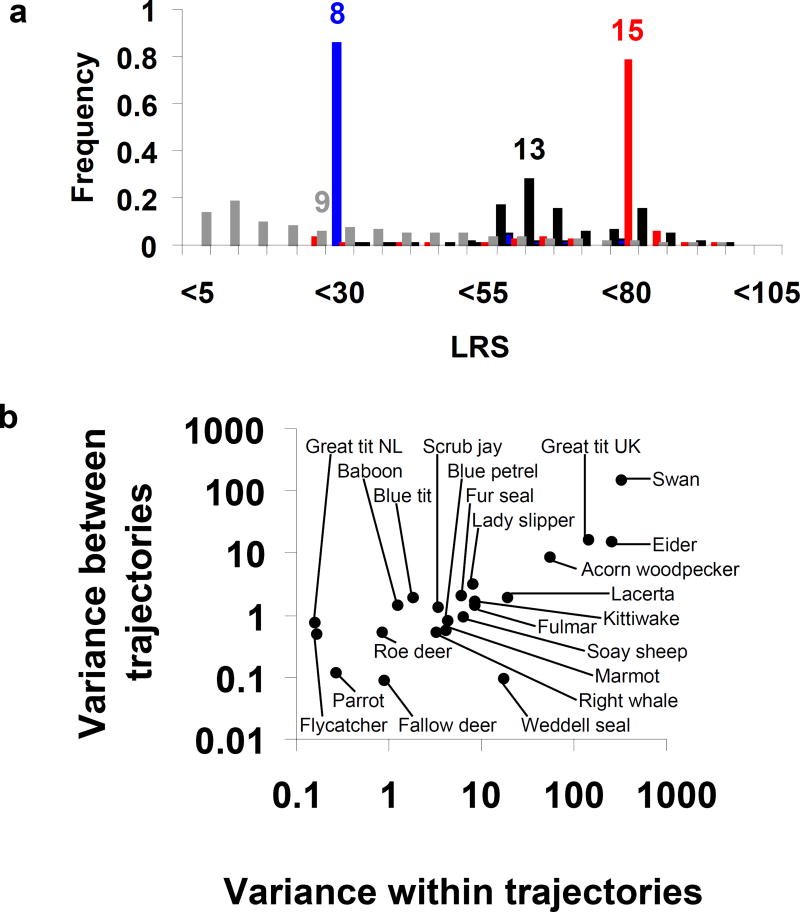
This LRS varies among individuals because of differences in both age at death and in the reproductive trajectories that were followed until death. Recall Fig 1a, which showed three reproductive trajectories for the Swans. Along each of these trajectories, the LRS varies because individuals may die at different ages, as shown by the red, blue and black distributions in Fig 4a. If we simulate a large number of trajectories we obtain a population level distribution and also the frequency distribution of LRS across all possible trajectories, which is the grey histogram in Fig 4a. For the Swans, the average expected LRS is 24.1 eggs; the minimum and maximum are 2.6 and 101.2 respectively, showing that there is large variance between trajectories. Considering all trajectories for the Swans, the variance of LRS between trajectories is 150.25 and the variance within trajectories is 336.1.

Fig. 4.

a) Distribution of Lifetime Reproductive Success (LRS) for the three trajectories ω₁,ω₂,ω₃ shown in Fig. 1 for Mute Swans, and for the population based on a large number of trajectories (in grey). The color coded numbers are the median age at death for the three trajectories and the population mean. They are shown above the corresponding median LRS for each of the trajectories and the expectation across the population.

b) Variance of expected Lifetime Reproductive Success (LRS) within trajectories versus variance in expected LRS between trajectories for 22 species. Note the difference in scales of the axes.

Within-trajectory variance of LRS is larger than between-trajectory variance for most of the species we analyzed (Fig 4b). The variance within trajectories is shaped by the stage-specific relationship between mortality and reproduction, and the variance between trajectories reflects the diversity of reproductive sequences that are followed over time. In short-lived species such as the Pied Flycatcher and the Great Tits, individuals may only be successful at recruiting offspring once or twice in their lives, so we might expect the variance within (short) trajectories to be smaller than the variance between them. The Pied Flycatcher and the Netherlands Great Tits exhibit this pattern, but for the English Great Tits within-trajectory variance is much larger than between-trajectory variance and both variances are large. There are at least two possible reasons for the difference. The data concern number of recruits for the Netherlands Great Tits but only clutch sizes for the English Great Tits; the correlation between numbers of recruits in successive years may differ from that between clutch sizes. In addition, there may be differences in ecological conditions between the two populations.

Distribution of Lifetime Reproductive Success

We can predict a population distribution of LRS, or predict the cumulative reproduction for an observed sample by sampling among trajectories according to an appropriate observational design. To compare observations and simulations of LRS, we need to correct for the possibility that resighting probabilities are < 1 and for the influence of right censoring (some individuals are still alive when data collection stops).

To correct for less-than-perfect resighting probabilities for different strata (as estimated from the data using CMR methods) at each time step in a simulation we make a binary choice between resighting and no sighting, and in the latter case set reproduction for that period to 0 in the trajectory ω (for the Swans, resighting probabilities of breeding stages were assumed to be 1).

To correct for the influence of right censoring, we record the observed distribution of ages of last observation d in the actual sample and then generate the distribution of LRS for a synthetic population of the same size as the actual sample, e.g., the 510 Swans in the Abbotsbury sample. For each individual in the observed sample with its age of last observation d, select one of the possible trajectories ω (sampling with replacement) using as probability weights the survivorship at age d. Record the cumulative reproduction on the chosen trajectory ω up to age d, and continue until each individual has been assigned an LRS.

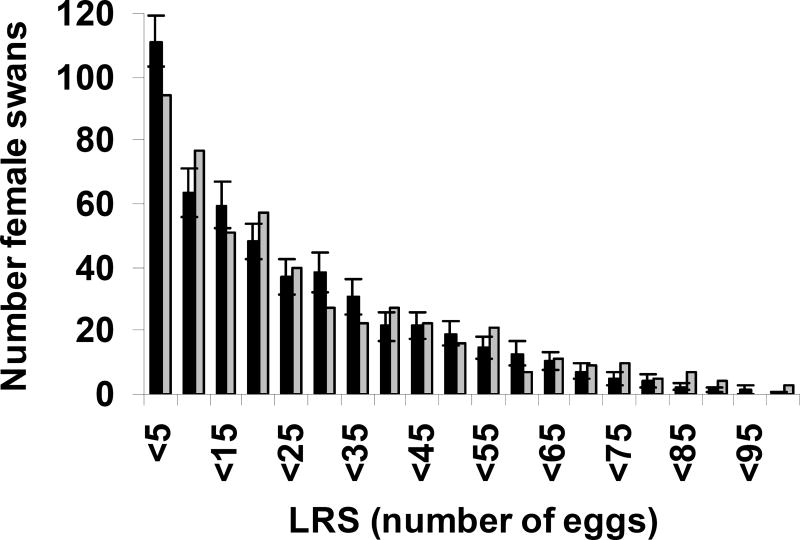
In order to assess the influence of stochastic sampling variability on the expected LRS distribution generated by dynamical heterogeneity, we generate 50 synthetic cohorts using this algorithm and calculate the average LRS distribution (the standard errors generated in this way are shown in Figure 5). This distribution for the Swans is shown in Figure 5; a Kolmogorov-Smirnov test indicates that cumulative distribution functions of the observed and predicted distributions are not significantly different from one another at the 0.05 level (Orzack et al. 2008a, submitted). We have found similar results for a number of other species (Orzack et al. 2008b, submitted).

Fig. 5.

Distribution of Lifetime Reproductive Success (LRS) for female Mute Swans. The observed distribution is shown by grey bars and the average distribution for 50 simulated synthetic populations is shown by black bars (± standard error). Synthetic populations exclude any fixed heterogeneity.

Old-age Mortality and Plateaus

There has been substantial recent interest in late-age "plateaus" of mortality rates in various species (Carey and Tuljapurkar 2003). In typical examples, a cohort’s mortality rate increases at young ages but the rate of increase eventually decreases to zero. One well-known hypothesis explaining such plateaus is that they result from intracohort selection operating on fixed frailty differences (Vaupel & Yashin 1985). However, even when there are no frailty differences a mortality plateau can arise when stage-specific survival is independent of age (Horvitz & Tuljapurkar 2008). To understand why, suppose we follow individuals in a large cohort starting at birth. As the cohort ages, the distribution of survivors over stages becomes nearly stable at older ages and the cohort’s average mortality becomes constant. In other words, a mortality plateau emerges so that population average survivorship eventually decreases at a constant rate

$$\frac{1}{a}\text{log }\overline{l_a}\to \text{log }{P}^{\ast }.$$ (6)

At the mortality plateau a cohort has constant average survival rate P*. This plateau is generated by reproductive trajectories that are both probable (i.e., have a high ν(ω)) and have relatively high survivorship (i.e., have a high l_a(a)). These need not be the trajectories that yield the highest survivorship. For example, in our equation (1) the highest possible survivorship occurs on a trajectory ω = (1, 3, 3,…, 3,…) but this ω has a low probability unless the entropy H is very small.

Such plateaus generated by dynamic heterogeneity are very different from plateaus generated by fixed heterogeneity. Consider a population with no dynamic heterogeneity in which newborns are either frail or robust, and that frail individuals have a mature survival rate P₂ whereas robust individuals have mature survival rate P₃ > P₂. As a cohort of such individuals ages, the population average survival rate will converge to a plateau at the value P₃. In contrast, in our model (1), there is no fixed frailty and dynamic heterogeneity produces a plateau in survival rates at a value P* which depends on P₂,P₃,ψ₂₂, and ψ₃₃. For example, suppose that P₂ ≫ P₃ and ψ₂₃ ≪ 1,ψ₂₂ ≪ 1, and that every individual first reaches maturity in stage 2. Every cohort will start out in low mortality stage 2 but in later years a large fraction of cohort survivors will be in high mortality stage 3. Thus the average late-life mortality will be dominated by the high mortality in stage 3. Under such conditions, dynamic heterogeneity can generate a late-age plateau at which mortality is higher than during most of life, as is the case for medflies and possibly for humans (Carey and Tuljapurkar 2003).

As a practical matter, a mortality plateau, however generated, is relevant only if a meaningful fraction of individuals reach the age at which the plateau appears. Mortality plateaus in medflies have been detected only through observation of very large cohorts. When mortality rates for all individuals increase steadily with age for all stages (or latent traits), neither fixed nor dynamic heterogeneity will generate a mortality plateau.

Dynamic Heterogeneity as a Neutral Model

Dynamical heterogeneity can provide a "neutral" standard by which one can assess whether the observed distribution of fitness components, such as the LRS or average annual reproduction, are influenced by certain kinds of fixed heterogeneity. In particular, a lack of fit between an observed distribution of, say, the LRS and a distribution generated solely by dynamic heterogeneity suggests that the observed distribution is influenced by fixed differences among individuals.

For example, an unobserved trait may cause some individuals to have lower expected survival in all strata as compared to other individuals who have a different value of the trait. Intra-population selection will benefit the latter individuals and likely increase the variance of the distribution of LRS as compared to the variance generated only by dynamic heterogeneity (since more individuals will likely have relatively low or high LRS). A similar argument applies if individuals differ in a latent factor that influences the probabilities to enter or leave stages with high breeding success. As shown in Fig. 5 and discussed above, we find a reasonable fit between simulations and data for Mute Swans, a result which suggests that fixed heterogeneity in survival or reproduction has little effect on the variation in LRS between females.

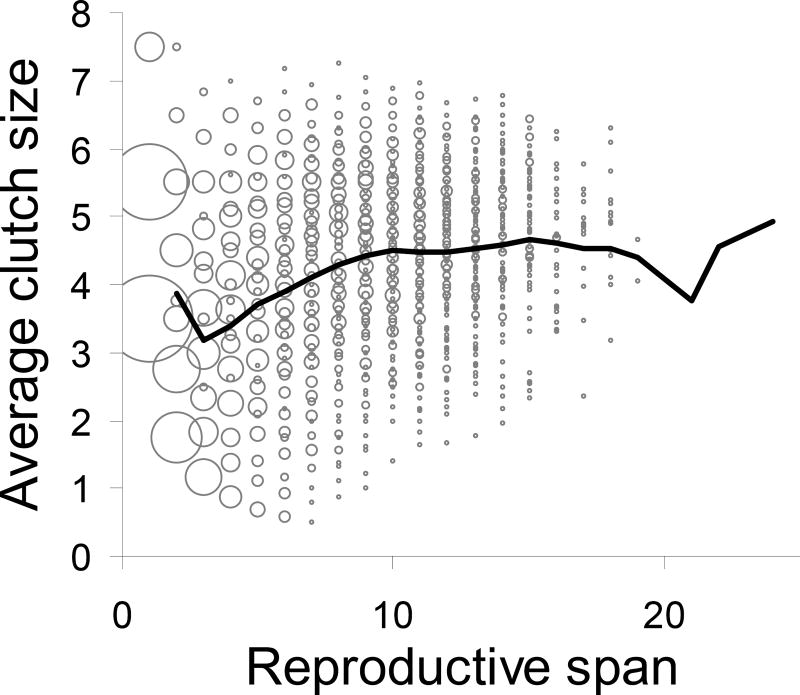
Multi-stage models can also be used as neutral models for fitness components other than the LRS, such as age at death, reproductive span, or average annual reproductive output. Suppose we find an association between the length of an individual’s breeding span and average annual reproduction during that span. One possible explanation is that fixed “quality” differences between individuals affect fitness components; a random-effects model fitted to the data would provide an estimate of these differences. But such variation is not the only possible cause for the observed association. Fig. 6 shows the distribution for Mute Swans of average annual clutch size versus reproductive span from simulations generated purely by dynamic heterogeneity based on our estimated models. There is considerable variance at each reproductive span and across spans. The average relationship, indicated by the solid line, yields a positive correlation between average annual clutch size and reproductive span. A statistical model for a sample of these individuals would yield an estimate of “quality” differences in average annual clutch size and reproductive span. But the variation in Fig 6 is entirely due to dynamic heterogeneity and does not provide evidence of fixed quality differences between individuals.

Fig. 6.

Reproductive span versus average clutch size during the reproductive span for 1000 simulated Mute Swans. Reproductive span is defined as the number of years between the ages of first and last reproduction. The thick black line shows the average clutch size by reproductive span across individuals. The size of the grey circle at a point denotes the number of individuals at the point.

Life Histories as Dynamic Processes

The concept of dynamic heterogeneity leads to new insights into life history evolution. The traditional focus on life history evolution concerns the age-pattern of reproduction and survival and how natural selection determines the levels of these traits and their age-pattern. But as shown in the examples discussed here, the same individual can have very different reproductive success at different ages. For such life histories, the traits of interest are the transition probabilities between stages and the dependence of mortality on stage. These, rather than the age-pattern and levels of vital rates, are the targets of natural selection and the phenotypes whose evolution we must understand. To do so requires theory and data analytic tools that we discuss in this closing section.

Studying Fitness and Selection

How do we define fitness for the dynamic life histories we have discussed? We can write a generalized version of Lotka’s equation for multi-stage models in the form,

$$1=E\{\sum _{a=1}^{a=T}{F}_a(\omega )e^{-\mathit{\text{ra}}}\}.$$ (7)

Here r is the rate of increase, the average E is over the distribution ν(ω) of reproductive trajectories, and T is age at death. When all individuals follow the same trajectory, equation (7) reduces to Lotka’s equation for the population. If we leave out the exponential factor in (7), then for each ω and T, the sum on the right of (7) is lifetime reproductive success (LRS). If we leave out the expectation in (7), the resulting solution r is an “individual” fitness for a given ω and T (Caswell 2001, Link et al. 2002).

When there is no explicit age-dependence in transition rates and in mortality and fertility rates, the multi-stage models here reduce to stage-structured models of the kind that has been widely used to study plants, invertebrates and some vertebrates (Lefkovitch 1965). Standard results for the latter models (Caswell 2001) show that the dynamics of a population of individuals governed by a multi-stage model without explicit age-dependence are given by a matrix recursion equation involving a population projection matrix. The fitness r in equation (7) is precisely equal to the logarithm of the dominant eigenvalue of this projection matrix. For the transition matrix in our example (1) this projection matrix is

$$\left(\begin{array}{ccc}\hfill P_1{\psi }_{11}\hfill & \hfill F_2\hfill & \hfill F_3\hfill \\ \hfill P_1{\psi }_{12}\hfill & \hfill P_2{\psi }_{22}\hfill & \hfill P_3{\psi }_{32}\hfill \\ \hfill P_1{\psi }_{13}\hfill & \hfill P_2{\psi }_{23}\hfill & \hfill P_3{\psi }_{33}\hfill \end{array}\right).$$ (8)

Caswell (2001) also shows how to compute the expected lifetime T̅ and the total variance in age at death using a related matrix analysis.

The elements of the matrix (8) show that dynamic heterogeneity is a determinant of evolutionary success. It is not just demographic noise. If the transition matrix (1) changes, so does the population projection matrix (8), and hence so must the rate of increase. Sensitivity analysis of r with respect to changes in the transition probabilities and other vital rates (Caswell 2001) can be used to explore the relationship between fitness and dynamic heterogeneity, and to generate or test hypotheses about the evolution of dynamic life histories. In small populations, demographic stochasticity adds to the variability generated by dynamic heterogeneity, and this additional variation can be analyzed using multi-type branching processes (Caswell 2001). Generalizations of equation (7) and (8) to include age-specific variation in addition to stage-specific variation can be based on multi-stage demography (Houllier & Lebreton 1986; Lebreton 1996, 2005).

The correspondence between multi-stage CMR models and stage-structured models reveals a clear parallel between the life histories of animals and plants. Both kinds of organisms can display stochastic dynamic heterogeneity, even though some of the biological processes driving stochastic transitions in these two classes of life history are different.

A traditional theoretical approach treats life histories in terms of “decisions” about energy allocation and behavior, subject to constraints, with optimal decisions leading to optimal life histories. In the presence of dynamic heterogeneity, such “decisions” are sequential stochastic choices and an optimal life history is a stochastic process. Optimization in life-history models incorporating dynamic heterogeneity can be analyzed using methods developed to study behavioral optimization (McNamara & Houston 1996). In dynamic life history models, we may also need to consider the effects of environmental variability and physiology as drivers of stage transitions. These may act sequentially, e.g., the environment in one year may affect energy expenditures, inputs, and storage, and thus constrain energy allocations in the following year. Dynamic energy budget methods (Kooijmans 2000) will be a suitable framework for studying such matters.

Extending Multi-Stage Models

Several potentially important influences on a species’ demography are not captured by the simple multi-stage models we describe here. One is duration dependence, e.g., survival rate and possibly fertility of a life history stage may depend on the amount of time an individual spends in that stage. Finite durations are easily accommodated by expanding the definition of stages to include both stage and time-in-stage (Hestbeck et al. 2002, Brownie et al. 1993). Such models will typically have a higher dimensionality than the models discussed here, but will have similar features. Models for duration-dependence fit more naturally into a semi-Markov framework (Huzurbazar 2004); the relevant theory especially for mortality plateaus and growth rates needs to be developed. Another direction is to expand the definition of stages by moving from discrete stages to continuous stages, say for size or mass; integral population models (IPMs) (Ellner & Rees 2006) provide a natural extension of our discrete stage models. Other needed developments include the incorporation of variable environments, and further analysis of age-and-stage dependent models.

Dynamic and Fixed Heterogeneity

The biological implications of dynamic heterogeneity differ from those of fixed heterogeneity. Perhaps most real populations are influenced by both kinds of heterogeneity. It will be worth exploring the evolution of fixed observable (or even latent) traits that influence the transition probabilities Ψ, survival, and fertility. We can examine the effects of such fixed traits on fitness using sensitivity analysis of the matrix in equation (8); the dynamics of a distribution of fixed heterogeneity can be followed using a mixture of these matrices. A useful further step would be to develop a quantitative genetic theory of life history evolution that develops for stage-structured populations an extension of existing theory for age-structure (Lande 1982, Charlesworth 1993).

Further progress in the analysis of CMR data is also needed so as to allow us to jointly analyze the contributions of fixed heterogeneity (via individual random effects), dynamic heterogeneity (via models of stage transitions), age-specific effects on life history components, and the effects of temporal variability (as opposed to secular trends) (compare with Gimenez et al. 2007). A joint model would allow us to test whether there are individual random effects in transitions, survival, or reproduction, and would also quantify the relative significance of fixed and dynamic heterogeneity. A related issue is the difficulty of discriminating between and testing complex models, often when relatively limited data are available. It should be helpful to develop tools that supplement the standard methods (Lebreton et al. 1992) with methods based on randomization and simulation that are effective on small samples.

A final point concerns alternative ways to characterize dynamic heterogeneity. We focus on the underlying Markov process because it is the generating process from which we can deduce and analyze the distribution of individual fitness components. But it would be useful to also characterize the distribution of survival-weighted trajectories. One approach would be to compute the entropy of the stage distribution of a cohort as a function of age. As the cohort ages, this stage distribution will converge to a quasi-stationary distribution and so the entropy of that distribution will also converge. Another option would be to do the kind of analysis that we have done with Ψ, but instead to work with probabilities of stage transitions conditional on non-absorption. The latter can be approximately described by a transformed version of a submatrix of the projection matrix (8), as discussed by Matthews (1970). We will explore these possibilities in future work.

Conclusions

We find that CMR studies naturally motivate a dynamic picture of life histories, in which individuals change their reproductive strata and mortality many times during their lives. Dynamic heterogeneity is observable and easily characterized, has a direct effect on individual fitness components (age at death, Lifetime Reproductive Success), and is a determinant of overall fitness. We have shown that residence in reproductive strata is ephemeral in a variety of species, that there is substantial diversity in reproductive trajectories in many species, and that senescent mortality is an average over distinct stages in a life history. Using the methods we have presented, CMR studies can play an important role in investigations of the character of trade-offs between survival and reproduction and the extent and kind of senescence of natural populations. Vindenes et al. (2008) have recently discussed some effects of demographic heterogeneity that complement our discussion here. The further study of dynamic heterogeneity should lead to unprecedented advances in our view of the structure and evolution of life histories.

Table 3.

Measuring Dynamic Heterogeneity through Ψ

Quantity	Definition
Stationary distribution	π = (πi),π′ = π′Ψ (prime indicates transpose)
Entropy	$H=-{\sum }_{i=1}^K{\sum }_{j=1}^K{\pi }_i{\psi }_{\mathit{\text{ij}}}\text{ log }{\psi }_{\mathit{\text{ij}}}$ (with 0 log(0) = 0)
Subdominant Eigenvalue	λ1 ≠ 1, solves det(λI − Ψ) = 0
Correlation Time	τ = −1/(log λ1)
Expected time to leave stage	For stage i, t̄i = 1/(1 − ψii)