The role of negative conductances in neuronal subthreshold properties and synaptic integration

Abstract

Based on passive cable theory, an increase in membrane conductance produces a decrease in the membrane time constant and input resistance. Unlike the classical leak currents, voltage-dependent currents have a nonlinear behavior which can create regions of negative conductance, despite the increase in membrane conductance (permeability). This negative conductance opposes the effects of the passive membrane conductance on the membrane input resistance and time constant, increasing their values and thereby substantially affecting the amplitude and time course of postsynaptic potentials at the voltage range of the negative conductance. This paradoxical effect has been described for three types of voltage-dependent inward currents: persistent sodium currents, L- and T-type calcium currents and ligand-gated glutamatergic N-methyl-D-aspartate currents. In this review, we describe the impact of the creation of a negative conductance region by these currents on neuronal membrane properties and synaptic integration. We also discuss recent contributions of the quasi-active cable approximation, an extension of the passive cable theory that includes voltage-dependent currents, and its effects on neuronal subthreshold properties.

What is a negative slope conductance?

Ion channels are considered to be biological conductors in the neuronal membrane. By definition, the conductance of a single channel is positive following the linear Ohm’s law. According to the passive cable model of the biological membrane, the opening of the channels increases ionic permeability and decreases membrane resistance (R _m) and the time constant (τ _m). Each neuronal type has a distinct membrane resistance which affects its excitability, integrative and temporal properties. Potassium background leak channels are considered to be the classical determinants of R _m (Enyedi and Czirják 2010). For example, in a heterogeneous neuronal population, membrane input resistance, action potential latency and threshold are inversely correlated with the expression of potassium leak currents (Dagostin et al. 2015). It is also well known that volatile anesthetics decrease membrane excitability by opening neuronal potassium leak channels (Ries and Puil 1999).

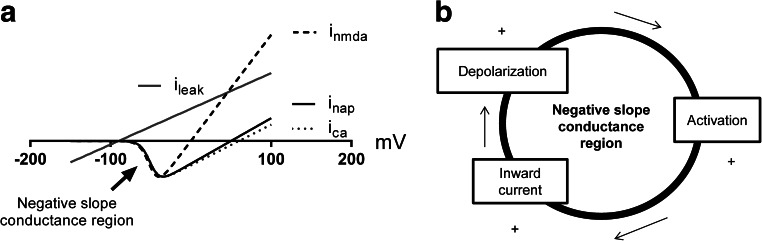
Ohmic leak currents have a linear current–voltage relationship (the I–V curve), producing a positive slope conductance (Fig. 1). However, voltage-gated channels present nonlinear I–V relationships and under certain circumstances can create regions of negative slope conductance by a positive feedback between a change of the membrane potential and the activation variables (Hutcheon and Yarom 2000; Izhikevich 2007; Remme and Rinzel 2011). In terms of current behavior, a negative slope conductance means that an inward current increases its magnitude with depolarization or that an outward current increases its magnitude with hyperpolarization. In the case of inward currents, a negative slope conductance region is created when the current is activated by depolarization which leads to a positive feedback between the activation and the amplitude of the current through a regenerative mechanism. The activation phase of the voltage-gated sodium and calcium currents are typical examples of regions of negative slope conductances (Fig. 1).

Fig. 1.

a Current–voltage characteristic (I–V curves) of the persistent sodium current (I _nap), calcium current (I _ca), N-methyl-D-aspartate current (I _nmda) and leak current (I _leak), and negative slope conductance region (arrow). b Positive feedback between depolarization and the activation variable that increases the inward currents regeneratively and creates the negative slope conductance region

However, what is exactly a negative slope conductance? The infinitesimal or differential definition of the membrane conductance in the steady state is G _m = dI/dV _ss, where V _ss is the steady-state membrane potential. This definition is also commonly known as the slope conductance, since it corresponds to the slope of the steady-state I–V plot (Johnston and Wu 1994). The slope conductance at the steady state of a voltage-dependent current I _v = g(V, t)(V − E _rev) is obtained by differentiating its current equation, G = dI _v/dV _ss =  g ^chord + G ^Der, where g ^chord is the so-called chord conductance, and G ^Der = (V − E _rev)(dg/dV) is the so-called derivative conductance. Interestingly, g ^chord is always positive, whereas G ^Der can be positive or negative, and when G ^Der is negative and larger than g ^chord the slope conductance is negative (Koch 1998; Wessel et al. 1999). The membrane conductance G _m of a membrane that contains linear ionic currents (I_L) and voltage-dependent ionic currents (I_V) is obtained by differentiating the sum of the currents G _m =  ∑ G _V +  ∑ g _L where G _V is the slope conductance of the voltage-dependent currents and g _L is the conductance of the linear currents. The inverse of the membrane conductance is the slope resistance, or membrane resistance $R_m=\frac{1}{G_m}$. In practical terms the R _m is also referred as input resistance (R _in) which is the sum of the membrane resistance R _m and the series resistance R _s of the electrode.

The basic concepts and mathematical analysis of the chord conductance and the slope conductance of voltage-dependent currents have been well described elsewhere (Finkelstein and Mauro 2011; Johnston and Wu 1994; Koch 1998). However, only recently have explicit equations been developed for the slope conductance of voltage-dependent currents. These equations use the Hodgkin–Huxley Formalism to describe currents and the Boltzmann equation to describe activation and inactivation kinetics (Ghigliazza and Holmes 2004; Remme and Rinzel 2011). This has allowed the possibility of an analytically tractable approach to study the effects of the negative slope conductance.

Remme and Rinzel (2011) studied the effects of a persistent sodium current (I_NaP) on synaptic inputs propagating through dendritic cables using the so-called quasi-active description of cables, an extension of the classical passive cable theory. This approach relies on linearizing voltage-dependent cable conductances around the membrane potential V _R. The method was first employed by Sabah and Leibovic (1969) and further worked on by Koch (1984), and it elucidates certain general principles of quasi-active cables. This approach allowed classifying I_NaP as a regenerative current, which produces a positive feedback and amplifies membrane potential changes, boosting and broadening excitatory postsynaptic potentials (EPSPs). The effectiveness of I_NaP in modulating the shape of EPSPs is determined by the activation time constant: the faster the activation time constant, the stronger its effect on EPSP amplitude (Ceballos et al. 2017). These effects are controlled by a single dimensionless parameter μ.

$$\mu \equiv \gamma \left(V_R-E_{\mathit{rev}}\right)\frac{\partial s^{\infty }\left(V_R\right)}{\partial V},$$

where V _R is the membrane potential around linearization, s ^∞ is the activation variable in the steady state, γ is the ratio of the maximal conductance of the current to the leak conductance and the partial derivative conveys the slope of the activation curve at V _R. The parameter μ denotes the strength of the positive feedback provided by I_NaP. The central parameters that qualitatively determine the effects of I_NaP on EPSP shape are the current-type μ, the activation time constant τ _act and the relative current density γ. The parameter μ is negative for regenerative or amplifying currents, such as the persistent sodium current, which is activated by depolarization (i.e. the partial derivative is positive) and has a depolarized reversal potential (relative to V _R) (Goldberg et al. 2007). These currents are called amplifying currents due to the amplified response in the low frequencies relative to the passive cable (Hutcheon and Yarom 2000). It is important to note that regenerative currents can be either inward or outward currents; for example, positive feedback results from both an inward current that activates or an outward current that deactivates upon depolarization.

The activation time constant of the amplifying current is central in determining the degree to which this current affects the shape of the EPSP. For example, a relatively slow current (τ _act> > τ _m) is not able to react to voltage transients and simply acts as a passive current on the time scale of an EPSP, attenuating and narrowing the EPSPs. The effect of a slowly gated active current on the EPSP shape is caused by its contribution to the chord conductance, since τ _act is typically too slow for its dynamics (characterized by the parameter μ) to significantly affect the shape of a single EPSP. In contrast, a very fast current (τ _act < <τ _m) varies continuously in steady state with the voltage and will therefore effectively act via its negative slope conductance (Ceballos et al. 2017; Remme and Rinzel 2011). A disadvantage of the linear approximation is that it is only valid for small voltage changes; the larger the voltage changes, the more the linearized system will deviate from the nonlinear system. Therefore, in principle this approach is well suited for small EPSPs.

Electrical impedance of neurons characterizes their voltage response to sinusoidal current inputs with varying frequency. Impedance is the frequency-domain extension of the concept of resistance and links the amplitudes and phases of the output/input oscillatory signals (Hutcheon and Yarom 2000). Using the quasi-active cable approximation, Káli and Zemankovics (2012) recently derived an explicit mathematical expression for the somatic membrane impedance of a model neuron consisting of a somatic compartment coupled to an infinite dendritic cable with voltage-gated conductances. These authors conceptualized all voltage-gated conductances as parallel impedances in the cell membrane. Since the negative slope conductance of the regenerative inward currents represents negative admittance, the final result of the inclusion of this kind of current into the model neuron is a net increase in the total impedance. As expected, their study predicted a significant contribution from I_NaP in amplifying the impedance profile of CA1 pyramidal neurons. The effect of amplifying currents, mainly I_NaP, and their effects on the impedance profiles of simple neuron models have been studied in several other theoretical and computational works (Richardson et al. 2003; Rotstein 2015, 2016; Rotstein and Nadim 2014).

Interestingly, the parameter μ is also central in these works and determines the contribution of the voltage-gated conductances to the impedance profile. Furthermore, τ _act is an explicit term of the impedance equation that divides the parameter μ: thus, the bigger the τ _act, the smaller the effect of μ on the impedance. Making a parallel between the parameter μ obtained using quasi-active cable approximation and the mathematical description of the slope conductance obtained by differentiating the current equation as in Koch (1998), one can say that the parameter μ and the derivative conductance are equivalent (Moore et al. 1995). Recently, Ceballos et al. (2017) were able to measure experimentally the derivative conductance of the I_NaP, suggesting that it is possible to test these theories experimentally.

Negative slope conductances increase the membrane resistance, time constant and impedance

The concept of negative slope conductance creates an interesting paradox. If a neuron depolarizes and activates voltage-dependent inward conductances, which creates a region of negative slope conductance, would R _m and τ _m decrease, as expected by an increased ionic conductance (i.e. permeability), or they would increase by the negative slope conductance? Early observations (Hirsch and Oertel 1988; Stafstrom et al. 1982) related the presence of a negative slope conductance created by I_NaP with an increase in R _m. Other studies found that activation of glutamatergic N-methyl-D-aspartate (NMDA) currents (I_NMDA) induced a region of negative slope conductance with an increased R _m (Crunelli and Mayer 1984; MacDonald et al. 1982). Later studies showed that I_NaP can be activated during a single EPSP, slowing its decay phase (Hirsch and Oertel 1988; Stafstrom et al. 1985). Thomson et al. (1988) showed that the amplitude and duration of EPSPs are voltage dependent and that depolarization of the membrane potential to values close to the action potential threshold amplifies the EPSP amplitude and prolongs its decay phase. It was subsequently established that these effects are mediated mainly by I_NaP (Andreasen and Lambert 1999; Deisz et al. 1991; Lipowsky et al. 1996; Schwindt and Crill 1995; Stuart and Sakmann 1995; Urban et al. 1998). Voltage-dependent calcium currents (I_Ca) can similarly produce these effects (Gillessen and Alzheimer 1997). These three currents (I_NaP, I_Ca and I_NMDA) are generally accepted to be amplifying currents that increase R _m and amplify EPSPs by their negative slope conductances at subthreshold voltages (MacDonald et al. 1982; Putzier et al. 2009; Stafstrom et al. 1982) (Fig. 1).

It has been observed in several types of neurons that R _m and τ _m increase in a voltage-dependent manner and that this effect is abolished by tetrodotoxin (TTX) application (Agrawal et al. 2001; Curti et al. 2008; Economo et al. 2014; Fernandez et al. 2015; Hirsch and Oertel 1988; Klink and Alonso 1993; Stafstrom et al. 1982; Yamada-Hanff and Bean 2015). The authors of these studies suggested that the negative slope conductance region generated by I_NaP caused this paradoxical increase in R _m. Recently, Yamada-Hanff and Bean (2015) have shown, in hippocampal pyramidal cells, that I_NaP activation increases R _m and τ_m simultaneously, whereas I_h, which does not produce a negative slope conductance region, decreases both R _m and τ _m. The increase or decrease of these parameters matches with regions of negative and positive slope conductance of the I–V curves, respectively. Similar results were obtained by Hirsch and Oertel (1988) in fusiform cells of the dorsal cochlear nucleus of mice where a TTX-sensitive increase in R _m with depolarization was observed. These authors also observed a concomitant decrease in R _m and τ _m with hyperpolarization, in parallel with the deactivation of I_NaP which is present in these neurons (Leao et al. 2012).

Activation of NMDA receptors can also produce an increase in R _m. A pioneering study by MacDonald et al. (1982) showed that L-aspartic acid induced a region of negative slope conductance in cultured spinal cord neurons concomitantly with an increased in R _m. In accordance with the negative conductance hypothesis, Crunelli and Mayer (1984) observed that in the absence of Mg²⁺, which abolishes NMDA-receptor current outward rectification, the depolarizing response to NMDA was accompanied by a decrease in R _m, but that in the presence of Mg²⁺ the response to NMDA was accompanied by an increase in R _m. Later, Moore et al. (1994) observed that the increase in R _m after the application of the glutamate agonist NMDA was voltage dependent and that the Mg²⁺ block of NMDA channels at the hyperpolarized membrane potential produced this voltage dependency. All of this evidence suggests that the anomalous R _m increase observed during the activation of NMDA receptors can be explained as a consequence of a negative slope conductance region.

Compelling evidence that the increase in R _m is the result of the negative slope conductance comes from the work of Fernandez et al. (2015). These authors injected artificial linear negative and positive conductance using a dynamic clamp in entorhinal stellate cells and observed that negative conductance increased R _m while a positive conductance decreased R _m, suggesting that is the negative slope conductance—and not the positive chord conductance—that determines R _in and τ _m (Ceballos et al. 2017). In a case like this, slope conductances (positive and negative) from each current (linear and voltage-dependent) are simply added up algebraically, and it is this sum that determines R _m and τ _m following a simple mathematical rule: R _m = 1/ΣG and τ _m = R _mC _m, (where C _m is membrane capacitance) (Buchanan et al. 1992; Moore et al. 1994; Yoshii et al. 1988). Thus, in the subthreshold region, the negative slope conductances of I_NaP and I_NMDA oppose the positive slope conductance of the leak current, which leads to a decrease in the total positive slope conductance and increases in both R _m and τ _m.

In order to increase R _m and τ _m, a critical feature for a current with a negative slope conductance is a fast activation (Ceballos et al. 2017; Manuel et al. 2007; Remme and Rinzel 2011). But how fast? In principle, the speed should be faster than the cell membrane time constant because the negative slope conductance is created proportionally to the rate of change of the conductance. Thus, an almost instantaneously activated current (current time constant <<τ _m) is able to reach its steady state so fast that it might be able to control R _m and τ _m by its steady state slope conductance. Since I_NaP has the fastest activation of all the voltage-activated inward currents (τ_act ≈ 250 μs; Carter et al. 2012), we speculate that the effect of I_NaP on R _m and τ _m is more powerful than that of the other currents.

It has been observed that I_NaP increases the impedance of neurons (Boehlen et al. 2012; Curti et al. 2008; Economo et al. 2014; Gutfreund and Segev 1995; Hu et al. 2002; Hutcheon et al. 1996a; Hutcheon et al. 1996b; Jacobson et al. 2005; Klink and Alonso 1997; Manuel et al. 2007; Pape and Driesang 1998; Saint Mleux and Moore 2000; Sun et al. 2014; Wu et al. 2001; Wu et al. 2005; Yang et al. 2009; Yaron-Jakoubovitch et al. 2008). This increase in the membrane impedance is thus a function of membrane voltage, increasing as the neuron is depolarized towards the spike threshold. Buchanan et al. (1992) showed that the activation of I_NaP causes an impedance increase that leads directly to an amplification of the EPSPs. Other studies have also reported that Ca⁺⁺ currents amplify the neuronal membrane impedance (Manuel et al. 2007; Matsumoto-Makidono et al. 2016; Saint Mleux and Moore 2000). Theoretical modeling has also shown that I_Ca has an amplifying effect on neuronal impedance (Ghaffari et al. 2015). Finally, there are some reports showing that NMDA currents increase the impedance in neurons (Moore et al. 1994, 1995, 1999) due to negative slope conductance.

Summarizing, the main effect of the negative slope conductance on neuronal impedance is to increase it. One the most important consequences of increases in R _m, τ _m and impedance is the amplification of synaptic inputs, i.e. their amplitude is increased and the decay phase is prolonged. This will be discussed in depth in the following section.

Negative slope conductance amplifies postsynaptic potentials

It is known that the amplitude and duration of EPSPs are voltage dependent and that depolarization of the membrane potential to values close to action potential threshold amplifies the EPSP amplitude and prolongs its decay phase (Deisz et al. 1991; Thomson et al. 1988; Zsiros and Hestrin 2005). Experiments using sodium and calcium blockers in the perfusion bath could be performed in order to determine whether these postsynaptic conductances are responsible for this effect, but since these blockers also impair glutamate release by the presynaptic fiber it is complicated to assess their effect on the EPSPs. Several approaches have been considered to circumvent this limitation, such as the injection of artificial EPSCs directly into the postsynaptic neuron (Stuart and Sakmann 1995; Ceballos et al. 2017), local application of sodium or calcium blockers to the postsynaptic neuron (González-Burgos and Barrionuevo 2001; Stuart and Sakmann 1995) and the use of intracellular sodium channel blockers, such as QX 314 (Deisz et al. 1991; González-Burgos and Barrionuevo 2001). Recently, more advanced techniques have been used, such as glutamate uncaging (Carter et al. 2012; Liu and Shipley 2008) or knockout animals of Na_v channels (Branco et al. 2016). Additional strategies, such as canceling the endogenous I_NaP or applying an artificial I_NaP with dynamic clamp (Ceballos et al. 2017; Vervaeke et al. 2006), have also been employed to analyze the effects of this conductance on the EPSPs.

The amplification of EPSPs by I_NaP has been extensively observed in neurons from the neocortex (Andreasen and Lambert 1999; Carter et al. 2012; Deisz et al. 1991; Fricker and Miles 2000; González-Burgos and Barrionuevo 2001; Hirsch and Gilbert 1991; Lipowsky et al. 1996; Rotaru et al. 2007; Schwindt and Crill 1995; Stafstrom et al. 1985; Stuart and Sakmann 1995; Thomson et al. 1988; Zsiros and Hestrin 2005), hippocampus (Ceballos et al. 2017; Urban et al. 1998; Vervaeke et al. 2006), entorhinal cortex (Economo et al. 2014; Rosenkranz and Johnston 2007), dorsal cochlear nucleus (Hirsch and Oertel 1988), subthalamic nucleus (Farries et al. 2010), hypothalamus (Branco et al. 2016), olfactory bulb (Liu and Shipley 2008), dorsal horn of the spinal cord (Prescott and De Koninck 2005), medial superior olive (Scott et al. 2010) and substantia nigra pars compacta (Yamashita and Isa 2004). In most of these experiments, blocking I_NaP with TTX abolished the voltage dependence of the EPSP amplitude and area.

The mechanism for the amplification of the EPSP amplitude is attributed to the almost instantaneous activation of I_NaP, which boosts depolarization and increases R _m by its negative slope conductance (Ceballos et al. 2017). EPSP amplification was observed upon the injection of both an artificial I_NaP or a linear negative conductance after TTX application, using the dynamic clamp method (Ceballos et al. 2017; Economo et al. 2014). Further evidence supporting the hypothesis that the negative slope conductance of I_NaP prolongs EPSP decay is provided by the recently proposed quasi-active cable theory approximation (Remme and Rinzel 2011). Moreover, Zsiros and Hestrin (2005) showed that injecting a positive conductance shortens the prolongation of the EPSP decay enhanced by I_NaP.

Pharmacological blockage of calcium currents also decreases the voltage dependence of the amplitude and area of EPSPs (Connelly et al. 2016; Gillessen and Alzheimer 1997; Liu and Shipley 2008; Prescott and De Koninck 2005; Urban et al. 1998). Amplification of EPSP by calcium currents seems to be mediated mostly by T-type Ca²⁺ currents rather than by L-type Ca²⁺ currents (Liu and Shipley 2008). In addition, calcium currents tend to prolong EPSP decay rather than amplify EPSP amplitude (Prescott and De Koninck 2005).

On the other hand, the negative slope conductance of NMDA currents has very small effect on EPSP amplitude and decay in neocortical neurons. Blocking NMDA currents with AP5 did not affect substantially the EPSP (Deisz et al. 1991; González-Burgos and Barrionuevo 2001; Hirsch and Gilbert 1991; Stuart and Sakmann 1995; Thomson et al. 1988). However, the effect of NMDA currents in some other areas appears to be more significant. For example, Fricker and Miles (2000) showed a decrease in EPSP area when blocked by AP5 in hippocampal pyramidal cells, and Connelly et al. (2016) showed strong EPSP amplification by NMDA currents in thalamocortical neurons. In addition, Porres et al. (2011) observed an EPSP decay phase prolongation in neurons of the dorsal nucleus of the lateral lemniscus caused by NMDA currents.

Interestingly, regenerative inward currents also amplify inhibitory postsynaptic potentials (IPSPs). For example, I_NaP amplifies IPSPs in neocortical pyramidal neurons (Stuart 1999; Williams and Stuart 2003), hippocampal pyramidal neurons (Hardie and Pearce 2006) and stellate cells of the medial entorhinal cortex (Economo et al. 2014). Ca⁺⁺ currents also amplify IPSPs in cat motoneurons (Bui et al. 2008). These observations suggest that a negative slope conductance amplifies the voltage changes independently of the direction of the membrane potential change, i.e. amplifies both depolarization and hyperpolarization of the membrane.

Reinforcing that negative slope conductance creates amplification of EPSPs, the activation of I_h, which is an inward depolarizing current activated by hyperpolarization, decreases the amplitude of EPSPs and reduces their decay time (Magee 1998), similar to the effect of some outward potassium currents (Hoffman et al. 1997; Mathews et al. 2010). In addition, the inwardly rectifying potassium current, an outward potassium current that has a negative slope conductance region in depolarized potentials, amplifies hyperpolarizations in endothelial cells (Jackson 2016), striatal cholinergic interneurons (Wilson 2005) and vascular smooth muscles (Smith et al. 2008), and also amplifies EPSPs in the AP cell of the leech (Wessel et al. 1999). All of these observations together suggest that the amplification of membrane voltage changes is caused by negative slope conductance rather than by current amplitude.

One interesting consequence of the EPSP prolongation by I_NaP is the near-perfect synaptic integration (i.e. the opposite of ideal coincidence detection) that has been observed in different brain regions and which is physiologically relevant since it enhances temporal summation (Prescott and De Koninck 2005). Farries et al. (2010) showed in neurons of the subthalamic nucleus that negative slope conductance of I_NaP can oppose the positive slope conductance produced by other subthreshold currents, creating a wide region with zero slope conductance which establishes an infinite time constant and strongly reduces the decay phase of EPSPs. Moreover, Branco et al. (2016) showed that in hypothalamic neurons, the prolonged EPSPs produced by I_NaP are critical for the regulation of body weight.

Conclusion

We have reviewed the nature and physiological impact of the negative conductance created by inward voltage-dependent currents such as I_NaP, I_Ca and I_NMDA. Normally the effects of these currents on the membrane potential and neuronal excitability are attributed only to their depolarizing effects on the membrane potential, but it is clear that the dynamical effects they produce in membrane resistance and the time constant and in their activation potentials have a profound impact on neuronal synaptic integration in the subthreshold range.

Compliance with ethical standards

Conflicts of interest

All of the authors declare that they have no conflicts of interest.

Ethical approval

This article does not contain any studies with human participants or animals performed by any of the authors.