Robust recovery of complex exponential signals from random Gaussian projections via low rank Hankel matrix reconstruction

Abstract

This paper explores robust recovery of a superposition of R distinct complex exponential functions with or without damping factors from a few random Gaussian projections. We assume that the signal of interest is of 2N − 1 dimensions and R < 2N − 1. This framework covers a large class of signals arising from real applications in biology, automation, imaging science, etc. To reconstruct such a signal, our algorithm is to seek a low-rank Hankel matrix of the signal by minimizing its nuclear norm subject to the consistency on the sampled data. Our theoretical results show that a robust recovery is possible as long as the number of projections exceeds O(Rln² N). No incoherence or separation condition is required in our proof. Our method can be applied to spectral compressed sensing where the signal of interest is a superposition of R complex sinusoids. Compared to existing results, our result here does not need any separation condition on the frequencies, while achieving better or comparable bounds on the number of measurements. Furthermore, our method provides theoretical guidance on how many samples are required in the state-of-the-art non-uniform sampling in NMR spectroscopy. The performance of our algorithm is further demonstrated by numerical experiments.

1. Introduction

Many practical problems involve signals that can be modeled or approximated by a superposition of a few complex exponential functions. In particular, if we choose the exponential function to be complex sinusoid, it covers signals in acceleration of medical imaging [16], analog-to-digital conversion [25], inverse scattering in seismic imaging [1], etc. Time domain signals in nuclear magnetic resonance (NMR) spectroscopy, that are widely used to analyze the compounds in chemistry and protein structures in biology, are another type of signals that can be modeled or approximated by a superposition of complex exponential functions [19]. How to recover those superpositions of complex exponential functions is of primary importance in those applications.

In this paper, we will consider how to recover those complex exponentials from linear measurements of their superposition. More specifically, let x̂ ∈ ℂ^{2N − 1} be a vector satisfying

$${\widehat{x}}_j=\sum _{k=1}^R{c}_k{z}_k^j,j=0,1,\dots ,2N-2,$$ (1)

where z_k ∈ ℂ, k = 1, …, R, are some unknown complex numbers. In other words, x̂ is a superposition of R exponential functions. We assume R < 2N − 1. When |z_k| = 1, k = 1, …, R, x̂ is a superposition of complex sinusoids. When z_k = e^−τ_ke^2πιf_k, k = 1, …, R, x̂ models the signal in NMR spectroscopy.

Since R < 2N − 1, the degree of freedom to determine x̂ is much less than the ambient dimension 2N − 1. Therefore, it is possible to recover x̂ from its under-sampling [3,5,8,12]. In particular, we consider to recover x̂ from its linear measurement

$$\mathit{b}=\mathit{A}\widehat{\mathit{x}},$$ (2)

where A ∈ ℂ^{M × (2N − 1)} with M < 2N − 1.

We will use a Hankel structure to reconstruct the signal of interest x̂. The Hankel structure originates from the matrix pencil method [15] for harmonic retrieval for complex sinusoid. The conventional matrix pencil method assumes fully observed x̂ as well as the model order R, which are both unknown here. Following the ideas of the matrix pencil method in [15] and enhanced matrix completion (EMaC) in [10], we construct a Hankel matrix based on signal x̂. More specifically, define the Hankel matrix Ĥ ∈ ℂ^N×N by

$${\widehat{\mathit{H}}}_{jk}={\widehat{\mathit{x}}}_{j+k},j,k=0,1,\dots ,N-1.$$ (3)

Throughout this paper, indices of all vectors and matrices start from 0, instead of 1 in conventional notations. It can be shown that Ĥ is a matrix with rank R. Instead of reconstructing x̂ directly, we reconstruct the rank-R Hankel matrix Ĥ, subject to the constraint that (2) is satisfied.

Low rank matrix recovery has been widely studied [2,5,6,20]. It is well known that minimizing the nuclear norm tends to lead to a solution of low-rank matrices. Therefore, a nuclear norm minimization problem subject to the constraint (2) is proposed. More specifically, for any given x ∈ ℂ^{2N − 1}, let H(x) ∈ ℂ^N×N be the Hankel matrix whose first row and last column is x, i.e., [H(x)]_jk = x_j+k. We propose to solve

$$\underset{\mathit{x}}{min}{\Vert \mathit{H}(\mathit{x})\Vert }_{\ast },\text{subject}\text{to}\mathit{Ax}=\mathit{b},$$ (4)

where ||·||_* is the nuclear norm function (the sum of all singular values), and A and b are from the linear measurement (2). When there is noise contained in the observation, i.e.,

$$\mathit{b}=\mathit{A}\widehat{\mathit{x}}+\mathit{\eta },$$

we solve

$$\underset{\mathit{x}}{min}{\Vert \mathit{H}(\mathit{x})\Vert }_{\ast },\text{subject}\text{to}{\Vert \mathit{Ax}-\mathit{b}\Vert }_2\le \delta ,$$ (5)

where δ = ||η||₂ is the noise level. The reconstruction of low-rank Hankel matrices via nuclear norm minimization were also proposed in [13] for system identification and realization.

An important theoretical question is how many measurements are required to get a robust reconstruction of Ĥ via (4) or (5). For a generic unstructured N × N matrix of rank R, standard theory [6,7,9,20] indicates that O(NR · poly(logN)) measurements are needed for a robust reconstruction by nuclear norm minimization. This result, however, is unacceptable here since the number of parameters of Ĥ is only 2N − 1 with the actual degrees of freedom R. The main contribution of this paper is then to prove that (4) and (5) give a robust recovery of Ĥ (hence x̂) as soon as the number of projections exceeds O(Rln² N) if we choose the linear operator A to be some scaled random Gaussian projections. This result is further extended to the robust reconstruction of low-rank Hankel or Toeplitz matrices from its few Gaussian random projections.

Our result can be applied to various signals of superposition of complex exponentials, including, but not limited to, signals of complex sinusoids and signals in accelerated NMR spectroscopy. When applied to complex sinusoids, our result here does not need any separation condition on the frequencies, while only requiring O(Rln² N) measurements instead of O(Rln⁴ N) in [10]. Furthermore, our theoretical result provides some guidance on how many samples to choose for the model proposed in [19] to recover NMR spectroscopy.

• Complex sinusoids. When |z_k| = 1 for k = 1, …, R, we must have z_k = e^2πιf_k for some frequency f_k. In this case, x̂ is a superposition of complex sinusoids, for example, in the analog-to-digital conversion of radio signals [25]. We often encounter the problem of signal recovery from compressed linear measurements of the superposition of complex sinusoids in various applications. For example, in compressed sensing of spectrally sparse bandlimited signals [25], the random demodulator obtains linear mixing measurements of spectrally sparse bandlimited signals through matching filters. We refer the reader to Sections III and IV of [25] for details. In array signal processing for Direction of Arrival (DoA) estimation of electromagnetic waves [26], the signals received at the antennas of the antenna array are a superposition of complex sinusoids with different frequencies. Suppose that the battery-powered antenna array aims to save energy in sending the measurements to the fusion center where the DoAs are calculated, the antenna array can send linear projections of the signals received across the antenna array. Moreover, if the antenna array is a non-uniform antenna array, the observations across the antenna array are also linear non-uniform compressive sampling of the uniform antenna array.

  The problem on recovering x̂ from its as few as possible linear measurements (2) may be solved using compressed sensing (CS) [8]. One can discretize the domain of frequencies f_k by a uniform grid. When the frequencies f_k indeed fall on the grid, x̂ is sparse in the discrete Fourier transform domain, and CS theory [8,12] suggests that it is possible to reconstruct x̂ from its very few samples via ℓ₁-norm minimization, provided that R ≪ 2N − 1. Nevertheless, the frequencies f_k in our setting usually do not exactly fall on a grid. The basis mismatch between the true parameters and the grid based on discretization degenerates the performance of conventional compressed sensing [11].

  To overcome this, the authors of [4,23] proposed to recover off-the-grid complex sinusoid frequencies using total variation minimization or atomic norm [9] minimization. They proved that the total variation minimization or atomic norm minimization can have a robust reconstruction of x̂ from a non-uniform sampling of very few entries of x̂, provided that the frequencies f_k, k = 1, …, R, has a good separation. Another method for recovering off-the-grid frequencies is enhanced matrix completion (EMaC) proposed by Chen et al. [10], where the Hankel structure plays a central role similar to our model. The main result in [10] is that the complex sinusoids x̂ can be robustly reconstructed via EMaC from its very few non-uniformly sampled entries. Again, the EMaC requires a separation of the frequencies, described implicitly by an incoherence condition.

  When applied to complex sinusoids, compared to the aforementioned existing results, our result in this paper does not need any separation condition on the frequencies, while achieving better or comparable bounds on the number of measurements.

• Accelerated NMR spectroscopy. When z_k = e^−τ_ke^2πιf_k, k = 1, …, R, x̂ models the signal in NMR spectroscopy, which arises frequently in studying short-lived molecular systems, monitoring chemical reactions in real-time, high-throughput applications, etc. Recently, Qu et al. [19] proposed an algorithm based on low rank Hankel matrix. In this specific application, A is a matrix that denotes the under-sampling of NMR signals in the time domain. We remark that linear non-uniform subsampling measurements of the signal can greatly speed up the NMR spectroscopy [19]. Numerical results show its efficiency in [19] for which theoretical guarantee results are still needed. It is vital to give some theoretical results on this model since it will give us some guidance on how many samples should be chosen to guarantee the robust recovery. Though the result in [10] applies to this problem, it needs an incoherence condition, which remains uncertain for diverse chemical and biology samples. Our result in this paper does not require any incoherence condition. Moreover, our bound is better than that in [10].

The rest of this paper is organized as follows. We begin with our model and our main results in Section 2. Proofs for the main result are given in Section 3. Then, in Section 4, we extend the main result to the reconstruction of generic low-rank Hankel or Toeplitz matrices. The performance of our algorithm is demonstrated by numerical experiments in Section 5. Finally, in Section 6, we conclude the paper and point out some possible future works.

2. Model and main results

Our approach is based on the observation that the Hankel matrix whose first row and last column consist of entries of x̂ has rank R. Let Ĥ be the Hankel matrix defined by (3). Eq. (1) leads to a decomposition

$$\widehat{\mathit{H}}=\left[\begin{array}{ccc}1& \dots & 1\\ z_1& \dots & z_R\\ ⋮& ⋮& ⋮\\ z_1^{N-1}& \dots & z_R^{N-1}\end{array}\right]\left[\begin{array}{ccc}{c}_1& & \\ & \ddots & \\ & & c_R\end{array}\right]\left[\begin{array}{ccc}1& z_1\dots & z_1^{N-1}\\ ⋮& ⋮& ⋮\\ 1& z_R\dots & z_R^{N-1}\end{array}\right]$$

Therefore, the rank of Ĥ is R. Similar to Enhanced Matrix Completion (EMaC) in [10], in order to reconstruct x̂, we first reconstruct the rank-R Hankel matrix Ĥ, is satisfied. Then, x̂ is derived directly by choosing the first row and last column of Ĥ. More specifically, for any given x ∈ ℂ^{2N − 1}, let H(x) ∈ ℂ^N×N be the Hankel matrix whose first row and last column is x, i.e., [H(x)]_jk = x_j+k. We propose to solve

$$\underset{\mathit{x}}{min}\text{rank}(\mathit{H}(\mathit{x})),\text{subject}\text{to}\mathit{Ax}=\mathit{b},$$ (6)

where rank(H(x)) denotes the rank of H(x), and A and b are from the linear measurement (2). When there is noise contained in the observation, i.e., b = Ax̂ + η, we correspondingly solve

$$\underset{\mathit{x}}{min}\text{rank}(\mathit{H}(\mathit{x})),\text{subject}\text{to}{\Vert \mathit{Ax}-\mathit{b}\Vert }_2\le \delta ,$$ (7)

where δ = ||η||₂ is the noise level.

These two problems are all NP hard problems and not easy to solve. Following the ideas of matrix completion and low rank matrix recovery [6,7,9,20], it is possible to exactly recover the low rank Hankel matrix via nuclear norm minimization. Therefore, it is reasonable to use nuclear norm minimization for our problem and it leads to the models in (4) and (5).

Theoretical results are desirable to guarantee the success of this Hankel matrix completion method. The results in [6,7,9,20] do not consider the Hankel structure. For generic N × N rank-R matrix, they require O(NR·poly(log N)) measurements for robust recovery which is too much since there are only 2N − 1 degrees of freedom in H(x). The theorems proposed in [23] work only for a special case where signals of interest are superpositions of complex sinusoids, which excludes, e.g., the signals in NMR spectroscopy. While the results from [10] extend to complex exponentials, the performance guarantees in [4,10,23] require incoherence conditions, implying the knowledge of frequency interval in spectroscopy, which are not available before the realistic sampling of diverse chemical or biological samples. This limits the applicability of these theories.

It is challenging to provide a theorem guaranteeing the exact recovery for model (4) with arbitrarily linear measurements A. In this paper, we provide a theoretical result ensuring exact recovery when A is a scaled random Gaussian matrix. Our result does not assume any incoherence conditions on the original signal.

Theorem 1

Let A = BD ∈ ℂ^{M×(2N − 1)}, where B ∈ ℂ^{M×(2N − 1)} is a random matrix whose real and imaginary parts are i.i.d. Gaussian with mean 0 and variance 1, D ∈ ℝ^{(2N − 1)×(2N − 1)} is a diagonal matrix with the j-th diagonal $\sqrt{j+1}$if j ≤ N − 1 and $\sqrt{2N-1-j}$ otherwise. Then, there exists a universal constant C₁ > 0 such that, for an arbitrary ε > 0, if

$$M\ge {(C_1\sqrt{R}lnN+\sqrt{2}\epsilon )}^2+1,$$

then, with probability at least $1-2e^{-\frac{M-1}{8}}$, we have

1. x̃ = x̂, where x̃ is the unique solution of (4) with b = Ax̂;

2. ||D(x̃ − x̂)||₂ ≤ 2δ/ε, where x̃ is the unique solution of (5) with ||b − Ax̂||₂ ≤ δ.

The scaling matrix D is introduced to preserve energy. In particular, we will introduce a variable y = Dx, and then the operator 𝒢 induced by 𝒢y = H(x) satisfies ||y||₂ = ||𝒢y||_F; see details in (9). This energy preserving property is critical in our estimation that will be seen later.

The number of measurements required is O(Rln² N), which is reasonable small compared with the number of parameters in H(x). Furthermore, there is a parameter ε in Theorem 1. For the noise-free case (a), the best choice of ε is obviously a number that is very close to 0. For the noisy case (b), we can balance the error bound and the number of measurements to get an optimal ε. On the one hand, according to the result in (b), in order to make the error in noisy case as small as possible, we would like ε to be as large as possible. On the other hand, we would like to keep the measurements M of the order of Rln² N. Therefore, a seemingly optimal choice of ε is $\epsilon =O(\sqrt{R}lnN)$. With this choice of ε, the number of measurements M = O(Rln² N) and the error ${\Vert \mathit{D}(\stackrel{\sim }{\mathit{x}}-\widehat{\mathit{x}})\Vert }_2\le O\left(\frac{\delta }{\sqrt{M}}\right)$.

Compared to results in [10,23], our theorem does not require any incoherence condition of the matrix Ĥ. In particular, our proposed approach for complex sinusoid signals does not need any separation condition on frequencies f_k’s for k = 1, 2, …, R. The reason for not needing a separation condition in noiseless case may be due to the Hankel matrix reconstruction method. Our proof of this fact also depends on the assumption of Gaussian measurements, for which we have the tool of Gaussian width analysis framework. For generic low-rank matrix reconstruction, it is well known that incoherence condition is necessary for successful reconstruction if partial entries of the underlying matrix are sampled [6,7]; however, incoherence is not required if Gaussian random projections are used [9,20]. We are in the same situation except for the additional Hankel structure. Our proposed approach uses Gaussian random projections of Ĥ, while the methods in [10,23] sample partial entries Ĥ. However, empirically, even for non-uniform time-domain samples, we observe that Hankel matrix completion does not seem to require the separation condition between frequencies. We thus conjecture that Hankel matrix completion does not require separations-between-frequencies condition to recover missing data from noiseless measurements under non-uniform time-domain samples, for which we currently do not have a proof.

2.1. Hankel matrix completion for recovering off-the-grid frequencies

Our results also apply to recovering frequencies in superposition of complex sinusoids, instead of recovering only the superposition of complex sinusoids. We divide our discussion into two cases.

The first case is the noise-free case, where the observations are not contaminated by additive noises. In this case, since we can recover the full signal of the superposition of the underlying sinusoids, we can use the single-snapshot MUSIC algorithm [27] to recover the underlying frequencies precisely.

The second case is the noisy case, where the observation is contaminated by additive noises. For this case, we have obtained a bound on the recovery error for the superposition signal (Theorem 1 of our paper). We can further recover the frequencies using the single-snapshot MUSIC algorithm by choosing the R smallest local minimum of surrogate criterion function R(ω) in [27]. In [27], the authors provided the stability result of recovering frequency using the single-snapshot MUSIC algorithm (Theorem 3 of [27]). Specifically, the error in surrogate criterion function R(ω) is upper bounded by the Euclidean norm of the observation noise multiplied by a constant C, where the constant C depends on the largest and smallest nonzero singular values of the involved Hankel matrix. Moreover, the recovered frequency deviates from the true frequency in the order of noise standard deviation when the noise is small (Remark 9 of [27]). We remark that this stability result from [27] is applicable without imposing separation condition on frequencies.

For frequencies satisfying a certain separation condition (Equation (23) of [27]), the authors of [27] further provide stronger and more explicit bounds on the stability of recovering frequencies from noisy data (by explicitly bounding the singular values of the involved Hankel matrix).

Moitra [28] proved that stability of recovering frequencies from noisy observations depends on the separation of frequencies. In particular, [28] shows a sharp phase transition for the relationship between the cutoff time observation index m (namely 2N − 1 in this paper) and the frequency separation δ. If m > 1/δ + 1, there is a polynomial-complexity estimator converging to the true frequencies at an inverse polynomial rate in terms of the magnitude of the noise. And conversely, when m < (1 − ε)/δ, no estimator can distinguish between a particular pair of δ-separated signals if the magnitude of the noise is not exponentially small.

However, the converse results in [28] are dealing with worst-case frequencies and worst-case frequency coefficients. Namely if the separation condition is not satisfied, one can always finds a worst-case pair of signals x and x′ such that telling them apart requires exponentially small noise. Thus Moitra’s result in [28] is not for an average-case, fixed signal x. Moreover, Moitra’s results does not mean that the single-snapshot MUSIC cannot tolerate small noises in recovering frequencies. By comparison, in this paper, our stability result is an average-case stability result, where our spectrally sparse signal is a fixed signal of superposition of complex exponentials, and our stability result is obtained over the ensemble of random Gaussian measurements. Our results are especially useful when the observations are noiseless or have high SNR.

3. Proof of Theorem 1

In this section, we prove the main result Theorem 1. The most crucial factors are that i) one has an explicit formula for the subdifferential of the objective function, and ii) the Gaussian width under the current measurement model is computable.

3.1. Orthonormal basis of the N × N Hankel matrices subspace

In this subsection, we introduce an orthonormal basis of the subspace of N × N Hankel matrices and use it to define a projection from ℂ^N×N to the subspace of all N × N Hankel matrices.

Let E_j ∈ ℂ^N×N, j = 0, 1 …, 2N − 2, be the Hankel matrix satisfying

$${[{\mathit{E}}_j]}_{kl}=\{\begin{array}{ll}1/\sqrt{K_j},\hfill & \text{if}k+l=j,\hfill \\ 0,\hfill & \text{otherwise},\hfill \end{array}k,l=0,\dots ,N-1,$$ (8)

where K_j = j + 1 for j ≤ N − 1 and K_j = 2N − 1 − j for j ≥ N − 1 is the number of non-zeros in E_j. Then, it is easy to check that ${\{{\mathit{E}}_j\}}_{j=0}^{2N-2}$ forms an orthonormal basis of the subspace of all N × N Hankel matrices, under the standard inner product in ℂ^N×N.

Define a linear operator

$$\mathcal{G}:\mathit{x}\in {ℂ}^{2N-1}\mapsto \mathcal{G}\mathit{x}=\sum _{j=0}^{2N-2}{x}_j{\mathit{E}}_j\in {ℂ}^{N\times N}.$$ (9)

The adjoint 𝒢^* of 𝒢 is

$${\mathcal{G}}^{\ast }:\mathit{X}\in {ℂ}^{N\times N}\mapsto {\mathcal{G}}^{\ast }\mathit{X}\in {ℂ}^{2N-1},{[{\mathcal{G}}^{\ast }\mathit{X}]}_j=\langle \mathit{X},{\mathit{E}}_j\rangle .$$

Obviously, 𝒢^*𝒢 is the identity operator in ℂ^{2N − 1}, and 𝒢𝒢^* is the orthogonal projector onto the subspace of all Hankel matrices.

3.2. Recovery condition based on restricted minimum gain condition

First of all, let us simplify the minimization problem (4) by introducing D ∈ ℂ^{(2N − 1)×(2N − 1)}, the diagonal matrix with j-th diagonal $\sqrt{K_j}$. Then, by letting y = Dx, (4) is rewritten as,

$$\underset{\mathit{y}}{min}{\Vert \mathcal{G}\mathit{y}\Vert }_{\ast }\text{subject}\text{to}\mathit{By}=\mathit{b},$$ (10)

where B = AD⁻¹. Recall that 𝒢 satisfies 𝒢^*𝒢 = ℐ, which is crucial in the proceeding analysis. Similarly, for the noisy case, (5) is rearranged to

$$\underset{\mathit{y}}{min}{\Vert \mathcal{G}\mathit{y}\Vert }_{\ast }\text{subject}\text{to}{\Vert \mathit{By}-\mathit{b}\Vert }_2\le \epsilon .$$ (11)

By our assumption in Theorem 1, B ∈ ℂ^{M×(2N − 1)} is a random matrix whose real and imaginary parts are both real-valued random matrices with i.i.d. Gaussian entries of mean 0 and variance 1. We will prove ỹ = Dx̂ (respectively ||ỹ − ŷ||₂ ≤ 2δ/ε) with dominant probability for problem (10) for the noise free case (respectively (11) for the noisy case).

Let the descent cone of ||𝒢 ·||_* at ŷ be

$$\mathfrak{T}(\widehat{\mathit{y}})=\{\lambda \mathit{z}\mid \lambda \ge 0,{\Vert \mathcal{G}(\widehat{\mathit{y}}+\mathit{z})\Vert }_{\ast }\le {\Vert \mathcal{G}\widehat{\mathit{y}}\Vert }_{\ast }\}.$$ (12)

To characterize the recovery condition, we need to use the minimum value of $\frac{{\Vert \mathit{Bz}\Vert }_2}{{\Vert \mathit{z}\Vert }_2}$ for nonzero z ∈ 𝔗(ŷ). This quantity is commonly called the minimum gain of the measurement operator B restricted on 𝔗(ŷ) [9]. In particular, if the minimum gain is bounded away from zero, then the exact recovery (respectively approximate recovery) for problem (10) (respectively (11)) holds.

Lemma 1

Let 𝔗(ŷ) be defined by (12). Assume

$$\underset{\mathit{z}\in \mathfrak{T}(\widehat{\mathit{y}})}{min}\frac{{\Vert \mathit{Bz}\Vert }_2}{{\Vert \mathit{z}\Vert }_2}\ge \epsilon .$$ (13)

1. Let ỹ be the solution of (10) with b = Bŷ. Then ỹ = ŷ.

2. Let ỹ be the solution of (11) with ||b − Bŷ||₂ ≤ δ. Then ||ỹ − ŷ||₂ ≤ 2δ/ε.

Proof

Since (a) is a special case of (b) with δ = 0, we prove (b) only. The optimality of ỹ implies ỹ − ŷ ∈ 𝔗(ŷ). By (13), we have

$${\Vert \stackrel{\sim }{\mathit{y}}-\widehat{\mathit{y}}\Vert }_2\le \frac{1}{\epsilon }{\Vert \mathit{B}(\stackrel{\sim }{\mathit{y}}-\widehat{\mathit{y}})\Vert }_2\le \frac{1}{\epsilon }({\Vert \mathit{B}\stackrel{\sim }{\mathit{y}}-\mathit{b}\Vert }_2+{\Vert \mathit{B}\widehat{\mathit{y}}-\mathit{b}\Vert }_2)\le 2\delta /\epsilon .$$

Minimum gain condition is a powerful concept and has been employed in recent recovery results via ℓ₁ norm minimization, block-sparse vector recovery, low-rank matrix reconstruction and other atomic norms [9].

3.3. Bound of minimum gain via Gaussian width

Lemma 1 requires to estimate the lower bound of ${min}_{\mathit{z}\in \mathfrak{T}(\widehat{\mathit{y}})}\frac{{\Vert \mathit{Bz}\Vert }_2}{{\Vert \mathit{z}\Vert }_2}$. Gordon gave a solution using Gaussian width of a set [9,14] to estimate the lower bound of minimum gain.

Definition 1

The Gaussian width of a set S ⊂ ℝ^p is defined as:

$$w(S):={\mathrm{E}}_{\mathit{\xi }}\left[\underset{\mathit{\gamma }\in S}{sup}{\mathit{\gamma }}^T\mathit{\xi }\right],$$

where ξ ∈ ℝ^p is a random vector of independent zero-mean unit-variance Gaussians.

Let λ_n denote the expected length of a n-dimensional Gaussian random vector. Then ${\lambda }_n=\sqrt{2}\mathrm{\Gamma }(\frac{n+1}{2})/\mathrm{\Gamma }(\frac{n}{2})$ and it can be tightly bounded as $\frac{n}{\sqrt{n+1}}\le {\lambda }_n\le \sqrt{n}$ [9]. The following theorem is given in Corollary 1.2 in [14]. It gives a bound on minimum gain for a random map Π: ℝ^p ↦ ℝⁿ.

Theorem 2. (See Corollary 1.2 in [14].)

Let Ω be a closed subset of {x ∈ ℝ^p|||x||₂ = 1}. Let Π ∈ ℝ^n×p be a random matrix with i.i.d. Gaussian entries with mean 0 and variance 1. Then, for any ε > 0,

$$\mathrm{P}\left(\underset{\mathit{z}\in \mathrm{\Omega }}{min}{\Vert \mathbf{\Pi }\mathit{z}\Vert }_2\ge \epsilon \right)\ge 1-e^{-\frac{1}{2}{({\lambda }_n-w(\mathrm{\Omega })-\epsilon )}^2},$$

provided λ_n − w(Ω) − ε ≥ 0. Here $\frac{n}{\sqrt{n+1}}\le {\lambda }_n\le \sqrt{n}$, and w(Ω) is the Gaussian width of Ω.

By converting the complex setting in our problem to the real setting and using Theorem 2, we can get the bound of (13) in terms of Gaussian width of ${\mathfrak{T}}_{ℝ}(\widehat{\mathit{y}})\cap {\mathbb{S}}_{ℝ}^{4N-3}$, where 𝔗_ℝ(ŷ) is a cone in ℝ^{4N − 2} defined by

$${\mathfrak{T}}_{ℝ}(\widehat{\mathit{y}})=\left\{\left[\begin{array}{c}\mathit{\alpha }\\ \mathit{\beta }\end{array}\right]|\mathit{\alpha }+\iota \mathit{\beta }\in \mathfrak{T}(\widehat{\mathit{y}})\right\}.$$ (14)

Lemma 2

Let the real and imaginary parts of entries of B ∈ ℂ^{M×(2N − 1)} be i.i.d. Gaussian with mean 0 and variance 1. Let 𝔗_ℝ(ŷ) be defined by (14) and ${\mathbb{S}}_c^{2N-2}$ be the unit sphere in ℂ^{2N − 1}. Then for any ε > 0,

$$\mathrm{P}\left(\underset{\mathit{z}\in \mathfrak{T}(\widehat{\mathit{y}})\cap {\mathbb{S}}_c^{2N-2}}{min}{\Vert \mathit{Bz}\Vert }_2\ge \epsilon \right)\ge 1-2e^{-\frac{1}{2}{\left({\lambda }_M-w({\mathfrak{T}}_{ℝ}(\widehat{\mathit{y}})\cap {\mathbb{S}}_{ℝ}^{4N-3})-\frac{\epsilon }{\sqrt{2}}\right)}^2},$$

where ${\mathbb{S}}_{ℝ}^{4N-3}$ is the unit sphere in ℝ^4N−2.

Proof

In order to use Theorem 2, we convert the complex setting in our problem to the real setting in Theorem 2. We will use Roman letters for vectors and matrices in complex-valued spaces, and Greek letters for real valued ones. Let B = Φ + ιΨ ∈ ℂ^M×(2N−1), where both Φ ∈ ℝ^M×(2N−1) and Ψ ∈ ℝ^M×(2N−1) are real-valued random matrices whose entries are i.i.d. mean-0 variance-1 Gaussian. Then, for any z = α + ιβ ∈ ℂ^2N−1 with α, β ∈ ℝ^2N−1,

$$\begin{array}{l}{\Vert \mathit{Bz}\Vert }_2={\Vert (\mathbf{\Phi }+\iota \mathbf{\Psi })(\mathit{\alpha }+\iota \mathit{\beta })\Vert }_2={\Vert (\mathbf{\Phi }\mathit{\alpha }-\mathbf{\Psi }\mathit{\beta })+\iota (\mathbf{\Psi }\mathit{\alpha }+\mathbf{\Phi }\mathit{\beta })\Vert }_2\\ ={\left({\Vert [\begin{array}{cc}\mathbf{\Phi }& -\mathbf{\Psi }\end{array}]\left[\begin{array}{c}\mathit{\alpha }\\ \mathit{\beta }\end{array}\right]\Vert }_2^2+{\Vert [\begin{array}{cc}\mathbf{\Psi }& \mathbf{\Phi }\end{array}]\left[\begin{array}{c}\mathit{\alpha }\\ \mathit{\beta }\end{array}\right]\Vert }_2^2\right)}^{-1/2}\end{array}$$

Then

$$\underset{\mathit{z}=\mathit{\alpha }+\iota \mathit{\beta }\in \mathfrak{T}(\widehat{\mathit{y}})\cap {\mathbb{S}}_c^{2N-2}}{min}{\Vert [\begin{array}{cc}\mathbf{\Phi }& -\mathbf{\Psi }\end{array}]\left[\begin{array}{c}\mathit{\alpha }\\ \mathit{\beta }\end{array}\right]\Vert }_2\ge \epsilon /\sqrt{2},\text{and}\underset{\mathit{z}=\mathit{\alpha }+\iota \mathit{\beta }\in \mathfrak{T}(\widehat{\mathit{y}})\cap {\mathbb{S}}_c^{2N-2}}{min}{\Vert [\begin{array}{cc}\mathbf{\Psi }& \mathbf{\Phi }\end{array}]\left[\begin{array}{c}\mathit{\alpha }\\ \mathit{\beta }\end{array}\right]\Vert }_2\ge \epsilon /\sqrt{2}$$ (15)

implies

$$\underset{\mathit{z}\in \mathfrak{T}(\widehat{\mathit{y}})\cap {\mathbb{S}}_c^{2N-2}}{min}{\Vert \mathit{Bz}\Vert }_2\ge \epsilon .$$

Therefore,

$$\mathrm{P}\left(\underset{\mathit{z}\in \mathfrak{T}(\widehat{\mathit{y}})\cap {\mathbb{S}}_c^{2N-2}}{min}{\Vert \mathit{Bz}\Vert }_2\ge \epsilon \right)\ge \mathrm{P}((15)\text{holds}\text{true}).$$

It is easy to see that both [Φ −Ψ] and [Ψ Φ] are real-valued random matrices with i.i.d. Gaussian entries of mean 0 and variance 1. By Theorem 2,

$$\mathrm{P}((15)\text{holds}\text{true})\ge 1-2e^{-\frac{1}{2}{\left({\lambda }_M-w({\mathfrak{T}}_{ℝ}(\widehat{\mathit{y}})\cap {\mathbb{S}}_{ℝ}^{4N-3})-\frac{\epsilon }{\sqrt{2}}\right)}^2},$$

and therefore we get the desired result.

3.4. Estimation of Gaussian width $w({\mathfrak{T}}_{ℝ}(\widehat{\mathit{y}})\cap {\mathbb{S}}_{ℝ}^{4N-3})$

Denote ${\mathfrak{T}}_{ℝ}^{\ast }(\widehat{\mathit{y}})$ be polar cone of 𝔗_ℝ(ŷ) ∈ ℝ^4N−2, i.e.,

$${\mathfrak{T}}_{ℝ}^{\ast }(\widehat{\mathit{y}})=\{\mathit{\delta }\in {ℝ}^{4N-2}\mid {\mathit{\gamma }}^T\mathit{\delta }\le 0,\forall \mathit{\gamma }\in {\mathfrak{T}}_{ℝ}(\widehat{\mathit{y}})\}.$$ (16)

Following the arguments in Proposition 3.6 in [9], we obtain

$$w({\mathfrak{T}}_{ℝ}(\widehat{\mathit{y}})\cap {\mathbb{S}}_{ℝ}^{4N-3})=\mathrm{E}\left(\underset{\mathit{\gamma }\in {\mathfrak{T}}_{ℝ}(\widehat{\mathit{y}})\cap {\mathbb{S}}_{ℝ}^{4N-3}}{sup}{\mathit{\xi }}^T\mathit{\gamma }\right)\le \mathrm{E}\left(\underset{\mathit{\gamma }\in {\mathfrak{T}}_{ℝ}^{\ast }(\widehat{\mathit{y}})}{min}{\Vert \mathit{\xi }-\mathit{\gamma }\Vert }_2\right),$$ (17)

where ξ ∈ ℝ^4N−2 is a random vector of i.i.d. Gaussian entries of mean 0 and variance 1. Hence, instead of estimating Gaussian width $w({\mathfrak{T}}_{ℝ}(\widehat{\mathit{y}})\cap {\mathbb{S}}_{ℝ}^{4N-3})$, we bound $\mathrm{E}({min}_{\mathit{\gamma }\in {\mathfrak{T}}_{ℝ}^{\ast }(\widehat{\mathit{y}})}{\Vert \mathit{\xi }-\mathit{\gamma }\Vert }_2)$. For this purpose, let ℱ : ℝ^4N−2 ↦ ℝ be defined by

$$\mathcal{F}\left(\left[\begin{array}{c}\mathit{\alpha }\\ \mathit{\beta }\end{array}\right]\right)={\Vert \mathcal{G}(\mathit{\alpha }+\iota \mathit{\beta })\Vert }_{\ast }.$$ (18)

The following lemma gives us a characterization of $\mathrm{E}\left({min}_{\mathit{\gamma }\in {\mathfrak{T}}_{ℝ}^{\ast }(\widehat{\mathit{y}})}{\Vert \mathit{\xi }-\mathit{\gamma }\Vert }_2\right)$ in terms of the subdifferential ∂ℱ of ℱ.

Lemma 3

Let ${\mathfrak{T}}_{ℝ}^{\ast }(\widehat{\mathit{y}})$ and ℱ be defined by (16) and (18) respectively. Let ω̂₁, ω̂₂ ∈ ℝ^2N−1 be the real and imaginary parts of ŷ respectively and denote $\widehat{\mathit{\omega }}=\left[\begin{array}{c}{\widehat{\mathit{\omega }}}_1\\ {\widehat{\mathit{\omega }}}_2\end{array}\right]$. Then

$${\mathfrak{T}}_{ℝ}^{\ast }(\widehat{\mathit{y}})=\text{cone}(\partial \mathcal{F}(\widehat{\mathit{\omega }}))=\{\lambda \mathit{\delta }\mid \lambda \ge 0,\mathcal{F}(\mathit{\gamma }+\widehat{\mathit{\omega }})\ge \mathcal{F}(\widehat{\mathit{\omega }})+{\mathit{\gamma }}^T\mathit{\delta },\forall \mathit{\gamma }\in {ℝ}^{4N-2}\}.$$ (19)

Proof

It is observed that 𝔗_ℝ(ŷ) in (14) is the descent cone of the function ℱ

$${\mathfrak{T}}_{ℝ}(\widehat{\mathit{y}})=\{\delta \mathit{\gamma }\mid \delta \ge 0,\mathcal{F}(\mathit{\gamma }+\widehat{\mathit{\omega }})\le \mathcal{F}(\widehat{\mathit{\omega }})\}.$$

According to Theorem 23.4 in [21], the cone dual to the descent cone is the conic hull of subgradient, which is exactly (19).

The following lemma gives us an estimation of Gaussian width $w({\mathfrak{T}}_{ℝ}(\widehat{\mathit{y}})\cap {\mathbb{S}}_{ℝ}^{4N-3})$ in terms of E(||𝒢g||₂).

Lemma 4

Let 𝔗_ℝ(ŷ) and 𝒢 be defined by (14) and (9) respectively. Then

$$w({\mathfrak{T}}_{ℝ}(\widehat{\mathit{y}})\cap {\mathbb{S}}_{ℝ}^{4N-3})\le 3\sqrt{R}·\mathrm{E}({\Vert \mathcal{G}\mathit{g}\Vert }_2),$$

where E(||𝒢g||₂) is the expectation with respect to g ∈ ℂ^2N−1. Here g is a random vector whose real and imaginary parts are i.i.d. mean-0 and variance-1 Gaussian entries.

Proof

By using (17) and Lemma 3, we need to find ∂ℱ(ω̂) and thus ${\mathfrak{T}}_{ℝ}^{\ast }(\widehat{\mathit{y}})$. Let Ω̂₁ = 𝒢ω̂₁ and Ω̂₂ = 𝒢ω̂₂. Then 𝒢ŷ = Ω̂₁ + ιΩ̂₂. Let a singular value decomposition of the rank-R matrix 𝒢ŷ be

$$\mathcal{G}\widehat{\mathit{y}}=\mathit{U}\mathbf{\sum }{\mathit{V}}^{\ast },\text{with}\mathit{U}={\mathbf{\Theta }}_1+\iota {\mathbf{\Theta }}_2,\mathit{V}={\mathbf{\Xi }}_1+\iota {\mathbf{\Xi }}_2,$$ (20)

where Θ₁, Θ₂, Ξ₁, Ξ₂ ∈ ℝ^N×R and Σ ∈ ℝ^R×R, and U ∈ ℂ^N×R and V ∈ ℂ^N×R satisfies U^*U = V^*V = I. Then, by direct calculation,

$$\mathbf{\Theta }\equiv \left[\begin{array}{cc}{\mathbf{\Theta }}_1& -{\mathbf{\Theta }}_2\\ {\mathbf{\Theta }}_2& {\mathbf{\Theta }}_1\end{array}\right]\in {ℝ}^{2N\times (2R)},\mathbf{\Xi }\equiv \left[\begin{array}{cc}{\mathbf{\Xi }}_1& -{\mathbf{\Xi }}_2\\ {\mathbf{\Xi }}_2& {\mathbf{\Xi }}_1\end{array}\right]\in {ℝ}^{2N\times (2R)}$$ (21)

satisfy Θ^TΘ = Ξ^TΞ = I. Moreover, if we define $\widehat{\mathbf{\Omega }}=\left[\begin{array}{cc}{\widehat{\mathbf{\Omega }}}_1& -{\widehat{\mathbf{\Omega }}}_2\\ {\widehat{\mathbf{\Omega }}}_2& {\widehat{\mathbf{\Omega }}}_1\end{array}\right]$, then

$$\widehat{\mathbf{\Omega }}=\mathbf{\Theta }\left[\begin{array}{cc}\mathbf{\sum }& \\ & \mathbf{\sum }\end{array}\right]{\mathbf{\Xi }}^T$$ (22)

is a singular value decomposition of the real matrix Ω̂, and the singular values Ω̂ are those of 𝒢ŷ, each repeated twice. Therefore,

$$\mathcal{F}(\widehat{\mathit{\omega }})={\Vert \mathcal{G}\widehat{\mathit{y}}\Vert }_{\ast }={\Vert \mathbf{\sum }\Vert }_{\ast }=\frac{1}{2}{\Vert \widehat{\mathbf{\Omega }}\Vert }_{\ast }.$$ (23)

Define a linear operator ℰ : ℝ^4N−2 ↦ ℝ^2N×2N by

$$\mathcal{E}\left(\left[\begin{array}{c}\mathit{\alpha }\\ \mathit{\beta }\end{array}\right]\right)=\left[\begin{array}{cc}\mathcal{G}\mathit{\alpha }& -\mathcal{G}\mathit{\beta }\\ \mathcal{G}\mathit{\beta }& \mathcal{G}\mathit{\alpha }\end{array}\right],\text{with}\mathit{\alpha },\mathit{\beta }\in {ℝ}^{2N-1}.$$

By (23) and the definition of Ω̂, we obtain $\mathcal{F}(\widehat{\mathit{\omega }})=\frac{1}{2}{\Vert \mathcal{E}\widehat{\mathit{\omega }}\Vert }_{\ast }$. From convex analysis theory and Ω̂ = ℰω̂, the subdifferential of ℱ is given by

$$\partial \mathcal{F}(\widehat{\mathit{\omega }})=\frac{1}{2}{\mathcal{E}}^{\ast }\partial {\Vert \widehat{\mathbf{\Omega }}\Vert }_{\ast }.$$ (24)

On the one hand, the adjoint ℰ* is given by, for any $\mathbf{\Delta }=\left[\begin{array}{cc}{\mathbf{\Delta }}_{11}& {\mathbf{\Delta }}_{12}\\ {\mathbf{\Delta }}_{21}& {\mathbf{\Delta }}_{22}\end{array}\right]\in {ℝ}^{2N\times 2N}$ with each block in ℝ^N×N,

$${\mathcal{E}}^{\ast }\mathbf{\Delta }=\left[\begin{array}{l}{\mathcal{G}}^{\ast }({\mathbf{\Delta }}_{11}+{\mathbf{\Delta }}_{22})\hfill \\ {\mathcal{G}}^{\ast }({\mathbf{\Delta }}_{21}-{\mathbf{\Delta }}_{12})\hfill \end{array}\right].$$ (25)

On the other hand, since (22) provides a singular value decomposition of Ω̂,

$$\partial {\Vert \widehat{\mathbf{\Omega }}\Vert }_{\ast }=\{\mathbf{\Theta }{\mathbf{\Xi }}^T+\mathbf{\Delta }\mid {\mathbf{\Theta }}^T\mathbf{\Delta }=\mathbf{0},\mathbf{\Delta }\mathbf{\Xi }=\mathbf{0},{\Vert \mathbf{\Delta }\Vert }_2\le 1\}.$$ (26)

Combining (24), (25), (26) and (21) yields the subdifferential of ℱ at ω̂

$$\partial \mathcal{F}(\widehat{\mathit{\omega }})=\left\{\left[\begin{array}{l}{\mathcal{G}}^{\ast }({\mathbf{\Theta }}_1{\mathbf{\Xi }}_1^T+{\mathbf{\Theta }}_2{\mathbf{\Xi }}_2^T+\frac{{\mathbf{\Delta }}_{11}+{\mathbf{\Delta }}_{22}}{2})\hfill \\ {\mathcal{G}}^{\ast }({\mathbf{\Theta }}_2{\mathbf{\Xi }}_1^T-{\mathbf{\Theta }}_1{\mathbf{\Xi }}_2^T+\frac{{\mathbf{\Delta }}_{21}-{\mathbf{\Delta }}_{12}}{2})\hfill \end{array}\right]|\mathbf{\Delta }=\left[\begin{array}{cc}{\mathbf{\Delta }}_{11}& {\mathbf{\Delta }}_{12}\\ {\mathbf{\Delta }}_{21}& {\mathbf{\Delta }}_{22}\end{array}\right],{\mathbf{\Theta }}^T\mathbf{\Delta }=\mathbf{0},\mathbf{\Delta }\mathbf{\Xi }=\mathbf{0},{\Vert \mathbf{\Delta }\Vert }_2\le 1\right\}.$$

We are now ready for the estimation of the Gaussian width. Let the set 𝔖 be a subset of the set of complex-valued vectors

$$\mathfrak{S}=\{{\mathcal{G}}^{\ast }(\mathit{U}{\mathit{V}}^{\ast }+\mathit{W})\mid {\mathit{U}}^{\ast }\mathit{W}=\mathbf{0},\mathit{WV}=\mathbf{0},{\Vert \mathit{W}\Vert }_2\le 1\},$$ (27)

where U, V are in (20). Then, it can be checked that

$$\mathfrak{H}\equiv \left\{\left[\begin{array}{c}\mathit{\alpha }\\ \mathit{\beta }\end{array}\right]\mid \mathit{\alpha }+\iota \mathit{\beta }\in \mathfrak{S}\right\}\subset \partial \mathcal{F}(\widehat{\mathit{\omega }}).$$ (28)

Actually, for any W = Δ₁ + ιΔ₂ satisfying U^*W = 0, WV = 0 and ||W||₂ ≤ 1, we choose $\mathbf{\Delta }=\left[\begin{array}{cc}{\mathbf{\Delta }}_1& -{\mathbf{\Delta }}_2\\ {\mathbf{\Delta }}_2& {\mathbf{\Delta }}_1\end{array}\right]$. Obviously, this choice of Δ satisfies the constraints on Δ in ∂ℱ(ω̂). Furthermore, $\mathit{U}{\mathit{V}}^{\ast }+\mathit{W}=({\mathbf{\Theta }}_1{\mathbf{\Xi }}_1^T+{\mathbf{\Theta }}_2{\mathbf{\Xi }}_2^T+{\mathbf{\Delta }}_1)+\iota ({\mathbf{\Theta }}_2{\mathbf{\Xi }}_1^T+{\mathbf{\Theta }}_1{\mathbf{\Xi }}_2^T+{\mathbf{\Delta }}_2)$. Therefore, (28) holds.

With the help of (28), we get

$$\underset{\mathit{\gamma }\in {\mathfrak{T}}_{ℝ}^{\ast }(\widehat{\mathit{y}})}{min}{\Vert \mathit{\xi }-\mathit{\gamma }\Vert }_2=\underset{\lambda \ge 0}{min}\underset{\mathit{\gamma }\in \partial \mathcal{F}(\widehat{\mathit{\omega }})}{min}{\Vert \mathit{\xi }-\lambda \mathit{\gamma }\Vert }_2\le \underset{\lambda \ge 0}{min}\underset{\mathit{\gamma }\in \mathfrak{H}}{min}{\Vert \mathit{\xi }-\lambda \mathit{\gamma }\Vert }_2.$$ (29)

We then convert the real-valued vectors to complex-valued vectors by letting g = ξ₁ + ιξ₂ and c = γ₁ + ιγ₂, where ξ₁ and ξ₂ are the first and second half of ξ respectively and so for γ₁ and γ₂. This leads to

$$\underset{\mathit{\gamma }\in {\mathfrak{T}}_{ℝ}^{\ast }(\widehat{\mathit{y}})}{min}{\Vert \mathit{\xi }-\mathit{\gamma }\Vert }_2\le \underset{\lambda \ge 0}{min}\underset{\mathit{\gamma }\in \mathfrak{H}}{min}{\Vert \mathit{\xi }-\lambda \mathit{\gamma }\Vert }_2=\underset{\lambda \ge 0}{min}\underset{\mathit{c}\in \mathfrak{S}}{min}{\Vert \mathit{g}-\lambda \mathit{c}\Vert }_2.$$

Since 𝒢*𝒢 is the identity operator and 𝒢𝒢* is an orthogonal projector, for any λ ≥ 0 and c ∈ 𝔖,

$$\begin{array}{l}{\Vert \mathit{g}-\lambda \mathit{c}\Vert }_2={\Vert \mathcal{G}\mathit{g}-\lambda \mathcal{G}\mathit{c}\Vert }_F={\Vert \mathcal{G}\mathit{g}-\lambda \mathcal{G}{\mathcal{G}}^{\ast }(\mathit{U}{\mathit{V}}^{\ast }+\mathit{W})\Vert }_F\\ ={({\Vert \mathcal{G}\mathit{g}-\lambda (\mathit{U}{\mathit{V}}^{\ast }+\mathit{W})\Vert }_F^2-{\Vert \lambda (ℐ-\mathcal{G}{\mathcal{G}}^{\ast })(\mathit{U}{\mathit{V}}^{\ast }+\mathit{W})\Vert }_F^2)}^{1/2}\\ \le {\Vert \mathcal{G}\mathit{g}-\lambda (\mathit{U}{\mathit{V}}^{\ast }+\mathit{W})\Vert }_F,\end{array}$$ (30)

where W satisfies the conditions in the definition of 𝔖 in (27). Define two orthogonal projectors ℘₁ and ℘₂ in ℂ^N×N by

$${\mathcal{P}}_1\mathit{X}=\mathit{U}{\mathit{U}}^{\ast }\mathit{X}+\mathit{XV}{\mathit{V}}^{\ast }-\mathit{U}{\mathit{U}}^{\ast }\mathit{XV}{\mathit{V}}^{\ast },{\mathcal{P}}_2\mathit{X}=(\mathit{I}-\mathit{U}{\mathit{U}}^{\ast })\mathit{X}(\mathit{I}-\mathit{V}{\mathit{V}}^{\ast }).$$

Then, it can be easily checked that: ℘₁X and ℘₂X are orthogonal, X = ℘₁X + ℘₂X, and

$${\mathcal{P}}_1\mathit{U}{\mathit{V}}^{\ast }=\mathit{U}{\mathit{V}}^{\ast },{\mathcal{P}}_2\mathit{U}{\mathit{V}}^{\ast }=\mathbf{0},{\mathcal{P}}_1\mathit{W}=\mathbf{0},{\mathcal{P}}_2\mathit{W}=\mathit{W},$$ (31)

where U, V, W are the same as those in (27). We choose

$$\lambda ={\Vert {\mathcal{P}}_2(\mathcal{G}\mathit{g})\Vert }_2,\mathit{W}=\frac{1}{\lambda }{\mathcal{P}}_2(\mathcal{G}\mathit{g}).$$

Then, W satisfies constraints in (27). This, together with (29), (30), (31), implies

$$\begin{array}{l}\underset{\mathit{\gamma }\in {\mathfrak{T}}_{ℝ}^{\ast }(\widehat{\mathit{y}})}{min}{\Vert \mathit{\xi }-\mathit{\gamma }\Vert }_2\le \Vert \mathcal{G}\mathit{g}-{\Vert {\mathcal{P}}_2(\mathcal{G}\mathit{g}){\Vert }_2\mathit{U}{\mathit{V}}^{\ast }-{\mathcal{P}}_2(\mathcal{G}\mathit{g})\Vert }_F=\Vert {\mathcal{P}}_1(\mathcal{G}\mathit{g})-{\Vert {\mathcal{P}}_2(\mathcal{G}\mathit{g}){\Vert }_2\mathit{U}{\mathit{V}}^{\ast }\Vert }_F\\ \le {\Vert {\mathcal{P}}_1(\mathcal{G}\mathit{g})\Vert }_F+{\Vert {\mathcal{P}}_2(\mathcal{G}\mathit{g})\Vert }_2{\Vert \mathit{U}{\mathit{V}}^{\ast }\Vert }_F={\Vert {\mathcal{P}}_1(\mathcal{G}\mathit{g})\Vert }_F+\sqrt{R}{\Vert {\mathcal{P}}_2(\mathcal{G}\mathit{g})\Vert }_2.\end{array}$$

We will estimate both ||℘₁(𝒢g)||_F and ||℘₂(𝒢g)||₂. For ||℘₁(𝒢g)||_F, we have

$$\begin{array}{l}{\Vert {\mathcal{P}}_1(\mathcal{G}\mathit{g})\Vert }_F={\Vert \mathit{U}{\mathit{U}}^{\ast }(\mathcal{G}\mathit{g})+(\mathcal{G}\mathit{g})\mathit{V}{\mathit{V}}^{\ast }-\mathit{U}{\mathit{U}}^{\ast }(\mathcal{G}\mathit{g})\mathit{V}{\mathit{V}}^{\ast }\Vert }_F={\Vert \mathit{U}{\mathit{U}}^{\ast }(\mathcal{G}\mathit{g})+(\mathit{I}-\mathit{U}{\mathit{U}}^{\ast })(\mathcal{G}\mathit{g})\mathit{V}{\mathit{V}}^{\ast }\Vert }_F\\ \le {\Vert \mathit{U}{\mathit{U}}^{\ast }(\mathcal{G}\mathit{g})\Vert }_F+{\Vert (\mathit{I}-\mathit{U}{\mathit{U}}^{\ast })(\mathcal{G}\mathit{g})\mathit{V}{\mathit{V}}^{\ast }\Vert }_F\le {\Vert \mathit{U}{\mathit{U}}^{\ast }(\mathcal{G}\mathit{g})\Vert }_F+{\Vert (\mathcal{G}\mathit{g})\mathit{V}{\mathit{V}}^{\ast }\Vert }_F\\ \le 2\sqrt{R}{\Vert \mathcal{G}\mathit{g}\Vert }_2\end{array}$$

where in the last line we have used the inequality

$${\Vert \mathit{U}{\mathit{U}}^{\ast }(\mathcal{G}\mathit{g})\Vert }_F\le {\Vert \mathit{U}{\mathit{U}}^{\ast }\Vert }_F{\Vert \mathcal{G}\mathit{g}\Vert }_2\le \sqrt{R}{\Vert \mathcal{G}\mathit{g}\Vert }_2$$

and similarly ${\Vert (\mathcal{G}\mathit{g})\mathit{V}{\mathit{V}}^{\ast }\Vert }_F\le \sqrt{R}{\Vert \mathcal{G}\mathit{g}\Vert }_2$. For ||℘₂(𝒢g)||₂,

$${\Vert {\mathcal{P}}_2(\mathcal{G}\mathit{g})\Vert }_2={\Vert (\mathit{I}-\mathit{U}{\mathit{U}}^{\ast })(\mathcal{G}\mathit{g})(\mathit{I}-\mathit{V}{\mathit{V}}^{\ast })\Vert }_2\le {\Vert \mathit{I}-\mathit{U}{\mathit{U}}^{\ast }\Vert }_2{\Vert \mathcal{G}\mathit{g}\Vert }_2{\Vert \mathit{I}-\mathit{V}{\mathit{V}}^{\ast }\Vert }_2\le {\Vert \mathcal{G}\mathit{g}\Vert }_2.$$

Altogether, we obtain

$$\underset{\mathit{\gamma }\in {\mathfrak{T}}_{ℝ}^{\ast }(\widehat{\mathit{y}})}{min}{\Vert \mathit{\xi }-\mathit{\gamma }\Vert }_2\le 3\sqrt{R}{\Vert \mathcal{G}\mathit{g}\Vert }_2,$$

which together with (17) gives

$$w({\mathfrak{T}}_{ℝ}(\widehat{\mathit{y}})\cap {\mathbb{S}}_{ℝ}^{4N-3})\le 3\sqrt{R}·\mathrm{E}({\Vert \mathcal{G}\mathit{g}\Vert }_2).$$

3.5. Bound of E(||𝒢g||₂)

The estimation of E(||𝒢g||₂) plays an important role in proving Theorem 1 since it is needed to give the tight bound of the Gaussian width $w({\mathfrak{T}}_{ℝ}(\widehat{\mathit{y}})\cap {\mathbb{S}}_{ℝ}^{4N-3})$. The following theorem gives us a bound for E(||𝒢g||₂).

Theorem 3

Let g ∈ ℝ^2N−1 be a random vector whose entries are i.i.d. Gaussian random variables with mean 0 and variance 1, or g ∈ ℂ^2N−1 a random vector whose real part and imaginary part have i.i.d. Gaussian random entries with mean 0 and variance 1. Then,

$$\mathrm{E}({\Vert \mathcal{G}\mathit{g}\Vert }_2)\le C_{1}lnN,$$

where C₁ are some positive universal constants.

We will use the moment method (see Chapter 2.3 in [24] for more details) to prove Theorem 3. In order to help the reader easily understand the proof, we begin with the real case and introduce some ideas and lemmas first. Assume g ∈ ℝ^2N−1 has i.i.d standard Gaussian entries with mean 0 and variance 1. Notice that 𝒢g is symmetric. Therefore, for any even integer k, (tr (𝒢g)^k)^1/k is the k-norm of vector of singular values, which implies ||𝒢g||₂ ≤ (tr (𝒢g)^k)^1/k. This together with Jensen’s inequality,

$$\mathrm{E}({\Vert \mathcal{G}\mathit{g}\Vert }_2)\le \mathrm{E}\left({(\text{tr}{(\mathcal{G}\mathit{g})}^k)}^{1/k}\right)\le {\left(\mathrm{E}(\text{tr}{(\mathcal{G}\mathit{g})}^k)\right)}^{1/k}.$$ (32)

Thus, in order to get an upper bound of E(||𝒢g||₂), we estimate E(tr((𝒢g)^k)). Denote M = 𝒢g. It is easy to see that

$$\mathrm{E}(\text{tr}({\mathit{M}}^k))=\sum _{0\le i_1,i_2,\dots ,i_k\le N-1}\mathrm{E}(M_{i_1{i}_2}{M}_{i_2{i}_3}\dots M_{i_{k-1}{i}_k}{M}_{i_k{i}_1}).$$ (33)

Therefore, we only need to estimate Σ_{0≤i1, i2,..., ik≤N−1} E(M_i1i2M_i2i3... M_ik−1ikM_iki1).

To simplify the notation, we denote i_k+1 = i₁. Notice that $M_{ij}=\frac{g_{i+j}}{\sqrt{K_{i+j}}}$, where g_i+j is a random Gaussian variable and K_j is defined in (8). Hence, M_{iℓ, iℓ+1} = M_{iℓ′, iℓ′+1} if and only if i_ℓ + i_ℓ+1 = i_ℓ′ + i_ℓ′+1. In order to utilize this property, we would like to introduce a graph for any given index i₁, i₂, ..., i_k and its equivalent edges on the graph. More specifically, we construct graph 𝔉_{i1, i2,..., ik} with nodes to be i₁, i₂, ..., i_k and edges to be (i₁, i₂), (i₂, i₃), ..., (i_k−1, i_k), (i_k, i₁). Let the weight for the edge (i_ℓ, i_ℓ+1) be i_ℓ + i_ℓ+1. The edges with the same weights are considered as an equivalent class. Obviously, M_{iℓ, iℓ+1} = M_{iℓ′, iℓ′+1} if and only if (i_ℓ, i_ℓ+1) and (i_ℓ′, i_ℓ′+1) are in the same equivalent class. Assume there are p equivalent classes of the edges of 𝔉_i1,i2,...,ik. These equivalent classes are indexed by 1, 2, ..., p according to their order in the graph traversal i₁ → i₂ → ... → i_k → i₁. We associate with the graph 𝔉_i1,i2,...,ik a sequence c₁c₂ ... c_k, where c_j is the index of the equivalent class of the edge (i_j, i_j+1). We call c₁c₂ ... c_k the label for the equivalent classes of the graph 𝔉_i1,i2,...,ik.

The label for the equivalent classes of the graph 𝔉_i1,i2,...,ik plays an important role in bounding E(||𝒢g||₂). In order to help the reader understand this concept better, we give two specific examples here. For N = 6, k = 6, i₁ = 1, i₂ = 4, i₃ = 1, i₄ = 3, i₅ = 1, i₆ = 4, we have a corresponding graph and its label for the equivalent classes of the graph is 112211. For N = 6, k = 6, i₁ = 2, i₂ = 3, i₃ = 2, i₄ = 4, i₅ = 2, i₆ = 3, the label for the equivalent classes of the corresponding graph is 112211 as well. Therefore, there may be several different index sequences i₁i₂ ... i_k that correspond to the same label for the equivalent classes of the corresponding graph. Let 𝔄_c1c2...ck be the set of indices whose label of equivalent class of the corresponding graph is c₁c₂ ... c_k, i.e.

$${\mathfrak{A}}_{c_1{c}_2\dots c_k}=\{i_1{i}_2\dots i_k\mid \text{the}\text{label}\text{for}\text{the}\text{equivalent}\text{class}\text{of}\text{the}\text{graph}{\mathfrak{F}}_{i_1,i_2,\dots ,i_k}\text{is}{c}_1{c}_2\dots c_k\}$$ (34)

For given c₁c₂ ... c_k, 𝔄_c1c2...ck is a subset of {i₁i₂ ... i_k |i_j ∈ {0, 1, ..., N − 1}, ∀ j = 1, ..., k}. The following lemma gives us an estimate for the bound Σ_{i1,i2...ik∈𝔄c1c2...ck} E(M_i1i2M_i2i3 ...M_ik−1ikM_iki1).

Lemma 5

Let ζ be the Riemann zeta function and 𝔄_c1c2...ck be defined in (34). Define B(s) = ln(N + 1) if s = 2 and B(s) = ζ (s/2) ≤ π²/6 for s ≥ 4. Then

$$\sum _{i_1{i}_2\dots i_k\in {\mathfrak{A}}_{c_1{c}_2\dots c_k}}\mathrm{E}(M_{i_1{i}_2}{M}_{i_2{i}_3}\dots M_{i_{k-1}{i}_k}{M}_{i_k{i}_1})\le N\prod _{\ell =1}^{p}B(s_{\ell })(s_{\ell }-1)!!$$ (35)

where p is the number of equivalent classes shown in c₁c₂ ... c_k, and s_ℓ, ℓ = 1, ..., p, is the frequency of ℓ in c₁c₂ ... c_k.

Proof

We begin with finding free indices for any i₁, i₂, ..., i_k in the set 𝔄_c1c2...ck. Let (j₁, j₂) be the first edge of the class 1. Therefore, the weight of the first class is j₁ + j₂. For convenience, we define k₁(j₁) = j₁. The first edge of the class 2 must have a vertex k₂(j₁, j₂), depending on j₁ and j₂, and a free vertex, denoted by j₃. The weight of the second class is k₂(j₁, j₂) + j₃. Similarly, the first edge in class 3 has a vertex k₃(j₁, j₂, j₃) and a free vertex j₄, and the weight is k₃(j₁, j₂, j₃) + j₄, and so on. Finally, the first edge in class p has a vertex k_p(j₁, j₂, ..., j_p) and a free vertex j_p+1, and the weight is k_p(j₁, j₂, ..., j_p) + j_p+1. Recall that the entry M_ij is $\frac{g_{i+j}}{\sqrt{K_{i+j}}}$, where g_i+j is a random Gaussian variable. Therefore, for any i₁i₂ ... i_k ∈ 𝔄_c1c2...ck,

$$\mathrm{E}(M_{i_1{i}_2}{M}_{i_2{i}_3}\dots M_{i_{k-1}{i}_k}{M}_{i_k{i}_1})=\prod _{\ell =1}^p\frac{1}{K_{m_{\ell }}^{s_{\ell }/2}}\mathrm{E}(g_{m_{\ell }}^{s_{\ell }}),$$ (36)

where m_ℓ = k_ℓ (j₁, j₂, ..., j_ℓ) + j_ℓ+1. Therefore, it is non-vanishing if and only if s₁, s₂, ..., s_p are all even. In these cases,

$$\mathrm{E}(M_{i_1{i}_2}{M}_{i_2{i}_3}\dots M_{i_{k-1}{i}_k}{M}_{i_k{i}_1})=\prod _{\ell =1}^p\frac{(s_{\ell }-1)!!}{K_{m_{\ell }}^{s_{\ell }/2}}.$$ (37)

Summing (37) over 𝔄_c1c2...ck, we obtain

$$\begin{array}{l}\sum _{i_1{i}_2\dots i_k\in {\mathfrak{A}}_{c_1{c}_2\dots c_k}}\mathrm{E}(M_{i_1{i}_2}{M}_{i_2{i}_3}\dots M_{i_{k-1}{i}_k}{M}_{i_k{i}_1})\le \sum _{j_1=0}^{N-1}\sum _{j_2=0}^{N-1}\cdots \sum _{j_p=0}^{N-1}\sum _{j_{p+1}=0}^{N-1}\prod _{\ell =1}^p\frac{(s_{\ell }-1)!!}{K_{m_{\ell }}^{s_{\ell }/2}}\\ =\sum _{j_1=0}^{N-1}\sum _{j_2=0}^{N-1}\left(\frac{(s_1-1)!!}{K_{k_1(j_1)+j_2}^{s_1/2}}\sum _{j_3=0}^{N-1}\left(\frac{(s_2-1)!!}{K_{k_2(j_1,j_2)+j_3}^{s_2/2}}\sum _{i_4=0}^{N-1}\left(\cdots \sum _{j_{p+1}=0}^{N-1}\frac{(s_p-1)!!}{K_{k_p(j_1,\dots ,j_p)+j_{p+1}}^{s_p/2}}\right)\cdots \right)\right)\end{array}$$

Since, for any 0 ≤ c ≤ N − 1,

$$\sum _{\ell =0}^{N-1}\frac{1}{K_{c+\ell }^{s/2}}\le \{\begin{array}{ll}1+1/2+1/3+\dots 1/N\le ln(N+1)\hfill & s=2,\hfill \\ 1+1/2^{s/2}+\dots +1/N^{s/2}\le \zeta (s/2)\hfill & s=4,6,\dots \hfill \end{array}$$

where ζ is the Riemann zeta function. By defining B(s) = ln(N + 1) if s = 2 and B(s) = ζ (s/2) ≤ π²/6 for s ≥ 4, the desired result easily follows.

The desired bound for E(||𝒢g||₂) can be obtained if we know how many different sets of 𝔄_c1c2…ck are available in the set {i₁i₂ … i_k|i_j ∈ {0, 1, …, N − 1}, ∀ j = 1, …, k}. Let 𝔅_s1s2…sp be the set of all labels of p equivalent classes with ℓ-th class containing s_ℓ equivalent edges respectively, i.e.

$${\mathfrak{B}}_{s_1{s}_2\dots s_p}=\left\{c_1{c}_2\dots c_p\mid \begin{array}{l}{c}_1{c}_2\dots c_p\text{is}\mathrm{a}\text{valid}\text{label}\text{of}\text{equivalent}\text{classes}\text{in}\text{graph}{\mathfrak{F}}_{i_1{i}_2\dots i_k}\hfill \\ \text{and}\text{there}\text{are}{s}_{\ell }\ell \text{'}\mathrm{s}\text{in}\text{the}\text{label}{c}_1{c}_2\dots c_p\hfill \end{array}\right\}$$ (38)

Let ℭ_p be the set of all possible choice of p positive even numbers s₁, …, s_p satisfying s₁ +s₂ +…+s_p = k. Then

$$\begin{array}{l}\mathrm{E}(\text{tr}({\mathit{M}}^k))=\sum _{0\le i_1,i_2,\dots ,i_k\le N-1}E(M_{i_1{i}_2}{M}_{i_2{i}_3}\dots M_{i_{k-1}{i}_k}{M}_{i_k{i}_1})\\ \le \sum _{p=1}^{k/2}\sum _{s_1\dots s_p\in {\mathfrak{C}}_p}\sum _{c_1{c}_2\dots c_k\in {\mathfrak{B}}_{s_1{s}_2\dots s_p}}\sum _{i_1{i}_2\dots i_k\in {\mathfrak{A}}_{c_1{c}_2\dots c_k}}\mathrm{E}(M_{i_1{i}_2}{M}_{i_2{i}_3}\dots M_{i_{k-1}{i}_k}{M}_{i_k{i}_1})\end{array}$$ (39)

By bounding the cardinality of 𝔅_s1s2…sp and ℭ_p, we can derive the bound E(tr(M^k)) hence E(||𝒢g||₂) for the real case. The complex case can be proved by directly using the results for the real case. Now, we are in position to prove Theorem 3.

Proof of Theorem 3

Following (39), we need to count the cardinality of 𝔅_s1s2…sp. For any c₁c₂ … c_k ∈ 𝔅_s1s2…sp, we must have c₁ = 1. Therefore, there are $\left(\begin{array}{c}k-1\\ s_1-1\end{array}\right)$ choices of the positions of remaining 1’s in c₁c₂ … c_k. Once positions for 1’s are fixed, the position of the first 2 has to be the first available slot, we have $\left(\begin{array}{c}k-s_1-1\\ s_2-1\end{array}\right)$ choices for the positions of remaining 2’s, and so on. Thus,

$$\begin{array}{l}\mid {\mathfrak{B}}_{s_1{s}_2\dots s_p}\mid \le \left(\begin{array}{c}k-1\\ s_1-1\end{array}\right)·\left(\begin{array}{c}k-s_1-1\\ s_2-1\end{array}\right)·\dots ·\left(\begin{array}{c}k-s_1-\dots -s_{p-1}-1\\ s_p-1\end{array}\right)\\ =\frac{(k-1)(k-2)\dots (k-s_1+1)}{(s_1-1)!}\frac{(k-s_1-1)\dots (k-s_1-s_2+1)}{(s_2-1)!}\dots 1\\ =\frac{(k-1)!}{{\prod }_{\ell =1}^p(s_{\ell }-1)!{\prod }_{\ell =1}^{p-1}(k-s_1-\dots -s_{\ell })},\end{array}$$

which together with (35) implies, for any s₁s₂ … s_p ∈ ℭ_p,

$$\begin{array}{l}\sum _{c_1{c}_2\dots c_k\in {\mathfrak{B}}_{s_1{s}_2\dots s_p}}\sum _{i_1{i}_2\dots i_k\in {\mathfrak{A}}_{c_1{c}_2\dots c_k}}\mathrm{E}(M_{i_1{i}_2}{M}_{i_2{i}_3}\dots M_{i_{k-1}{i}_k}{M}_{i_k{i}_1})\\ \le N\frac{(k-1)!}{{\prod }_{\ell =1}^p(s_{\ell }-2)!!{\prod }_{\ell =1}^{p-1}(k-s_1-\dots -s_{\ell })}\prod _{\ell =1}^{p}B(s_{\ell })\end{array}$$ (40)

Summing (40) over ℭ_p yields

$$\begin{array}{l}\sum _{s_1\dots s_p\in {\mathfrak{C}}_p}\sum _{c_1{c}_2\dots c_k\in {\mathfrak{B}}_{s_1{s}_2\dots s_p}}\sum _{i_1{i}_2\dots i_k\in {\mathfrak{A}}_{c_1{c}_2\dots c_k}}\mathrm{E}(M_{i_1{i}_2}{M}_{i_2{i}_3}\dots M_{i_{k-1}{i}_k}{M}_{i_k{i}_1})\\ \le N(k-1)!\sum _{s_1\dots s_p\in {\mathfrak{C}}_p}\frac{{\prod }_{\ell =1}^{p}B(s_{\ell })}{{\prod }_{\ell =1}^p(s_{\ell }-2)!!{\prod }_{\ell =1}^{p-1}(k-s_1-\dots -s_{\ell })}\end{array}$$ (41)

Let us estimate the sum in the last line. Let s be the number of 2’s in s₁s₂ … s_p. Then,

$$\prod _{\ell =1}^{p}B(s_{\ell })\le {ln}^s(N+1){\left(\frac{{\pi }^2}{6}\right)}^{p-s}.$$ (42)

Since each s₁, …, s_p ≥ 2 and there are p − s terms greater than 4 among them, we have

$$\prod _{\ell =1}^p(s_{\ell }-2)!!\ge 2^{p-s}$$ (43)

and k − s₁ − … − s_ℓ = s_ℓ+1 + … + s_p ≥ 2(p − ℓ), which implies

$$\prod _{\ell =1}^{p-1}(k-s_1-\dots -s_{\ell })\ge \prod _{\ell =1}^{p-1}2(p-\ell )=2^{p-1}(p-1)!.$$ (44)

There are $\left(\begin{array}{c}p\\ s\end{array}\right)$ choices of the positions of the s 2’s. Moreover, once the s 2’s in s₁s₂ … s_p are chosen, there are at most

$$\left(\frac{k}{2}-s\right)·\left(\frac{k}{2}-s-1\right)·\dots ·\left(\frac{k}{2}-s-(p-s+1)\right)\le {\left(\frac{k}{2}\right)}^{p-s}$$

choices of the remaining p − s s_j ‘s. Altogether,

$$\begin{array}{l}\sum _{s_1\dots s_p\in {\mathfrak{C}}_p}\sum _{c_1{c}_2\dots c_k\in {\mathfrak{B}}_{s_1{s}_2\dots s_p}}\sum _{i_1{i}_2\dots i_k\in {\mathfrak{A}}_{c_1{c}_2\dots c_k}}\mathrm{E}(M_{i_1{i}_2}{M}_{i_2{i}_3}\dots M_{i_{k-1}{i}_k}{M}_{i_k{i}_1})\\ \le N(k-1)!\sum _{s=0}^p\left(\begin{array}{c}p\\ s\end{array}\right){\left(\frac{k}{2}\right)}^{p-s}{ln}^s(N+1){\left(\frac{{\pi }^2}{6}\right)}^{p-s}\frac{1}{2^{p-s}{2}^{p-1}(p-1)!}\\ =2N(k-1)!\frac{1}{(p-1)!}\sum _{s=0}^p\left(\begin{array}{c}p\\ s\end{array}\right){\left(\frac{k}{2}\right)}^{p-s}{ln}^s(N+1){\left(\frac{{\pi }^2}{6}\right)}^{p-s}\frac{1}{4^{p-s}{2}^s}\\ =\frac{2N(k-1)!}{(p-1)!}\sum _{s=0}^p\left(\begin{array}{c}p\\ s\end{array}\right){\left(\frac{{\pi }^{2}k}{48}\right)}^{p-s}{\left(\frac{ln(N+1)}{2}\right)}^s\\ =2N(k-1)!\frac{{\left(\frac{{\pi }^2}{48}k+\frac{ln(N+1)}{2}\right)}^p}{(p-1)!}\end{array}$$ (45)

Finally, (45) is summed over all possible p and we obtain

$$\begin{array}{l}\mathrm{E}(\text{tr}({\mathit{M}}^k))=\sum _{i_1,i_2,\dots ,i_k}\mathrm{E}(M_{i_1{i}_2}{M}_{i_2{i}_3}\dots M_{i_{k-1}{i}_k}{M}_{i_k{i}_1})\\ \le \sum _{p=1}^{k/2}\sum _{s_1\dots s_p\in {\mathfrak{C}}_p}\sum _{c_1{c}_2\dots c_k\in {\mathfrak{B}}_{s_1{s}_2\dots s_p}}\sum _{i_1{i}_2\dots i_k\in {\mathfrak{A}}_{c_1{c}_2\dots c_k}}\mathrm{E}(M_{i_1{i}_2}{M}_{i_2{i}_3}\dots M_{i_{k-1}{i}_k}{M}_{i_k{i}_1})\\ \le 2N(k-1)!\sum _{p=1}^{k/2}\frac{{\left(\frac{{\pi }^2}{48}k+\frac{ln(N+1)}{2}\right)}^p}{(p-1)!}\end{array}$$ (46)

By using the fact that, for any A > 0,

$$\sum _{p=1}^{k/2}\frac{A^p}{(p-1)!}=A\left(1+A+\frac{A^2}{2!}+\dots +\frac{A^{k/2-1}}{(k/2-1)!}\right)\le A{e}^A,$$

(46) is rearranged into

$$\begin{array}{l}\mathrm{E}(\text{tr}({\mathit{M}}^k))\le 2N(k-1)!\left(\frac{{\pi }^2}{48}k+\frac{ln(N+1)}{2}\right)e^{\frac{{\pi }^2}{48}k+\frac{ln(N+1)}{2}}=2N\sqrt{N+1}(k-1)!\left(\frac{{\pi }^2}{48}k+\frac{ln(N+1)}{2}\right)e^{\frac{{\pi }^2}{48}k}\\ \le 2{(N+1)}^{\frac{3}{2}}{k}^k\left(\frac{{\pi }^2}{48}+\frac{ln(N+1)}{2k}\right)e^{\frac{{\pi }^2}{48}k}.\end{array}$$

Let k be the smallest even integer greater than $\frac{24}{{\pi }^2}ln(N+1)$. Then using ||M||₂ ≤ (tr(M^k))^1/k lead to

$$\begin{array}{l}\mathrm{E}({\Vert \mathit{M}\Vert }_2)\le \mathrm{E}({(\text{tr}({\mathit{M}}^k))}^{1/k})\le {\left(\mathrm{E}(\text{tr}({\mathit{M}}^k))\right)}^{1/k}\le {(2{(N+1)}^{\frac{3}{2}})}^{1/k}k{\left(\frac{{\pi }^2}{48}+\frac{ln(N+1)}{2k}\right)}^{1/k}{e}^{\frac{{\pi }^2}{48}}\\ \le 2^{\frac{{\pi }^2}{24ln(N+1)}}·e^{\frac{{\pi }^2}{16}}·\frac{24}{{\pi }^2}ln(N+1)·{\left(\frac{{\pi }^2}{24}\right)}^{\frac{{\pi }^2}{24ln(N+1)}}·e^{\frac{{\pi }^2}{48}}\le C_{1}lnN,\end{array}$$

where the constant C₁ is some universal constant.

Next, we estimate the complex case. In this case, g ∈ ℂ^2N−1, where both its real part and imaginary part have i.i.d. Gaussian entries. Write g = ξ + ıη, where ξ, η ∈ ℝ^2N−1 are real-valued random Gaussian vectors. From the real-valued case above, we derive

$$\mathrm{E}({\Vert \mathcal{G}\mathit{\xi }\Vert }_2)\le C_{1}lnN,\mathrm{E}({\Vert \mathcal{G}\mathit{\eta }\Vert }_2)\le C_{1}lnN.$$

Therefore,

$$\mathrm{E}({\Vert \mathcal{G}\mathit{g}\Vert }_2)=\mathrm{E}({\Vert \mathcal{G}\mathit{\xi }+\iota \mathcal{G}\mathit{\eta }\Vert }_2)\le \mathrm{E}({\Vert \mathcal{G}\mathit{\xi }\Vert }_2)+\mathrm{E}({\Vert \mathcal{G}\mathit{\eta }\Vert }_2)\le 2C_{1}lnN.$$

3.6. Proof of Theorem 1

With Lemmas 1, 2, 4, and Theorem 3 in hand, we are in position to prove Theorem 1.

Proof of Theorem 1

Since (10) is equivalent to (4) by the relation y = Dx, we only need to prove that ŷ = ỹ for noise free data (||ŷ−ỹ||₂ ≤ 2δ/ε for noisy data) with dominant probability. According to Lemma 1, we only need to prove (13). By Lemma 2,

$$\mathrm{P}\left(\underset{\mathit{z}\in \mathfrak{T}(\widehat{\mathit{y}})\cap {\mathbb{S}}_c^{2N-2}}{min}{\Vert \mathit{Bz}\Vert }_2\ge \epsilon \right)\ge 1-2e^{-\frac{1}{2}{\left({\lambda }_M-w({\mathfrak{T}}_{ℝ}(\widehat{\mathit{y}})\cap {\mathbb{S}}_{ℝ}^{4N-3})-\frac{\epsilon }{\sqrt{2}}\right)}^2}.$$

Lemma 4, Theorem 3, and the inequality ${\lambda }_M\ge \frac{M}{\sqrt{M+1}}$ imply that

$${\lambda }_M-w({\mathfrak{T}}_{ℝ}(\widehat{\mathit{y}})\cap {\mathbb{S}}_{ℝ}^{4N-3})-\frac{\epsilon }{\sqrt{2}}\ge \frac{M}{\sqrt{M+1}}-3C_1\sqrt{R}lnN-\frac{\epsilon }{\sqrt{2}}\ge \sqrt{M-1}-3C_1\sqrt{R}lnN-\frac{\epsilon }{\sqrt{2}}.$$

When $M\ge {(6C_1\sqrt{R}lnN+\sqrt{2}\epsilon )}^2+1$, we can easily get $\mathrm{P}\left({min}_{\mathit{z}\in \mathfrak{T}(\stackrel{.}{\mathit{y}})\cap {\mathbb{S}}_c^{2N-2}}{\Vert \mathit{Bz}\Vert }_2\ge \epsilon \right)\ge 1-2e^{-\frac{M-1}{8}}$. We get the desired result.

4. Extension to structured low-rank matrix reconstruction

In this section, we extend our results to low-rank Hankel matrix reconstruction and low-rank Toeplitz matrix reconstruction from their Gaussian measurements.

Since the proof of Theorem 1 does not use the specific property that ŷ is an exponential signal, Theorem 1 holds true for any low-rank Hankel matrices. We have the following corollary, which reads that any Hankel matrix of size N × N and rank R can be recovered exactly from its O(Rln² N) Gaussian measurements, and this reconstruction is robust to noise.

Corollary 1 (Low-rank Hankel matrix reconstruction)

Let Ĥ ∈ ℂ^N×N be a given Hankel matrix with rank R. Let x̂ ∈ ℂ^2N−1 be satisfying x̂_i+j = Ĥ_ij for 0 ≤ i, j ≤ N − 1. Let A = BD ∈ ℂ^M×(2N−1), where B ∈ ℂ^M×(2N−1) is a random matrix whose real and imaginary parts are i.i.d. Gaussian with mean 0 and variance 1, D ∈ ℝ^{(2N−1)×(2N−1)} is the same as defined in Theorem 1. Then, there exists a universal constant C₁ > 0 such that, for any ε > 0, if

$$M\ge {(C_1\sqrt{R}lnN+\sqrt{2}\epsilon )}^2+1,$$

then, with probability at least $1-2e^{-\frac{M-1}{8}}$, we have

1. H(x̃) = Ĥ, where x̃ is the unique solution of

   $$\underset{\mathit{x}}{min}{\Vert \mathit{H}(\mathit{x})\Vert }_{\ast }\mathit{subject}to\mathit{Ax}=\mathit{b}$$

   with b = Ax̂;

2. ||H(x̃) − Ĥ )||_F ≤ 2δ/ε, where x̃ is the unique solution of

   $$\underset{\mathit{x}}{min}{\Vert \mathit{H}(\mathit{x})\Vert }_{\ast }\mathit{subject}to{\Vert \mathit{Ax}-\mathit{b}\Vert }_2\le \delta$$

   with ||b − Ax̂||₂ ≤ δ.

Moreover, Theorem 1 can be extended to the reconstruction of low-rank Toeplitz matrix from its Gaussian measurements. Let T̂ ∈ ℂ^N×N be a Toeplitz matrix. Let x̂ ∈ ℂ^2N−1 be a vector satisfying x̂_{N−1+(i−j)} = T̂_i,j for 0 ≤ i, j ≤ N − 1. Let P ∈ ℂ^N×N be an anti-diagonal matrix with anti-diagonals of 1. Then, it is easy to check that T̂ = H(x̂)P. Thus, we define a linear operator T that maps a vector in ℂ^2N−1 to a N × N Toeplitz matrix by T(x) = H(x)P. Since P is a unitary matrix, one has ||T(x)||_* = ||H(x)P||_* = ||H(x)||_*. Therefore, the above corollary can be adapted to low-rank Toeplitz matrices.

5. Numerical experiments

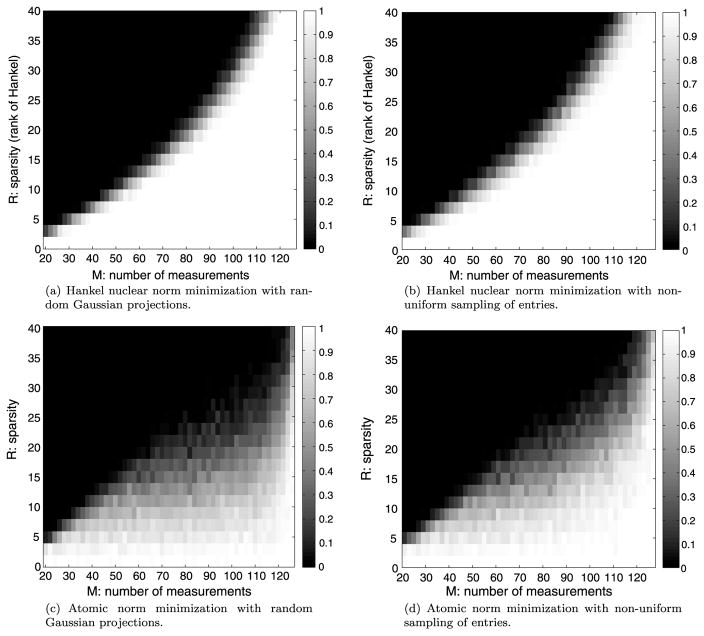
In this section, we use numerical experiments to demonstrate the empirical performance of our proposed approach, and compare it with other methods including those in [10,23]. We use superpositions of complex sinusoids as test signals. Note that the application of our approach is not limited to such signals but any signals that are superpositions of complex exponentials. We are going to consider two sampling schemes, namely, the random Gaussian sampling model in Theorem 1 and the non-uniform sampling of entries studied in [10,23]. For the latter sampling scheme, it randomly observes M entries of x̂ whose locations are uniformly distributed in all M-subsets of {0, 1, …, 2N −2}. We also consider two signal reconstruction algorithms, the Hankel nuclear norm minimization and the atomic norm minimization, from the given samples. Therefore, we have four different approaches to compare: the Hankel nuclear norm minimization with random Gaussian sampling (our proposed approach), the Hankel nuclear norm minimization with non-uniform sampling of entries (EMaC in [10]), the atomic norm minimization with random Gaussian sampling, and the atomic norm minimization with non-uniform sampling of entries (off-the-grid CS in [23]).

We fix N = 64, i.e., the dimension of the true signal x̂ is 127. We conduct experiments under different M and R for different approaches. For each approach with a fixed M and R, we test 100 runs, where each run is executed as follows. We first generate the true signal x̂ = [x̂(0), x̂(1), …, x̂(126)]^T with $\widehat{x}(t)={\sum }_{k=1}^R{c}_k{e}^{\iota 2\pi f_{k}t}$ for t = 0, 1, …, 126, where f_k are frequencies drawn from the interval [0, 1] uniformly at random, and c_k are complex coefficients satisfying the model c_k = (1+10^0.5m_k)e^i2πθ_k with m_k and θ_k being uniformly randomly drawn from the interval [0, 1]. Then we get M samples of x̂ according to the corresponding sampling scheme. Finally, a reconstruction x̃ is obtained by solving the corresponding reconstruction algorithm, which is numerically implemented by alternating direction method of multipliers (ADMM). If $\frac{{\Vert \stackrel{\sim }{\mathit{x}}-\widehat{\mathit{x}}\Vert }_2}{{\Vert \widehat{\mathit{x}}\Vert }_2}\le {10}^{-3}$, then we regard it as a successful reconstruction.

We plot in Fig. 1 the rate of successful reconstruction with respect to different M and R for different approaches. The black and white region indicate a 0% and 100% of successful reconstruction respectively, and a grey between 0% and 100%. From the figure, we see that the atomic norm minimization has similar performance under the random Gaussian sampling and the non-uniform sampling of entries. Moreover, the Hankel nuclear norm minimization also has similar performance under these two types of different sampling schemes. Compared with the atomic norm minimization, the Hankel nuclear norm minimization method is more robust when neighboring frequencies are close, despite different sampling schemes used.

Fig. 1.

Numerical results.

6. Conclusion and future works

In this paper, we study compressed sensing of signal that is a weighted sum of R complex exponential functions with or without damping factor. The measurements are obtained by random Gaussian projections. We prove that, as long as the number of measurements is greater than O(Rln² N) with N the dimension of the signal, minimization (4) is guaranteed to get a robust reconstruction of the underlying signal. Compared to results in [10,23] where partial entries of the underlying signal are observed, our proposed approach does not require any incoherence condition (i.e. does not require any separation condition on frequencies for signals without damping).

The bound O(Rln² N) we obtained is not optimal. There are several possible direction to improve it. Firstly, we may improve the estimation of E(||𝒢g||₂), a key step in our proof. We empirically observed that $\mathrm{E}({\Vert \mathcal{G}\mathit{g}\Vert }_2)=O(\sqrt{\mathit{R}lnN})$, which is better than the bound in Theorem 3. We would prove this bound theoretically. Secondly, we may borrow techniques from compressed sensing to get the optimal bound under Gaussian measurements. Actually, there has been recent work that yields precise bounds [17,18,22]. These results assume Gaussian measurements, but all quantities involved are reals. It is interesting to explore whether those results can be extended to our setting.