A Meta-Analysis Suggests Different Neural Correlates for Implicit and Explicit Learning

SUMMARY

A meta-analysis of non-human primates performing three different tasks (Object-Match, Category-Match, and Category-Saccade associations) revealed signatures of explicit and implicit learning. Performance improved equally following correct and error trials in the Match (explicit) tasks but it improved more after correct trials in the Saccade (implicit) task, a signature of explicit vs implicit learning. Likewise, error-related negativity, a marker for error processing, was greater in the Match (explicit) tasks. All tasks showed an increase in alpha/beta (10–30 Hz) synchrony after correct choices. However, only the implicit task showed an increase in theta (3–7 Hz) synchrony after correct choices that decreased with learning. In contrast, in the explicit tasks, alpha/beta synchrony increased with learning and decreased thereafter. Our results suggest that explicit vs implicit learning engages different neural mechanisms that rely on different patterns of oscillatory synchrony.

eTOC Blurb

In brief, Loonis et al. find that explicit and implicit learning use feedback about correct choices vs errors differently. Implicit learning relies more on theta synchrony (3–7 Hz) while explicit learning relies on alpha/beta synchrony (10–30 Hz).

INTRODUCTION

Learning was once believed to be a unitary process. As it turned out, however, patient HM and other amnesia patients have preserved skill learning despite an inability to retain and recall new facts and episodes (Scoville and Milner, 1957; Milner, 1962; Milner et al. 1968; Cohen and Squire, 1980). This led to the notion that there are at least two major forms of learning: one, hippocampal-dependent and episodic in content (explicit learning) and, another, non-hippocampal and largely unconscious (implicit learning).

While it is clear that explicit and implicit learning engage distinct brain systems, differences in their neural mechanisms have been less clear. For the most part, studies of the neural correlates of both types of learning report similar findings. On the neuron level, tuning sharpens, signal-to-noise ratio improves and their activity becomes a better predictor of task events (Antzoulatos and Miller, 2011; Asaad and Miller, 1998; Brincat and Miller, 2015; Chen and Wise, 1995; Sakai and Miyashita, 1991; Pasupathy and Miller, 2005; Williams and Eskandar, 2006; Wirth et al., 2003; Wirth et al., 2009). On the network level, learning enhances oscillatory activity, improves synchrony between neurons, and even sculpts unique oscillatory ensembles (Antzoulatos and Miller, 2014; Brincat and Miller, 2015; Buschman et al., 2012; Hargreaves et al., 2012; Jutras et al., 2009; Jutras et al. 2013). Animal studies are generally agnostic as to whether this plasticity is related to explicit or implicit learning. Assignment to one or the other is typically made by whether the brain area in question has been associated with explicit learning (e.g., the hippocampus) or implicit learning (e.g., the basal ganglia) and whether learning is fast (explicit) or slow (implicit). There is no clear neural signature differentiating the two.

This is due, in part, to practical considerations. A typical experiment trains animals to learn one task. That is difficult enough. Training animals to learn two or more tasks is prohibitively time-consuming. It occurred to us, however, that we had data from three experiments that differed in their formal demands in two ways: one, in the content of what was learned (paired associations between objects vs category membership), and, two, in how that learning was “read out” (via a match decision or visuomotor association). Fortuitously, there was enough overlap in the tasks for us to isolate these different factors. We found different patterns of post-choice synchrony that varied with the read-out, not with the content. Examination of the animals’ behavior and neural activity supported the conclusion that these different synchrony patterns were signatures of explicit and implicit learning.

RESULTS

Tasks

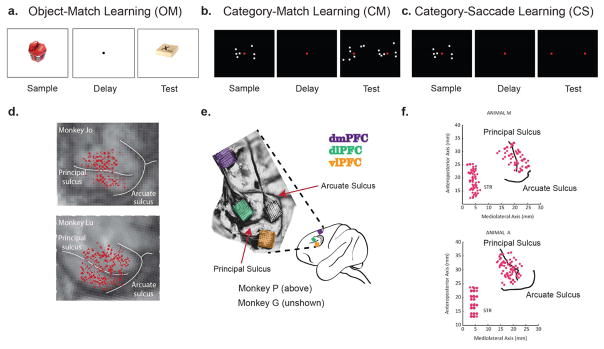
Six monkeys (three different pairs) performed three different learning tasks (Fig. 1A–C). During each session of the Object Match task (OM; Fig. 1A), animals learned through trial-and-error four novel associations between pairs of objects (see Methods). They saw two objects in succession: first a sample and then a test. If the test object was the pre-assigned paired associate of the sample, they were rewarded with juice for making a saccade to a subsequently displayed, randomly positioned target. If the test object was not the pre-assigned paired associate of the sample, then they had to withhold a response to this target and await the presentation of the correct test object. If they responded to the wrong test object, they received error feedback, i.e. there was no reward and a red screen flashed on.

Figure 1.

A. In the Object-Match, task the animal was instructed to learn by trial- and error- whether a sample and test object were the correct pair. In each trial, the animal was first presented a sample object for 0.5s, and after a delay of 0.75s, a test object. The animal had to confirm whether the test object was the correct associate of the sample object (i.e. the correct match). In every session, each animal learned to associate 4 different sample objects with 2 test objects (Brincat and Miller, 2015). B, In the Category-Match task, each animal had to learn by trial-and-error two different, de novo dot-pattern categories. In each trial, the animal was first presented with a sample exemplar from one of two possible and, then after a variable delay (.85–1.25s), test exemplars one from each of the two possible categories. In order to select the test exemplar corresponding to the category of the sample, the animal had to fixate on it for .7s. In this task, the animals were matching the category of the sample to the category of the test, hence Category-Match learning. C. In the Category-Saccade task, each animal had to learn two different, de novo categories. In this task, the animal was presented with a sample exemplar for 0.6s, held fixation through a 1s delay, and had to indicate the category membership of this exemplar by making a saccade to the right or left target (Antzoulatos and Miller, 2011). D. In the Object-Match task, we recorded from 617 pairs within prefrontal cortex (PFC) and 941 pairs between PFC and hippocampus (HPC). Electrodes within PFC were spread equally across ventrolateral and dorsolateral prefrontal cortex (vlPFC and dlPFC). E. In the Category-Match task, we recorded from 64 electrode arrays in each vLPFC, dLPFC, and dorsomedial PFC (dmPFC). For PFC, we combined vlPFC and dlPFC electrode pairs, and recorded from 4032 pairs. For PFC-dmPFC, we recorded from 8192 pairs of electrodes. F. In the Category-Saccade task, we recorded from 240 PFC pairs (across both vl- and dlPFC), and 426 PFC-striatal (STR) electrode pairs.

The other two tasks required animals to categorize dot patterns that were distortions of prototype patterns (Fig. 1B, C). These prototypes were jittered according to a set of statistical rules to produce a large number of exemplars for each category. For each recording session, two novel categories were generated, and the animals had to learn through trial-and-error which exemplars belonged to which categories. The animals were first presented with a sample exemplar from one of the categories, which was then followed by a short delay. In the Category Match task (CM), two test exemplars appeared side-by-side after this delay – one on the right side of the screen, and the other on the left (Fig. 1B). One of the exemplars was from the same category as the sample (a category match); the other was from the other category. The left vs right location of the matching exemplar was random. The monkeys free-viewed the test exemplars and were rewarded for maintaining fixation on the correct one. If incorrect, the animals received error feedback: there was no reward and the chosen stimulus turned red. In the Category-Saccade task (CS), at the end of the delay, two green dots appeared on the right and left side of the screen. Each of the categories was arbitrarily associated with a saccade to the right or left dot. (Fig. 1C). The monkeys learned by trial-and-error which saccade was associated with which category. As before, an incorrect response was followed by error feedback (no reward and a presentation of the sample exemplar at the correct location).

In order to facilitate learning in the category tasks, each session was organized into a set of blocks. In the first block, the animals were presented with only two exemplars from each category. To move on from one block to the next, the animals had to perform at or above 70% correct. With every subsequent block, a greater number of novel exemplars from each category was used. In each block, there were a total of 2^block exemplars (Antzoulatos and Miller, 2011). Thus, each time they reached criterion, the animals were challenged with more novel exemplars, facilitating their gradual acquisition of the categories.

For all three tasks, the animals were well trained on the formal demands of the tasks, but had to learn new stimuli for each recording session. In each task, animals started near, or at, chance and gradually reached a good level of performance (> 75% correct) within a single recording session (average 2–3 hours). Mean performance during Category-Saccade and Category-Match learning was no different (CM, 79.3%; CS, 82.1%; p = 0.1637), while performance during Object-Match learning was somewhat lower (69.1%, vs. CS p = 1 × 10⁻⁷; vs. CM, p = 2 × 10⁻²⁴, two-sided t-test). Recordings were obtained from sites distributed evenly across dlPFC and vlPFC, anterior to the origin of the principal sulcus (Fig. 1D–E). Additional recordings were obtained in the Object-Match task from the hippocampus (HPC), in the Category-Saccade task from the anterior caudate (STR, striatum), and in the Category-Match task from dorsomedial Prefrontal Cortex in the vicinity of the supplementary eye fields (dmPFC).

For the sake of analysis, we divided learning into stages. In the Object-Match task, the animals gradually acquired the paired associations. Thus, we evenly divided the session into Early (first third of trials), Middle (middle third) and Late (final third) learning stages. Because of the blocked structure of the category learning tasks, defining the learning stages was less straightforward. In order to do so, we focused on the acquisition of category information to determine learning stages, as we had in our prior work (Antzoulatos and Miller, 2015). Category knowledge was assessed by performance to the novel exemplars. Early in learning, the monkeys had not yet acquired any category information. When novel exemplars were introduced at the start of a block of trials, performance to novel exemplars was substantially diminished, if not at chance (i.e., they guessed). By contrast, late in learning, they had acquired the categories and performance to novel exemplars was at a high level (75% correct) and stable (i.e. the animal’s performance to novel stimuli reached an asymptote). In order to characterize this asymptote, we tested sequentially whether or not performance on novel exemplars in the first n trials differed from performance on novel exemplars on trials n+1 to the end of the day. When the null hypothesis could no longer be rejected, we considered those trials as late learning. To reject this null hypothesis, we used a two-sided t-test and set a threshold of p < .05. In the Category-Saccade task, this plateau of novel exemplar performance occurred in block 5, and, in the Category-Match task, it occurred in block 2.

As a result, in the Category-Saccade task, we identified an Early stage of learning (prior to acquisition of category information, i.e., chance performance to novel exemplars) as the first 80 trials (the first two blocks of trials, on average). The Late learning stage occurred in blocks 5 to 8 (on average, trials 210–550), when performance to novel exemplars was high and stable (and thus the categories were learned). We could also identify a Middle stage (around trials 81–209 and blocks 3–4, on average) in which performance to novel exemplars did not drop to chance, but was below criterion and improved over the block of trials (and thus categories were being acquired). Finally, in the Category-Match task, learning occurred more rapidly. Within the first 100 trials, and by block 2, the monkeys’ average performance to novel exemplars reached an asymptote. There was no clear middle stage. Therefore, in the Category-Match task, the first 100 trials were classified as Early learning, and the following 100 trials were classified as Late.

The idea in comparing these three tasks was that they overlapped in different ways. Two of them shared the requirement to make a match decision (but to different types of stimuli - a paired associate object vs dot category exemplars). The other two shared similar stimuli (dot category exemplars) but differed in response (match decision vs performing an associated visuomotor response).

Correct Feedback was Emphasized During the Visuomotor Learning Task

An examination of the animals’ behavior suggested that the match tasks relied on explicit learning while the visuomotor (saccade) task relied on implicit learning. Prior studies have shown that implicit learning relies more on correct than error feedback. For example, skill learning in amnesia patients is better when correct feedback is emphasized (Evans et al., 2000; Squires et al., 1997; Roberts at al., 2016; Maxwell et al., 2001; Poolton et al., 2005). The different use of feedback information for learning seemed to divide our Match and Saccade tasks.

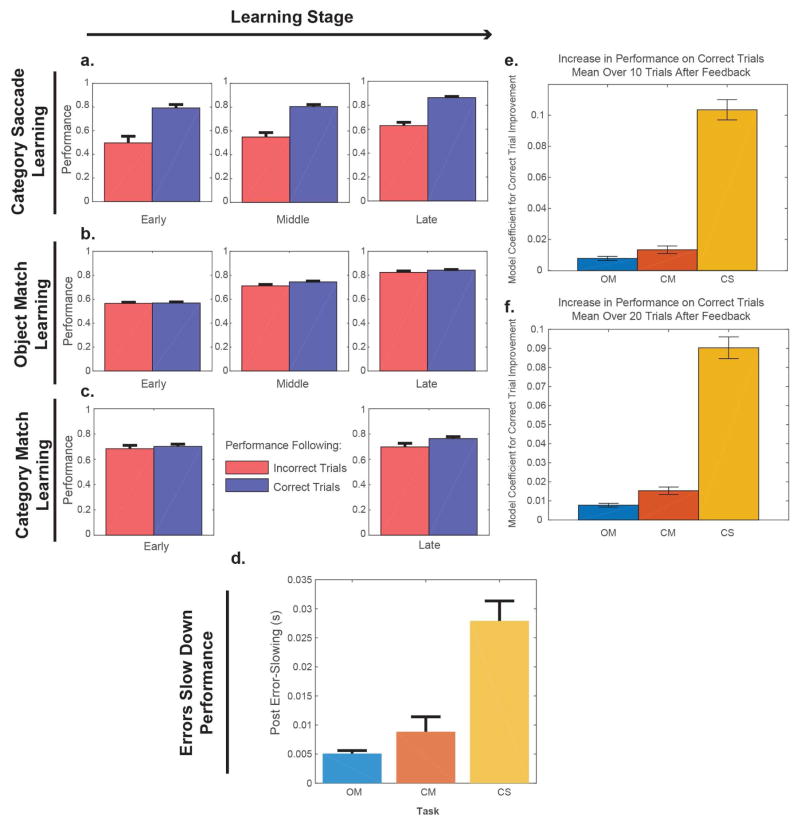
We found that Category-Saccade learning improved more after correct choices (and correct feedback) than after incorrect choices (and error feedback). In fact, error feedback in this task appeared to be disruptive; performance worsened immediately after an incorrect trial and reaction times increased. Figure 2A shows performance on Category-Saccade trials that were immediately preceded by either a correct response (and correct feedback) or an incorrect response (and error feedback). Performance on the Category-Saccade task was significantly better if the preceding trial was correct (blue bars) than if the previous trial was incorrect (red bars) (+23.97% after correct choices, p < 1 × 10⁻⁴, for all stages, bootstrap). This performance advantage after correct trials held throughout learning, even as overall performance improved, and extended over several trials (Figure S1). Further, reaction times on those trials following an incorrect trial increased by 27.9ms (Fig. 2D, p < 1 × 10⁻⁴). This increase in reaction times was not driven exclusively by a rise in the number of errors, for even correctly performed trials after an error had much higher reaction times (23.9ms, p < 1 × 10⁻⁴).

Figure 2.

In A, each bar represents performance separated out by monkey on trials following either an incorrect response (red bar) or a correct response (blue bar) during Category-Saccade learning. All trials were pooled across days for each stage of learning (presented as separate columns). Error bars show 95% confidence interval generated from a binomial distribution. In B, C we again plotted performance following a correct and incorrect trial for both the Object-Match and Category-Match tasks; however, both monkeys in each task were pooled. D. Post-error slowing across the 3 different learning tasks: Object-Match (OM), Category-Match (CM), and Category-Saccade (CS). CM and OM post-error slowing were not significantly different (p = 0.172). CS post-error slowing was significantly larger than both Match tasks (p < 1 × 10⁻⁴). Error bars represent the SEM. In E, F mean performance changes over 10 trials and 20 trials following feedback (correct vs. error) after regressing out total mean performance. In both Match tasks, performance increased marginally following correct trials, while in the Category-Saccade task performance improved by 10-fold relative to the Match tasks. See also Figure S1.

By contrast, during the two Match tasks (OM and CM), there was barely a difference in performance (+1.86% in Object-Match task, p < .005, Fig. 2B; +3.75%, in Category-Match, p < 0.025, bootstrap, Fig. 2C) and in reaction times (Fig. 2D: OM: 5.1ms, p < 1 × 10⁻⁴; CM: 8.8ms, p < 1 × 10⁻⁴) on trials following correct trials vs incorrect trials. Only early in learning did both Match tasks differ marginally in their performance improvement after correct trials (Early, +2.86% CM > OM, p = 0.0524; Late, +2.32%, CM > OM, p = .1048). Moreover, this difference in performance was minor relative to those differences between both Match tasks and the Saccade task (CS vs. OM, +29.24% (early), +21.45% (late), p < 1 × 10⁻⁴; CS vs CM, +26.31% (early), +19.13% (late), p < 1 × 10⁻⁴). In contrast, the differences in reaction times following an error were not statistically different between Match tasks (p = 0.172), and were significantly smaller than in the Saccade task (vs. OM. −22.8ms, vs. CM, −17.7ms, p < 1 × 10⁻⁴).

Moreover, these performance differences following error and correct feedback persisted across trials and independent of learning stage classification (Fig. 2E, F). We estimated a bivariate linear model examining whether both the mean performance of all trials prior to feedback and the type of feedback (correct or an error) influenced mean performance in the 10 (Fig. 2E) or 20 (Fig. 2F) trials post-feedback. Again, we found that in the Saccade tasks there was significantly better performance after correct than error trials than in the Match tasks (20 trial model – OM: +0.0078, CM: +0.0153, CS: +0.0903; CM, OM < CS, p < 0.0004; 10 trial model – OM: +0.0078, CM: +0.0134, CS: +0.1034; CM, OM < CS, p < 0.0004, bootstrap). We will see next that these task differences were also mirrored in differences in an evoked potential called the error-related negativity.

Error-Related Negativity was Stronger for Match than Saccade Learning

Error-related negativity (ERN) is an event-related potential observed after committing errors during learning. It has been correlated with error awareness (Frank et al., 2005; Gehring and Willoughby, 2002; Scheffers and Coles, 2000; Walsh and Anderson, 2012; Wessel et al., 2011; Wessel, 2012). The behavioral analysis described above suggested that Category-Saccade learning was less reliant on errors than the two match tasks. This was paralleled in a weaker error-related negativity (ERN) in the Category-Saccade task relative to the match tasks.

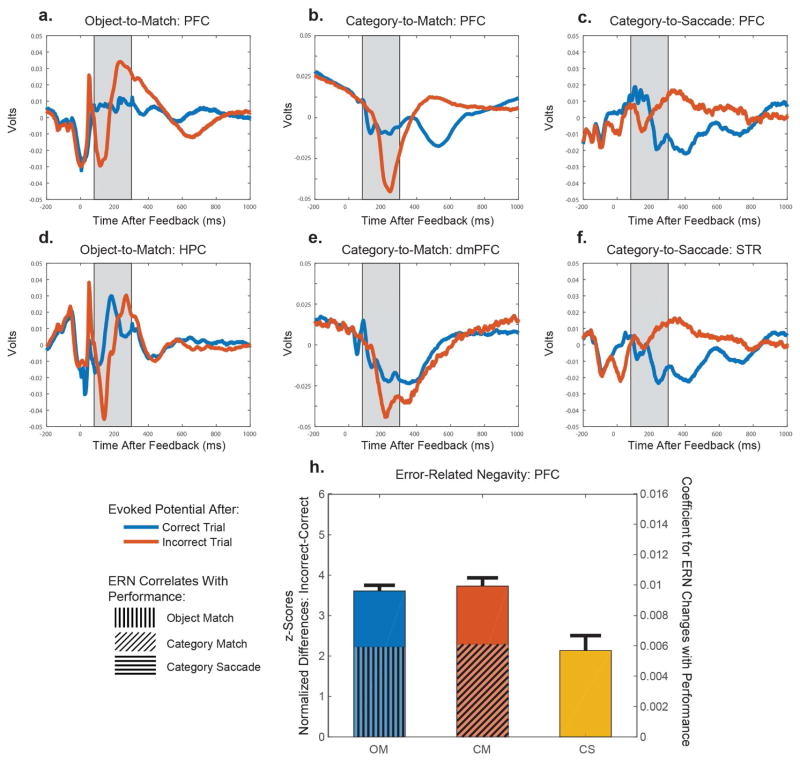
Figure 3 shows the event-related potentials (ERPs) following correct (blue) or error (red) feedback, averaged across all electrodes, for the Object-to-Match (left column), Category-to-Match (middle column), and Category-to-Saccade (right column) tasks. In humans, the ERN typically peaks between 80–300ms after an error. This time period is shaded grey in Figure 3A–F. As predicted, during Category-Saccade learning, there was no prominent ERN in the expected time window in either the PFC (top right) or STR (bottom right) (Fig. 3C, F). In contrast, in that same time window, during both Object-Match and Category-Match learning, there was a prominent negative potential, an ERN, following errors (Fig. 3A, D). This sharp negative potential on error trials (red line) was most clear when compared to its absence following a correct response (blue line). The ERNs in both Match tasks were seen in PFC, dmPFC, and HPC (Fig. 3A, B, D, E).

Figure 3.

A–C. Across all electrodes in prefrontal cortex, we computed the evoked potentials in each task separately. The blue line is the evoked potential averaged across correct trials, and the red line is the evoked averaged across the incorrect trials. The shaded grey region represents the time of an expected error-related negativity, between 80–300 ms after feedback. In the Object-Match and Category-Saccade tasks, we averaged across 242 and 64 electrodes distributed across vl- and dlPFC, respectively. In the Category-Match task, we averaged across each array within vl- and dlPFC (n = 97 arrays). D. Evoked potentials within the hippocampus (n= 162 electrodes), E. the supplementary eye fields (n = 30 arrays), and F. the striatum (n=65 electrodes) during the Object-Match, Category-Match, and Category-Saccade tasks respectively. G. The error-related negativity is plotted here for each task. The error-related negativity was computed by subtracting the evoked potentials on correct and incorrect trials, and aligned to the maximal differences across tasks. We compared the peak negativity by averaging around this peak (+/− 25 ms). The error bars represent +1 SEM. The hatched lines over lying the bars reflect the estimated coefficients for the change in the ERN as a function of performance (10 trial mean prior to feedback). In both Match tasks, the ERN increased with performance and hence behavioral certainty. The estimated coefficient in the Saccade task was near to 0, and not statistically significant. See also Figure S2.

In order to account for any differences associated with different neural latencies across the tasks, we recomputed the ERN by z-scoring the raw voltage differences to a within trial mean and STD, and aligning each of the tasks to their maximal difference. We quantified these differences over a 50-ms window centered on the peak negativity for each of the 3 tasks (Fig. 3H). There was no significant difference between the match tasks (p = 0.911, bootstrap). By contrast, the ERN in the Match tasks was significantly greater than in the Saccade task (p < .001). This supported the conclusion that errors were of greater use in the match tasks and, thus, that they depended on explicit learning. The lack of an ERN during the Saccade task supports its reliance on implicit learning.

In order to assess the relationship between ERN and task performance, we defined the ERN on each trial as the distance between the maximum and minimum recorded value following an error. As in Figure 3H, we found that the ERN was significantly greater on Match tasks than that on Saccade tasks (Figure S2). This did not depend on the time window investigated, and this pattern extended to the HPC, dmPFC, and STR (Figure S2). There was also a correlation between behavioral performance and ERN. To compute this correlation, we found for each session and each trial the mean ERN across electrodes, and the mean performance over the 20 preceding trials. In order to account for the variability in the ERN across sessions, we then subtracted from each trial’s ERN the magnitude of the ERN at the 75% performance level for each session, and linearly regressed these corrected ERN’s on performance. In the end, we found that in the Match tasks as performance increased so did the ERN. This was not true in the Saccade task (Fig. 3H; OM: +0.0059, p = 0.002; CM: +0.0061, p < 1×10⁻³; CS: −1.46×10⁻⁴, p = 0.996, bootstrap). These coefficients are plotted as hatched lines in Figure 3H. Next, we’ll show that feedback-period patterns of oscillatory synchrony also differed between the Match vs Saccade tasks.

Neural Synchrony Differentiates Learning Styles

In a previous report using the Object-Match task, Brincat and Miller (2015) found differences in LFP-LFP synchrony between and within the PFC and HPC during the feedback period. After correct responses, there was long-latency, long-duration synchrony, mainly at 10–30 Hz (the alpha-2/beta band). By contrast, after incorrect responses, there was short-latency, short-duration synchrony at 3–7 Hz (i.e., delta/theta band). This was interpreted as reflecting the network interactions that guide learning by signaling success or failure. The differences in how animals responded to success and failure between the Match tasks vs Category-Saccade task in this report raised the question of whether feedback-related network interactions also differed: they did.

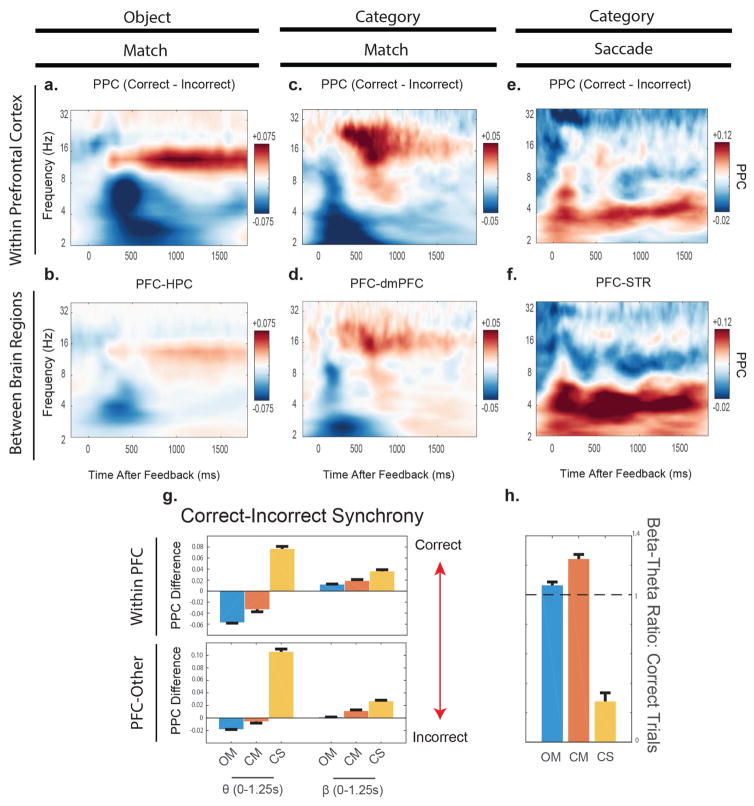
Figure 4 plots differences in synchrony as estimated by the pairwise phase consistency statistic (PPC) during the feedback period between correct and error trials. PPC quantifies whether there are any stable phase relationships between signals of the same frequency across trial conditions. Because the tasks involved eye movement responses tied to the correct exemplar, we removed the potentials related to the saccade away from the response target so that it would not contribute to any synchrony effects.

Figure 4.

In panels A–E., plotted is the difference in pairwise phase consistency between correct and incorrect trials. Red means a greater synchrony value on correct trials, and blue means a greater synchrony value on incorrect trials. Note the difference in color scales among the 3 panels. In G., we compared how the magnitude of these normalized synchrony values differed within the theta (3–7 Hz) and the alpha-2/beta bands (10–30 Hz) over time. In H, we computed that the ratio of beta-theta synchrony on correct trials varied for each task. We found that in both Match tasks the beta-theta ratio was greater than 1. This was not true in the Category-Saccade task (ratio = 0.2759). The error bars represent +1 SEM. See also Figure S3.

Both of the Match tasks showed the same pattern: an increase in alpha-2/beta synchrony after a correct response and an increase in delta/theta synchrony after an incorrect response. During the Object-Match task, there was an increase in alpha-2/beta synchrony on correct trials (red colors) both within the PFC (Fig. 4A) and between the PFC and HPC (Fig. 4B). On error trials, there was an increase in delta/theta synchrony (blue colors), especially within the PFC (Fig. 4A). Note that the increase in alpha-2/beta on correct trials tended to be long in duration and peaked after a long latency (750–1000ms), whereas the increase in theta/delta synchrony on incorrect trials peaked earlier (400–500ms). This is consistent with our prior report (Brincat and Miller, 2015). Similar results were obtained from the Category-Match task (Fig. 4C, D), especially within the PFC (Fig. 4C).

By contrast, the Category-Saccade task produced a different pattern of results. Like the Match tasks, there was an increase in alpha-2/beta after correct responses (light red colors). However, correct responses in the Category-Saccade produced a large increase in theta/delta (darker red colors), unlike the Match tasks in which delta/theta synchrony only increased after incorrect responses. This was true both within the PFC (Fig. 4E) and especially between the PFC and STR (Fig. 4F).

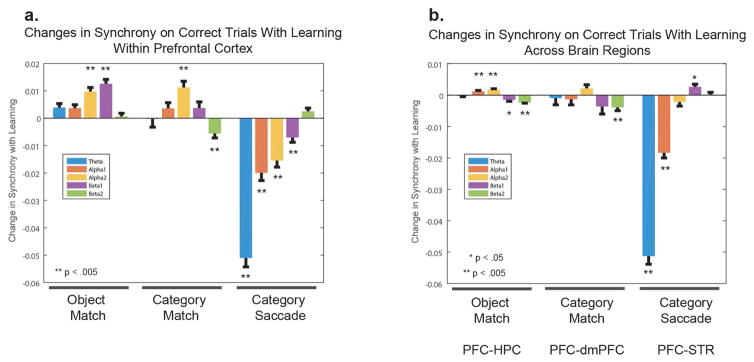
We quantified these differences by averaging over the 1.25 seconds after feedback was delivered (time zero in Fig. 4A–F). The results are shown in Fig. 4G. Positive values indicate greater synchrony after a correct response; negative values indicate greater synchrony after an incorrect response. In the alpha-2/beta band, all three tasks showed a significant increase in synchrony after correct trials only, within the PFC (OM, +0.012; CM, +0.0186; CS, +0.0358; p < 2 × 10⁻⁴, bootstrap) and, albeit weaker, between PFC and other areas (OM, +0.0012, p = 0.002; CM, +0.0112, p < 2 × 10⁻⁴; CS, +0.0268, p < 2 × 10-4). In the delta/theta band, there was a marked difference between the Match tasks and the Category-Saccade task. The Match tasks showed a significant increase in delta/theta synchrony after incorrect responses, especially within the PFC (OM, −0.0517; CM, −0.0129, p < 2 × 10⁻⁴) but also between PFC and HPC, and PFC and dmPFC (“PFC-Other”, OM, −0.018, p < 2 × 10⁻⁴; CM, −0.0054, p = 0.0458). By contrast, in the Category-Saccade task there was an increase in delta/theta synchrony after correct responses within the PFC (CS, +0.067, p < 2 × 10⁻⁴) and, more prominently, between PFC and STR (CS, +0.1057, p < 2 × 10⁻⁴).

Because there were small differences in the error feedback across tasks (red screen in the OM task, correct test exemplar turning red in the CM task, and correct exemplar presented in the correct location in the CS task), we also examined whether these synchrony patterns (i.e. differences in the prevalence of theta and beta oscillations) were present on correct trials alone. We compared the relative amount of synchrony in different frequency bands by calculating the ratio of alpha-2/beta synchrony relative to delta/theta synchrony. A value greater than 1 indicates that synchrony in the alpha-2/beta band was greater than that in the delta/theta band. Values less than one indicate stronger delta/theta synchrony relative to alpha-2/beta. This is plotted in Figure 4H.

Both Match tasks had beta-theta ratios significantly above 1 (OM, ratio = 1.0641, p = 0.0034; CM, ration = 1.2425, p < 2 × 10⁻⁴, bootstrap). This shows that alpha-2/beta dominated over delta/theta synchrony on correct trials during the Match tasks. By contrast, in the Category-Saccade task, the ratio was significantly less than 1 (ratio= 0.2759, p < 2 × 10⁻⁴), indicating the dominance of delta/theta over alpha-2/beta on correct trials. Taking the absolute values of the ratio differences from 1 showed that the increase in delta/theta synchrony following correct Category-Saccade responses was greater than the increase in alpha-2/beta synchrony following correct trials in the Object-Match (+0.66, p < 2 × 10⁻⁴) or Category-Match (+0.4816, p < 2 × 10⁻⁴) tasks. None of these effects were influenced by the time window chosen for analysis (Figure Supplemental 3). These results suggest explicit and implicit learning may be differentiated by distinct patterns of network synchrony in response to feedback.

Neural Synchrony Changes with Learning and Learning Style

We next examined whether synchrony during the feedback period changed with learning and, if it did, whether it did so differently for the putative explicit vs implicit learning tasks. To investigate these changes, we focused on correct trials, because, for one, in the Category-Match task, animals learned rapidly and we only had a small number of incorrect trials. Two, longer duration synchrony (~1–2s) tended to be seen after correct trials in all three tasks (albeit at different frequencies), and these longer duration events helped reduce the noise in our synchrony estimates. And three, whether the task was implicit or explicit, performance levels following correct trials was comparable (Fig. 2). To compute a frequency profile of the changes with learning, we computed PPC values using the traditional frequency bands: theta (3–7 Hz), alpha-1 (8–9 Hz), alpha-2 (10–12 Hz), beta-1 (13–17 Hz), and beta-2 (18–30 Hz). We used the entire 1.7 second interval following delivery of feedback and compared the average values from early vs late in learning (as defined previously).

Figure 5 shows the change in PPC from early to late in learning. Fig. 5A shows these changes within PFC alone and Fig. 5B shows them between the PFC and other areas (PFC-dmPFC, PFC-STR, and PFC-HPC). Positive values indicate an increase with learning, and negative values, a decrease. The largest effect was seen during Category-Saccade learning. There was a decrease in theta synchrony within PFC (Fig. 5A) and between PFC and STR (Fig. 5B) (PFC: −0.0472; PFC-STR: −0.0472, p < .005, bootstrap). By contrast, there was little or no change in theta synchrony with learning during either Object-Match or Category-Match tasks. Instead, Match learning showed a moderate, but significant, increase in synchrony in the higher frequencies, especially in the alpha-2/beta-1 band, within PFC (OM: alpha-2, +0.0097; beta-1, +0.0126, p<.005; CM: alpha-2, +0.0113, p <.005, bootstrap). There was also a modest, but significant, drop in beta-2 band synchrony across brain regions during the Match tasks, but not the Saccade task (OM: PFC-HPC, beta-2, −0.0023, p<.005; CM: PFC-dmPFC, beta-2, −0.0046, p <.005). There were other increases and decreases in alpha-1, and beta-2 with learning in the Match tasks, but they were modest and not consistent across tasks (OM: PFC-HPC, alpha-1, +0.0012, p<.005; beta-2, −0.0023, p<.005; CM: PFC, beta-1, −0.0013, p<.005). Moreover, there were no shared changes in synchrony in any frequency band between any of the Match tasks and the Saccade task (CS: PFC, theta, −0.0472; alpha-1, −0.0213; alpha-2, −0.0172; beta-1; −0.009, p < .005; PFC-STR, theta −0.0513, alpha-1, −0.0183, p <.005; beta-1, +0.0026). We replotted these results pooling alpha-2/beta-1 bands and computed these changes with learning over the entire feedback epoch. All time windows yielded similar results (Figure S4).

Figure 5.

We compared synchrony on correct trials early and late in learning. The bar plots represent a change from early to late learning, a positive value is associated with an increase in synchrony with learning and a negative value, a decrease. We computed synchrony at 5 different frequency bands: theta (3–7 Hz), alpha-1 (8–10 Hz), alpha-2 (10–12 Hz), beta-1 (13–17 Hz), and beta-2 (18 – 30 Hz). Error bars represent the SEM, and the stars represent significance. In A., we compared synchrony increases within PFC. In B. we compared synchrony changes with learning across different brain regions (OM: PFC-HPC, CM: PFC-dmPFC, CS: PFC-STR). See also Figure S4.

During Match Learning, Alpha-2/Beta-1 Synchrony Increased then Decreased

Above, we showed a moderate increase in alpha-2/beta-1 synchrony with learning during the Match tasks. A closer examination revealed something more complex. Alpha-2/beta-1 first increased with learning, but then late in learning, after the animals reached criterion, it decreased. Because the animals’ learning rate varied from task to task, from session to session, and even within a session itself, we could not simply relate PPC to an average learning curve. To better assess how alpha-2/beta-1 synchrony changed with performance, we computed PPC on correct trials over bins of 20 non-overlapping trials. We plotted average PPC values as a function of the animals’ level of behavioral performance over the trials bracketed by this same 20 correct-trial window. To maximize statistical power, we averaged across all electrodes both within and outside the PFC for each session.

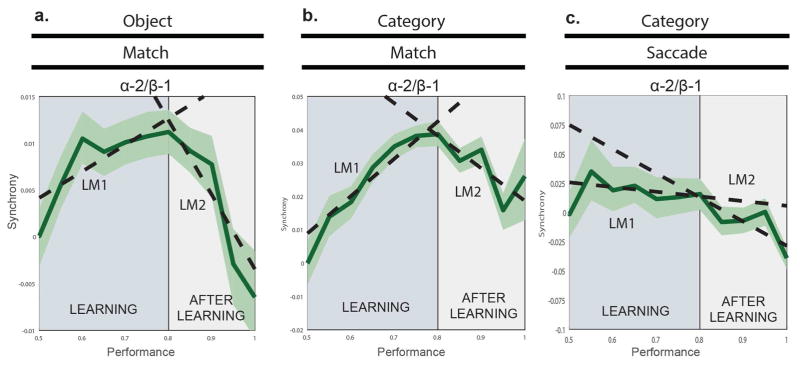
Figure 6 shows the outcome of this analysis. Figure 6A, B shows the results for the Match tasks in the 10–17 Hz (alpha-2/beta-1) band where we observed an increase with learning (Fig. 5). This revealed that 10–17 Hz synchrony increased as task performance improved. That is, until the animals had largely learned the tasks. For both the Object-Match (Fig. 6A) and Category-Match (Fig. 6B) tasks, alpha-2/beta-1 synchrony increased until the animals reached around 80% correct performance and after that, synchrony decreased. This drop-off largely erased prior learning-related increases. A piecewise linear model, made up of two linear models, LM1 and LM2, confirmed these changes with performance (Fig. 6A, B). Linear Model 1 estimated the changes in synchrony with performance increases from 50 to 80%, and Linear Model 2 estimated the changes in synchrony with performance increases from 80 to 100%. The coefficients for synchrony changes with performance were significant and opposite in sign around the 80% performance mark (OM: LM1, β = 0.028449, p =0.0068933; LM2, β = −0.079505, p = 0.0013742; CM: LM1, β = +0.11223, p = 4.7148e-9; LM2, β = −0.09765, p = 0.0087861, two-sided t-test).

Figure 6.

Synchrony binned by non-overlapping, 20-trial window intervals. Error-bars represent the standard error of the mean. The dotted lines represent the fits of two different linear models, accounting for changes with learning. The mean synchrony at 50% performance level has been subtracted from each graph for visual purposes only. Linear Model 1 estimated the changes in synchrony with performance increases from 50% to 80%. Linear Model 2 estimated the changes in synchrony with performance increases from 80% to 100%. In A., all electrodes from within and between PFC and HPC in the OM task were used to obtain a single synchrony value for each performance bin. In B., we took all electrodes from within PFC and again obtained a single synchrony value for each 20-trial non-overlapping bin. C. We applied the same methods (as above) for all PFC electrodes within the Category-Saccade task. We repeated the same analysis with the PFC-STR electrodes (not shown), and still found no change before or after the criterion. The error bars represent ± SEM.

Even though the drop in alpha-2/beta-1 synchrony occurred in both Match tasks when performance was above average, there was still sufficient trials for analysis (11% and 20% of both the OM and CM datasets were available for analysis at or above 90% performance, respectively). We applied this same analysis in the Category-Saccade task both to PFC pairs alone and PFC-STR pairs included (where we saw a decrease with learning, see Fig. 6A), and yet we still did not find any increase with performance (PFC alone: LM1, β = −0.04015, p = 0.61026; PFC-STR included: LM1, β = −0.13447, p = 0.067499, two-sided t-test). Instead, the observed drops in alpha-2/beta synchrony were restricted to after the learning criterion was reached (PFC alone: LM2, β = −0.20717, p = 0.0054737; PFC-STR: LM2, LM2, β = −0.039018, p = 0.55914) (Fig. 7C).

Figure 7.

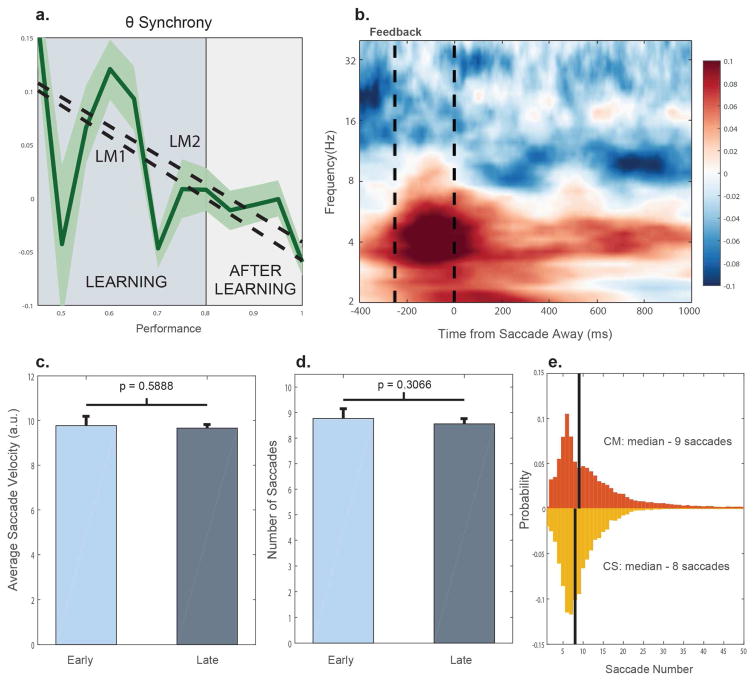
A, Theta band synchrony binned by non-overlapping, 20-trial window intervals in the Category-Saccade task. LM1 and LM2 estimate changes with learning from 50–80% learning, and 80–100% learning respectively. B, Instead of aligning the LFPs to the feedback, all of the data was aligned to the saccade away from the target – which occurred on average 339ms after feedback. For the sake of visualization, this data has been normalized to the mean synchrony across the theta and beta bands. Here, theta synchrony increased on correct trials prior to the saccade away. C, Average saccade velocity early and late in learning (the mean of the first derivative of the eye position signal relative to the center of the screen). D, The number of saccades was taken as the number of threshold crossings of the eye signal during the entire feedback period (1.7s). E, Probability distributions of the number of saccades for both the Category-Match and Category-Saccade tasks. All of the error bars reflect ± SEM.

During Saccade Learning, Theta Synchrony Drops Continuously

In the Category-Saccade task, we found that theta synchrony dropped with learning (Fig. 7A). Because alpha-2/beta changed differently before and after learning, we sought to identify whether theta synchrony changed at the same rate before and after performance levels reached 80%. This was the case. In Figure 7A, we found that theta synchrony dropped both early (LM1, β = −0.28891, p = 0.027735, two-sided t-test) and late (LM1, β = −0.27005, p = 0.015615). In other words, we did not see any difference in the change in theta synchrony before and after learning, like we did for alpha-2/beta-1.

Eye movements tend to be made in the theta range (3–7 Hz), and a concern was that these movements (and their correlates) could contribute to the observed changes in theta synchrony. However, we found little evidence that this was the case. We first sought to control for timing differences in saccades made during the feedback period, both on correct and incorrect trials. To do so, we aligned all of the data on a trial-by-trial basis to the first saccade the animal made away from the target that was chosen. After this re-alignment, we recomputed the PPC and we found that, despite this realignment, theta synchrony remained significantly higher on correct trials (−200 to 0ms prior to the saccade away, +0.1012, p < 2 × 10⁻⁴, bootstrap, Fig. 7B). In fact, it appeared that the rise in the theta synchrony preceded this eye movement away and was more closely time locked to the delivery of the feedback. Specifically, we found that theta synchrony on correct trials peaked 81–119ms before the saccade and approximately 231–269ms after the feedback (95%, CI).

Alternatively, using the eye tracking data, we assessed both saccade velocity and the average number of saccades made over the feedback period. We found that, while there was an increase in the number of saccades on incorrect trials (+4 saccades, p < 2 × 10⁻⁴, bootstrap), there were neither any changes with learning in the number of detectable saccades nor in the average saccade velocity over the entire feedback period analyzed (0–1.7s) (Fig. 7C, D). Finally, it was possible that the theta synchrony present in the Category-Saccade task may be tied to eye movements that do not occur in the match tasks. Again, this was not the case. We found that over the 1.7s feedback period there was a median number of 9 saccades in the Category-Match task, strikingly similar to the median number of 8 saccades found in the Category-Saccade task (Fig. 7E).

DISCUSSION

We found evidence that two tasks involving match decisions engaged explicit learning, whereas a task involving a visuomotor (Saccade) association engaged implicit learning. Further, we demonstrated that these putative explicit and implicit learning tasks had different patterns of neural synchrony following correct vs incorrect behavioral choices. During the explicit (Match) tasks, there was an increase in alpha-2/beta synchrony following a correct choice and an increase in delta/theta synchrony following an incorrect choice. The implicit (Saccade) task showed a different pattern. Like the explicit (Match) tasks, alpha-2/beta synchrony increased after correct choices. But unlike the Match tasks, which showed increases in delta/theta synchrony after incorrect choices, the implicit (Saccade) task showed increased delta/theta synchrony after correct choices. The two types of tasks also showed differences in how synchrony changed with learning. Alpha-2/beta-1 synchrony increased during explicit learning (both Match tasks) until the animals reached a high level of performance, then it dropped off. By contrast, during the implicit (Saccade) task, alpha-2/beta-1 did not increase with learning and theta synchrony decreased.

The evidence that the tasks engaged different learning systems came from how errors were treated. During the implicit (Saccade) task, performance was better immediately following a correct than following an incorrect trial. Correct responses drove improvements in performance. This is consistent with observations that amnesia patients (who rely on implicit learning) acquire new skills more rapidly, and retain them longer, with errorless learning (Squires et al., 1997; Evans et al., 2000; Maxwell et al., 2001; Poolton et al., 2005; Roberts et al. 2016).

By contrast, during the explicit (Match) tasks, performance was nearly equivalent following correct and incorrect trials. In other words, explicit learning also utilizes feedback about incorrect responses to improve behavior. The greater error-related negativity (ERN) in the explicit (Match) tasks than in the implicit (Saccade) task further supports this conclusion. In humans, the ERN is correlated with error awareness, conflict monitoring, and the use of errors to improve learning, all hallmarks of explicit learning (Frank et al., 2005; Scheffers and Coles, 2000; Walsh and Anderson, 2012; Wessel et al. 2011; Wessel et al. 2012). For example, explicit learners of a sensorimotor sequence task exhibited an enhanced ERN relative to implicit learners (Russeler et al. 2003). Our results are also consistent with other reports that use of correct vs error feedback differentiates implicit vs. explicit learning tasks (Morrison et al., 2015; Smith et al. 2013). Moreover, in the Match tasks, when errors arose in the context of higher behavioral certainty, the ERN was larger and could have reflected a prediction error. This was not the case in Saccade (implicit) task. Explicit, not implicit, learning relies on the evaluation of specific rules (predictions) to guide performance. The Saccade task was likely more amenable to implicit learning because it allowed a motor response to be associated with the sample stimulus.

Category learning, and more specifically the dot-category learning employed here, has been found to rely on either implicit or explicit learning systems, depending on the task structure and instructions (Ashby and O’Brien, 2005; Ashby and Maddox, 2011; Carpenter et al., 2016; Reber et al. 1998; Milton et al., 2011; Seger and Miller, 2010). If the dot learning was accompanied by motor instructions (such as point to center of dot pattern), or the task was an A-/not-A category distinction, implicit memory was used (Squire and Knowlton, 1995; Zeithmova et al., 2008). If instead, participants were told that there were different patterns, explicit memory was used (Aizenstein et al.,2000; Reber et al.,2003). Likewise, two of our tasks (Category-Match and Category-Saccade) required categorization of dot patterns, but had different behavioral requirements that seemed to engage explicit vs implicit learning, the latter based on a motor decision. Our results are also in line with other observations that working memory tasks that seem formally equivalent (e.g., “remember objects”) can have different neural correlates depending on whether those memories are reported by actively choosing a match from alternatives or recognizing their match (Warden and Miller, 2011).

During explicit learning, alpha-2/beta band synchrony increased on correct choices, increased over the course of learning, and decreased after learning. Alpha-2/beta band synchrony has been tied to cognitive functions such as attention, top-down control, and feedback processing. This seems consistent with its role in explicit memory formation. Moreover, in a previous report, this feedback-period, alpha-2/beta band synchrony had been found to first arise from the hippocampus (Brincat and Miller, 2015). Together, all of this information suggests that the alpha-2/beta band synchrony found in the feedback period may reflect the activity of specialized neural circuits originating from the hippocampus responsible for explicit learning.

Theta synchrony, on the other hand, has been linked with learning, memory, and conflict monitoring (Colgin, 2013). Theta oscillations and theta stimulation have been known to facilitate both long-term potentiation (LTP) and long-term depression (LTP) in vitro and in vivo (Huerta et al., 1995; Hyman et al. 2003). Theta synchrony has never been reported in non-human primates in response to correct feedback, nor has its decrease with learning. It has been found to become more prevalent in patients with even mild Alzheimer’s, who by definition increasingly rely on implicit learning strategy (Coben et al., 1989; Jeong, 2014). Our observations of theta synchrony within prefrontal cortex and between prefrontal cortex and striatum, in addition to the hippocampus, suggest that theta synchrony is a widespread plasticity signal. Implicit learning, therefore, may depend on global changes in LTD and LTP, rather than the activation of specific hippocampal-based networks.

Alternatively, theta oscillations may act as a mechanism organizing neural activity between brain areas. Previous studies have suggested that low frequency synchronizations facilitate long-distance communication. For instance, theta synchrony has been reported to coordinate activity between regions, such as V4-FEF (Liebe et al., 2012), STR-HPC (DeCouteau et al., 2007), FEF-ACC (Babapoor-Farrokhan et al., 2017), PFC-HPC (Benchenane et al. 2010), PFC-STR-HPC (Herweg et al., 2016), and LIP-TEO-V4-Pulvinar (Wang et al., 2012). In particular, one study found that as animals learned a procedural task, theta oscillations within STR and HPC became anti-phasic (DeCouteau et al., 2007). The presence of theta synchrony, hence, between PFC and STR may facilitate the functional connectivity between PFC and STR over that of PFC and HPC.

In sum, our results suggest that explicit vs implicit learning not only engages different brain systems, it may also engage different neural mechanisms that rely on different patterns of oscillatory synchrony.

STAR★METHODS

CONTACT FOR REAGENT AND RESOURCE SHARING

Further information and requests for resources and reagents should be directed to and will be fulfilled by the Lead Contact, Earl K. Miller (ekmiller@mit.edu)

EXPERIMENTAL MODEL AND SUBJECT DETAILS

All experiments were performed in adult (~8–10 years old) rhesus macaques (Macaca mulatta), ranging from 5 to 13 kg. All procedures followed the guidelines of the MIT Animal Care and Use Committee and the US National Institutes of Health. In total, 4 females and 2 males were trained in this study. They were pair-housed, and on a normal 12-hr diurnal schedule. In the Category-Saccade task, one of the animals had been previously trained on a conditional association task. In the Category-Match task, one of the animals was being actively treated with cyclosporine daily. All animals spent approximately 1–2 years of training on their respective tasks.

METHOD DETAILS

Task Details

The details of the Object-Match task have been presented previously (Brincat and Miller, 2015). In each session, six novel objects were chosen from an image database (Hemera Photo-Objects). Four were randomly designated as cue objects, and the remaining two as associate objects. In turn, each cue object was randomly paired with an associate object. The monkeys’ task throughout each session was to learn, through trial-and-error, which associate was paired with each cue. To initiate a trial, each monkey fixated on a central white dot for 0.5s. After this fixation period, a cue object (foveal, 3° wide) was presented for 0.5s, followed by a blank delay of 0.75s. Two associate objects were then presented in a randomly-ordered series. Each object presentation lasted 0.5s, and was then followed by another a brief delay of 0.6s. To indicate that an object was a match, the monkey had to saccade to a subsequently presented visual target, a white dot presented 7.5° to the left or right of fixation. And if it did so, the animal received juice and a new trial began within 3s. If incorrect, instead of juice, a red “error screen” flashed on for 1.5 s, and the animal had to wait 6s for the subsequent trial. The location (left versus right) of the response target after each associate was randomized and unrelated to task performance.

The details of Category-Saccade task have also been presented previously (Antzoulatos and Miller, 2011 and 2014). In this task, animals had to learn to classify a number of category exemplars generated from two different prototypes into two categories. Each category was directly tied to a specific saccadic target (right or left). To start a trial, animals first fixated within 1.5–2° of a red, central target (0.4° in diameter) for 0.7s. After this fixation period, a randomly chosen category exemplar (6° by 6°) from either category was presented for 0.6s. Trials from both categories were randomly interleaved throughout the session. One second after the end of the exemplar period, two saccade targets (a green dot, 0.6° in diameter) appeared on the left and right of the center of fixation (5° from the center). In order t o indicate a response, the animals had to make a single, direct saccade within 1s of target presentation and maintain fixation on it for 0.2s. If the animal chose correctly, it was rewarded with drops of juice. If the animal did not, it was punished with a 5-s timeout, during which the cue was presented again at the location of the corresponding target.

In each session of the Category-Match, animals had to classify a number of category exemplars generated from two novel different prototypes into two categories. Each category here, however, was neither tied to any particular saccade nor saccade location. Instead at the test period, the animal had the opportunity to freely investigate two exemplars, one of which matched the category of the sample exemplar, and then had to choose by fixating on this match. To initiate each trial, each animal had to fixate within 2.5° of a centrally located, red dot (0.2° i n diameter) for 0.5s. After this fixation, an exemplar of one of the two categories was presented at the center of the screen (7° by 7°) for 1s. If the animal continued to fixate throu gh this sample period, and a subsequent delay of 0.85s (with an additional jitter of 0.4s), then the central fixation dot disappeared and two new exemplars were presented on the left and right side of the screen (9° from the center of the screen). Once the test exemplars appeared, the animal had the opportunity to freely view both of the exemplars presented and make the correct choice. To indicate this choice, the animal had to fixate on one of the two peripherally presented exemplars for 0.7s. If it made the correct choice, the white dots of the chosen exemplar turned green and the animal received juice. If the animal did not make the correct choice, the chosen exemplar turned red and no juice was given. Depending on the animal, the length of timeout incurred on error trials varied from 5–16s.

Neurophysiology and Hardware

In both the Category-Saccade and Object-Match task stimulus presentation and reward delivery were controlled by Cortex (NIMH, Laboratory of Neuropsychology) and presented on a 100 Hz CRT monitor. Eye movements and pupil size were monitored and recorded using an infrared eye tracking system (Eyelink I & Eyelink II, SR Research @ 500 Hz). In these tasks, up to 16 electrodes were lowered in PFC, HPC, or STR acutely. All recordings from PFC and STR, and most from HPC, were performed with epoxy-coated tungsten microelectrodes (FHC). On some HPC recordings, 24-channel linear probes with 300-um spacing between adjacent platinum iridium contacts were used (U-probes, Plexon). For targeting, the animals’ implanted chambers were co-registered with structural MRI images. For all of the PFC, STR, and some HPC recordings, these electrodes were lowered daily though the dura using custom-built, screw micro-drives. The exact location on the grid and orientation of the grid were varied to limit cortical damage and maximize coverage of the intended regions. For the linear probes, electrodes were lowered through a 25-gauge transdural cannula using a motorized drive system (NAN-S4, NAN instruments). The electrodes would be lowered until spiking was detected, and then electrodes were allowed to sit for about an hour to limit apparent neural drift. Neural activity was amplified, filtered, digitized and stored using an integrated multichannel recording system (Multichannel Acquisition Processor, Plexon). The signal from each electrode was amplified by a high input–impedance, unitary gain headstage (HST/8o50-G1, Plexon), referenced to ground, filtered from 0.7–300 Hz, and amplified 1000-fold. LFPs were recorded continuously at 1 kHz. Only electrodes with cells present on them were included for these analyses and, after trial cutting, evoked potentials were subtracted out from each individual trial.

In the Category-Match task, stimulus presentation and reward delivery were controlled by custom software written in Matlab using PsychToolbox. All stimuli were presented on a LCD screen at 144 Hz (ViewSonic VG2401mh 24″ Gaming Monitor). Eye movements and pupil size were monitored using EyeLink II at 1000 Hz sampling. Four 8×8 channel Blackrock Cereport arrays with 1mm long electrodes were implanted in dorsomedial prefrontal cortex (dmPFC), dorosolateral prefrontal cortex (dlPFC), and ventrolateral prefrontal cortex (vlPFC). Each electrode was separated by 400 um. vlPFC, dlPFC, and dmPFC were all defined by anatomical landmarks following the craniotomy. The vlPFC array was placed 1 mm ventral to the principal sulcus and was centered at 9–12 mm anterior to the genu of the arcuate sulcus. In contrast, the dlPFC array was positioned slightly more rostral, 12–15 mm anterior to the genu of the arcuate and 1 mm dorsal to the principal sulcus. Finally, we placed the dmPFC (dorsomedial prefrontal cortex) array in the vicinity of where others have reported to identify the supplementary eye fields. The medial edge of the array was placed 5mm from the midline, and 5mm anterior to the genu of the arcuate sulcus. We recorded using Blackrock headstages (Blackrock Cereplex M and Cereplex E). Signals were sampled at 30 kHz, band-passed between 0.3 Hz and 7.5 kHz (1^st order Butterworth high-pass and 3^rd order Butterworth low-pass), and digitized at a 16-bit, 250 nV/bit. All LFPs were recorded with a low-pass 250 Hz Butterworth filter, referenced to ground, sampled at 1 kHz, and AC-coupled. In Monkey G, an error in the design of the Cereplex E head-stage made the system susceptible to ground loops and to DC-drifts in the signal. This required us to apply a high-pass, 0.5 Hz FIR filter in both directions on the whole dataset to avoid any phase distortions. All arrays had units present on at least 5, if not typically a large proportion of channels. All channels were included in this analysis, and for all synchrony analyses the evoked potentials averaged across trials were subtracted from each individual trial.

Prototype and Exemplar Generation

In both the Category-Match and Category-Saccade tasks, the visual stimuli were composed of 7 randomly located dots on a black background. To construct the categories, we followed previously published procedures (Posner et al., 1967; Vogels et al., 2002, Antzoulatos and Miller, 2011). Every day, two novel prototypes were created at random. These prototypes (as would be the exemplars) were generated as 7 arbitrarily positioned, 7-pixel dots on a grid of 140 by 140 pixels. In order to control for difficulty and ease, these arbitrarily constructed prototypes had to obey a number of rules: (1) They had no dot centers that fell within 14 pixels of one another. (2) The average dot position of the prototype was at the center of the grid. (3) No dots from each exemplar fell within a 10-dot margin on the edge. And, (4) the minimum Euclidean distance between all pairs of dots between each prototype was no greater than 200 pixels. Each of these 140 × 140 pixel exemplars subtended 6–7 degrees of visual angle.

In order to generate the exemplars, the prototype dot patterns were jittered according to a procedure first established by Posner and colleagues (Posner et al., 1967). To determine this jitter, we first defined 5 concentric annular regions. These annuli were centered around each dot, and spaced apart radially by 7 pixels. Region 1 refers to the annulus immediately surrounding the dot center, 1 dot-diameter away, and region 5 refers to the annulus 5 dot-diameters away from this dot. Next, each dot from each prototype was shifted away from its prototypical location by at least 1 region; no exemplar was identical to the prototype. Whether any particular dot was moved to regions 2 to 5 depended on the distortion level desired. Each exemplar had to be unique, different from any other exemplar, and, to ensure such, no more than 2 dots from each exemplar could be less than 10 pixels away from any other exemplar’s dots.

Posner et al. defined 9 distinct levels of distortion, based on the probability of a dot to shift to each of these 5 concentric regions. Two of these 9 distortions were used in this task. At distortion level 1, 88% of dots were shifted to region 1, 10% to region 2, 1.5% to region 3, 0.4% to region 4, and 0.2% to region 5. At distortion 2, 75% of dots were shifted to region 1, 15% to region 2, 5% to region 3, 3% to region 4, and 2% to region 5. In the Category-Saccade task, the generated exemplars were largely at distortion level 2. In the Category-Match task, which appeared more difficult for animals to acquire, distortion level 1 exemplars were used for both animals. As a side note, in order to rule out that any of the reported effects were a result of the level distortion, we repeated 3 sessions in one of the two monkeys at distortion level 2. The results were similar; the monkey showed an enhancement of synchrony in the beta band on correct trials and theta band on incorrect trials.

Overall, the use of these visual stimuli in both tasks provided for us a number of advantages: (1) These categories were not imbued with any overt meaning to the subject, for they held no apparent relationship to objects seen in daily life. (2) The exemplars which could, in fact, look distinctively different from one another were always perceptually related and averaged out to the original prototype. And (3), these categories could not be distinguished by any simple rule.

Block Design

To facilitate learning, in both the Category-Match and Category-Saccade task, each learning session was organized into blocks. The blocks were defined by a progressively growing pool of available exemplars from which any could be used for a given trial and any task period (sample or test). In any given block, with the exception of block 1 in the Category-Saccade task, there were a total of 2^block number of exemplars for each category. In the Category-Saccade task, in the first block, there was a single exemplar per category. The pool of available exemplars grew by accretion, “new” exemplars were added to a bank of “familiar” ones, so that the total available exemplar was equal to 2^block. The terms novel and familiar are not an indication for how familiar any exemplar was to an animal, but simply a reflection of when it became available in the pool of potentially usable exemplars. As the blocks progressed, the chances for only seeing novel exemplars increased substantially, and performance on these novel exemplars suggested successful categorization. In fact, block transition was not possible without successful categorization, and the overlap of available exemplars between blocks favored a smoother learning process.

In order to pass from one block to another, each animal had to achieve a particular behavioral criterion. The criteria diverged somewhat between the two category tasks. In the Category-Saccade task, a block transition occurred when the animal had correctly responded to 80% of the previous 20 trials. In the Category-Match task, both animals had a tremendous capacity for being biased in either choosing a particular location and/or a particular category. In order to limit these behavioral biases, each animal had to successfully complete 70% of the previous 10 trials for each potential condition (Category A – on left, Category A – on right, Category B – on left, and Category B – on right). Because of these behavioral criteria in both tasks, not all available exemplars were presented in each block. In the Category-Match task, an additional restraint was imposed on the pool of available exemplars presented in block 1. Because both animals struggled to pass block one, in which two exemplars from each category were presented, the exemplars from each category had to have a Euclidean distance of less than 20 pixels apart. This constraint reduced the difficulty of the first block, promoted rapid block passage, and ultimately favored category abstraction. Following block one, there was no limitation on the presented exemplars.

Bias Correction

The Category-Match was a more difficult task to maintain high levels of performance and, as a result, if left to each of their own devices, each of the animals engaged in suboptimal strategies and would fail to learn to categorize stimuli. To avoid these aberrant behaviors, we detected the animals’ biases, and scaled the probability that any particular condition was shown to counteract these “easier,” inefficient strategies. In order to assess bias in any one of the four conditions enumerated above, we compared performance in each of the four conditions to one another, and computed the Mann Whitney U test statistic (U) for each of these comparisons. R₁ represents the sum of ranks for condition 1 and the n₁ represents the sample size for sample 1. From this test statistic, we obtained the area under the curve, subtracted 0.5 to obtain a bias measure, and remapped this bias measure to a value between [0–1] by dividing it by 0.5. We then used this measure to scale the probability that any particular condition would be seen. We only implemented this bias correction algorithm after 20 trials were performed in each of the blocks.

$$U=R_1-\frac{n_1(n_1+1)}{2}$$ Eqn. 1

$$\mathit{AUC}=\frac{U}{n_1{n}_2}$$ Eqn. 2

$$\mathit{Bias}=\frac{(\mathit{AUC}-0.5)}{0.5}$$ Eqn. 3

QUANTIFICATION AND STATISTICAL ANALYSIS

Learning Stages

In a previous report, which analyzed this same Category-Saccade task, block 5 similarly marked the transition towards a late stage of learning (Antzoulatos and Miller, 2011). In that study, early learning (alternatively called stimulus-response association) was defined as the first two blocks of the task, where novel exemplar performance was at chance. By contrast, late learning (alternatively called category-performance) was defined as those blocks when novel performance on each category in a 16-trial window was above 75% correct. This behavioral criterion was reached on average by block 5. The middle stage of learning (alternatively called category learning) was defined, therefore, as those blocks which remained, i.e. those blocks between the early and late stages of learning, and hence blocks 3 and 4. Due to the congruence of the sliding t-test first presented here and those previously published behavioral results, we separated learning into the same learning stages.

In the Category-Match task, novel performance had already plateaued by block 2 (on average, trial 89), and a division of learning stages by blocks was not appropriate. Because future analyses divided behavioral curves by 20 trial bins, we rounded the 89- trial criterion to the next multiple of 20, and defined early learning as the first 100 trials and late learning as the next 100. Moreover, because of the rapid learning particularly present in the Category-Match task, we restricted these analyses involving the learning stages in both the Category-Saccade and Category-Match tasks to those days in which learning was a bit more difficult and performance on all trials (not just novel) was less than or equal to 80% in the first 20 trials. In the Category-Match task, 39 days matched these criteria, evenly spread across both monkeys (23 days from Monkey P, 16 days from Monkey G). In the Category-Saccade task, 12 days matched these criteria (8 days from Monkey 1, 4 days from Monkey 2). All days from all monkeys in each task were pooled together. As we will see, learning in these analyses was assumed to be somewhat linear, and we expected to see physiological changes that correlated with average changes in performance in late vs. early trials. And while we did, we also show (when binning trials from the entire session by performance) that none of these results depend on a particular learning stage classification nor any assumption that learning need be linear.

Because the Object-Match task was not blocked, unlike the category tasks, the behavioral criteria for learning stages differed as well. As previously reported, in the Object-Match task, only those sessions for which each of the final cue-associate pairings were performed at 32 correct response over the final 50 trials (p ≅ .01, binomial test) were included in this final analysis. 61 sessions met these criteria, and trials within them were simply divided into thirds. The first-third of the session was early learning, the second-third middle learning, and the last-third late learning.

Behavioral Analyses

In all three tasks, we computed performance in the trial following a correct trial or an incorrect trial irrespective of the following category or cue-associate presented. A binomial distribution was fit to each of the post-correct and post-incorrect trial performances, and 95% confidence intervals were generated. During these same trials, we compared reaction times on trials following correct and incorrect trials. In both the Category-Saccade task and Object-Match task, we computed the differences in the time it took the animals to respond following target presentation between correct and incorrect trials. In the Category-Match task, because the task involved free viewing, we computed the differences in time between the presentation of the match exemplars and the chosen response after controlling for the number of saccades. To control for saccade number, we subtracted correct and incorrect trial times when the animal completed a single saccade, and the same for two saccades. All significance testing was done on a distribution generated through 10,000 bootstraps of correct-incorrect trial time differences over sessions in each task. From these distributions, we computed 95% confidence intervals by finding the 2.5% and 97.5% quantiles of each distribution.

In order to confirm that performance following errors was greatly reduced in the Saccade task relative to the Match tasks, we also examined whether mean performance over 10 and 20 trials after a correct or an error differed in each task. We computed a linear regression model without interactions and treated both total trial performance pre-feedback, and the type of feedback (correct or an error) as independent variables, and mean trial performance in those 10 or 20 post-feedback trials as the response variable. The type of feedback (correct or error) was treated as a categorical variable and, thus, the design matrix had a single column of 1’s or 0’s for feedback type. We then pooled all combinations of trial feedback, post-feedback performance, and pre-feedback performance (10 or 20 trials) across all sessions, and used normal equations to analytically compute the coefficients for intercept, pre-feedback influence, and correct-incorrect post-feedback differences. We then randomly sampled all of the trials from all days, and computed an empirical distribution for each coefficient of the model. In Figure 2E and 2F, we plotted correct-incorrect feedback coefficient for each of the tasks. In Figure 2E, we examined the post feedback coefficient for 10 trials, and in Figure 2F for 20 trials.

In Figure S1, we visualized performance differences after correct and incorrect trials across a sequence of 8 trials post-feedback. Again, we pooled all post feedback trials after correct and incorrect trials across all sessions, and randomly sampled the trials from across the days to obtained a mean performance difference for each post-feedback trial (i.e. post-feedback trial 1, post-feedback trial 2, etc.). We plot in Figure S1, an error-bar reflecting the standard deviation of this bootstrapped distribution.

Evoked Potential and Error-Related Negativity

In three tasks, we computed evoked potentials on correct and incorrect trials by averaging across trials on each electrode from each region. As in previous work, in both the Object-Match and Category-Saccade tasks, recordings from each of these acute electrodes were considered independent (Brincat and Miller 2014, Antzoulatos and Miller 2011). In these two sets of recordings, pairs of electrodes were placed >1.5 mm apart across a large swath of ventrolateral and dorsolateral prefrontal cortex. Evoked potentials from all of these sites were averaged and plotted. For these analyses and others, we performed statistical testing by bootstrapping the trials and pairs to ensure that the reported findings were not dependent on any independence assumption. In the Category-Match task, evoked potentials were computed across an entire array and averaged across sessions. The error-related negativity is an evoked potential that arises more prominently on incorrect trials and occurs in epochs spanning 80–300 ms following feedback. In order to compute the error-related negativity, the evoked potential from incorrect trials was subtracted from correct trials. We aligned all of the tasks to their maximal peak (i.e. where the error-related negativity is greatest), and then normalized the entire signal by the mean and standard deviation of the differences across the entire trial and feedback (-2s to 1.7s post-feedback). To compare the error-related negativity across the tasks, we computed the mean value of the normalized voltage differences for a 50ms period of time centered around the maximum difference from each task. We computed 10,000 bootstraps and found the empirical value for each comparison. In order to account for multiple comparisons, we applied a Bonferroni correction and multiplied all p-values by 3.

In order to further test that the ERN was greater in the Match tasks than in the Saccade task, we defined the ERN by estimating the amplitude of the evoked potential arising subsequent to an error. In order to compute this amplitude, we found the maximum and minimum value for each z-scored signal averaged across all incorrect trials in the feedback period for each electrode. The magnitude of the ERN was equal to the distance between the max and min values, and we compared the mean ERN across electrodes. To avoid questions on the independence of different electrodes, we first bootstrapped the trials and then the electrodes 1,000 times to obtain an empirical probability distribution on the size of the ERN. However, given both the large number of electrodes recorded daily (PFC, n=128; dmPFC, n=64) and the large number of error trial counts, we chose to be conservative for the Category-Match task and bootstrapped across the sessions. In order to test our a priori hypothesis that the ERN in the Match tasks was greater than in the Saccade task, we computed the p-values by finding the number of bootstraps that were greater in the match distributions than that in the saccade distribution, and dividing by the total number of bootstraps. To visualize the independence between the specific timing and the magnitude of the ERN computed, we took the maximum and minimum values found within three different time windows (Figure S2: 50–350ms, 100–400ms, and 150–450ms). Also un-plotted we compared those results when taking the entire 50–450ms interval; the p-values were equal equivalent to those in the 50–350ms window. Regardless of the interval chosen, we found that the ERN in the Match tasks in the PFC was greater than that in the Saccade task. We also repeated these analyses in the HPC (OM), dmPFC (CM), and STR (CS). Again, the same pattern was true: the ERN in both the HPC and the dmPFC was greater than that in the STR.

Using a similar method to that described above, we also obtained the magnitude of the ERN on a per trial basis. We again found the distance between the maximum and minimum value in the feedback; however, in this case we did not average across trials. Instead, before taking this distance, we averaged across all PFC electrodes. For each session, we had a single ERN magnitude for each incorrect trial. Moreover, for each incorrect trial, we found the mean performance over the previous 20 trials. Since we were carrying out a regression analysis examining how performance interacts with the ERN, we corrected the ERN magnitudes in each session by subtracting its mean magnitude at 75% performance. This was meant to facilitate the comparison of the ERN magnitudes by removing any day-specific effects. We next pooled trials across all sessions and used robust regression (as described below in the Linear Regression section) to assess how a single trial ERN correlated with prior performance (Fig. 2G). To compute statistical differences, we again randomly sampled across all of the magnitude-ern pairs, and the compared the computed coefficient to zero.

Time-Frequency Analysis

Spectrogram and coherograms were computed by applying the continuous wavelet transform to the trial-by-trial data. In order to compute the transform efficiently, for each complex-valued Morlet wavelet of wave number 6, we multiplied its Fourier transform by the Fourier transform of the trial data, and took the inverse Fourier transform of this product (Torrence and Compo, 1998). The 61 daughter wavelets sampled the frequency space exponentially (base of 2), starting at a max frequency of 80 Hz, and ending 6 (num_octaves) exponential decreases later (here, 80/2⁶ = 1.25 Hz). For every exponential decrease, here, for every halving, we sampled 10 frequencies (num_per_octave). All of the sampled frequencies from this paper can be given by the following equation:

$$\mathit{Sampled}\mathit{Frequenci}es=\frac{\mathit{max}\_\mathit{frequency}}{2^{(0:\frac{1}{\mathit{num}\_\mathit{per}\_\mathit{octave}}:nu{m}_{\mathit{octaves}})}}$$ Eqn. 5

In order to obtain the amplitude or power from the complex output of the wavelet transform, we took the complex modulus of wavelet coefficients. Alternatively, for phase values, we took the inverse tangent of the ratio of the real and imaginary components of the wavelet coefficients.

Synchrony Analysis

To estimate synchrony, we computed the pairwise phase consistency (PPC), an unbiased estimator of the magnitude squared resultant (Vinck et al., 2010). In other words, the pairwise phase consistency statistic is a measure equivalent on the population level to the square of the oft-used phase locking value (PLV) but which is uninfluenced in its average by trial number. In this study, differences in trial number were prominent, as there were both differences in the number of incorrect and correct trials for any given session, as well as differences in the number of correct trials in any given 20-trial window. In order to implement the PPC statistic, we used a simplification derived previously (Kornblith, Buschman, and Miller, 2016)

$$\begin{gathered} \text{PPC}=\frac{2}{N(N-1)}\sum _{j=1}^{N-1}\sum _{k=j+1}^N\left(cos{\theta }_{j}cos{\theta }_k+sin{\theta }_{j}sin{\theta }_k\right) \\ =\frac{1}{N(N-1)}\left[{\left|\sum _{j=1}^{N}exp\left(i{\theta }_j\right)\right|}^2-N\right] \\ =1-var(cos\theta )-var(sin\theta ) \end{gathered}$$ Eqn. 6

where θ is the vector of angular differences between two channels at any given point in frequency and time. N is the number of trials. For every single channel-pair, we subtracted the phases (obtained from the wavelet-transformed data) of one channel from those of another, took the variance of the sine and cosine of these angle differences across trials, and subtracted both of these variances from 1. To compute changes in synchrony early and late in learning, we bootstrapped the channels or sessions 1,000 times and obtained an empirical distribution. We used this distribution to estimate p-values. Because we were looking for differences above or below 0, we applied both a two-way test as well as a Bonferroni correction. The Bonferroni correction was used, instead of a more statistically powerful multiple comparisons correction, because it is particularly effective at controlling the type I error when different tests are potentially correlated.

Subtraction of Eye Movement Away

Because one of the animals in the Category-Match task had some stereotyped eye movements after correct responses, we removed from both eye movement tasks (in this case, both Category tasks) the saccade related to the eye movement away from the response target. In order to do so, we identified the time of the saccade away by taking the derivative of the eye trace and setting a voltage threshold (+0.02V for the Category-Saccade, +0.05V for the Category-Match). We determined each of these thresholds based on the threshold evoked by the saccade to the target. Once this threshold was reached, we cut the data prior to the threshold crossing (50 ms) and after (Category-Match, 450ms; Category-Saccade, 250 ms). These times were determined by the shape of the evoked potentials in each of the tasks (i.e. when the mean saccade potential returned to 0V). Different time windows around the saccade were used, and none changed the results. After all of the saccadic periods were cut from each trial, we obtained a template for a saccade for each electrode by taking the mean across all of saccades. Once we obtained this template, we returned to the original data, and applied linear regression to obtain an optimal fit of the template to the saccade potential on each individual trial. Once we found the optimal fit of the template to the data, we subtracted the template from the original data. In order to avoid spurious edge effects, we re-filtered all of the data in both directions by two FIR equiripple filters. Filter 1 was a 106 order, low pass, equiripple FIR filter at 80 Hz (Fpass = 80 Hz, Fstop = 100, Apass = 1, Astop = 60). Filter 2 was a 1047 order, high pass, equiripple FIR filter at 1.5 Hz (Fstop = 0.7, Fpass = 1.5, Astop = 20, Apass = 1).

Linear Regression

To both better assess the synchrony changes across learning, and avoid particular assumptions regarding whether learning occurred linearly over time, we estimated synchrony using PPC across all electrode pairs over 20-trial window bins across each session. We computed the PPC only on correct trials, for we had previously found that most of the longer duration synchrony events occurred on correct trials. These 20-trial windows were non-overlapping, and hence independent. For every 20-trial bin, we had a single PPC value (averaged across all electrode pairs of interest) and an average performance value. We pooled all 20-trial PPC values across all sessions in each of the 3 tasks, and performed linear regression to assess whether PPC varied directly with performance. Our design matrix was simply a column of 1s (our intercept) for each 20-trial bin and another column for performance. After solving the normal equation and calculating the residuals, we computed a t-value and a corresponding p-value. In order to confirm that the assumptions underlying linear regression were met, we plotted how synchrony varied performance from chance (50%) to high performance (100%). We found that over the range of different performance level the variances at each level were largely equivalent with the exception at 100%. To ensure that our results were resistant to this possible violation of heteroscedasticity, we performed both linear regression on a reduced performance range from 50% to 95% (where variances were equal), and robust regression using iteratively reweighted least squares with a bi-square weighting function and a tuning constant of 4.685. Robust regression, unlike ordinary least squares regression, minimizes the influence of data points that are outliers by penalizing their influence. Neither of these methods changed the results; and are unreported here.

Category-Saccade Controls

Because eye movements tend to be rhythmic and occur in the 3–4 Hz range, we wanted to ensure that both correct-incorrect synchrony differences and learning-related synchrony decreases were unrelated to changes in eye movements. To address these concerns, we did two things: One, we controlled for the latency differences in the saccade away from the target that arose between correct and incorrect trials. Two, we examined whether eye movements, like theta synchrony, changed with learning. To control for the latency differences in the eye movement away from the target, we first estimated when saccades were made following the initial saccade to the target using analog outputs from the eye monitoring system. After computing our wavelets and removing the evoked potentials related to the feedback, we aligned each individual trial to this saccade away from the target. Despite this procedure controlling for eye movements, theta synchrony differences emerged immediately following feedback, and did not appear influenced by the realignment procedure.

In order to investigate eye movement changes with learning, we compared the mean saccade velocity and the number of saccades made in the feedback period (0–1.7s). To assess saccade velocity, we cut the raw eye signal into trials, computed the animal’s position on the screen relative to center (by taking the square root of the sum of squares of the X and Y eye position signals), and took the 1^st derivative of the resulting position signal. Saccade velocity was averaged across the 1.7s of the feedback period, and the number of saccades identified was equal to the number of time points that exceeded a voltage threshold of .025V (~178 deg/s). The feedback period is a difficult time to capture behavioral events such as saccades, because the animal may move out of eye tracking limits. As a result, the values computed here may be underestimates of the true saccade count. Moreover, while visual inspection of the eye traces at the thresholds given above suggests that many of these events are saccades, we cannot preclude that some of the saccadic events are, in fact, eye blinks. Note that their inclusion here is conservative, and these flaws of behavioral observation are shared across tasks. To compute significance, we bootstrapped the trials and sessions 10,000 times.

DATA AND SOFTWARE AVAILABILITY

Custom code for analyses will be provided upon request to the Lead Contact.

KEY RESOURCES TABLE

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Experimental Model: Organisms/Strains
Rhesus Macaque (Macaca Mulatta)	Primate Center	N/A
Software and Algorithms
MATLAB	Mathworks	https://www.mathworks.com
CORTEX	National Institute of Mental Health	https://www.nimh.nih.gov/labs-at-nimh/research-areas/clinics-and-labs/ln/shn/index.shtml
Psychtoolbox-3	Brainard, 1997; Pelli, 1997	http://psychtoolbox.org/
Other
64 ch. (8×8) Utah Array (Electrodes)	Blackrock Microsystems	N/A
FHC-Electrodes	FHC	N/A
U-probe (24 ch.)	Plexon	N/A
Cereplex M Headstage	Blackrock Microsystems	PN#8603
Cereplex E Headstage	Blackrock Microsystems	PN#8010
Eyelink I/II	SR Research	N/A
Custom built microdrives		N/A
Cerebrus (128 channels)	Blackrock Microsystems	PN#4176
Multichannel Acquisition Processor	Plexon	N/A
HST/8o50-G1 (Headstage)	Plexon	N/A
VG2401mh 24″ Gaming Monitor	Viewsonic	N/A
5-RLD-E2-C Gravity feed dispenser	Crist	N/A

Highlights.

• Explicit vs implicit learning have different post-choice oscillatory synchrony.

• Explicit learning exploits feedback about errors, implicit learning does not.

• Alpha/beta synchrony increases with explicit learning.

• Theta synchrony decreases with implicit learning.