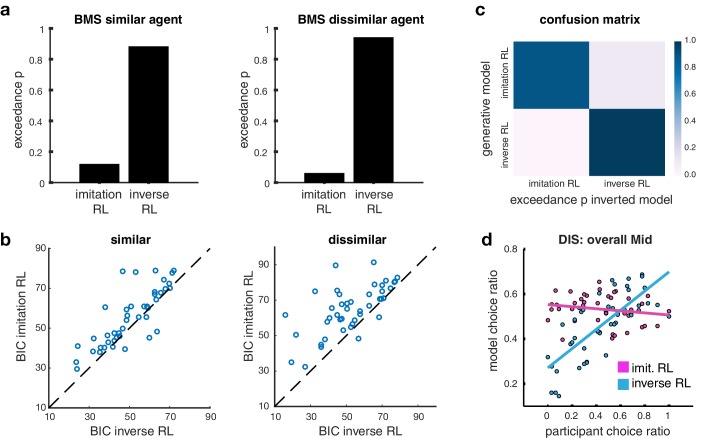
Figure 2. Model comparison.

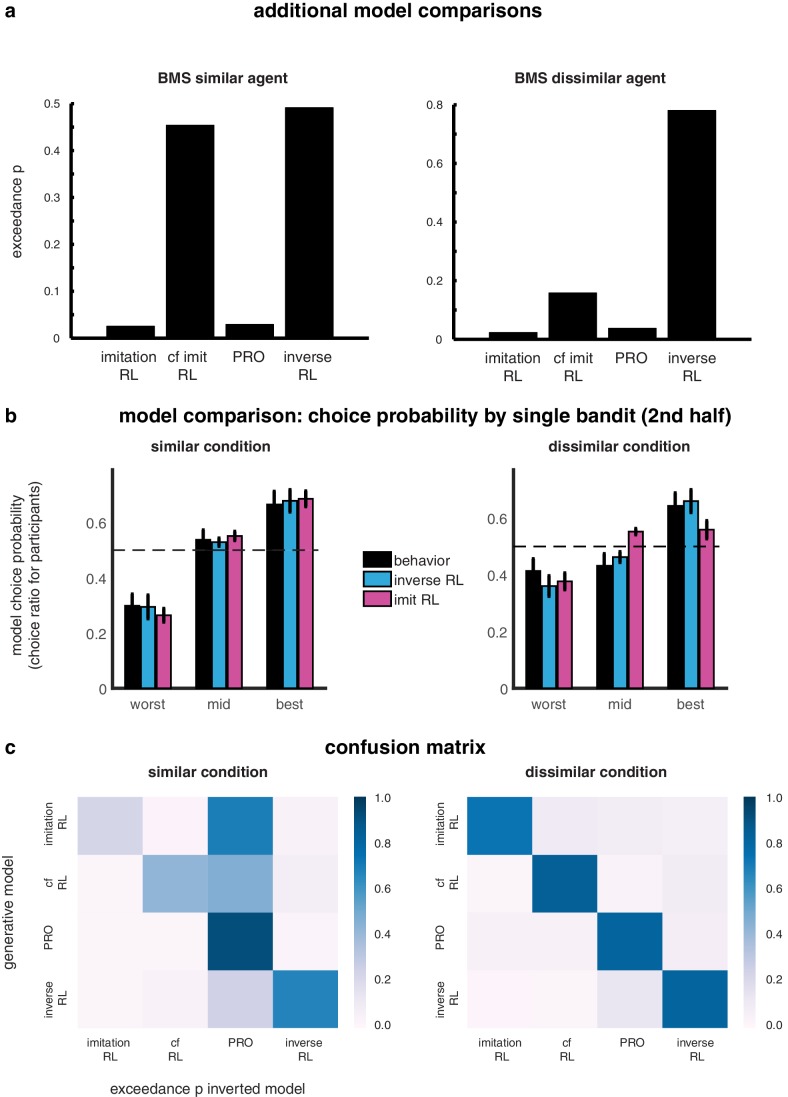
(A) Bar plots illustrating the results of the Bayesian Model Selection (BMS) for the two main model frameworks. The inverse RL algorithm performs best, across both conditions (similar and dissimilar). On the left, the plot depicts the BMS between the two models in the similar condition; on the right the plot shows the BMS in the dissimilar condition (BMS analysis of auxiliary models are shown in Figure 2—figure supplement 1A). (B) Scatter plots depicting direct model comparisons for all participants. The lower the Bayesian Information Criterion (BIC), the better the model performs, hence if a participant’s point lies over the diagonal, the inverse RL explains the behavior better. The figure on the left illustrates the similar condition; the plot on the right depicts the dissimilar condition. (C) Confusion matrix of the two models to evaluate the performance of the BMS, in the dissimilar condition. Each square depicts the frequency with which each behavioral model wins based on data generated under each model and inverted by itself and all other models. The matrix illustrates that the two models are not 'confused’, hence they capture different specific strategies. Confusion matrices of the similar condition and for auxiliary models are shown in Figure 2—figure supplement 1C) (D) Scatter plots depict the participant choice ratio of the mid slot machine plotted against the predictions of the inverse and imitation RL models.

Figure 2—figure supplement 1. Additional model information.

(A) Bayesian Model Selection with additional models: the imitation RL with counterfactuals as described in the main text, and the PRO model (probabilistic rank order): In the PRO model, the observer assumes that the agents have distributions over the preference rankings for the different slot machines without considering the outcome distributions per se. Each rank-order has a certain likelihood of being the actual agent’s preferences over the n slot machines to be ranked. At feedback, the beliefs over the rank orders are updated in a Bayesian fashion, according to the likelihood of each rank order to be correct given the observed choice of the agent. Subsequently the participant’s choice is expressed as a soft-max function between the expected rank value of the chosen and the unchosen slot machine, with a free parameter $\beta$ characterizing the choice stochasticity. We find again that the inverse RL gives a better explanation of participant behavior, especially in the dissimilar condition. (B) mean choice ratio for participants (black) and choice probability for fitted models, separately for similar and dissimilar conditions (C) Confusion matrix of these four models to evaluate the performance of the BMS. Each square depicts the frequency with which each behavioral model wins based on data generated under each model and inverted by itself and all other models. The matrix illustrates that the four models are not 'confused’, especially in the dissimilar condition, hence they capture different specific strategies.