LONGITUDINAL MULTI-SCALE MAPPING OF INFANT CORTICAL FOLDING USING SPHERICAL WAVELETS

Abstract

The dynamic development of brain cognition and motor functions during infancy are highly associated with the rapid changes of the convoluted cortical folding. However, little is known about how the cortical folding, which can be characterized on different scales, develops in the first two postnatal years. In this paper, we propose a curvature-based multi-scale method using spherical wavelets to map the complicated longitudinal changes of cortical folding during infancy. Specifically, we first decompose the cortical curvature map, which encodes the cortical folding information, into multiple spatial-frequency scales, and then measure the scale-specific wavelet power at 6 different scales as quantitative indices of cortical folding degree. We apply this method on 219 longitudinal MR images from 73 healthy infants at 0, 1, and 2 years of age. We reveal that the changing patterns of cortical folding are both scale-specific and region-specific. Particularly, at coarser spatial-frequency levels, the majority of the primary folds flatten out, while at finer spatial-frequency levels, the majority of the minor folds become more convoluted. This study provides valuable insights into the longitudinal changes of infant cortical folding.

1. INTRODUCTION

The human cerebral cortex is a highly folded structure, which grows dramatically during the first two years of postnatal life [1]. The cortical folding is related to cognitive functions, and the abnormality of cortical folding has been associated with many neurodevelopmental disorders rooted during infancy, such as autism and schizophrenia [2]. Hence, quantitative analysis of cortical folding is of great importance in longitudinal infant development research.

For measuring cortical folding, the existing methods can be split into two major categories: global measurement-based and local measurement-based methods. For the first category, the most widely used global descriptor is gyrification index (GI). For instance, two dimensional (2D) GI was introduced as the perimeter ratio of the total folded cortex over the superficial cortex on 2D coronal sections [3]. Although 2D GI is easy to compute and implement, it is somewhat biased since the perimeter is calculated on 2D slices, thus ignoring the three dimensional (3D) nature of the cortex. To solve this, 2D GI was extended to 3D GI, defined as the area ratio between the cortical surface and the cerebral hull surface [4]. However, as a global measurement, GI cannot provide rich spatial information, which leads to the proposition of local measurements.

Methods for examining local cortical folding can be roughly divided into two groups. The first one includes the Local GI (LGI), which calculates 3D GI in specific local regions, ranging from a few vertices to a large region containing several sulcal-gyral folds [4][5][6]. The second group involves curvature and sulcal depth based methods, which estimate the vertex-wise measurements of curvature and sulcal depth [7]. Nonetheless, the curvature, sulcal depth and LGI typically only capture a single-scale information of the rich and complex geometry of the cortex, thus ignoring the intrinsic multi-scale characteristics of the cortical folding.

To measure the complex and multi-scale nature of the cortical folding in infants, we propose to decompose the curvature map of the cortical surface using over-complete spherical wavelets. Since the underlying wavelet basis functions have local supports in both space and frequency, the wavelet coefficients naturally characterize the cortical folding at multiple spatial-frequency scales, thus capturing the richness and complexity of the cortical folding. Note that although wavelet-based decomposition of 3D coordinate functions of the cortical surface at multiple scales has been proposed for studying fetal cortical folding in limited imaging samples [8], the decomposed coordinate information remains difficult to interpret. Since curvature is an intuitive feature of geometric shape, its multi-scale decomposition is more meaningful and interpretable. We apply this method on 219 longitudinal MR images from 73 healthy infants at 0, 1, and 2 years of age. We reveal both the scale-specific and region-specific changing patterns of cortical folding during the first two postnatal years.

2. METHODS

2.1. Subjects and Image Acquisition

MR images for 73 normal neonates (0 year) with follow-up scans at 1 and 2 years of age were acquired on a Siemens head-only 3T scanner. T1-weighted images were obtained with 3D magnetization-prepared rapid gradient echo sequence using the parameters: TR, 1900 ms; TE, 4.38 ms; resolution, 1×1×1 mm³. T2-weighted images were acquired by using a turbo spin-echo sequence with the parameters: TR, 7380 ms; TE, 119 ms; resolution, 1.25×1.25×1.95 mm³.

2.2. Cortical Surface Construction and Mapping

All MR images were processed through an infant-dedicated computational pipeline [1][5]. For preprocessing, briefly, it contained the following procedures: skull striping and cerebellum removing, intensity inhomogeneity correction, tissue segmentation using a longitudinal level-set method, and separation of left and right hemispheres. Topologically-correct inner and outer cortical surfaces were reconstructed using a deformable surface method. The inner cortical surface was further smoothed, inflated, and mapped to a standard sphere. Both intra-subject and inter-subject vertex-to-vertex cortical correspondences were finally established using Spherical Demons [9].

2.3. Cortical Folding Analysis using Spherical Wavelets

2.3.1. Over-complete Spherical Wavelets

The mean curvature map, which partly encodes the geometry of the cortical surface, was calculated on each inner cortical surface with a spherical topology. Herein, we use the over-complete spherical wavelet transform [8] to decompose the curvature map into multi-scales in spatial-frequency domains. Of note, we cannot adopt the conventional orthogonal or biorthogonal spherical wavelets, as they suffer from sampling aliasing and thus a subtle but inevitable rotation error of the surface causes dramatic changes in wavelet coefficients. In contrast, over-complete spherical wavelets resolve this issue by ensuring sufficient sampling at each scale, and thus are more robust and accurate [8]. Let I(θ, φ) be the input spherical curvature map and ${\{{\stackrel{\sim }{h}}_n(\theta ,\phi )\}}_{n=1}^N$ be the spherical analysis filters, which are the dilations of a mother wavelet. By performing spherical convolutions between them, we output a set of wavelet coefficients ω_n = I * h̃_n. When convolving ω_n with the corresponding spherical synthesis filter h_n inversely, we can obtain the reconstructed spherical curvature map by summarizing the outputs: Î= Σ_n ω_n * h_n [8]. Note that the analysis-synthesis filter bank ${\{{\stackrel{\sim }{h}}_n,h_n\}}_{n=1}^N$ is invertible. To construct a spherical continuous wavelet transform (SCWT), the analysis filter h̃_n is defined as:

$${\stackrel{\sim }{h}}_n=D_n\psi$$ (1)

where n is the frequency level and ψ is the mother wavelet. D_nψ represents the dilations of ψ. The synthesis filter is defined as [8]:

$$h_n^{l,m}=\{\begin{array}{c}\hfill {\stackrel{\sim }{h}}_n^{l,m}/H_{\stackrel{\sim }{h}}(l),\text{for }{H}_{\stackrel{\sim }{h}}(l)>0\hfill \\ \hfill 0,\text{otherwise}\hfill \end{array}$$ (2)

where h^l,m denotes the function h(θ, φ)’s l-th degree and m-th order spherical harmonic coefficient. Herein, H_h̃ (l) denotes the frequency response defined as follows [8]:

$$H_{\stackrel{\sim }{h}}(l)=\frac{8{\pi }^2}{2l+1}{\sum }_{n=1}^N{\sum }_{m\prime =-l}^l{\left|{\stackrel{\sim }{h}}_n^{l,m\prime }\right|}^2$$ (3)

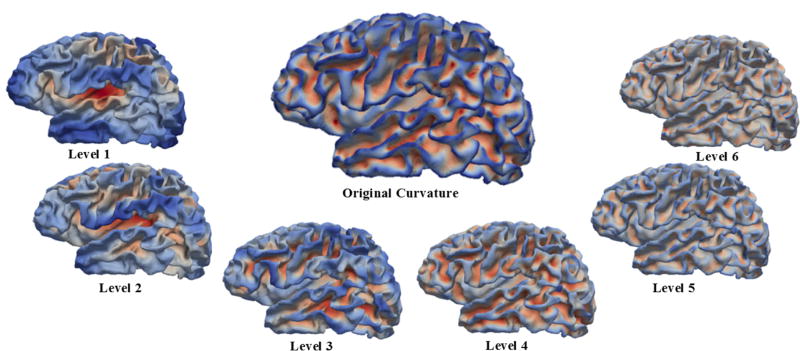
To decompose the spherical curvature map into multi-scales, we convolved the curvature function with the analysis multi-level filters in the spherical domain, thereby generating a series of wavelet coefficients ω_n at each level n. Herein, we used the Laplacian-of-Gaussian as the mother wavelet ψ [8]. For a rotation-invariant shape analysis, we over-sampled the estimated wavelet coefficients ω_n on the sphere with 163,842 vertices. As shown in Fig. 1, in the original surface (in the middle), each vertex is colored by the mean curvature value, where blue indicates gyri and red indicates sulci. In the decomposed curvature maps at levels 1–6, each vertex is colored by its corresponding wavelet coefficients. As we can see, wavelet coefficients of the curvature map at coarser levels capture larger-scale folding information, while coefficients at finer levels encode smaller-scale folding information, thus leading to a natural multi-scale characterization of cortical folding.

Fig. 1.

Decomposition of the cortical curvature map into multiple scales (levels 1–6) via over-complete spherical wavelets. The large surface (in the middle) is the original cortical mean curvature map of a neonate. The smaller ones are decomposed curvature maps at levels 1–6. Blue indicates large negative values, while red indicates large positive values.

2.3.2. Cortical Folding Analysis

For each vertex x at each scale n, its wavelet power was used to indicate the cortical folding degree as:

$$p_n^t(x)={\omega }_n^t{(x)}^2,n\in \{1,2,3,\dots ,6\}$$ (4)

where ω denotes the wavelet coefficient of the vertex x at the level n, and t represents the age (0, 1, and 2 years) of a subject.

For each ROI R at each scale n, its average wavelet power was defined as:

$$P_n^t(R)=\frac{1}{M_R}{\sum }_{x\in R}{p}_n^t(x)$$ (5)

where M_R represents the number of vert ices in this ROI.

We also calculated the mean change rate of wavelet power in each ROI across all subjects through age 0–1 and 1–2, separately. The change rate G of wavelet power was defined as:

$$G_n^{t\to t+1}(R)=\frac{1}{s}{\sum }_{s=1}^S\frac{P_n^{t+1}(R_s)-P_n^t(R_s)}{P_n^t(R_s)}$$ (6)

where Sdenotes the total subject number (here 73) and R_s indicates the region R in subjects.

2.4. Statistical Analysis

To study the statistical significance of cortical folding changes during 0–1 year and 1–2 years, a paired t-test was performed. Specifically, for each subject, we paired the wavelet power of each ROI at each scale estimated at two adjacent time points. Next, we used the paired sample t-test with p < 0.05 to identify the significant change regions between age 0 and 1 year, as well as age 1 and 2 years, respectively. Finally, we performed multiple comparisons correction using the false discovery rate (FDR).

3. RESULTS

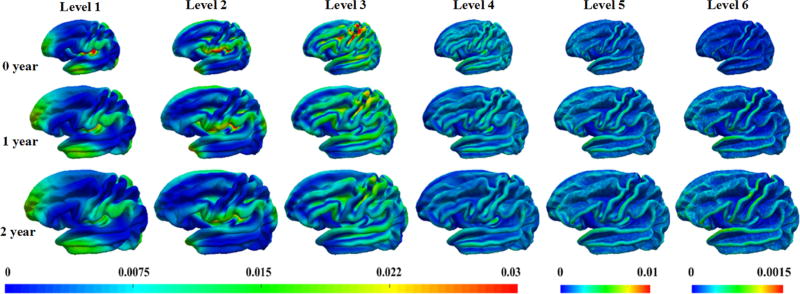
Fig. 2 depicts the vertex-wise average of the wavelet power of the decomposed curvature maps at levels 1–6 at 0, 1, and 2 years of age, each based on 73 normal subjects. As we can see, the wavelet power is both region-specific and scale-specific and changes substantially during the first two years. Specifically, in levels 1 and 2, regions with higher wavelet power locate in the frontal pole, temporal pole, occipital pole, insula cortex, supramarginal gyrus, superior parietal cortex, perisylvian cortex, and superior frontal gyrus, mainly capturing large-scale folding information of the cortex; in levels 3 and 4, regions with higher wavelet power are largely in the sulcal bottoms and their adjacent gyral crests of primary folds, such as the central sulcus, precentral sulcus, postcentral sulcus, superior temporal sulcus, inferior frontal sulcus and superior frontal sulcus, capturing the sulcal-gyral scale geometric information of primary folds. In levels 5 and 6, regions with higher wavelet power are more variable and mainly locate on the gyral crests, reflecting fine-scale folding information. In general, the spatial and scale-specific distribution patterns of the wavelet power are largely preserved from 0 to 2 years of age. As for the magnitude patterns, they display an interesting trend, specifically, slight decrease in coarser levels 1–4, while slight increase in finer levels 5–6.

Fig. 2.

Vertex-wise average of the wavelet power of the decomposed curvature maps at levels 1–6 at 0, 1, and 2 years of age, each based on 73 normal subjects.

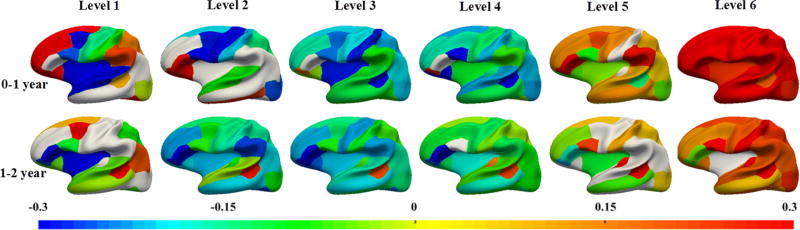
Fig. 3 shows the change rate of the wavelet power in ROIs at various scales. Overall, the mean change rate of all ROIs in 6 levels are 0.30, −0.01, −0.14, −0.11, 0.18, 0.74, respectively, in year 1, while −0.04, −0.17, −0.16, −0.08, 0.03, 0.21, respectively, in year 2. These indicate overall large increase in cortical folding in both the very coarse level and very fine level in year 1, and also large increase in cortical folding at the very fine level in year 2. In Fig. 3, the colored regions indicate statistically significant regions after FDR correction, whereas the white regions lack statistical significance. As we can see, the change of wavelet power is regionally heterogeneous and age-specific. During the first year, at level 1, the unimodal cortices, such as sensorimotor area, auditory cortex, and visual cortex, as well as Broca’s area, decrease in wavelet power, whereas high-order association cortices, such as the prefrontal cortex and parietal cortex, increase in wavelet power, indicating differential change patterns between unimodal and high-order association regions. Interestingly, the insula cortex and caudal middle frontal cortex also decrease. At level 2, most regions decrease in wavelet power, whereas several high-order association regions increase in wavelet power, including the pars triangularis, pars orbitalis, orbitofrontal region and inferior temporal cortex. At levels 3 and 4, all regions, except the pars orbitalis, decrease in wavelet powers. At levels 5 and 6, most regions increase in wavelet power, indicating that the cortical folding in fine scales becomes more folded. Interestingly, across all 6 levels, the pars orbitalis always increases in wavelet power.

Fig. 3.

Longitudinal multi-scale wavelet power changing rate of decomposed curvature maps in the first 2 years, based on 73 subjects.

During the second year, the overall change trends at different levels are similar to those in the first year to some extent. Specifically, at level 1, while the wavelet power peaks in caudal middle frontal cortex, banks of superior temporal sulcus (STS) and inferior parietal cortex, it largely drops in insula cortex, pars triangularis and pars orbitalis. At levels 2 to 4, most regions decrease in wavelet power, except the banks of STS. At levels 5 and 6, most regions increase in wavelet power. Interestingly, across all 6 levels, the banks of STS always increase in wavelet power. It is also interesting that the insula cortex exhibits a large negative change both at year 0–1 and year 1–2 at level 1. Together, these results may indicate that: as the brain volume grows, at very coarser spatial-frequency levels, primary folds of specific regions, such as the insula and unimodal cortex, flatten out (i.e., negative change rate), especially in the first year; while at very finer spatial-frequency levels, small folds in most regions become more complex and convoluted (i.e., positive change rate). Furthermore, we notice that most regions in the frontal cortex become more folded, especially in the first year, consistent with the results in [5].

4. CONCLUSION

In this paper, we proposed a new approach to map the longitudinal changes of infant cortical folding. We leveraged spherical wavelets to decompose the cortical curvature maps into multi-scales, with each scale encoding the folding information at a different level, and then adopted the wavelet power to quantify cortical folding. We revealed both scale-specific and region-specific changes in cortical folding. Specifically, folds in unimodal cortex and insula cortex at coarser spatial-frequency levels become flat, and the majority of smaller folds at finer spatial-frequency levels become more folded; while most folds in the frontal cortex become more folded at coarser levels during the first two years, providing new insights into the longitudinal changes of infant cortical folding. Future work includes studying gender and cognition functions in relation to cortical folding and applying other features, to further examine the infant brain development. 5.