Improved Quantum Chemical NMR Chemical Shift Prediction of Metabolites in Aqueous Solution Toward the Validation of Unknowns

Abstract

A quantum-chemistry based protocol, termed MOSS-DFT, is presented for the prediction of ¹³C and ¹H NMR chemical shifts of a wide range of organic molecules in aqueous solution, including metabolites. Molecular motif-specific linear scaling parameters are reported for five different density functional theory (DFT) methods (B97-2/pcS-1, B97-2/pcS-2, B97-2/pcS-3, B3LYP/pcS-2 and BLYP/pcS-2), which were applied to a large set of 176 metabolite molecules. The chemical shift root-mean-square deviations (RMSD) for the best method, B97-2/pcS-3, are 1.93 ppm and 0.154 ppm for ¹³C and ¹H chemical shifts, respectively. Excellent results have been obtained for chemical shifts of methyl and aromatic ¹³C and ¹H that are not directly bonded to a heteroatom (O, N, S, or P) with RMSD values of 1.15/0.079 ppm and 1.31/0.118 ppm, respectively. This study not only demonstrates how NMR chemical shift predictions in aqueous environment can be improved over the commonly used global linear scaling approach, but also allows for motif-specific error estimates, which are useful for an improved chemical shift-based verification of metabolite candidates of metabolomics samples containing unknown components.

Graphical Abstract

1. Introduction

The analysis of complex metabolic mixtures of a wide range of biological systems using NMR spectroscopy has become increasingly popular over the past decade in the context of the rapidly growing field of metabolomics.^1–4 This is in part due to the ability to simultaneously provide detailed spectroscopic information on many different metabolites in the same sample. In that way, new insights into the state of biological systems as well as into metabolic pathways are possible.^5–8

The concomitant development of databases and web-based query tools, like the Complex Mixture Analysis by NMR (COLMAR) database⁹, The Human Metabolome Database (HMDB)¹⁰ and the Biological Magnetic Resonance Data Bank (BMRB)¹¹, has further increased the usefulness of NMR spectroscopy and enabled the automated assignment of metabolites. However, the identification of unknown metabolites, which are metabolites that give rise to signals in the NMR spectra, but that have not been identified previously or are not part of commonly accessible NMR databases, remains a key challenge. In this regard, empirical chemical shift predictors, such as NMRPredict¹² as used by the MNova software,¹³ or the ACD/NMR predictor¹⁴ are useful to efficiently compare experimental chemical shift information with predicted chemical shifts of a large number of candidate structures, but their accuracy is determined by the nature and size of the underlying database.

As a consequence, one often encounters excellent prediction results for structures that are part of the underlying database, but structures (or substructures) that have not been considered during the fitting procedure are usually predicted with significantly reduced accuracy. Therefore, predictors that are less dependent on or even entirely independent of databases, potentially allow for the more balanced and more accurate chemical shift prediction for both known and unknown structures. In this context, quantum-chemical (QC) methods offer a promising alternative. However, their computational cost is in most cases several orders of magnitude larger and they require the use of high performance computing resources when a large number of predictions is needed. To keep the computational costs manageable, several approximations are usually employed, both regarding the system under study and the QC method itself. Although other procedures have been put forward in the literature,^15–16 a widely-used approach is to calculate shielding constants only for a limited number of relevant conformers and to account for solvent effects implicitly. Among the various QC methods, density functional theory (DFT) has been shown to yield both the accuracy and numerical efficiency to allow for NMR chemical shift calculations on a routine basis.^17–24 Nevertheless, recent developments in wave function-based methods, especially MP2, offer potentially useful alternatives for small to medium-sized molecules.^25–27

The calculated shielding constants can be converted to chemical shifts in three ways: (i) by subtracting them from the shielding constant of an internal reference, such as tetramethylsilane (TMS) or 4,4-dimethyl-4-silapentane-1-sulfonic acid (DSS), (ii) by intermediate references or multi-standards, and (iii) by means of (linear) regression. Whereas the first two approaches usually rely on (often fortuitous) error cancellation between shielding constants calculated for the query and reference atom, linear regression allows for the correction of systematic errors as a function of the shielding constant. Several studies have reported excellent agreements with experimental shifts by using DFT together with linear regression and provided fitting parameters for several exchange-correlation/basis set combinations^{20, 28–30}, where some of them used multiple motif-dependent standards.³¹ However, most of them were conducted in organic solvents, such as chloroform, for a relatively small number of molecules. While these results are helpful in the field of general organic chemistry, they are somewhat less practical for metabolomics studies, because NMR chemical shifts are usually measured in aqueous solution. Naturally, the presence of water poses additional challenges for the prediction of NMR chemical shifts of metabolites, especially if combined with implicit solvent models. For example, chemical shifts of atoms in close proximity to hydrogen bond donors or acceptors will have different systematic errors than shifts of those atoms that are further away.³² Moreover, molecules that allow for intramolecular hydrogen bonding often exhibit large chemical shift deviations when implicit solvent models are employed. This is because conformational search and geometry optimization in implicit solvent favor geometries that are stabilized by intramolecular hydrogen bonds, which often leads to a biased conformational ensemble compared to the one in explicit water. As a result, atoms in different microscopic solvation environments will have different systematic errors.

In the present work, we report a DFT-based protocol, termed MOlecular motif-Specific Scaling of Density-Functional-Theory-based chemical shifts (MOSS-DFT), for NMR chemical shift predictions, which is based on a set of 176 molecules that are relevant for metabolomics studies. Chemical shielding constants are converted to chemical shifts by a motif-specific linear regression approach of calculated shielding constants to experimental chemical shift measured with 2D ¹H-¹³C HSQC spectroscopy. In the first part, details about the MOSS-DFT database construction and the computational methods are given. Thereafter, we provide the definition of motifs and compare our prediction results with those from earlier studies that employ global linear regressions. In the last part, we discuss the influence of basis set size and the exchange-correlation functional by comparing the results to various functional-basis set combinations.

2. Methods

For the MOSS-DFT database construction, a number of molecules were randomly picked from the COLMAR database. We used Open Babel³³ to generate 3D coordinates from 2D structures and to adjust the protonation state of ionizable groups to pH 7, that is, all carboxylic, phosphonic and sulfonic acid groups were deprotonated and all amino groups were protonated. For the calculation of the chemical shifts we largely follow the approach described previously.²¹ All molecules were subjected to a conformational search, which was conducted with the MacroModel program³⁴ that is part of the Schrödinger suite. The OPLS 2005 force field³⁵ was used together with an implicit solvent model for water.³⁴ For sampling, the Monte Carlo Multiple Minimum (MCMM) algorithm was chosen^36–37 with the maximum step number set to 5000. Other program options have been set to their default values or set automatically by MacroModel, which is part of the automatic setup. To avoid unphysical conformational ensembles due to the implicit solvation model, the resulting conformers were checked for intramolecular hydrogen bonds, defined by a donor (D) – acceptor (A) distance of less than 3.5 3 and a D-H-A angle of 180° ± 30°. In the case of intramolecular hydrogen bonding in at least one of the conformers, the compound was removed from the database. In addition, molecules with long carbon hydride chains were excluded, if the conformational search yielded a large number (>100) of similarly low energy structures. The conformers obtained from the conformational search were further optimized at the DFT level using the Gaussian 09 program.³⁸ The B3LYP³⁹ exchange correlation functional was used together with the D3 dispersion correction⁴⁰ and the def2-TZVP basis set.⁴¹ In order to capture solvation effects, the conductor polarized continuum model (CPCM) was adopted using water as solvent.^42–43 To ensure well-converged local minimum geometries, extremely tight convergence criteria have been used along with an ultrafine integration grid.

Convergence to local minimum structures has been additionally monitored by normal mode analysis at the same level of theory. In cases where two initially different conformers had essentially identical total energies (ΔE ≤ 10⁻⁹ Hartree), it was assumed that the DFT optimization led to the same minimum structure and calculations were continued only for one of the structures. The conformer population p_i at 298.15 K was estimated from a Boltzmann analysis

$$p_i=\frac{e^{-E_i/RT}}{{\sum }_{j=1}^N{e}^{-E_j/RT}}$$ (1)

where E_i denotes the relative free energy (electronic + thermal free energy) of conformer i as estimated from the thermochemical analysis in Gaussian 09 with respect to the most stable conformer. RT is the product of the ideal gas constant and the absolute temperature, respectively, and N is the total number of distinct conformers as obtained from geometry optimization. NMR shielding constants were calculated based on the gauge-independent atomic orbitals (GIAO) approach as implemented in Gaussian 09.^44–48 We calculated NMR shielding constants at the DFT level employing 5 different functional-basis set combinations (see Table 3). The computed NMR shielding values have been averaged according to the weights of the Boltzmann analysis. Because calculated shielding constants have been referenced to chemical shifts obtained from ¹H-¹³C HSQC experiments, the MOSS-DFT database only contains ¹³C-¹H pairs of covalently bonded atoms. The calculated shielding constants of methyl and methylene protons have been averaged to reduce misassignments in the case of magnetically inequivalent protons. In our calculations, about 4% of the atoms had chemical shift deviations larger than 7 ppm and 0.6 ppm for ¹³C and ¹H, respectively. A closer inspection of the problematic compounds suggests in some cases misassignments in the experimental spectra or obvious problems in conformational sampling, such as errors in dihedral angles, especially for some tertiary carbon atoms. However, for the majority of outliers it was not easily possible to identify the specific cause for the deviation, such as less common functional groups. To prevent biased linear regression parameters, the molecules containing those atoms have been removed from the database, and the linear fit was repeated for the remaining 176 molecules. Finally, to convert the shielding constants to chemical shifts, a motif-specific linear regression approach was used according to

Table 3.

RMS Deviations of Chemical Shifts for Different Exchange-Correlation Functionals and Basis Sets.

XC Functional / Basis Set	RMSD 13C (ppm)	RMSD 1H (ppm)
B97-250 / pcS-151	2.05	0.222
B97-2 / pcS-251	1.96	0.164
B97-2 / pcS-351	1.93	0.154
B3LYP39 / pcS-2	2.03	0.165
BLYP52–54 / pcS-2	2.62	0.166

$$\delta =a_i{\sigma }_{\mathit{iso}}+b_i$$ (2)

where σ_iso denotes the shielding constant; a_i and b_i are model parameters for motif i (details on motifs are given below) and δ is the chemical shift value.

3. Results and Discussion

3.1 Motif-Specific Linear Regressions for the More Accurate Chemical Shift Prediction

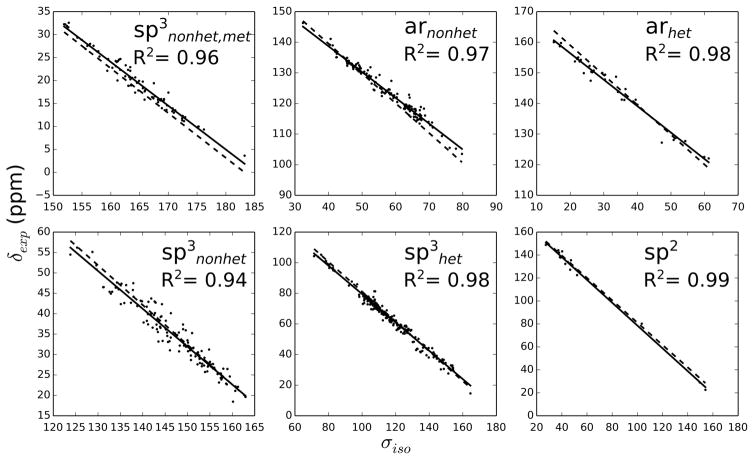
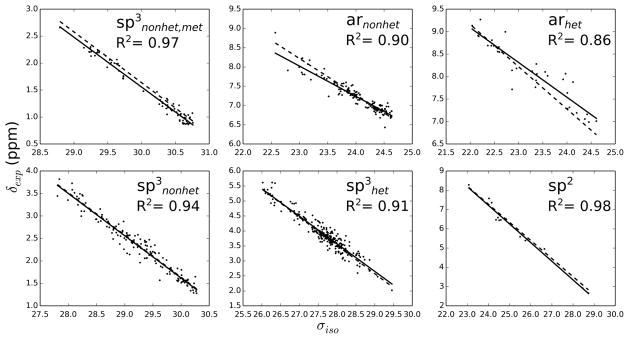
Table 1 shows the definition and names of motifs that are used to convert the calculated shielding constants to chemical shifts. We assigned each ¹³C-¹H pair to one of the motifs based on the chemical environment of its carbon atom. That is, we determined in a first step whether the carbon atom is sp³ or sp² hybridized, and subsequently, whether it is bonded to any element other than carbon or hydrogen. For sp² carbons, we further discriminated between aromatic and aliphatic carbons, where we assigned aromatic atoms to ar_het and ar_nonhet depending on whether they are bonded to a hetero atom or not. Aliphatic sp² atoms were assigned to the sp² motif. Due to the relatively small number of atoms within this motif, it was not further divided into hetero or non-hetero bonded carbons. Note, these definitions are mutually exclusive, that is, every ¹³C-¹H pair is assigned to only one of the motifs. Our motivation for the present classification is threefold: we aim (I) to correct for errors due to the implicit modeling of solute-water interactions that will affect carbons bonded to heteroatoms differently than carbon atoms bonded to other carbon atoms, (II) to identify and obtain groups of atoms with superior or inferior prediction accuracy, and optimize their scaling parameters to further reduce errors within these groups, and (III) to account for slightly different slopes of aliphatic and aromatic carbons and protons. As part of the fitting process, we carried out a quadratic fit for each of the motifs and found no significant improvements.

Table 1.

Definitions, Names, and Examples of the Molecular Motifs Used in the Linear Regression Approach.

Motif Definition:	Methyl groups not bonded to a heteroatom	sp3 carbon centers not bonded to a heteroatom, excluding methyl groups	sp3 carbon centers bonded to a heteroatom	Aromatic carbon centers not bonded to a heteroatom	Aromatic carbon centers bonded to a heteroatom	sp2 carbon centers
Motif Name:	sp3nonhet, met	sp3nonhet	sp3het	arnonhet	arhet	sp2
Examples:

The RMSD values and slopes of the linear regressions for the best performing method, B97- 2/pcS-3, are reported in Table 2, where the considered RMSD intervals were limited to 0–7 ppm (¹³C) and 0–0.6 ppm (¹H), respectively. Our findings show a good overall performance of the MOSS-DFT approach as indicated by RMSD values of 1.93 and 0.154 ppm for ¹³C and ¹H, respectively. A particularly good prediction is achieved for motif sp³_nonhet,met with RMSD values of 1.15 and 0.079 for ¹³C and ¹H, respectively. Therefore, the chemical shift prediction of methyls that are not bonded to any heteroatom should be given a higher weight when such information is used for the identification and validation of unknown metabolites.

Table 2.

RMSDs with respect to Experimental NMR Chemical Shifts along with Linear Regression Parameters for the B97-2/pcS-3 Method.

Nucleus		sp3nonhet,met	arnonhet	arhet	sp3nonhet	sp3het	sp2	total
13C	a	−0.9532	−0.8433	−0.8634	−0.9277	−0.9261	−0.9936
	b	176.5288	172.4185	173.6563	171.0732	172.1137	177.9458
	RMSD	1.15	1.31	1.76	2.05	2.32	3.03	1.93
1H	a	−0.9244	−0.7854	−0.7725	−0.9399	−0.9181	−0.9677
	b	29.2860	26.0863	26.0812	29.8153	29.2769	30.4447
	RMSD	0.079	0.118	0.239	0.146	0.177	0.214	0.154
	No. of 13C-1H pairs	87	192	35	141	285	16	756

As a general trend, a higher prediction accuracy is achieved for ¹³C-¹H pairs that are not directly bonded to a heteroatom, with carbons in the group ar_het being a notable exception. The worst prediction results are found for sp² carbons and protons, as well as for protons within the ar_het group. Nevertheless, with the MOSS-DFT prediction approach we obtained an accuracy that is comparable to earlier studies of organic solvents using global scaling factors and intercepts.^{20, 24, 28–30} We also note that in our case the RMSD values for global scaling are 2.36 and 0.170 ppm for ¹³C and ¹H, respectively, and thus significantly larger than those for the motif-specific scaling. To cross-validate our approach, a new training set was created by randomly excluding 20% of the compounds from the original MOSS-DFT training set and assigning them to a test set. The obtained linear regression parameters for the new training set and the RMSD values of the test set are reported in Table S3. We find overall RMSD values of 1.94 ppm and 0.133 ppm for ¹³C and ¹H, respectively, which are well comparable to the ones reported above. In addition, a comparison of the linear regression parameters in Table S3 with the original MOSS-DFT parameters shows only marginal differences, which confirms that the MOSS-DFT parameters are robust, i.e. they are insensitive to the exact choice of the database. As a result, a good prediction accuracy can be expected when applying the MOSS-DFT parameters to targets outside of the training set, provided that the conformational ensemble of the query compound has been obtained in a similar way.

Figures 1 and 2 show the correlation between shielding constants and experimental chemical shifts within the considered RMSD interval. The high R² coefficients indicate very good correlations considering the narrow chemical shift ranges of most of the motifs. Usually, better correlations are found for ¹³C than for ¹H. This is not unexpected, since the chemical shift ranges are much smaller in the latter case. Furthermore, there are significant differences between global and motif-specific fits. The largest discrepancies between global and motif-specific slopes are found for ar_nonhet and ar_het, indicating larger systematic errors in these cases. It has been previously proposed for Hartree-Fock that the larger degree of electron correlation in aromatic compounds is responsible for larger systematic errors,⁴⁹ but this is still under debate for DFT. Nevertheless, Table 2 shows that the RMSD values of the aromatic groups are mostly lower than those for sp3_nonhet, which illustrates the importance of the motif-specific corrections used here. Another interesting observation is found for motif sp3_nonhet,met: the correlation plots for ¹³C and ¹H show almost parallel ‘best fit’ lines for global and motif-specific regressions. At this point, it is unclear whether this result is intrinsic to our model (i.e. GIAO-DFT with implicit water model and the use of optimized geometries) or whether it is of purely statistical nature. The use of a larger sample size with a concomitant reduction of the spread of the error distribution might be able to resolve this issue.

Figure 1.

Experimental chemical shifts versus computed isotropic shielding constants of ¹³C using the B97-2/pcS-3 method. The solid lines belong to the best fit for each motif, while the dashed lines correspond to the global fit.

Figure 2.

Experimental chemical shifts versus computed isotropic shielding constants of ¹H using the B97-2/pcS-3 method. The solid lines belong to the best fit for each type, while the dashed lines correspond to the global fit.

3.2 Choice of Basis Set and Exchange-Correlation Functional

The computational cost of chemical shift predictions is especially crucial in the field of metabolomics as often large sets of candidate compounds exist for which predictions are needed. Clearly, the computational time required for any QC method to calculate shielding constants will depend on the size of the basis set. To find an acceptable tradeoff between computational cost and prediction accuracy, the dependence of RMSD values for ¹³C and ¹H chemical shifts on the basis set size has been examined. The results for the sequence pcS-1, pcS-2 and pcS-3 are shown in Table 3. Note that the average computational time for a single NMR shielding calculation increases from 1 minute for pcS-1 to around 4 hours for pcS-3 on 12 cores. It is found that the RMSD value for ¹³C chemical shifts decreases by 0.09 ppm when the pcS-2 basis set is used instead of pcS-1. The use of pcS-3 only yields a marginal improvement of 0.03 ppm. Although, on an absolute scale, the differences between RMSD values of ¹H are comparable to those of ¹³C, it is clear that changes in the second digit after the decimal point are already a major accuracy gain for ¹H. Like for ¹³C, our results indicate a consistent improvement for ¹H chemical shifts when going to larger basis sets, where the difference between pcS-1 and pcS-2 is as large as 0.058 ppm. However, unlike for ¹³C, the use of B97-2/pcS-3 still leads to a small improvement by 0.01 ppm compared to B97-2/pcS-2. It is also interesting to note that there is no obvious relation between a scaling factor closer to one and a lower RMSD value (see Tables S1 and S2). Nevertheless, one observes convergence of the scaling factors in the case of ¹³C for pcS-2 to pcS-3. Thus, we can conclude that the accuracy gain results from an improved correlation between calculated shielding constants and experimental chemical shifts, but not from the reduction of the method’s systematic error as reflected by the scaling factor.

In addition to the basis set convergence, we compared the performances of two other exchange-correlation functionals. The results are reported in Table 3. The first functional, B3LYP, is one of the most widely used hybrid DFT functionals for organic molecules, whereas the second, BLYP, is a GGA functional often used in explicit solvent ab-initio molecular dynamics simulations and NMR shielding calculations due to its numerical efficiency. Compared to B97-2/pcS-2, both functionals perform slightly worse for ¹³C with RMSDs of 0.07 and 0.66 ppm for B3LYP and BLYP, respectively. Interestingly, the prediction performance of both functionals for ¹H is consistent with that of B97-2. Unlike the basis set dependence, our findings show a correlation between a lower RMSD and a slope closer to one (see Tables S1 and S2), which indicates a smaller systematic error.

3.3 Comparison with Empirical Predictions

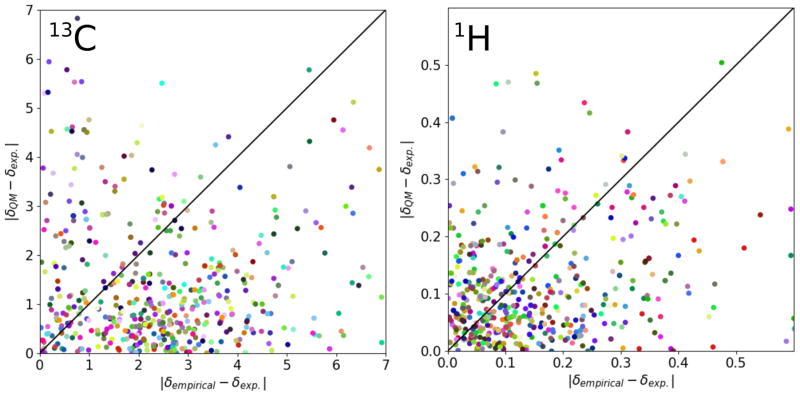
Since the time needed for QC predictions is typically orders of magnitudes larger than for empirical predictions, the former need to deliver a substantial accuracy increase to justify their use in metabolomics studies. To verify this, we compared the RMSD values of our MOSS-DFT method to empirical predictions in Table 4. Likewise, for the QC results above, all molecules that contained ¹³C/¹H atoms, whose empirically predicted shifts deviated by more than 7 ppm / 0.6 ppm, have been omitted in the RMSD calculation. We note, however, that a completely unbiased comparison between both methods is not possible in our case, because it would require an independent validation set and therefore the knowledge of the training set of the NMRPredict program, which is not available. Our findings show an improvement of more than 1.2 ppm for ¹³C and 0.1 ppm for ¹H of the QC method in terms of RMSD over the empirical NMRPredict program. Even by using only a global correction, our QC predictor still outperforms the empirical predictor. However, predictions that are closely related to those in the training set are usually predicted by the empirical method with a very high accuracy, whereas structures that are dissimilar to the training set tend to be predicted significantly less accurately. We also investigated the correlation between the predictions by MOSS-DFT and NMRPredict (Figure 3) and find that there is no obvious correlation between the two. Nevertheless, both methods seem to be complementary in the sense that there are only few predictions that have large errors in both cases. The low probability of large errors for either method could be used as additional scoring information as part of the identification protocol. For example, if both predictors show a relatively large error for a candidate structure, it can be assigned a lower matching score.

Table 4.

RMSD Values for MOSS-DFT (B97-2 / pcS-3) and NMRPredict Chemical Shift Predictions with respect to experiment.

13C	RMSDMOSS-DFT	1.93 ppm
	RMSDNMRPredict	3.15 ppm*
1H	RMSDMOSS-DFT	0.154 ppm
	RMSDNMRPredict	0.255 ppm*

^*Outliers above 7 ppm (¹³C) / 0.6 ppm (¹H) have been excluded

Figure 3.

Absolute deviations of predictions by MOSS-DFT versus NMRPredict for ¹³C and ¹H. The diagonal is shown to guide the eye. Points marked with the same color belong to the same molecule. Note that the chemical shift error ranges for ¹³C and ¹H have been limited to the intervals indicated in the figure.

4. Conclusion

In this work, we have presented a new DFT-based chemical shift prediction approach in aqueous solution, MOSS-DFT, that is specifically suited for the analysis of metabolites. To correct for systematic errors, a motif-specific model was introduced, which goes beyond a common global scaling correction. Our approach is based on a set of 176 molecules, where ¹³C-¹H atom pairs have been classified into 6 motifs based on hybridization, aromaticity, and heteroatom bonding of the carbon atom. Subsequently, linear regression parameters have been derived separately for each of the motifs. We found a total RMSD value with respect to experimental data of 1.93/0.154 ppm for ¹³C/¹H. This value is 0.43/0.016 ppm lower than that of the global linear correction. As a general trend, predictions of atoms that are not bonded to a heteroatom exhibit a lower error. The best motif-specific RMSD values were obtained for sp³_nonhet,met and ar_nonhet with 1.15/0.079 ppm and 1.31/0.118 ppm for ¹³C/¹H atoms. The non-aromatic sp² atoms have the highest RMSD (3.03 ppm) for ¹³C, whereas for ¹H the highest RMSD of 0.239 ppm was found for ar_het. A comparison of different functional/basis set combinations suggests that B97-2/pcS-2 is most economical, although B97-2/pcS-3 is slightly more accurate for ¹H. In the case of ¹H, no significant improvement is found for B97-2 and B3LYP functionals over BLYP. A limitation of the MOSS-DFT approach is for molecules that form intramolecular hydrogen bonds. Therefore, future developments and applications of numerically efficient protocols should focus on the improved sampling and selection of relevant conformations for further improvements toward accurate calculations of chemical shifts of a growing spectrum of synthetic and naturally occurring molecules.