Probing bacterial cell biology using image cytometry

Abstract

Advances in automated fluorescence microscopy have made snap-shot and time-lapse imaging of bacterial cells commonplace, yet fundamental challenges remain in analysis. The vast quantity of data collected in high-throughput experiments requires a fast and reliable automated method to analyze fluorescence intensity and localization, cell morphology and proliferation as well as other descriptors. Inspired by effective yet tractable methods of population-level analysis using flow cytometry, we have developed a framework and tools for facilitating analogous analyses in image cytometry. These tools can both visualize and gate (generate sub-populations) more than 70 cell descriptors, including cell size, age, fluorescence, etc. The method is well suited to multi-well imaging, analysis of bacterial cultures with high cell density (thousands of cells per frame), and complete cell cycle imaging. We give a brief description of the analysis of four distinct applications to emphasize the broad applicability of the tool.

Introduction

Quantitative fluorescence imaging has become an important tool for the study of the bacterial cell biology (van Teeffelen et al., 2012). Most cellular processes, from chromosome segregation to replication, are stochastic in nature and exhibit significant cell-to-cell variation (Kuwada et al., 2013; Kuwada et al., 2015a; Cass et al., 2016). This variation makes the quantitative statistical analysis of a significant number of cells essential (Kuwada et al., 2015a). For many biological problems, flow cytometry offers a tractable approach for the analysis of thousands of cells per second and offers powerful methods for sub-population analysis: Cells are gated (or selected) by fluorescence or scattering intensity, or a combination of intensities. Gating is used for both analytic applications (i.e. the determination of the relative abundance of a sub-populations or the removal of cell debris from the analysis) and functional applications (i.e. Fluorescence Activated Cell Sorting, FACS).

Although flow cytometry is fast and efficient, many important cell biology questions demand an imaging approach where cellular ultrastructure can be characterized and the cell cycle dynamics captured for individual cells. In contrast to flow cytometry, the use of time-lapse imaging has the potential for complete cell cycle analysis and characterization of cells. While it is tractable to capture time-lapse images of tens-to hundreds of-thousands of cells with modern automated fluorescent microscopes, significant challenges remain in the analysis of these data sets.

Cell segmentation and analysis packages have been developed (e.g. (Ducret et al., 2016; Paintdakhi et al., 2016)) and include some automated tools for analysis of these large data sets, but they are not as powerful and flexible as the tools commonly used in the analysis of flow cytometry data. For instance, although some existing packages can generate histograms of cell descriptors from segmented data, it is often necessary to define and analyze subpopulations of cells (e.g. removal of cell debris or non-proliferating cells, etc). In this paper we describe a powerful tool for sub-population analysis inspired by flow cytometry.

Our Clist (or Cell list) framework, and tool for data gating and visualization gateTool, facilitate efficient capture and manipulation of image cytometry data, including the generation of sub-populations from over 70 pre-programmed cell descriptors and provide a flexible framework for analyzing many cell biology problems. These descriptors include birth time, division time, old pole age, long axis length, mean fluorescence intensity and cell area, as well as the ability to add additional customized descriptors as required. We have recently described a cell segmentation and analysis package for bacterial cells (SuperSegger) (Stylianidou et al., 2016); SuperSegger and the gateTool are designed to be part of the same complete package, but can be used independently. That is, SuperSegger will automatically output segmented cell data as a Clist for seamless input to the gateTool for analysis, but a custom user-constructed Clist can also be used. In principle, the gateTool framework could be applied more broadly, to classify objects and facilitate analysis in a wide range of image analysis applications. However, the SuperSegger software is designed specifically for the segmentation of bacteria cells. We will discuss the gateTool in the context of bacterial cell analysis.

We have already used this method, without detailed description, in a number of papers (Wiggins et al., 2010; LeRoux et al., 2012; Kuwada et al., 2013; LeRoux et al., 2015; Stylianidou et al., 2014; Kuwada et al., 2015b; Kuwada et al., 2015a; Cass et al., 2016; Stylianidou et al., 2016), and the software is available for download from the Wiggins Lab website (http://mtshasta.phys.washington.edu/website/ssodownload.php). The purpose of the current report is to describe the method and to demonstrate its potential. Here, we first give a brief description of the tools used for sub-population analysis, then we analyze a number of representative cell biology problems. In particular, we investigate a number of common assumptions (e.g. cell length is a good proxy for cell age) and interesting recent claims in the literature (e.g. aging in Escherichia coli), using the Clist tools to explore the robustness of these observed phenomena.

Results and Discussion

A matrix-based summary of time-courses

Our segmentation suite SuperSegger provides three partially redundant outputs: (i) frames files which contain all the data from a single time-point, (ii) cell files which contain all the data for a single cell for all time-points and (iii) the Clist (or cell list matrix) which is a matrix-structured summary of all cells and all time-points (Stylianidou et al., 2016). This paper focuses on analysis of the Clist matrix.

Due to the size of the typical processed data set, it is usually not practical to load the entire data set into memory. The purpose of the Clist matrix is to load only the data pertinent for population-level analyses. The schematic form of the matrix is shown in Table 1. Each row represents an individual cell tracked through the time-course and the columns represent a subset of the > 70 cell descriptors.

Table 1.

Clist data structure. A schematic picture of the Clist matrix. The matrix columns represent cellular descriptors (one value per cell) and the rows correspond to individual cells. At typical Clist generated from a single field of view can contain 5,000 cells, each with >70 cellular descriptors.

Cell ID	Mother ID	Daughter 1 ID	Daughter 2 ID	Birth Time	Division Time	Age (frames)	Old Pole Age	Long Axis	Short Axis	GFP Mean	…
1	0	2	3	1	124	123	NaN	1.4	0.76	148.57	…
2	1	4	5	125	163	38	NaN	2.6	0.81	143.15	…
3	1	6	7	125	166	41	NaN	2.6	0.84	147.75	…
4	2	8	9	164	202	38	NaN	2.5	0.82	150.63	…
5	2	12	13	164	210	46	2	2.2	0.77	141.07	…
6	3	14	15	167	214	47	2	2.2	0.82	139.83	…
⋮	⋮	⋮	⋮	⋮	⋮	⋮	⋮	⋮	⋮	⋮

SuperSegger assigns each cell a unique cell ID which is preserved throughout the time course and is used as an identifier for subsequent analysis. The cell ID can been seen in the first column of the Clist matrix (Table 1). The ID of mother and daughter cells is also recorded (see columns 2-4 of the Clist matrix in Table 1).

Cell cytometry and the Clist

SuperSegger performs a detailed characterization of the cell at each time-point. A summary of this information is stored in the Clist matrix. It is important to note that each element of the matrix is a single number (not time-dependent). Although this makes sense for some descriptors (Cell ID, duration of the cell cycle, etc) other cell descriptors change from frame-to-frame (e.g. cell length and fluorescence intensity). For most frame dependent descriptors, the value at cell birth (or in some cases cell death) is retained. For example, the length of a cell (Long axis) which grows throughout the experiment is stored as two Clist variables: Long axis at birth and Long axis at death. The Clist construction is easily customizable; addition to or removal of any cell characteristic from the Clist requires editing only a single line of the SuperSegger software. The name of each descriptor is also saved in the Clist. (See Supplemental Information for details on the included cell descriptors, and how to add your own cell descriptors.)

Cell birth and death

Although the Clist is most powerful when used in the context of time-lapse complete cell cycle imaging, the matrix can still be computed for snapshot (or short time-lapse) analysis. If there is only a single frame, birth and death descriptors are identical. It is also important to note that the descriptions birth and death refer only to the appearance (and disappearance) of cells from the analysis. All cells present in the first frame are assigned frame one as their birth time, but new cells also appear due to cell division and cell tracking errors. The last frame in which the cell is observed is defined as its death time. Cell death could be the result of cell division (since new cells are assigned new IDs), the cell drifting from the field-of-view, a cell tracking error, the experiment ending, etc. Note that there are many equivalent strategies for ensuring that only new born cells that result from cell division (not tracking errors, etc) contribute to an analysis, as will be described below.

Time-dependent Clist

For some applications, the retention of only birth and death cell descriptors is too limiting. In addition to the standard Clist, we provide a second time-dependent Clist, called Clist3D, which contains time-dependent descriptors for each frame, each cell and a subset of the cell descriptors. The matrix contains Not-a-Number (NaNs) in frames where the cell does not exist. In general, the direct manipulation of the Clist3D matrix is cumbersome although it is useful for some applications. One example is given in the Length as a Proxy For Cell Age section of this paper.

Visualization and analysis of data

Once the Clist is constructed, we have efficient methods for visualizing and analyzing population-level characteristics. We streamline the data analysis process using a function called gateTool. By passing keywords into this single function, the user can extract data, and implement a number of population visualization tools, including one and two dimensional histograms, kernel density estimates (KDEs; see Supplement for details) (Fig. 2, Fig. 3 and Fig. 4), and dot plots (Fig. 1A), etc. An easy to use GUI version of the gateTool is also available (See Supplemental Information).

Fig. 2. Conditional probability of cell age given a cell length.

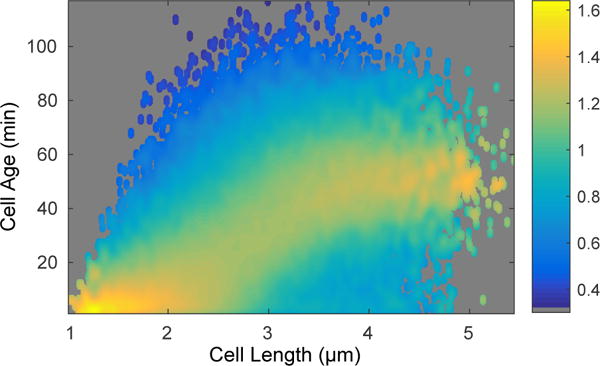
This bivariate histogram displays the cell length and age from over 56,000 measurements. The coloring of the points shows the resulting conditional probability of the cell age, given the cell’s length.

Fig. 3. Over-expression phenotypes. Panel A.

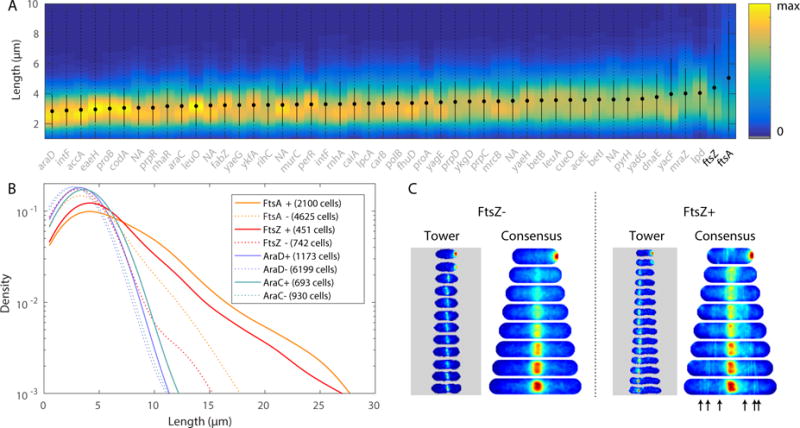
KDE of cell length (at death) for 48 strains (including ftsZA fusion strains) and statistics: minimum to maximum (dotted), mean (circle) and standard deviation (solid line). Genes labeled as NA are currently not annotated genes in MG1655. Strains are ordered by mean length. Panel B: Analysis of high (+) and low (−) expression sub-populations of four strains. High-expression sub-populations of FtsA and FtsZ have long length. Panel C: Single cell tower and consensus images for FtsZ high and low expression sub-populations. The consensus image for the + sub-population shows a cloud around midcell, reflecting the averaging of tower images of z-rings with aberrant localization. Arrows have been included to point out the various clouds of higher intensity, localized away from cell center, resulting from misplaced z-rings in many cells.

Fig. 4. Effect of cell growth characteristics on cell age. Panel A-C.

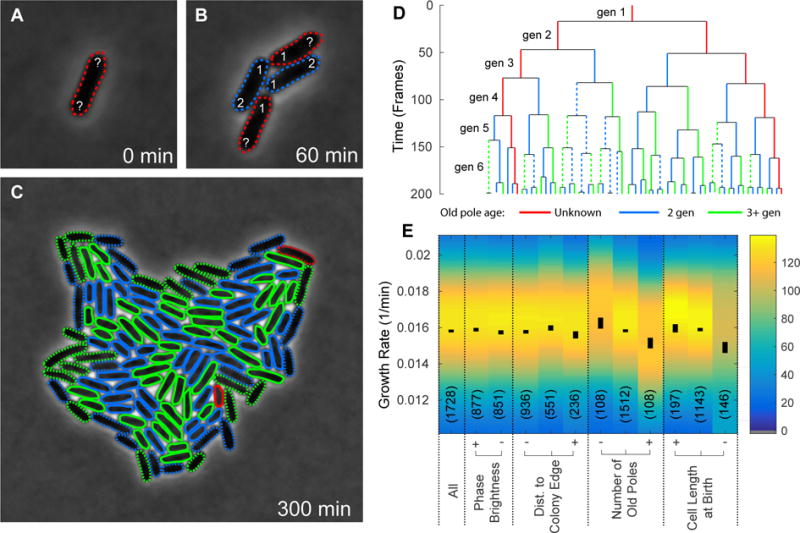
A sample field of view of a colony growing from a single progenitor cell, shown at t = 0, 60 and 300 minutes. The color of each cell outline indicates the old pole age: two (blue), greater than two (green), or inherited from progenitor/unknown (red). The lines are dashed (or solid) to represent cells at the edge (or inside) of the colony at birth. Panel D: A sample lineage tree from a single progenitor cell. The length of each line gives the age of the cell. The color and style of the lines again indicate the old pole age and position of the cell within the colony. Panel E: We compare the mean cell age for six different conditions of cell growth: (i) on the edge of a colony, (ii) on the inside of a colony (iii) inheriting the oldest poles (iv) inheriting the most new poles (v) longest at birth, and (vi) shortest at birth. Each cell descriptor is gated into three groups: low (−), medium, and high (+). It is clear from this figure that the mean cell cycle duration (or cell age) and standard error on the mean are consistent, independent of pole age.

Fig. 1. Identification by morphology verses fluorescence. Panel A.

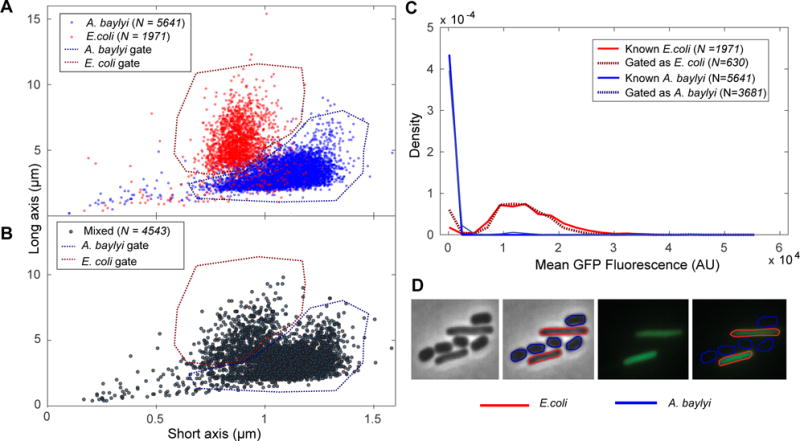
A dot plot of long and short axes for the A. baylyi (blue) and E. coli (red) cells, imaged separately. Based on this data, appropriate gates for A. baylyi and E. coli based on morphology are selected (dotted). Panel B: A dot plot of long and short axes for the mixed A. baylyi and E. coli cells, with the A. baylyi and E. coli gates from Panel A applied. Panel C: Histogram of mean GFP fluorescence for known A. baylyi (solid blue) and E. coli (solid red) cells, as well as mixed cells sorted as A. baylyi (dotted blue) and E. coli (dotted red). We find that the fluorescence data for the mixed cells sorted by morphology closely match the fluorescence data for the known populations. Panel D: Bright field and fluorescence images of a sample field of view, with and without cell outlines determined by morphology and fluorescence gates.

To complement the population-level visualization tools, we also include tools for the analysis of fluorescence localization in single cells. Single Cell Towers, or mosaics, are time-lapse images of a single cell, stacked in chronological order, with consistent pole orientation (Fig. 3). In order to visualize fluorescence localization averaged over cell-to-cell variation, we have also implemented Consensus Images, the mean cell cycle dependent fluorescence localization pattern from sets of single cell towers, spatially scaled to the same cell length and width (See: Fig. 3). A detailed description for the implementation of Single Cell Towers and Consensus Images can be found in (Kuwada et al., 2015a).

In addition, the gateTool will also compute basic statistics (mean, std, error, min and max, population size, etc) on any cellular descriptor and the raw data can be exported as matrices into MATLAB, as well as saved in csv and excel file formats.

Sub-population selection by gating

Tools for cell selection by image cytometry (Lamprecht et al., 2007; Ducret et al., 2016) allow users to classify cells, however we implement a more flexible system inspired by flow cytometry to provide a robust tool for cell selection. In flow cytometry, a canonical method for the identification of sub-populations of cells is the definition of a gate: a subset of cell descriptors corresponding to a population of interest. Usually these gates are defined by selecting an interval of a single descriptor which is often visualized on the descriptor histogram. For gating in two-dimensions, we implemented a polygon-based definition of the gated region in the two-dimensional descriptor space, shown for the long and short axes in Panels A and B of Fig. 1.

Although a single descriptor gate (selection) is straightforward to implement on a single population in MATLAB or R without the use of gateTool, it is often necessary to gate in two descriptor dimensions, or perform multiple sequential selections on two different populations. These more complicated but routine manipulations are easily performed in gateTool. For instance, the interactive tool for selecting gates is particularly powerful in two dimensional where custom shapes are often the most convenient method for defining a population but specifying the vertex coordinates numerically would be time consuming. E.g. see Fig. 1B. Another key feature of gateTool is the ability to nest an arbitrary number of gates. Importantly, data that are gated out are retained in the Clist, but ignored in subsequent analysis. After gating, we can choose to restore the complete un-gated dataset by simply empty the gate. This facilitates the ability to divide data from a single Clist into sub-populations in many different ways. This implementation also makes it straightforward to copy gates between Clists; this is useful when we wish apply consistent constraints to two separate Clists (i.e. Fig. 1)A and 1B.

Finally, the analysis can be applied simultaneously to any number of Clists, which can be treated as replicate experiments where cells are pooled, or from distinct conditions where the data are analyzed independently. For instance, we discuss an example below where the analysis is performed simultaneously on Clists generated for 48 strains.

Comparison to existing packages

Although other packages allow for image analysis, and some offer tools for sub-population selection, our gateTool method offers a more extensive and flexible framework for cell analysis and sorting. For example, Oufti (Paintdakhi et al., 2016) stores data as a “cell list” containing 18 cell descriptors for all cells in all frames, and the ability to “filter” cells by a single cell descriptor at a time, from a list of five cell descriptors. In comparison, the SuperSegger generated Clist contains 70 cell descriptors and frame-independent structure offers users a more extensive quantitation of user data, in a more compact structure. In addition, gateTool’s capabilities for two-dimensional gating from the set of 70 cell descriptors greatly enhances the ability to perform novel analyses. Another package, MicrobeJ (Ducret et al., 2016), allows users to filter cells by using a cutoff value; although this does allow users to gate out cells, the use of a single cutoff value limits the flexibility in sub-population selection. Histograms can be generated, but there are no two-dimensional visualization (or gating) options. Neither Oufti nor MicrobeJ offers users the ability to add their own customized variables to the set of cell descriptors which can be analyzed. Our Clist and gateTool offer users a novel image analysis tool for highly customized analysis with an easy-to-use framework.

Removal of debris from analysis

In practice, it is difficult to prepare samples completely free from microscopic debris that can be mistakenly identified as cells during the cell segmentation process. Although SuperSegger generates few false positive events for the analysis of wild-type E. coli (False positive rate α < 0.01 (Stylianidou et al., 2016)), some mutants, like minC, can significantly increase the amount of cell-like debris (e.g. (Bi and Lutkenhaus, 1993)). Gating can therefore provide an effective method for removing debris from the analysis.

Snapshot analysis

In image-based cytometry of snap-shot images, we have used the following descriptors to remove debris: (i) major axis length, (ii) minor axis length, (iii) area, (iv) phase gray level, and (v) region score. The first three identifiers need little explanation and usually offer sufficient discrimination without additional descriptors. Phase gray level can be quite informative since isolated cells are phase dark. The region score is a proxy for the likelihood of a region being a cell, generated automatically by SuperSegger using a machine learning algorithm trained on test data sets. It combines information from many descriptors not included in the Clist and can be an effective tool, provided that the cells of interest are similar in morphology to the training set.

For time-lapse analysis

For the removal of debris from time-lapse analysis over complete cell cycles, we usually use of the stat0 descriptor alone. stat0 is the cell tracking status defined as follows:

stat0	Birth Div.	Death Div.	No Errors
0	✗
1	✓	✗
1	✓	✓	✗
2	✓	✓	✓

For example, Supplemental Movie 1 shows the proliferation of E. coli, starting from a single progenitor cell. The cells are colored by stat0 value and a segmentation error is automatically detected and labeled. For many analyses, restricting the analysis to cells for which a complete cell cycle is observed ( stat0= 2) makes additional gating unnecessary.

For short duration time-lapse imaging of cells that do not complete a full cell cycle, we have used a number of other methods for removing debris and cells with segmentation errors in addition to the descriptors described for snap-shot analysis. The descriptor error frame contains the frame number of the first error (or a NaN if there is no error). Descriptors are also included for the maximum ( dL max) and minimum ( dL min) change in the cell length (major axis length) between frames over the course of the time-lapse experiment. These descriptors enable the detection of segmentation errors by large changes in cell length. A useful descriptor for intermediate duration time-lapse is the estimated rate of growth:

$$k\equiv (\text{log}{L}_{t+\tau }-\text{log}{L}_t)/\tau ,$$ [1]

where L_t is the cell length at time t and τ is the interval between frames.

Distinguishing cells in a mixed population

Although bacteria are single-celled organisms, they interact and exhibit many forms of cooperative behavior (West et al., 2007). To study these phenomena, it is necessary to distinguish between the bacterial species. We have recently made a quantitative characterization of T6SS-based contact-mediated cell killing in Pseudomonas aeruginosa (LeRoux et al., 2012). Like many previous studies, we introduced an exogenous fluorescent label to differentiate between cells and used the observed cellular fluorescence (descriptor fluor mean) to differentiate between T6SS^± cells (LeRoux et al., 2012). In our experience this is a good, although not perfect, descriptor for distinguishing cells.

To measure the quality of fluorescence as a proxy for cell identity, we cultured wild-type MG1655 E. coli and the same strain expressing GFP (expressed from plasmid pZA12-GFP), then considered the mutual information of the cell fluorescence and various morphological cell descriptors. The mutual information is a measure of how much two distributions depend on one another; given the set of values for one variable, how well can you predict the set of values for the second variable? For a mathematical explanation of the mutual information, please see the Estimation of the Mutual Information section of the Supplement. In the context of inference on the cell identify given an equal number of GFP ± cells, the average information content of the fluorescence intensity (i.e. the mutual information) is:

$$M(\text{GEP intensity},\text{strain})=0.99\text{bits,}$$ [2]

compared to one bit, which is the information required to unambiguously identify the cell. This corresponds to an average information loss of just 0.01 per cell relative to perfect information about cellular identity and this loss results from the small overlap in the fluorescence intensities of GFP± cells.

Distinguishing cells by morphology

Although the use of cytoplasmic fluorescence to differentiate between strains is a canonical method in cell biology, it is not always convenient. We decided to explore the possibility of differentiating between bacterial cells based on cell morphology alone, rather than using a fluorescence-based descriptor. To determine whether this approach would be feasible, we considered a co-culture of Acinetobacter baylyi and Escherichia coli. When grown in liquid minimal media, E. coli cells have a long, thin rod-like morphology (bacillus), while A. baylyi are quite round in comparison (coccobacillus). We would therefore expect the eccentricity ε, defined as the ratio of the major to minor axis length, to be a good proxy for cell identity. In the context of inference on the cell identify given an equal number of A. baylyi and E. coli cells, the average information content of the eccentricity (i.e. the mutual information) is:

$$M(\epsilon ,\text{species})=0.8\text{bits},$$ [3]

compared to one bit, the information required to unambiguously identify the cell. This information loss corresponds to an average information loss of 0.2 bit per cell relative to perfect information about cellular identity. Again, this loss results from the small overlap in the eccentricity of A. baylyi and E. coli cells. For these cells with ambiguous eccentricity, the cell identify cannot be reliably determined.

The eccentricity is a convenient one dimensional measurement which combines information about major and minor axis length; however, inference on cell identify using both the major and minor axes length descriptors is more informative. The mutual information between morphology (using both descriptors) and species is:

$$M(\text{morphology},\text{species})=0.9\text{bits},$$ [4]

roughly a 10% increase in information content over the eccentricity. Although the information loss for cell morphology is greater than it is for fluorescence, the morphology may be sufficient. Remember that for many applications, ambiguous cells can simply be removed by a judicious choice of the gates. A table of the estimated mutual information for morphological and fluorescence cell descriptors is provided in Table 2. An example of morphology based gating is shown in Panel B of Fig. 1.

Table 2.

We computed the mutual information from morphological cell descriptors and mean cellular fluorescence. Fluorescence is the most informative descriptor for sorting bacterial species; however the combination of short and long axis information trails by less than 0.1 bit, serving as a suitable pair of cell descriptors for sorting bacterial species.

Descriptor	Mutual Information M (bits)
Fluorescence	0.99
Long and Short	0.9
Eccentricity	0.8
Long	0.5
Short	0.5
Area	0.4

Gating on fluorescence versus morphology

To demonstrate the process of gating with gateTool, we create A. baylyi and E. coli sub-populations using either the fluorescence or the morphology descriptor. We cultured (non-fluorescent) A. baylyi and E. coli (expressing GFP) both (i) separately and (ii) mixed together, then collected snap-shot images of all three cultures. Panel A of Fig. 1, shows the dot plot of the long and short axis lengths of the individually grown E. coli and A. baylyi cells. Using this information about the cells of known species, we created gates that can be used to sort the two species by morphologies.

In Panel B, those gates are applied to the dot plot of the mixed cells’ lengths, to predict which cells are A. baylyi (blue gate) and which are E. coli (red gate). In Panel C, we provide the histogram of fluorescence for the known A. baylyi and E. coli cells, as well as the “sorted” mixed cells. We find that the predicted fluorescence distributions for both species closely match their known fluorescence distributions.

Panel D of Fig. 1 displays the phase and fluorescence images of a sample field of view containing A. baylyi and E. coli cells. Each of these images is accompanied by the same image, with cell outlines of blue (A. baylyi) and red (E. coli), based on the chosen cell sorting gates. Based on our training data and gates, we estimate the A. baylyi misclassification rate as 1.3% and the unclassified rate as 2.9%. The E. coli misclassification rate is 6.0% and unclassified rate is 5.3%. “Unclassifed” cells are those cells which were not sorted by any gate. In general, a lower misclassification rate can be achieved by setting stricter gates, at the cost of a higher unclassified rate.

Length as a proxy for cell age

In flow cytometry and snap-shot experiments (where cell age information is unavailable) relative cell lengths are commonly used as a proxy for cell age (e.g. (Youngren et al., 2014; Helgesen et al., 2015)). The natural cell-to-cell variation in cell length implies that it is an imperfect proxy for cell age. To place cell-length dependent data in context, it is interesting to determine how informative this data is with respect to true time-lapse imaging for determining the timing of cellular events. Again, it is useful to formulate this problem in terms of mutual information, or the information content of cell length with respect to cell age. In this case, we will compute the number of codewords, i.e. $\mathcal{N}\approx 2^M$, which is comparable to effective temporal resolution, in frames per cell cycle achieved by snapshot imaging.

To analyze the information content of cell length, we characterized wild-type MG1655 E. coli proliferation over two hours with one minute time resolution. A kernel density estimate showing cell age, conditioned on cell length, is shown in Fig. 2. It is immediately clear from the plot that due to the significant variation in cell length, length will be an uninformative predictor of cell age.

We computed the mutual information for three pairs of descriptors and the results are shown in Table 3 (the additional conditional probability plots for these descriptor pairs are provided in the Supplement Fig. S3). The most relevant mutual information is between cell length (L) which is observed and relative age τ, defined as the cell age relative to the cell cycle duration. This mutual information is the smallest, a fraction of a bit per cell. The effective temporal resolution is only ≈ 1.5 frames per cell cycle.

Table 3.

Estimated Mutual information of cell length and age. We estimated the mutual information of three combination of four variables: t is the age of the cell in minutes, τ is age of the cell relative to the length of the cell cycle, L is the length of the cell is microns, and λ ≡ log(L/L₀)/ log(L/L₁) is the log length, re-scaled by initial and final length. The effective resolution is effective number of frames per cell cycle: $\mathcal{N}\equiv 2^M$.

Variable 1	Variable 2	Mutual information M (bits)	Effective resolution: $\mathcal{N}$
t	L	0.8	1.8
τ	L	0.5	1.5
τ	λ	2.8	7.1

To demonstrate that the variation in both cell length and cell cycle duration are responsible for the low mutual information, we also computed mutual information for relative length and relative age, which is almost 3 bits and corresponds to an effective frame rate of 7 frames per cell cycle. (The relative length cannot be determined in snapshot imaging.)

There are two important implications of this experiment: (i) cell-length based analysis of cell cycle dynamics is a poor substitute for true time-lapse imaging since the significant variation in both the duration of the cell cycle and the length of cells makes inference of cell age from cell length uninformative. (ii) Although the typical information content of this data is quite low, the sub-population of the shortest and the longest cells are still somewhat informative implying that cell-length based analysis, while inefficient, is sufficient for some problems.

Over-expression phenotypes

To demonstrate the analysis potential of the Clist and gateTool in the context of a high-throughput time-lapse analysis, we analyzed data from a near-complete library of fluorescent fusions. We had previously imaged the ASKA library (Kitagawa et al., 2005), a genome-scale, plasmid-based collection of inducible fluorescence fusions to genes of E. coli (Kuwada et al., 2015a) to characterize protein localization dynamics in a model bacterium. An interesting potential feature of the ASKA library is the ability to characterize the effect of protein expression on cell morphology, where protein expression is quantified via fluorescence. We harness the natural variation in gene expression to generate a range of protein expression levels (Elowitz and Leibler, 2000; Elowitz et al., 2002). A natural test case are the genes ftsAZ whose gene products assemble to form the z-ring, responsible for septation, but whose over expression results in a loss-of-function phenotype: filamentation (Errington et al., 2003; Lutkenhaus, 2007).

For previous studies, our lab imaged all ASKA fusions displaying nondiffuse localization (Kuwada et al., 2015a; Kuwada et al., 2015b). We re-analyzed the data from these high-throughput imaging experiments, which included both the FtsZ and FtsA fusions. This is accomplished with a single command using the gateTool. For compactness, we show data only from the 48 strains imaged with the FtsZ and FstA strains, rather than from the roughly 800 strains imaged.

We computed the statistics on the cell length at death and ordered the 48 strains by average length. (See Fig. 3A.) The ftsAZ strains (bolded in Fig. 3A) were longest of the 48 strains. We then constructed two sub-populations: protein expression level above (+) and below (−) the mean expression level, as measured by mean fluorescence intensity. The distributions of cell lengths are shown for ftsZ, ftsA, araC, and araD fusion strains. (The strains araCD are included as a control.) Although all strains had longer length in the (+) populations, the ftsAZ strains show a pronounced increase in the number of long cells relative to the (−) population, exactly as predicted. (See Fig. 3B.) The mechanism for cell filamentation is clear from the consensus images: The (−) population shows a precisely localized z-ring forming at midcell, whereas the (+) population shows a cloud of intensity from z-rings with aberrant localization. (See Fig. 3C.)

Determinants of growth rate

F. Taddei and coworkers have recently proposed a mechanism for aging in cells which divide symmetrically (Stewart et al., 2005), based on the definition of a pole age. Pole age is defined as the number of divisions since the pole was created by septation (Stewart et al., 2005). For instance, a single progenitor cell is shown in Panel A, Fig. 4 with poles of unknown age. After two rounds of division, there are four progeny, including two new daughters (old pole age 2) and two old daughters (old pole age greater than 2). Taddei and coworkers tracked cell proliferation on an agarose pad by microscopy and, intriguingly, reported that old cells grow more slowly than new cells, consistent with existence of an aging mechanism in E. coli. However, in subsequent work using a microfluidic chamber that retained the cells with the oldest poles (mother machine), S. Jun, Taddei and coworkers reported a constant growth rate of cells as a function of pole age (Wang et al., 2010). Although the authors were careful to note that these new results were not explicitly in conflict with the previous report, they suggest that E. coli growth rate and the aging phenomenology may be more subtle than initially proposed (Kysela et al., 2013).

It is important to note that the reported reduction in growth rate is very small (approximately 7%) and therefore the analysis of the aging phenomena necessitates the characterization of a significant number of cells and is therefore a natural application of the gateTool. Due to the small size of the reported change in the growth rate, many subtle mechanisms could contribute. We reconstituted the proliferation experiment using wild-type MG1655 E. coli, without the exogenous YFP protein which is highly transcribed from a phage promoter and therefore has the potential to generate replication conflicts (Merrikh et al., 2012), and without the potential of DNA damage due to phototoxicity from fluorescence excitation (Ge et al., 2013). Both changes were possible since our cell segmentation (SuperSegger) is generated from phase contrast images rather than from fluorescence images so YFP and fluorescence imaging are not required for our experiment and analysis.

To characterize the cell proliferation, we inoculated single log-phase cells from liquid media onto agarose pads and imaged individual cells with one minute time resolution for 300 minutes. The images were then segmented and a small number of segmentation errors were corrected by hand such that we had 50 cells tracked through six complete generations without errors (Stylianidou et al., 2016). Images from a typical single-cell proliferation experiment are show in Panels A-C in Fig. 4.

We investigated a number of hypothetical determinants of cell growth rate that could be measured by microscopy: cell length at birth, position in the colony, pole age and phase brightness. (Phase brightness is included as a control and it not expected to be a determinant of cell growth rate.) Since growth on agarose pads is not rigorously steady-state log growth, we analyzed only cells in the sixth generation. To analyze the role of cell length at birth we gated the cells into two sub-populations short and long, corresponding to cells shorter or longer at birth than the mean cell length at birth. To analyze the role of colony position at birth, we gated the cells into two sub-populations outside and inside, corresponding to cells that contact the boundary of the colony versus cell that do not contact the boundary respectively. (Inside (outside) cells are shown with solid (dashed) outlines in Panels A-C in Fig. 4.) Finally we considered old and new cells, as defined above. Old (green), new (blue) and cell with the progenitor pole (red) are shown in Panel A-C in Fig. 4. A lineage tree of the cells shown in Fig. 4A–C is provided in Panel D. In this tree, the length of each vertical line on the lineage tree is the length of a cell’s complete cell cycle; once the cell divides, a vertical line is drawn for each of its two daughters. Again, the color and style of the vertical line is chosen according to old pole age and position within the colony.

The KDEs, the error on the mean and standard deviation for the growth rates of the gated sub-populations are shown in Panel E of Fig. 4. (The p-values for the (+) and (−) sub-populations of each cell descriptor are provided in Table 6 of the Supplemental Information.) This sub-population analysis revealed that cell length at birth and number of old poles are notably the best predictors of cell cycle duration of the four determinants we investigated, with the difference in colony position and phase brightness being statistically insignificant. In this context, the “oldest” cells are those cells with the most old poles (five or six generations of old poles) in their lineage; the middle and smallest group contain cells with two to four (middle) and zero or one (−) old poles in their lineage. Note that although both cell length and number of old poles have a similar sized effect on growth rate (7%), the correlation between cell length and number of old poles is weak. Our results recapitulating the lower growth rate of cells with older poles are consistent with the original reports of F. Taddei and coworkers (Stewart et al., 2005). On the other hand, the statistical significance of other factors, like cell length at birth, suggest that there may be many determinants of cell growth rate with comparable statistical significance.

Conclusion

In this paper, we have described a framework (Clist) and tools ( gateTool) for visualizing and analyzing image cytometry data, inspired by the standard tools used for flow cytometry. This approach facilitates efficient analysis of sub-populations defined by cell descriptors such as fluorescence intensity and localization, cell morphology, growth rate, etc. We provided four representative examples relevant to bacterial cell biology. In these examples, we demonstrate how the robust and efficient Clist framework provides a flexible image cytometry tool, making large-scale bacterial studies tractable.

Experimental Procedures

The analysis for this work was applied to data taken from a variety of new and previous studies. Data for the “Over-expression Phenotypes” and “Length as a proxy for cell age” experiments were initially collected for previous studies (respectively, (Kuwada et al., 2015a; Kuwada et al., 2015b) and (Cass et al., 2016). For a complete list of strains and imaging procedures used in this work, see the Strains and data collection section and Supplemental Information Table 5.

All imaging was conducted using a Nikon Ti-E inverted wide-field fluorescence microscope with a large format sCMOS camera (Andor NEO) and controlled by NIS-Elements. Image processing and analysis was completed using SuperSegger custom MATLAB (Natick, MA) software (Stylianidou et al., 2016). This software is available for download from the Wiggins Lab website (http://mtshasta.phys.washington.edu/website/ssodownload.php). For complete information about the download and manual for SuperSegger, please see the Software Availability and Documentation section of the Supplemental Information.