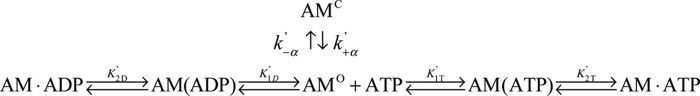N-terminal splicing extensions of the human MYO1C gene fine-tune the kinetics of the three full-length myosin IC isoforms

Abstract

The MYO1C gene produces three alternatively spliced isoforms, differing only in their N-terminal regions (NTRs). These isoforms, which exhibit both specific and overlapping nuclear and cytoplasmic functions, have different expression levels and nuclear–cytoplasmic partitioning. To investigate the effect of NTR extensions on the enzymatic behavior of individual isoforms, we overexpressed and purified the three full-length human isoforms from suspension-adapted HEK cells. MYO1C^C favored the actomyosin closed state (AM^C), MYO1C¹⁶ populated the actomyosin open state (AM^O) and AM^C equally, and MYO1C³⁵ favored the AM^O state. Moreover, the full-length constructs isomerized before ADP release, which has not been observed previously in truncated MYO1C^C constructs. Furthermore, global numerical simulation analysis predicted that MYO1C³⁵ populated the actomyosin·ADP closed state (AMD^C) 5-fold more than the actomyosin·ADP open state (AMD^O) and to a greater degree than MYO1C^C and MYO1C¹⁶ (4- and 2-fold, respectively). On the basis of a homology model of the 35-amino acid NTR of MYO1C³⁵ (NTR³⁵) docked to the X-ray structure of MYO1C^C, we predicted that MYO1C³⁵ NTR residue Arg-21 would engage in a specific interaction with post-relay helix residue Glu-469, which affects the mechanics of the myosin power stroke. In addition, we found that adding the NTR³⁵ peptide to MYO1C^C yielded a protein that transiently mimics MYO1C³⁵ kinetic behavior. By contrast, NTR³⁵, which harbors the R21G mutation, was unable to confer MYO1C³⁵-like kinetic behavior. Thus, the NTRs affect the specific nucleotide-binding properties of MYO1C isoforms, adding to their kinetic diversity. We propose that this level of fine-tuning within MYO1C broadens its adaptability within cells.

Introduction

Myosins are molecular motors that utilize ATP binding, hydrolysis, and product release to perform mechanical work along actin filaments. All myosins share a highly conserved motor domain, a lever arm, and a tail domain that exhibits substantial diversity. The mechanochemical transduction pathway of the ATPase cycle and the major structural biochemical intermediates are conserved across the myosin family (1). Importantly, to perform their myriad biological functions, myosins have evolved unique kinetic adaptations by modulating the rate and equilibrium constants of the ATPase cycle (2–4).

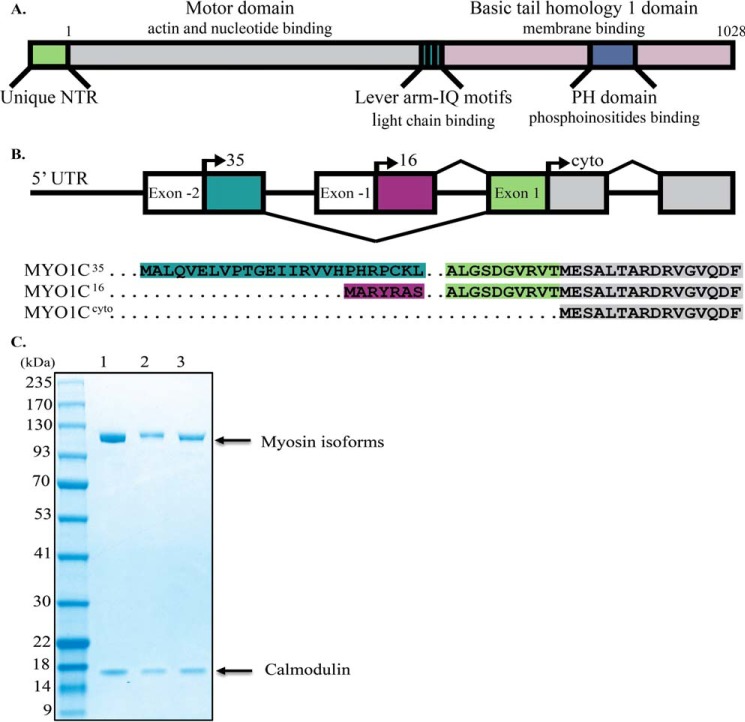
Myosin IC (MYO1C),² a class I myosin, is produced as three splice isoforms that differ only at the N-terminal region (NTR) (Fig. 1) (5). Although they share identical motor domains, three calmodulin-binding IQ motifs containing a nuclear localization signal (6) and a membrane-binding tail domain (Fig. 1A), each isoform has acquired differences in function and nuclear–cytoplasmic partitioning. MYO1C^C, the first isoform to be identified, localizes mostly to the cytoplasm and interacts with plasma membrane phosphoinositides via its PH domain; functionally, it participates in the generation of membrane tension, cell migration, vesicle trafficking, signal transduction, and hearing (7–14). MYO1C^C nuclear import is regulated by calcium (15), but its nuclear functions remain unknown. MYO1C¹⁶ has a 16-amino acid (aa) extension at the NTR, which includes a nucleolar localization signal (16). MYO1C¹⁶, previously referred to as nuclear myosin I (or NMI), localizes mostly to the nucleus (17), and its nuclear localization is moderately affected by calcium (15). In the nucleus, MYO1C¹⁶ is involved in transcription by all three RNA polymerases, mRNA maturation, chromatin remodeling, and chromosome movement (18–23). MYO1C¹⁶ also localizes to the cytoplasm, where, like MYO1C^C, it contributes to the regulation of cell membrane tension (24). MYO1C¹⁶ knock-out mice do not exhibit any obvious phenotype (25). MYO1C³⁵ has an additional 35-aa extension at the NTR (partially overlapping with MYO1C¹⁶ (Fig. 1B)) and also localizes mostly to the nucleus, where it interacts with RNA polymerase II but not RNA polymerase I (5). In mouse, MYO1C³⁵ is expressed at low levels in a tissue-specific pattern, whereas MYO1C¹⁶ and MYO1C^C are ubiquitously expressed at comparable levels in most tissues (26).

Figure 1.

Alignment of isoforms and domain structure of MYO1C. A, schematic representation of MYO1C domain structures. B, splicing pattern and alignment of the initial sequences of MYO1C isoforms. NCBI RefSeq: NP_001074248.1, NP_001074419.1, NP_203693.3 for MYO1C³⁵, MYO1C¹⁶, and MYO1C^C, respectively. C, Coomassie Blue-stained SDS-polyacrylamide gel of the human MYO1C³⁵ (lane 1), MYO1C¹⁶ (lane 2), and MYO1C^C (lane 3). Molecular masses are 121.7, 119.6, and 117.9 kDa for MYO1C³⁵, MYO1C¹⁶, and MYO1C^C, respectively. The associated calmodulin light chain can be seen in all lanes (∼17 kDa).

Although the biological functions and localization of all three MYO1C isoforms have been thoroughly investigated, only MYO1C^C has been characterized enzymatically. MYO1C^C is a low-duty-ratio myosin (i.e. it spends most of the ATPase cycle in the weak actin-binding states), despite the fact that its actin attachment lifetime is relatively long (27, 28). It exhibits a weak coupling between ADP and actin binding, and ADP release is coupled to an additional lever arm movement, which facilitates additional work subsequent to the power stroke (29, 30). The force-sensitive transition in the ATPase cycle is the isomerization that follows ATP binding, and the rate-limiting step has been proposed to be a transition that precedes entry to the strong-binding state (28). Because of these properties, MYO1C^C may be viewed as a tension sensor or slow transporter (3, 28, 29). The kinetics of the additional two isoforms have not been investigated previously, and the impact of alternative splicing on the enzymology of MYO1C isoforms is not fully understood.

A recently solved crystal structure of the closely related protein Myo1b shows that its NTR interacts with calmodulin bound to the first IQ motif (31). Deletion of nine aa of the NTR of MYO1C^C, or replacement of this sequence with residues from the N terminus of Myo1b, dramatically changes the kinetics and tension-sensing properties of MYO1C^C (32). This region is shared by all three isoforms of MYO1C, but the functions of the NTR extensions remain to be elucidated.

We investigated how the kinetic properties of the MYO1C isoforms are affected by alternative splicing of the NTR. To this end, we expressed and purified the three full-length human MYO1C isoforms in a human cell line and characterized their steady-state ATPase and nucleotide-binding activities by both kinetic and equilibrium measurements. Our detailed kinetic analysis revealed that the diverse NTRs affect isomerization of the nucleotide pocket. Specifically, the NTR stabilizes both the AM^O (open state) and the AMD^C (ADP closed state preceding isomerization). The open–closed transitions are dependent on the length of the NTR. Next, we computationally analyzed the interaction between the 35-aa NTR with the myosin heavy chain by molecular dynamic modeling and docking to the recently solved crystal structure of MYO1C^C-1IQ (33). Finally, we found that the addition of the NTR³⁵ peptide in trans to the MYO1C^C isoform mimicked the ATP-induced acto·MYO1C·ADP dissociation kinetics of the MYO1C³⁵ isoform and stabilized the AMD^C state.

Results

N-terminal sequence alignments and purification of full-length human MYO1C isoforms

MYO1C³⁵ and MYO1C¹⁶ share 10 aa from exon 1 and an additional 6 or 25 aa from exons −1 or −2, respectively (Fig. 1, A and B). The remaining identical 1028 aa constitute the motor domain, which binds nucleotides and actin; the lever arm, which consists of three IQ motifs for calmodulin light-chain binding; and the PH domain in the tail, which binds phosphoinositides. To better match the cellular environment in which MYO1C functions, we established an expression and purification system for human myosins using a suspension adapted human HEK293SF-3F6 cell line. This system may be of use in future studies aimed at expanding the options for expression of other myosins with more complex architectures. For our experiments, we purified the three human MYO1C isoforms as full-length constructs with calmodulin as their light chain (Fig. 1C) and determined whether they display full calmodulin light-chain binding motif occupancy by preforming actin co-sedimentation followed by SDS-PAGE and densitometry (supplemental Fig. S1) with calmodulin standards to determine light-chain concentration. We found that all MYO1C isoforms bound three molecules of calmodulin (2.9 ± 0.10, 2.75 ± 0.13, and 3.1 ± 0.07 for MYO1C³⁵, MYO1C¹⁶, and MYO1C^C, respectively).

Actin-activated steady-state ATPase activity of full-length human MYO1C isoforms

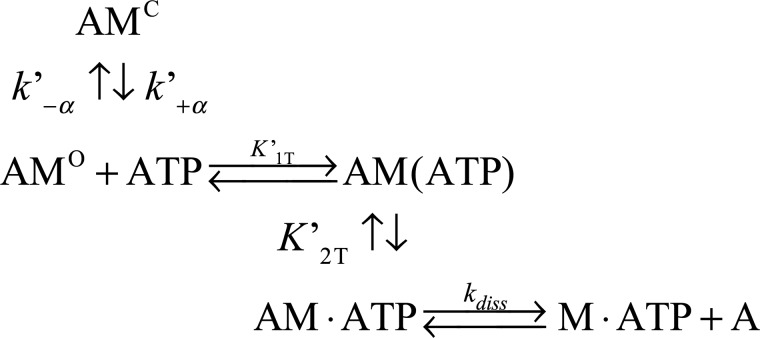
Under our reaction conditions, all three isoforms exhibited actin-activated steady-state ATPase activity with hyperbolic dependence on actin concentration, which allowed us to determine the steady-state parameters according to the Michaelis-Menten model (supplemental Fig. S2 and Table S2). Our results revealed that the steady-state kinetic parameters did not indicate whether the different NTRs of these isoforms impact their enzymology. Hence, we reasoned that a detailed kinetic dissection of the ATPase cycle of each isoform might reveal modulation of the rate constants of their ATPase cycle (see Scheme 1).

Scheme 1.

ATP induced an acto·MYO1C population of weakly bound states

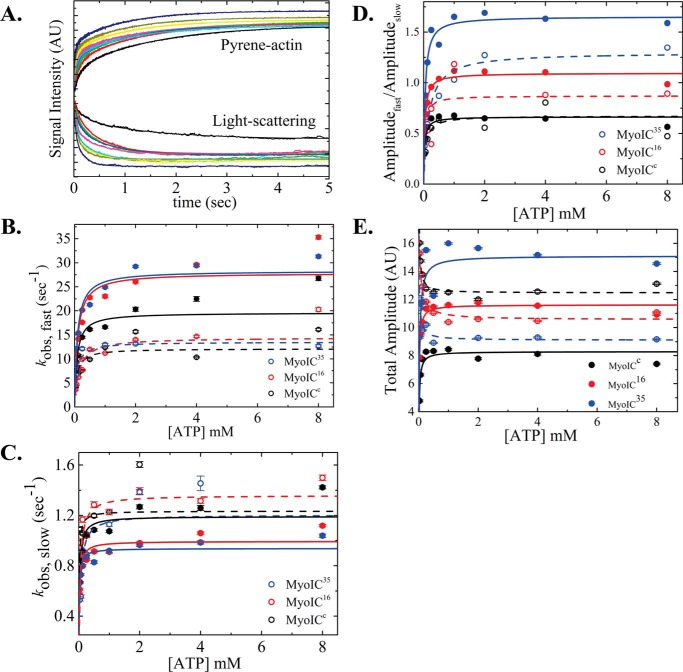
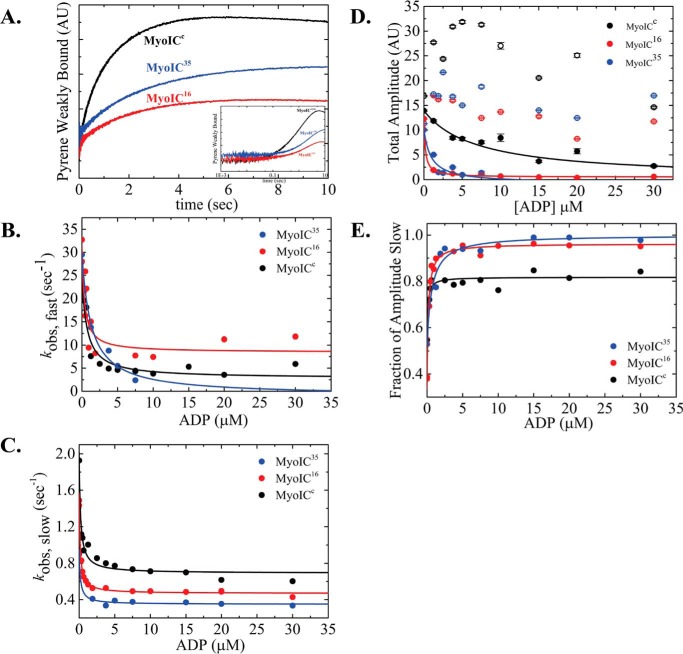
The increase in pyrene-labeled actin fluorescence and the decrease in light scattering upon ATP binding to acto·MYO1C isoforms were monitored as a function of [ATP]. The signal arises from the induced weak-binding states (pyrene-actin, Fig. 2A) or dissociation from actomyosin (light scattering, Fig. 2A). For all three isoforms, both signals were best fitted to double-exponential equations, suggesting that the isoforms have similar ATP-binding mechanisms (Fig. 2A). This is explained by actomyosin existing in two states: the fast phase reflects ATP binding to the AM^O state, and the slow phase represents the conversion from AM^C to AM^O (29, 30). The equilibrium for this transition is termed K′_α (where K′_α = k′_−α/k′_+α) as shown in Scheme 2. The observed rate constants of the fast phase (k_obs,fast) were hyperbolically dependent on [ATP] (Fig. 3B), yielding K′_1T and k′_+2T (Scheme 2 and Equation 1).

$$k_{\text{obs},\text{fast}}=\frac{K{\prime }_{1\text{T}}k{\prime }_{+2\text{T}}\left[\text{ATP}\right]}{1+K{\prime }_{1\text{T}}\left[\text{ATP}\right]}$$ (Eq. 1)

Figure 2.

ATP-induced population of weakly bound acto·MYO1C states. A, representative time courses of pyrene fluorescence enhancement and normalized light scattering reduction after rapid mixing of 25 nm acto·MYO1C¹⁶ isoform with 0, 0.03125, 0.0625, 0.125, 0.25, 0.5, 1, 2, 4, or 8 mm ATP. Data are averaged transients (n = 3). The data were best fitted to a double-exponential equation. MYO1C^C (black), MYO1C¹⁶ (red), and MYO1C³⁵ (blue) are shown as solid circles for pyrene fluorescence data and as open circles for light-scattering data. The solid lines for pyrene and dashed lines for light scattering represent the best fits to the data. B, the fast-phase k_obs was best fitted to a rectangular hyperbola (Scheme 2 and Equation 1), giving the equilibrium constant for MgATP binding to actomyosin, K′_1T, and the kinetic constant for isomerization after MgATP binding, k′_+2T. C, slow-phase k_obs,slow values plotted as a function of [MgATP]. The slow k_obs was best fitted to a rectangular hyperbola (Scheme 2 and Equation 2), yielding the kinetic constant for the closed-to-open isomerization of the ATP-binding pocket, k′_+α. D, a rectangular hyperbola was fitted to the data of the ratio between the fast (A_fast) and slow (A_slow) time-course amplitudes, giving the closed-to-open nucleotide pocket equilibrium constant, K′_α. E, amplitude of ATP-induced dissociation. The error bars of the fitting are within data points.

Scheme 2.

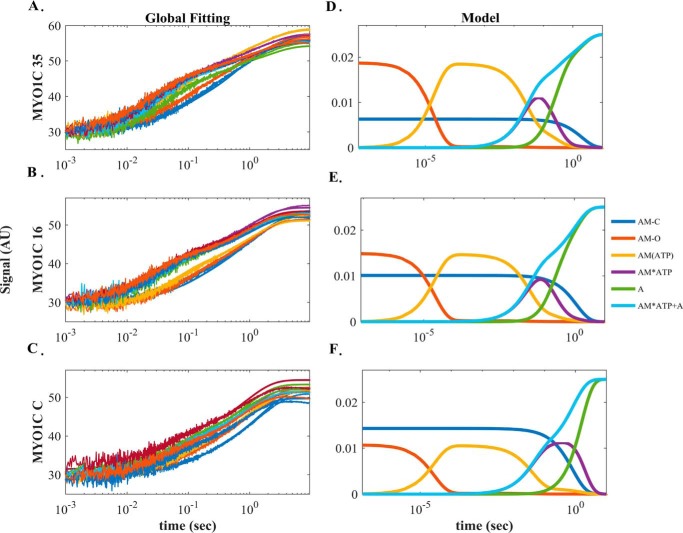
Figure 3.

Global numerical simulation of time-dependent distribution of the reaction intermediates of Scheme 2. A–C, simulated data sets of the ATP-induced population of weakly bound acto·MYO1C states fitted to raw data from MYO1C³⁵, MYO1C¹⁶, and MYO1C^C. Each graph shows in solid lines the time courses of data collected at 0.03125 (blue), 0.0625 (brown), 0.125 (yellow), 0.25 (purple), 0.5 (green), 1 (light blue), 2 (dark red), 4 (blue), and 8 (orange) mm ATP as presented in Fig. 2A for pyrene-labeled acto·MYO1C ATP-induced dissociation. The solid lines through the data sets are the fitted curves resulting from performing global numerical analysis on the entire set of data for each isoform. The fitting was to the sum of the AM·ATP and A states according to Scheme 2. D–F, time-dependent distribution of biochemical intermediates of the reaction according to the simulation mechanism shown in Scheme 2 for MYO1C³⁵, MYO1C¹⁶, and MYO1C^C, respectively. Blue, AM^C; red, AM^O; yellow, AM(ATP); purple, AM·ATP; green, A state. The light blue line represents the sum of the AM·ATP and A states, which reflect the pyrene signal of weakly bound or dissociated states.

The k_obs,fast of MYO1C¹⁶ and MYO1C^C continued to increase above 8 mm MgATP, but the total amplitudes of the fluorescence increase arising from the fast phase reached saturation above 4 mm MgATP (Fig. 2E). This observation suggests the existence of a small population exhibiting faster kinetics. The apparent equilibrium constants for ATP binding, K′_1T, as determined by pyrene-actin fluorescence, were similar among isoforms (K′_1T,p = 11.5 ± 1.94, 10.3 ± 2.37, and 12.9 ± 3.59 mm⁻¹ for MYO1C³⁵, MYO1C¹⁶, and MYO1C^C, respectively (Table 1)). However, the apparent equilibrium constants measured by light scattering, K′_1,LS, was ∼2-fold smaller for MYO1C¹⁶ (K′_1,LS = 13.9 ± 2.49, 6.9 ± 1.51, and 14.01 ± 5.3 mm⁻¹ for MYO1C³⁵, MYO1C¹⁶, and MYO1C^C, respectively (Table 1)). Furthermore, for all isoforms, k′_+2T values measured by light scattering were ∼2-fold smaller than those obtained by the pyrene-actin fluorescence assay (k′_+2T,LS = 13.5 ± 0.61, 14.4 ± 0.84, and 12.1 ± 1.07 s⁻¹ for MYO1C³⁵, MYO1C¹⁶, and MYO1C^C, respectively (Table 1)).

Table 1.

ATP-induced acto·MYO1C dissociation measured by pyrene-actin and light scattering

Conditions used were: 20 mm MOPS, pH 7.0, 25 mm KAc, 2 mm MgCl₂, 0.2 mm EGTA, and 1 mm DTT at 20 ± 0.1 °C.

Constant	MYO1C35		MYO1C16		MYO1CC
	Pyrene-actin	Light scattering	Pyrene-actin	Light scattering	Pyrene-actin	Light scattering
k′+α (s−1)	0.9 ± 0.03	1.2 ± 0.11	1.0 ± 0.03	1.4 ± 0.05	1.2 ± 0.05	1.2 ± 0.06
k′−α (s−1)a	0.6 ± 0.03	0.9 ± 0.15	0.9 ± 0.05	1.6 ± 0.14	1.8 ± 0.14	1.8 ± 0.26
K′α	1.6 ± 0.04	1.3 ± 0.09	1.1 ± 0.02	0.9 ± 0.04	0.7 ± 0.02	0.7 ± 0.06
K′1T·k′+2T (μm−1 s−1)	0.33 ± 0.07	0.19 ± 0.04	0.29 ± 0.09	0.10 ± 0.03	0.25 ± 0.09	0.17 ± 0.08
K′1T (mm−1)	11.5 ± 1.94	13.9 ± 2.49	10.3 ± 2.37	6.9 ± 1.51	12.9 ± 3.59	14.0 ± 5.28
k′+2T (s−1)	28.3 ± 1.32	13.5 ± 0.61	27.9 ± 2.06	14.4 ± 0.84	19.6 ± 1.51	12.1 ± 1.07

^a Calculated.

The observed slow phase in ATP-induced dissociation from actomyosin mostly represents the decrease in the population of the AM^C state over time. The [ATP]-dependence of the observed slow-phase rates were fitted to a rectangular hyperbola, yielding k'_+α (Fig. 2B) according to Scheme 2 and Equation 2.

$$k_{\text{obs},\text{slow}}=\frac{k_{+\alpha }\left[\text{ATP}\right]}{K_{0.5}+\left[\text{ATP}\right]}$$ (Eq. 2)

The rate constant for the nucleotide pocket transition from closed to open, k′_+α, did not differ significantly among the MYO1C isoforms in either assay (k′_+α,p = 0.9 ± 0.03, 1.0 ± 0.03, and 1.2 ± 0.05 s⁻¹ and k′_+α,LS = 1.2 ± 0.11, 1.4 ± 0.05, and 1.2 ± 0.06 s⁻¹ for MYO1C³⁵, MYO1C¹⁶, and MYO1C^C, respectively (Table 1)). The ratio between the amplitudes of the fast and slow phases (Fig. 2D) represents the equilibrium constant, reflecting the distribution of the closed and open states, K′_α (34).

Interestingly, unlike MYO1C^C, which favors the closed state, MYO1C³⁵ favors the open state, and MYO1C¹⁶ populates both states equally (K′_α,p = 1.6 ± 0.04, 1.1 ± 0.02, and 0.7 ± 0.02 and K′_α,LS = 1.3 ± 0.09, 0.9 ± 0.04 and 0.7 ± 0.06 for MYO1C³⁵, MYO1C¹⁶, and MYO1C^C, respectively (Table 1)). The observed changes in K′_α in both assays were consistent with an overall shift toward population of the AM^O state as the NTR grew longer.

Global numerical curve fitting of ATP-induced population of weakly bound acto·MYO1C states

The explicit solutions for the mechanism shown in Scheme 2 cannot extract the four parameters k′_+1T, k′_−1T, k′_−2T, and k′_diss. Therefore, we performed numerical integration (simulation) using KinTek Explorer (35, 36) by globally fitting our time-dependent reaction curves. The kinetic parameters extracted by performing simulation on the complete data sets for each isoform are presented in Fig. 3 and Table 2. The signal represents the sum of the AM·ATP and A states (weak-binding states). As shown in Table 4, the results of the simulation were in good agreement with the experimentally determined parameters K′_1T and k′_+2T, and the data provided numeric solutions for k′_+1T, k′_−1T, k′_−2T, and K′_2T. k′_+1T decreased, whereas k′_−1T did not differ between the isoforms (k′_+1T = 6.6, 5.1, and 4.3 s⁻¹ and k′_−1T = 548, 568, and 531 s⁻¹ for MYO1C³⁵, MYO1C¹⁶, and MYO1C^C, respectively). k′_−2T of MYO1C³⁵ was 2- and 8-fold lower than the values for MYO1C¹⁶ and MYO1C^C, respectively (Table 2). K′_2T, the equilibrium constant for isomerization after ATP binding, was 2- and 6-fold higher in MYO1C³⁵ than in MYO1C¹⁶ and MYO1C^C, respectively (Table 2). Both the forward and reverse rate constants for the nucleotide-binding isomerization from the closed-to-open state, k′_+α and k′_-α, were smaller than the experimentally determined constants (Table 2). The equilibrium rate constant for the closed-to-open isomerization, K′_α, was similar between the experiment and simulation for MYO1C^C. However, for MYO1C¹⁶ and MYO1C³⁵, the predicted values were 1.5- and 2-fold larger, respectively, than the experimentally measured values (K′_α = 3.0, 1.5, and 0.8 for MYO1C³⁵, MYO1C¹⁶, and MYO1C^C, respectively). Overall, the results were statistically significant in terms of the goodness of the fits per set of each isoform (Fig. 3, A–C). The confidence of the fitting results is expressed as the ratio of χ²/minimum χ² for the forward versus reverse constants, which assures that the fits reached a global minimum. The signal arising from the summation of the weak-binding states in the simulation allowed determination of the rate of actomyosin dissociation, k′_diss. Interestingly, we found that the value for MYO1C^C (k′_diss^C = 1.0 s⁻¹) was 5-fold smaller than the values for MYO1C³⁵ and MYO1C¹⁶ (k′_diss = 5.1 and 5.7 s⁻¹, respectively). This analysis yielded additional rate constants that describe ATP binding to acto·MYO1C in greater detail and, more importantly, identified specific steps that differed among MYO1C isoforms.

Table 2.

ATP-induced pyrene(acto)·MYO1C dissociation by global fit simulation

Conditions used were: 20 mm MOPS, pH 7.0, 25 mm KAc, 2 mm MgCl₂, 0.2 mm EGTA, and 1 mm DTT at 20 ± 0.1 °C.

Constant	MYO1C35	MYO1C16	MYO1CC
k′+α (s−1)	0.50	0.86	1.20
k′−α (s−1)	0.17	0.58	1.60
K′α	2.99	1.48	0.75
K′1T k′+2T (μm−1 s−1)a	0.33	0.24	0.19
k′+1T (μm−1s−1)	6.25	5.13	4.34
k′−1T (s−1)	548.00	568.00	531.00
K′1T (mm−1)	11.41	9.03	8.17
k′+2T (s−1)	29.00	26.80	23.00
k′−2T (s−1)	7.79	3.97	0.97
K′2T	3.72	6.75	23.66
k′Diss (s−1)	5.08	5.71	1.02

^a Calculated.

Table 4.

ATP-induced prebound pyrene·acto·MYO1C·ADP dissociation by global fit simulation

Constant	MYO1C35	MYO1C16	MYO1CC
k′+1D (s−1)	4.5 ± 0.83	3.3 ± 0.17	3.6 ± 0.13
k′−1D (μm−1·s−1)	1.7 ± 0.14	6.4 ± 0.35	4.6 ± 0.17
K′1D (μm)	2.6	0.5	0.8
k′+2D (s−1)	0.9 ± 0.10	1.0 ± 0.03	1.2 ± 0.01
k′−2D (s−1)	5.2 ± 0.37	2.1 ± 0.12	1.3 ± 0.05
K′2D	0.2	0.4	0.9
K′AD (K′1D·K2D) (μm)	0.5	0.2	0.7
kobs,AMDC (s−1)a	0.4 ± 0.00	0.4 ± 0.00	0.5 ± 0.04
AAMDCa	15.6 ± 0.00	12.8 ± 0.01	16.9 ± 0.42
kobs,fast,AMDO (s−1)a	10.9 ± 0.09	6.6 ± 0.37	5.05 ± 0.25
Afast,AMDOa	1.02 ± 0.00	1.9 ± 0.05	7.5 ± 0.24

^a The parameters obtained by fitting the exponential function to the simulated AMD^O and AMD^C states shown in Fig. 5.

ADP-binding kinetics to acto·MYO1C isoforms

The rate of ADP release can be determined by measuring the kinetics of ATP-induced dissociation of actomyosin·ADP as a function of [ADP] (37, 38). Fig. 4A shows representative time courses of acto·MYO1C·ADP premixed with 3.75 μm ADP (final concentration) upon rapid mixing with 1 mm ATP. The transient time courses were best fitted to a sum of two exponentials for all three isoforms (supplemental Fig. S3). The fast phase is thought to reflect ATP binding to free actomyosin, whereas the slow phase reflects the fraction of ADP dissociation from the acto·MYO1C·ADP complex (37, 39). Although acto·MYO1C^C and acto·MYO1C¹⁶ sustained the fast and the slow phases throughout the entire range of [ADP], acto·MYO1C³⁵·ADP prebound to ADP at a concentration of 7.5 μm or higher lost the fast-phase component due to loss of the fast amplitude (Fig. 4, B and D). Similar behavior has been reported for MYO1C^C-1IQ and MYO1C^C-3IQ (28, 30).

Figure 4.

ADP dissociation determined by ATP-induced dissociation of acto·MYO1C·ADP. A, representative time courses of pyrene-actin fluorescence enhancement after rapid mixing of 2 mm MgATP with an equilibrated mixture of 25 nm pyrene-labeled acto·MYO1C isoforms with 7.5 μm ADP. MYO1C^C, MYO1C¹⁶, and MYO1C³⁵ are shown in black, red, and blue, respectively. The data were best fitted to a double-exponential equation. Inset, the same data plotted on a logarithmic time scale. Data are averaged transients (n = 3). B and C, fast-phase k_obs (B) and slow-phase k_obs (C) plotted as a function of [MgADP]. The fast and the slow k_obs were best fitted to a rectangular hyperbola (Scheme 3 and Equation 3) yielding I_fast, K′_0.5,fast and k′_min,fast, and I_slow, K′_0.5,slow and k′_min,slow, respectively (Scheme 3 and Equation 3). D, total amplitudes of the fast and slow k_obs are represented by the solid and open circles, respectively. The fast amplitude showed hyperbolic dependence on [MgADP] (solid line through the data). The MYO1C³⁵ fast phase was not observed above 7.5 μm ADP due to the loss of the fast amplitude E, plot of the fraction of amplitude_slow fitted to a rectangular hyperbola (Equation 4). The error bars of the fitting are within the data points.

For all three isoforms, the dependence of both fast and slow k_obs on [ADP] exhibited hyperbolic behavior, suggesting that ADP dissociation occurs via at least two transitions preceding the complete dissociation from actomyosin (Fig. 4, B and C). This is described as actomyosin·ADP isomerization from AMD^C (ADP closed binding state) to AMD^O (ADP open binding state), which has been observed in several other myosins (34, 40). However, for MYO1C^C, AMD isomerization has not been kinetically identified in previous studies. A reaction mechanism that accounts for these events is presented in Scheme 3.

Scheme 3.

According to Scheme 3, in the absence of ADP, the signal arises from ATP-induced dissociation of the AM^C and AM^O states. Preincubation with higher [ADP] increases population of the AMD^O and AMD^C states, and at saturating ADP, AMD^O and AMD^C are the predominant states. Thus, the fast and slow k_obs values measured upon rapid mixing with 1 mm ATP reflect the summation of all of these states. k_obs,fast and k_obs,slow are described by Equation 3 (Fig. 4, B and C).

$$k_{\text{obs}}=\frac{c+\left[\text{ADP}\right]}{K_{0.5}\left[\text{ADP}\right]}+I_{\text{intercept}};k_{\min }=c+I_{\text{intercept}}$$ (Eq. 3)

The y intercept of k_obs,fast (I_fast) at [ADP] = 0 represents the rate constant for nucleotide binding by the AM^O state. Indeed, I_fast values (29.4 ± 1.68, 30.6 ± 2.48, and 24.6 ± 1.86 s⁻¹ for MYO1C³⁵, MYO1C¹⁶, and MYO1C^C, respectively (Table 3)) are very similar to the rate of isomerization after ATP binding, k′_+2T (Table 2 and Scheme 3 for 1 mm ATP). At saturating ADP, AMD^C and AMD^O are the predominant states, and k_obs,fast reports the decay of the AMD^O state. ADP release was ∼4-fold faster for MYO1C¹⁶ than for MYO1C^C (k′_min,fast = 8.4 ± 3.90 and 2.2 ± 2.69 s⁻¹ for MYO1C¹⁶ and MYO1C^C, respectively (Table 3)). The fast phase of MYO1C³⁵ was not observed above 7.5 μm ADP due to a loss of the fast amplitude (Fig. 4D). This suggests that, for MYO1C³⁵, AMD^C is the predominant state and ADP release occurs sequentially. For MYO1C¹⁶ and MYO1C^C, the two ADP states co-existed over the entire range of the measured [ADP]. K_0.5,fast was 2-fold lower for MYO1C¹⁶ than for MYO1C^C (K_0.5,fast = 0.4 ± 0.16 and 0.8 ± 0.26 μm for MYO1C¹⁶ and MYO1C^C, respectively). The y intercept of k_obs,slow (I_slow) represents the rate of AM^C-to-AM^O isomerization (Fig. 5C). Indeed, I_slow values (I _slow = 0.9 ± 0.02, 1.5 ± 0.02, and 1.9 ± 0.07 s⁻¹ for MYO1C³⁵, MYO1C¹⁶, and MYO1C^C, respectively (Table 3)) were very similar to k′_+α (Table 3). At saturating ADP, the slow k_obs represents the rate of AMD^C decay. k′_min,slow differed among the isoforms (k′_min,slow = 0.4 ± 0.03, 0.5 ± 0.02, and 0.7 ± 0.10 s⁻¹ for MYO1C³⁵, MYO1C¹⁶, and MYO1C^C, respectively (Table 3)). For MYO1C³⁵ and MYO1C¹⁶, K′_0.5,slow was similar and 1.4-fold lower than for MYO1C^C (K′_0.5,slow = 0.15 ± 0.07, 0.16 ± 0.01, and 0.21 ± 0.04 μm for MYO1C³⁵, MYO1C¹⁶, and MYO1C^C, respectively).

Table 3.

ADP binding to acto·MYO1C measured by kinetic competition with ATP

Conditions used were: 20 mm MOPS, pH 7.0, 25 mm KAc, 2 mm MgCl₂, 0.2 mm EGTA, and 1 mm DTT at 20 ± 0.1 °C.

Constant	MYO1C35	MYO1C16	MYO1CC
k′max,fast (s−1)	≈0	8.4 ± 3.90	2.2 ± 2.69
K′0.5,fast (μm)	1.3 ± 0.51	0.4 ± 0.16	0.8 ± 0.26
Ifast (s−1)	29.4 ± 1.68	30.6 ± 2.48	24.6 ± 1.86
k′max,slow (s−1)	0.4 ± 0.03	0.5 ± 0.02	0.7 ± 0.10
K′0.5,slow (μm)	0.15 ± 0.07	0.16 ± 0.01	0.21 ± 0.04
Islow (s−1)	0.9 ± 0.02	1.5 ± 0.02	1.9 ± 0.07
K′AD (μm)	0.68 ± 0.23	0.19 ± 0.03	0.12 ± 0.05

Figure 5.

Global numerical simulation of time-dependent distribution of reaction intermediates of Scheme 3. A–C, simulated data sets of the ATP-induced population of weakly bound acto·MYO1C·ADP states fitted to raw data from MYO1C³⁵, MYO1C¹⁶, and MYO1C^C. Each graph shows the time course of data collected after preincubation with 1.25 (blue), 2.5 (brown), 5 (yellow), 7.5 (purple), 10 (green), 20 (light blue), or 30 (dark red) μm prebound ADP mixed rapidly with 1 mm ATP, as presented in A for pyrene-labeled acto·MYO1C³⁵·ADP ATP-induced dissociation. The solid lines through the data sets are fitted curves resulting from performing global numerical analysis on the entire set of data for each isoform. D–F, time-dependent distribution of biochemical intermediates according to the simulation mechanism shown in Scheme 3 for MYO1C³⁵, MYO1C¹⁶, and MYO1C^C. Blue, AM^C; red, AM^O; yellow, AM(ATP); purple, AM·ATP; green, A; light blue, AMD^C; dark red, AMD^O. The light blue line represents the sum of the AM·ATP and A states, which represent the pyrene signal of weakly bound or dissociation states. AMD^C and AMD^O traces were fitted to single and double-exponential equations, respectively. The fitting parameters, k_obs,AMD^C, A_AMD^C, k_obs,fast,AM^O, and A_fast,AMD^O, are shown in Table 4.

For all three isoforms, the slow-phase amplitudes remained constant as a function of [ADP] (Fig. 4D) in contrast to k_obs,slow, which exhibited hyperbolic dependence on [ADP]. At saturating ADP, both AMD^O and AMD^C should be fully occupied. Thus, the K′_0.5 value for the fraction of the slow amplitude as a function of [ADP] indicates the overall affinity for ADP. The fraction of the slow phase (Fig. 3E) was fitted according to Equation 4.

$$A_{\text{slow}}=\frac{\left[\text{ADP}\right]}{1/K{\prime }_{\text{AD}}+\left[\text{ADP}\right]}$$ (Eq. 4)

The overall affinity for ADP (reflected by K′_AD) was ∼3-fold stronger for MYO1C¹⁶ and MYO1C^C than for MYO1C³⁵ (0.68 ± 0.23, 0.19 ± 0.03, and 0.12 ± 0.05 μm for MYO1C³⁵, MYO1C¹⁶, and MYO1C^C, respectively).

Global numerical curve fitting of ATP-induced acto·MYO1C·ADP dissociation

The minimum mechanism for dissociation of prebound ADP from actomyosin·ADP upon ATP binding involves at least five biochemical transitions (Scheme 3). Previously, we analyzed our data only in the defined AM or AMD states in the absence of ADP or under saturating ADP conditions. However, to analyze our data throughout the entire range of [ADP], considering all intermediates, we globally fitted the entire data set according to Scheme 3 (Fig. 5). To constrain the simulation, we used the parameters determined in the ATP-induced dissociation experiments (Table 4). Only four rate constants describing ADP binding and dissociation were determined by the model [k′_+1D (s⁻¹), k′_−1D (μm⁻¹·s⁻¹), k′_+2D (s⁻¹), k′_-2D (s⁻¹)]. The fitting iterations to the data sets were allowed to run until they converged to the best possible fitting parameters to reach a global minimum (χ²/degree of freedom < 1.1, S.D. (σ) < 0.85). The good of the fitting results is expressed as the ratio of χ²/minimum χ² for the forward versus reverse constants, which assures that the fits reached a global minimum (supplemental Fig. S5). The rate constant for ADP release from the AMD^O state, k′_+1D, was 1.4-fold larger for MYO1C³⁵ than MYO1C^16/C (Table 4). The rate for ADP binding for MYO1C³⁵, however, was 3.7- and 2.7-fold smaller than those of MYO1C¹⁶ and MYO1C^C (Table 4). As a result, the ADP-binding affinities of MYO1C¹⁶ and MYO1C^C were 5.2- and 3.2-fold stronger than that of MYO1C³⁵ (Table 4). The rate constant for isomerization of AMD^C to AMD^O, k′_+2D, increased gradually as the NTR became shorter (Table 4). The rates for the closed-to-open nucleotide pocket isomerization were very similar to those for the isomerization of AM^C to AM^O (Table 3 and Scheme 2). By contrast, the reverse rate for the open-to-closed isomerization decreased as the NTR became shorter (Table 4). Consequently, two of the three isoforms populate the AMD^C state to a greater extent than the AMD^O state but with different ratios. MYO1C³⁵ populates the closed state 5-fold more than the open state; MYO1C¹⁶ favors the closed state by 2.5-fold; and MYO1C^C populates both states with almost equal probability (Table 4). The overall ADP affinity (K′_AD = 0.5, 0.2, and 0.7 μm for MYO1C³⁵, MYO1C¹⁶, and MYO1C^C, respectively) agreed with the measured K′_AD for MYO1C^35/16, but was 5-fold smaller than the measured K′_AD for the measured MYO1C^C.

The simulated progression curves allowed us to follow the decay upon addition of ATP of AMD^C and AMD^O equilibrated with 30 μm ADP. AMD^C decayed exponentially, with k_obs and amplitude similar to the measured k_obs,slow for all three isoforms (Figs. 4 and 5 and Tables 3 and 4). However, AMD^O exhibited double-exponential decay with a fast phase that was not completely consistent with the measured fast phase, even though the fitted curve yielded a fast phase identical to the measured data (Figs. 4 and 5 and Tables 3 and 4). This suggests that the measured slow phase reflects AMD^C decay, whereas the measured fast phase reflects a mixture of several states in the system.

Structural homology modeling and molecular dynamic docking of the NTR³⁵ domain with MYO1C^C

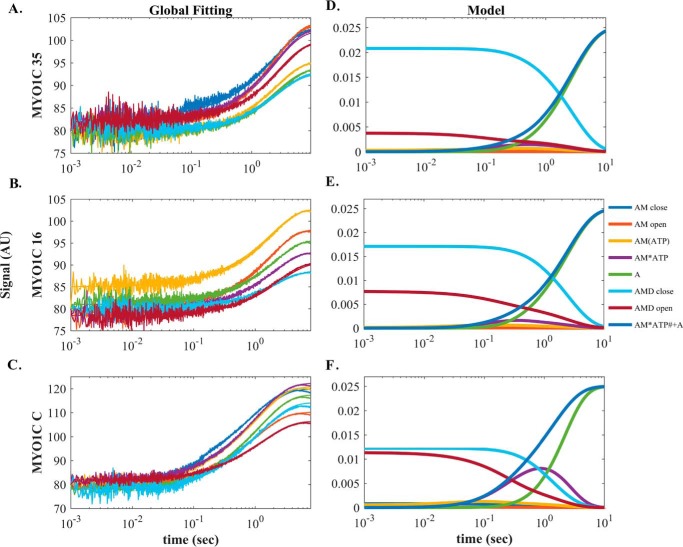
To gain further insights into how the NTRs impact the structural properties of MYO1C isoforms, we applied structure-based molecular dynamics and docking routines. First, we used PSIPRED version 3.3 to perform a secondary structure prediction of the NTR of MYO1C³⁵, which indicated that this region consists of four β-strands interrupted by three coils (Fig. 6A). A FASTA search against structured proteins revealed that the NTR of MYO1C³⁵ shares 18.4% sequence identity (44.7% sequence similarity) with desulforedoxin in (PDB ID: 1DHG) (Fig. 6B). Remarkably, desulforedoxin adopts a compact β-barrel fold comprising four β-strands, which is similar to the PSIPRED prediction. Therefore, the homology model of MYO1C³⁵-NTR was based on desulforedoxin (PDB ID: 1DHG). In that model, a HPH motif (similar to the WPH motif of Myo1B (31)) is exposed at the tip of the β-barrel. Next, we performed docking experiments of the predicted folded motif of MYO1C³⁵-NTR. For this procedure, we used Maestro in the Schrödinger Software Suite to generate different states of the predicted homology model by molecular dynamics simulations (41, 42). These different conformations of the NTR model were used as ligands for protein-protein docking studies using the crystal structure of MYO1C^C (0, 6.4, 8.6, 15.5, and 25 ns after energy minimization) (PDB ID: 4BYF). For this purpose, we used the ClusPro online docking tool for protein-protein docking studies (43). Different constraints were added for the docking procedures. For example, the HPH motif (H18-P19-H20) of the NTR model was involved in the interaction, and the C-terminal Phe-57 of the NTR model exhibited a repulsive interaction. Most of the resulting docking models were out of range of the experimentally solved N terminus. The best hit within a reachable range is shown in Fig. 6D. In this model, the MYO1C³⁵ NTR interacts with the experimentally solved crystal structure. Interestingly, according to this model, the NTR of the MYO1C³⁵ interacts with amino acid region 619–636, which was identified by Schwab et al. (16) as corresponding to one of the two nucleolar localization signals of MYO1C¹⁶. The second nucleolar localization signal of MYO1C¹⁶ is located on the NTR itself, suggesting that the two are connected. Besides numerous electrostatic and hydrophobic contacts between the N terminus of the crystal structure and the nucleolar localization signal, one specific interaction stands out: residue Arg-21 engages in polar contact with Glu-469 of the loop directly after the relay helix, which could have a mechanical impact on the myosin power stroke. Consistent with this model, our kinetic studies revealed that MYO1C³⁵ has a >2-fold faster AMD^O-to-AMD^C isomerization and a 3-fold slower ADP-binding rate constant than MYO1C¹⁶ and MYO1C^C.

Figure 6.

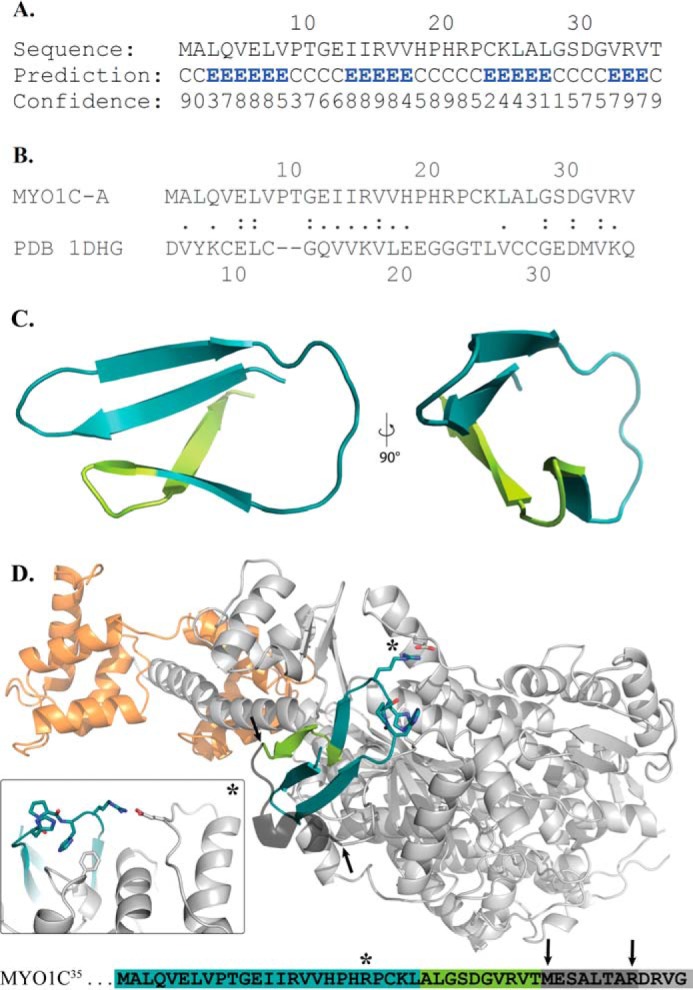
Structural homology modeling and molecular dynamics docking of the NTR extension. A, secondary structure prediction of NTR of MYO1C³⁵. B, FASTA search against structured proteins revealed that the NTR of MYO1C³⁵ shares sequence homology with desulforedoxin. C, homology model of the MYO1C³⁵ NTR from two angles, showing the unclosed β-barrel-like structure. The model was based on desulforedoxin (PDB ID: 1DHG). D, overview of experimentally determined structure of MYO1C (PDB ID: 4BYF) shown in gray. The bound calmodulin is shown in orange and the NTR model in cyan/light green after the best protein-protein docking hit. The black arrows indicate the termini of the model and the solved myosin structure. The connector part of both is built after sequence similarity of nonredundant PDB sequences (52) with YASARA. It shows a qualitative possibility of this connectional part. Inset, a close-up of the contact between the NTR model and the post-relay helix region is marked with a star. The detailed view illustrates the possible salt bridge between Arg-21 and Glu-469 and the interaction of His-20 with Phe-57. At the bottom, an overview of the sequence shows the color code and position markers.

Determination of NTR³⁵, NTR³⁵-R21G, and NTR¹⁶ secondary structure by circular dichroism

To test our structural homology modeling, we synthesized three peptides corresponding to the 35-aa NTR (NTR³⁵), NTR³⁵-R21G (a mutant peptide based on the results of molecular dynamic modeling), and 16-aa NTR (NTR¹⁶). We then determined their secondary structures by performing circular dichroism (CD) measurements and deconvolution of their spectra (Fig. 7 and supplemental Tables S4 and S5). NTR³⁵ exhibits a strong negative peak at 208 nm. Deconvolution of its spectrum yielded a prediction of 38% anti-parallel β-sheet, 47% unstructured, and 15% turns at 20 °C (Fig. 7 and supplemental Table S5). This is highly similar to the predicted model based on the structural homology presented in Fig. 6C. Point mutation of R21G within this peptide to generate NTR³⁵-R21G shifted the negative peak to 209 nm (Fig. 7). We also determined the secondary structure of the shorter NTR¹⁶, which shares 10 aa with NTR³⁵ (Fig. 7). According to the predicted secondary model, ∼43% of the identical amino acids fall within the predicted anti-parallel β-sheet (Fig. 6C).

Figure 7.

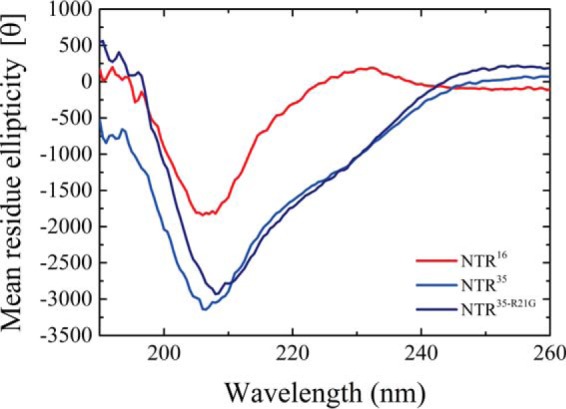
CD spectrum of the NTR peptides. Shown are the CD spectra of NTR¹⁶ peptide (red), NTR³⁵ (blue), and NTR³⁵-R21G (dark blue) at 20 °C. The data presented are an average of three measurements.

NTR³⁵ peptide added in trans to MYO1C^C induces MYO1C³⁵-like kinetic behavior

The CD measurements of the various NTRs showed that these peptides form independently folded domains. Hence, they may invoke similar effects whether they are presentin trans or covalently attached to the polypeptide chain. We studied the effect of the NTR³⁵ and NTR³⁵-R21G peptides on ATP-induced dissociation of acto·MYO1C^C·ADP and compared this effect among the three isoforms (Fig. 8). These experiments were performed in the presence of 20 μm folded peptide, high enough to saturate binding to MYO1C^C (both 50 and 100 μm folded peptides yielded similar results). Interestingly, we observed the same kinetic behavior in k_obs,fast and k_obs,slow of ATP-induced dissociation of acto·MYO1C³⁵·ADP as with acto·MYO1C^C·ADP preincubated with NTR³⁵. This remarkable finding demonstrates that NTR³⁵ impacts the nucleotide-dependent transition in trans in the same way as when it is present on a continuous polypeptide chain. NTR³⁵-R21G did not affect MYO1C^C kinetic behavior to the same extent, confirming the predicted interaction of Arg-21 with the rest of the myosin heavy chain. Finally, the addition of the NTR peptides in trans influenced the fraction of the slow amplitude (Fig. 8B). This shifted the population of AMD^C and AMD^O toward the closed states, as predicted by our model.

Figure 8.

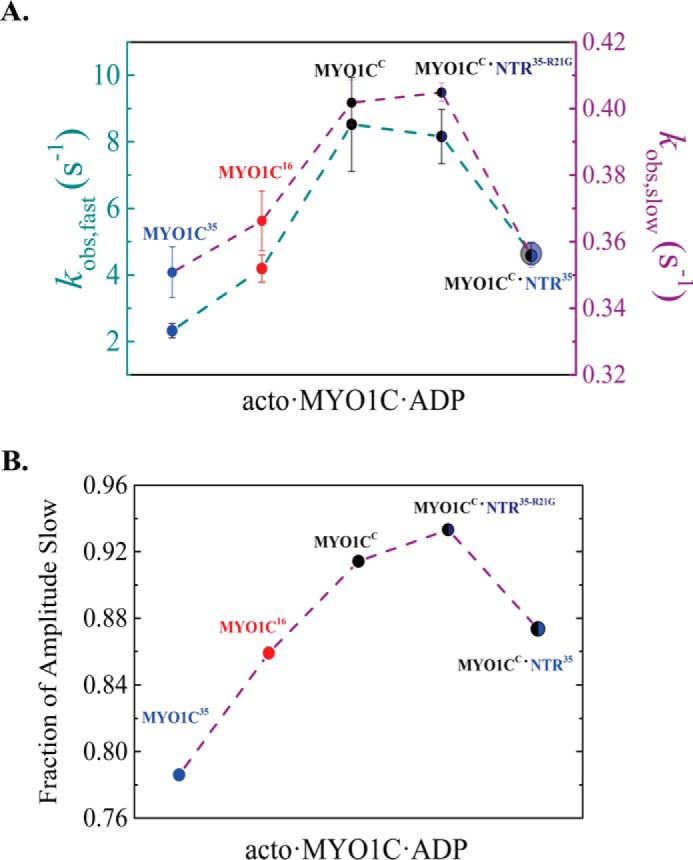
NTR³⁵ peptide added in trans to MYO1C^C induces MYO1C³⁵-like kinetic behavior. A, fast-phase (dark cyan) and slow-phase (purple) k_obs of the double-exponential fit to transients obtained after rapid mixing of 1 mm MgATP with an equilibrated mixture of 50 nm pyrene-labeled acto·MYO1C isoforms with 2.5 μm ADP. Shown are MYO1C^C (black), MYO1C¹⁶ (red), MYO1C³⁵ (blue), and MYO1C^C (black) in the presence of 20 μm NTR³⁵-R21G (dark blue) or NTR³⁵ (blue). B, fraction of the slow amplitude of the same measurements. Data are from averaged transients (n = 6). The error bars of fitting are within the data points.

Discussion

We performed comparative studies of MYO1C splice isoforms in the context of their full-length proteins with the goal of achieving accurate allosteric awareness as proposed by Preller and Manstein (44). The steady-state parameters did not show dramatic changes in overall ATPase behavior among the isoforms. However, a detailed kinetic analysis revealed intrinsic divergence among the isoforms that either balanced out or had a low impact on k_cat and K_ATPase.

We compared our results with those obtained to date with truncated MYO1C^C constructs. We determined the equilibrium constant of MYO1C nucleotide-binding pocket isomerization using both pyrene-actin and light-scattering approaches. Previous studies on the MYO1C^C-1IQ/3IQ motor domain with variable lever arm constructs showed that the MYO1C^C isoform populates mostly the AM^C state (27, 28, 29, 30). Our results supported these findings but also demonstrated that the equilibrium of full-length MYO1C^C is shifted from AM^C toward AM^O by 7-fold relative to the 1IQ construct and 2-fold relative to the 3IQ construct.

ADP-binding kinetics to acto·MYO1C isoforms reveal conservation of ADP isomerization states

ADP-binding kinetics contribute to the dwelling time of myosin in the strong-binding state and hence its effect on the duty ratio (40, 45). Both EM and mechanical measurements show that the ADP release mechanism of MYO1C^C is biphasic and depends upon additional movement of the lever arm and load (29, 30). However, kinetic measurements of ATP binding to prebound actomyosin·ADP using the 1IQ and 3IQ MYO1C^C constructs could not detect intrinsic isomerization prior to ADP release due to the loss of the fast-phase k_obs (27–30). Here, we show for the first time that full-length MYO1C undergo closed-to-open isomerization before ADP is released. This isomerization was also detected using truncated constructs of the closely related Myo1b (32). Therefore, we suggest that the addition of the tail domain shifts the equilibrium toward the AMD^O state.

NTR effect on actomyosin nucleotide pocket isomerization

The NTR extensions altered the closed-to-open isomerization of the nucleotide pocket by stabilizing the AM^O and AMD^C states. As a result, the differences in behavior imply that each isoform has different kinetics depending on the ATP/ADP ratio. Related to this finding, the simulated models (Figs. 3 and 5) demonstrated that the larger the population of the AM^O and AMD^C states, the larger the population of the AM(ATP) state and the faster it forms, at a given [ATP]. The simulation also revealed differences in k′_−2T and k′_diss. MYO1C^C populated the AM·ATP (weak-binding state) longer than MYO1C³⁵, suggesting that the NTR extensions destabilize the weak-binding state and could be responsible for differences in the tension-sensing features between the two isoforms (32).

Communication between nucleotide- and actin-binding sites

The communication between the nucleotide- and actin-binding sites can be described by a closed thermodynamic square, in which ADP (D) and actin (A) binding to myosin (M) are linked by four equilibrium constants as shown in Scheme 4.

Scheme 4.

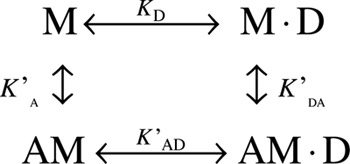
Myosins that generate rapid sliding velocities (e.g. muscle myosins) have large thermodynamic coupling constants (>10) and hence strong coupling between actin and ADP binding. On the other hand, myosins that function as gated/processive or tension sensors (e.g. myosins V, VI, and VII) (3, 40, 45, 46) have small thermodynamic coupling constants (<5). Table 3 and supplemental Fig. S4 and Table S3 show K′_A, K′_DA, and K′_AD for each of the isoforms (see supplemental information text, Fig. S4, Scheme S1, and Equation S1 for a description of the equilibrium-binding experiments). The K_D values of each isoform according to Scheme 4 are K′_DA/K′_A = 1.40, 0.99, and 1.39 for MYO1C³⁵, MYO1C¹⁶, and MYO1C^C, respectively, and the affinities for ADP in the absence of actin are K_D = 0.3, 0.18, and 0.28 μm, respectively. The results support weak thermodynamic coupling between ADP and actin binding, consistent with a role for MYO1C isoforms as tension sensors or slow transporters in ensembles.

Consideration of the structural impact of the NTR in light of current models

Greenberg et al. (32) studied how MYO1C^C-3IQ NTR impacts load dependence and kinetics, either by deleting the first nine residues of MYO1C^C or replacing them with the first 13 residues of Myo1b. This region is shared by all three MYO1C spliced isoforms. Greenberg et al. (32) performed comprehensive biochemical and mechanical (under load) studies to investigate how such structural changes affect the motor properties of MYO1C^C; specifically, the results of the unloaded kinetics revealed that isomerization after nucleotide binding and AM^C-to-AM^O isomerization are strongly affected by the identity of the NTR, which can alter k′₊₂, k′_+α, and k′_−α quite significantly. They found that the addition or deletion of these structural elements affects the active site isomerization by increasing its flexibility. Finally they proposed that the NTR plays an important role in stabilizing the post-power-stroke conformation (32). Our results show that the extended NTRs affect nucleotide pocket isomerization by decreasing both k′_+α and k′_−α without affecting k′₊₂. Moreover, unlike MYO1C^C, which tended to populate the AM^C state in the ATP-induced dissociation experiment, MYO1C³⁵ populated mostly the AM^O state, whereas MYO1C¹⁶ populated both states equally (Fig. 2). Together, our results indicate that the lengthening of the NTR increases the rigidity of the nucleotide pocket and stabilizes the AM^O state. In the prebound ADP measurements, all three isoforms tended to populate the AMD^C state but to varying extents (MYO1C³⁵ > MYO1C¹⁶ > MYO1C^C) (Fig. 4). This suggests that the NTR extensions stabilize the post-power-stroke state, similar to what was observed previously in NTR mutants as well as Myo1b (32). Our results indicate some degree of correlation between ATP- and ADP-binding kinetics in all three isoforms. It may be that these transitions are linked in terms of structural reorganization, i.e. the open-to-closed isomerization of the nucleotide-binding pocket. In addition, consistent with the findings of Greenberg et al. (32), our results support the idea that the nucleotide-binding pocket is affected by the NTR region. We propose that the extended NTRs of the isoforms form a structural domain (Fig. 7) that affects pocket rigidity and stabilizes the AM^O and AMD^C states.

Higher level of fine regulation by MYO1C NTRs

Our results show changes in the kinetic parameters that may yield additional specific kinetic adaptations for each of the three isoforms. Several studies have suggested that in addition to their distinct functions, some overlap could occur in the event that one isoform is lost. Knock-out mice lacking the NM1 (MYO1C¹⁶) start codon (without affecting MYO1C^C or MYO1C³⁵) exhibit interchangeability and redundancy of myosin isoforms in the cell nucleus, suggesting that both isoforms can substitute for each other in nuclear processes (25). Partial rescue and functional overlap between closely related MYO1C isoforms are likely to minimize the observed cellular and whole-animal knockdown phenotypes (47). MYO1C¹⁶, although displaying specific nuclear functions, localizes to the plasma membrane. Furthermore, knock-out of MYO1C¹⁶ has strong effects on the elasticity of the plasma membrane around the actin cytoskeleton, as determined by atomic force microscopy (24). Overall, MYO1C isoforms possess overall nearly identical structural domains and most likely are subject to similar post-translational modifications and binding to similar partners. Thus, different mixtures or ensembles of MYO1C isoforms could serve to fine-tune a specific biological function. Finally, to distinguish between the ensemble effects and redundancy of isoforms, all three knockouts should be compared individually.

Experimental procedures

Reagents

All chemicals and reagents were of the highest purity commercially available. ATP was purchased from Roche Applied Science, and ADP was purchased from Bio Basic (Markham, Ontario, Canada). Nucleotide concentrations were determined by measuring absorbance at 259 nm using ϵ₂₅₉ = 15,400 m⁻¹ cm⁻¹. In all experiments, 1 molar equivalent of MgCl₂ was added to nucleotide solutions immediately before use. N-(1-Pyrene)iodoacetamide (Molecular Probes, Eugene, OR), MOPS, EGTA, apyrase (potato grade VII), and phalloidin were purchased from Sigma-Aldrich. MgCl₂·6H₂O came from Bio Basic and KCl from Merck (Darmstadt, Germany).

Cell culture

All media reagents were purchased from Sigma. Fetal calf serum, l-glutamine, HEPES-KOH, pH 7.4, penicillin, streptomycin, and amphotericin B were purchased from Biological Industries (Beit Haemek, Israel).

Cloning of full-length human MYO1C isoforms

Full-length human MYO1C isoforms (residues 1–1063, 1044m, and 1028 for MYO1C³⁵, MYO1C¹⁶, and MYO1C^C, respectively) were cloned into the HaloTag-pFC14K Flexi vector (Promega). Human cDNA (HsCD00365758 clone ID), purchased from the ORFeome Collaboration, was used as the template for cloning human isoforms by primer extension PCR using the primers listed in supplemental Table S1. All constructs were fully sequenced and compared with the published sequences of human MYO1C isoform (NCBI RefSeq NM_001080779.1, NM_001080950.1, and NM_033375.4 for MYO1C³⁵, MYO1C¹⁶, and MYO1C^C, respectively). Human calmodulin was cloned into pF4A.

Expression and purification of full-length human MYO1C isoforms

Human isoform constructs with co-expressed calmodulin were purified from suspension-adapted HEK293SF-3F6 cells using the Promega HaloTag mammalian expression system. Briefly, 1 liter of suspension HEK293SF-3F6 cells (10⁶ cells/ml) was grown in serum-free EX-CELL medium (Sigma-Aldrich) as reported previously (48) or in proprietary cell culture medium made in-house, co-transfected with pFC14K-MYO1C and pF4A-calmodulin, and harvested after 48 h. The cells were lysed (20 mm MOPS, pH 7, 5 mm MgAc, 2 mm K-EGTA, 150 mm KAc, 0.025% Nonidet P-40, 0.025% Triton X-100, 0.5 mm DTT, Promega protease inhibitor mixture, 1 μm E-64, and 2 μm calmodulin) using a Dounce homogenizer followed by centrifugation at 100,000 × g for 1 h in the presence of 2 mm MgATP (4 °C). The supernatant was incubated with HaloTag beads overnight, washed (20 mm MOPS, pH 7, 5 mm MgAc, 2 mm K-EGTA, 150 mm KAc, 0.0025% Nonidet P-40, and 0.5 mm DTT) with or without 2 mm ATP, and then cleaved from the beads using Promega HaloTEV protease. The eluted protein was dialyzed into storage buffer (50% glycerol, 20 mm MOPS, pH 7, 5 mm MgAc, 2 mm K-EGTA, 75 mm KAc, and 0.5 mm DTT) and stored at −20 °C. Purity was ≥95% for all constructs (Fig. 1C). All purifications and experiments were performed in the presence of 5 μm calmodulin. MYO1C isoform concentrations were determined using the predicted extinction coefficient at 280 nm (ExPASy ProtParam) in 6 m guanidine hydrochloride. Absorption spectra were acquired on a T90+ spectrometer (PG Instruments, Leicestershire, UK) controlled by UWin software.

Expression and purification of other proteins

Actin was purified from rabbit or chicken skeletal muscle (labeled with pyrene if needed) and gel-filtered over Sephacryl S-300 HR (49). Ca²⁺-actin monomers were converted to Mg²⁺-actin monomers by the addition of 0.2 mm EGTA and 40 μm MgCl₂ (excess over [actin]) immediately prior to polymerization by dialysis against KMg50 buffer (20 mm MOPS, 50 mm KAc, 2 mm MgCl₂, 0.2 mm EGTA, and 1 mm DTT, pH 7, at 25 °C). The final dialysis was performed against KMg25 buffer (20 mm MOPS, 25 mm KAc, 2 mm MgCl₂, 0.2 mm EGTA, and 1 mm DTT, pH 7 at 25 °C). Phalloidin (1:1 molar ratio) was used to stabilize actin filaments. Actin was purified from rabbit skeletal muscle, labeled with pyrene, and gel-filtered over Sephacryl S-300 HR 28 (49) Ca²⁺-actin monomers were converted to Mg²⁺-actin monomers with 0.2 mm EGTA and 50 μm MgCl₂ (excess over [actin]) immediately prior to polymerization by dialysis against KMg50 and followed by KMg25 buffer. Phalloidin (1.1 molar equivalent) was used to stabilize the actin filaments. Calmodulin was expressed in bacteria and purified as described (50).

Determination of light-chain calmodulin occupancy to the myosin isoforms

Light-chain calmodulin occupancy of myosin isoforms was performed by actin co-sedimentation of the MYO1C constructs as described elsewhere (51) with minor changes. Briefly, 60 nm MYO1C isoforms was incubated with 1 μm actin in KMg25 buffer for 30 min followed by ultracentrifugation in a TLA55 rotor (Beckman) at 186,000 × g for 25 min at 4 °C. The pellets were then washed gently with the KMg25 buffer and resuspended in protein sample buffer in the presence of 3 mm EGTA, heated for 5 min at 95 °C, resolved by gradient SDS-PAGE (10–20%), and visualized by staining with InstantBlue^TM (Expedeon, San Diego, CA). Calmodulin band intensities were quantified with ImageLab software using known quantities of calmodulin resolved on the same gel as standards.

Steady-state ATPase activity

The actin-activated steady-state ATPase activity of MYO1C was measured at 20 ± 0.1 °C in KMg25 buffer supplemented with 2 mm MgATP by monitoring changes in absorption at 340 nm for 10 min at 1-s intervals on a UV-spectrometer (37). The concentration of all myosins was 100 nm. Myosin concentrations were determined as described above and verified by gel densitometry.

Equilibrium fluorescence binding of pyrene-actin to myosin and actomyosin

Fluorescence measurements were performed on a PC1 spectrofluorimeter (ISS Inc., Urbana-Champaign, IL) set up in an L-format configuration using an emission channel monochromator. Samples were equilibrated (60 min at room temperature), measured with λ_ex = 365 nm, and monitored with emission monochromators scanning from 390 to 430 nm with a peak at λ_em = 409 nm.

Stopped-flow measurements

All experiments were performed in KMg25 buffer on a Hi-Tech Scientific SF-61DX2 stopped-flow apparatus (TgK Scientific Ltd., Bradford-on-Avon, UK) with temperature regulated by a thermostat at 20 ± 0.1 °C. For ATP-induced dissociation experiments, due to high [MgATP], buffer ionic strength (I) was held constant throughout the measurements at the ionic strength of KMg25. Unless noted otherwise, the concentrations stated throughout the text are final concentrations after mixing (i.e. in the observation cell). Light scattering was measured with excitation at 313 nm. Pyrene fluorescence was measured (λ_ex = 365) through a long-pass 400-nm filter. Most time courses shown are those of individual, 2000-point transients collected with the instrument in oversampling mode, where the intrinsic time constant for data acquisition is ≈64 μs. Typically, three time courses were averaged before analysis. Time courses exhibiting fast and slow phases were collected on a logarithmic time scale. Data analysis was performed using the Kinetic Studio software provided with the instrument or with Origin (OriginLab Corp., Northampton, MA). Time courses of changes in signal (fluorescence and light scattering) were fitted to a sum of exponentials according to Equation 5,

$$F\left(t\right)=F_{\infty }+{\displaystyle \sum _{i=1}^n{A}_i{e}^{-k_{i}t}}$$ (Eq. 5)

where F(t) is the signal at time t, F_∞ is the final signal value, A_i is the amplitude, k_i is the observed rate constant characterizing the i-th relaxation process, and n is the total number of observed relaxations. The value of n was either 1 (single exponential) or 2 (double exponential). Fitting was limited to data beyond 1 ms to account for the instrument dead time and to exclude data acquired during the continuous-flow phase of mixing, as recommended by the manufacturer.

Uncertainties are reported as standard errors in the fits, unless stated otherwise, and were propagated using the general formula shown in Equation 6,

$$da=\sqrt{{\left(\frac{\partial a}{\partial x_1}d{x}_1\right)}^2+\dots +{\left(\frac{\partial a}{\partial x_n}d{x}_n\right)}^2}$$ (Eq. 6)

where the experimental measurements x₁, x₂…x_n have uncertainties dx₁, dx₂…dx_n and a is a function of x₁, x₂…x_n. The Levenberg-Marquardt algorithm was used to solve the minimization of nonlinear least squares curve fitting.

Nucleotide-binding kinetics

The time courses of nucleotide binding were acquired under pseudo first-order conditions with [nucleotide] ≫ [myosin or actomyosin]. Actomyosin samples were prepared by mixing equimolar amounts of MYO1C and actin filaments or, where specified, with [actin] ≫ [myosin]. Actomyosin samples were treated with apyrase (0.01 unit/ml), used to deplete ATP and ADP from actomyosin when relevant, and equilibrated on ice for 10 min before measurements were made. After mixing, the final concentration of apyrase was 0.005 unit/ml (37).

Circular dichroism measurements

Far-UV CD was observed with an Applied Photophysics PiStar CD spectrometer (Surrey, UK) equilibrated with nitrogen gas, with the temperature regulated by a thermostat at 20 ± 0.1 °C. Changes in ellipticity were followed from 280 to 190 nm in 20 mm MOPS, 25 mm KCl in a 1-mm path-length fused quartz cell with a step size of 0.5 nm and bandwidth of 10 nm. Typically, three scans were averaged prior to analysis. Peptide concentrations were 0.2 mg/ml, corresponding to 54, 56.1, and 115 μm NTR³⁵, NTR³⁵-R21G, and NTR¹⁶, respectively (supplemental Table S4). The mean residue ellipticity ([θ], in mdeg·cm²·dmol⁻¹·residue⁻¹) was derived from the raw data (θ, in millidegrees (mdeg)) using the following formula: [θ] = θ × 100/(l × n × c), where l is the path length of the cuvette, c is the molar concentration of the peptides, and n is the number of residues in the peptides (i.e. 35 or 16 residues). The CD spectrum was deconvoluted using the BestSel server (http://bestsel.elte.hu/)³ (53). The normalized root-mean-square deviation represents the goodness of the deconvolution ( NRMSD, supplemental Table S5).

Kinetic simulations and modeling

We used KinTek Explorer (35, 36) to simulate the complex reaction shown in Schemes 3 and 4, utilizing numerical integration and global fitting of a family of data sets to a single model to extract mechanistic information directly from kinetic data. First, the transients were fitted to an analytic function to derive their standard deviation (σ), which was then incorporated into the statistical analysis of the goodness of the fits. The fitting parameters were then loaded into the Ode45 function in Matlab to produce the model and fitting.

Molecular dynamics simulation

For molecular dynamics simulation and energy minimization processes, we used Desmond in the Maestro 11 work suite (41, 42). The OPLS_2005 force field was used in a minimized 10 Å orthorhombic water box with 0.05 m sodium chloride ions. The simulation was performed with the TIP3P water model, including a 0.03-ns quick relaxation step. The simulation time was 25 ns at 300 K and 1 atmosphere.

Protein docking

Protein-protein docking was performed using the ClusPro online docking tool (43). The MYO1C^C crystal structure (PDB ID: 4BYF) was used as the receptor molecule. The ligand molecule was a homology model of an NTR in minimized conformation with four additional different plateau states of the molecular dynamics simulation (6.4, 8.6, 15.5, and 25 ns). Different parameters of attraction and repulsion were used, including determined attraction for His-18–Pro-19–His-20 of the NTR and repulsion for Val-31.

Author contributions

A. H. and L. Z. designed and performed the research, analyzed the data, and wrote the article. R. R. performed research, and M. U. developed the methodology to express constructs in suspension-adapted HEK293SF-3F6 cell line. P. Y. A. R. and A. O. S. performed the structural homology modeling, P. Y. A. R. preformed molecular dynamic modeling and docking, and P. Y. A. R., S. G., M. H. T., and D. J. M. analyzed data.