PaCeQuant: A Tool for High-Throughput Quantification of Pavement Cell Shape Characteristics^,

An ImageJ-based tool enables rapid and unbiased quantification of multiple shape features in leaf epidermis pavement cells

Abstract

Pavement cells (PCs) are the most frequently occurring cell type in the leaf epidermis and play important roles in leaf growth and function. In many plant species, PCs form highly complex jigsaw-puzzle-shaped cells with interlocking lobes. Understanding of their development is of high interest for plant science research because of their importance for leaf growth and hence for plant fitness and crop yield. Studies of PC development, however, are limited, because robust methods are lacking that enable automatic segmentation and quantification of PC shape parameters suitable to reflect their cellular complexity. Here, we present our new ImageJ-based tool, PaCeQuant, which provides a fully automatic image analysis workflow for PC shape quantification. PaCeQuant automatically detects cell boundaries of PCs from confocal input images and enables manual correction of automatic segmentation results or direct import of manually segmented cells. PaCeQuant simultaneously extracts 27 shape features that include global, contour-based, skeleton-based, and PC-specific object descriptors. In addition, we included a method for classification and analysis of lobes at two-cell junctions and three-cell junctions, respectively. We provide an R script for graphical visualization and statistical analysis. We validated PaCeQuant by extensive comparative analysis to manual segmentation and existing quantification tools and demonstrated its usability to analyze PC shape characteristics during development and between different genotypes. PaCeQuant thus provides a platform for robust, efficient, and reproducible quantitative analysis of PC shape characteristics that can easily be applied to study PC development in large data sets.

Leaves are the major sites of photosynthesis in most plants and play central roles in carbon fixation and energy supply. In addition, leaves control gas exchange and transport of water and nutrients from roots to shoots (Kalve et al., 2014). From a morphological perspective, leaves are remarkably diverse structures. The diversity is reflected in numerous species-specific shapes, which are reliable traits for taxonomic identification and classification of species (Viscosi and Cardini, 2011; Tsukaya, 2014). Leaf size and shape are not solely determined by genetic variability but also change during development and adapt to environmental conditions (Sultan, 1995, 2000; Cho et al., 2007; Bar and Ori, 2014). Phenotypic plasticity of leaf morphology helps plants to optimize sunlight harvesting, CO₂ gas exchange, and acclimatization to changing ambient temperatures (Nicotra et al., 2010; de Casas et al., 2011). Hence, understanding the cellular and molecular mechanisms of growth regulation is of central importance to improve plant yield, quality, and resource use efficiency.

Because of its high relevance in plant biology, leaf development has been extensively studied in the past decades in many plant species (Bar and Ori, 2014, 2015), including maize (Zea mays; Freeling, 1992), tomato (Solanum lycopersicum; Gray, 1957), and Medicago truncatula (Wang et al., 2008). Genetic and phenotypic analyses, mostly in the model species Arabidopsis (Arabidopsis thaliana), provide insights into the dynamics of cellular events that underlie the development from primordia to the final flat and polar organ (Tsukaya, 2010, 2013; Vanhaeren et al., 2015). Growth and development are controlled by complex molecular networks that integrate internal and external signals (Cho et al., 2007; Wolters and Jürgens, 2009). A central role in regulation of expansion is played by the leaf epidermis, which forms a rigid outer coat of the leaf (Savaldi-Goldstein et al., 2007; Kutschera, 2008; Bai et al., 2010; Marcotrigiano, 2010). In several plant species, including Arabidopsis, the leaf epidermis is composed of three different cell types, which are derived from specialized epidermal progenitor cells: pavement cells (PC), stomatal guard cells, and trichomes, also called leaf hairs (Glover, 2000). Out of these three cell types, PCs are always present in the epidermis and usually the most frequently occurring cell type in the epidermis. PCs can develop highly interlocked, jigsaw-puzzle-like shapes during expansion and provide a structural barrier against mechanical insults. This epidermal barrier is interrupted only by stomata, which form small pores required for gas exchange and transpiration (Glover, 2000).

At the macroscopic level, studies of leaf geometry were one of the first applications for shape analysis in biology (Dale et al., 1971; Ghent, 1973; Kalyoncu and Toygar, 2015). For example, shapes were quantified by use of Fourier-based descriptors (McLellan and Endler, 1998), moments, geometric codes, and margin statistics (Kalyoncu and Toygar, 2015), and leaf serration was quantified using hierarchy analyses (Biot et al., 2016). With improving imaging techniques, several studies addressed the dynamics and changes of PC shape during leaf development and expansion (Iwata and Ukai, 2002; Andriankaja et al., 2012; Elsner et al., 2012; Barbier de Reuille et al., 2015; Vanhaeren et al., 2015). Key regulators of PC interdigitation were identified by mutant phenotyping (Xu et al., 2010; Lin et al., 2012; Li et al., 2013; Guo et al., 2015). In many cases, PC characteristics were described by global descriptors, such as area or circularity, or by skeleton-based approaches (Horiguchi et al., 2006; Staff et al., 2012). These methods oversimplify PC shape and contain no informational value on the number and degree of lobes (Ivakov and Persson, 2013; Wu et al., 2016). To quantify lobe numbers, two main approaches are widely used: skeleton-based detection and manual quantification, which typically underestimate the number of lobes or calculate the number of lobes per area rather than per cell, respectively (Xu et al., 2010; Gao et al., 2015). More recently, a MATLAB-based tool was developed, which aims to provide a platform for objective and robust quantification of lobe number and shape characteristics by analysis of a refined convex hull (Wu et al., 2016). The number of features extracted by these tools, however, is limited to only a few parameters and thus is not capable to cover the shape variability observable in PCs.

In addition, most methods that quantify PC shape rely on manual segmentation of individual cell outlines. The manual preparation has two major disadvantages. First, it is very time consuming and laborious and prevents high-throughput analysis of PC shape. Second, unless segmentation is carried out in blind studies, it is prone to bias by the experimenter (Vanhaeren et al., 2015). Hence, for objective quantification of PC shape characteristics, robust and fully automatic techniques for the segmentation of cell regions, as well as meaningful and clearly defined shape descriptors are required. Powerful descriptors combined with an unbiased automatic segmentation would enable comparative analysis of PC shapes not only within a single set of experiments but also between data from independent studies (Ivakov and Persson, 2013). Ideally, such tool should be user-friendly and run on publicly available open source platforms.

Here, we present our newly developed tool, PaCeQuant, for fully automatic segmentation of individual PCs from confocal input images and simultaneous extraction of 27 different shape parameters. In addition, PaCeQuant optionally offers the analysis of shape characteristics of individual lobes at two-cell and three-cell contact points. The tool is implemented as plugin for the widely used open-source image analysis software ImageJ and publicly available under GPL v3.0. It features a graphical user interface for user-friendly data input of large data sets. We provide a supplemental R script for extended data analysis (including statistical analysis) and comfortable data visualization by box plots or violin plots. Extensive comparative evaluations prove that PaCeQuant is able to produce high-quality segmentations of PCs and to provide robust, reliable, and reproducible quantification of PC shape characteristics suitable for shape analysis during development and for mutant phenotyping.

RESULTS

Overview of PaCeQuant Workflow

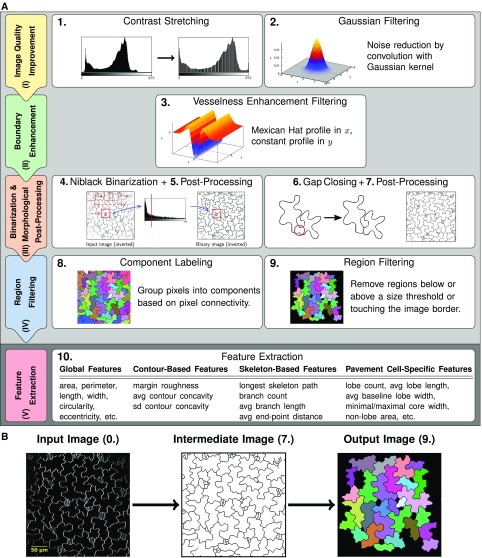
The workflow for cell segmentation and feature extraction implemented in PaCeQuant is composed of two parts. In the first part, we offer an optional automatic segmentation of PCs from confocal microscopy input images, which consists of four basic stages covering (I) improvement of the image quality, (II) cell boundary enhancement, (III) binarization and morphological postprocessing, and (IV) region filtering. In the second part, we provide a pipeline for feature extraction from segmented cell regions, which runs on cell regions, either defined by the automatic segmentation, after manual correction of automatic segmentation results or from manually segmented input images (Fig. 1).

Figure 1.

Workflow of cell segmentation and feature extraction. A, Workflow implemented in PaCeQuant for automatic detection of cell outlines (part 1, light gray) and extraction of shape features (part 2, dark gray). In the first part, input images are processed in four basic stages (image quality improvement [I] to region filtering [IV], left column) via nine individual processing steps (panels on the right). In the second part, the feature extraction (step 10) is performed. B, Example of an input image (step 0), the processed image after outline extraction (step 7), and an image containing identified and filtered regions (step 9) used for feature extraction. For an overview of all image-processing steps, see Supplemental Figure S1.

We implemented PaCeQuant in a platform-independent fashion in Java as part of the Microscope Image Analysis Toolbox (MiToBo; Möller et al., 2016). Most of the individual algorithms and processing steps that are part of the complete workflow are directly implemented as operators in MiToBo. If external functionality is used, it is explicitly indicated below. The PaCeQuant tool is publically available under GPL License 3.0 as part of the MiToBo distribution at MiToBo’s website (http://www.informatik.uni-halle.de/mitobo/) and integrates seamlessly in ImageJ/Fiji (Schindelin et al., 2012) via MiToBo’s own update site (see “Installation and Usage of PaCeQuant” in “Materials and Methods” for more information). The source code of MiToBo and the PaCeQuant plugin is available from the MiToBo website or on Github (https://github.com/mitobo-hub/mitobo); detailed documentation can be found on PaCeQuant’s webpage (http://mitobo.informatik.uni-halle.de/index.php/Applications/PaCeQuant). PaCeQuant takes full benefit of all built-in features of MiToBo and its core library Alida (Posch and Möller, 2017). Alida provides a framework for the development of data analysis applications in a modular fashion and supports the automatic generation of graphical user interfaces for operators (Möller and Posch, 2013). Since Alida also provides command line interfaces for all implemented operators, PaCeQuant can be run optionally without graphical interaction, e.g. remote on a server.

Cell Boundary Segmentation and Region Filtering

To develop an automatic segmentation method, we used confocal images as input (Fig. 1B), which is a common method for cell shape analysis (Xu et al., 2010; Wu et al., 2016). We initially focused our studies on cotyledons of 5-d-old Arabidopsis seedlings. Cotyledons resemble the characteristics of true leaves in many aspects and have therefore been developed into a popular model system to study leaf development (Tsukaya et al., 1994). Cell outlines were visualized by staining of cotyledons with the lipophilic dye FM4-64 and imaged as single optical sections covering groups of adjacent epidermis cells at a resolution of 2.2 to 3.2 pixels/µm.

To extract cell boundaries, images are processed as follows. First, we use a global contrast stretching to enhance the contrast of the input images (step 1), followed by applying a Gaussian filter (with sd σ = 1) for noise removal (Fig. 1A; Supplemental Fig. S1; step 2). In stage (II), we further enhance the cell structures by vesselness enhancement filtering (step 3), which is used typically to enhance thin elongated structures, such as, e.g. blood vessels, in digital images (Chaudhuri et al., 1989; Zhang et al., 2010; Fraz et al., 2012). Here, we apply a filter kernel, as proposed in Sofka and Stewart (2006). The rectangular kernel mask is composed of a Mexican hat profile in normal and a constant profile in tangential direction. The Mexican hat profile is defined by a second-order Gaussian derivative (Fig. 1A; Supplemental Fig. S1). Each image is convolved with the filter mask in 18 different orientations from 0° to 170°, in successive steps of 10° increase. The resulting 18 filter responses are joined into a single filter response image by selecting for each pixel the maximal response to any of the 18 filters while setting negative maxima to zero.

The filtered image is postprocessed with a local median filter of radius r = 1 pixel to account for locally varying contrasts. To segment cell boundaries, in stage (III) a local Niblack binarization is applied to the filter response images (Niblack, 1986; Fig. 1A; Supplemental Fig. S1; step 4). The Niblack algorithm only yields reliable thresholds if intensity variance is present within the local sliding window. Thus, we introduced an additional test for local variance prior to threshold extraction, and thresholds are only calculated for window positions with sufficient local variance. All other positions are classified as background. To account for small breaks in the boundaries, the resulting binary image is dilated (r = 3 pixels) and eroded (r = 5 pixels). Very small components (e.g. dots, linear structures, etc.), which most likely refer to noise artifacts, are eliminated and the detected boundary components are thinned to a width of 1 pixel (step 5).

An optional gap-closing step may be subsequently performed on the 1-pixel-boundary images to eliminate larger gaps in the cell boundaries (step 6). For this, two different heuristics are implemented in PaCeQuant, a very simple heuristic based on end-point distances and a second heuristic, relying on a watershed transformation on binary images. In the first case, all boundary end points with an empirically determined maximum distance of d = 20 pixels are linked to close gaps in between. In the second case, we apply a Euclidean distance transformation to the binary image, followed by a watershed transformation on the distance image using the implementation available in ImageJ according to Leymarie and Levine (1992). To remove implausible boundaries resulting from oversegmentation of the watershed segmentation, we apply a combination of different criteria for filtering boundary segments. A segment is preserved only if it existed in the binary image already, if it is shorter than 40 pixels and its end points are located close to previously detected end points, if it extends a skeleton branch with a sufficient length, or if it crosses an image region with sufficiently dark intensity values most likely referring to a cell boundary. In the resulting binary image, individual cell regions are segmented according to the postprocessed watersheds detected in the distance image. To ensure that neighboring cell regions are not merged, boundaries are dilated (radius r = 3 pixels) and holes within regions are filled (step 7). This is achieved by applying a component-labeling algorithm to each detected region, where the region is treated as background and potential holes are identified as foreground components. By adding their pixels to the corresponding region, holes are eliminated. In the final step of stage (III), cell boundaries are thinned again to a width of 1 pixel using the skeletonization algorithm of ImageJ (Zhang and Suen, 1984), short open branches are removed, and boundaries are extended to a final width of three pixels. As a result, the grayscale input image is converted into a binary output image where the cell boundaries are represented by black pixels and the cell regions by white pixels.

Stage (IV) starts with assigning a unique identifier to each detected cell region by applying component labeling to the binary image resulting from the previous stage (Fig. 1B; step 8). Regions with boundaries that exceed the image border are removed since these reflect incomplete cells (Fig. 1; Supplemental Fig. S1; step 9). The remaining regions are filtered for size to remove unspecific regions that likely reflect noise from the data set.

Quantification of Shape Characteristics

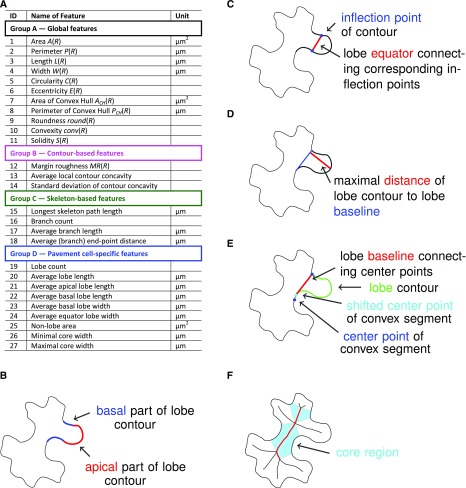
To analyze and quantify shape characteristics, we implemented the automatic extraction of 27 features for each segmented cell in part 2 (or alternatively stage IV) of our PaCeQuant workflow (Figs. 1 and 2; part 2 (or alternatively stage IV), step 10). The features cover four major groups: (A) global features, (B) contour-based features, (C) skeleton-based features, and (D) special features of PCs, e.g. the number and length of lobes (Fig. 2A; Supplemental Table S1). Group A features characterize the cell as a whole with a focus on its global shape (e.g. circularity, degree of elongation). In group B, we quantify the boundary characteristics, such as changes in local contour concavity and tangent orientations, which correlate with the degree of contour folding. The third group of features analyzes shape characteristics relative to the skeleton of the cell, which we extract using the algorithm of Zhang and Suen (1984). The skeleton is defined as the 1-pixel-wide main axis or backbone of a cell region. It consists of a set of branches, end points, and branch points and is frequently used to quantify morphological characteristics of regions in images (Marchand-Maillet and Sharaiha, 1999; Xiong et al., 2010). In the set of group C features, we included the length of the longest path in the skeleton, the number of branches (as a rough estimate for the number of lobes), the average branch length, and the average radius of the lobes associated with detected branches. In group D, we extract specific features for PCs, i.e. their lobe and neck characteristics.

Figure 2.

List of PaCeQuant cell shape features and basic definitions of PC-specific features. A, List of cell shape features extracted by PaCeQuant and their units. For a detailed description of feature characteristics, see Supplemental Table S1. B to F, Basic definitions used for the quantification of PC-specific shape features, including (B) apical and basal parts of a lobe, (C) lobe equator, (D) lobe baseline, (E) neck point and neck point correction, and (F) core region dimensions.

Definition of PC-Specific Features

The automatic extraction and analysis of features suitable to characterize PC shapes requires a unique definition of relevant components of PCs involved in the calculation of shape features, e.g. of lobes or neck regions. So far, however, most PC shape characteristics lack such clear definitions, and only vague ideas are reported in the existing literature that discuss how lobes are localized along a contour or how their exact dimensions are quantified. Similarly, a clear definition for the neck width of PCs, which is a common measure for the growth restriction at neck regions, is lacking. Instead, the neck width is calculated based on manually selected line segments that appear reasonable to the individual user (Li et al., 2003; Bannigan and Baskin, 2005; Fu et al., 2005). This quantification is highly biased since the selection and definition of the line segments is highly variable. Thus, we first provide clear definitions of all relevant components of a PC, which form the fundament for the set of PC-specific features automatically extracted by PaCeQuant.

We define lobes and necks along the cell contour based on local curvature orientation (Fig. 2, B–E). First, the local curvature is estimated for each point along the contour by applying the robust algorithm of Freeman and Davis (1977) available in MiToBo. Resulting curvature values are convolved with a Gaussian filter mask to smooth the profile, which increases the quality of feature extraction from curvature values. Values for positions where no curvature is extracted are interpolated by a nearest neighbor approach. The resulting contour contains concave and convex segments that are defined by positive and negative curvature values, respectively. Lobes and necks are detected by analyzing the signs of local curvature (Fig. 2B). Points where signs change refer to inflection points connecting the apical parts of lobe contours (Fig. 2C). We define a neck point as the center point of a convex contour segment (Fig. 2E). This definition turned out to be more robust than selecting the point with a maximal curvature value since local curvature values may suffer from noise and numerical instabilities due to discretization. The distance between two adjacent neck points, termed lobe baseline, represents the basal width of an individual lobe. If the lobe baseline intersects with the background of the image (Fig. 2E), we heuristically adapt the positions of the boundary points of a lobe section, resulting in virtual neck points. In detail, the neck points defining a lobe section are virtually shifted toward each other along the contour until the baseline connecting the two virtual points no longer intersects with the image background. By shifting a neck point to a new virtual position, the original neck point is expanded to a neck region, which is flanked by the original neck point and the new virtual neck point. If shifts for both adjacent lobe regions of a neck point are necessary, two virtual neck points will flank the neck region.

A lobe is defined as the contour segment between two adjacent neck points. To increase detection robustness and to distinguish lobes from unspecific curvature variations due to segmentation inaccuracies, we set the threshold for lobe detection by default to contour segments with a length of ≥8 pixels. If necessary, the threshold can be adjusted by the user. The number of inflection points divided by two refers to the number of lobes. The line connecting the two inflection points of a lobe defines the lobe equator and represents the equator width of a lobe (Fig. 2C). The lobe length is calculated as the maximal distance between the lobe baseline and the lobe contour (Fig. 2D). In addition, we calculate the distances between baseline and equator, and equator and contour as estimates for the basal and apical lobe lengths (Supplemental Table S1).

The area enclosed by the baseline and the contour segments of the lobe represents the lobe region. As a measure for the relative proportion of lobes to the total cell area, we calculate the nonlobe area, which yields a first estimate of the growth restriction/expansion of the core cell region (i.e. the region between the necks). The nonlobe area is the area of a cell enclosed by the lobe baselines and, if neck points were virtually shifted, by additional pixels of the resulting neck regions (Supplemental Table S1). As an additional value for the size of the cellular core region, we quantify the width of the core region. For this, we utilize the parts of the region skeleton not belonging to any branch, i.e. the core skeleton, as an estimate of the cellular core region (Fig. 2F). We exclude the skeleton branches as they usually refer to lobes of a region. For each pixel of the core skeleton, the Euclidean distance to the background is calculated, and the width of the core region is double the Euclidian distance. To characterize the core region more globally, we sort all distances along the core skeleton in ascending order. Since the region skeleton is very sensitive to changes in contour shape, extreme values of this sorted list, i.e. the minimum and maximum distances, often refer to outliers. To increase the robustness of the core width values, we thus extract the first and third quartile entries as estimates for the minimum and maximum core widths, respectively.

Accuracy of the Automatic Detection

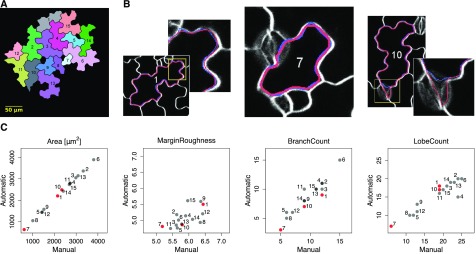
To assess the quality of PaCeQuant’s segmentation approach, we compared the results from the fully automatic cell segmentation with manually extracted cell outlines. For a subset of 15 individual cells from one input image (data set 1) we calculated recall and precision measures of segmented cell areas and distance measures between manually and automatically extracted cell contours (Fig. 3; Supplemental Table S2). The recall quantifies the fraction of the cell area in the manually segmented cell, which has also been extracted by the automatic approach. Vice versa, precision quantifies the ratio of the area detected by automatic segmentation, which is also part of the manually segmented cell. For both measures, a value of 1 represents an optimal fit. To compare the similarity of the two samples, we calculated the F1-score (also known as Sørensen-Dice index), which is the harmonic mean of recall and precision and ranges from 0 to 1, with 1 representing highest similarity. To compare the accuracy of the detected contours, we computed the Hausdorff distance, which measures the (dis)similarity between two sets of points. For each point of one set it extracts the minimal distance to a contour pixel in the second set, and vice versa. Next, the maximum over all minimal distances is identified within the two sets, hence the Hausdorff distance refers to the maximal distance that occurs between two contours at any position.

Figure 3.

Comparison between automatic and manual segmentation of cells based on PaCeQuant features. A, Sample image containing 15 individual cells, which were segmented fully automatically and manually. Numbers correspond to cell identifiers. B, Overlay of cell outlines detected by automatic (red) and manual (blue) segmentation for sample cells with high congruence and different cell sizes (left, ID 1, large cell; and middle, ID 7, small cell) and with local deviations (right, ID 10). C, Scatterplots of one exemplary feature for each of the four feature groups (see Fig. 2 and Supplemental Table S1) from a pairwise comparison between automatic and manual segmentation of all 15 cells. Cells shown in B are highlighted in red (for a summary of all features, see Supplemental Fig. S2).

For the 15 cells in our evaluation set (Fig. 3A) we found an average recall of 0.976 ± 0.0088 (sd) and an average precision of 0.973 ± 0.0121, resulting in an average F1-score of 0.975 ± 0.0079 (Supplemental Table S2). The values are consistent, with a large overlap between manual and automatic segmentation (Fig. 3B, left and middle). For 12 of the 15 test cells, the Hausdorff distance was smaller than 6.5 pixels. For 3 cells, distances of 12.2, 11.7, and 44.2 pixels were found, resulting in contour changes of maximum 1 or 2 µm. These are due to short contour segments where larger deviations between manual and automatic segmentation appear, often caused by low contrasts along the contour or by stomata accidentally classified as part of a cell (Fig. 3B, right).

To further validate the accuracy of the automatic segmentation and to assess the impact of differences in segmentation on feature values, we performed a pairwise comparison of all 27 extracted features between manually and automatically segmented cells (Fig. 3C; Supplemental Fig. S2). For the 11 global features (group A), the values from manual and automatic segmentation are almost identical in all 15 cells, as revealed by straight diagonal lines in the scatterplots. Thus, short sections at which automatically segmented boundaries deviate from manual cell boundaries have only minor effects on this feature class. The three other groups of contour-based (group B), skeleton-based (group C), and PC-specific (group D) features are slightly more sensitive to the different segmentation methods. A tendency for higher values in manually segmented cells is seen for margin roughness (group B), as indicated by an accumulation of points below the diagonal. Variation without a clear tendency toward the segmentation method is seen for “average branch length” and “average end point distance” (group C), and “average lobe length” (group D; Supplemental Fig. S2). Notably, feature values sometimes differ significantly even for cells with a high overlap of cell boundaries between manual and automatic segmentation, as seen e.g. in cell ID 7 for “average branch length” (group C) or “average lobe length” (group D; see Fig. 3B; Supplemental Fig. S2; Supplemental Table S2). The differences are consistent with a general sensitivity of skeleton-based features (group C) to even small changes in region shape (Gonzales and Woods, 1996). Likewise, the quantification of contour-based features (group B) and PC-specific features (group D) relies on analyzing curvatures and concavities of the region boundary and thus is sensitive to small variations in shape contours (e.g. Utcke, 2003).

Variance can be generated by manual segmentation due to bias caused by different persons and even by a single person between segmentations generated at different time points (Vanhaeren et al., 2015). The accuracy of manual segmentation further depends on the sampling density, i.e. the frequency of sampling points along the cell boundary. To reduce the impact of geometrical discontinuities in manual segmentation, extracted contours are commonly smoothed, e.g. using ImageJ’s spline fitting (Wu et al., 2016), which additionally affects the curvature of the contour. Automatic segmentation, on the other hand, mostly depends on the image quality. Local regions of low contrast are prone to segmentation inaccuracies, and the optional watershed gap closing potentially leads to oversegmentation of actual cell borders. In a direct comparison, however, bias introduced by PaCeQuant is identical for all images, and PaCeQuant reproducibly detects cell regions from experiments conducted at different times. Thus, our first experiment suggests that PaCeQuant is suitable to detect cell outlines automatically and to quantify cell shape characteristics with a very high quality.

The automatic segmentation step works best with input images with a high image quality, which sometimes is difficult to obtain, e.g. when leaves are curled or wavy. In such cases, results from the automatic segmentation can be exported from PaCeQuant and can be manually corrected in ImageJ to remove local inaccuracies. PaCeQuant supports two formats for exporting segmentation results. Segmented cell regions can be saved as ImageJ ROI files or exported as label images, which can be edited directly in ImageJ via the ROI manager or allow for manual corrections by editing pixel intensities in, e.g. programs like Gimp, respectively. Alternatively, if only a few cells are detectable in the input image or if input images are not compatible with the automatic segmentation method implemented in PaCeQuant, as is the case, e.g. for agarose imprints of cell outlines, segmentation can be conducted manually in ImageJ. In both cases, manually corrected or manually defined cell regions can be imported into PaCeQuant for automatic feature quantification and data analysis.

Precision of Lobe Detection

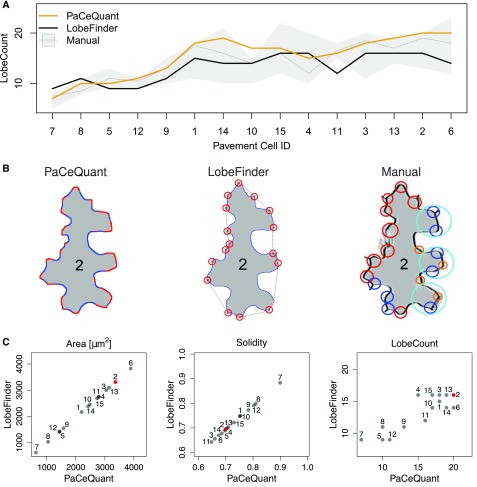
The formation of lobes and indentations is a specific property of PCs. Thus, lobes are quantified commonly to describe shape characteristics, mostly by manual counting or by skeleton-based approaches, which are prone to bias and often inaccurate. Recently, the LobeFinder program was released, which automatically measures lobe numbers by analysis of a refined convex hull (Wu et al., 2016). However, the LobeFinder tool still relies on manual segmentation of individual cells and tends to underestimate lobes when compared to manual counting (Wu et al., 2016). To investigate the quality and suitability of lobe detection based on sign changes of curvature, which we implemented in PaCeQuant, we compared the efficiency of PaCeQuant’s lobe detection with LobeFinder and with manual lobe counting using the sample set of 15 cells (Fig. 4). For manual counting, lobes were quantified in the original input image by four individuals with expertise in PC shape analysis in a blind study. To compare PaCeQuant with LobeFinder, cell boundaries automatically extracted by PaCeQuant were used as input, and all features for which quantification algorithms are implemented in both tools (e.g. area, solidity, and circularity) were quantified and compared.

Figure 4.

Evaluation of lobe detection accuracy by comparison between PaCeQuant results with LobeFinder and manual lobe counting. A, Number of lobes detected in the 15 sample cells (ID 1–ID 15) after automatic segmentation by PaCeQuant (orange), LobeFinder (black), and by manual lobe counting (gray). For manual counting, lobes were analyzed by four independent researchers. The gray line represents the mean lobe number per cell of the four measurements; the gray strip represents the range of the independent measurements. Cells are sorted by their area from small (left) to large (right). B, Lobe count results in one exemplary cell (ID 2) analyzed with PaCeQuant (left, 20 lobes), LobeFinder (middle, 16 lobes), and manually (right, 13–20 lobes). Lobes identified by PaCeQuant or LobeFinder are marked in red. Lobes identified manually are marked in red (nine lobes), blue (eight lobes), pink (four lobes), and turquoise (three lobes) if identified by four, three, two, or at least one person, respectively. C, Pairwise comparison of features computed by PaCeQuant and LobeFinder in the sample set of the 15 automatically segmented cells. Scatterplots are shown for area, solidity, and lobe count (for a summary of all features, see Supplemental Fig. S3). The cell shown in B is highlighted in red.

For all three approaches, a tendency for increased lobe counts was detected with increasing cell size (Fig. 4A). Notably, manual counting resulted in large differences between individual persons in the number of detected lobes for some of the analyzed cells (Fig. 4, A and B). The deviations within the four sets of manually detected lobes increased with increasing size and complexity of the analyzed cells. For some cells (e.g. cell ID 15, ID 14, and ID 6) manual counting resulted in differences of 8 to 11 lobes per cell, which refers to a deviation of up to 100% for single cells. Nevertheless, a significant number of lobes is consistently detected in all four manual annotations and by both tools, as shown for cell ID 2 (Fig. 4B). PaCeQuant and LobeFinder are in the range of lobe numbers counted by the four individuals. In general, PaCeQuant tends to detect more lobes than LobeFinder, and lobe numbers detected by PaCeQuant are in the upper range of manual lobe counts (Fig. 4, A and C). For all other features, such as area, solidity, and convex hull characteristics, we obtained identical results with LobeFinder and PaCeQuant, as expected for identical input contours (Fig. 4C; Supplemental Fig. S3). Thus, we conclude that PaCeQuant is suitable to quantify lobes efficiently. The comparison of the three methods further highlights the subjectivity of manual lobe counting and demonstrates a requirement for automatic lobe quantification to generate comparable and reproducible data with a constant bias.

Application of PaCeQuant to Large Data Sets

The main goal of PaCeQuant is to enable high-throughput analysis of PC characteristics. We thus validated the quality of PaCeQuant results on a larger data set (data set 2) consisting of 14 individual images of PCs from cotyledons of 5-d-old wild-type seedlings (Supplemental Fig. S4). In total, 373 cells were identified in the sample set within a time span of 10 min, starting from data input to result output, which refers to 1.6 s per cell. As seen for the initial set of 15 cells (see Fig. 3), some cells, in particular cells adjacent to stomata or with regions of low contrast, were not detected correctly (Supplemental Fig. S4B). To study the impact of such detection inaccuracies on the overall feature quantification we manually filtered the automatic PaCeQuant segmentation results. Thirty-one cells showed locally incorrect cell borders and failed to pass the manual quality control, which represents ≤10% of all detected cells. A pairwise comparison of the distributions for all 27 features between the unfiltered data set, and the manually filtered data set revealed that the manual filtering step has only minor effects on feature distributions and set properties, which are not statistically significant (P values of 0.623–0.997; Supplemental Fig. S4A). Thus, detection errors within individual cells are compensated by the analysis of large data sets, which can easily be generated with PaCeQuant, and time-intense manual filtering is not required for reliable PC shape quantification with PaCeQuant. Compared to manual segmentation, PaCeQuant offers the advantage of a much faster and unbiased segmentation. Thus, PaCeQuant is capable of increasing the amount of quantitative data, which improves the power of statistical analyses and guarantees a larger objectivity and reproducibility of extracted data.

Analysis of Cell Shape Characteristics during Development

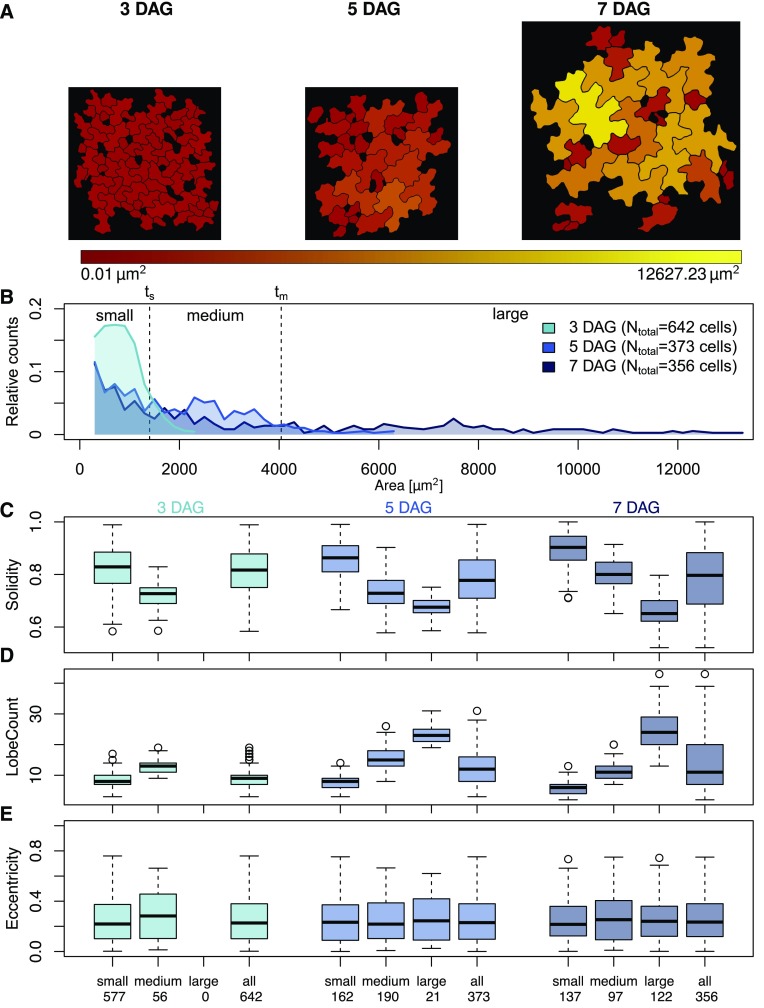
To assess the usability of high-throughput cell shape analysis in a biological context, we applied PaCeQuant to a developmental series of Arabidopsis cotyledons (Fig. 5). We analyzed PCs of the adaxial side of wild-type cotyledons at stages of early cell expansion (3 d after germination [DAG]), of rapid expansion (5 DAG), and at a stage with first fully expanded cells (7 DAG; data set 3; Zhang et al., 2011). At 3 DAG, cells range in size between 245 and 2,320 µm², with 90% of the cells being smaller than 1,400 µm² (Fig. 5, A and B). At 5 DAG, cells span sizes between 245 and 6,367 µm². At this stage, 90% of the cells are smaller than 4,042 µm², and approximately 50% of all detected cells range in size between 1,400 and 4,042 µm². The number of small cells decreased to <40% when compared to 3-d-old seedlings. At 7 DAG, roughly one-third of the detected cells belongs to the groups of small and medium-sized cells each, and the last third consist of cells with sizes larger than 4,040 µm², ranging up to 12,600 µm². The detected cell sizes are in the range of previous reports (Zhang et al., 2011), which further demonstrates the accuracy of the PaCeQuant measurements. In leaves, neighboring cells differ largely in their shapes ranging from small and simple-shaped cells to large and highly complex cells (Elsner et al., 2012). Consistent with large differences in cell size and cell differentiation, we observed high variability within the feature values calculated from analysis of the complete set of detected cells as input (Fig. 5, C–E, Supplemental Fig. S5A). The variability increases with increasing age of the analyzed cotyledons (Supplemental Fig. S5) and reflects the increasing diversity of cell shape and size during later stages of cotyledon (Zhang et al., 2011) and leaf growth (Elsner et al., 2012).

Figure 5.

Analysis of pavement cell shape characteristics during development. A, Epidermal pavement cell shape in the adaxial side of cotyledons from wild-type (Col-0) seedlings 3, 5, and 7 DAG. The color gradient represents the area of the detected cells (red, small to yellow, large). B, Relative distribution of cell areas in cotyledons of 3-, 5-, and 7-d-old seedlings. Cells were categorized into small cells (threshold t_s ≤ 1400 µm², which includes 90% of the cells in 3-d-old seedlings), medium-sized cells (threshold t_m ≤ 4042 µm², which includes 90% of the cells in 5-d-old seedlings that exceed t_s), and large cells (≥t_m), which represent the different stages of cell differentiation. C to E, Quantification of cell shape features during differentiation. Cells were grouped according to (B) or treated as a single input set (all). Numbers on the x axis refer to the number of cells analyzed per sample set. Feature values are shown in box plots. Results are medians; boxes range from first to third quartile. For a summary of all features and statistical analysis of feature values, see Supplemental Figure S5. (C) Solidity decreases with increasing cell size and differentiation, which is consistent with (D) an increased number of lobes, while other parameters, as shown for (E) eccentricity are largely unaffected during differentiation.

We next aimed to analyze PC shape transitions during development of cotyledons in more detail. To quantify shape characteristics in cells at similar stages of cellular expansion, we categorized them into small, medium, and large cells by applying the 90% thresholds from 3 DAG and 5 DAG as small size threshold (t_s) and medium size threshold (t_m), respectively (Fig. 5B). We analyzed the 27 PC shape features in the three sets and in the three size categories and compared the feature distributions by applying the Dunn’s test and by adjusting P values with the Benjamini-Hochberg procedure (Fig. 5, C–E; Supplemental Fig. S5). As expected, values of parameters such as perimeter, length, width, convex hull perimeter, lobe count, and lobe width increased significantly (P < 0.001) with increasing cell size (Fig. 5C; Supplemental Figure S5, A and B). Consistent with increased lobe formation and growth, inversely related parameters such as solidity, circularity, or convex hull roundness decreased significantly (P < 0.001). Other parameters, in particular cellular eccentricity, were unaffected by cell size or by the developmental stage (Fig. 5E). Within the individual developmental stages, we observed highly significant differences between small and medium and small and large cells for almost all analyzed features. Between medium and large cells, significant differences were visible at 7 DAG (P < 0.001). Within the 5 DAG set, only a few features differed significantly (P < 0.01) between medium and large cells. The tendencies, however, were identical to those measured at 7 DAG.

To analyze geometries of similar-sized cells during leaf growth, we next compared the three cell populations (small, medium, and large) across the three developmental stages. Small cells at 3 DAG differed significantly from small cells at 7 DAG in 23 out of the 27 analyzed parameters (P < 0.05). Large differences were observed for PC-specific features such as lobe count and lobe length and for circularity and solidity (Supplemental Fig. S5, A and B). Similarly, medium-sized cells differed between the analyzed developmental stages. Only weak differences were observed between the shape characteristics of large cells at 5 DAG and 7 DAG samples, and differences were restricted mostly to PC-specific shape features. These results are consistent with previous studies, which revealed age-dependent differences in cell shape of similar sized cells throughout development (Zhang et al., 2011; Wu et al., 2016). Differences in shape characteristics are more pronounced in expanding cell populations and disappear once cells are fully expanded. Thus, our data provide the first evidence that automatic analysis of large populations of PCs with PaCeQuant in combination with size filtering is a suitable approach to quantify developmental changes of PC shape.

Analysis of Lobe Type Characteristics

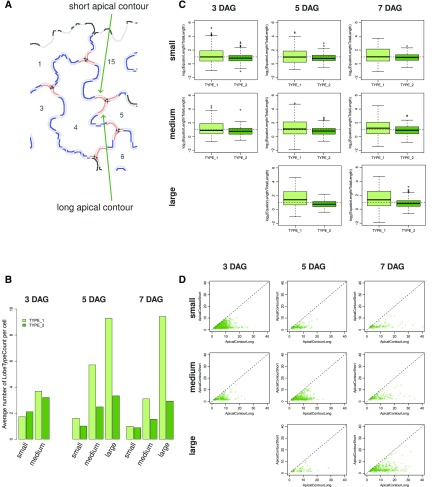
Most interdigitations are formed at two-cell contact points between two adjacent cells and form lobes referred to as type I lobes (Wu et al., 2016). In addition, some lobes form at three-cell contact points, referred to as type II lobes. So far, however, analyses of type I and type II lobe characteristics are limited because lobe classification has to be done manually, and methods for the quantification of lobe characteristics are missing. With its automatic segmentation and feature extraction capabilities, PaCeQuant provides a framework for the automatic classification of lobe types and shape quantification. We implemented an optional analysis of shape characteristics of individual lobes within single cells, which allows discriminating between lobes at two-cell contact points (TYPE-1) and three-cell contact points (TYPE-2; Fig. 6).

Figure 6.

Analysis of type I and type II lobes and quantification of lobe characteristics. A, Image of an exemplary group of adjacent PCs after neighborhood analysis of individual lobes. Apical contours of type I and type II lobes are shown in blue and red, respectively. In type II lobes, three-cell contact points (shown as black dots) separate the lobe contours corresponding to the contact sides with the two neighboring cells (referred to as short and long contour segments). B to D, Analysis of lobe characteristics in PCs from the three developmental time points (3 DAG, 5 DAG, and 7 DAG) and the three size categories (small, medium, large; see Fig. 5). For an overview of quantified lobe features and statistical analysis, see Supplemental Figure S6. B, Bar plots showing the average number of type I (TYPE_1) and type II (TYPE_2) lobes per PC. C, Average ratio of lobe equator length to total contour length in type I and type II lobes in a logarithmic scale. D, Analysis of the length of the two parts of type II lobe contours that span the distances from the lobe equator to the three-cell contact point. Scatterplots of all individual type II lobes compare the short (ApicalContourShort) and long (ApicalContourLong) fragments.

We classify lobes into TYPE-1 or TYPE-2 based on the analysis of their neighborhood in fields of adjacent cells (Fig. 6A). All lobes for which information on neighboring cells is missing, e.g. at border regions or adjacent to stomata, and which thus cannot be sorted in either of the two groups, are classified as UNDEFINED. For classification, we use the output label images generated during stage (IV) of the image analysis workflow implemented in PaCeQuant (see Supplemental Fig. S1, image 9). In these images, cell boundaries are represented as a black line with a width of 3 pixels that refers to the background of the image, and regions belonging to individual cells are defined by unique labels. In a first step, cell regions are expanded by dilation with a mask size of ≤5 using a built-in MiToBo function. The dilation locally stops as soon as two adjacent cell regions touch, which removes the boundaries between two adjacent cells and prevents the fusion of individual cell labels. Remaining black pixels thus exclusively refer to background regions, which do not belong to a cell boundary nor to any cell. Subsequently, for each individual lobe within each analyzed cell, the total number of different labels in its vicinity, defined by an 11 × 11 pixel-sized neighborhood around each pixel of the lobe, is counted and yields the base for type classification. If two different labels are present, i.e. the label of the analyzed lobe region and one additional neighboring region, the lobe is classified as TYPE-1 (Fig. 6A). In case of three labels present at the vicinity of a single lobe, it belongs to the TYPE-2 group of lobes. The presence of one or more background pixels at the lobe indicates that it is located close to an undefined image region where no further information is available, and the lobe thus is classified as UNDEFINED.

We applied the lobe classification approach to the developmental series (see Fig. 5) and quantified the number of type I and type II lobes within the small-, medium-, and large-sized cells at 3 DAG, 5 DAG, and 7 DAG (Fig. 6B; Supplemental Figure S6A). We observed only small increases in the number of type II lobes per cell between small (average lobe number of 1 to 2)- and medium-sized cells (average lobe number of 2 to 3.5), and only weak differences between small, medium, and large cells (averaeg lobe number of 1 to 3.8), respectively, during development (Fig. 6B). In contrast, the number of type I lobes increased during cellular expansion from an average lobe number of 2 to an average lobe number of 10 in small- and large-sized cells, respectively. In medium- and large-sized cells, most lobes form at two-cell junctions (Fig. 6B). Thus, consistent with earlier studies, our data suggest that type II lobes are established mostly during cytokinesis, while most of the lobes formed during cellular expansion are type I lobes (Jura et al., 2006; Wu et al., 2016).

To quantify shape characteristics of individual lobes, PaCeQuant extracts five lobe features per lobe, including the equator length, the baseline length, the apical and basal lengths, and the contour length of each lobe (Supplemental Fig. S6B). In addition, for type II lobes, we quantify the distance of the contour segments from the equator to the three-cell-junction point. To estimate the bending of a lobe from these features, we calculated the ratio of the lobe equator length to the total length of the lobe contour (Supplemental Fig. S6, C–E). In a direct comparison, type II lobes displayed a larger contour length relative to the equator than type I lobes, as indicated by log(Equator Length/Total LobeContour Length) values of ≤1 and ≥1 in type II and type I lobes, respectively (Fig. 6C). This points to a higher degree of asymmetric expansion at three-cell junctions. We measured the length of the lobe contour segments corresponding to the contact sides with the two neighboring cells and compared the ratio of the short versus the long contour segments (Fig. 6D; Supplemental Fig. S6, E and F). Our data revealed a tendency for a more similar length of the two lobe contours in small cells when compared to large cells, which suggests that different levels of expansion of the two neighboring cells contributed to these changes in type II lobe characteristics. During development, the difference between the two nonuniformly growing parts of the lobes increased further. Our results suggest that predominant expansion of one the two neighboring cells contributes to the higher degree of asymmetric expansion at type II lobes, which is consistent with previous reports (Jura et al., 2006). Together, we conclude that our novel method robustly detects and classifies type I and type II cells based on the analysis of the lobe neighborhood and quantifies characteristics of individual lobes, which provides a platform to study effects of, e.g. gene functions specifically involved in the formation of type II lobes.

Phenotype Analysis of Cell Shape Mutants

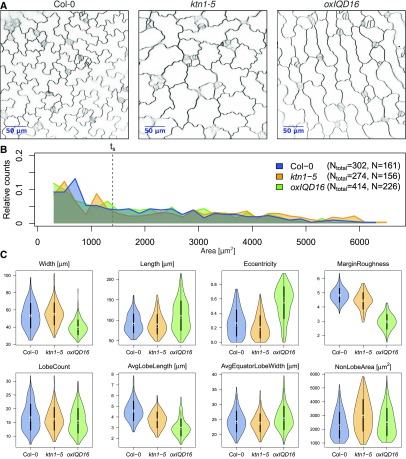
We next applied the PaCeQuant program to analyze shape characteristics in mutants that differ in PC shape compared to wild-type seedlings (data set 4; Fig. 7). We selected a mutant impaired in KATANIN (KTN1) function. KTN1 encodes a protein with microtubule severing function, and ktn mutant lines have extensively been studied with respect to microtubule ordering and PC shape characteristics (Lin et al., 2013; Lindeboom et al., 2013; Zhang et al., 2013). In particular, lobe growth has been shown to be impaired in ktn1 mutants, which results in a reduced length of lobes (Lin et al., 2013). In addition, we included transgenic Arabidopsis Pro-35S:IQ67-DOMAIN (IQD)16 lines in our analysis. IQD16 belongs to a novel class of calmodulin-binding proteins with potential roles in cellular calcium signaling (Abel et al., 2005; Abel et al., 2013). Most IQD family members localize to microtubules, and overexpression of IQD16 alters microtubule organization and induces cell elongation (Bürstenbinder et al., 2017a; Bürstenbinder et al., 2017b). As input, we used 10 images per genotype of cotyledons from 5-d-old seedlings (Fig. 7A). We selected 5-d-old seedlings because at this stage cotyledons are flat, which facilitates fast and easy image acquisition. In addition, a large number of PCs is actively expanding at 5 DAG and has developed pronounced lobes (see Fig. 5), which is a prerequisite for reliable lobe quantification.

Figure 7.

Phenotypic analysis of pavement cell shape mutants. PC shape analysis in cotyledons of 5-d-old seedlings from wild type (Col-0) and two mutants, ktn1-5 and transgenic Pro-35S:IQD16 (oxIQD16) plants. A, Inverted confocal images of wild type and the two mutants stained with FM4-64. B, Relative distribution of cell areas in the three data sets. Numbers in the legend refer to the total number of cells (N_total) from 13 images of the wild type, 13 of ktn1-5, and 17 of oxIQD16. Cells larger than size threshold t_s = 1,400 μm² (N) were used for further analysis (see Fig. 5). C, Violin plots of value distributions for four global (top) and four PC-specific features (bottom). Circles and crosses refer to medians and means; the vertical black lines in each category represent the sd (thick lines) and the 95% confidence intervals (thin lines). The width of each violin box represents the local distribution of feature values along the y axes. For a summary of all features and a statistical analysis, see Supplemental Figure S7.

We observed comparable distributions of cell sizes in the two mutant lines when compared to the wild-type control (Fig. 7B). Since medium- and large-sized cells are highly similar in cotyledons of Arabidopsis wild-type seedlings at 5 DAG (see Fig. 5) we assumed that removal of only small cells from the sample set is sufficient for size filtering and reliable quantification (see Supplemental Fig. S5B). We thus applied the empirically determined small size threshold t_s from the developmental analysis of wild-type seedlings (see Fig. 5) to the mutant data set and quantified PC shape characteristics in all cells larger than 1,404 µm². After size filtering, we retained 161, 156, and 226 cells for wild-type, ktn1-5, and Pro-35S:IQD16, respectively (Fig. 7B). Thus, approximately 50% of all cells detected by PaCeQuant are included in the subsequent data analysis.

Consistent with previous reports, we detected a significantly reduced average lobe length in ktn1-5 (P < 0.001; Fig. 7C; Supplemental Fig. S7B). The lobe length automatically measured with our novel algorithm resembles lobe length values measured manually by Lin et al. (2013) and correlates with lobe length values measured in ktn1 mutants. The total number of lobes is not altered in ktn1-5 when compared to wild-type seedlings, which points to roles of KTN1 in lobe growth, but not in lobe initiation. In addition, we observed increases in cell size (area), but not in cellular elongation (eccentricity). Nonlobe area as well as minimum and maximum core width are increased in ktn1-5 mutants. Thus, our data suggest that loss of KTN1 promotes isotropic expansion of PCs, possibly by preventing growth restriction at the neck regions. In transgenic Pro-35:IQD16 lines, lobe length is reduced even stronger than it is in ktn1-5 (P ≤ 0.001). The reduced lobe growth is further reflected by an increased nonlobe area ratio and by a reduced irregularity of the cell contour, as reflected by a decreased margin roughness in Pro-35S:IQD16 < ktn1-5 < Col-0 (Fig. 7C; Supplemental Fig. S7, A and B). Compared to wild-type and ktn1-5 mutants, we observed a significant elongation of individual cells in Pro-35:IQD16 seedlings (P < 0.001), which is represented by increased length (P < 0.001), reduced width (P < 0.001), and increased eccentricity (P < 0.001) values of cells from Pro-35:IQD16 lines. The cell sizes, however, are not altered in Pro-35S:IQD16 lines, which suggests that IQD16 does not promote cellular expansion but alters the direction of cellular growth. Thus, our data suggest distinct functions of KTN1 and IQD16 in regulation of cell growth and cellular expansion and provide first insights into potential roles of IQD16 in establishment of cellular polarity or growth anisotropy. Together, the combined analysis of 27 shape descriptors provides a platform for comparative and quantitative analyses with statistical support suitable for mutant phenotyping and developmental analyses.

DISCUSSION

In this study, we present PaCeQuant, a novel ImageJ-based tool for automatic segmentation of leaf epidermal PCs and simultaneous quantification of PC shape characteristics. The fully automatic segmentation of individual cells by PaCeQuant is a major advance because currently all measurements of PCs require manual segmentation. Manual segmentation is very time consuming and prone to bias introduced by the subjectivity of sample choice and contour labeling (Vanhaeren et al., 2015; Wu et al., 2016). PaCeQuant efficiently detects cell outlines in confocal input images using a combination of contrast and boundary enhancement, analysis of skeletons in binary images and watershed-based gap closing (Fig. 1).

We validated the accuracy of the automatic segmentation implemented in PaCeQuant by comparison to results from manually segmented cells (Fig. 3; Supplemental Fig. S2; Supplemental Table S2). In few cases, PaCeQuant locally determined cell contours with low accuracy, mostly at regions of lower contrast (Fig. 3; Supplemental Fig. S4). Local regions of deviation from manually segmented contours, however, only had weak effects on calculated shape properties of individual cells (Fig. 3; Supplemental Fig. S2). When applied to a larger data set of 373 cells, PaCeQuant partially failed to segment the contours of less than 10 percent of the cells (Supplemental Fig. S4). Manual filtering did not affect the calculated feature values significantly (Supplemental Fig. S4), which suggests that the large number of analyzed cells generates data sets robust enough to compensate for minor detection errors. When compared to manual segmentation, PaCeQuant reduces the variance in segmentation results due to its high reproducibility, and bias induced by PaCeQuant is constant irrespective of when or by whom segmentations are performed. Thus, PaCeQuant provides a robust platform for cell segmentation, which can be used for shape quantification without manual postprocessing. To account for input data sets with medium to low quality of input images and to increase the compatibility of PaCeQuant with independent imaging techniques such as agarose imprints or scanning electron microscopy images, we additionally implemented an optional semiautomatic or manual segmentation mode, respectively, into PaCeQuant.

The automatic segmentation of individual PCs implemented in PaCeQuant provides the basis for high-throughput shape quantification. To study developmental shape transitions and molecular and genetic modes of shape establishment, imaging must be combined with the quantification of PC shape characteristics. A combination of advanced imaging, automatic quantification of shape features, and computational modeling has been used to study the development of embryos (De Rybel et al., 2014; Yoshida et al., 2014), of root meristems (Campilho et al., 2006), of shoots apical meristems (Reddy et al., 2004; Kierzkowski et al., 2012; Serrano-Mislata et al., 2015), and of flower organs (Tauriello et al., 2015). In these studies, the direction of cell division and cell expansion is tracked over time from semi- and fully automatic 3D segmentations of individual cells using the MorphoGraphX software (de Reuille et al., 2014; Barbier de Reuille et al., 2015). In combination with molecular and developmental data imaging-based analyses enabled the generation of comprehensive models of the underlying regulatory processes (Roeder et al., 2011; Sozzani et al., 2014). All cell types analyzed by these approaches, however, are simple shaped cubic or cylindrical cells, whereas PCs form much more complex and diverse cell shapes during expansion. The algorithms used to track and measure growth in these model systems cannot directly be applied to quantify PC characteristics, as they oversimplify PC shape geometry, and comparable quantification methods suitable for robust analysis of PCs are lacking. In most existing studies that analyzed PC characteristics, differences in PC shape between mutants and wild type were quantified by the analysis of single shape parameters only (Tisné et al., 2008; Xu et al., 2010; Li et al., 2013) or by a combination of a few select shape parameters (Fu et al., 2005; Guo et al., 2015). Although sufficient for direct comparison of phenotypes, the limited shape information reduces the informational value of the individual measurements and hampers a comprehensive comparison of phenotypes identified in different studies and from different laboratories (Ivakov and Persson, 2013; Wu et al., 2016).

To provide a standardized platform for PC shape phenotyping, we included the simultaneous quantification of 27 different shape parameters in PaCeQuant. The 27 features include global geometric and morphological features, such as area, perimeter, and circularity (Fig. 2; Supplemental Table S1). In addition, we quantify the number, length, and width of lobes, which are specific characteristics of PCs, by analysis of the local curvature along the cell contour. In a direct comparison with the recently released LobeFinder tool (Wu et al., 2016), PaCeQuant quantifies more shape features than LobeFinder (27 versus 8, respectively), including the length of lobes and the degree of cellular elongation. PaCeQuant detects in average one to three lobes more per cell than LobeFinder (Fig. 4). The lobe numbers detected by PaCeQuant are in the range of lobes detected by individuals (Fig. 4; Supplemental Fig. S3). The large differences in the lobe numbers measured by four independent individuals further demonstrate the high variability of manual image analysis and highlight the requirement for automated phenotyping platforms. Another important parameter in PC shape development is the degree of growth restriction at neck regions, sometimes estimated by the quantification of the neck width (Li et al., 2003; Bannigan and Baskin, 2005; Fu et al., 2005). The definition of the neck width, however, is not clear and renders objective measurements difficult. We thus developed novel objective and well-defined algorithms to quantify the extent of the cellular core region. These two features, the minimal and maximal core width (Fig. 2; Supplemental Table S1), quantify the widths of narrow and wide parts of the core region of PCs, defined by distance of the cell contour to the central skeleton branch. Small values represent a small neck width, while large values correspond to a larger neck width. In combination with the analysis of the nonlobe area and the ratio of nonlobe area to total area, these values provide information on the growth restriction at neck regions.

Finally, PaCeQuant is the first tool that not only analyzes and quantifies shape features per cell but also extracts data per lobe. It provides length and width measurements of various parts of an individual lobe, e.g. of the overall lobe length as well as of baseline and equator lengths. PaCeQuant additionally includes an automatic identification of type I and type II lobes at two-cell and three-cell contact points, respectively, for cells with sufficient neighborhood information (Fig. 6; Supplemental Fig. S6). This allows detailed analyses of the characteristics in particular of three-cell contacts, e.g. at different time points during development, with regard to lobe symmetry. By applying PaCeQuant on a developmental time series of Arabidopsis cotyledon PCs, we demonstrate that PaCeQuant accurately quantifies shape features over a wide range of cellular sizes and differing shapes (Fig. 5). In our sample sets, PaCeQuant automatically detected between 21 and 34 cells per image and simultaneously quantified the 27 shape features with an average processing speed of 1.6 s per cell. The supplemental R script enables fast and easy data visualization, statistical analysis and data processing, and supports high-throughput data analysis. Thus, PaCeQuant is suitable to generate large data sets in a short period of time, which are free from biased selection of individual cells. The data sets contain information on the number and distribution of cells from different stages of cellular expansion. To quantify and compare shape geometries in defined subsets of cells during development we applied size filters and analyzed shape features in small-, medium-, and large-sized cells. Our data reveal age-dependent differences in cell shape between populations of similar sized cells, which likely reflect different stages of differentiation (Fig. 5). The results are in agreement with previous studies, which reported changes of shape in actively expanding PCs during development (Zhang et al., 2011; Elsner et al., 2012).

Analysis of lobe types and feature characteristics of individual lobes indicated that, in a direct comparison, type II lobes are less regular shaped (Fig. 6). These differences might be caused by higher growth rates of one of the two neighboring cells, which is consistent with earlier reports (Jura et al., 2006). The optional analysis of lobe types implemented in PaCeQuant thus provides the first tool to study effects of gene functions specifically involved in the formation of three-cell junctions and to measure shape characteristics of individual lobes. For the phenotypic analysis of mutants that, e.g. affect PC shape globally it, however, is not necessary to distinguish between these two lobe types. If desired, the user thus can optionally activate lobe type classification and analysis in the graphical user interface.

We additionally validated the usability of PaCeQuant for PC shape quantification in mutant phenotyping as a first proof of concept (Fig. 7). Consistent with previous reports, we observed a reduced length of lobes in ktn1-5 lines (Lin et al., 2013), which confirms that the analysis of contour curvature implemented in PaCeQuant is suitable for measurements of lobe characteristics. We provide evidence that the combined analysis of 27 shape features with PaCeQuant generates information on multiple aspects of PC shape and growth, including the size of the cellular core region and the number and characteristics of lobes. The analyzed features reflect the geometrical complexity of PCs. Thus, PaCeQuant enables comparative analyses between mutants or during development even across different laboratories with a more complex description of PC shapes than other existing tools.

We will establish a future database where PaCeQuant results can be uploaded and directly compared to existing data sets. Such a database will enable the identification of, e.g. mutants with highly similar defects in shape formation, which might point to similar cellular functions and could assist the molecular and physiological characterization. In the long term, we aim to implement the collected data in systems biology approaches to model the underlying molecular and genetic pathways.

In conclusion, our data demonstrate that PaCeQuant is suitable for automatic segmentation of PCs, which builds a prerequisite for the generation of objective and reproducible data. Together with the implemented feature analysis, PaCeQuant offers the possibility of high-throughput PC shape analysis. It thus provides a user-friendly platform for large-scale shape quantification with potential application in studies of cell shape changes in response to external stimuli, during development or in mutant phenotyping.

MATERIALS AND METHODS

Plant Material and Growth Conditions

Arabidopsis (Arabidopsis thaliana; ecotype Col-0) seeds were originally obtained from the Arabidopsis Biological Resource Center. Seeds of the ktn1-5 T-DNA line (SAIL_343_D12) were obtained from the Nottingham Arabidopsis Stock Centre (NASC). Transgenic Pro-35S:IQD16 lines were generated by Agrobacterium tumefaciens-mediated transformation using the floral-dip method (Clough and Bent, 1998), as described in Bürstenbinder et al. (2017b). Arabidopsis seeds were surface-sterilized with chlorine gas, and after 2 d of stratification at 4°C grown vertically on square plates containing Arabidopsis salt (ATS) medium and 0.5% (w/v) agar (Lincoln et al., 1990) at 20°C with cycles of 16 h light and 8 h dark.

Confocal Microscopy

For analysis of epidermal pavement cell shape, seedlings were incubated 10 to 30 min in 50 µm FM4-64 dye (Synapto-Red, Sigma). Imaging was performed with an LSM 700 inverted laser scanning microscope (Carl Zeiss) using a 20× plan neofluar objective. The laser line 555 nm was used for FM4-64 excitation, and fluorescence emission was detected between 560 and 590 nm. Single optical sections of the adaxial site of FM4-64-stained cotyledons were acquired with pixel dwell times between 0.8 and 1.3 µs and an averaging of 4 to increase the signal-to-noise ratio. For each developmental stage and line, 10 to 17 cotyledons from 5 to 10 individual seedlings were scanned. Groups of adjacent pavement cells were imaged with a resolution of 3.19 pixels/µm in 3-d-old and 5-d-old seedlings and with a resolution of 2.24 pixels/µm in 7-d-old seedlings.

Data Sets

For the evaluation of PaCeQuant, we used four data sets, which were comprised as follows:

• Data set 1: 15 individual cells from one input image of 5-d-old Arabidopsis Col-0 seedlings.

• Data set 2: 373 cells identified from 14 input images of cotyledons from 5-d-old Arabidopsis Col-0 seedlings. After manual postprocessing, 342 cells were retained in the curated data set.

• Data set 3: 642 cells from 10 input images of Arabidopsis Col-0 seedlings 3 DAG, 373 cells from 14 input images of seedlings 5 DAG, and 356 cells from 13 images of seedlings 7 DAG.

• Data set 4: 302 cells from 13 input images of Col-0 wild type, 274 cells from 13 input images of ktn1-5 mutants, and 414 cells from 17 input images of transgenic Pro-35S:IQD16 lines from 5-d-old seedlings. After size filtering for removal of small cells (≤1400 µm²), the data set contains 161, 156, and 226 cells from Col-0, ktn1-5, and Pro-35S:IQD16, respectively.

Installation and Usage of PaCeQuant

PaCeQuant is part of the Microscope Image Analysis ToolBox MiToBo. The PaCeQuant plugin can be added to ImageJ/Fiji by activation of MiToBo’s update site via the update site manager of Fiji. Alternatively, binary packages of MiToBo, including the PaCeQuant plugin for direct use with ImageJ/Fiji, can be downloaded from MiToBo’s website. A detailed description of PaCeQuant, including installation instructions can be found at PaCeQuant’s website (http://mitobo.informatik.uni-halle.de/index.php/Applications/PaCeQuant).

After installation, PaCeQuant can be found in ImageJ’s plugin menu. After selection of Plugins > MiToBo > PaCeQuant, a graphical user interface opens, which allows easy configuration and execution of the tool (Supplemental Fig. S8).

First, the general workflow and data input format have to be configured. For this purpose, PaCeQuant offers three options:

SEGMENTATION_AND_FEATURES

In this mode, PaCeQuant uses confocal input images for automatic cell segmentation and feature quantification. As output, images showing the segmentation results, ImageJ ROI files containing the region data and for each image a text file including all extracted feature values per analyzed cell are exported and saved in the result directory.

SEGMENTATION_ONLY

By choosing this mode, PaCeQuant performs automatic segmentation of individual cells on confocal input images. As output, images and ImageJ ROI files are exported and saved in the result directory, which subsequently can be reimported to ImageJ for manual correction of segmentation inaccuracies.

FEATURES_ONLY

In this mode, either manually corrected segmentation data or input ROIs generated by, e.g. manual segmentation of individual cells, can be imported, and for each image or ROI set a text file including all extracted feature values per analyzed cell are exported and saved in the result directory.

For feature analysis, PaCeQuant accepts the following input formats:

• BINARY_IMAGE: a binary image where the background is marked by intensity value 0 and the foreground by intensity value 255.

• LABEL_IMAGE: a grayscale image where each cell region is marked by a unique label.

• IMAGEJ_ROIs: ImageJ ROI files with region data, e.g. exported from ImageJ’s ROI manager

PaCeQuant supports two basic working modes:

INTERACTIVE

Only the image or ROI set currently selected in ImageJ/Fiji is analyzed.

BATCH

All images or region files in a selected directory, and all its subdirectories are analyzed.

Depending on the chosen option for image analysis and the selected working mode, the configuration of the GUI dynamically changes, and mode-specific entry fields appear. For segmentation, the user has to specify how the cells in the images are labeled, i.e. if the boundaries are darker than the background or vice versa. Note that these are the only settings that are required to run PaCeQuant. Optionally, PaCeQuant offers to activate a gap-closing heuristic to account for incomplete cell boundaries due to low contrast and to define thresholds on the size of valid regions, which we recommend to set properly. For expert users, further configuration options are available via the parameter “Morphology Analyzer Operator.” It allows for changing thresholds and parameter values applied in lobe detection and enables deactivation of subsets of features. Users, however, should be aware that any change in these parameters might hamper comparative evaluations between experiments and thus is not recommended. Finally, the analysis of lobe types (TYPE-1, TYPE-2, UNDEFINED) and the quantification of shape features of individual lobes can be activated optionally. These results will be exported to a separate table per cell and can be analyzed separately. At the bottom of the configuration, window options for generating supplemental results are provided, e.g. for an image stack including additional intermediate result images and for a stack with additional images visualizing the feature values of each cell by mapping them to the intensity values of the cell in the corresponding image. Lastly, additional verbose output to console can be activated.

Clicking the button “Run” starts the processing. If a single image is analyzed, the results will directly pop up, while in batch mode, the results are written to file. For each input image in each processed folder, several files with segmentation data and an output text file are generated and saved to a new subfolder “results.” The text files contain row-wise for each cell the set of feature values extracted by PaCeQuant. If the optional lobe type classification is activated, additional text files are generated for each individual cell per image. These files contain information on the lobe type and on lobe-specific feature values for each lobe of the particular cell. Note that a complete documentation of all configuration options and all general information about PaCeQuant can be found at MiToBo’s Web site in the documentation section:

http://mitobo.informatik.uni-halle.de/index.php/Applications/PaCeQuant.

Automatic Cell Shape Analysis and Data Visualization with R

For analysis of the data output, we provide an R script that visualizes the features and performs basic statistical evaluations. As data input the path to the results directory of the PaCeQuant output has to be provided by the user. Each subdirectory within the results directory defines a sample set. First, all detected cells are sorted according to size, and a histogram of the size distribution is generated for each individual sample set. In the next step, size filtering can be applied to exclude small cells below a manually defined size threshold. Values between 0 and 1 are considered as percentages of the total number of detected cells. Values larger than 1 are considered as absolute PC areas in µm². The size filtering can be performed on the global level, where the same threshold is applied to all analyzed sample sets. Alternatively, local thresholds can be set separately for individual data sets. Since size reflects the developmental stage of PCs and thus has a large impact on most analyzed features, we recommend comparing the size distributions of the analyzed sample sets before selecting a threshold for further analysis. We recommend using global thresholds if all samples have comparable size distributions. For comparison of, e.g. mutants with generally reduced cell sizes compared to wild-type seedlings, locally defined thresholds might be useful to compare cells at similar stages of cell differentiation. Lastly, we suggest using absolute sizes as threshold, which, however, requires careful analysis of size distributions and of size impacts prior to threshold selection. For comparative analyses in Arabidopsis (also across different laboratories), we recommend to use developmental stages and thresholds introduced in this work (t_s = 1400 µm²). To visualize the data, the results of all individual features are plotted as histograms, boxplots, or violin plots.

Statistical Analysis

Analysis of the data sets with the Kolmogorov-Smirnov test revealed nonnormal distribution for most sample sets and features. For statistical analysis, we thus applied the nonparametric Kruskal-Wallis test provided by the R package stats, which is the equivalent of the parametric one-way ANOVA (Kruskal and Wallis, 1952). The Kruskal-Wallis test is intended for testing whether samples originate from the same distribution. Specifically, it tests for the null hypothesis that the location parameters (medians) of the distributions of the given samples are the same in each group. The alternative is that they differ in at least one group. In the latter case, we applied the Dunn’s test (Dunn, 1964) provided by the R package dunn.test as post hoc test to analyze each pair of samples separately.

Accession Numbers

Sequence data for KTN1 and IQD16 can be found in the EMBL/GenBank data libraries under accession numbers At1g80350 and At4g10640, respectively.

Supplemental Data

The following supplemental materials are available.

• Supplemental Figure S1. Effects of the individual processing steps implemented in PaCeQuant on the input image.

• Supplemental Figure S2. Comparison of PaCeQuant features between manually and automatically segmented cells.

• Supplemental Figure S3. Pairwise comparison of features computed by PaCeQuant and LobeFinder.

• Supplemental Figure S4. Comparison of feature values between Raw PaCeQuant output data and after cell removal by manual filtering.

• Supplemental Figure S5. Quantification and statistical analysis of pavement cell shape features during development.

• Supplemental Figure S6. Classification and quantification of type I and type II lobe characteristics.

• Supplemental Figure S7. Quantification of pavement cell shape features in wild-type and mutant lines.

• Supplemental Figure S8. Graphical user interface of PaCeQuant.

• Supplemental Table S1. Detailed definitions of features analyzed by PaCeQuant.

• Supplemental Table S2. Quantitative evaluation of segmentation quality.