Thermosensitivity of growth is determined by chaperone-mediated proteome reallocation

Significance

How do bacteria adapt to the diverse thermal niches on earth? Evidence accumulates in the protein sequence and structural determinants of thermosensitivity and mechanisms by which molecular chaperones aid protein folding. However, a comprehensive understanding of how thermoadaptation is achieved at the systems level is still missing. Here we reconstruct an integrated genome-scale protein-folding network for Escherichia coli, termed FoldME, that couples both contributing factors to the metabolic state of a cell. FoldME simulations reproduce the asymmetrical bacterial temperature response and delineate the multiscale strategies cells use to resist unfolding stresses induced by high temperature and destabilizing mutations in a single gene. The results highlight how global proteome allocation regulates thermoadaptation through balance between chaperones for folding and translational machinery for biosynthesis.

Abstract

Maintenance of a properly folded proteome is critical for bacterial survival at notably different growth temperatures. Understanding the molecular basis of thermoadaptation has progressed in two main directions, the sequence and structural basis of protein thermostability and the mechanistic principles of protein quality control assisted by chaperones. Yet we do not fully understand how structural integrity of the entire proteome is maintained under stress and how it affects cellular fitness. To address this challenge, we reconstruct a genome-scale protein-folding network for Escherichia coli and formulate a computational model, FoldME, that provides statistical descriptions of multiscale cellular response consistent with many datasets. FoldME simulations show (i) that the chaperones act as a system when they respond to unfolding stress rather than achieving efficient folding of any single component of the proteome, (ii) how the proteome is globally balanced between chaperones for folding and the complex machinery synthesizing the proteins in response to perturbation, (iii) how this balancing determines growth rate dependence on temperature and is achieved through nonspecific regulation, and (iv) how thermal instability of the individual protein affects the overall functional state of the proteome. Overall, these results expand our view of cellular regulation, from targeted specific control mechanisms to global regulation through a web of nonspecific competing interactions that modulate the optimal reallocation of cellular resources. The methodology developed in this study enables genome-scale integration of environment-dependent protein properties and a proteome-wide study of cellular stress responses.

Temperature is one of the most important environmental parameters that dictate the evolution of bacterial species. Our current understanding of thermoadaptation is based on deep investigations from a few different standpoints. First, sequence and structural determinants of thermosensitivity are identified through comparison of homologous enzymes between psychrophilic, mesophilic, and thermophilic organisms (1, 2) or fitness-increasing mutations that arise during laboratory evolution at high temperatures (3–5). Second, efforts have been made to comprehend the detailed mechanisms by which molecular chaperones promote efficient folding, minimize toxic aggregation, and maintain a properly folded proteome under stressful perturbations (6–8). In particular, two major chaperone families that are well conserved across bacteria, the Hsp70 (9) and Hsp60 (10) systems, share the majority of the folding load in a cell. Therefore, physicochemical principles (11–15) and chaperone–substrate interactions (16–18) that regulate efficient folding for a single protein are extensively studied in in vitro experiments and theoretical models.

Empirical and population genetics models of bacterial growth try to explain the general principles for various species to adapt to diverse thermal niches. For example, temperature responses fit nicely using the activation enthalpy of a single rate-limiting reaction and thermodynamic parameters of its catalyzing enzyme (19). In another approach, focusing on marginally stable proteomes that may experience sharp and cooperative denaturation, thermo-response can be simply described by two parameters, a dominant metabolic activation barrier and the number of proteins controlling replication process in an organism (20, 21).

Apparently, evolution of protein thermodynamics and the function of a rate-limiting response reaction (presumably chaperone-assisted folding) are both critical to the temperature dependence of bacterial growth. To date, most studies provide in-depth investigation on the effect of only one aspect. However, the cytoplasm of a living cell is an active complex medium, where a large number of protein molecules with varied thermal qualities compete to achieve diverse cellular functions. How do proteins with different evolutionarily developed thermal features respond to instant temperature perturbations? How do molecular chaperones catch these changes and distribute their folding service to optimize growth? How do these two determinants interact at the systems level to modulate temperature response of a cell under different environmental conditions?

To answer these questions, we use the genome-scale network reconstructions and computational models of metabolism and protein expression [ME Models (22–24)] for Escherichia coli. The E. coli ME Model is capable of generating fine-grained descriptions of proteome composition that optimizes cellular growth in a given environment. Furthermore, the decoupling of protein expression from metabolic requirement enables incorporation of multiple protein states, providing the framework to characterize the changing properties of proteins and lay out how chaperones are distributed to maintain protein quality control in vivo.

Herein, we present the reconstruction of the genome-scale protein-folding and chaperone network in E. coli K-12 MG1655. This reconstruction is then integrated into the ME Model to form FoldME. FoldME describes the in vivo protein folding as a competition between de novo spontaneous folding and assisted folding, using the HSP70 (DnaK/DnaJ/GrpE) and the HSP60 chaperonin system (GroEL/GroES). With the chaperones being allowed to respond dynamically to changes in the proteomic folding state, FoldME delineates how organismal fitness is affected by a variety of perturbations, such as temperature fluctuations, nutrient availability shifts, and genetic mutations. Importantly, we demonstrate that cellular response to unfolding stresses is more complicated than a simple decision about which folding pathway to choose for each unfolded peptide. It involves a systems-level proteome reallocation in accordance with empirical bacterial growth laws (25), to balance availability of chaperones for folding and the biosynthesis machinery to synthesize the proteome, including the chaperones.

Results

Model Reconstruction.

Environmental and genetic perturbations modulate cell growth by changing the properties of the cell’s protein components, followed by a subsequent reallocation of cellular resources in response to that alteration. To assess this effect, we first associate all biochemical reactions in the E. coli genome-scale ME Model [iOL1650 (24)] with the sequences and structures of their catalytic enzymes, using the protocols developed in our group (26, 27). Next, we compute the temperature-dependent protein kinetic folding rate [$k_f(T)$], thermostability [free energy of unfolding $\mathrm{\Delta }G(T)$], equilibrium constant of unfolding $K_{eq}(T)\triangleq \exp \{-\mathrm{\Delta }G(T)/RT$}, and aggregation propensity (agg) from first principles (Materials and Methods) for every protein in FoldME. The calculation provides us with a condition-specific characterization of the folding state of the proteome, which is then coupled to cell growth through flux balance formulation of the folding reactions described below.

Three pathways that actively fold nonspecific protein targets in vivo are incorporated to form the folding network (Fig. 1A): (i) the spontaneous folding pathway, (ii) the DnaK-assisted folding pathway, and (iii) the GroEL/ES-mediated folding pathway. Spontaneous folding occurs in the presence of trigger factor once a nascent peptide chain exits the ribosome. We describe the temperature-dependent unfolded fraction of an individual protein with the coupling constraint $V_{dilution}\ge (\frac{\mu }{k_f(T)}+K_{eq}(T))\cdot V_{folding}$, where $\mu$ is the growth rate.

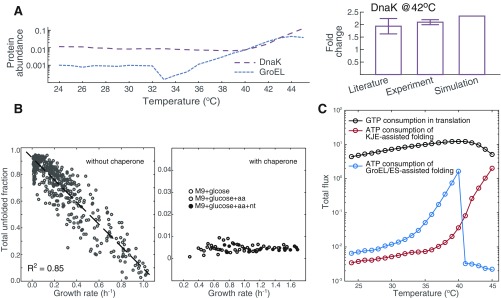
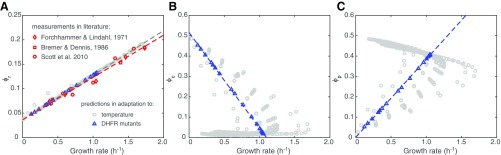
Fig. 1.

FoldME reconstruction and validation. (A) Elementary model reactions for the three folding pathways. The flux going through each reaction is denoted $V_{reaction\text{\_}label}$, and the coupling constraints are explained in the text. (B) Illustration of how temperature dependence of each biophysical property is combined to compute their collective effect on cell growth. CR stands for chaperone requirement calculated from agg alone; CR(T) takes into account both agg and $\mathrm{\Delta }G(T)$. (C) FoldME predictions (circles connected with a solid line) of relative growth rates of E. coli over temperatures, compared with data obtained from the literature (16, 50, 51) (diamonds) and in-house experiments (triangles).

DnaK- and GroEL/ES-assisted folding pathways have been studied extensively due to their central role in maintaining cellular proteostasis (12, 18, 28). Without loss of generality, we describe each chaperone-assisted folding pathway with three kinetically controlled elementary steps (Fig. 1A) that are constrained with the corresponding enzymatic turnover rates measured experimentally (29, 30). To reflect the fact that multiple repeated cycles of complete release and rebinding of the peptide are required for the substrate to reach its native state (31, 32), we design a pair of duplicated reactions, one for the successful folding event ($V_{K3}$ and $V_{G3}$) and another unfruitful chaperone-interaction cycle that releases the unfolded peptide ($V_{K3\prime }$ and $V_{G3\prime }$). The ratio between the flux of these two reactions is set to an effective temperature-dependent chaperone requirement, $CR(T)=agg\cdot (1+K_{eq}(T))$, to estimate the number of repeated cycles required for a particular peptide. Derivations and additional details for modeling the three folding pathways are described in SI Materials and Methods.

The E. coli protein-folding network has been developed in more detail based on the concerted action of the molecular chaperones and proteases to predict the folding outcome of a single protein (14, 15, 33). However, such a kinetic model gives no clue on how the chaperones should be partitioned simultaneously among the folding request from the whole proteome and how proteome folding is coupled to the metabolic state of a growing cell. Here, we allow the three folding pathways to compete for folding of any protein instead of being designated a priori to any particular clients. Through integration into iOL1650, this unique computational model, termed FoldME, is capable of dynamically adjusting the in vivo folding pathway of each protein based on its folding characteristics, as well as the proteome composition and metabolic state in a given environment.

Asymmetrical Temperature Dependence of Cell Growth.

We simulated FoldME at different temperatures by computing the enzyme catalytic rate $k_{cat}$ and proteomic biophysical profile according to statistical mechanical laws depicted in Fig. 1B. FoldME computes the proteins’ folding properties separately from their metabolic activities and can thus assess how each property contributes to the nonlinear nature of the cell’s temperature response over a wide range of temperatures (Fig. 1C). Remarkably, without any further assumptions or parameter fitting, the predicted relative growth rate agrees quantitatively with the independent experimental data from 24 °C to 46 °C, in both minimal glucose and defined rich media.

Over the Arrhenius growth temperatures (24$\sim$37 °C, region in pink in Fig. 1C), change in growth rate is governed by the temperature dependence of enzyme catalytic rates. We estimated the equivalent Arrhenius activation energy for cell growth to be 55.9 $\pm$ 1.1 kJ/mol, consistent with the experimental value 56.5 kJ/mol previously measured for E. coli in rich media (34). Between 38 °C and 42 °C, growth rate varies only in a small range, and the optimal growth temperature is dependent on the medium type. Consistent with our experimental measurements, FoldME predicted that the optimal growth temperature in rich medium was slightly higher ($\sim$1 °C) than that in the minimal glucose medium. Relatively constant growth in this temperature range is maintained by an intricate competition between all contributing factors. At higher temperatures ($T\ge$42  °C, region in blue in Fig. 1C), neither the increased kinetic folding rate nor the elevated enzyme catalytic rate is enough to compensate for the cost of maintaining stability of the unfolding proteins; hence, the growth rate decreases sharply.

In addition to predictions of growth behavior, FoldME simulations correctly capture the intracellular abundance and temperature response of the molecular chaperones. At 37 °C, FoldME estimates DnaK to contribute 0.72% to the total mass in defined rich medium, consistent with the estimation of $\sim$1% total proteome mass during exponential growth (35). At 42 °C, DnaK is calculated to increase by 2.3-fold, which is very close to our experimental measurements ($2.1\pm \mathrm{\hspace{0.17em}0.1}$). Although abundances of GroEL vary in different experiments, FoldME predictions capture the general trend that GroEL is slightly lower in mass fraction than DnaK at physiological temperatures (Fig. S1A).

Fig. S1.

Model-predicted cellular cost related to the chaperone-assisted folding process. (A) Biosynthetic cost of the chaperones. Shown is the mass fraction of DnaK and GroEL in defined rich medium predicted by FoldME simulations. The calculated fold change of DnaK abundance at 42 °C compares well with measurements in the literature and in-house experiments. (B) Cost of the unfolded peptides. To show how the chaperone network controls the total unfolded protein fraction in the proteome, we simulated cell growth with and without the DnaK-assisted and GroEL/ES-assisted folding pathways. Without the chaperones, we simulated cell growth by sampling $K_{eq}$ of each protein independently from the calculated $K_{eq}$ distribution at 37 °C. The results showed an anticorrelation between growth rate and the mass fraction of the unfolded proteome. With chaperones functioning in the designed network, the total unfolded fraction is kept at a low level regardless of how the temperature changes the growth rate. (C) Energy cost of chaperone-assisted folding reactions, compared with that consumed by protein translation.

Quantitative consistency in the up-regulation of chaperones at higher temperatures is obscured due to the difference between FoldME simulations that reflects an evolved global optimum and experiments usually performed for the WT cells. Nevertheless, in a study that evolved E. coli to an extreme temperature of 48.5 °C, GroEL is determined to increase 16-fold over its WT level (36), partially supporting our FoldME estimations. The increased level of chaperones is used to keep the total unfolded protein fraction below 1% of the proteome mass under all temperatures (Fig. S1B). Therefore, FoldME simulations faithfully recapitulate the critical function of the chaperone network in buffering the temperature-induced unfolding stresses and maintaining robust cell growth.

Chaperone-Mediated Proteome Reallocation Details the Empirical Bacterial Growth Law.

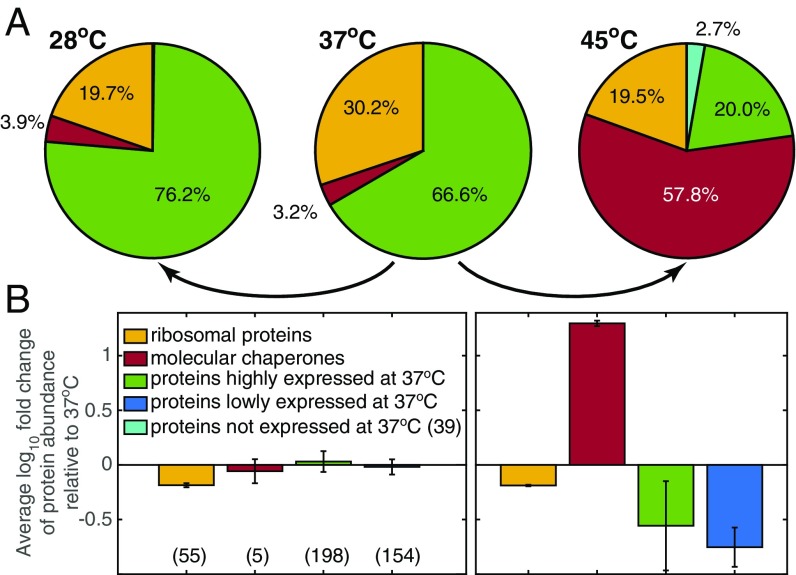
The phenotypic change adapted to different temperatures is reflected in proteome allocation strategies. We compared computed gene expression profiles at 28 °C and 45 °C, where the growth rates are similar (Fig. 2 and Fig. S2). In the Arrhenius temperature range, the shift in gene expression is minor and homogeneously distributed to all metabolic enzymes to compensate for the overall decrease in enzymatic efficiency. In contrast, under severe unfolding stress at 45 °C, the up-regulation of chaperones significantly drains cellular resources away from ribosome synthesis, limiting the synthesis of all other cellular components. Thus, chaperones not only respond to unfolding needs, but also mediate global proteome reallocation by setting a constraint on the use of cellular resources for biomass synthesis.

Fig. 2.

Proteome reallocation with change in temperature. (A) Pie charts of the computed mass fraction for ribosomal proteins (yellow); molecular chaperones (red); and proteins that are highly expressed (green), lowly expressed (blue), and not expressed (cyan) at 37 °C. Percentage is calculated with respect to all expressed proteins in FoldME (454, 446, and 448 at 28 °C, 37 °C, and 45 °C, respectively). (B) The average fold change in protein abundance at 28 °C (Left) and 45 °C (Right) with respect to 37 °C. The number of expressed proteins used for fold change calculation is shown in parentheses for each colored category. The error bars indicate variation of fold change in the particular protein fraction shown.

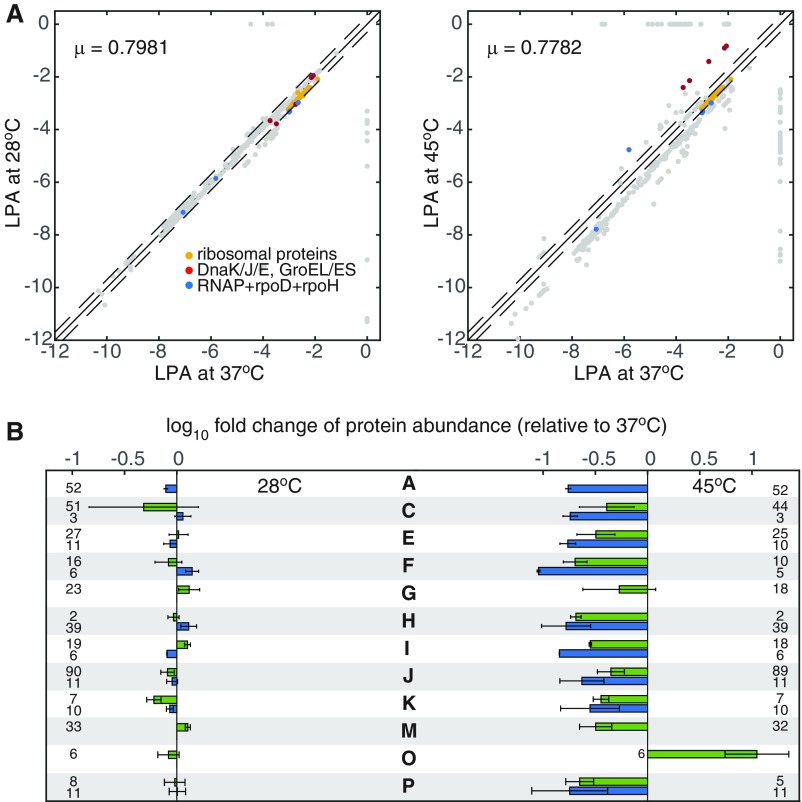
Fig. S2.

Comparison of the computed differential gene expression at 28 °C and 45 °C. (A) Logarithm of the protein abundance (LPA) at 28 °C and 45 °C is compared with LPA at 37 °C. LPAs of the ribosomal proteins (yellow), molecular chaperones (red), and RNA polymerase complex (blue) are highlighted for reference. (B) Average fold change of protein abundance in each main COG. For easy comparison with Fig. 2 in the main text, proteins in each COG category are grouped into those that are highly expressed at 37 °C (green) and those that are lowly expressed at 37 °C (blue). Numbers of proteins in every group are indicated in the same row. Error bars represent the SD of fold change within each protein group. COG categories are listed as follows: A, RNA processing and modification; C, energy production and conversion; E, amino acid metabolism and transport; F, nucleotide metabolism and transport; G, carbohydrate metabolism and transport; H coenzyme metabolism; I, lipid metabolism; J, translation; K, transcription; M, cell wall/membrane/envelope biogenesis; O, protein turnover and chaperone functions; and P, inorganic ion transport and metabolism.

We further detailed the constraints associated with proteome allocation, using large-scale simulations of 21 nutrients that were previously shown to best represent the diversity of the proteome under different conditions (37). With implementation of the chaperone network, computed growth rates showed consistent temperature response from 24 °C to 46 °C for all nutrients considered (Fig. S3).

Fig. S3.

Robust temperature adaptation under different nutrient conditions. (A) Simulated E. coli growth rate for 19 single-carbon (gray)/nitrogen (blue)/phosphate (yellow) nutrient conditions and two rich media (red) at 37 °C. These growth rates are used as reference to rank the nutrient quality in Fig. 3B. Relative growth rate is shown for all 21 nutrient conditions from 24 °C to 46 °C. The slope in the Arrhenius range is used to calculate the averaged activation energy for cell growth. Growth in xanthine (star) and hexanoate (triangle) shows slight deviations compared with that in the other nutrient conditions, likely due to different metabolic pathway use because of their low nutrient quality (low growth rate at 37 °C).

The mechanism underlying these detailed predictions is consistent with reported coarse-grained bacterial growth laws (25, 38, 39). Three overall fractions of the expressed proteome, ribosomal proteins (${\mathrm{\Phi }}_r$), molecular chaperones (${\mathrm{\Phi }}_c$), and metabolic proteins (${\mathrm{\Phi }}_p$), each show a different type of growth-rate dependency (Fig. 3 A–C). The number of ribosomes in a cell directly determines how much biomass a cell can produce; therefore ${\mathrm{\Phi }}_r$ increases linearly with growth rate under all simulated conditions. Consistent with the empirical bacterial growth law, growth rate increases with better nutrient quality, representing a higher translational efficiency. In the Arrhenius temperature range, ${\mathrm{\Phi }}_c$ remains constant so that the allocation trade-off between ribosomal and metabolic proteins gives rise to the conjugate growth-related change between ${\mathrm{\Phi }}_r$ and ${\mathrm{\Phi }}_p$. In the stressed temperature range, growth is modulated by the partition among all three fractions. ${\mathrm{\Phi }}_c$ becomes linearly dependent on the growth rate with a negative slope, similar to the relationship between ${\mathrm{\Phi }}_r$ and growth rate under translational inhibition by antibiotics (25). The slope changes according to the nutrient quality, which likely modulates the overall folding efficiency of the chaperone. Between the two temperature ranges, nonlinearity arises within an “optimal plateau” (38), due to the suboptimal level of both folding and translational efficiency.

Fig. 3.

Growth law for the chaperone-regulated proteome. (A–C) The linear relationship between growth rate and mass fraction of the ribosomal proteins (${\mathrm{\Phi }}_r$), molecular chaperones (${\mathrm{\Phi }}_c$), and metabolic proteins (${\mathrm{\Phi }}_p$). Arrows indicate the direction of nutrient quality or temperature increase. Nutrient quality is ordered within each nutrient group by predicted growth rate at 37 °C (Fig. S3). (D) Schematic of the bacterial growth law and chaperone’s regulatory role in proteome allocation. ${\mathrm{\Phi }}_t$ denotes the total expressed proteome.

The chaperones’ regulatory role in growth-coupled proteome partition originates from the need to maintain a low cellular level of unfolded peptides at the lowest biosynthetic cost. Under stress, increasing translational efficiency leads to increased levels of unfolded peptides and native enzymes simultaneously, resulting in an inefficient regulation and significant waste of cellular resources (Fig. 3D). The evolutionary invention of chaperones resolves this dilemma by producing a balanced cellular process that increases the flux from a pool of unfolded peptides to native proteins while suppressing the production of both unfolded peptides and ribosomes.

Multiscale Predictions for the Cellular Adaptation Mechanisms.

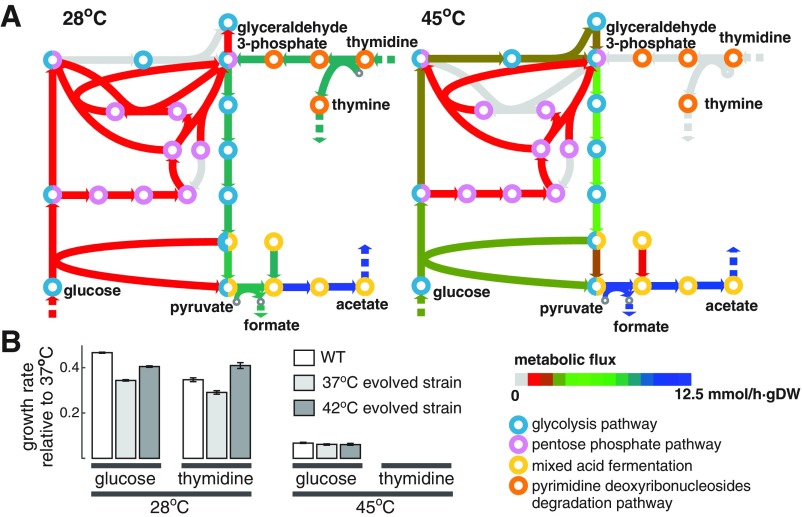
FoldME is a multiscale model that describes not only global regulation of proteome composition but also the statistical effects on in vivo folding at the level of metabolic pathways or upon perturbation of a single gene. At the pathway level, FoldME predicts that at high temperatures, DeoA, an enzyme involved in the pyrimidine degradation pathway, becomes unstable and extremely expensive to produce. The high cost of maintaining DeoA leads to a shift in sugar uptake from pyrimidine degradation to the glycolysis and pentose phosphate pathway (Fig. S4A). This prediction is confirmed by our experiment showing that E. coli cells grow on glucose, but not on thymidine at high temperatures (Fig. S4B). Additional support comes from a long-term evolution experiment of E. coli subjected to high temperature in LB medium, where the steady-state levels of enzymes involved in pyrimidine degradation including DeoA, DeoB, and DeoC are significantly down-regulated upon adaptation (36).

Fig. S4.

Metabolic flux shift upon temperature change. (A) At high temperature, glyceraldehyde 3-phosphate production switched from the pyrimidine deoxyribonucleoside degradation pathway to the glycolysis and pentose phosphate pathway. (B) Model prediction is observed in experiments. Growth measured for cells in minimal media supplemented with glucose or thymidine shows that E. coli could not use thymidine at high temperature.

To evaluate the effect of perturbation of a single gene, we used FoldME to compute the consequences of point mutations in the core metabolic enzyme dihydrofolate reductase (DHFR), which were shown to affect the cellular abundance of a large number of E. coli proteins (40). We reproduced the sharp decrease in growth rate within small variations of DHFR stability (Fig. 4A) and correctly predicted that DHFR mutants used GroEL/ES for folding (41). Upon destabilization of the DHFR protein, FoldME predicted the differential expression of a large number of proteins. Consistent with discoveries reported in Bershtein et al. (40), the overall SD of protein expression level increases as DHFR stability and organism fitness decrease (Fig. 4B).

Fig. 4.

Systems-level responses to DHFR mutations. (A) FoldME predicts sharp decrease in growth rate (circles) as the stability of DHFR decreases. Experimental values for four DHFR mutants (crosses) are taken from the literature (40, 52). (B) SD of the LRPA is anticorrelated with growth rate. (C) The average z scores for transcriptomic data (40) and model prediction are highly correlated (Pearson’s r = 0.84) for the shown COG categories (53). The width and height of each oval are proportional to the SD of z scores within the group. Gray scales with the number of proteins included in each category (darker color represents larger number).

For quantitative comparisons between experiments and FoldME predictions, we calculated z scores for genes expressed in both experiment and FoldME: $z=\frac{Y_i-<Y>}{{\sigma }^Y}$, where $Y_i$ is the logarithm of relative protein abundance (LRPA) with respect to the WT level for gene $i$. Average variations in expression for individual proteins correlated quantitatively between transcriptomic data and FoldME predictions for the majority of the clusters of orthologous group (COG) categories (Fig. 4C). Importantly, the biosynthetic resource is distributed to the three proteome partitions with the same growth-coupling relationships as shown in Fig. 3 (Fig. S5). Similar down-regulation of coenzyme biosynthetic pathways was observed for temperature elevation and destabilizing mutations (Fig. S6), indicating a consistent energy allocation strategy in chaperone-mediated adaptation to environmental and genetic perturbations.

Fig. S5.

Growth coupling of proteome partitions. (A–C) The coupling relationship between growth rate and (A) the mass fraction of ribosomal proteins (${\mathrm{\Phi }}_r$), (B) molecular chaperones (${\mathrm{\Phi }}_c$), and (C) metabolic enzymes (${\mathrm{\Phi }}_p$). Data from nutrient and temperature shift simulations (Fig. 3) are shown in gray for comparison. Experimental data are taken from three sources (25, 60, 61). The experimental data of RNA/protein ratio are first scaled by 0.46 into mass fraction of the ribosomal proteins (39) and then scaled again by 0.85 to account for the fact that 85% of the ribosomes are actively involved in biosynthesis. The slope of the linear fitting in A is 0.0865 and 0.0911 for experimental measurements and FoldME simulations, respectively.

Fig. S6.

Comparison of differential gene expression under temperature and genetic perturbations. LPAs are compared between six different conditions (labeled on the y axis) and that of the WT strain at 37 °C under minimal glucose medium. The six different conditions are (A) 30 °C; (B) 44 °C; (C) 46 °C; (D) mutation in DHFR with destabilizing effect equivalent to the V75H+I155A mutant; (E) mutation in DHFR with destabilizing effect equivalent to the V75H+I91L+I155A mutant; and (F) mutation in DHFR with destabilizing effect equivalent to the I91L+W133V mutant.

SI Materials and Methods

Additional Details for Protein Thermostability Prediction.

The Dill and Oobatake expressions for protein thermostability prediction are detailed below.

The Dill expression (21) is formulated based on abundant experimental evidence and theoretical studies that show thermal quantities like enthalpy $\mathrm{\Delta }H$, entropy $\mathrm{\Delta }S$, and $\mathrm{\Delta }{C}_p$ all mainly depend on the number of amino acids in the protein. Such linear dependencies are well fitted for the 59 mesophilic proteins by the expressions from ref. 21

$$\mathrm{\Delta }G(N,T)=\mathrm{\Delta }H(T_h,N)+\mathrm{\Delta }{C}_p(N)(T-T_h)-T\mathrm{\Delta }S(T_s,N)-T\mathrm{\Delta }{C}_p(N)ln(T/T_s)$$ [S1]

$$\begin{array}{c}\mathrm{\Delta }H(T=T_h,N)=(4.0N+143)kJ/mol\\ \mathrm{\Delta }S(T=T_s,N)=(13.27N+448)J/(mol\cdot K)\\ \mathrm{\Delta }{C}_p(N)=(0.048N+0.85)kJ/(mol\cdot K)\end{array},$$ [S2]

where the two reference temperatures are taken to be $T_h=373.5\hspace{0.17em}\text{K}$ and $T_s=385\hspace{0.17em}\text{K}$.

The Oobatake method (46) evaluates the unfolding free energy empirically against experimental values based on the assumptions that (i) thermodynamic data of each functional group are proportional to the solvent accessible surface area of the chemical group itself and (ii) the free energy of unfolding of a protein is the sum of contributions from all individual groups. After fitting the thermodynamic contributions from each type of amino acid using available structure information from the PDB database, the unfolding free energy of a protein can be predicted from the weighted sum of contributions from its amino acid sequence directly at the reference temperature (T₀ = 25 °C). For all other temperatures, $\mathrm{\Delta }G(T)=\mathrm{\Delta }H(T_0)+\mathrm{\Delta }{C}_p(T-T_0)-T\mathrm{\Delta }S(T_0)-T\mathrm{\Delta }{C}_{p}ln(T/T_0)$, assuming $\mathrm{\Delta }{C}_p$ is independent of temperature.

Additional Details for Model Reconstruction.

FoldME is reconstructed with three basic pathways: the spontaneous folding pathway, the DnaK-assisted folding pathway, and the GroEL/ES-mediated folding pathway. All three pathways are enabled for every eligible protein in the model, leading to a large increase in the number of reactions of the model. At the same time, this redundancy of the network offers great flexibility in proteome responses and robust growth of the cell under changing environments. The elementary reactions for each pathway are depicted in Fig. 1A, and additional details for the chaperone-assisted folding reactions are explained below.

The flux of the spontaneous folding pathway is, by definition, written as $V_{folding}=k_f(T){[U]}_{eq}$, where ${[U]}_{eq}$ is the equilibrium cellular abundance of the unfolded protein. Dilution of the unfolded peptide due to growth is defined by $V_{dilution}=\mu {[U]}_{eq}$, where $\mu$ is the growth rate. Because ${[U]}_{eq}$ depends on protein stability according to the Boltzmann law, $\frac{{[U]}_{eq}}{{[P]}_{total}}=\frac{K_{eq}(T)}{1+K_{eq}(T)}$, we capture the temperature-dependent change in the unfolded fraction for individual proteins using the coupling constraint

$$\frac{V_{dilution}}{V_{folding}}\ge \frac{\mu }{k_f(T)}+K_{eq}(T).$$ [S3]

DnaK-assisted folding has been studied extensively due to its variety in functions and central role in maintaining cellular proteostasis (18, 28). In E. coli, DnaK binds and releases the substrate peptide by switching between the low-affinity ATP-bound state and the high-affinity ADP-bound state, which is controlled by its cochaperone DnaJ and the nucleotide exchange factor GrpE. We denote the reaction cycle with three basic steps (Fig. 1A): (i) DnaJ-mediated substrate binding to DnaK ($V_{K1}$), (ii) DnaJ-stimulated ATP hydrolysis and conformational change from the ATP- to the ADP-bound state of the DnaK$\cdot$peptide complex ($V_{K2}$), and (iii) GrpE-induced nucleotide exchange and subsequent substrate release. The apparent reaction rates measured from real-time kinetics (29) are used to constrain $V_{K1}$ ($0.04\hspace{0.17em}{\text{s}}^{-1}$) and $V_{K2}$ ($1.0\hspace{0.17em}{\text{s}}^{-1}$), respectively.

The third step is then duplicated into two equivalent reactions, representing a successful folding event assisted by DnaK ($V_{K3}$) and an unfruitful DnaK-interaction cycle that releases the unfolded peptide ($V_{K3\prime }$). This pair of duplicated folding reactions is designed to reflect the fact that one single chaperone-binding cycle is usually not enough to fully repair the sick protein. For both HSP70 (31) and the chaperonin system (32), repeated cycles of complete release and rebinding of the peptide were shown to be required for the substrate to reach its active state. The idea of a pair of duplicated folding reactions has been applied previously to build a kinetic model of HSP70 (11). The model showed the HSP70 to fold firefly luciferase with a probability factor of 2.68% in any given cycle, i.e., an average of 38 cycles for successful refolding. The author suggested that this refolding probability should be a “characteristic parameter depending on the nature of the substrate, its sequence, fold, and energy landscape for folding” (ref. 11, p. 502). We try to capture this protein-specific characteristic with some intuitive assumptions: (i) For stable proteins, each chaperone-binding cycle can fix one aggregation-prone sequence on the unfolded peptide, so that the maximum number of chaperone-binding cycles to fold a peptide is equal to its agg; (ii) for unstable peptides, every agg cycle of the chaperone-binding cycle can fold the peptide with a probability equal to its native protein fraction at equilibrium $P_N=1/(1+K_{eq})$. Taken together, the total number of chaperone-binding cycles needed to fold an average protein is agg$\mathrm{\cdot }\mathrm{(}\mathrm{1}\mathrm{+}{K}_{e\mathit{}q}\mathrm{)}$, resulting in the following coupling constraints between the fluxes of this pair of reactions:

$$V_{K3}\cdot agg\cdot (1+K_{eq}(T))\le V_{K3\prime }.$$ [S4]

Considering that most of the proteins are marginally stable ($0<K_{eq}<1$) and their aggs vary between 0 and 28, the number of chaperone-binding cycles required should be comparable to that estimated for firefly luciferase in ref. 11 and for class I–III GroEL clients in ref. 33. Therefore, we consider that our formulation largely reflects the physiological amount of chaperones required in in vivo folding.

GroEL/ES-mediated folding is described with three basic steps (12): (i) binding of the unfolded peptide and ATPs and then the GroES to encapsulate the GroEL ring; (ii) ATP hydrolysis that induces further conformational changes and allows the peptide to fold within the cage; and (iii) release of the GroES, ADP molecules, and the peptide contained inside. Unlike the DnaK-assisted folding where substrate release is the rate-limiting step, ATP hydrolysis is measured to be one to three orders of magnitude slower than the other elementary reactions in the GroEL/ES-mediated folding cycle (30). We constrain the flux through the GroEL/ES-mediated folding reaction cycle, using the experimentally measured ATP hydrolysis rate of $0.12\hspace{0.17em}{\text{s}}^{-1}$. Similarly, the third step is duplicated to produce either the unfolded peptide or the native enzyme.

The closed GroEL/ES cavity provides an isolated hydrophobic environment with negatively charged surface that may change the protein’s energy landscape and thus increase the folding rate. Proteins with molecular weight $\le 60\text{kDa}$ can be fully encapsulated and are allowed to fold freely inside the cage until all seven ATPs are hydrolyzed and the GroES cap is released. This process should facilitate folding much more efficiently than the DnaK chaperone. However, without proper information to compare the two chaperone systems, we now use a single scaling factor ($propensity\text{\_}scaling$) to couple the duplicated reactions $V_{G3}$ and $V_{G3\prime }$:

$$V_{G3}\cdot agg\cdot propensity\text{\_}scaling\cdot (1+K_{eq}(T))\le V_{G3\prime }.$$ [S5]

$propensity\text{\_}scaling$ is set to 0.45 in FoldME, so that both the DnaK-assisted and the GroEL/ES-mediated folding processes consume the same amount of ATPs for each successful folding event. This parameter was varied from 0.1 to 1 in a series of simulations, giving no obvious change of the phenotypic prediction.

Comparison Between Model Prediction With and Without Molecular Chaperones.

The chaperone network maintains the cellular level of the total unfolded fraction of the proteome. Without chaperones in the model, the simulations show no growth of the cell. Therefore, we independently sample the kinetic folding rate and thermostability for each protein in the simulations. As a result, we observed an anticorrelation between the simulated growth rates and the total unfolded fraction of proteome (Fig. S1B). With chaperones functioning in the designed network, the total unfolded fraction is kept at a low level between 0.1% and 1% regardless of how growth rate changes with temperature.

Energy Consumption of the Chaperone-Assisted Folding Reactions.

The energy requirement of chaperone-assisted folding is explicitly accounted for in the form of ATP hydrolysis reactions (Fig. 1A). DnaK-assisted folding consumes one ATP molecule per cycle, and GroEL/ES-assisted folding consumes seven. The number of chaperone-binding cycles required to fold a protein is related to the thermodynamic properties of the protein in question. Hence, the energy cost of chaperone-assisted folding increases as the protein’s aggregation propensity increases and/or its stability decreases.

To get a rough idea of the overall energy cost of chaperone-assisted folding in a growing cell, we compared the total ATP consumption on DnaK- and GroEL/ES-assisted folding to the GTP consumption on translation (Fig. S1C). Considering that hydrolysis of GTP and ATP is approximately energetically equivalent, we estimate the chaperone-assisted folding to consume about 1.6% of the energy consumed by translation at the physiological temperature 37 °C. This number increases dramatically to $\sim$38% at 45 °C. We argue that energy cost of chaperone activity modulates cell growth in two aspects: (i) The relative energy cost between different chaperone systems adds another complication to partitioning of the proteome folding burden and (ii) the total energy involved in protein folding is a significant amount of cellular resource to be optimized for adaptation at high temperatures. However, we have not found a direct experimental measurement to validate this estimation.

Comparison of Differential Gene Expression Under Temperature and Genetic Perturbations.

At similar growth rates, unfolding stresses induced by genetic mutations and by a heat shock both exhibit biased expression toward the more abundant proteins, while heat shock causes larger overall variations. Many cofactor biosynthesis pathways that are identified as thermosensitive in Chang et al. (26) (e.g., flavin, heme) are consistently down-regulated. Nevertheless, the proteome allocation scheme to adopt for any particular condition can be hard to predict without such multilevel network simulation. For example, the proteome composition of the DHFR mutant shares some features with the cell evolved to grow at 30 °C where unfolding stress is low. Among many others, ion transporters and the glycine cleavage complex are down-regulated in both conditions; and the pyrimidine deoxyribonucleotide biosynthesis pathway is up-regulated in both conditions. In another example, similar groups of genes are down-regulated in response to unfolding stresses induced by high temperature (46 °C) and the destabilizing DHFR mutation (I91L+W133V). However, genes responsible for heme and tetrapyrrole biosynthesis are up-regulated at 46 °C, but down-regulated in the latter situation. The comparison presented here highlights the complexity of cellular response to the genetic and environmental unfolding stresses, indicating that a systems-level investigation is required for understanding the protein quality-control system and proteostasis network.

Effect of the Enzyme in Vivo Turnover Rate on Model Prediction.

The effective enzyme turnover ($k_{eff}$) rate is fundamental to our understanding of biological processes and cellular phenomena. The current version of the FoldME model inherited $k_{eff}$ from ref. 24, where we assume $k_{eff}$ to be proportional to the enzyme’s solvent-accessible surface area (SASA). The scaled $k_{eff}$ is centered on a median enzyme efficiency of 65 ${\text{s}}^{-1}$, consistent with findings reported in ref. 54. This is, of course, a first approximation to extend in vivo enzyme efficiency assignment on the genome scale. There are potentially two ways to improve $k_{eff}$ assignment in such a genome-scale model. First, ongoing studies suggest that in vitro and in vivo maximal catalytic rates generally concur (55), so that we could use experimentally measured rates whenever necessary and possible. In FoldME, we constrain the chaperone-assisted folding with real-time kinetics measurements, which differ from the SASA-scaled $k_{eff}$ by two to three orders of magnitude. After this correction, we were able to reproduce the correct physiological concentrations of the chaperones.

Second, sampling over the $k_{eff}$ space (56) is shown to improve model predictions by large-scale fitting to achieve known protein abundance distributions. Unfortunately, the lack of temperature-dependent proteomics data and the size of our model currently prevent efficient sampling over the large number of values. Furthermore, the in vivo $k_{eff}$ calculated from sampling simulations represent the result of certain regulation (supposedly including the folding regulation), without addressing the underlying mechanism of it. For these reasons, we stay with the first principle estimation of $k_{eff}$ as described above, yet we should be aware of the uncertainty involved in this choice. In Fig. S7A, we show a comparison between the mass fractions of all proteins predicted to express under M9 minimal medium supplemented with glucose at 37 °C. For about 70% of these proteins (within the red circle), the abundance correlates well with the experimental value. The abundance of the remaining 30% of proteins is dominantly underestimated due to overestimation of the corresponding $k_{eff}$. Considering that the chaperone client proteins are generally highly expressed (Fig. S7B), the error in protein abundance likely leads to an underestimation of the corresponding portion of chaperone requirement for folding.

Fig. S7.

Effect of the enzyme in vivo turnover rate on model prediction. (A) Comparison of protein abundance between model prediction and that calculated from in-house RNASeq experiments measured for an evolved E. coli strain adapted to using glucose as the only carbon source. For approximately 70% of the proteins (within the red circle), the predicted abundances correlate well with experimentally measured values. The abundances for the remaining proteins (within the blue circle) are underestimated due to overestimation of their enzyme catalytic rate. (B) Comparison of expression levels for four groups of proteins. Protein abundance is taken from the same RNASeq experiment shown in A. The number of proteins used in each group is indicated in parentheses.

Sensitivity Analysis of Kinetic Folding Rate.

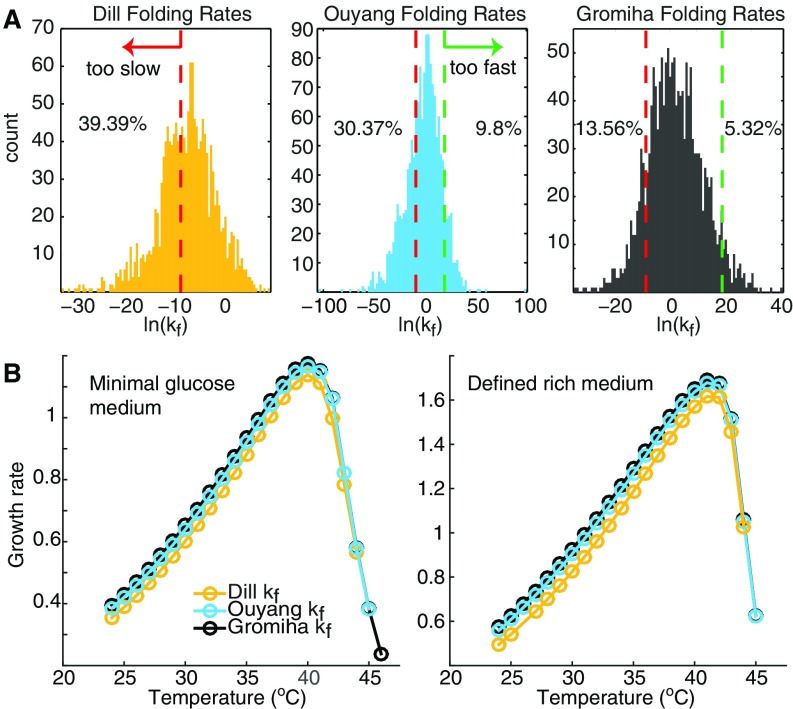
To ensure that the calculated kinetic folding rates are physiologically relevant on the proteome level, we compared the folding rate distribution estimated using the Gromiha method and two other algorithms, the Dill method (21) and the Ouyang method (58). The distributions of the kinetic folding rate calculated from these three methods are shown in Fig. S8A. The Gromiha method gives the highest average protein-folding rate ($\sim 7.7{\text{s}}^{-1}$), whereas the other two methods predict much lower mean values (Dill $\sim 0.000466{\text{s}}^{-1}$ and Ouyang $\sim 0.188{\text{s}}^{-1}$). We also consider two more criteria to judge the overall goodness of prediction: (i) No protein should fold faster than 4 ns (green dashed lines in Fig. S8A) as estimated by the Ouyang method and (ii) the majority of the proteome should fold within one cell cycle of the slow-growing E. coli (e.g., 1 h, red dashed lines in Fig. S8A). Accordingly, the Gromiha method predicts more than 80% of the proteome folds within the “normal” timescale.

Fig. S8.

Kinetic folding rate distributions and their effect on growth rate. (A) Distribution of the kinetic folding rate for all proteins in the model, predicted using the Dill method (yellow), the Ouyang method (cyan), and the Gromiha method (gray), respectively. (B) Predicted temperature-dependent growth rate follows the same trend using the three formulations for kinetic folding rate calculation, respectively. Absolute values of the growth rate differ only by a small amount despite the orders of magnitude difference in the predicted kinetic folding rate.

Then we simulated cell growth with $k_f$ calculated using the three methods, respectively. Growth rate over the temperature follows the same trend with each of three formulations (Fig. S8B). The absolute value of growth rate differs by only $\sim$5% between the Dill and Gromiha methods, whose average folding rates are five orders of magnitude apart. Hence, we conclude that kinetic folding rate prediction will not affect growth prediction significantly. We then made the choice to use the Gromiha method, which gives the most physiologically meaningful folding-rate distribution.

In Vivo vs. in Vitro Thermostability.

The relationship between protein thermostability and cell growth is extremely interwoven. On one hand, temperature response of the cell is dependent on the stability distribution of its proteome. On the other hand, protein stability is also strongly influenced by the complex cellular environment including and not limited to cotranslational folding, chaperone interactions, molecular crowding, and intermolecular interactions. The complexity involved herein raised a practical question regarding which thermodynamic parameter, the in vitro or in vivo protein stability, is the most appropriate for our modeling purpose.

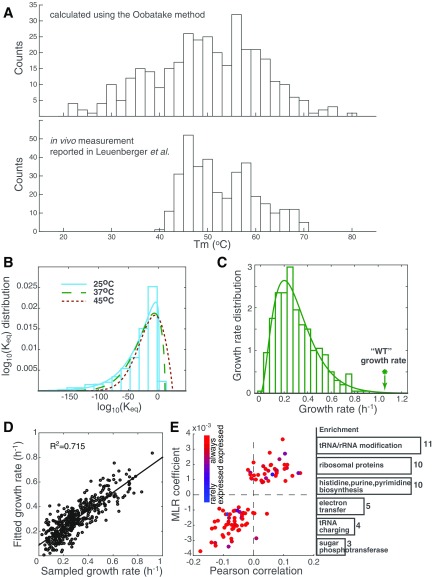
The in vitro folding parameters are empirically fitted from biochemical characterizations of protein thermodynamics at equilibrium in an ideal dilute solution. These quantities have been studied for a large number of proteins in detail and are easily accessible. Therefore, we built the FoldME model based on theoretical predictions of the in vitro protein thermostability. In vivo characterization of protein thermodynamics has been extremely difficult on the proteome level. Recently, Leuenberger et al. (57) developed a high-throughput structural proteomic strategy to measure protein thermostability on a proteome-wide scale, enabling a first comparison between in vitro and in vivo protein thermostability on the systems level. As discussed above, a one-to-one correlation between melting temperatures ($T_m$) from theoretical prediction and the in vivo thermostability assay is obscured by the differences in the experimental conditions to obtain these measurements. However, the distributions of $T_m$ (Fig. S9A) show a very similar two-peak feature (one around 46–48 °C and the other around 56–58 °C) for the 350 proteins whose thermostability is determined by the Oobatake method in FoldME. The average values of $T_m$ are also close, 50.0 °C and 53.1 °C for theoretical prediction and in vivo assay, respectively. The major discrepancy lies in the wider distribution of unstable proteins from theoretical predictions. This is likely due to the fact that in the cellular environment, factors such as crowding and chaperones will increase the effective stability of the less stable proteins, but have a smaller effect on proteins that are already stable in vitro.

Fig. S9.

Validation and sensitivity analysis of protein thermostability. (A) Distribution of the melting temperatures calculated using the Oobatake method (Top) and extracted from the in vivo thermostability assay from ref. 57 (Bottom). (B) Distribution of the logarithm of equilibrium folding constant ($K_{eq}$) for all modeled proteins, predicted using a combination of the Dill and Oobatake methods. The distribution is shown for 25 °C (cyan bar) and fitted to a generalized extreme value distribution for 25 °C (cyan), 37 °C (green), and 45 °C (red), respectively. (C) Distribution of the computed growth rate in 400 sampling simulations. (D) Result of a stepwise multiple linear regression of the sampling simulations shows that the stability fluctuations in 92 proteins could explain 71.5% of the variations in growth rate. (E) The 92 proteins that are identified as the major contributors to variations in cell growth are enriched in growth-coupled essential genes (red circles).

We further explain how the differences between in vitro and in vivo thermostability may affect FoldME model reconstruction, using the ribosomal proteins as an example. Ribosomal proteins are highly positively charged and unstable in solution unless bound to the rRNA. Consequently, one might expect them to require a chaperone for folding, at least before reaching the ribosome for assembly. Consistently, 32 of the 55 ribosomal proteins are observed to interact with DnaK in experiment (18). On the other hand, in a cellular environment, the ribosome is extremely stable as an intact complex once assembled. Hence it is also intuitive to see ribosomal proteins constantly appearing as the most stable proteins in the cell-wide thermostability assay. This example shows that theoretical prediction tends to overestimate the chaperone requirement by ignoring stabilization from protein complexes, while the in vivo assay underestimates it by ignoring various dynamic aspects during folding. Limited by our current understanding of in vivo protein folding and availability of quantitative experimental characterizations, the decision of choosing the in vitro or in vivo thermostability for modeling is blurred by the complexity of the cellular environment and may be evaluated only on a case-by-case basis for a small number of proteins.

Without loss of generality, we stick to using theoretical predictions based on in vitro protein thermodynamics to evaluate the function of chaperone-assisted folding in the cellular environment. We also list here a couple of practical limitations that prevent us from using the in vivo thermostability assay reported in Leuenberger et al. (57): (i) The assay could not cover the full proteome currently. For the E. coli cell, the assay is able to provide quantitative measurements for 2,416 peptides, mapped onto 729 unique proteins. Our model currently contains 1,554 protein-coding genes in total, among which only 485 have high-quality $T_m$ data from the experiment. (ii) Leuenberger et al. (57) reported only the $T_m$ and $T_{90\%}$ values. It is not clear whether the $\mathrm{\Delta }G(T)$ measurement is of equal high quality and can be extended to a larger temperature range. (iii) As discussed above, this in vivo thermostability assay is likely condition specific. Leuenberger et al. (57) has not provided information on whether or how much the thermo-profile of the proteome will change under different nutrient conditions. As experimental technique improves and our understanding of in vivo protein folding advances, additional descriptions of the thermodynamic parameters are expected to be incorporated to elaborate on model prediction.

Sampling Simulations and Sensitivity Analysis of Protein Thermostability.

Thermostability of the entire proteome was shown to affect cell growth significantly, especially at high temperatures. We investigated whether an (and which) individual protein’s stability may dominate phenotypic predictions by sampling the $K_{eq}$ value for each protein from the predicted (WT) distribution at 37 °C (Fig. S9B, green dashed line). The result of 400 such sampling simulations showed a broad distribution of growth rate centered on 0.305 h⁻¹, and none outcompeted the WT (Fig. S9C). As temperature increases, the distribution shifts to the right, showing that larger fractions of the proteome become unstable. None of the 100 samples drawn from the 45 °C distribution were calculated to be viable, although the stability distribution shift is moderate. Stability of individual proteins only weakly correlated with cellular growth, with a maximum absolute Pearson correlation lower than 0.2. We used stepwise multiple linear regressions (MLR) to narrow down 92 proteins whose stability fluctuations explain 71.5% of the variations in the simulated growth rate (Fig. S9D). With the chaperone network buffering a wide range of unfolding stresses, we no longer see single proteins or pathways limiting cell growth (26). Instead, the cell was able to survive under severe perturbations, unless a large number of proteins involved in growth-related essential functions such as RNA modification, ribosomal biogenesis, nucleotide biosynthesis, and tRNA charging failed to fold properly at the same time (Fig. S9E).

Simulated Growth Media.

The 21 nutrient conditions simulated using FoldME are listed below: 11 single-carbon source media [glucose, fumarate, hexanoate, L-serine, 2-(alpha-D-mannosyl)-D-glycerate, sn-glycero-3-phosphocholine, trehalose, xanthine, dAMP, IMP, UMP]; 5 phosphorus source media (3′-AMP, dCMP, dIMP, N-acetyl-D-glucosamine 1-phosphate, glycerophosphoserine); 3 nitrogen source media (nitrate, putrescine, UMP); and 2 defined rich media both with supplementation of 20 aa and one of them with additional nucleotide including adenine, guanine, thymine, uracil, cytosine, adenosine, guanosine, thymidine, uridine, cytidine, AMP, GMP, IMP, UMP, and CMP.

Bacterial Strains and Growth Media.

E. coli K-12 MG1655 (ATCC 700926) was grown in minimal M9 medium supplemented with four nutrient mixtures: (i) 0.2% (wt/vol) glucose; (ii) 0.2% (wt/vol) thymidine; (iii) 0.2% (wt/vol) glucose, with 50 mg/L of the 20 basic amino acids; and (iv) 0.2% glucose, plus the nutrient mixtures including 20 basic amino acids, adenine, guanine, cytosine, and thymine (50 mg/L each). Water bath circulation and heating were performed for selected temperatures from 25 °C to 45 °C. Two additional strains were used for comparison of cell growth using glucose or thymidine as a carbon source: strain 7 from a 37 °C adaptive laboratory evolution (ALE) experiment (59) and strain 8 from a 42 °C ALE experiment (5).

RT-PCR Measurements of Chaperone Expression Level.

Cells were grown in 250-mL flasks until reaching midlog phase (OD₆₀₀ = 0.5) and then transferred in triplicate into fresh media and harvested at 42 °C and 37 °C. Samples were RNA stabilized with the RNAProtect Bacterial Reagent, and total RNA was isolated with the RNeasy mini kit (Qiagen). cDNA was prepared from the total RNA, cleaned up with QIAquick PCR purification kits (Qiagen), and then quantified for subsequent RT-PCR assays. To determine the primer efficiencies, we generated a standard curve using different amounts of genomic DNA instead of cDNA with fixed primer concentrations.

Discussion

To obtain a comprehensive understanding of bacterial thermoadaptation that bridges the knowledge from the molecular to the systems level, we have reconstructed the E. coli protein-folding network. We used this reconstruction to formulate a computational model, FoldME, through integration with the genome-scale model of metabolism and protein expression. Even with uncertainties in model parameters for single proteins (SI Materials and Methods and Figs. S7–S9), FoldME simulations are capable of reproducing robust cell growth in conditions that vary in nutrient, temperature, and gene content. The results illustrate the complexity of protein folding in vivo, such that thermostability of a single protein has only very limited influence on cellular fitness (Fig. S9E). Instead, interwoven interactions between protein thermodynamics and chaperone regulation lead to multilevel strategies, ranging from gene to pathway to network that a cell uses to deal with unfolding stresses. Moreover, we highlight the systems-level regulatory role of the chaperone network that has been overlooked in previous studies. During bacterial thermoadaptation, the molecular chaperone takes a “service” function that mediates proteome allocation and cellular fitness in two interconnected ways. First, the chaperone pool is shared by the whole proteome; thus occupancy of a chaperone by one unfolded protein sets a constraint on the structural integrity of all other proteins. Second, the increased expression of chaperones under stress drains available resources from protein synthesis, setting a stringent translational constraint on the entire proteome.

Three critical factors contribute to FoldME’s ability to achieve a deep multiscale understanding of bacterial thermoadaptation. First, we incorporate a metabolically inactive unfolded state of protein to facilitate assessment of the proteome’s biophysical profile. This profile serves as an internal “sensor” to reflect the environmental and genetic perturbations. Second, we design a mathematical formulation for the chaperones to respond to the folding request of the proteome independent of its metabolic state. Third, instead of imposing the chaperone-assisted folding reactions only on the few experimentally validated substrates, we enable competition among the spontaneous, DnaK-assisted, and GroEL-mediated folding pathways, for all modeled proteins. As such, changes in the proteostatic state of the cell induced by environmental and genetic perturbations can be calculated based on first principles, evaluated by the protein quality-control machinery, and coupled to the whole cell’s economics. The approach adopted in this study opens up fundamental unique possibilities for genome-scale integration of environment-dependent protein properties, which enables proteome-wide study of cellular stress responses to environmental and genetic perturbations.

Materials and Methods

Kinetic Folding-Rate Calculation.

The kinetic folding rate $k_f$ is calculated using the Gromiha method, which is reported with a correlation of 0.97 between predicted and experimentally measured folding rates for a sample of 32 proteins (42). To calculate $k_f$ for each modeled protein, we first compute its secondary structures using the DSSP tool (43) in ProDy (44) and then submit the protein sequence along with the assigned secondary structure class to the FOLD-RATE web server (https://www.iitm.ac.in/bioinfo/fold-rate/). Finally, the predicted values are set as the reference folding rate at 37 °C and scaled according to the relationship $ln{k}_f\propto \mathrm{\hspace{0.17em}1}/T$ to cover the temperature range between 24 °C and 46 °C (45).

Thermostability Calculation.

Gibbs free energy of unfolding ($\mathrm{\Delta }G=G_{unfolded}-G_{folded}$) is predicted using a combination of the Dill expression (21) and the Oobatake method (46). The Dill expression is formulated based on the empirical correlation between protein length and thermostability. It generates a homogeneously stable proteome with melting temperatures varying in a small range, between 53.9 °C and 58.7 °C. The Oobatake method generates a more diverse thermostability profile, using information from protein sequence and structure. To maintain both heterogeneity and a low level (5%) of E. coli proteome being intrinsically disordered (47), we assign the unfolding free energy in two steps: (i) Calculate $\mathrm{\Delta }G(T)$ for $T\in [24\text{,}46]\hspace{0.17em}°\text{C}$ using the Oobatake method; and (ii) if $\mathrm{\Delta }G(T)<0$ for all calculated temperatures, recalculate $\mathrm{\Delta }G(T)$ using the Dill expression; otherwise, assign $\mathrm{\Delta }G(T)$ using the values calculated in step i. Folding constraints and chaperone requirements in FoldME are expressed in equilibrium constant ($K_{eq}={[U]}_{eq}/{[N]}_{eq}$) calculated using $\mathrm{\Delta }G(T)=-RTln(K_{eq}(T))$. More details for the calculation and sensitivity analysis of $k_f(T)$ and $\mathrm{\Delta }G(T)$ are discussed in SI Materials and Methods and Figs. S8 and S9.

agg Calculation.

agg is defined as the number of “aggregation-prone” segments on an unfolded protein sequence. These aggregation-prone regions have been extensively studied and shown to be highly correlated with chaperone selectivity (48). We choose a consensus method (49), which incorporates 11 popular algorithms that use different aspects of the sequence property to predict aggregation propensity of the E. coli proteome. Sequences of the modeled proteins are submitted to the web server (aias.biol.uoa.gr/AMYLPRED2/) for evaluation. To obtain the best balance between sensitivity and specificity, we follow the author’s guidelines to consider every five consecutive residues agreed among at least five methods contributing 1 to the agg.

Bacteria Strains and Growth Media.

E. coli strains, culture conditions, and characterizations of the media used in this study are described in SI Materials and Methods.