Visual perception as retrospective Bayesian decoding from high- to low-level features

Significance

The nature of perceptual decoding remains an open, fundamental question. Many studies assume that decoding follows the same low- to high-level hierarchy of encoding, yet this assumption was never rigorously tested. We performed such a test, which refutes the assumption to the extent that absolute and relative/ordinal orientations are features of different levels. Additionally, the backward aftereffect we discovered cannot be explained by the efficient-coding theories of adaptation. Finally, we proposed a new theory that explains our data as retrospective Bayesian decoding from high to low levels in working memory. This decoding hierarchy is justified by considering memory stability/distortion of high/low-level features. Thus, our work rejects the currently dominant decoding scheme and offers a framework that integrates perceptual decoding and working memory.

Abstract

When a stimulus is presented, its encoding is known to progress from low- to high-level features. How these features are decoded to produce perception is less clear, and most models assume that decoding follows the same low- to high-level hierarchy of encoding. There are also theories arguing for global precedence, reversed hierarchy, or bidirectional processing, but they are descriptive without quantitative comparison with human perception. Moreover, observers often inspect different parts of a scene sequentially to form overall perception, suggesting that perceptual decoding requires working memory, yet few models consider how working-memory properties may affect decoding hierarchy. We probed decoding hierarchy by comparing absolute judgments of single orientations and relative/ordinal judgments between two sequentially presented orientations. We found that lower-level, absolute judgments failed to account for higher-level, relative/ordinal judgments. However, when ordinal judgment was used to retrospectively decode memory representations of absolute orientations, striking aspects of absolute judgments, including the correlation and forward/backward aftereffects between two reported orientations in a trial, were explained. We propose that the brain prioritizes decoding of higher-level features because they are more behaviorally relevant, and more invariant and categorical, and thus easier to specify and maintain in noisy working memory, and that more reliable higher-level decoding constrains less reliable lower-level decoding.

Visual stimuli evoke neuronal responses (a process termed encoding), which lead to our perceptual estimation of the stimuli (decoding). Experimental studies have firmly established that encoding is hierarchical, progressing from lower-level representations of simpler and less invariant features to higher-level representations of more complex and invariant features along visual pathways (1). Researchers have also studied decoding by using models to relate neuronal responses to perceptual estimation. Most models posit, explicitly or implicitly, that decoding follows the same low- to high-level hierarchy, often in the form of what we call the absolute-to-relative assumption (2–6). For example, these models may decode V1 responses to a line into a perceived orientation of, say 51.2° (or a distribution around it). Psychophysically, this is termed an absolute judgment. To determine the relationship between two lines, the models first decode each orientation separately and the two resulting absolute orientations are then compared. For instance, the two absolute orientations may be subtracted to obtain the angle between the lines (relative orientation), or the sign of the difference may be used to determine whether the second line is clockwise or counterclockwise from the first (ordinal orientation discrimination). Absolute orientation of a single line is a simpler, less invariant, lower-level feature than relative/ordinal relationship between two lines, and physiological and computational evidence suggests that these features are encoded according to the standard low- to high-level hierarchy (Discussion). The absolute-to-relative assumption then implies that their decoding follows the same hierarchy.

The absolute-to-relative assumption is common to many decoding models including population average (7), maximum likelihood (3), and Bayesian (8) when they are applied to discrimination. The assumption is also used in signal detection theory’s definition of d′ (2) and thus the use of Fisher information to calculate d′ (3, 4). Models based on the idea of relating tuning-curve slopes to discrimination (6, 9, 10) are no exception: after the absolute distributions are determined by tuning curves and a noise model, they are compared to calculate ordinal discriminability.

Despite its widespread use in both theoretical studies and data analyses, the absolute-to-relative assumption was never rigorously tested. Typically, people choose model parameters to simulate observed ordinal discriminability without checking the relationship between absolute and relative/ordinal judgments (2–6). In particular, the assumption predicts that absolute-judgment distributions fully determine the corresponding relative-judgment distribution, yet no study measured distributions of both absolute and relative judgments to provide a strong test of the assumption. Indeed, comparing d′ values between one- and two-stimulus paradigms produced mixed results probably because such studies did not measure the required distributions to provide the strong test (2, 11). Moreover, d′ definition already uses the absolute-to-relative assumption so these studies are not designed to test the assumption.

Surprisingly, previous studies on absolute/relative judgments also cannot refute the absolute-to-relative assumption, which perhaps explains why the assumption is still widely used. For example, Westheimer (12) showed that the disparity threshold for detecting a line’s jump in depth was much greater when the line was alone than when it was flanked by other lines. Note that, even for the single line alone, there was a relative disparity between its prejump and postjump absolute disparities. He thus concluded (in modern terms) that relative disparity across time is much worse than relative disparity across space, and discussed that vergence might contribute to the difference. He did not test whether we judge relative disparity (across time or space) by comparing absolute disparities. Similarly, motion studies focused on position- vs. velocity-based mechanisms (13, 14), and vernier studies examined contributions of size, position, and orientation mechanisms (15, 16), without testing whether a relative judgment results from comparing corresponding absolute judgments. Like disparity, vernier acuity across time is also much worse than that across space (17, 18). In sum, although the brain is known to be sensitive to relationships, the sensitivity is not always good when the relationship is defined across time. More importantly, it is unclear whether absolute judgments are compared to reach relative judgments as assumed by most decoding models, or generally, whether decoding follows the same low- to high-level hierarchy of encoding.

Contrary to the standard hierarchy, there are also theories arguing for global-first perception or reversed hierarchy (19–21), or bidirectional processing (22, 23). However, these theories are descriptive without quantifying the relationship between feature decoding at different levels (19–21) or comparing with perception (22, 23). In fact, they usually do not distinguish between encoding and decoding. Additionally, interpretations of some relevant experiments have been discussed due to stimulus complexity (24–27).

We therefore measured distributions of both absolute- and relative-orientation judgments to test the absolute-to-relative assumption and the underlying low- to high-level decoding assumption. We used simple line stimuli to avoid interpretation complications. Our results not only unequivocally refuted the assumption but also lead to a different computational framework. The common low- to high-level decoding assumption is perhaps based on the implicit notion that encoding and decoding occur in the same sensory neurons and at the same time. However, under natural viewing conditions, our small fovea and frequent saccades introduce delays between the encoding of different parts of a scene and the perceptual integration of the whole scene. Similarly, in many psychophysical experiments (including ours), there are delays between stimuli, and/or between the disappearance of the last stimulus and the report. We therefore propose that, while encoding occurs in sensory neurons at the time of stimulus presentation, decoding often happens later in working memory. Once relevant features are encoded and enter working memory, their decoding could, in principle, follow any order. To understand decoding hierarchy, then, one must consider working-memory properties of stimulus features. Importantly, we propose that when the memory stability (or distortion) and behavioral relevance (or irrelevance) of more categorical, higher-level (or more continuous, lower-level) features are considered, then decoding should start with high-level features which then constrain the decoding of lower-level features. We show that this framework explains our psychophysical data, including the new phenomena of backward aftereffect and interreport correlation, whereas the common low- to high-level decoding assumption or standard adaptation theories cannot. Our model is formally similar to Stocker and Simoncelli’s model (28) for Jazayeri and Movshon’s (29) experiment, but we focus on the logical consequence of integrating working memory and perceptual decoding while they do not (Discussion).

Results

Perceptual Decoding Does Not Follow the Standard Low- to High-Level Hierarchy of Encoding.

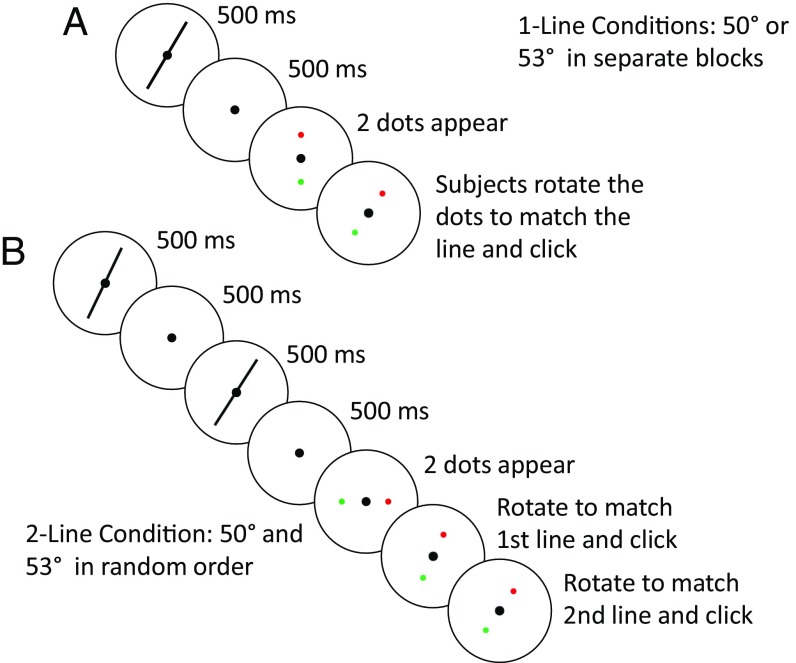
To probe decoding hierarchy, we designed a stimulus protocol involving either one or two lines in a trial (1-line and 2-line conditions, respectively; Fig. 1). When a single line is flashed on the screen, subjects only perceive low-level features such as its orientation. When two lines are presented sequentially, in addition to the orientation of each line, subjects also perceive higher-level features such as relationships between the lines. We compared and modeled the reported line orientations in these two conditions.

Fig. 1.

The 1-line and 2-line test conditions. (A) Trial sequence of the 1-line test conditions. The 50° and 53° lines were run in separate blocks. (B) Trial sequence of the 2-line test condition. The 50° and 53° lines were presented in each trial in counterbalanced, pseudorandomized order. For each condition, the marker dots appeared randomly at either horizontal or vertical initial positions, and subjects rotated them and clicked to report orientation(s). See Methods for details and the actual stimulus parameters.

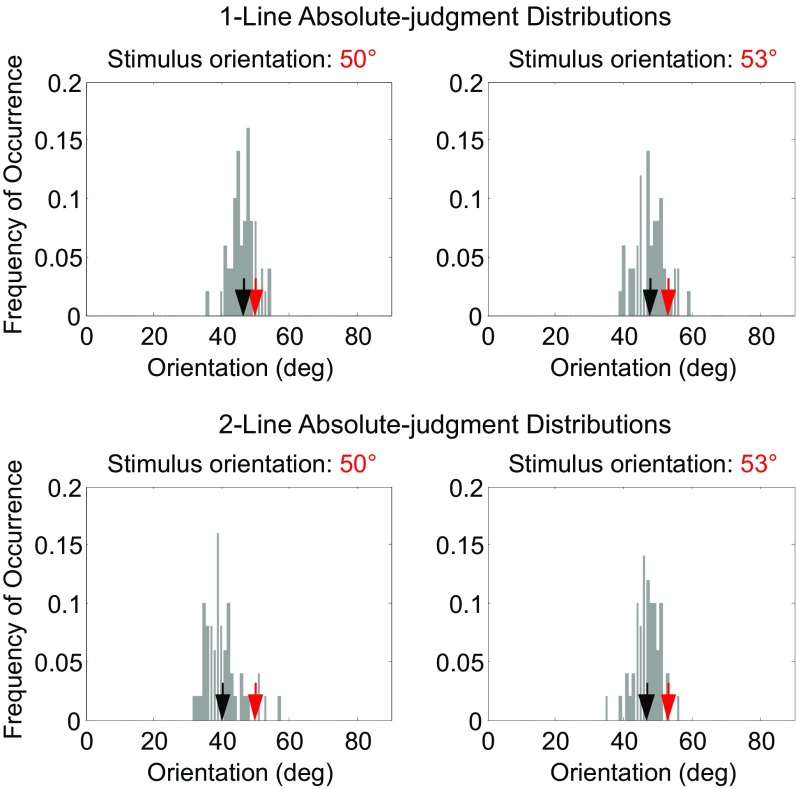
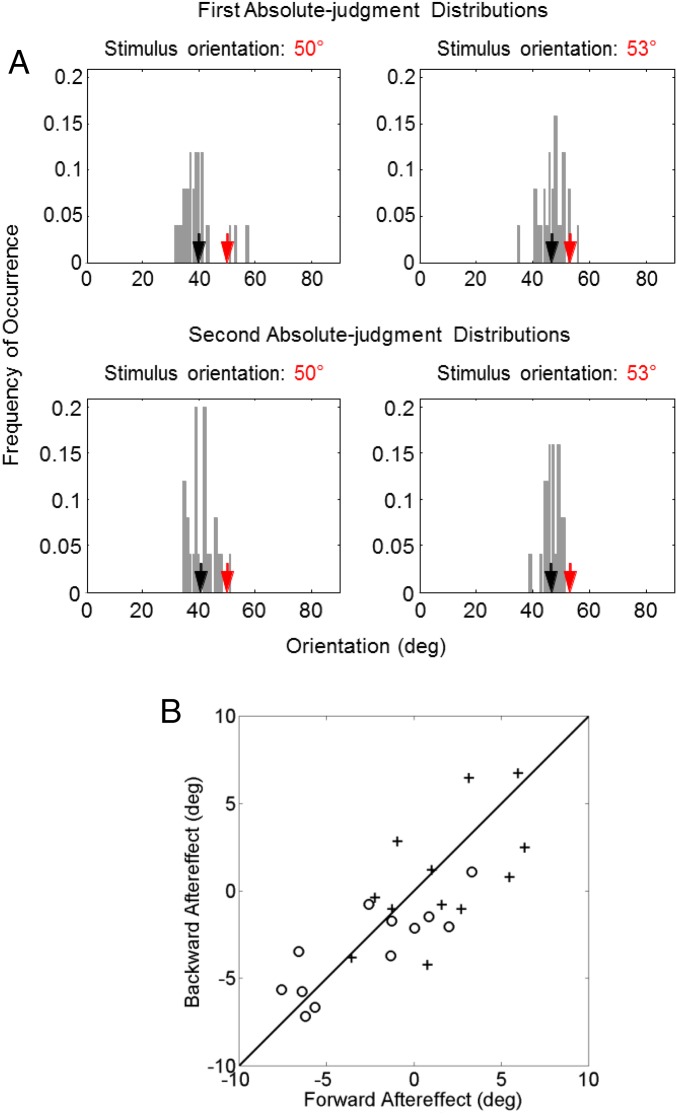
We employed two 1-line conditions in which a single line of either 50° or 53° orientation was shown for 500 ms. Following a 500-ms delay, subjects reported the line orientation by rotating two marker dots (Methods). A subject’s reported orientations over 50 repeated trials produced an absolute-judgment distribution for either the 50° or 53° stimulus. These 1-line absolute distributions for one naïve subject are shown in Fig. 2, Top. Prominent features of the distributions are large spreads and biases away from the true orientations which cannot be explained by motor variability (SI Appendix). We therefore conclude that the decoding of absolute orientations is unreliable, likely due to noise accumulation in working-memory representations during the delay between stimulus presentation and report (30, 31).

Fig. 2.

A naive subject’s absolute-judgment distributions from the 1-line test conditions (Top row) and 2-line test condition (Bottom row). The distributions for the 50° and 53° stimuli are shown on the Left and Right, respectively. In each panel, the red and black arrows indicate the actual stimulus orientation and the mean of the distribution (i.e., the mean of the subject’s reported orientations), respectively. See SI Appendix, Fig. S1, for comparisons of variances and biases between all 12 subjects’ 1-line and 2-line absolute distributions. deg, degrees.

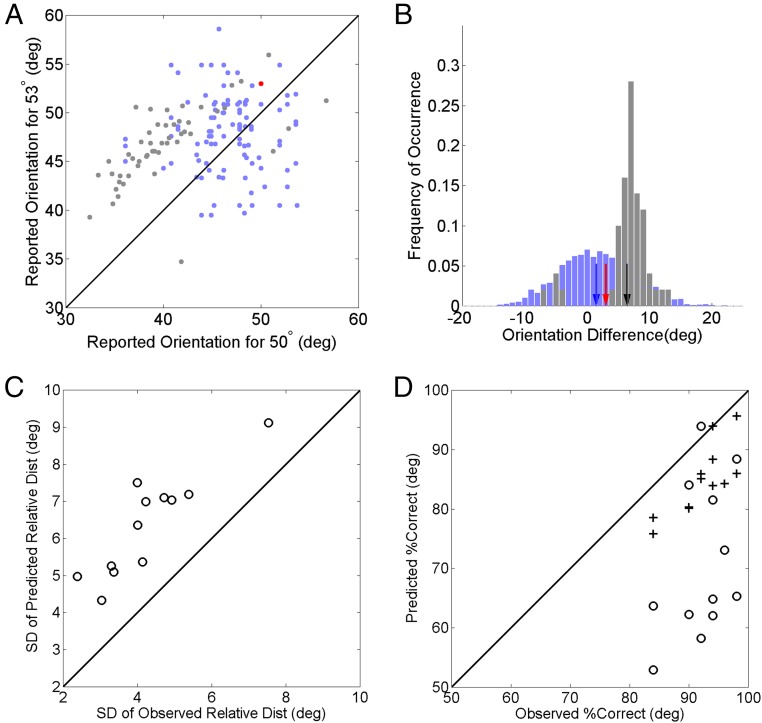
In the 2-line condition, the 50° and 53° lines were shown sequentially in counterbalanced, pseudorandomized order, with a 500-ms interstimulus interval to eliminate apparent motion (32). After a 500-ms delay, subjects rotated the marker dots to report the two orientations in the perceived order. We first analyzed the two orientations separately (as the absolute-to-relative assumption suggests) by compiling the histogram of the reports for each orientation. The resulting 2-line absolute distributions are shown in Fig. 2, Bottom, for the same subject. These distributions are even less reliable compared with those from the 1-line conditions (Fig. 2, Top), with greater variances and biases (see SI Appendix, text and Fig. S1, for details). This is not surprising given that more time elapsed between presentations and reports in the 2-line condition. We then examined the relationship between the two reports in a trial by plotting the subject’s report for the 53° line against that for the 50° line. This joint distribution (Fig. 3A, gray dots) reveals a striking pattern not predicted by either the 1-line or 2-line absolute distributions. The gray dots form an elongation demonstrating that the reports for the 50° and 53° lines in a 2-line trial were correlated (interreport correlation; Pearson correlation coefficient = 0.63, P = 9.3 × 10⁻⁷). Most dots are clustered above the positive diagonal line, indicating that in most trials the subject correctly discriminated the ordinal relationship between the lines. Moreover, the trials with correct and incorrect ordinal discrimination (gray dots above and below the diagonal) are separated from the diagonal by a gap, which can also be seen in the relative-orientation distribution (Fig. 3B, gray histogram) obtained by subtracting the 50°-line report from the 53°-line report (equivalent to projecting gray dots of Fig. 3A to the negative diagonal axis).

Fig. 3.

Observations from the 2-line condition and the corresponding predictions by the absolute-to-relative assumption. (A) A naive subject’s joint distribution with the reported orientation for the 53° stimulus plotted against that for the 50° stimulus in each trial of the 2-line condition (gray dots). Predictions from the subject’s 1-line absolute distributions are shown for comparison (light blue dots). The trials with correct and incorrect ordinal discrimination of the stimulus orientations are above and below the diagonal line, respectively. The red dot indicates the actual orientations. (B) The subject’s reported relative-judgment distribution (gray histogram) and that predicted from the 1-line absolute distributions (light blue histogram). They were obtained by projecting the dots in A along the negative diagonal. The red, black, and blue arrows indicate the actual orientation difference (3°), the mean of the reported orientation difference, and the mean predicted by the 1-line absolute distribution, respectively. SI Appendix, Fig. S2, shows the individual plots for the other 11 subjects. Note that 10,000 simulated samples were used to define the simulated relative distributions well but only 100 of them were randomly selected for the scatter plot of the simulated joint distribution to avoid clutter. (C) Relative-distribution SD predicted by the absolute-to-relative assumption vs. the observation for all 12 subjects. (D) Percentage of correct ordinal discrimination predicted with the 1-line (open dots) and 2-line (crosses) absolute distributions plotted against the observation for all 12 subjects. (Two of the 12 crosses happened to superimpose.) deg, degrees.

None of these observations is predicted by the absolute-to-relative assumption with either the 1-line or 2-line absolute distributions. To avoid clutter, only predictions from the 1-line absolute distributions are shown (Fig. 3A, light blue dots for the predicted joint distribution; Fig. 3B, light blue histogram for the predicted relative distribution); they were simulated by repeatedly drawing two numbers, one from the 50° absolute distribution and the other from the 53° absolute distribution, and subtracting them. The predicted distributions, by definition, cannot have the interreport correlation or the gap between trials with correct and incorrect ordinal discrimination; they also have much larger percentages of trials with incorrect ordinal discrimination compared with the observation (Fig. 3D).

All 12 subjects showed very similar results (SI Appendix, Fig. S2). In particular, every subject showed a significant trial-by-trial interreport correlation (mean Pearson correlation coefficient, 0.56 ± 0.04; all values of P < 0.025) that cannot be explained by the absolute-to-relative assumption. To quantify this difference further, note that the absolute-to-relative assumption predicts that, in the 2-line condition, the variance of the relative distribution should equal the summed variances of the two corresponding absolute distributions. Fig. 3C shows the predicted against the observed SDs for the 12 subjects, demonstrating that, contrary to the prediction, the former is significantly larger than the latter (two-tailed Wilcoxon signed rank test, P = 4.9 × 10⁻⁴).

A common measure of relative judgment is the percentage of trials with correct ordinal discrimination. This is simply the percentage of the points above the diagonal in the joint distribution (Fig. 3A) or to the right of zero in the relative distribution (Fig. 3B). Fig. 3D shows that, across the subjects, the observed percent correct discrimination is significantly better than those predicted by the absolute-to-relative assumption with either the 1-line absolute distributions (open dots; two-tailed Wilcoxon signed rank test, P = 9.8 × 10⁻⁴) or the 2-line absolute distributions (crosses; P = 4.9 × 10⁻⁴). Interestingly, although the 2-line absolute distributions have larger variances and biases than do the 1-line absolute distributions (SI Appendix, text and Fig. S1), the former produced better ordinal discrimination than the latter (Fig. 3D), mainly because of the exaggerated orientation difference (Fig. 4B). This further contradicts the absolute-to-relative assumption, which predicts that good ordinal discriminability requires small variance of corresponding absolute distributions (2, 3).

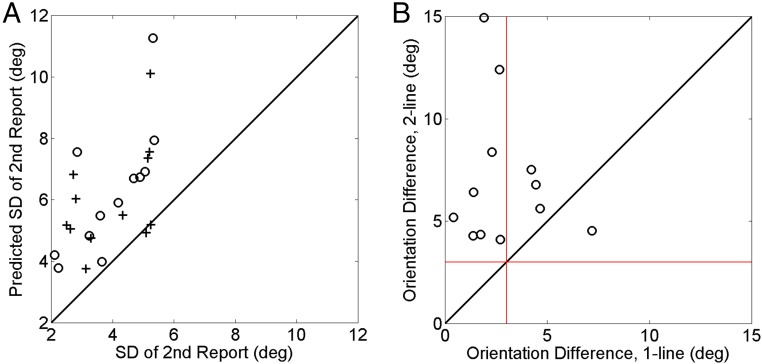
Fig. 4.

Second-report variability and orientation difference in the 2-line condition. (A) Second-report SD predicted by a sequential theory vs. the observation. The open dots and crosses are results for the 50° and 53° stimulus orientations, respectively. (B) The perceived orientation difference in the 2-line condition vs. that in the 1-line conditions for each subject. The red lines indicate the actual orientation difference of 3° between the 50° and 53° stimulus orientations. The orientation difference was exaggerated in the 2-line condition, but not in the 1-line conditions. deg, degrees.

We conclude that our data clearly refute the widely used absolute-to-relative assumption and the broader low- to high-level decoding assumption (2–6).

Perceptual Decoding Cannot Be Explained by a Sequential Mechanism or by Conventional Adaptation.

The interreport correlation above indicates that, in the 2-line condition, the two lines in a trial are not decoded independently. One might argue that a sequential mechanism could explain the correlation. Specifically, subjects might decode the absolute orientation of the first line and then decode the second line relative to the first. If the first, absolute decoding is more variable than the second, relative decoding (an assumption that already contradicts the common absolute-to-relative assumption), then the observed interreport correlation could occur. This sequential theory predicts that the second-line variance should equal the summed variances of the first line and the angular difference. Fig. 4A plots the predicted SD against the actual SD of the second line, demonstrating that the former is significantly larger than the latter (two-tailed Wilcoxon signed rank test, P = 4.9 × 10⁻⁴) and rejecting the theory. The theory also cannot explain the gap between the correct and incorrect discrimination trials in Fig. 3 A and B.

Additionally, the sequential theory cannot readily explain the exaggerated angular difference between the lines in the 2-line condition. Fig. 4B plots the reported angular difference for the 2-line condition against that for the 1-line condition; the former (mean, 7.0° ± 1.0°) is significantly larger than the actual 3° (two-tailed Wilcoxon signed rank test, P = 4.9 × 10⁻⁴), whereas the latter (mean, 2.7° ± 0.6°) is not (P = 0.47). We show below some additional properties of the data (see Figs. 5 and 7) that cannot be explained by the sequential theory.

Fig. 5.

Forward/backward aftereffects between two lines in a trial. (A) The same naive subject’s first and second absolute-judgment distributions from the 2-line test condition. (They are obtained by splitting each of the distributions in the Bottom of Fig. 2; see Perceptual Decoding Cannot Be Explained by a Sequential Mechanism or by Conventional Adaptation.) The top and bottom rows represent the first and second absolute-judgment distributions, respectively; the left and right columns are for the 50° and 53° stimulus orientations, respectively. In each panel, the red and black arrows indicate the stimulus orientation and the mean of the distribution (i.e., the mean of the subject’s reported orientations), respectively. (B) The backward aftereffect plotted against the forward aftereffect for each of the 12 subjects. The open dots and crosses are results for the 50° and 53° stimulus orientations, respectively. Open dots in the third quadrant and crosses in the first quadrant indicate repulsive aftereffects. The figure show that large aftereffects were repulsive, but small ones were a mixture of repulsion and attraction. deg, degrees.

Fig. 7.

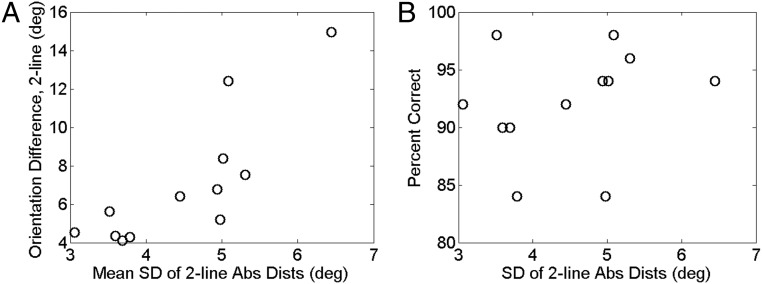
Test of two predictions of the retrospective Bayesian decoding theory. (A) Reported orientation difference as a function of the mean SD of the absolute distributions in the 2-line condition for all 12 subjects. (B) Percentage of correct ordinal discrimination as a function of the mean SD of the absolute distributions in the 2-line condition for all 12 subjects. As predicted, the reported orientation difference increased with the SD, whereas the ordinal discrimination performance did not decrease with the SD. deg, degrees.

Finally, the exaggerated orientation difference in the 2-line condition could simply be repulsive tilt aftereffect of orientation adaptation. First note that the tilt aftereffect cannot explain the interreport correlation. Indeed, different aftereffect magnitudes across trials should produce an elongation parallel to the negative diagonal, instead of the observed elongation parallel to the positive diagonal, in the joint distribution (Fig. 3A). We show further data analysis below that cannot be accounted for by conventional adaptation and its theories.

In conventional adaptation paradigm, two orientations are presented sequentially in a trial and subjects only report the second orientation (test) but not the first (adaptor) (33, 34). It studies how the first line affects the perception of the second one, which we will call forward aftereffect. Our 2-line condition was different in that the subjects reported the orientations of both lines in a trial, affording an opportunity to investigate both forward aftereffect and backward aftereffect (how the second line affected the perception of the first one at the time of report). To this end, we split each 2-line absolute distribution into two according to whether a given orientation appeared first or second in a trial, resulting in four absolute distributions referred to as 50°-first, 50°-second, 53°-first, and 53°-second distributions (four panels of Fig. 5A). By comparing the mean of, for example, the 50°-first distribution (black arrow in the Fig. 5A, Top Left) with the mean of the baseline, 1-line 50° distribution (the black arrow in the Fig. 2, Top Left), we obtained the backward aftereffect on the 50° stimulus; it indicates how the 53° stimulus that appeared second affected the report of the 50° stimulus that appeared first. Fig. 5B shows the backward aftereffects against the forward aftereffects for each subject. The open dots and crosses are for the 50° and 53° lines, respectively. The backward and forward aftereffects are similar for a subject and significantly correlated across subjects (Pearson correlation coefficient, 0.78; P = 6.3 × 10⁻⁶), suggesting mutual influence between the two lines in working memory. Such bidirectional, temporal interactions are not considered or explained by standard adaptation theories, which interpret adaptation as a consequence of using past stimulus statistics to efficiently transmit future stimuli and therefore predict only forward aftereffect (35–39). Similarly, sequential physiological mechanisms, such as previous response history affecting current responses, cannot explain the backward aftereffect.

One might argue that, in the 2-line condition, the second line in a trial could adapt the first line in the next trial so that the backward aftereffect could actually be the cross-trial forward aftereffect. However, the average time from the offset of the second line in a trial to the onset of the first line in the next trial was 6.03 s (including a 2-s intertrial interval), much longer than the 0.5-s interstimulus interval between the two lines within a trial. Given the exponential decay of the tilt aftereffect (40, 41), the cross-trial adaptation should be negligible compared with the within-trial adaptation. However, the observed backward aftereffect was as large as the forward aftereffect, ruling out the cross-trial interpretation.

Perception as Retrospective Bayesian Decoding in Working Memory from High to Low Levels.

To elucidate functional significance of feature interactions in working memory revealed by the backward and forward aftereffects and the exaggerated angular difference, we first consider how lines’ absolute orientations and their ordinal relationship are stored in working memory during the delay between stimulus disappearance and report. Absolute orientation of a line has a continuous value requiring a continuous attractor to represent it in neuronal working memory (42). Such representations are unstable in the presence of noise and become distorted with time (30, 31), contributing to the biases and variances in the observed absolute distributions (Fig. 2 and SI Appendix, Fig. S1). In contrast, ordinal relationship between two lines is categorical requiring only 1 bit of information to specify, and can be reliably maintained in point attractors which are resistant to noise (43). We therefore hypothesize that once all relevant features are represented in working memory, at the report time, the brain first decodes the reliable ordinal relationship and then uses this information to retrospectively constrain and improve the decoding of the distorted absolute-orientation representations in working memory.

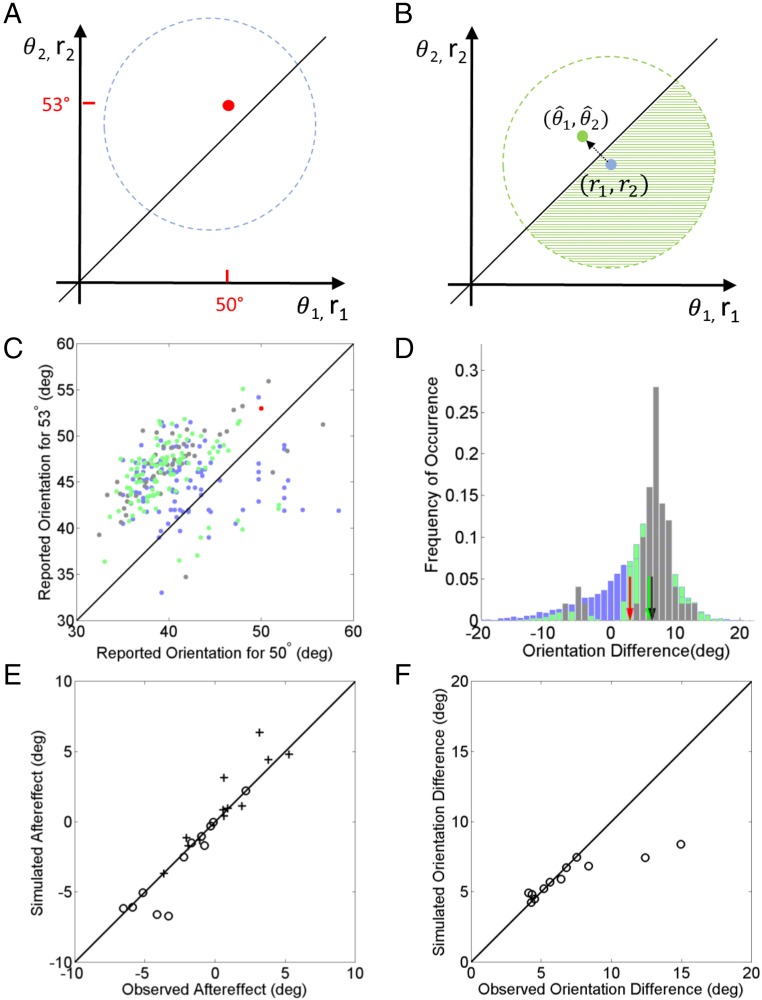
Specifically, consider trials in which lines with orientations $\theta \equiv \left({\theta }_1,{\theta }_2\right)=\left(50°,53°\right)$ are flashed successively (red dot in Fig. 6A), evoking brief visual responses along the standard encoding hierarchy (44, 45). Because these orientations and their relationship are task relevant, they are represented in visual working memory after the stimuli’s disappearances. By the time of reporting, the memory representations $r\equiv \left(r_1,\hspace{0.5em}{r}_2\right)$ of the lines’ absolute orientations have distorted forming a distribution $P\left(r|\theta \right)$ across trials (blue circle in Fig. 6A). If the brain were to use these noisy representations to decode the lines’ absolute orientations, the ordinal relationship between the lines would be wrong on a considerable portion of trials (area of the blue circle below the diagonal). Instead, we hypothesize that, at the report time, the ordinal relationship is still stably maintained in working memory. Since it was encoded as soon as the second line was flashed, before further noise accumulation in the lines’ absolute representations, the stored ordinal relationship is more likely to be correct than the absolute-to-relative assumption’s prediction at the report time. The brain should first decode this ordinal relationship and use it to constrain the decoding of the distorted memory representations of the continuous absolute orientations. Consider a trial with a particular realization of memory representations ($r_1,r_2$) of the absolute orientations shown as a blue dot in Fig. 6B. In the following, we assume that they are drawn from Gaussian distribution around the stimulus orientations:

$$P\left(r|\theta \right)=\frac{1}{2\pi \sqrt{{\sigma }_1{\sigma }_2}}{e}^{-\frac{{\left(r_1-{\theta }_1\right)}^2}{{2{\sigma }_1}^2}-\frac{{\left(r_2-{\theta }_2\right)}^2}{{2{\sigma }_2}^2}},$$

where σ₁ and σ₂ are the SDs for the first and second orientations, respectively. We ignored the biases here as they can be readily included by shifting $\left({\theta }_1,{\theta }_2\right)$. Viewed as a function of $\left({\theta }_1,{\theta }_2\right)$, this expression becomes a likelihood function of the stimulus orientations given current memory representations and is illustrated with a green circle in Fig. 6B. Absent any other information, the estimated orientations would be computed as the means of the likelihood function, that is, they would coincide with memory representations ($r_1,r_2$). If, however, the decoded ordinal relationship happens to be ${\theta }_1<{\theta }_2$, then it constrains the absolution orientations to be above the diagonal line in the joint space of Fig. 6B, effectively imposing a prior distribution that is a step function along the diagonal line. This prior distribution then eliminates the part of the likelihood distribution below the diagonal (shaded area in Fig. 6B), giving rise to a posterior distribution of orientations that is entirely above the diagonal, that is, compatible with the ordinal relationship. The reported orientations will then be computed as the means of the posterior distribution, illustrated with the green dot $\left({\widehat{\theta }}_1,{\widehat{\theta }}_2\right)$ in Fig. 6B. Regardless of the ordinal relationship between r₁ and r₂, that between ${\widehat{\theta }}_1$ and ${\widehat{\theta }}_2$ agrees with the decoded ordinal relationship. For the Gaussian $P\left(r|\theta \right)$ above, $\left({\widehat{\theta }}_1,{\widehat{\theta }}_2\right)$ can be derived analytically as follows:

$${\widehat{\theta }}_1=r_1-\sqrt{\frac{2}{\pi }}\frac{{{\sigma }_1}^2}{\sqrt{{{\sigma }_1}^2+{{\sigma }_2}^2}}{e}^{-\frac{{\left(\mathrm{\Delta }r\right)}^2}{2\left({{\sigma }_1}^2+{\sigma }_2^2\right)}}\frac{1}{\mathrm{erfc}\left(\frac{\mathrm{\Delta }r}{\sqrt{2\left({\sigma }_1^2+{\sigma }_2^2\right)}}\right)},$$ [1]

$${\widehat{\theta }}_2=r_2+\sqrt{\frac{2}{\pi }}\frac{{\sigma }_2^2}{\sqrt{{\sigma }_1^2+{\sigma }_2^2}}{e}^{-\frac{{\left(\mathrm{\Delta }r\right)}^2}{2\left({\sigma }_1^2+{\sigma }_2^2\right)}}\frac{1}{\mathrm{erfc}\left(\frac{\mathrm{\Delta }r}{\sqrt{2\left({\sigma }_1^2+{\sigma }_2^2\right)}}\right)},$$ [2]

where $\mathrm{\Delta }r=r_1-r_2$ and erfc is the complementary error function (see Methods for details). We note that, in standard Bayesian models, priors are based on previous experiences such as image statistics. In contrast, our model derives the prior from the ordinal relationship, which is decoded before the absolute orientations in working memory (but encoded after the absolute orientations in sensory neurons).

Fig. 6.

Perception as retrospective Bayesian decoding in working memory. (A and B) Schematic illustration of the theory. The x and y axes represent the first and second orientations, respectively. θ’s and r’s stand for stimulus orientations and their working-memory representations, respectively. The red dot indicates the actual orientations in a trial of the 2-line condition. The blue circle in A and the blue dot in B indicate the distribution of the two lines’ memory representations and a specific sample from it, respectively, at the report times in the 2-line condition. The area of the blue circle in A under the diagonal is the portion of incorrect ordinal discrimination based on the memory representations. For the blue-dot sample in B, the green circle indicates its likelihood function, and the Bayesian prior of ordinal relationship eliminates the shaded green portion, shifting the means of the posterior distribution to the green dot. (C) Simulated joint distribution for the subject of Fig. 3A, with the estimate for the 53° line against that for the 50° line in the 2-line condition (light green dots). The actual data are shown as gray dots (same as the gray dots in Fig. 3A). The light blue dots indicate simulated samples of memory representations (see Perception as Retrospective Bayesian Decoding in Working Memory from High to Low Levels). (D) Relative distributions obtained from the joint distributions in C by projecting them along the negative diagonal line. The gray, light blue, and light green histograms represent the relative distributions from the observation, the memory representation, and the retrospective Bayesian decoding, respectively. The black, blue, and green arrows indicate the mean of these relative distributions. The blue arrow is at the 3° and occluded by the red arrow, whereas the green arrow exaggerates the angular difference similar to the observation (black arrow). Note that 10,000 simulated samples were used to define each simulated relative distribution well, but only 100 of them were randomly selected for the corresponding scatter plot of the simulated joint distribution to avoid clutter. (E) The aftereffects predicted by the retrospective Bayesian decoding against the observations across subjects. The open dots and crosses are results for the 50° and 53° stimulus orientations, respectively. (F) The angular differences predicted by the retrospective Bayesian decoding against the observations across subjects. The simulations underestimated the angular difference for 2 of the total 12 subjects; this discrepancy can be eliminated by introducing a free parameter (see Perception as Retrospective Bayesian Decoding in Working Memory from High to Low Levels). deg, degrees.

We applied this retrospective Bayesian theory, which uses the higher-level ordinal-orientation decoding to constrain the lower-level absolute-orientation decoding, to explain our 2-line data. Since the Bayesian prior mostly changes the joint distribution without affecting the absolute (marginal) distributions much (Fig. 6B), we used each subject’s 2-line absolute distributions to produce samples $\left(r_1,\hspace{0.5em}{r}_2\right)$ and the SDs of these distributions as the σ’s in Eqs. 1 and 2 to decode $\left({\widehat{\theta }}_1,{\widehat{\theta }}_2\right)$. We shifted each subject’s two absolute distributions by opposite amounts to make their mean angular difference equal 3°, and hence the exaggeration of the simulated angular difference is strictly the consequence of our decoding scheme. (Without the shifting, the simulations matched the data even better.) For each subject, we used his/her actual ordinal discrimination performance (x axis of Fig. 3D) to determine the fraction of trials with correct and incorrect ordinal relationship. The simulations had no other free parameters.

Fig. 6 C and D show the decoded joint distribution (green dots) and relative distribution (green histogram), respectively, for the naive subject of Fig. 3. They were similar to the observed joint distribution (gray dots) and relative distributions (gray histogram), respectively. (The joint and relative distributions of the memory samples were shown as light blue dots and histograms.) SI Appendix, Fig. S3 shows the same results for the other subjects. For a memory sample $\left(r_1,\hspace{0.5em}{r}_2\right)$, its decoded estimate $\left({\widehat{\theta }}_1,{\widehat{\theta }}_2\right)$ was always shifted away from the diagonal (Eqs. 1 and 2), exaggerating the angular difference and producing similar backward and forward aftereffects for similar σ₁ and σ₂ (Fig. 6 B and C). Across memory samples, the estimates spread along the positive diagonal showing interreport correlation similar to the data (Fig. 6C). In the few trials where the ordinal relationship between the lines was incorrect, the estimates shift to the other side of the diagonal (Fig. 6C), reproducing the gap between the trials with correct and incorrect ordinal relationships (Fig. 6D).

Fig. 6E compares the observed and the simulated aftereffects across the subjects. Since the forward and backward aftereffects were similar according to both the data and theory, they were combined in this comparison to reduce variability. Open dots and crosses represent the results for the 50° and 53° lines, respectively. Fig. 6F compares the observed and the simulated angular difference between the lines. The theory explained the data well for 10 of the total 12 subjects. For the other two subjects (see also the 2nd and 10th rows of SI Appendix, Fig. S3), the simulated angular differences were smaller than the observed. This discrepancy can be easily eliminated by introducing a free parameter to scale the σ’s in Eqs. 1 and 2. This means that, for these two subjects, the SDs of the 2-line absolute distributions were not good approximations of the SDs of the corresponding memory representations.

Eqs. 1 and 2 predict that for small $\mathrm{\Delta }r$ and similar σ₁ and σ₂ (as in our experiment), average reported angular difference, ${\widehat{\theta }}_2-{\widehat{\theta }}_1$, increases with σ. The 12 subjects we tested showed different SDs of their 2-line absolute distributions, which must be related to the SDs (σ₁ and σ₂) before application of Bayesian prior. The prediction then becomes that subjects with large (small) SDs should also show large (small) reported angular difference between the two lines. Fig. 7A confirms this prediction (Pearson correlation coefficient, 0.83; P = 0.00090). Also as predicted, the percentage of correct ordinal discrimination did not decrease significantly with SDs (Fig. 7B; Pearson correlation coefficient, 0.24; P = 0.45), supporting our hypothesis that ordinal relationship between the lines was stably maintained in working memory and unaffected by the noise in memory representations of the absolute orientations accumulated over the delay period between presentations and reports. Note that different subjects’ SDs at the report time differed by more than a factor of 2 while their ordinal discrimination performances were in the narrow range from 84% to 98% correct. This suggests that the subjects’ noise differences at the time of second-line presentation must be small and that the large SD differences at the report time must mostly reflect different rates of their memory distortion with time.

Discussion

By measuring joint distributions of two judgments in a trial, which contained distributions of both absolute and relative judgments, we refuted the absolute-to-relative assumption which has been widely used in neural decoding models and signal detection theory. To the extent that absolute and relative/ordinal orientations are features of different levels (see below), our study also rejected the general low- to high-level decoding assumption. We proposed a computational theory that views visual perception as retrospective decoding in working memory from high- to low-level features. We demonstrated that the theory accounts for all essential aspects of the data including interreport correlation, bimodal relative distribution with a gap near zero, exaggerated orientation difference, and similar backward and forward aftereffects. We also confirmed two predictions of the theory, namely that orientation difference, but not ordinal discrimination performance, depends on the noise in absolute judgments at the time of report. These findings argue for a paradigm of perception that integrates perceptual decoding and working memory.

We considered the relationship between two sequentially presented orientations as a higher-level feature than the individual orientations themselves for a few reasons. Physiologically, most V1 neurons are tuned to single orientations (44) while a significant fraction of V2 neurons are tuned to combinations of orientations (45). Computationally, successful object recognition models (including HMAX and related deep-learning networks) encode single orientations and their relationships in two successive layers of processing [e.g., the study by Riesenhuber and Poggio (46)]. Conceptually, the relationship between two orientations depends on the two individual orientations but not vice versa. Although, in principle, V1 neurons or the first layer of neural networks could directly encode all combinations of angular differences between two orientations (or even more complex objects), this is not the case presumably because of computational difficulties.

Our experiment, like most psychophysical experiments, required working memory because of the delays. Under natural conditions, because of frequent saccades and small foveas, our coherent perception of the world must also depend on working memory. Compared with lower-level features (e.g., absolute orientation, luminance), higher-level properties (e.g., ordinal orientation, facial expression) are more invariant and categorical, and are thus easier to specify and maintain in working memory. They are also more behaviorally relevant (47). For example, the absolute orientation of a person’s eyebrow varies constantly with viewers’ head and eye orientations, providing little useful information. However, whether the eyebrow tilts more clockwise or counterclockwise from a moment ago (or with respect to the eye) is invariant over a broad range of viewing parameters and conveys facial emotion (48). Although lower-level features are encoded earlier along visual pathways, once all task-relevant features reach working memory their later decoding does not have to follow the order of encoding. Indeed, decoding should focus on behaviorally relevant, high-level features. Lower-level features are decoded only when necessary, and because their continuous values render their memory representations unreliable (30, 31), their decoding should be constrained by more reliable, higher-level decoding for consistency and accuracy. Our work provides evidence for such high- to low-level decoding.

Since we used a Bayesian approach, our model is formally similar to previous Bayesian models, particularly those on how categorization affects perception (28, 29, 49). It is also related to studies on visual working memory (50–52), especially the memory combination of categories and particulars (53). However, our study focuses on the integration of perceptual decoding and memory properties of low- and high-level features and the logical implications of this integration on decoding hierarchy whereas the previous studies do not. This key difference leads to very different interpretations of formally similar models. Specifically, in our study, successively presented lines and their relationship clearly defined a low- to high-level encoding hierarchy, and delays between stimuli and between the last stimulus and report engaged working memory. This allowed us to demonstrate that perceptual decoding did not follow the same hierarchical order of encoding but, instead, was accounted for by a retrospective, high- to low-level procedure in working memory. Importantly, this procedure makes logical sense only because higher-level stimulus features are more categorical and thus easier to maintain in working memory, and are more important behaviorally. In contrast, previous studies (28, 49, 53) focused on integrating categorical and continuous cues without discussing the absolute-to-relative assumption, decoding hierarchy, or stability differences between low- and high-level memories. A model by Stocker and Simoncelli (28) assumes that a commitment to one category leads to a suboptimal model of conditional perception and estimation biases. Instead, our memory considerations logically lead to the framework that ordinal relationship should be decoded first and then produce a Bayesian prior to constrain the decoding of absolute orientations. This decoding hierarchy improves the reliability of decoded orientations because, according to our theory, the binary ordinal relationship does not deteriorate in working memory whereas continuous absolute orientations (and their angular difference) do.

The trial-by-trial interreport correlation we found suggests that neural representations for the two stimuli being compared must be correlated. This correlation differs from the commonly studied noise correlation or synchronization among different neurons’ responses to the same stimulus (54–58). The backward aftereffect cannot be explained by optimal (or efficient) encoding/transmission theories of adaptation and perceptual bias, although the theories have been very successful in accounting for many other phenomena (35–39, 59, 60): by the time the second orientation is presented after a 0.5-s interval, the first orientation must already be encoded in V1 and transmitted to higher areas; any perceptual influence from the second to the first orientation must not be for efficient encoding/transmission of the first orientation.

In summary, our findings not only reject the absolute-to-relative assumption and the associated low- to high-level decoding assumption widely used in theoretical studies and data analyses, but also call for a revision of popular theories of adaptation. By separating encoding and decoding hierarchies and assigning high- to low-level decoding to working memory, we propose a computational framework for understanding perception. The framework may be applicable to a broad range of demonstrations that higher-level properties influence the perception of lower-level properties (19, 61–66). For example, higher-level segmentation cues such as transparency may produce a Bayesian prior to constrain lower-level decoding of motion integration (65, 66). Our work also raises the question of whether generally, higher-level, more categorical memories (e.g., person A is good) are more stable than lower-level, less categorical memories (e.g., the things person A did or tweeted), and if so, whether the former influences the latter more strongly than the other way around, regardless of the memories’ temporal order of formation.

Methods

Subjects.

Twelve subjects consented to participate in the experiment; 10 of them are naive to the purpose of the study. They all had normal or corrected-to-normal vision. The study was approved by the Institutional Review Board of the New York State Psychiatric Institute and was carried out in accordance with the Code of Ethics of the World Medical Association (Declaration of Helsinki).

Apparatus.

The visual stimuli were presented on a 21-inch Viewsonic P225f monitor controlled by a PC computer. The vertical refresh rate was 60 Hz, and the spatial resolution was 1,024 × 786 pixels. The monitor was calibrated for linearity with a Minolta LS-110 photometer. In a dimly lit room, subjects viewed the monitor from a distance of 75 cm through a black, cylindrical viewing tube (10-cm inner diameter) to exclude potential influence from external orientations. Each pixel subtended 0.03° at this distance. A chin rest with a head band or bite bars were used to stabilize the head (see below). All experiments were run in Matlab with PsychToolbox 3 (67, 68).

Visual Stimuli.

A round, black (0.15 cd/m²) fixation dot, 0.3° in diameter, was always shown at the center of the white (55.5 cd/m²) screen. All stimuli were black lines of 3° (length) by 0.03° (width), centered on the fixation dot, and oriented either 50° or 53° counterclockwise from horizontal. The dot and lines were created with antialiasing (Screen BlendFunction of Psychtoolbox 3) to ensure smooth appearance under the viewing condition.

Procedures.

The main experiment consisted of five conditions, each run in a separate block of trials. Subjects were instructed to always look at the fixation dot in the center of the viewing tube. They initiated a block of trials by clicking a mouse button, and 500 ms later the first stimulus appeared. There were two 1-line test conditions (Fig. 1A), in which a single line of a fixed orientation (either 50° or 53° counterclockwise from horizontal in separate blocks) was flashed for 500 ms in each trial. Five hundred milliseconds after the disappearance of the line, a red marker dot and a green marker dot, each 0.12° in diameter, appeared on opposite sides of the fixation dot either vertically or horizontally (randomly chosen with equal probability). Subjects then used the mouse to rotate the dots, which were always constrained on opposite sides of an invisible circle centered at the fixation point, to match the perceived orientation of the flashed line as closely as possible and clicked a mouse button to report. The invisible circle had a diameter of 2.4°, smaller than the 3° line length, so that subjects had to use the line orientation, instead of the line end points, to place the marker dots. After a 2-s intertrial interval, the same line was flashed for the next trial and the process repeated for a total of 50 trials.

To ensure that the mouse control of the dots’ rotation had fine enough resolution in orientation, the Matlab code first rotated the dots on a (invisible) circle of a diameter equal to the screen height (786 pixels or 23.6°). It then radially (toward the fixation) projected the dots onto the circle of 2.4° diameter (without rounding off) and drew them with antialiasing. Both circles had the fixation point as the center. Consequently, the smallest movement of the mouse (1 pixel) changes the orientation of the dots by at most ${\tan }^{-1}\left(1/786\right)$ = 0.073°. This resolution is adequate because it was more than two orders of magnitude smaller than the spread of a typical distribution of orientation judgments (Fig. 2).

There was one 2-line test condition (Fig. 1B) in which two lines of fixed orientations (again 50° and 53°) were presented sequentially in each trial, with an interstimulus interval of 500 ms between them to eliminate apparent motion (32). The order of presenting the two orientations was counterbalanced and randomized across 50 trials. Subjects used the mouse to rotate the marker dots, which appeared 500 ms after the disappearance of the second orientation, to match the first orientation and click, and then to match the second orientation and click. They were told that the order of the two different clicks must match the order of the lines so this condition required orientation discrimination. The 3° difference between the two lines was chosen so that subjects could readily discriminate them (69–72). All other aspects of this condition, including the 2-s intertrial interval, were identical to those for the 1-line test conditions above.

Finally, there were two 1-line control conditions. These were identical to the two 1-line test conditions above except that, in each trial, the line stayed on the screen until subjects rotated the marker dots to match its orientation and clicked, and that there were 20 trials per condition. Since the line stayed on to provide visual feedback for the placement of the marker dots, these control conditions measured the variability arising from subjects’ fine-motor control capabilities, namely, how well subjects were able to place the marker dots at the intended orientation.

The block orders between the two 1-line test conditions and between the 1-line and 2-line test conditions were pseudorandomized. For all subjects, the two 1-line control conditions were always run last.

In all conditions, subjects always indicated the perceived orientation by rotating the marker dots without reporting any numbers. This experimental design ensured a fair comparison among absolute and relative judgements and ordinal discrimination. Before data collection, subjects were given detailed instructions and sufficient practice trials to understand the tasks and familiarize with the mouse control of the dot rotation. For all conditions, subjects were instructed to take time to match the perceived orientations as closely as possible.

Subjects received no feedback on their performance at any time; this minimized their learning of stimulus statistics across trials (SI Appendix, text and Figs. S4–S6).

Note that we ran the 1-line test conditions in separate blocks so that we could measure the absolute distribution of each orientation without interference from the other. It is important for us to have a reliable measure of the absolute distributions to show that even these absolute distributions failed to explain the relative/ordinal judgments. These 1-line conditions also served as the baseline condition for calculating forward and backward aftereffects (see Perceptual Decoding Cannot Be Explained by a Sequential Mechanism or by Conventional Adaptation). The 2-line condition did mix the two orientations to measure their interactions.

Head Stabilization.

For a given line on the screen, its retinal and perceived orientations may vary with the roll of the head and eye. Specifically, voluntary head roll can induce counter eye roll (torsion), and since they do not cancel completely (73), the retinal image orientation can change. We therefore stabilized the head, with two methods. We collected data from 12 subjects with a chin rest and a head band. We repeated all measurements on two subjects (one naive) using bite bars (Bite Buddy; University of Houston, Houston, TX). Since the results from the two methods were identical, we report the results from the first method in the text but mention the results from the second method in SI Appendix. Note that because the subjects used the marker dots to match the perceived orientation in each trial, only the head roll between the stimulus presentation and the mouse click within a trial could affect the matching result; head rolls between trials would not matter. Also note that small horizontal and vertical eye movements would not change the stimulus orientation. Large eye movements were unlikely because the subjects looked through the viewing tube and the fixation point and a small line were the only visual stimuli inside the tube.

To further control for possible motor noise (explained in SI Appendix), when the two subjects used the bite bars to repeat the experiment, there was a small modification for the 2-line condition: the initial marker dot orientation was closer to the first line. They repeated the other conditions without modification.

Data Analysis and Statistics.

For each 1-line test condition, the 50 reported orientations of a given subject were sorted and binned into a histogram with a bin size of 1°; this produced the absolute-judgment distributions for the 50° and 53° stimulus orientations, to be referred to as the 1-line absolute distributions. We applied the same analysis to the 1-line control conditions to demonstrate that variability from motor control was negligible for our tasks.

For the 2-line test condition, we plotted the reported orientation for the 53° line against that for the 50° line in a trial as a joint distribution to reveal interreport correlation for each subject. We also subtracted the reported orientation of the 50° line from that of the 53° line in each trial, and then sorted and binned the differences from 50 trials into a histogram; this produced the relative-judgment distribution for each subject, to be referred to as the observed relative distribution.

According to the absolute-to-relative assumption, for each subject, the absolute distributions completely determine the corresponding joint and relative distributions. We therefore computed the predicted joint and relative distributions by repeatedly drawing a number from the 50° absolute distribution and a number from the 53° absolute distribution, and subtracting the former from the latter. This was done 10,000 times to define the predicted distributions well, but only 100 samples were shown in scatter plots of joint distributions to avoid clutter.

We also generated absolute distributions from the 2-line condition. This was done by simply compiling a subject’s reported orientations for the 50° and 53° lines separately across trials, regardless of when a given line appeared. We refer to these absolute distributions as the 2-line absolute distributions to distinguish them from the 1-line absolute distributions above.

When comparing predictions of the absolute-to-relative assumption and the corresponding observations, we used the nonparametric Wilcoxon signed-rank test.

Derivations for the Retrospective Bayesian Decoding Theory.

We outline the derivations of Eqs. 1 and 2. We consider two continuous variables, denoted as $\theta =\left({\theta }_1,{\theta }_2\right)$, for the two line orientations in a trial. We assume that their noisy working-memory representations $r=\left(r_1,r_2\right)$ obey Gaussian distribution:

$$P\left(r|\theta \right)\sim \exp \left(-\frac{{\left(r_1-{\theta }_1\right)}^2}{{\sigma }_1^2}-\frac{{\left(r_2-{\theta }_2\right)}^2}{{\sigma }_2^2}\right).$$

When viewed as a function of $\theta$ for a given r, this is the likelihood function. To decode the estimated values of $\theta$ from their memory representations, we assume that the ordinal relation between them (e.g., ${\theta }_1<{\theta }_2$) was decoded earlier and can now be used as a Bayesian prior, resulting in the following posterior distribution:

$$P\left(\theta |r\right)\sim 1_{{\theta }_1<{\theta }_2}\exp \left(-\frac{{\left({\theta }_1-r_1\right)}^2}{{\sigma }_1^2}-\frac{{\left({\theta }_2-r_2\right)}^2}{{\sigma }_2^2}\right),$$

which is the product of the likelihood and the prior. We then find the estimated values for $\theta$ as averages over the posterior distribution. This results in Eqs. 1 and 2.