Significance
Investigations of the conditions of truth wins in social groups present mixed findings and have not included a network science modeling of the opinion dynamics that alter individuals’ positions. This paper presents evidence that an attention to such dynamics substantially clarifies how truth wins. The findings of our experiments on groups of human subjects suggest that the mixed findings on truth wins in social groups can be integrated as special-case realizations of a general model of opinion dynamics on influence networks.
Keywords: network science, opinion dynamics, truth statements
Abstract
How truth wins in social groups is an important open problem. Classic experiments on social groups dealing with truth statement issues present mixed findings on the conditions of truth abandonment and reaching a consensus on the truth. No theory has been developed and evaluated that might integrate these findings with a mathematical model of the interpersonal influence system that alters some or all of its members’ positions on an issue. In this paper we provide evidence that a general model in the network science on opinion dynamics substantially clarifies how truth wins in groups.
Max Planck’s famous null hypothesis on truth propagation is that “a new scientific truth does not triumph by convincing its opponents and making them see the light, but rather because its opponents eventually die.” Classic experiments in social psychology have probed the conditions of “truth wins” in social groups. This evidence presents mixed findings, and no dynamical system model has been advanced that integrates them. Thorndike and Barnlund (1, 2) show that an initial consensus is adopted without scrutiny whether or not it is true. Asch (3–5) shows that individuals are likely to abandon the truth if they are located in a group in which all other members have a fixed agreement on a false position. Sherif (6) shows that a group converges to a false consensus when all its members are uncertain about the true position. Laughlin and Adamopoulos (7) and Laughlin and Ellis (8) find that reaching consensus on a true position depends on the size of the faction of individuals with the correct position on an issue. Clearly, truth propagation is not a viral contagion in which a true position is automatically adopted by anyone who comes into contact with it, and the hazard rate of adopting false positions on issues is substantial.
The above referenced findings of the classical literature on truth wins in social groups are based on statistical tests of hypotheses on input–output associations and do not specify the groups’ throughput mechanisms that alter individuals’ positions on issues. Understanding the mechanisms by which truth wins or fails to win is an open problem. It is a problem that has become increasingly important with the development of social media that allow a rapid widespread dissemination of true and false information. Unfortunately, we are currently confronted with such a hazard in which a faction of policy makers have concluded that the numerical evidence on global warming does not indicate any trajectory toward a dangerous threshold level that would require immediate action.
Investigations of the conditions of truth wins have not included a network science modeling of the opinion dynamics that determine groups’ outcomes. We present evidence that an attention to such dynamics substantially clarifies how truth wins in groups. Given information on a group’s initial opinions and influence network on a quantitative issue, network science models of opinion dynamics are motivated by the idea that complex sequences of opinion updates are triggered by individuals’ exposure to a set of one or more other individuals’ fixed or changing positions on an issue. An interdisciplinary field of research has developed on the problem of predicting group members’ displayed settled positions on an issue. Such predictions require a mathematical model of interpersonal influence systems in which repetitive individual-level updates of quantitative opinions are occurring. Numerous models of such systems have been proposed; see refs. 9 and 10 for reviews. Consistent with all mathematically based science on dynamical natural systems, the goal of this field is to find an empirically supported parsimonious general mechanism of opinion updating that unfolds on any influence network topology and, thus, explains a large domain of observed realizations of influence system outcomes. The open fundamental question is whether or not there exists an elementary “cognitive algebra” (11, 12) in individuals’ integration of their own and others’ displayed opinions. The most widely accepted candidate is a weighted averaging mechanism with which each individual automatically allocates weights to his or her own and others’ fixed or changing opinions to obtain an updated opinion that is a convex combination of opinions. The set of all group members’ allocated weights defines the influence network of the group. Thus, a group issue-specific influence network is automatically assembled as an implication of individuals’ information integration mechanism; that is, the weights are in the mechanism used by individuals to adjust their own opinion on an issue. In this literature, the Friedkin–Johnsen (13, 14) generalization of the seminal French–Harary–DeGroot (15–17) weighted-averaging opinion update mechanism is currently the only model on which a sustained line of human-subject experiments (14, 18–20) have been conducted to evaluate predictions of opinion changes. This model is given by
| [1] |
where , , , and . The corresponding matrix equation for the influence system is
| [2] |
where is the system’s matrix of weights and is the system’s diagonal matrix of individuals’ levels of stubborn attachment to their initial opinions ( , ). In the special case of , the model reduces to a French–Harary–DeGroot system without resistances to opinion change. Mathematical analysis has shown that this system’s equilibrium equation,
| [3] |
is consistent with relaxations of the model’s simplifying assumptions of synchronous opinion updates (21, 22) and time-invariant (23) that allow random asynchronous updates and time-varying weights. The model provides theoretical foundations for widely used measures of the influence centralities of individuals in a group: In the special case of an , its measure is equivalent to eigenvector centrality, and in the special case of an , , its measure is equivalent to PageRank centrality (24–26). See SI Text on other relevant properties of this model. Experiments on groups of human subjects have evaluated the model’s predictive accuracy on quantitative issues of judgment for which there are no true or false numerical positions. The designs of these experiments include groups in face-to-face interaction (20) and groups in which interaction is constrained by different telephonic communication structures that prohibit direct conversations among particular pairs of individuals and allow random dyadic conversations of varying length (14, 18, 19). Its predictive accuracy includes exact predictions of observed final opinions such as in the following case that appears in the findings of the experiments reported in this paper. Before the group discussion, the four members of this group privately recorded their initial opinions,
A direct measure of the cognitive weights of Eq. 1 (relating to the way an individual is integrating information in his or her own mind) is based on the four individuals’ independent postdiscussion reports of the extent to which each of the other group members influenced their own final opinions; see SI Text on this measure. In this group on this issue, 1 reports according no weight to itself or to 4, and equal weights to 2 and 3, and the group’s matrix of such reports is:
The model’s predicted equilibrium opinions are
Let . Its elements correspond to the total relative (direct and indirect) influence of group member ’s initial opinion on the final opinion of group member . Each and . Thus, for this group, the model’s predicted final opinions are
and, in this case, they are exact predictions of the individuals’ observed privately reported final opinions. We will show that the model’s predictive accuracy is high in the pool of all cases reported in this article on intellective (truth statement) issues. Note that there is nothing in this prediction that indicates whether any opinion is correct or incorrect.
The fact that the issue is intellective, in contrast to the judgment issues that have been involved in all previously conducted experiments, is irrelevant to the model’s explanation of the observed opinion changes. Here, and in general, the foundations of this model’s success rests (i) on its assumption of a weighted averaging mechanism of opinion updates that allows for levels of stubborn attachment to initial opinions and (ii) on an equilibrium equation that is robust to violations of its simplifying assumptions of synchronous updates on a time-invariant influence network.
However, there are important implications of quantitative intellective issues that distinguish them from quantitative judgment issues. Note that in the above example two individuals reported identical initial opinions. Henceforth, we refer to a subset of individuals with identical initial opinions as a faction. Such factions frequently occur on the intellective issues of the conducted experiments. In contrast, in previous experiments on quantitative judgment issues (14, 19, 20), initial opinion factions rarely occur so that typically any initial opinion in a group is a distinct position that is associated with one individual. On the issues investigated in this paper, because the same initial position is often held by two or more individuals the displayed position of a faction-as-a-unit has an influence value. This idea has motivated the classical work on truth wins and abandonment referenced in the Introduction. We break from the tradition of treating the relative sizes of factions as an explanatory variable. Consistent with a network science approach, we define the influence of a faction-as-a-unit on any individual as the sum of the faction members’ total influences on . Thus, one member of the faction may explain most its influence, and other individuals may be more or less influenced by different members of a faction. On this basis, we can formulate a prediction of the relative total influence of the truth, that is a value in the interval, in determining each ’s final opinion on an issue as follows:
| [4] |
For each individual , regardless of whether his or her own initial opinion is true or false, the hypothesis is that predicts whether will hold a true or false final opinion. For each group, the hypothesis is that predicts whether a group consensus is reached on a true or false position. This formulation allows for cases in which a true initial position is abandoned, or a true initial opinion of one member alters all other members’ false opinions, or the true initial position of a faction alters or fails to alter other members’ opinions. We will show that our findings support this network science approach for explaining how truth wins in groups.
In addition, we show that a deeper level of persuasion is involved in group discussions of truth statements. In the classic Asch (3–5) and Sherif (6) experiments, individuals voiced their positions without discussion. Group discussion allows not only a display of opinions but also a display of the calculative logics upon which different initial opinions are based. The abandonment of an opinion may be associated with the adoption of a true or false calculative logic that applies to the issue, and to all other issues to which the logic can be applied. This deeper level of persuasion, based on social learning, allows a growth of initial opinion factions along a sequence of issues on which a common calculative logic can be adapted to each issue. In the conducted experiments, the structure of each issue varies over the issue sequence so that formulaic rote learning may fail in the absence of a more abstract understanding of the logic involved. Although individuals may have been persuaded to accept a true opinion, they may present either a true or false initial opinion on the next issue of the issue sequence, depending on whether they acquired an abstract understanding of how to obtain a true opinion. Similarly, they may be persuaded to accept a false opinion without acquiring an abstract understanding of its calculative logic. We show that both true and false initial opinion factions grow in size along a sequence of intellective issues on which a true or false calculative logic can be adapted to each issue. In our data, faction growth includes cases of group trajectories along an issue sequence to extremal states of initial consensus. In these extremal cases, all group members have the same initial opinion (true or false) and maximal levels of attachment to it. Finally, we consider the net resultant of these intimately intertwined processes of interpersonal influence and social learning. When there are various false calculative logics and only one true calculative logic, the distribution of initial opinion errors (for all individuals nested in independent groups) evolves over time along an issue sequence toward a distribution in which the frequency of true initial opinions dominates. Although the bulk of initial opinions may be based on false calculative logics, they are group-specific. Thus, truth wins in a decentralized population of individuals nested in independent groups under the condition of one-true versus many-false calculative logics on a class of intellective issues.
We conducted experiments on risk evaluation issues—analytical reliability problems—for which there are objectively correct numerical positions. We assembled 45 face-to-face groups of three to four individuals. Each group dealt with a random permutation of the same issues under the instruction that they should try to reach a consensus on each issue. With 161 individuals nested in 45 groups with three to four members, each dealing with a sequence of eight issues, the experiments set up group-issue occasions in which individuals present an initial and final opinion and 1,288 individual-level behavioral observations of (initial, final) tuples of opinion. The individuals were recruited from the undergraduate subject pool of our university and paid for their participation. The University of California, Santa Barbara Institutional Review Board approved the study, and all subjects provided written informed consent. The experiment is a standard prepost group-discussion randomized design. One of the eight issues is posed to a group. (i) Individuals privately record their initial positions on the issue, (ii) a group discussion is then opened and concluded, and (iii) individuals privately record their final positions and their subjective weights indicating the extent to which each of the other group members influenced their own final opinion. Then another issue is posed, and so on, until the concluding issue of the random permutation of the eight issues is reached. For each group-specific issue, the obtained data are the group’s -vectors of initial and final opinions and its matrix of allocated weights, which are measures of the model’s , , and constructs, respectively. See SI Text on the detailing of these experiments. Because the data structure is a longitudinal multilevel design in which individuals are nested in groups, the statistical analysis draws on methods suitable to such clustered data (SI Text). We also conducted a baseline experiment on 30 individuals who worked independently on random permutations of the same eight issues.
Results
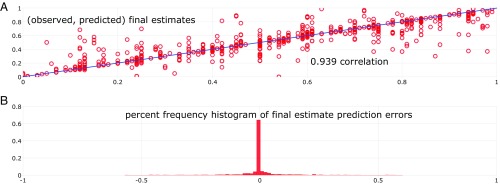
First, we evaluate the predictions of the opinion dynamics model. The experiments provided individual-level behavioral observations of (initial, final) tuples of opinion. Fig. 1 evaluates the model’s predicted final opinions. The Pearson product-moment correlation coefficient of observed and predicted final opinions is (P < 0.001, ).
Fig. 1.
The F-J model of group influence systems is applied to 161 individuals nested in 45 groups, each dealing with a sequence of eight issues, setting up group-task occasions in which the individuals nested in a group presented an initial and final opinion and 1,288 individual-level behavioral observations. (A) Individuals’ observed and F-J model-predicted final opinions. The Pearson product-moment correlation of the observed and predicted final opinions is . (B) Percent frequency histogram of the F-J model prediction errors of final estimates.
Opinion changes were prevalent, and the model’s predictions of the direction and magnitude of these changes are associated with the observed changes (P < 0.001). Regressing individuals’ observed final opinions on their predicted final opinions and observed initial opinions, the estimated coefficient for the predicted values is 0.983 (P < 0.001, SE = 0.041) and the coefficient for initial opinions is insignificant (P = 0.496). These findings on quantitative intellective issues are strongly consistent with previous findings on quantitative judgment issues (14, 19, 20). The network science speculation that there may be an elementary mechanism of opinion updates, based on weighted averaging, is buttressed by these findings. With respect to the specialized literature of experiments on groups dealing with intellective problems, referenced in the Introduction of this paper, these findings suggest that a network science model of opinion dynamics may serve to integrate this literature’s observations. The special cases of this model cover all realizations of initial opinions (initial consensus, faction structures, and complete heterogeneity), levels of stubborn attachments to initial opinions, and influence network topologies. In the present experiments we have not constrained these realizations as in the classic Asch (3–5) experiments and have allowed them to naturally arise.
Second, we evaluate the Eq. 4 hypothesis that the probability of an individual’s adopting a true final opinion on an issue depends on whether one or more true initial opinions exist in a group and their influence on an individual’s opinion. We find that the hazard of a false final opinion given a false initial opinion is (i) near 100% if an individual is not exposed to a true initial opinion and (ii) reduced but not eliminated (in these data to 18%) if an individual is exposed to a true initial opinion. The existence of a true initial opinion in a group is necessary but not sufficient to explain its adoption (who adopts it or who does not). The Eq. 4 hypothesis is that its adoption by a particular individual depends on the existence of one or more true initial opinions and on the influence of the one or more individuals who are advocating it. In our data, a group’s array of initial opinions is not constrained by the experimental design as in the classic Asch (3–5) experiments on truth abandonment, where a single naive subject with a true initial opinion is confronted with two or more confederates of the experimenter who display an identical false fixed opinion on each issue of a sequence of similar issues. We allow true or false factions of initial opinions to naturally occur along an issue sequence, and we place no design constraints on individuals’ levels of stubbornness. In the 360 occasions that present arrays of initial opinions of true or false factions, all feasible faction structures of initial opinion were observed. In the 152 group-issue-specific occasions involving triads, the distribution of the number of unique initial opinions is 40, 50, and 62 occasions with one, two, and three unique initial opinions, respectively. In the 208 group-issue-specific occasions involving tetrads, the distribution of the number of unique initial opinions is 34, 63, 54, and 57 occasions with one, two, three, and four unique initial opinions, respectively. The existence of initial opinion factions presents an open question in the network science on opinion dynamics. Can the effects of initial opinion factions on group members’ final opinions be understood as a simple aggregation of the relative total interpersonal influences of the individuals who are advocating a particular position on an issue? We address this question with a logistic regression of the individuals’ observed binary adoptions of true versus false final opinions on the Eq. 4 predicted influence value of the truth on their final opinions, controlling for the truth state of their observed initial opinions. The estimated coefficient for the predicted influence of the truth is 7.747 (P < 0.001, SE = 1.040) and the estimated coefficient of the truth state of their initial opinions is insignificant (P = 0.552). Thus, Eq. 4 captures instances of maintained or adjusted initial-to-final opinions and predicts the log odds of adopting true final positions. Since and its observed values span its feasible values, the estimated 7.747 coefficient indicates a strong association (linear increases in the log odds of adopting a true final opinion up to a nearly eight-fold increase) consistent with the predictions of the entertained opinion dynamics model.
For each group, the hypothesis is that the group’s mean predicts whether a group consensus is reached on a true position. From the opinion dynamics model, this mean value must be 0 if all group members have false initial opinions or if any true initial opinion has no influence on final opinions, and its positive values indicate the extent to which one or more true initial opinions in a group influence final opinions. The data present 360 occasions on which a consensus might be reached. We evaluate the hypothesis with a logistic regression of the observed events of a true versus false final consensus on the mean Eq. 4 predicted total influence of the truth on final opinions, controlling for the number of group members with true initial opinions. The estimated coefficient for the predicted influence of the truth is 6.888 (P < 0.001, SE = 1.651) and the estimated coefficient for the number of group members with true initial opinions is insignificant (P = 0.317). Since and its observed values span its feasible values, the estimated 6.888 coefficient indicates a strong association (linear increases in the log odds of a true final consensus up to a nearly sevenfold increase) consistent with the predictions of the entertained opinion dynamics model. The insignificant coefficient for the number of group members with true initial opinions is consistent with the hypothesis that the opinion dynamics model explains the association of initial factions of true positions on true consensus outcomes.
Third, we show that a deeper level of persuasion is involved in group discussions of truth statements. Group discussion allows not only a display of opinions but also a display of the calculative logics upon which different initial opinions are based. The abandonment of an opinion may be associated with adoption of a true or false calculative logic that applies to the issue, and to all other issues to which the logic can be applied. This deeper level of persuasion, based on social learning, allows a growth of initial opinion factions along a sequence of issues on which a common calculative logic can be adapted to each issue. On the analytical reliability issues of this experiment, the structure of each issue varies over the issue sequence so that formulaic rote learning may fail in the absence of a more abstract understanding of the logic involved. Although individuals may have been persuaded to accept a true opinion, they may present either a true or false initial opinion on the next issue of the issue sequence, depending on whether they acquired an abstract understanding of how to obtain a true opinion. Similarly, they may be persuaded to accept a false opinion without acquiring an abstract understanding of its calculative logic. Thus, true and false social learning is manifested in the growth of initial opinion factions along an issue sequence.
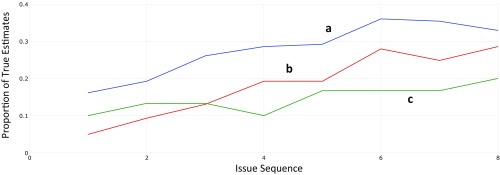
Fig. 2 reports the proportion of true opinions along the issue sequence for 30 isolated individuals and the 161 individuals nested in 45 groups. The effect of groups is the difference between the (a) curve for the final opinions of individuals nested in groups and the (c) curve for the isolated individuals. The (b) curve for the initial opinions of the individuals nested in groups signals the occurrence of social learning events that alter the conditions under which the opinion dynamics of the groups unfold. The difference of the (a) and (b) curves for final and initial opinions is based on the additional factor of interpersonal systems in which the influence of one or more true initial opinions elevates the adoption of a true final opinion whether or not the adopter understands how such opinions were obtained. Note that the maximum proportion of true final opinions on the (a) curve is below 0.40. A substantial proportion of the groups in these data fail to present any true opinion. In such groups, factions of initial opinion grow along the issue sequence based on false learning.
Fig. 2.
The proportion true opinions along the issue sequence for (a) the final opinions of the 161 individuals nested in groups, (b) the initial opinions of the 161 individuals nested in groups, and (c) the opinions of the 30 isolated individuals.
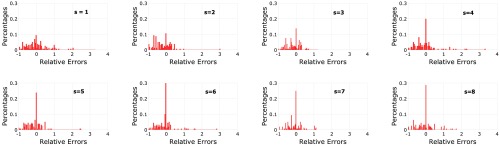
Finally, we consider the net resultant of these intimately intertwined processes of interpersonal influence and social learning. When there are various false calculative logics and only one true calculative logic, the resulting distribution of individuals’ initial opinion errors is an evolving distribution in which the frequency of true initial opinions is elevated. Fig 3 shows the evolving distribution of relative initial opinion errors. Truth wins in a decentralized population of individuals nested in independent groups that are dealing with a sequence of intellective issues on which a common calculative logic can be adapted to each issue. Such evolution will occur when the application of incorrect facts and logic is group-idiosyncratic and, thus, fails to form any substantial between-group faction with a common error bias. Such evolution may be derailed by social movements or social media that elevate the adoption of a particular set of false facts and logic.
Fig. 3.
The emergence of a dominant faction of individuals with true initial opinions in the sample of 161 individuals nested in 45 disconnected groups.
Discussion
The research reported in this paper suggests that a network science of opinion dynamics may advance our understanding of how truth wins in groups. It presents an approach that contrasts with the literature on the wisdom of crowds (27–30) in which true numerical estimates are obtained from the mean value of the distribution of independent individual estimates. This work also contrasts with the literature on groupthink (31–35) with its implication that the definitional properties of groupthink are not necessarily associated with flawed decisions. Both positive and negative groupthink outcomes are permissible. We have noted that a group’s array of initial opinions evolves along an issue sequence and includes cases of group trajectories to extremal states of both true or false initial consensus based on the adoption of a particular calculative logic. If the shared calculative logic is false, then an instance of negative groupthink is expressed. If the shared calculative logic is true, then an instance of positive groupthink is expressed. Formally, both outcomes are consistent with the conditions of groupthink. Moreover, this work contributes a way of thinking about how truth wins in a population of independent groups. Social science has long emphasized the importance shared norms in large-scale populations (6, 36, 37), because shared norms appear to be the only basis on which independent groups might have similar initial opinions on the same class of issues, and reach a similar consensus on each issue. It is for this reason that shared norms have been emphasized by social scientists as a basis of societal coherence. We have shown how a dominant faction with opinions based on a true calculative logic, for a class of issues, may emerge in a population of independent groups. Although the bulk of initial opinions in such a population may be based on false calculative logics, they are group-specific. Truth wins in a decentralized population of individuals nested in independent groups under the condition of one-true versus many-false calculative logics. Its dominance is based on the property that any individual who understands the relevant science or mathematics must come to the same conclusion, while those who do not understand the relevant science or mathematics are likely to adopt diverse group idiosyncratic conclusions. This one-true versus many-false calculative logics condition of truth wins is not satisfied when social movements or social media elevate the adoption of a particular set of false facts and logic. Macro-level belief system dynamics that generate shared constraints on individuals’ opinions are complex (26, 38) and not easily controlled. Both history and social science present the evidence that the hazard rate of adopting false positions on truth statements is substantial and that truth propagation is not a viral contagion in which a true position is automatically adopted by anyone who comes into contact with it. Incentivizing correct opinions, to lower this hazard rate, has not been investigated. Fact checks that are exogenous feedbacks to groups would incentivize a rethinking of the method being used to obtain problem solutions. However, the conditions affecting the willingness or capacity of groups to alter their agreed-upon methods of solving problems are currently not well understood. More broadly, the advancement of a network science modeling of the group dynamics that alter individuals’ positions on issues is currently limited by the absence of a technology that provides more direct evidence on the causal basis of these dynamics and, in particular, a more direct measurement of the weights in the automatic convex combination mechanism that is the widely assumed cognitive algebra of iterative opinion update processes.
The Model
The Friedkin–Johnsen model does not assert that all, or any, members of a group are influenced by the positions of other members of the group. Whether such influence occurs depends on the individual-level self-weights of the group’s members. This formalization, in which self-weights correspond to individuals’ anchorage on their initial positions on an issue and the extent to which they are open or closed to the interpersonal influence of other individuals, is specified by a discrete time process of iterated weighted averaging:
| [S1] |
where , , , and is the initial position of the group member on an issue. The self-weights may be heterogeneous. For an individual with , the individual is not subject to interpersonal influence, , and the fixed position of the individual is his/her initial position. For an individual with , , and at each time the individual’s position is updated to a weighted average of the time positions of those group members to whom has allocated influence,
| [S2] |
For an individual with , the initial position of the individual makes a continuing direct contribution to any iteration of the influenced position of . This contribution depends on extent to which the individual is open or closed to interpersonal influence. In this case, the value is the weight that allocates to his or her own updated positions during the interpersonal influence process. This weight varies from to (achieved for ) and corresponds to ’s resistance to opinion change per se. Thus, the system of equations for the influence system on a specific issue is described by the matrix equation
| [S3] |
where is a diagonal matrix, with values on the main diagonal and zeros elsewhere, and I is the identity matrix (with ones on the main diagonal and zeros elsewhere). Note that A is determined by group members’ self-weights in W, and that the matrix W is a group-level construct derived from the mechanism specified by the theory. The mechanism is assumed to be the cognitive algebra of any individual’s automatic information integration activity, and the influence network is the social cognition structure assembled by the weights that individuals allocate to themselves and others in their information integration activity.
The process of interpersonal influence, which unfolds in the influence network (A,W), may involve direct and indirect influences. The direct influences, at each time , are described by Eq. S1. Indirect interpersonal influences on an individual arise from the repetitive responses of individuals to the changing opinions of those to whom they have allocated direct influence. For instance, if a particular group member , to whom has allocated influence, has been affected by some other group member , then influences indirectly. At each time , we have a matrix of direct and indirect influences that defines the relative net influence of each group member ’s initial opinion on the opinion of at time ,
| [S4] |
where for all , and , and
for all and . The matrix may be obtained either with the matrix recursion, ,
| [S5] |
or equivalently with the evolving matrix polynomial of walks in the graph of AW,
| [S6] |
The sequence converges, and thus opinions converge to steady values for any choice of , if and only if exists (such matrices AW are called “regular”). Necessary and sufficient conditions for such a convergence are covered in ref. 26. Two sufficient conditions for this apply to the most interesting case where (that is, when the F-J model does not reduce to the French–Harary–DeGroot model). A sufficient condition is strong connectivity of the influence network, that is, the existence of mutual influence (direct or indirect) between opinions of any two individuals. The other sufficient condition is in which case individuals’ levels of closure-openness are for all . In both situations the matrix AW proves to be Schur-stable, which means that and the sequence converges to
| [S7] |
When the influence process reaches an equilibrium, that is, the matrix is regular, the model admits a control matrix, , hereafter denoted as , that describes the total (direct and indirect) influences of group member ’s initial opinion on group member ’s settled opinions on an issue
| [S8] |
for each . The equilibrium matrix equation for the system is
| [S9] |
With for all and , and for all , is the equilibrium relative total contribution of group member ’s initial opinion to the settled opinion of group member . Thus, each group member has a mean relative influence centrality, that is,
| [S10] |
where each is the total relative influence of ’s initial opinion on ’s equilibrium opinion. Since is a stochastic matrix, the mean influence centralities sum to 1. A useful practical and remarkable technical property of the model is that Eq. S7 is well-behaved when and the inverse matrix in Eq. S7 does not exist. It appears (26) that
| [S11] |
is not ill-conditioned as , and the equilibrium opinion satisfies Eq. S9 with
| [S12] |
Violations of the regularity property for are exceptional; it fails only in presence of some “closed” community in the network, whose members’ opinions obey the French–Harary–DeGroot model with a periodic influence graph and are completely independent on the positions of the remaining individuals.
Materials and Methods
The model assumes a closed deterministic system (without exogenous disturbances) in groups where some or all individuals’ opinions are altered by the specified mechanism of interpersonal influence. As such, the model gives the necessary and sufficient constructs that must be measured to generate predictions. With measures of the group’s initial opinions and influence matrix , predicted final opinions are generated without estimation of unknown parameters. The experiments described in this section allow a measure of individuals’ independent initial opinions on an issue, a measure of their final opinions, and a measure of . The subjective self-reported weights, with which we assemble a measure of , are as close as we currently can get to the construct definition of this matrix. Under the assumptions of the model specification, if our measures are without error, then there should be an exact correspondence of individuals’ observed and predicted final opinions. Measurement errors will attenuate this correspondence, that is, bias it toward 0. Similarly, given that there are no model-intrinsic unknown parameters that require statistical estimation, model specification errors will also directly attenuate this correspondence.
The Issue Sequence.
A random permutation of eight analytical reliability problems of varying complexity is presented to each group. Such problems involve a determination of the probability that at least one component of a set of redundant components will not fail, where each component involves some number of subcomponents each with a probability of failure. The simplest form of such problems occurs under the assumption of independence. An example of such a problem on two components is
where , , , , and are the probabilities of subcomponent successes and is the estimate for probability that at least one of the two components will not fail. The problems proposed to the groups varied in their structure. Both the number of components and the number of subcomponents were varied. Moreover, the problems were constructed so that the estimated reliability values ranged from low to high reliabilities.
Medical research.
Two medical teams are working independently to achieve a cure for a disease. The hope is that least one of these teams will succeed. The success of Research Team A depends on the successful solution of two problems A1 and A2: The probabilities of their successful solutions are and , respectively. The success of Research Team B depends on the successful solution of three problems B1, B2, and B3: The probabilities of their successful solutions are , , and , respectively. All of the above probabilities are independent. What is your estimate of the probability that at least one of these research teams will succeed in finding a cure?
Contractor work.
We have three contractors who are working independently to build a device. We are hoping that at least one of these contractors will succeed. The success of Contractor A depends on the successful completion of two tasks A1 and A2: The probabilities of their successful solutions are and , respectively. The success of Contractor B depends of the successful completion of two tasks B1 and B2: The probabilities of their successful solutions are and , respectively. The success of Contractor C depends on the successful completion of three tasks C1, C2, and C3: The probabilities of their successful solutions are , , and , respectively. All of the above probabilities are independent. What is your estimate of the probability that at least one of these contractors will succeed in building the device?
Procedural change.
We must change a procedure to correct an unusual deficiency that is creating problems in our organization. Two of our lawyers are working independently on different approaches to achieve a correction. The hope is that at least one of these lawyers will succeed in finding a legal pathway to a correction. The success of lawyer A depends on the successful solution of two complex legal issues A1 and A2: The probabilities of their successful solutions are and , respectively. The success of lawyer B depends of the successful solution of two simpler legal issues (B1 and B2), and one complex issue (B3): The probabilities of their successful solutions are: , , and , respectively. All of the above probabilities are independent. What is your estimate of the probability that at least one of these lawyers will succeed obtaining a procedural solution?
Tactical problem.
We are involved in a competitive contest with another organization, and we have assembled three teams who are now working independently to end it in our favor. Each team is pursuing a different approach. Our hope is that at least one of these approaches will succeed. The success of Team A depends on the success of one gambit A1: Our estimate of the probability of its success is . The success of Team B depends on two gambits B1 and B2: The probabilities of their successful solutions are and , respectively. The success of Team C also depends on two gambits C1 and C2: The probabilities of their successful solutions are and , respectively. All of the above probabilities are independent. What is your estimate of the probability that at least one of these teams will succeed in ending the contest in our favor?
Information technology.
Our organization is developing a novel technology to gather information. Two groups of engineers have proposed different approaches and are working independently to design the technology. We are hoping that at least one of these groups will succeed. The success of Group A depends on the successful completion of two tasks A1 and A2: The probabilities of their successful solutions are and , respectively. The success of Group B depends on the successful completion of three tasks C1, C2, and C3: The probabilities of their successful solutions are , , and . All of the above probabilities are independent. What is your estimate of the probability that at least one of these groups will succeed in designing the technology?
Opening negotiation.
Our organization (Ego) wants to settle a dispute with another organization (Alter). However, we need to covertly acquire information on the current attitude of Alter’s board of directors toward us. We plan to do this by using our social network ties. We have three possible pathways to get the information that we need. Pathway A involves activating one tie (A1): The probability of its activation . Pathway B involves activating two ties (B1 and B2): The probabilities of their activation are and , respectively. Pathway C requires activating three ties (C1, C2, and C3): The probabilities of their activation is , , and , respectively. All of the above probabilities are independent. What is your estimate of the probability that at least one of these pathways will succeed providing the information that we seek?
Information accuracy.
Our organization has tasked one group to design an intelligence system with four independent agencies (A, B, C, and D) with the responsibility to deliver accurate information to policy makers. Our hope is that at least one of the agencies will deliver verified true information on each occasion that we need such information. Our estimates of these agencies’ probabilities of successful delivery of verified true information are , , , and , respectively. All of the above probabilities are independent. What is your estimate of the probability that at least one of these agencies will deliver accurate information to policy makers?
Investments.
We have invested funds in three businesses (A, B, and C), and we hope that at least one of them will succeed. The success of a business depends on three factors: (i) the probability of its retaining key customers, (ii) the probability of its keeping up with changes in the marketplace, and (iii) the probability of its managing cash flow properly. Most business startups fail, but when they succeed the payoff may be large. We estimate the probabilities of A’s success on each of the three factors as follows: , , and . We estimate the probabilities of B’s success on each of the three factors as follows: , , and . We estimate the probabilities of C’s success on each of the three factors as follows: , , and . All of the above probabilities are independent. What is your estimate of the probability that at least one of these three businesses will succeed?
Experimental Designs.
Subjects nested in groups.
Subjects were recruited from the undergraduate subject pool of our university and paid for their participation. The University of California, Santa Barbara Institutional Review Board approved the study, and all subjects provided written informed consent. Data were collected on 161 individuals assembled into 45 groups (19 triads and 26 tetrads). Each group considered a random permutation of the eight problems. The design is a standard prepost randomized design. No manipulation or deception is involved. Each subject is seated at different side of a large table with a calculator and note pad. One of the eight problems is posed to the group. (i) Individuals privately record their initial positions on the problem in the “mere presence” of other group members. (ii) A group discussion is then opened with the instruction, “Discuss the problem with the other members of your group. The goal is to reach an agreement. However, the conversation that you will have may or may not lead you to alter your initial answer, and you may not come to an agreement as a group.” (iii) Upon concluding the discussion, individuals privately record their final positions on the problem plus other information requested by the investigators on each individual’s distribution of weights to other group members: “Imagine that you have been given a total of 100 chips. Distribute these chips to indicate the relative importance of each member to determining your own final answer on this problem. The number of chips that you allocate to a particular member should indicate the extent to which that member provided information that you personally found useful and caused you to modify your approach to the problem. The number of chips that you allocate to yourself should indicate the extent to which your final answer was not affected by the conversation. If the conversation had no influence on you, then put 100 beside your own sign (name). If the conversation caused you to abandon your approach to the problem, then put 0 beside your own sign, and allocate all of the chips to one or more of the other members. If you did not entirely abandon your own approach to the problem, then put a number greater than 0 beside your sign and allocate the remainder to one or more others.” (iv) Then, another problem is posed, and so on, until the concluding problem of the random permutation of the eight problems is reached. A group has up to 30 min to respond to each problem. For each problem, the obtained data are the group’s -vectors of initial and final estimates and its matrix of allocated weights, which are measures of the model’s , , and constructs, respectively. In general, when individuals report the relative influences of other group members on their own opinion, they have no realistic basis of estimating the total direct and indirect influences of all other members of the network in which are embedded. These total influences, which are given by , are resultants of all of the walks in the network. In small groups, it is plausible that individuals’ postdiscussion reports of the relative influences of others on their own opinions might be confounded with their perceptions of the relative net contributions of its members in determining a group’s consensus opinion, when a consensus was reached. This potential confound has been previously investigated (19) on judgment issues. The investigation was on small groups in which individuals’ communications were constrained to dyadic telephonic interactions such that only some pairs of individuals could directly communicate (the communication structures investigated were varied). The present experiment is a face-to-face open communication design. In either case, corresponds to the F-J model’s first opinion update in a French–Harary–DeGroot group, and this an important update with respect to opinion changes. In the data of this paper, it is again found that has an independent significant contribution to the prediction of individuals’ observed final opinions, controlling for and . With 161 individuals nested in 45 groups with three to four members, each dealing with a sequence of eight issues, the experiment set up group-issue occasions in which individuals present an initial and final opinion, and individual-level behavioral observations of (initial, final) tuples of opinion. The collected data are available upon request beginning 12 mo after the publication date of this paper, which will allow us to complete our research agenda on it.
Single subjects.
No manipulation or deception is involved. Each subject is seated at table with a calculator and note pad. No other subject is present in the room during the experiment. Each subject is presented with a random permutation of the eight problems. Subjects have up to 25 min to respond to each problem. Data were collected on 30 subjects. With 30 subjects, each dealing with eight problems, 240 individual-level behavioral observations were obtained.
Statistical Analysis.
With individuals nested in groups each dealing with a sequence of eight issues, the collected data structure is a multilevel longitudinal design. The statistical analysis uses estimation models suitable to such longitudinal clustered data: STATA v12’s xtmixed (maximum likelihood multiple regression robust error) model and the xtmelogit (logistic regression) model.
Supplementary Material
Acknowledgments
We thank Wenjun Mei, Victor Amelkin, and Sose Abraamyan for their helpful contributions to this work and Janelle Pham, who administered the data collection. This work was supported by US Army Research Laboratory and US Army Research Office Grant W911NF-15-1-0577.
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1710603114/-/DCSupplemental.
References
- 1.Thorndike RL. The effect of discussion upon the correctness of decisions, when the factor of majority influence is allowed for. J Soc Psychol. 1938;9:343–363. [Google Scholar]
- 2.Barnlund CD. A comparative study of individual, majority, and group judgment. J Abnorm Psychol. 1959;58:55–60. doi: 10.1037/h0040823. [DOI] [PubMed] [Google Scholar]
- 3.Asch SE. Effects of group pressure upon the modification and distortion of judgments. In: Guetzkow H, editor. Groups, Leadership, and Men. Carnegie; Pittsburgh: 1951. pp. 177–190. [Google Scholar]
- 4.Asch S. Social Psychology. Prentice Hall; Englewood Cliffs, NJ: 1952. [Google Scholar]
- 5.Asch SE. Studies of independence and conformity: I. A minority of one against a unanimous majority. Psychol Monogr Gen Appl. 1956;70:1–70. [Google Scholar]
- 6.Sherif M. The Psychology of Norms. Harper; New York: 1936. [Google Scholar]
- 7.Laughlin PR, Adamopoulos J. Social combination processes and individual learning for six-person cooperative groups on an intellective task. J Pers Soc Psychol. 1980;38:941–947. [Google Scholar]
- 8.Laughlin PR, Ellis AL. Demonstrability and social combination processes on mathematical intellective tasks. J Exp Soc Psychol. 1986;22:177–189. [Google Scholar]
- 9.Proskurnikov AV, Tempo R. A tutorial on modeling and analysis of dynamic social networks. Part I. Annu Rev Contr. 2017;43:65–79. [Google Scholar]
- 10.Castellano C, Fortunato S, Loreto V. Statistical physics of social dynamics. Rev Mod Phys. 2009;81:591–646. [Google Scholar]
- 11.Anderson NH. Integration theory and attitude change. Psychol Rev. 1971;78:171–206. [Google Scholar]
- 12.Anderson NH. Social Attitudes and Psychophysical Measurement. 1982. Cognitive algebra and social psychophysics; pp. 123–148. [Google Scholar]
- 13.Friedkin NE, Johnsen EC. Social influence and opinions. J Math Sociol. 1990;15:193–206. [Google Scholar]
- 14.Friedkin NE, Johnsen EC. Social influence networks and opinion change. Adv Group Process. 1999;16:1–29. [Google Scholar]
- 15.French JRP. A formal theory of social power. Psychol Rev. 1956;63:181–194. doi: 10.1037/h0046123. [DOI] [PubMed] [Google Scholar]
- 16.Harary F. A criterion for unanimity in French’s theory of social power. In: Cartwright D, editor. Studies in Social Power. Institute for Social Research, Univ of Michigan; Ann Arbor, MI: 1959. pp. 168–182. [Google Scholar]
- 17.DeGroot MH. Reaching a consensus. J Am Stat Assoc. 1974;69:118–121. [Google Scholar]
- 18.Friedkin NE, Cook KS. Peer group influence. Socio Meth Res. 1990;19:122–143. [Google Scholar]
- 19.Friedkin NE, Johnsen EC. Social Influence Network Theory: A Sociological Examination of Small Group Dynamics. Cambridge Univ Press; New York: 2011. [Google Scholar]
- 20.Friedkin NE, Jia P, Bullo F. A theory of the evolution of social power: Natural trajectories of interpersonal influence systems along issue sequences. Sociol Sci. 2016;3:444–472. [Google Scholar]
- 21.Ravazzi C, Frasca P, Tempo R, Ishii H. Ergodic randomized algorithms and dynamics over networks. IEEE Trans Control Netw Syst. 2015;2:78–87. [Google Scholar]
- 22.Frasca P, Ravazzi C, Tempo R, Ishii H. Gossips and prejudices: Ergodic randomized dynamics in social networks. IFAC Proc Vol. 2013;46:212–219. [Google Scholar]
- 23.Proskurnikov AV, Tempo R, Cao M, Friedkin NE. 2017. Opinion evolution in time-varying social influence networks with prejudiced agents. arXiv:170406900.
- 24.Friedkin NE. Theoretical foundations for centrality measures. Am J Sociol. 1991;96:1478–1504. [Google Scholar]
- 25.Friedkin NE, Johnsen EC. Two steps to obfuscation. Soc Network. 2014;39:12–13. [Google Scholar]
- 26.Parsegov SE, Proskurnikov AV, Tempo R, Friedkin NE. Novel multidimensional models of opinion dynamics in social networks. IEEE Trans Automat Contr. 2016;62:2270–2285. [Google Scholar]
- 27.Galton F. Vox populi (the wisdom of crowds) Nature. 1907;75:450–451. [Google Scholar]
- 28.Surowiecki J. The Wisdom of Crowds. Anchor; New York: 2004. [Google Scholar]
- 29.Golub B, Jackson MO. Naive learning in social networks and the wisdom of crowds. Am Econ J Microecon. 2010;2:112–149. [Google Scholar]
- 30.Lorenz J, Rauhut H, Schweitzer F, Helbing D. How social influence can undermine the wisdom of crowd effect. Proc Natl Acad Sci USA. 2011;108:9020–9025. doi: 10.1073/pnas.1008636108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Janis IL. Victims of Groupthink. Haughton Mifflin; Boston: 1972. [Google Scholar]
- 32.Janis IL. Crucial Decisions. Free; New York: 1989. [Google Scholar]
- 33.McCauley C. The nature of social influence in groupthink: Compliance and internalization. J Pers Soc Psychol. 1989;57:250–240. [Google Scholar]
- 34.McCauley C. Group dynamics in Janis’s theory of groupthink: Backward and forward. Organ Behav Hum Decis Process. 1998;73:142–162. doi: 10.1006/obhd.1998.2759. [DOI] [PubMed] [Google Scholar]
- 35.Park W-W. A comprehensive empirical investigation of the relationships among variables of the groupthink model. J Organ Behav. 2000;21:873–887. [Google Scholar]
- 36.Parsons T. The Social System. Routledge; New York: 1951. [Google Scholar]
- 37.Hechter M, Opp K-D. Social Norms. Russell Sage Foundation; New York: 2001. [Google Scholar]
- 38.Friedkin NE, Proskurnikov AV, Tempo R, Parsegov SE. Network science on belief system dynamics under logic constraints. Science. 2016;354:321–326. doi: 10.1126/science.aag2624. [DOI] [PubMed] [Google Scholar]