Competitive network determines the direction of the diversity–function relationship

Significance

Diverse communities typically have higher functional potential (e.g., biomass production) because species use different resources and respond to different environmental cues. Yet, in highly competitive communities, individuals often grow less efficiently together due to intense competition for shared resources. Here, we show that the structure of the competitive network (i.e., who beats who) ultimately determines whether an increase in diversity leads to an increase or a decrease in functioning. The diversity–function relationship depended both on whether communities exhibited “rock–paper–scissors” (i.e., intransitive) dynamics, and whether they comprised strong versus weak competitors. These results highlight that knowledge of the competitive network may be integral for predicting when losses in biodiversity will have positive or negative effects on ecosystem function.

Abstract

The structure of the competitive network is an important driver of biodiversity and coexistence in natural communities. In addition to determining which species survive, the nature and intensity of competitive interactions within the network also affect the growth, productivity, and abundances of those individuals that persist. As such, the competitive network structure may likewise play an important role in determining community-level functioning by capturing the net costs of competition. Here, using an experimental system comprising 18 wood decay basidiomycete fungi, we test this possibility by quantifying the links among competitive network structure, species diversity, and community function. We show that species diversity alone has negligible impacts on community functioning, but that diversity interacts with two key properties of the competitive network—competitive intransitivity and average competitive ability—to ultimately shape biomass production, respiration, and carbon use efficiency. Most notably, highly intransitive communities comprising weak competitors exhibited a positive diversity–function relationship, whereas weakly intransitive communities comprising strong competitors exhibited a negative relationship. These findings demonstrate that competitive network structure can be an important determinant of community-level functioning, capturing a gradient from weakly to strongly competitive communities. Our research suggests that the competitive network may therefore act as a unifying link between diversity and function, providing key insight as to how and when losses in biodiversity will impact ecosystem function.

The relationship between biological diversity and ecosystem functioning is a central question in ecology and conservation, providing tangible links between natural systems and the provision of ecosystem services to humans. In recent decades, a wealth of studies have explored how ecosystem functioning responds to changes in various types of diversity (e.g., species, trait, or phylogenetic diversity), revealing the highly idiosyncratic nature of this relationship across systems (1). Functionally unique species with mutually exclusive resource requirements can exhibit greater productivity in diverse communities (2), whereas highly similar species with overlapping niches exhibit minimal increases in functioning as diversity increases (1, 3). Although the field of biodiversity–ecosystem function (BEF) research continues to gain momentum, the sheer complexity of ecological communities complicates the search for unifying patterns (1). As such, in most systems, we still lack the ability to predict a priori how changes in biodiversity will alter ecosystem function.

The BEF relationship is often linked to the degree of functional redundancy, complementarity, or niche overlap among species (4–6). Yet this relationship can alternatively be formulated in terms of the nature, variability, and intensity of competitive interactions among species (7–9). Competitive dynamics and competitive relationships among species can attenuate or reverse BEF relationships (10–13), driven by both the direct effects of competition (e.g., reductions in per capita growth rate) and indirect effects (e.g., community turnover or overyielding of dominant species). Thus, the structure of the competitive network—that is, the complete set of pairwise competitive outcomes among species (14)—should play an important role in the BEF relationship by dictating the nature and intensity of competitive interactions (and corresponding functional costs) exhibited across species in the community. Although the structure of the competitive network is increasingly acknowledged as an important driver of biodiversity and coexistence in competitive communities (14–16), whether or not the competitive network likewise affects ecosystem function remains largely untested.

Here, we explore how the competitive network interacts with species richness to determine the BEF relationship in competitive fungal communities. We focus on two measures of the competitive network: (i) competitive intransitivity (a continuous measure of the extent to which the community exhibits rock–paper–scissors relationships) and (ii) mean competitive ability (a continuous measure of how competitive the individuals in the community are, based on fully factorial pairwise interactions). These two properties were selected because of their importance in determining biodiversity and coexistence patterns across systems (15–17). We use a saprotrophic basidiomycete fungal community for several reasons. First, these organisms provide a tractable means of measuring the full set of pairwise competitive outcomes among species, thereby allowing us to precisely quantify the full competitive network (15). Second, our knowledge of the mechanisms underlying the BEF relation remains particularly elusive in fungal and bacterial systems (18–20), in part due to complex competitive dynamics that drive both positive and negative BEF relationships (21–25). Last, basidiomycete fungi comprise an important functional guild from a carbon cycle perspective, being the dominant decomposers of recalcitrant organic material in forested ecosystems (26–29). Understanding how and when diversity affects function in basidiomycete communities therefore has important secondary implications for terrestrial carbon storage (30).

Using a set of 18 unique fungal species with previously measured traits, phylogenies, and competitive hierarchies (15, 31) (Table S1, Fig. S1, and Dataset S1), we explored how increasing levels of species richness interacted with the competitive network structure to determine community function. We selecting 150 unique communities comprising 3, 6, or 12 unique fungal species, with 50 unique communities per richness level (Materials and Methods and Dataset S2). Functioning was measured via biomass production, respiration, and carbon use efficiency (CUE; the ratio of carbon allocated to biomass vs. respiration), and we focus predominantly on CUE throughout, given its central role as a net measure of overall organismal function in fungi and bacteria (32). To capture the structure of the competitive network, we first competed all fungi against each other in all pairwise combinations (Dataset S1) (15). These outcomes were then used to calculate continuous measures of “average competitive ability” and “competitive intransitivity.” Both of these metrics vary between 0 and 1: A value of 0 indicates a community that is perfectly hierarchical or comprises the weakest competitors, and a value of 1 indicates a community that is perfectly intransitive or comprises the strongest competitors (Fig. S2; see also Materials and Methods and SI Materials and Methods). Using these network metrics, we quantified how species richness, intransitivity, and competitive ability interactively determine biomass production, respiration, and CUE.

Table S1.

The 18 wood decay basidiomycete fungi used in the experiment

Latin binomial	Reference name
Hyphoderma setigerum (Fr.) Donk	h.seti
Laetiporus caribensis Banik & D.L. Lindner	l.carib
Laetiporus conifericola Burds. & Banik	l.conif
Laetiporus gilbertsonii Burds.	l.gilb
Laetiporus huroniensis Burds. & Banik	l.huron
Lentinus crinitus (L.) Fr.	l.crin
Merulius tremellosus Schrad.	m.trem
Phellinus gilvus (Schwein.) Pat.	p.gilv
Phellinus hartigii (Alesch. & Schnabl.) Pat.	p.har
Phellinus robiniae (Murrill) A. Ames	p.robin
Phlebia rufa (Pers.) M.P. Christ.	p.rufa
Phlebiopsis flavidoalba (Cooke) Hjortstam	p.flav
Porodisculus pendulus (Schwein.) Schwein.	p.pend
Pycnoporus sanguineus (L.) Murrill	p.sang
Schizophyllum commune (Fr.)	s.comm
Tyromyces chioneus (Fr.) P. Karst.	t.chion
Xylobolus subpileatus (Berk. & M.A. Curtis) Boidin	x.sub

“Reference names” refer to the shorthand names used in Datasets S1 and S2. All trait data, pairwise competitive outcomes, and competitive rankings are given in Dataset S1. In addition to phylogenetic relatedness, a suite of functional traits was measured for each fungus, including wood decomposition rate over 12 wk, hyphal extension rate, hyphal density, the production of five hydrolytic enzymes (leucine aminopeptidase, cellobiohydrolase, acid phosphatase, N-acetyl-ß -glucosaminidase, and β-glucosidase), and the production of three oxidative enzymes (two phenol oxidases and one peroxidase). Trait data were used to calculate functional dissimilarity (Rao’s Q), which was included as a predictor in the statistical models (Table S2). Detailed methods for trait measurements are given in ref. 15.

Fig. S1.

The phylogenetic tree for the 18 fungi. DNA sequences were aligned using MAFFT version 6 (55) using the Q-INS-I algorithm for the alignment of ITS and the G-INS-I algorithm for LSU sequences. The combined LSU+ITS dataset was constructed by concatenating both alignment files, and the evolutionary history was inferred by using Maximum Likelihood methods by calculating the bootstrap consensus tree from 500 replicates. The tree is drawn to scale, with branch lengths measured in the number of substitutions per site. Phylogenetic pairwise distances were calculated for all 18 isolates using MEGA version 5 (56) using the number of differences for all nucleotide positions with greater than 95% site coverage. Phylogenetic dissimilarity (mean pairwise distance) was calculated for each community and included as a predictor in the statistical models (Table S2).

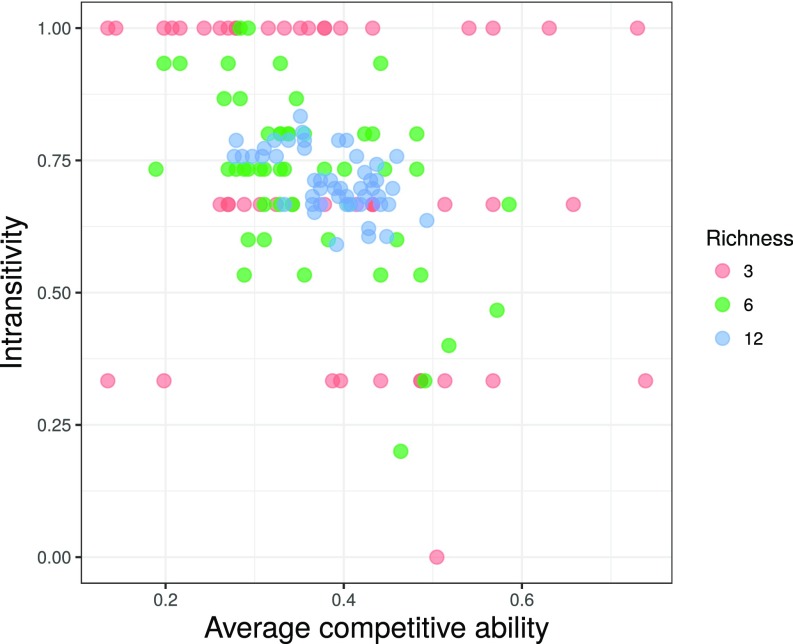
Fig. S2.

The community-level values of intransitivity and competitive ability for the 150 communities used in the experiment. Communities with low intransitivity values (i.e., reflecting a hierarchical community) are relatively rare, particularly at high species richness. This is driven by the fact that even the strongest competitors deadlock or lose to roughly 30% of the other species (see Dataset S1 for full competitive outcomes). Furthermore, as richness increases, the law of large numbers causes communities to cluster closer to the mean competitive ability of $\sim$0.5, and an intransitivity level of $\sim$0.65. Because of these inherent correlations between richness, intransitivity, and competitive ability, we used a simulation approach to explore the patterns that emerge across a random subset of communities (Fig. 4 and Fig. S4).

Due to inherent relationships among network properties, some network structures and corresponding diversity–function patterns may be exceedingly rare in natural systems. For example, at high richness levels, it is increasingly unlikely that communities comprising weak competitors will, by chance alone, happen to exhibit a perfectly hierarchical structure, since these weak competitors, by definition, have low rates of overgrowth. Alternatively, because of the law of large numbers, the average competitive ability of species in a community should start to converge to 0.5 at high richness levels (e.g., Fig. S2). Such phenomena are not otherwise reflected in statistical models. Thus, to gain insight into how such constraints might alter the “realized” diversity–function patterns across the landscape, we secondarily used a simulation approach to quantify the BEF patterns that emerge across a broad set of communities. We randomly selected 20,000 unique communities comprising the 18 fungal isolates (richness ranging from 3 to 12), and used the statistical models to calculate the CUE of each community (Materials and Methods). By reflecting the underlying relationships and constraints between competitive network properties, this complementary approach allows us to explore how the statistical patterns scale to larger metacommunities.

SI Materials and Methods

Calculating Intransitivity.

There are numerous approaches for calculating competitive intransitivity; however, most assume a binary win/loss outcome, such that they cannot easily allow for deadlocks among species. Thus, we use an approach proposed by ref. 47 to calculate “transitivity in probability,” where the measure of intransitivity refers to the stochastic probability that one species displaces another. The competitive outcomes (win, loss, tie) for all pairings were converted into a pairwise competition matrix, with a value of “1” representing a win and a value of “0” representing a loss. Pairings that resulted in a draw were assigned a value of 0.5, representing only stochastic fluctuations in outcomes when interacting (see Dataset S1). Following ref. 47, we calculated a measure of intransitivity for each of the 150 communities used in the experiment by first permutating the rows and columns of their competition matrix to find the ordering with the maximum number of matrix entries > 0.5 in the upper right triangle (an approach first proposed by ref. 50). Note that this can be computationally intensive, requiring nearly 500 million permutations to be checked for a 12-species community. After sorting, we calculated a normalized measure of intransitivity, taken as the relative proportion of entries in the upper right triangle that were less than their corresponding entry in the lower left triangle. That is,

$$\text{Intransitivity}=\frac{\sum I(a_{ij}<a_{ji})}{n(n-1)/2},$$

where the summation is taken over all $i<j$, and the operator $I\mathit{\text{(}}\cdot \mathit{\text{)}}$ is the indicator function, which equals 1 if $a_{ij}<a_{ji}$ and 0 otherwise. This value ranges between 0 (completely hierarchical) and 1 (completely intransitive). See Dataset S2 for the community-level intransitivity measurements.

Competitive Rankings and Average Competitive Ability.

Some isolates were strongly defensive, neither winning nor losing against strongly combative fungi; others were strongly offensive, rarely deadlocking but having high rates of wins and losses (Dataset S1). To capture this variation in combative strategies, we used the Elo Ranking system (48) in the PlayerRatings package in R. As opposed to standard rankings, Elo penalizes a highly ranked competitor if it loses against a weak competitor, and assigns a higher rank to a weak competitor if it draws or wins against stronger competitors. Whereas a simple hierarchy based on win percentage would assign a low rank to a species with a high number of draws but no wins, the Elo system ranks these species closer to the middle of the hierarchy. This approach better captured variation among “defensive” competitors and “weak” competitors in our study system (15).

Given that the Elo rating system was originally designed for ranking chess players, it does not return readily interpretable values (the raw rankings ranged between 2,000 and 2,500 for this system). Thus, these values were subsequently standardized between 0 and 1 for use here. Note that the full ranking was obtained using a more diverse community comprising 37 isolates (15), and so the lowest rated species used here has a value of 0.05 (Laetiporus huroniensis) rather than exactly 0.

For each experimental community, an estimate of average competitive ability and variance in competitive ability was calculated by taking the simple average and the empirical variance of these ranks across all species in the community. See Dataset S1 for the individual rankings and all of the pairwise competitive outcomes, and see Dataset S2 for the community-level values of average competitive ability and variance in competitive ability.

Functional and Phylogenetic Dissimilarity.

Functional dissimilarity and phylogenetic dissimilarity were calculated for each community and included as potential confounding variables, given that these community characteristics can independently affect functional outcomes (51, 52). Functional dissimilarity was calculated using Rao’s quadratic entropy (53) in the FD package in R, using 11 functional traits: wood decomposition rate (% mass loss over 12 wk), enzyme activity of five hydrolytic and three oxidative enzymes (given in units of fluorescence and absorbance, respectively), hyphal density (micrograms of dry mass per square centimeter), and growth rate (millimeter extension per day). See Dataset S1 for the complete data, and see ref. 15 for detailed methods of trait measurements. Functional dissimilarity was included as a predictor in the statistical models (Table S2), and is included in Dataset 2.

Table S2.

Model-based coefficients and corresponding standard errors

Variable	Biomass 13C	Respiration 13C	CUE
Avg. monoculture biomass	$-$0.235* (0.112)	$-$0.195* (0.098)
Avg. monoculture respiration	0.591* (0.271)	0.561* (0.221)
Avg. monoculture CUE
Richness	$-$0.008 (0.009)	$-$0.013 (0.007)	0.008 (0.010)
Functional dissimilarity (Rao’s Q)	$-$0.007 (0.007)	$-$0.022*** (0.005)	0.033*** (0.009)
Phylogenetic dissimilarity (MPD)	$-$0.001*** (0.0002)	$-$0.0004** (0.0001)
Variation in competitive ability	$-$0.018 (0.026)	$-$0.013 (0.020)
Average competitive ability	0.170 (0.087)	0.045 (0.066)	0.161 (0.107)
Intransitivity	0.091 (0.056)	0.073 (0.042)	0.002 (0.064)
Richness $\times$ variation in ability	0.011* (0.005)	0.008* (0.004)
Richness $\times$ avg. ability	$-$0.006 (0.009)	0.016* (0.007)	$-$0.033** (0.011)
Richness $\times$ intransitivity	0.018** (0.007)	0.002 (0.005)	0.022* (0.009)
Intransitivity $\times$ avg. Ability	$-$0.372*** (0.101)	$-$0.208*** (0.078)	$-$0.156 (0.113)
Observations	146	146	146
Adjusted R2	0.677	0.468	0.578
Residual SE	0.021 (df = 122)	0.016 (df = 122)	0.032 (df = 129)
F statistic	14.233*** (df = 23; 122)	6.535*** (df = 23; 122)	13.412*** (df = 16; 129)

Variables were retained in the final model if they had a corresponding P value of <0.10. Note that coefficients are not standardized here, as they are in Fig. 2 and as they are reported in the main text. An increase in phylogenetic dissimilarity and functional dissimilarity (FD) led to decreases in biomass and respiration. These decreases largely offset each other with regard to phylogenetic similarity and CUE (not retained in the final model, since P >0.10). The proportional decrease in respiration attributed to FD was significantly less than the corresponding decrease in biomass, leading to a significant increase in CUE with greater functional dissimilarity (P <0.001). Variation in competitive ability exhibited significant positive interactions with richness for both biomass and respiration (P =0.02 and P =0.03, respectively), but these effectively offset each other such that variation in competitive ability was uninformative with respect to CUE (P >0.10). Community-weighted average biomass and average respiration were both significant predictors of biomass and respiration, but were not predictive of community-level CUE. Average monoculture CUE was not predictive of any outcome and was not retained in any model. (^∗P <0.05; ^∗∗P <0.01; ^∗∗∗P <0.001.)

Phylogenetic dissimilarity was calculated using mean pairwise phylogenetic distance (54) using the concatenated ITS and LSU sequences for each fungus (Fig. S1). Phylogenetic analysis for these isolates is outlined in detail in ref. 15. Briefly, DNA sequences were aligned using Multiple Alignment using Fast Fourier Transform (MAFFT) version 6 (55) using the Q-INS-I algorithm for the alignment of ITS and the G-INS-I algorithm for LSU sequences. The combined LSU+ITS dataset was constructed by concatenating both alignment files, and the evolutionary history was inferred using Maximum Likelihood methods by calculating the bootstrap consensus tree from 500 replicates. Phylogenetic pairwise distances were calculated for all 18 isolates using Molecular Evolutionary Genetics Analysis (MEGA) version 5 (56) using the number of differences for all nucleotide positions with greater than 95% site coverage. Phylogenetic dissimilarity (mean pairwise distance) was calculated for each community and included as a predictor in the statistical models (Table S2), and is included in Dataset 2.

Results and Discussion

Without accounting for competitive network properties, an increase in species richness was not correlated with changes in biomass (Fig. 1A; $\beta$ = 0.001, $P=0.37$), nor with respiration (Fig. 1B; $\beta$ = 0.002, $P=0.10$), or CUE (Fig. 1C; $\beta$ = $-0.0002$, $P=0.83$), such that richness explained <1% of the variation in each of these functional outcomes. These same fungal species were previously found to exhibit reductions in biomass and CUE in mixtures relative to monoculture (31), such that our expectation was that increases in diversity would lead to further reductions in functioning. Yet the null effect of richness instead suggests that the induced costs of competition at the individual level are relatively fixed, regardless of the number of competitors present. Conversely, the fact that these communities likewise failed to exhibit a positive BEF relationship is in line with traditional BEF theory, given that the microcosms were intentionally designed to provide minimal opportunities for niche differentiation, facilitation, or environmentally driven species averaging, which can otherwise drive significant positive BEF relationships (7, 24, 25).

Fig. 1.

The mean relationships between species richness and biomass, respiration, and CUE. Without accounting for competitive network properties, an increase in species richness was unrelated to (A) biomass, (B) respiration, or (C) CUE. Richness explained <1% of the variation in each of these functional outcomes $(n=46)$.

However, once the competitive network variables were included in the model, there emerged strong pairwise interactions among intransitivity, competitive ability, and richness (Fig. 2 and Table S2). The coefficients for CUE largely mirrored the net response of the biomass and respiration functional endpoints (Fig. 2), reflecting the fact that CUE is calculated as the net allocation of carbon (C) to growth versus respiration. CUE was affected by a significant negative interaction between richness and competitive ability ($\beta$ = −0.27, P = 0.006), driven by their positive interactive effects on respiration and null interactive effect on biomass. CUE was likewise influenced by a significant richness-by-intransitivity interaction due to the positive interactive effects of these variables on biomass and null interactive effect on respiration. With all other variables held constant at their mean (including species richness), more competitive communities exhibited significantly lower CUE ($\beta$ = −0.39, $P<0.001$), whereas more intransitive communities exhibited higher CUE ($\beta$ = 0.37, $P=0.03$). These results suggest that the links between diversity and function differ markedly in communities with different competitive network structures, with both competitive intransitivity and mean competitive ability being significant drivers of community functioning.

Fig. 2.

Standardized effect sizes linking richness, intransitivity, and competitive ability to biomass, respiration, and CUE. Shown are the effect sizes with corresponding 95% CIs. Variables were standardized to have a mean of 0 and an SD of 1, such that the main effects are interpretable as the change in the outcome with all other variables held constant at their mean. The full regression models explained 68% of the variation in biomass, 47% of the variation in respiration, and 58% of the variation in CUE. Biomass and CUE largely showed matching trends, driven by the fact that biomass was more closely linked to CUE than to respiration (Fig. S3). Both biomass and CUE showed significant relationships with competitive ability, intransitivity, and richness. Respiration responded most strongly to the interaction between richness and competitive ability, and the interaction between intransitivity and competitive ability $(n=146)$.

Fig. S3.

Relationships among functional outcomes. (A) Net ¹³C in biomass was strongly correlated with total biomass (r = 0.85, $P<0.001$), with this relationship exhibiting higher variance in communities with large biomass. (B) Respiration and biomass were moderately correlated (r = 0.36, $P<0.001$), and (C) CUE was strongly correlated with biomass (r = 0.80, $P<0.001$) but (D) weakly correlated with respiration (r = −0.24, $P=0.004$). Point sizes denote richness levels (3, 6, or 12 species), with larger diameters indicating higher richness.

Most strikingly, when plotted against a range of intransitivity and competitive ability values, the slope of the diversity–function relationship depended on the interactions between intransitivity and mean competitive ability (Fig. 3). Among highly intransitive communities, an increase in richness increased biomass production, with this effect tapering off for more competitive communities at high intransitivity (Fig. 3A, blue portion). In contrast, the effect of richness on respiration was more strongly influenced by the average competitive ability of the community, such that highly competitive communities exhibited higher respiration in response to increasing richness (Fig. 3B, red portion), whereas weakly competitive communities exhibited lower respiration with increasing richness (Fig. 3B, blue portion). Combined, the contrasting interactions with intransitivity (for biomass) and competitive ability (for respiration) led to a positive diversity effect on CUE only among highly intransitive communities comprising weak competitors ($\sim$10% absolute increase, Fig. 3C, blue portion). In all other settings, an increase in richness led to an absolute decrease in CUE of as much as 5% (Fig. 3C, red portion), with this reduction being strongest in highly competitive communities with low intransitivity (Fig. 3C, upper left corner).

Fig. 3.

The effect of diversity on function. Shown are the marginal coefficients (slopes) denoting the change in functional outcomes for an increase in richness of three species, plotted across the full range of intransitivity and competitive ability values. Red denotes a decrease in functioning, and thus corresponds with a decrease in biomass and CUE in A and C, but an increase in respiration in B. (A) Increasing richness corresponds to a decrease in biomass for everywhere except highly intransitive communities, where the increase in biomass is stronger at lower levels of competitive ability. (B) Highly competitive communities (>0.4) exhibited an increase in respiration with the addition of more species (red), with this effect negligibly modified by intransitivity ($P>0.10$ for the interaction). (C) An increase in richness corresponds to a decrease in CUE for all but the least competitive communities. Among weak competitors, an increase in richness translates to an increase in CUE (blue portion, lower right), with this effect being more pronounced at high intransitivity levels $(n=146)$.

These results illustrate that the impact of diversity on fungal function exists along a continuum of competitive dynamics. In the absence of other ecological forces, communities strongly structured by competition may exhibit negative diversity–function relationships, due to greater investment in competitive activities with the addition of more competitors. Conversely, communities minimally structured by competition may instead exhibit positive diversity–function relationships. These positive relationships might arise because of negligible negative effects of competitive interactions on individual productivity, or, in fungal-specific cases, potentially due to greater investment in defensive activities that increase biomass [i.e., defensive wall building to prevent overgrowth by competitors (31)]. Quantifying the relative influences of exploitative versus interference competition may help to resolve why such a broad range of diversity–function relationships is observed for fungal communities (22, 24, 25, 33).

An often overlooked aspect of competitive network theory is that some competitive network structures are correlated with species richness, and should therefore become more or less likely to occur in diverse communities. Indeed, when our results were applied to 20,000 randomly selected communities, clear patterns emerged between CUE and richness (Fig. 4) that were not otherwise evident from the statistical models. In line with our empirical results, intransitive, strongly competitive communities had a neutral richness relationship ($\beta$ = 0.001, $P=0.273$; Fig. 4A), and hierarchically structured, weak competitors had a slightly positive relationship between CUE and richness ($\beta$ = 0.004, $P<0.001$; Fig. 4B). However, both of these community types became increasingly rare at higher richness levels—reflecting inherent constraints between network properties—such that they comprised less than 1% of the communities with more than 10 species. The low abundance of hierarchically structured, weak competitors is presumably due to the fact that weak competitors, by definition, have poor displacement ability, such that a random assemblage of weak competitors is unlikely to exhibit sufficient displacement to establish a perfectly hierarchical community. Conversely, the low abundance of intransitive, strong competitor communities is likely because strong competitors have high displacement ability, such that it becomes increasingly unlikely that a random assemblage of these species will exhibit perfect rock–paper–scissors relationships as the number of species increases. Collectively, these results suggest that these two network structures and their corresponding BEF relationships should be exceedingly rare in natural systems.

Fig. 4.

The realized patterns between richness and CUE across a random sample of communities: 20,000 randomly sampled communities were divided into high vs. low intransitivity and high vs. low competitive ability based on the 33rd and 66th percentiles across all communities. In line with the model predictions, (A) intransitive communities comprising strong competitors and (B) hierarchical communities comprising weak competitors showed moderate positive relationships. However, these two types of communities became increasingly rare as richness increased, ultimately comprising <1% of all communities with 10 or more species. At these higher richness levels, three clear groups emerged, each with pronounced differences in the slope of the BEF response: (C) Hierarchical communities comprising strong competitors exhibited a negative diversity–function relationship; (D) highly intransitive communities comprising weak competitors exhibited a positive diversity–function relationship; and, last, communities that fell into none of these four categories (data shown in Fig. S4) exhibited a null relationship between diversity and function. Thus, although on aggregate there appears to be no link between diversity and function (Fig. 1 and Fig. S4), this result can be attributed to offsetting BEF relationships between these different network structures (see SI Discussion).

At higher richness levels, the two most common network structures were intransitive communities comprising weak competitors and hierarchical communities comprising strong competitors (Fig. 4 C and D). The markedly different diversity–function relationships between these two groups highlights that the competitive network has the potential to promote fundamentally different diversity–function relationships across the landscape. Nevertheless, if we ignore the differential responses of these four groups, the overall relationship between diversity and function across all 20,000 communities is negligible (Fig. S4)—as seen in the experimental results (Fig. 1)—highlighting that these offsetting BEF patterns essentially negate each other when taken on aggregate (see SI Discussion). Thus, at the landscape level, these findings illustrate that knowledge of the competitive network can help to disentangle underlying BEF relationships by identifying which subsets of communities are likely to display significant positive or negative diversity–function responses.

Fig. S4.

(A) The model-based predictions for all 20,000 communities. Mirroring the experimental results in Fig. 1, there appears to be no relationships between diversity and function when taken on aggregate ($\beta$ = −0.0000007; $P=0.32$). Thus, although there are significant relationships between diversity, function, and competitive network structure, different network structures lead to contrasting responses (some with a negative BEF, some with a positive; Fig. 4), which effectively negate each other, leading to a null overall response if we fail to account for network structure. (B) Shown are the model-based CUE estimates for communities whose intransitivity value and/or mean competitive ability value fell between the 33rd and 66th percentiles across all communities, such that they were not classified into one of the four categories shown in Fig. 4. These “intermediate” communities showed a null relationship between richness and CUE ($\beta$ = 0.00001, $P=0.83$), and were common throughout the range of richness levels.

These results suggest that intransitivity is not only critical for maintaining diversity (14, 15), but is also a key driver of productivity and efficiency in competitive communities. Yet exactly how intransitivity affects community-level functioning is not immediately apparent. From a coexistence perspective, intransitive loops can provide a type of indirect benefit (or harm) to species by reducing the importance of direct pairwise outcomes (i.e., “the enemy of my enemy is my friend”) (15, 34). Analogous to indirect interactions in food webs (35), species’ abundances in competitive communities can thus be an emergent byproduct of the full set of interactions within the community (14, 36). From a functional perspective, it is therefore plausible that intransitivity predicts functional outcomes because it captures the net costs of these indirect interactions, and thereby reflects the average intensity of competition perceived by each individual. If indeed this is the case, then, as with trophic systems (37), the importance of intransitivity as a driver of functioning will likely depend on the relative importance of direct vs. indirect interactions in the system.

Intransitive competition and competitive hierarchies are important drivers of coexistence and biodiversity in nonfungal communities [e.g., grassland plant communities (16, 38)]. Nevertheless, an important outstanding question is whether or not these results extend to other systems. Indeed, the observed patterns among richness, intransitivity, competitive ability, and functioning are certain to be context-dependent, even among fungal communities. Some fungi (e.g., basidiomycetes, as used here) are known to prioritize competitive behaviors relative to other fungi (28), with these behaviors heavily modified by environmental conditions (18, 31, 39, 40). Alternately, in communities where interspecific interactions alter functioning predominantly via indirect changes in community composition or by differential responses to environmental variability—rather than via direct competitive interactions—the links between diversity and function should depend more strongly on the correlations between competitive ability and functioning (11, 12).

Over long timescales, or in the presence of environmental variability, various ecological processes such as species averaging, overyielding, or selection effects may overwhelm the short-term relationships observed here (4, 5, 25, 41). Such long-term processes should be particularly relevant in systems where the functional endpoint of interest (e.g., plant primary productivity) correlates strongly with competitive ability or environmental conditions, such that changes in community composition or environmental conditions correlate with predictable changes in community functioning (41). Disentangling the importance of direct effects (induced changes in functioning) vs. indirect effects (changes in functioning due to community turnover) is therefore an important next step for identifying when and where induced competitive costs scale to long-term patterns (42). Nevertheless, by showing that the competitive network structure has the potential to play a key role in linking diversity to function, we demonstrate a mechanism by which species interactions directly determine the strength and direction of the BEF relationship. The relative importance of this mechanism in situ will only be revealed by exploring its context dependency and its importance in relation to other biotic and abiotic controls.

SI Discussion

The goal of the simulation experiment is twofold: first, to explore how inherent correlations between richness and the competitive network constrain the realized patterns we observe across the metacommunity, and, second, to explore the relative importance of the competitive network structure and richness in relation to additional confounding factors (e.g., phylogenetic or functional diversity, or species-specific effects). Out of 20,000 communities, $\sim$4% were classified as highly intransitive, strong competitors (Fig. 4A), 3% were classified as hierarchical, weak competitors (Fig. 4B), 15% were classified as hierarchical, strong competitors (Fig. 4C), and 21% were classified as intransitive, weak competitors (Fig. 4D). The remaining 55% of communities (Fig. S4B) fell within the 33rd and 66th percentile for either intransitivity or average competitive ability, such that they were not classified into any of the four cases.

If we completely ignore the role of the competitive network, we see essentially no relationship between diversity and function (Fig. S4A), mirroring the experimental outcomes (i.e., Fig. 1). However, when we break down the communities into those that have high vs. low intransitivity and high vs. low competitive ability, we see clear patterns emerge (Fig. 4). Moreover, the two dominant groups that emerge—hierarchical, high competitive ability and intransitive, low competitive ability—have essentially offsetting trends. Thus, despite the fact that the competitive network plays an important role in determining community-level function, these contrasting relationships effectively offset each other, such that, when taken on aggregate, there appears to be no relationship.

Once richness is greater than approximately eight species, it becomes exceedingly rare that a community is hierarchical with low competitive ability, or that it is intransitive with high competitive ability, reflecting inherent correlations within the network that constrain the realized set of network structures (e.g., Fig. S2). Thus, our results suggest that there should be three clear groups (and three different corresponding BEF relationships) that we predominantly observe in natural settings: hierarchical communities with high competitive ability (negative BEF), intransitive communities with low competitive ability (positive BEF), and communities with moderate intransitivity and moderate competitive ability (null BEF).

Conclusion

We demonstrate that two key aspects of the competitive network structure—intransitivity and average competitive ability—interactively determine the direction and magnitude of the diversity–function relationship in a competitive fungal system. Our results suggest that the competitive network structure captures a continuum from highly competitive communities to minimally competitive communities, with these groups having widely different functional responses to increasing richness. In communities strongly structured by competitive activities (highly competitive, weakly intransitive assemblages), diversity had a negative effect on functioning, whereas, in communities with minimal investment in competition (weakly competitive, highly intransitive assemblages), diversity had a positive effect. By demonstrating that intransitivity can dictate functioning as well as diversity, our results identify a potential mechanism underpinning diversity–function relationships in competitive communities.

Materials and Methods

Fungal Isolates.

The 18 wood decay basidiomycete fungal isolates used in this study have been previously discussed in detail (15, 31) (see SI Materials and Methods, Table S1, Fig. S1, and Dataset S1). All were obtained from the culture collection at the US Forest Service Center for Forest Mycology Research, and were originally collected from fruiting bodies on dead wood in the early to middle stages of decay. All species are endemic to mixed hardwood forest throughout North America, with most having widespread global distributions. These 18 species were selected to capture a range of taxonomic, phylogenetic, and functional diversity values, while also ensuring that all species are prominent decomposers of dead wood during at least a portion of their life cycle. The original species pool included 23 unique species and 37 total unique isolates (15). Eighteen of these species were selected for inclusion here, based on those that showed adequate growth over the course of 20 d (at least 2-cm-diameter radial expansion). Large subunit (LSU) and internal transcribed spacer (ITS) sequences for these 18 isolates are available in GenBank (accession numbers KX065932–KX065968 and KX065969–KX066002), as submitted in ref. 15.

Community Selection.

Following the approach outlined in Dias et al. (43), communities were selected from among the $\sim$37,000 possible combinations using a stratified random sampling scheme to ensured that each richness level included a range of competitive abilities and intransitivity values. Specifically, for each richness level, communities were divided into high vs. low competitive ability crossed with high vs. low intransitivity, and communities were selected at random from each of these four quadrants ($\sim$12 communities for each combination for each richness level). The benefit of this approach is that it has the statistical power to identify underlying mechanistic relationships; the drawback is that it may not necessarily reflect which relationships (and functional outcomes) are most common across the metacommunity. Thus, we subsequently conducted a simulation experiment to explore how these model-based relationships scale to a fully random selection of communities (Quantifying Patterns Across Communities).

Microcosm Design.

Following traditional diversity–function study designs (41, 44, 45), all microcosms, including the monocultures, were “seeded” with the same initial number of fungal colonies, regardless of richness level, thus ensuring that any resulting effects were not confounded by differing colony densities among treatments. All plugs of each species were taken from a single colony, such that, after meeting other genetically identical individuals, they would fuse to form a single cohesive colony. However, some degree of “intraindividual” aggression is expected (e.g., a time delay before fusing), so that our design should be interpreted as quantifying the effect of species richness after accounting for intraindividual effects (31). Previous work showed that 10 d was sufficient for identifying the costs of competition (31). We extended this time period to 20 d to better capture complex community dynamics that may not manifest over shorter time periods (e.g., combative species overgrowing close neighbors but then deadlocking with species on the other side of the dish). To account for this longer time period, we increased the C in the media (2% vs. 4% malt extract agar) to ensure that C was nonlimiting over the course of the experiment.

Biomass Harvesting.

After 20 d, a total of 40 plugs, 7 mm diameter each, were subsampled from each dish using a sterilized cork borer (11% of the plate subsampled by area) and used to estimate the ¹³C present in the biomass plus agar media. The plugs were placed in a preweighed tin and dried at 65 °C to constant mass. Fungal biomass in the remaining media was recovered using standard approaches (26, 31). Briefly, the remaining media was heated to 121 °C for 5 min to melt the agar. The solution was filtered through a 53-μm sieve and rinsed with 1 L of 90 °C deionized water, agitating slightly to remove residual agar, and subsequently rinsed for 2 min with 20 °C deionized water. The resulting biomass was dried at 65 °C to constant mass and weighed. The dried biomass and the dried plugs (agar + biomass) were milled with a mortar and pestle into a fine powder, and analyzed for total %C and atm% ¹³C content (ESC4010; Costech Analytical Technologies Inc.).

Quantifying Community Function.

Community function was quantified three ways, via net productivity (biomass production), net respiration, and CUE, all of which were measured using the ¹³C label. Total biomass in the dish was estimated by scaling the recovered biomass by the inverse proportion of the dish that was subsampled for ¹³C content of the media (i.e., multiplied by 1/0.89 to account for the 11% removed). The atm% ¹³C label in both the dried biomass and plugs was calculated using the standard mixing equation: (¹³C in sample – ¹³C in media) × (99.995 – ¹³C in media)⁻¹, with the atm% ¹³C in the media previously estimated at 1.08. This percentage was then scaled to a mass basis (i.e., milligrams of ¹³C per sample) based on the %C and the total mass of the sample. Respired ¹³C was estimated by calculating the difference between the total ¹³C added to each plate and the amount of ¹³C recovered in the biomass plus the amount remaining in the plate. CUE was measured by taking the ratio of total mass of ¹³C in the biomass, relative to the total amount of ¹³C removed from the media [i.e., CUE = ¹³C in biomass $\cdot$ (¹³C in biomass + ¹³C in respiration)⁻¹] (31, 46).

Competition Experiments.

Pairwise competitive outcomes were obtained previously (15) and used to calculate competitive ranks and intransitivity. Briefly, all 18 fungi were competed against each other in all pairwise combinations ($n=153$ unique pairings; see ref. 15). Three 5-mm-diameter plugs were inoculated onto one side of the dish, 1 cm apart in a straight line, ∼2 cm from the center of the dish. Fungi were plated at different times, based on monoculture growth rate, to ensure that each was approximately 1 cm from the center of the dish at the “start” of the experiment. After both fungi were inoculated in each plate, the microcosms were sealed and incubated at 22 °C for up to 8 wk. Competitive outcomes were scored as a win, loss, or draw. The full data and competitive outcomes are available in Dataset S1.

Competitive Network Properties.

Using these pairwise outcomes, we calculated community-level intransitivity values for each community using a probabilistic approach, as given in refs. 16 and 47. Specifically, we first permuted the rows and columns of each community’s competition matrix to find the ordering with the maximum number of matrix entries > 0.5 in the upper right triangle. After sorting, we then calculated the relative proportion of entries in the upper right triangle that were less than their corresponding entry in the lower left triangle (47),

$$\text{Intransitivity}=\frac{\sum I(a_{ij}<a_{ji})}{n(n-1)/2},$$

where the summation is taken over all $i<j$, and the operator $I\mathit{\text{(}}\cdot \mathit{\text{)}}$ is the indicator function, which equals 1 if $a_{ij}<a_{ji}$ and 0 otherwise. This value ranges from 0 (completely hierarchical) to 1 (completely intransitive). See SI Materials and Methods for more details.

Next, we obtained a competitive ranking of species using the Elo ranking system (48) in the PlayerRatings package in R. This ranking was standardized to between 0 and 1, with 1 being the most dominant fungus, and 0 being the weakest (Dataset S1 and SI Materials and Methods for detailed calculations). We using this ranking to calculate community-level measures of “mean competitive ability” and “variance in competitive ability” by taking the average and variance, respectively, of this ranking across all members in that community (see Dataset S2). Variance was included as a potential confounding variable in the statistical analysis, although it is not otherwise a primary variable of interest in this analysis (Table S2).

Model Estimation.

Separate regression models were fit for biomass, respiration, and CUE. All models included species richness, mean competitive ability, intransitivity, and secondary confounding variables (variation in competitive ability, functional dissimilarity, and phylogenetic dissimilarity). Also included were the pairwise interactions among richness, intransitivity, and competitive ability. Species-specific effects were taken into account two ways. First, the community-specific average monoculture performance (e.g., average monoculture respiration) was included as a predictor for each outcome, thus accounting for baseline differences in communities’ functioning based solely on differences in community composition. Second, the relative proportions of each species in each community (i.e., 0, 1/3, 1/6, or 1/12) were included as fixed effects in all models to account for species-specific effects and autocorrelation among communities with shared species. Richness, intransitivity, and mean competitive ability—as well as their pairwise interactions—were included in all models regardless of significance; otherwise, variables were included in the final model only if they had a P value of <0.10. Note that potential confounding variables (phylogenetic and functional dissimilarity, variation in competitive ability) are not discussed in detail further, given that they were not the main variables of our hypothesis testing (but see Table S2 for the full model results). All P values were adjusted for multiple comparisons (49).

Estimating Marginal Effects.

In the presence of strong interactions, individual coefficients are difficult to interpret, even after standardizing variables. Therefore, to illustrate the marginal effect of each variable (richness, intransitivity, competitive ability), we plotted the model-based coefficients (i.e., slopes) for each variable across a grid of values. Thus, for example, we calculated the regression coefficient corresponding to species richness across a grid of intransitivity and competitive ability values (with all other values held constant at their mean), which gives the slope of the diversity–function relationship (or “diversity effect”) for any given competitive network structure.

Quantifying Patterns Across Communities.

Some competitive network structures are more likely than others to occur in a random sample of communities, due to correlations among variables and species. Thus, we used a simulation approach to explore how the relationships identified in our statistical models might translate to patterns in functioning across a much larger random sample of communities. We selected, at random, 20,000 unique communities from among the $\sim$350,000 possible, with species richness ranging from 3 to 12 species, and each community combination drawn from the 18 species used in the experiment. We then used the model-derived parameters to predict the CUE of each community. To explore the relative contribution of intransitivity and competitive ability, the communities were then split into high vs. low intransitivity and high vs. low mean competitive ability based on the <33rd and >66th percentiles of each of these values across all 20,000 communities. These four groups (low intransitivity and low competitive ability, low intransitivity and high competitive ability, high intransitivity and low competitive ability, and high intransitivity and high competitive ability) were then plotted, and simple linear regression was used to capture the resulting relationship between diversity and function among these four groups. This approach therefore reflects how innate relationships among variables among and between species can constrain or modulate the metacommunity patterns, thus capturing the “average” relationships that might be likely to occur under random community assembly.