Distinct ice patterns on solid surfaces with various wettabilities

Significance

Ice growth is essential to the final shape of ice crystals; therefore, it is of significant relevance to rich varieties of practical applications and fundamental research. A correlation between the surface wettability and ice growth has not been established, although ice often forms on solid surfaces. We discover experimentally that ice grows along surface when the contact angle of water drops on solid surfaces is below a critical value, and ice grows off surface when the contact angle is above this critical value. Our molecular dynamics simulation analysis reveals that the presence/absence of bilayer ice on solid surfaces of different surface wettabilities dictates the ice growth and therefore provides the molecular mechanism of ice growth on solid surfaces.

Abstract

No relationship has been established between surface wettability and ice growth patterns, although ice often forms on top of solid surfaces. Here, we report experimental observations obtained using a process specially designed to avoid the influence of nucleation and describe the wettability-dependent ice morphology on solid surfaces under atmospheric conditions and the discovery of two growth modes of ice crystals: along-surface and off-surface growth modes. Using atomistic molecular dynamics simulation analysis, we show that these distinct ice growth phenomena are attributable to the presence (or absence) of bilayer ice on solid surfaces with different wettability; that is, the formation of bilayer ice on hydrophilic surface can dictate the along-surface growth mode due to the structural match between the bilayer hexagonal ice and the basal face of hexagonal ice (ice I_h), thereby promoting rapid growth of nonbasal faces along the hydrophilic surface. The dramatically different growth patterns of ice on solid surfaces are of crucial relevance to ice repellency surfaces.

Ice crystals with rich morphologies are ubiquitous in nature, and understanding the ice formation mechanism on the molecular level has immense implications in diverse disciplines, such as atmospheric science, astrophysics, aerospace engineering, and food science (1–7). The natural patterns of ice crystals can be determined by the interplay between the external macroscopic forces and the microscopic interfacial behaviors (8, 9). The sixfold symmetry of snowflakes, for example, has reflected the transfer from the microscopic information to the macroscopic morphology (10, 11). However, things can be completely different when a solid surface is exposed to a growing ice crystal because of the introduction of the asymmetrical external force at the microscopic level (12, 13). Consequently, window frost, one of the unique sceneries of winter, usually exhibits almost infinite morphological variants. In particular, microscopic water structures have recently been studied on surfaces with various chemical composition and atom structures (e.g., metal, metal oxide, and mica) (13–17). However, a correlation between the microscopic water structures and the macroscopic patterns of ice crystals supported by solid surfaces has not been explored.

Ice Growth Patterns on Surfaces with Various Wettabilities

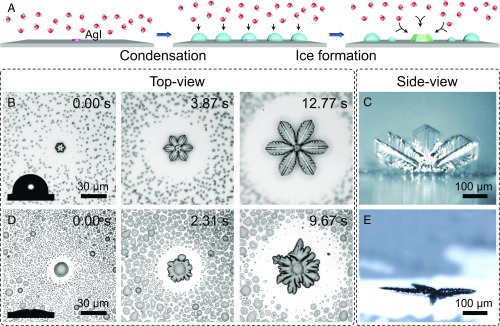
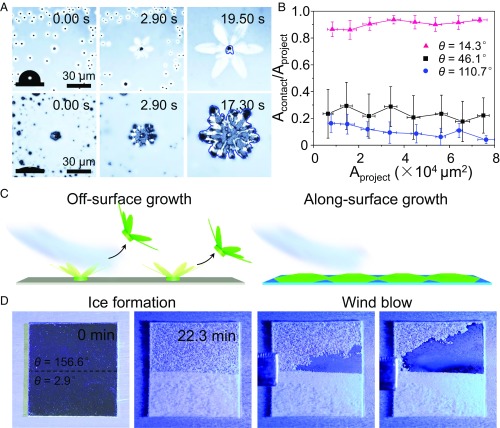
By introducing nanoparticles with inherently low nucleation barriers to ice formation onto surfaces (18), here we report distinct ice growth patterns on surfaces with adjusting wettabilities through changing the fluorine content of the fluoroalkyl silane modified surface. Fig. 1A presents a schematic illustration of the experimental design. Silver iodide (AgI) nanoparticles were chosen as ice nucleation active sites (19, 20) to allow ice nucleation to occur at the same time (and the same temperature) across the entire solid surface in the same experimental environment. Thus, many known factors that can affect ice formation, such as released heat, nucleation temperature, and relative humidity, were nonfactors (10). More importantly, isolated ice crystals surrounded by empty regions of the solid surface (without condensed water droplets) can be observed because the adjacent water droplets can be harvested by ice due to the local gradient in vapor pressures (21–23). This would allow the quantitative measurement of ice crystal growth on different solid surfaces. Fig. 1B shows top-view images of the growth process of six-leaf clover-like ice on a hydrophobic surface (contact angle, θ, is 107.3°) (see also Movie S1). Keeping the focal plane at the advancing edge as the ice grows over time from 0 to 12.77 s, the gradually blurring substrate indicates that ice on the hydrophobic surface undergoes an off-surface growth (OSG) mode. A side-view image further displays the morphology of OSG ice on the same hydrophobic surface as a conspicuously normal distance exists between the advancing edge and the substrate (Fig. 1C).

Fig. 1.

Two ice growth modes on hydrophilic and hydrophobic surfaces. (A) A schematic illustration of the experimental design used to investigate the effect of solid surfaces on ice growth via the introduction of ice nucleation active sites (AgI nanoparticles) on solid surfaces. This allowed ice nucleation to occur at almost the same time and temperature over the entire solid surfaces in the same environment. (B) Selected snapshots captured at different times using an optical microscope coupled to a high-speed camera. These top-view images show the growth process of six-leaf clover-like ice on a hydrophobic surface (θ = 107.3°). (C) A side-view snapshot that shows the morphology of the ice on the same hydrophobic surface produced by the OSG mode. (D) Selected snapshots captured at different times using an optical microscope coupled to a high-speed camera. These top-view images show the growth process of sunflower-like ice on a hydrophilic surface (θ = 14.5°). (E) A side-view snapshot of the ice morphology on the same hydrophilic surface resulting from the ASG mode. The surface temperature is −15 °C, and the supersaturation is 5.16.

By contrast, top-view images of the growth process of sunflower-like ice along a hydrophilic surface (i.e., with a measured contact angle of 14.5°) reveal that these ice crystals undergo the along-surface growth (ASG) mode (Fig. 1D; see also Movie S2), in which the ice continues to advance in the same focal plane as the substrate. A side-view snapshot visually presents the ASG mode of ice on the same hydrophilic surface (Fig. 1E). The generality of this observation was consolidated via employing other nucleating agents (24) such as surface scratches and a self-assembled monolayer 21 alcohol (C₂₁H₄₃OH). The growth modes of ice on solid surfaces can also be distinguished based on differences in the ice–substrate contact interface or by the dependence of the ice morphology on the substrate roughness or in the ice itself when the distribution of silver iodide nanoparticles was controlled (Fig. S1).

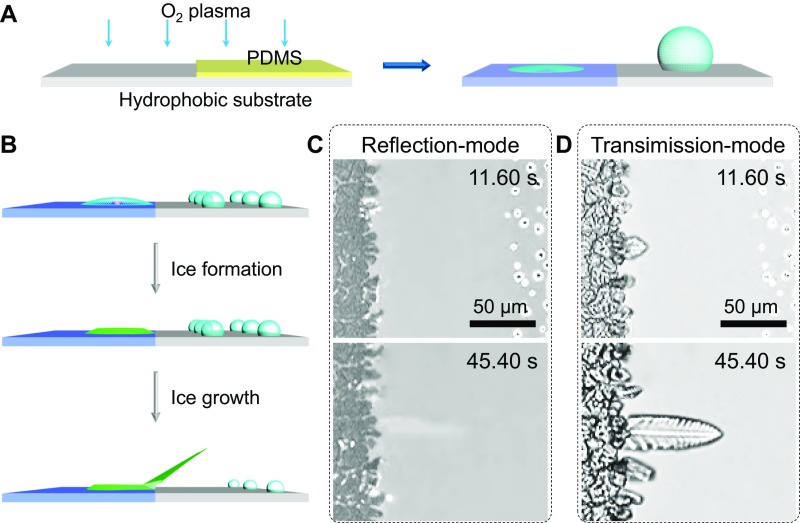
Fig. S1.

Methods for distinguishing the growth modes of ice on solid surfaces. (A–C) Differences between the outline of the ice–substrate interface and the ice can be used to distinguish between ice growth modes. (A and B) Two types of ice morphology were seen on solid surfaces, resulting from the initial orientation of the ice crystals on the surfaces. We observed the ice morphology on a transparent glass slide (θ = 46.7°) through an inverted optical microscope. The ice–substrate interface can be seen in (Upper) reflection mode and appears dark because little light is reflected back. By contrast, the profile of the ice can be clearly identified in (Lower) transmission mode. Clearly, for both types of ice morphologies, the outline of the ice–substrate interface is smaller than that of the ice, implying that both types of ice exhibit OSG mode. (C) The outline of the ice–substrate interface of ASG ice is almost the same as that of the ice itself. (D and E) The dependence of the ice morphology on the surface roughness can also be used to distinguish between ice growth modes. (D) A microscopic snapshot showing that the morphology of OSG ice bears little similarity to the surface structure (i.e., square micropores with a size of 5 μm and depth of 5 μm, θ = 123.9°). Inset shows the orientation of the surface structure. (E) A microscopic snapshot showing that the growth orientation of ASG ice is completely consistent with the surface structure (i.e., square micropores with a size of 5 μm and depth of 5 μm, θ ∼ 9.8°), as indicated by the red dashed lines. Distinctive ice growth modes of ice on (F) hydrophobic surface and (G) hydrophilic surface with different wetting properties when the distribution of the silver iodide nanoparticles was controlled. The distance of adjacent nucleation active sites is 80 μm. The surface temperature is −15 °C, and the supersaturation is 5.16.

We also designed a transparent surface in which half of the area was strongly hydrophilic (θ = 2.9°) and the other half was hydrophobic (θ = 107.3°) to further explore the dependence of the ice growth mode on surface wettability. Using this transparent surface, the structural evolution of both the ice itself and the ice–substrate contact interface was observed (Figs. S2 and S3). The flat ice, which evolved from water droplets located on the hydrophilic region and along the boundary, adopts the OSG mode as it grows toward the hydrophobic area, indicating that the initial shape of the ice has little effect on the ice growth mode (Fig. S2 B–D). When the ice front advances from the hydrophilic region to the hydrophobic region, the ice–substrate interface front is completely blocked by the hydrophobic–hydrophilic boundary, despite the ice starting to grow off of the surface (Fig. S3). Therefore, we conclude that a growth mode transition can occur when the wetting property of solid surfaces changes.

Fig. S2.

Preparation of a hybrid hydrophobic/hydrophilic surface and the effect of the initial shape of the ice on the growth mode. (A) A schematic showing the hybrid surface with one hydrophilic half (θ = 2.9°) and another hydrophobic half (θ = 107.3°) designed to explore the different growth modes of ice on surfaces with different wettabilities. (B) A schematic illustration showing that the ice evolved from a water droplet located on the hydrophilic region and along the boundary would demonstrate a flat initial shape, which is determined by the contact angle of the hydrophilic part. The ice exhibits the OSG mode at the boundary when its growth is oriented toward the hydrophobic side, indicating that the ice shape has very little effect on the ice growth mode. (C) Selected snapshots taken using an inverted microscope in reflection mode showing that when ice grows over the hydrophobic/hydrophilic boundary, no ice–substrate interface could be observed. (D) The outline of ice corresponding to that shown in C observed using an inverted microscope in transmission mode. The turned-up ice on the hydrophobic side indicates that the initial shape of the ice is not the main determining factor of the ice growth mode. The surface temperature is −15 °C, and the supersaturation is 5.16.

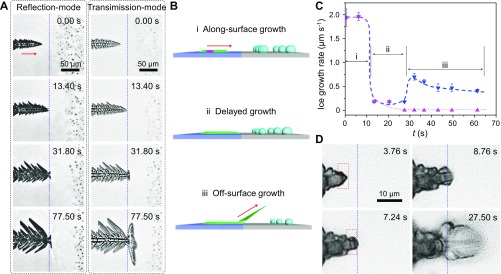
Fig. S3.

Effects of the surface wettability on the ice growth mode. (A) Reflection-mode images taken using inverted microscopy showing the evolution of the ice–substrate interface when the ice advances from a hydrophilic region to a hydrophobic region. Ice grew on the hydrophilic surface from 0.00 to 13.40 s, and subsequently, the advancing edge of the ice–substrate interface was restricted and gradually became parallel to the boundary of the two regions until 31.80 s. Then, until 77.50 s, the ice–substrate interface did not shift at all. Transmission-mode images reveal a small ice hand stretching away from the surface at 31.80 s, which subsequently continued to grow away from the surface, as shown in the image taken at 77.50 s. (B) Ice experiences three corresponding stages as it grows from hydrophilic regions to hydrophobic regions: (i) ASG, (ii) delayed growth, and (iii) OSG. (C) Accompanied by a switch in the ice growth mode, the growth rates of both projective ice (r_ice) and the ice–substrate interface (r_interface) advancing edge changed. Both growth rates decreased from 2.3 ± 0.2 μm⋅s⁻¹ to nearly 0 instantly when the ice grew to the boundary, and the growth mode switched from stage i to ii. Ice growth was delayed for ∼20 s by the high barrier of the boundary during stage ii, whereas r_interface = 0 and r_ice > 0 during stage iii. The decrease in r_ice in stage iii might be attributable to the increasing distance between the ice edge and the substrate. (D) Selected snapshots captured by high-speed camera showing the point at which ice transitions from the ASG mode to the OSG mode at a hydrophobic/hydrophilic boundary in detail. An obvious accumulation process was observed as the ice advanced over the boundary from the hydrophilic to the hydrophobic region. The surface temperature is −15 °C, and the supersaturation is 5.16.

Influence of Other Factors on Ice Growth Modes

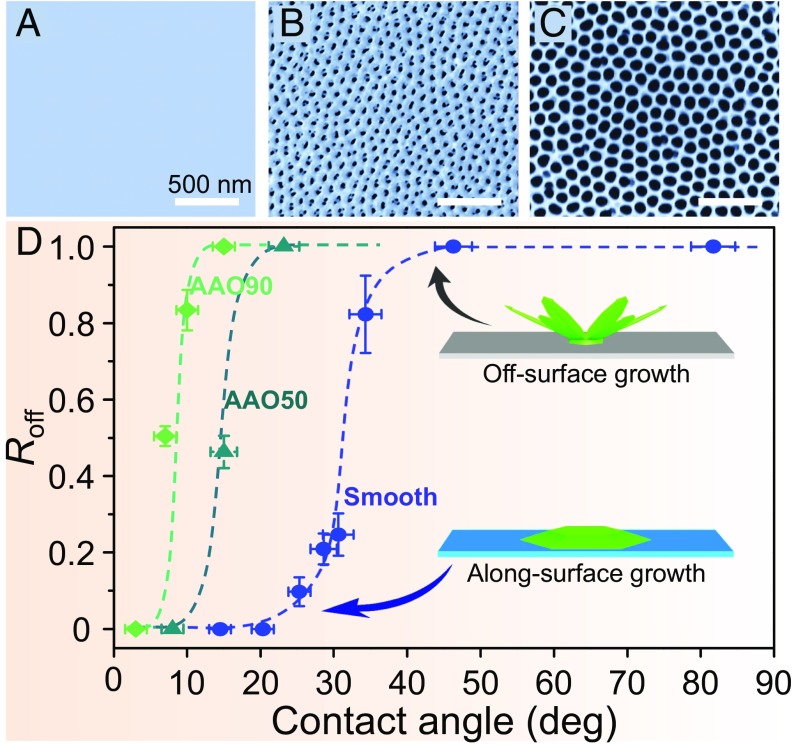
A strong dependence of the ice growth mode on the surface wettability and roughness is also demonstrated (Fig. 2D) when ice was grown on three different types of solid substrates: a smooth (at the 1-nm scale) aluminum surface and two anodic aluminum oxide (AAO) surfaces with different mean pore sizes (Fig. 2 A–C). On the smooth surface, the ASG-to-OSG transition in the ice growth mode occurs when the surface has a contact angle θ = 32.5° ± 1.9° (more detailed ice morphologies on solid surfaces with different wettabilities are shown in Fig. S4 A and B). The same ASG-to-OSG transition was also observed on the two AAO surfaces, but remarkably, as the pore size (or the surface roughness) increased (25), the ASG-to-OSG transition shifted to a lower contact angle θ.

Fig. 2.

Dependence of the ice growth mode on the surface wettability and roughness. Surfaces with different roughness were used to detect the ice growth mode on solid surfaces: (A) a nanometer-scale smooth surface (aluminum surface), (B) AAO-50 (AAO with a mean pore size of 50 nm), and (C) AAO-90 (AAO with a mean pore size of 90 nm). The average pitch of the nanopores of all AAO samples is 100 nm. (D) The ASG-to-OSG transition at a critical contact angle. On the smooth surface (blue dashed line), the transition from the ASG mode to the OSG mode occurs at θ = 32.5° ± 1.9°. R_off represents the appearance probability of OSG ice. As the mean pore size increases, the transition shifts to a smaller contact angle. We have investigated about 400 ice growth events to get the mean values of each dot. The different colored guide lines correspond to the substrates marked with the same color. Insets present the two distinct growth modes (ASG and OSG) of ice on solid surfaces. The surface temperature is −15 °C, and the supersaturation is 5.16.

Fig. S4.

Morphological details of ice on solid surfaces made of different materials having different wettabilities. (A) The water contact angles of nanosmooth surfaces (aluminum surfaces modified with FAS) could be changed by applying oxygen plasma for different durations. Corresponding AFM images were taken and show that the surface roughness on each surface modified with O plasma is almost the same despite the change in the contact angle. (B) Microscopic top-view images showing the ice morphology on smooth aluminum surfaces with different wettabilities. When the contact angle exceeds 32.5° ± 1.9°, ice undergoes the OSG mode. (C and D) The ice morphology on graphene and PET. When the contact angle is 19.3° on the graphene surface and 22.9° on the PET surface, the ice follows the ASG mode. By contrast, the ice exhibits the OSG mode when the contact angle is 82.6° on the graphene surface and 74.3° on the PET surface. (E) Ice grown on different surfaces, such as glass slide, copper, gold, and PDMS, follows the OSG mode because the contact angles of these materials are all >32.5° ± 1.9°. By contrast, ice grown on mica exhibits the ASG mode. The surface temperature is −15 °C, and the supersaturation is 5.16.

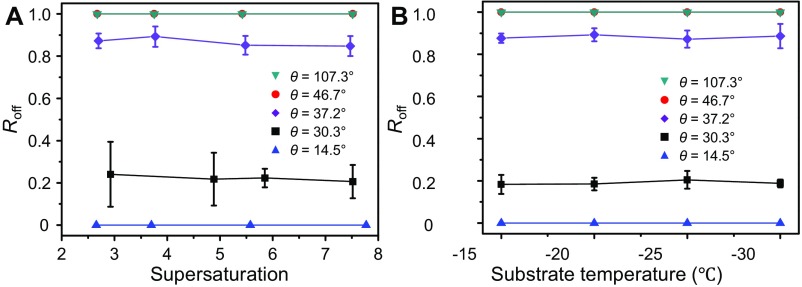
These ice growth modes were observed on surfaces made of different materials (Fig. S4 C–E), reaffirming the universality of the aforementioned wettability dependence. Surprisingly, many critical factors that are known to influence the growth habit of atmospheric ice (10, 26), such as supersaturation (in the range of 2.5 ∼ 8.0) and temperature (in the range of −15 °C ∼ −30 °C), appeared to exert little influence on the ice growth modes when the ice was supported by a solid surface (Fig. S5).

Fig. S5.

Effects of supersaturation and temperature on the ice growth mode on solid surfaces. R_off represents the appearance probability of OSG ice. (A) Evolution of R_off with supersaturation (the substrate temperature was −15 °C) showing that R_off remains almost unchanged as the supersaturation varied from 2.5 to 8 on flat aluminum surfaces with different contact angles (14.5° to 107.3°). (B) Evolution of R_off with the degree of supercooling showing that the value of R_off remains nearly constant when on surfaces with contact angles ranging from 14.5° to 107.3°. Clearly, neither the supersaturation nor the temperature strongly influence the ice growth mode on surfaces. Indeed, their effects were never able to overcome the gap in R_off caused by the surface wettability. We have investigated about 400 ice growth events to get the mean values of each dot.

Molecular Level Mechanism of Solid Surface Wettability on Ice Growth Modes

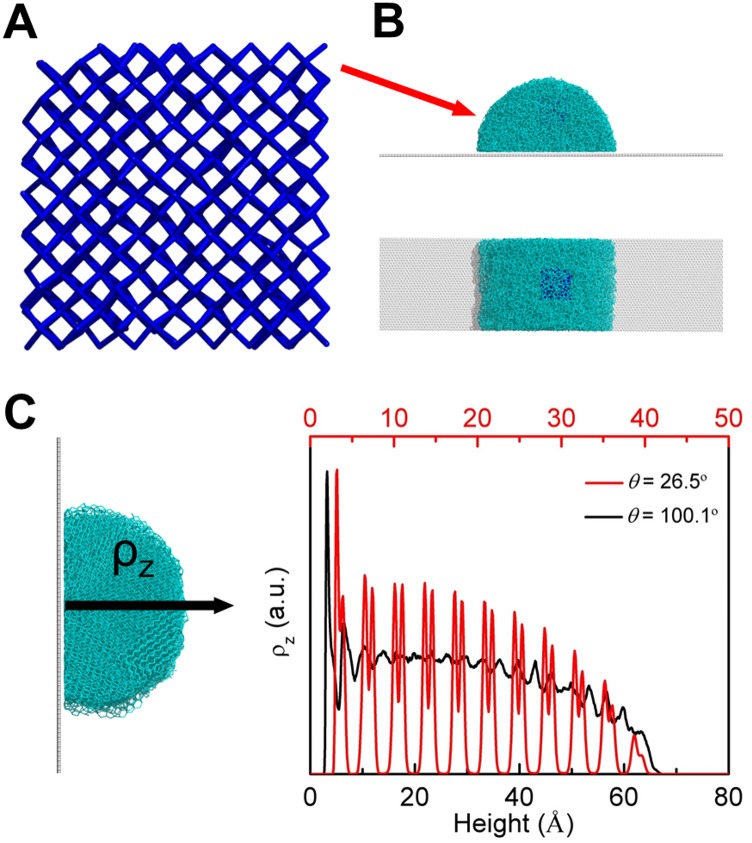
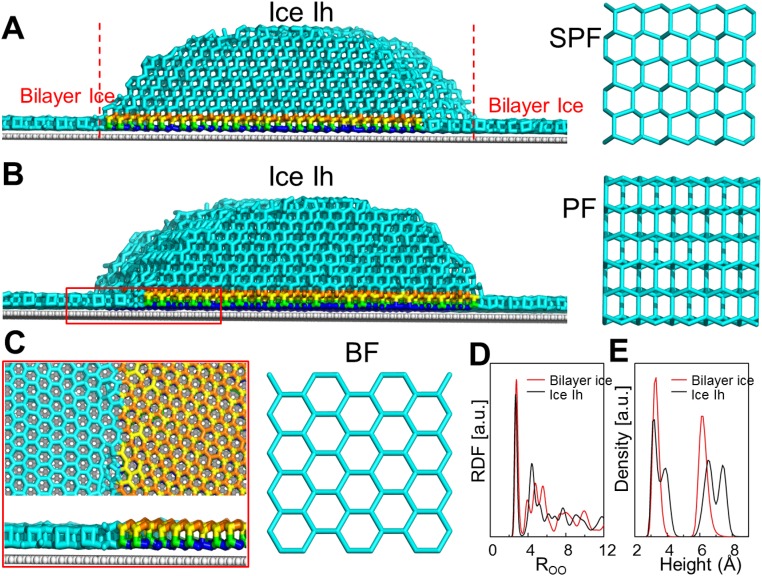
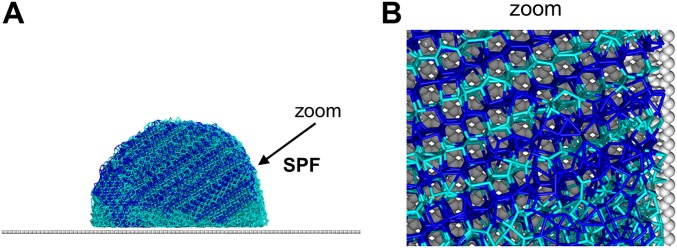
To understand the molecular-level mechanism (27–29) underlying the observed substrate wettability effect on the ice growth mode, we performed classical molecular dynamics (MD) simulations of ice growth on surfaces with various wettabilities (Fig. S6 A and B). Snapshots of the systems at different simulation times are shown in Fig. 3A. In the case of the hydrophilic surface (θ = 26.5° ± 1.2°), at the final equilibrium stage (∼200 ns) after freezing, the entire water droplet turns into ice. Notably, the single-crystal ice formed on the hydrophilic surface (Fig. 3A, Left) has its secondary prism face (SPF) (Fig. S7A) and prism face (PF) (Fig. S7B) oriented perpendicular to the solid surface, whereas its basal face (BF) is parallel to the surface (Fig. S7C). This result is in stark contrast to ice formation on the hydrophobic surface (θ = 100.1° ± 1.0°) (Fig. 3A, Right). Here polycrystalline ice is formed at the equilibrium stage (200 ns) with its SPF appearing as shown in Fig. S8.

Fig. S6.

MD simulations of water growth on a surface. (A) An ice core (blue) with 512 water molecules was introduced into the water droplet (B) to study the effects of substrate wettability on the ice growth mode at 250 K. (B) A (Upper) side view and (Lower) top view of the system are shown. (C) Density profile in the z direction (defined in Left) for water molecules near a hydrophilic surface, which show a characteristic double-peak behavior (red line in Right), indicating that the BF is parallel to the substrate. For comparison, the density profile in the z direction for water molecules near a hydrophobic surface (black line) shows no strong characteristics, indicating that a polycrystal is formed.

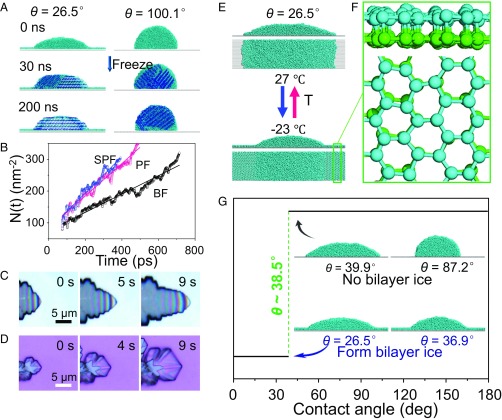
Fig. 3.

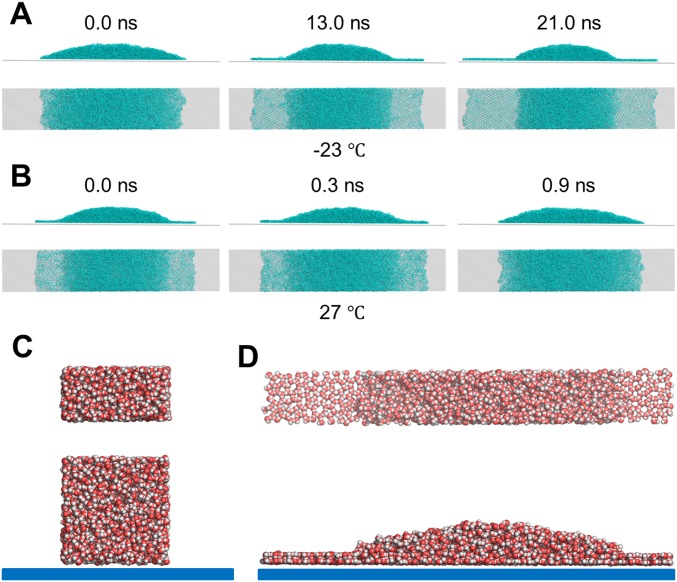
Understanding the mechanism underlying wettability-dependent ice growth modes. (A) Snapshots from the MD simulations of ice growth on a hydrophilic surface (θ = 26.5° ± 1.2°) or hydrophobic surface (θ = 100.1° ± 1.0°). After equilibration, the ice formed on the hydrophilic surface turns into a single crystal with the SPF and PF perpendicular to the substrate, whereas the ice formed on the hydrophobic surface becomes a polycrystal. (B) The number of water molecules per unit area within one of the three crystal faces of hexagonal ice I_h at −23 °C versus the simulation time: the BF (black curve), PF (red curve), and SPF (blue curve), for ice grown on the hydrophilic surface. (C and D) Selected snapshots captured using an optical microscope, revealing details of the ice growing (layer-by-layer fashion) in ASG mode (on mica, θ = 0°) and OSG mode (on a silicon wafer, θ = 63.6°) on solid surfaces at −20 °C. The supersaturation is 2.36. (E) Two illustrations (side and top views) of the simulation system showing the reversible (Lower) appearance and (Upper) disappearance of bilayer ice on a hydrophilic surface at low (−23 °C) and high temperatures (27 °C), respectively. (F) Side and top views of bilayer ice (the zoomed-in area marked by the rectangular box in E, Lower). (G) In the MD simulation, the critical contact angle is 38.5° for the formation of bilayer ice on a hydrophilic surface at −23 °C. The four Insets show snapshots of four independent simulations on solid surfaces with different wettabilities.

Fig. S7.

Equilibrium structure of ice on a hydrophilic surface. (A and B) A side view snapshot of the system with a hydrophilic surface (θ = 26.5° ± 1.2°) in which all water molecules are in the ice phase. Here the SPF and PF (A and B, Right) are perpendicular to the solid substrate. The first two layers near the surface are shown in C. Bilayer hexagonal ice is seen in the area surrounding the droplet. The first two water layers underneath the droplet are in the ice I_h phase, and the BF (C, Right) is parallel to the substrate. (D) Radical distribution functions (RDFs) for water and water in bilayer ice outside the droplet (red line) and in the first two layers underneath the droplet (black line). The RDFs for the water in bilayer ice and water in the first two layers underneath the water droplet exhibit peaks at distances of r = 2.76 Å and r = 2.69 Å, respectively, which are very similar. (E) Density profiles along the z axis for water molecules in bilayer ice outside the droplet (red line) and the first two layers under the droplet (black line). The density profile in the z direction for water molecules near the hydrophilic surface in the first two layers under the droplet shows characteristic double-peak behavior, indicating that it is in the ice I_h phase and that its BF is parallel to the substrate. By contrast, the density profile in the z direction for water molecules near the hydrophilic surface in bilayer ice outside the droplet shows single-peak behavior.

Fig. S8.

Equilibrium structure of ice on a hydrophobic surface. (A) A side-view snapshot of the system with a hydrophobic surface (θ = 100.1° ± 1.0°) in which all water molecules are in the ice phase. (B) Polycrystalline ice formed at the late equilibrium stage (∼200 ns) and a magnified zoom-in image of one of its SPFs.

Next, we performed a second series of independent MD simulations to study the growth of the three prism crystal faces of hexagonal ice (I_h), namely, BF, PF, and SPF (Fig. 3B and Fig. S7 A–C, Right). Our simulations show that the ice growth is anisotropic. The growth of the BF is the slowest; specifically, its growth rate is 43% and 51% slower than that of the PF and SPF, respectively. For the hydrophilic surface (θ = 26.5° ± 1.2°), because the SPF and PF are perpendicular to the solid surface (Figs. S6C and S7 A and B), the ice crystal grows along the surface (ASG mode). By contrast, for the hydrophobic surface (θ = 100.1° ± 1.0°), an angle is observed between the solid surface and SPF (Fig. S8), indicating that the ice crystal grows off the solid surface (OSG mode). These results are consistent with the ASG mode and OSG mode observed using an optical microscope (Fig. 3 C and D). The colored advancing edge shown in Fig. 3C indicates that ice grows in a layer-by-layer fashion on the hydrophilic mica surface according to the colors of ice (30), which is dramatically different from ice growth on the hydrophobic surface (10, 31–33). This feature is further supported by the growth process of ice when it advances over the hydrophilic/hydrophobic boundary (Fig. S3D), which suggests a change in the crystal orientation.

Why does the wettability of solid surfaces profoundly affect the orientation of the preferential growth face of an ice crystal? One reason derived from the MD simulation is that bilayer hexagonal ice forms only on the hydrophilic surface (Fig. 3 E and F and Fig. S7 C–E) and not on the hydrophobic surface at low temperature (−23 °C) (32) (Fig. 3A and Fig. S8). Indeed, another series of MD simulations demonstrated that the bilayer ice that formed on the hydrophilic surface disappeared as the temperature increased (to 27 °C), and this freezing/thawing process was reversible (Fig. 3E and Fig. S9). Moreover, because of the close lattice match between the bilayer hexagonal ice (2.76 Å) and the ice I_h BF (2.69 Å) (Fig. S7 D and E), the orientation of the ice crystal on the hydrophilic surface is dictated by the preexistence of the bilayer ice; this crystal growth mechanism is akin to molecular beam epitaxy (MBE) (20, 32). Note that the ASG mode observed on the hydrophilic mica surface (Fig. 3C) also indicates the high possibility of the bilayer ice leading to ASG because the presence of ice film with a height of 0.7–0.8 nm on mica surface at −19 °C was experimentally verified (34), consistent with our MD simulation results (Fig. S7E). We also conducted an additional independent MD simulation to locate the critical point at which bilayer ice can form on a solid surface (Fig. S10). We found that for $\theta \le 36.9°$, bilayer ice forms on the surface at −23 °C, whereas for $\theta \ge 39.9°$, no bilayer ice forms, indicating that the transition point for bilayer formation on a solid surface is located at ∼3$8.5°\pm 1.6°$ (Fig. 3G). This result is consistent with the ASG/OSG transition point observed (Fig. 2D) on a smooth surface.

Fig. S9.

MD simulations of a water droplet on a hydrophilic surface at different temperatures. (A) Snapshots of the MD simulations of a water droplet (using mW model) on a hydrophilic surface ($\theta =26.5°\pm 1.2°$) at 250 K after preequilibration of the initial structure at 300 K for 1 ns. (B) Snapshots of the MD simulations of a water droplet on the hydrophilic surface ($\theta =26.5°\pm 1.2°$) at 300 K using the initial structure taken from the MD simulation at 250 K performed as described above. Clearly, bilayer ice formed on the hydrophilic surface at low temperature (250 K) but disappeared as the temperature increased (300 K). This process is reversible. (C and D) Independent MD simulations of water droplets on the hydrophilic surface with the TIP4P/2005 water model were also performed. (Upper) Top view and (Lower) side views of the initial water droplet on a smooth hydrophilic substrate. Here the oxygen–wall interaction is described by the 9–3 LJ potential function, $U\left(r\right)=\epsilon \left[{\left(\sigma /r\right)}^9-{\left(\sigma /r\right)}^3\right]$, where the LJ parameters are ${\sigma }_{O-wl}=2.2578\hspace{0.17em}\mathrm{\AA }$ and ${\epsilon }_{O-wl}=8.0698$ kcal⋅mol⁻¹. All intermolecular interactions, including the long-range charge–charge interaction and the LJ interaction between oxygen atoms, are truncated at 10.0 Å. (D) (Upper) Top and (Lower) side views of the water droplet on the smooth substrate at the end of the MD simulation (10 ns). Bilayer hexagonal ice is observed, indicating that the formation of bilayer ice on the substrate is not sensitive to the water model (mW or TIP4P/2005).

Fig. S10.

Effects of surface wettability on bilayer ice formation on solid surfaces. Snapshots of the MD simulations of water droplets on surfaces with different wettabilities at 250 K. When $\theta \le 36.9°$ (D–F), bilayer ice is observed on the surface at 250 K. Note that this bilayer ice disappears when $\theta \ge 39.9°$ (A–C), indicating that the transition point for the observation of bilayer hexagonal ice is located at $38.5°\pm 1.6°$.

Construction of Antiicing Surfaces

The growth mode of ice crystals on solid surface also affects the realistic contact area A_contact between the ice and the substrate (Fig. 4A). Here A_contact for OSG ice is much smaller than the projected area (A_project) of the ice on the substrate. By contrast, A_contact for ASG ice is almost the same size as A_project. As a result, OSG ice presents a much smaller ice–substrate contact area than ASG ice (Fig. 4B). Consequently, OSG ice should exhibit much lower adhesion to the substrate than ASG ice and therefore can be easily removed from the surface by a small force, such as a wind gust, whereas ASG ice should stick to the solid surface more tightly (Fig. 4C). For many practical applications, airflow is likely a more realistic scenario for the ice removal. Therefore, a wind-blowing experiment was performed on a hybrid surface, of which one half was strongly hydrophilic (θ = 2.9°) and the other was superhydrophobic (θ = 156.6°). Indeed, the OSG ice was easily blown away by a breeze (velocity = 5.78 m⋅s⁻¹; the temperature was −3 °C), whereas the ASG ice was not (Fig. 4D and see also Movies S3 and S4). Given this wettability-dependent property, surfaces that can induce the OSG mode in ice may play an essential role in the preparation of antiicing surfaces (35–37).

Fig. 4.

Wettability-dependent ice–substrate contact area and its application for easy deicing. (A) Snapshots taken using an inverted optical microscope showing distinct contact areas between the ice and substrate (A_contact) depending on the wettability of the surface. The contact angles are (Upper) 107.3° and (Lower) 14.5°. The contact areas between ices and substrates are enclosed in blue lines. (B) The ratio of the ice–substrate contact area (A_contact/A_project) versus the projected ice area (A_project) for three substrates with different wettabilities. We have investigated about 100 ice growth events to get the mean values of each dot. (C) A scheme demonstrating that OSG ice can be easily blown away by a breeze, whereas ASG ice remains stuck to the solid surface. (D) An experiment designed to further verify the point made in C using a hybrid surface, of which one half had θ = 2.9° and the other half had θ = 107.3° (2 cm × 2 cm). The surface temperature was −20.2 °C to allow ice to grow simultaneously on both areas when the substrates were exposed to humid air at a relative humidity of 0.42 ± 0.05.

Discussion

Ice formation often initiates with heterogeneous nucleation on solid surfaces; how solid surfaces affect the subsequent ice growth therefore becomes critical (22, 38). Although effects of temperature and humidity on ice growth have been extensively investigated, the influence of solid substrates has not been paid deserved research (10). In our work, we introduced ice nuclei on solid surfaces to specifically investigate the effect of solid surfaces on ice growth. We found that ice grows distinctly on surfaces of different wettabilities and discovered a transition from the ASG mode to the OSG mode at a critical water contact angle on solid surfaces. Moreover, the effect of solid surfaces on ice growth persisted when the surface temperature was changed from −15 °C to −30 °C and the supersaturation was varied from 2.5 to 8.0.

In addition, MD simulation results indicate that the bilayer ice can form on hydrophilic surfaces, which can dictate the along-surface growth mode due to the structural match between the bilayer hexagonal ice and the basal face of ice I_h, thereby promoting rapid growth of nonbasal faces along the hydrophilic surface. Further MD simulations showed that the critical contact angle for bilayer ice formation on smooth surfaces is consistent with the experimentally observed critical contact angle for ASG/OSG transition. Therefore, we reported how the microscopic structure (presence or absence of bilayer ice structure) of the interfacial water layer influences the macroscopic morphology (wettability-dependent ice growth modes) of ice crystals on solid surfaces. The discovery of different ice growth modes on solid surfaces can be exploited to design better antiicing surfaces, such as windshields.

Materials and Methods

Materials.

Potassium iodide (KI, 99.99%) and silver nitrate (AgNO₃, 99.9999%) were purchased from Sigma–Aldrich. To synthesize the AgI nanoparticles, 10 μL of 1-M aqueous KI solution and 5 μL of 1-M aqueous AgNO₃ solution were rapidly mixed in a 20-mL borosilicate vial with 10 mL of deionized water. The mixed solution immediately turned yellowish white because of the formation of AgI nanoparticles. The size of the AgI nanoparticles was ∼100 nm. The 21 alcohol was purchased from Sigma–Aldrich. The smooth surface shown in Fig. 2 consisted of aluminum prepared by depositing a thin aluminum film on a silicon wafer [10-cm diameter, N-type doped with phosphorus, (100) oriented, 525 μm thick] using a Kurt J. Lesker PVD75 thin film deposition system (DC, 250 W, working air pressure: 3 mTorr, time: 500 s); the film thickness was ∼500 nm. Nanostructures could be introduced into the aluminum surface by immersing it in a 70 °C water bath for 10 min. The surface was made hydrophobic by modification with 1H,1H,2H,2H-perfluorodecyltrimethoxysilane (FAS-17) via chemical vapor deposition (CVD). Next, O plasma (FEMTO plasma cleaner; Diener) was applied, and the surface wettability was tuned by varying the treatment time. Other thin metal films (copper and gold) were also deposited on top of planar silicon surfaces to prepare different substrates. The film thickness was ∼50 nm. Glass slides were used as transparent substrates and modified with FAS-17 or O plasma. To prepare the polydimethylsiloxane (PDMS), the prepolymer and curing agent were sufficiently mixed (10:1 by mass) in a clean plastic Petri dish. After removing gas bubbles under vacuum, the sample was cured at 60 °C for 3 h. Porous AAO films with different pore sizes and pore distances were purchased from Shanghai Nateng Instrument & Technology Co., Ltd. To prepare the hybrid surface, one half of the FAS-17–modified glass slide or nanostructured surface was coated with PDMS, and the other part was made hydrophilic by O plasma. The graphene substrate and polyethylene terephthalate (PET) were purchased commercially. The samples used in this work were prepared by spraying AgI nanoparticle solution onto different surfaces to introduce ice nucleation active sites. The arrays of nucleation active sites on surfaces were prepared with the method reported in ref. 18.

Characterization.

Surface morphologies were characterized by field emission scanning electron microscopy (Hitachi S-4800). The growth process of ice on the samples was observed using an optical microscope (OLYMPUS BX51) coupled with a high-speed video camera (V7.3; Phantom). The interface between the ice and transparent substrate and the projective morphology of the ice were observed using an optical inverted microscope in reflection mode and transmission mode, respectively. The water contact angles on different samples were measured using a CA System (DSA100; Kruss Co.) at ambient temperature, and the droplet volume was 3.0 μL. The nanometer-scale roughness of the surface was characterized by atomic force microscopy (AFM; Multimode8; Bruker).

Experiment.

To observe the growth process of ice on the surfaces, the samples were first placed on a horizontal cryostage (THMS 600; Linkam) in a humidity-adjustable chamber. When the surface temperature of the cryostage was −15 °C, wet air was introduced into the chamber, and the humidity was adjusted by controlling the air flux. Then, the ice growth process was recorded by the high-speed camera, and the growth mode of ice could be easily determined based on the ice morphology. The wind-blowing experiment was conducted at an environmental temperature of 20.2 ± 1 °C and a relative humidity of 0.42 ± 0.05. The surface temperatures of the samples were cooled with a cooling bath circulation thermostat (Ministat 230-CC-NR) at −20 °C, and the blown air was first passed through supercooled saturated salt water to lower its temperature.

MD Simulations of Bilayer Formation on Different Substrates.

To understand the observed wettability-dependent growth mode, MD simulations were performed. For the MD simulations, a water nanodroplet (containing 13,651 molecules) was placed on a model graphene-like surface (Fig. S6 A and B); the simulation box size was 76.7 × 398.5 × 200 ų. Because of the large size of the simulation system, the water molecules were described by the coarse-grained mW model in which each H₂O molecule is treated as a single particle interacting through anisotropic short-ranged potentials (the Stillinger–Weber potential). Although explicit hydrogen atoms and electrostatic terms are not included, the mW model can correctly describe the thermodynamic properties and phase behavior of water in bulk and on substrate (Fig. S9 as an example). The water–surface interaction was modeled by the 12–6 Lennard-Jones (LJ) potential with the parameter ${\sigma }_{\text{SW}}=3.2\hspace{0.17em}\mathrm{\AA }$, and ${\epsilon }_{\text{SW}}$ was adjusted over a range from 0.05 to 0.18 kcal⋅mol⁻¹ on model surfaces ranging from hydrophobic to hydrophilic. Periodic boundary conditions were applied in three dimensions, and the equations of motion were integrated using the Velocity Verlet algorithm with a time step of 10 fs. Simulations were performed using the NVT ensemble; the temperature was controlled using the Nosé–Hoover thermostat, and the relaxation time was 0.1 ps. All simulations were performed using Large-Scale Atomic/Molecular Massively Parallel Simulator software.

MD Simulation of Ice Growth.

To simulate the growth process of ice on hydrophobic surfaces and hydrophilic surfaces, we used the same MD setup, as shown in Fig. S6 A and B. Fig. 1 shows that the difference in the growth mode on hydrophilic surfaces and hydrophobic surfaces cannot be observed unless the ice exceeds several micrometers in size. To observe the effect of wettability on the ice growth mode, a slab-like simulation box that is thin in the y direction and long in the x and z directions was adopted. Periodic boundary conditions were applied such that the water droplet was infinite in the x direction with a truncated cylindrical cross-section, as seen in Fig. S6B. After the water droplet reached an equilibrium state, an ice core (512 molecules) was introduced to the water droplet. The water–surface interaction was modeled with the following parameters: ${\sigma }_{\text{SW}}=3.2\hspace{0.17em}\mathrm{\AA }$ and ${\epsilon }_{\text{SW}}=0.1$ kcal⋅mol⁻¹ for the hydrophobic surface (θ = 100.1° ± 1.0°) and ${\sigma }_{\text{SW}}=3.2\hspace{0.17em}\mathrm{\AA }$ and ${\epsilon }_{\text{SW}}=0.18$ kcal⋅mol⁻¹ for the hydrophilic surface (θ = 26.5° ± 1.2°).

MD Simulations of the Growth Rates Along Three Primary Crystal of Ice I_h.

To study the crystal growth on the three primary crystal faces of hexagonal ice, three new simulation systems were prepared in which the growth of the BF, PF, and SPF (Fig. S7, Right) was simulated. The shapes of all systems are cuboids. To set up the simulation systems, bulk I_h consisting of 952 water molecules and bulk water consisting of 1,520 water molecules were prepared separately. The equilibrium structure of each phase was obtained from an MD simulation at T = −23 °C and P = 1 bar. Next, the liquid slab was placed in contact with the targeted ice slab surface. Periodic boundary conditions were imposed in all three directions of the systems. All of the MD simulations were performed using the constant volume and constant pressure (NPT) ensemble at a temperature and pressure of −23 °C and 1 bar, respectively, for 20 ns.

Our simulation results show that ice growth along the surface normal of the three primary crystal faces of hexagonal ice (i.e., the BF, PF, and SPF) is anisotropic. The growth rate of the BF was 0.28 nm⁻²⋅ps⁻¹, which is the slowest of the three faces. By contrast, the growth rates of the PF and SPF were 0.51 and 0.57 nm⁻²⋅ps⁻¹, respectively, which are ∼82% and 104% faster than that of the BF.